Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Предположим, что у вас шесть колокольчиков с разными тонами и вы хотите найти количество уникальных последовательностей, в которых каждый колокольчик можно запускать один раз. В этом примере вычисляются факториал из шести. Как правило, с помощью факториала можно подсчитать количество способов у организовать группу отдельных элементов (также называемых перестроениями). Чтобы вычислить факториал числа, используйте функцию ФАКТЫ.
В этой статье описаны синтаксис формулы и использование функции ФАКТР в Microsoft Excel.
Описание
Возвращает факториал числа. Факториал числа — это значение, равное 1*2*3*…* число.
Синтаксис
ФАКТР(число)
Аргументы функции ФАКТР описаны ниже.
-
Число — обязательный аргумент. Неотрицательное число, для которого вычисляется факториал. Если число не является целым, оно усекается.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ФАКТР(5) |
Факториал числа 5 или 1*2*3*4*5 |
120 |
|
=ФАКТР(1,9) |
Факториал целой части числа 1,9 |
1 |
|
=ФАКТР(0) |
Факториал числа 0 |
1 |
|
=ФАКТР(-1) |
Факториал отрицательного числа возвращает значение ошибки |
#ЧИСЛО! |
|
=ФАКТР(1) |
Факториал числа 1 |
1 |
Нужна дополнительная помощь?
Факториал в Excel
В этой статье я расскажу о факториале, его свойствах и о том, как вычислить его значение с помощью Excel. Мы проверим, как точно вычисляет значение факториала формула Стирлинга и разберем решение типовых задач с факториалами, а на закуску — несколько видеороликов (и конечно расчетный файл эксель). Удачи!
Лучшее спасибо — порекомендовать эту страницу
Что такое факториал?
Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. Факториал определен только для целых неотрицательных чисел.
$$n!=1cdot 2cdot 3 cdot … cdot (n-1) cdot n$$
По определению, считают, что $0!=1, 1!=1$. Далее:
$$
2!=1 cdot 2 = 2,\
3!=1 cdot 2 cdot 3= 6,\
4!=1 cdot 2 cdot 3cdot 4= 24,\
5!=1 cdot 2 cdot 3cdot 4cdot 5= 120,\
…
$$
Факториал растет невероятно быстро (недаром он обозначается восклицательным знаком!), существенно быстрее степенной $x^n$ или даже экспоненциальной функции $e^n$ (но медленее чем $e^{e^n}$)
Факториал широко применяется в комбинаторике — он равен числу всех перестановок $n$-элементного множества, а также входит в формулы для числа сочетаний и размещений. Факториал встречается в математическом анализе (чаще при разложениях функции в степенные ряды), а также в функциональном анализе и теории чисел.
Еще: онлайн калькулятор факториала.
Формулы и свойства факториала
Рекуррентная формула для факториала:
$$
n!=left{
begin{matrix}
1, & n=0,\
(n-1)!cdot n, & n gt 0.\
end{matrix}
right.
$$
Факториал связан с гамма-функцией по формуле: $n!= Gamma(n+1)$. Фактически, гамма-функция — обобщение понятия факториала на все положительные вещственные функции.
Для любого натурального $n$ выполняется:
$$
(n!)^2 ge n^n ge n! ge n.
$$
Любопытная формула связывает факториал и производную степенной функции:
$$ (x^n)^{(n)} = n!$$
Формула Стирлинга
Для приближенного вычисления факториала применяют асимптотическую формулу Стирлинга:
$$
n!=sqrt{2pi n} left( frac{n}{e}right )^n left(1+ frac{1}{12n}+ frac{1}{288n^2}- frac{139}{51840n^3}- frac{571}{2488320n^4}+… right )
$$
Обычно для расчетов берут только главный член:
$$
n! approx sqrt{2pi n} left( frac{n}{e}right )^n.
$$
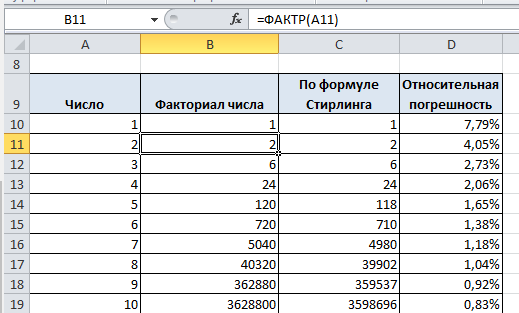
Ниже вы увидите пример расчета факториала по обычной формуле и с помощью формулы Стирлинга, которая, как видно, дает вполне хорошее приближение (начиная с $n=9$ относительная погрешность уже меньше 1%).
Расчет факториала в Эксель
Для нахождения факториала в Excel нужно использовать специальную функцию =ФАКТР($n$), где $n$ — число, факториал которого нужно найти.
Пример расчета и ввода формулы ниже на скриншоте, также вы можете скачать расчетный файл
Нужна помощь в решении задач по комбинаторике?
Примеры задач с факториалом
Рассмотрим решение типовых задач.
Пример 1. На полке стоят 8 дисков. Сколькими способами их можно расставить между собой?
Решение. Требуется найти число всех перестановок 8 различных объектов, что вычисляется как раз как факториал:
$$N=8!=1 cdot 2 cdot 3cdot 4cdot 5cdot 6cdot 7cdot 8=40320.$$
Пример 2. Вычислить
$$
frac{60!}{58!}-frac{6!}{5!}
$$
Решение.
$$
frac{60!}{58!}-frac{6!}{5!}=frac{58!cdot 59cdot 60}{58!}-frac{5! cdot 6}{5!}=59cdot 60-6=3534.
$$
Пример 3. Упростить выражение
$$
frac{n+3}{(n+1)!}-frac{1}{n!}
$$
Решение.
$$
frac{n+3}{(n+1)!}-frac{1}{n!} = frac{n+3}{(n+1)!}-frac{n+1}{n!(n+1)}=frac{n+3-(n+1)}{(n+1)!}= frac{2}{(n+1)!}
$$
Пример 4. Упростить дробь, содержащую факториал:
$$
frac{n!}{(n-2)!}
$$
Решение.
$$
frac{n!}{(n-2)!}=frac{ (n-1)! cdot n}{(n-2)!} =frac{(n-2)! cdot (n-1) cdot n}{(n-2)!} = (n-1) cdot n = n^2-n$$
Видео о факториале
Небольшое учебное видео про факториал — определение, свойства, как быстро растет, как вычислить в Excel по встроенной формуле и по приближенной формуле Стирлинга.
Расчетный файл из видео можно скачать
Напоследок — насколько быстро растет факториал!
Полезные ссылки
|
|
Решебник задач по комбинаторике
Понял, что на нашем сайте очень мало описаний математических функций. Хотя в Excel их превеликое множество. Есть описание НДС, всяких там печатных документов и форм. А вот описания основы основ табличного редактора — математических функций, почти нет. «Надо бы заняться этим пробелом» — подумал я. Вот занимаюсь. Первым на очереди факториал. Почему? Просто на днях делал одну задачу с этой функцией. Подробнее про факториал в Excel читаем далее.
Факториал в Excel. Введение
Думаю, углубляться в мат. часть сильно не стоит. Считаю, нужно рассказать, для чего используется эта функция и как ее считать в Excel.
Начнем с определения. Как говорит нам Википедия — Факториал числа n (от лат. factorialis — умножающий, действующий) — это произведение всех натуральных чисел от 1 до n включительно.
Для чего это может понадобиться? В первую очередь — это обозначение умножения нескольких чисел 3! = 1*2*3. Факториал очень часто используется в комбинаторике. Что такое комбинаторика? Как следует из названия — это наука изучающая математические комбинации.
Пример: Сколько сочетаний цветов получится из 10 разных цветов? Сходу знаете? Я, например, нет. Для вычисления кол-ва комбинаций применяется факториал.
Рассчитаем для 3 цветов: количество комбинаций цветов (желтый, красный, зеленый) = 3! =1*2*3 = 6. Какие это комбинации:
- ЖКЗ
- ЖЗК
- КЖЗ
- КЗЖ
- ЗЖК
- ЗКЖ
Действительно 6 
В более сложных задачах в жизни часто нужно узнать, к примеру, какое количество вариантов выполнения маршрута из 7 точек. Как видите, штука полезная!
Факториал в Excel. Как посчитать.
Для факториала есть специальная функция =ФАКТР() Реквизиты предельно просты: один аргумент, то число до которого нужно рассчитать факториал
Пример такой формулы
=ФАКТР(A1)
Рассчитав факториал 7, мы узнаем, что количество вариантов маршрута из 7 точек равно 5040. По-моему, это впечатляет!
Удачной комбинаторики!
Факториал числа часто используется, например, для расчета количества перестановок или вычисления биномиальных коэффициентов.
Рассмотрим особенности использования факториала в Excel.
Для начала освежим в памяти что же такое факториал числа.
Факториал числа n — произведение натуральных чисел от 1 до n (включительно), обозначается как n!.
В общем виде формула расчета факториала имеет вид n!=1*2*3*…*n, при этом по умолчанию считается, что 0!=1.
Наибольшее применение факториал имеет в комбинаторике и теории чисел.
Перейдем от теории к практике.
Для расчета факториала в Excel применяется функция ФАКТР:
ФАКТР(число)
Возвращает факториал числа, равный 1*2*3*…*число.
- Число (обязательный аргумент) — натуральное число (т.е. целое неотрицательное), факториал которого вычисляется.
В случае, если в качестве аргумента функции было введено нецелое число, то оно округляется в меньшую сторону.
Удачи вам и до скорой встречи на страницах блога Tutorexcel.ru!
Поделиться с друзьями:
Поиск по сайту:
Вычисление факториала натуральных (неотрицательных целых) чисел с помощью пользовательской функции Factorial. Ограничение для VBA Excel по типу данных.
Факториал и его вычисление
Факториал – это функция, определяемая для натурального числа n как произведение всех неотрицательных целых чисел от 1 до n включительно.
Формула, по которой вычисляется факториал, записывается следующим образом:
n! = 1 · 2 · ... · n
Пример: 3! = 1 · 2 · 3 = 6
В соответствии с формулой факториала, будет верным следующее соотношение:
(n-1)! = n! : n
Если принять для этого равенства n = 1, тогда получим:
0! = 1
Пользовательская функция Factorial
Для вычисления факториала натуральных чисел можно использовать следующую пользовательскую функцию:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
Public Function Factorial(n) Dim i, p If Not IsNumeric(n) Or n = Empty Then Factorial = «Аргумент не является числом» Exit Function ElseIf n < 0 Then Factorial = «Аргумент отрицательный» Exit Function End If p = 1 n = Format(n, 0) If n > 1 Then For i = 2 To n p = p * i Next End If Factorial = p End Function |
Первое условие функции Factorial (If Not IsNumeric(n) Or n = Empty) проверяет, не является ли значение ячейки не числом. Второе условие (ElseIf n < 0) проверяет, не является ли число в ячейке отрицательным.
Если значение ячейки окажется не числом или числом отрицательным, функция возвратит соответствующее сообщение и завершит работу (Exit Function).
Далее, если функция Factorial не завершила работу, переменной p присваивается значение 1, которое возвратит функция, если значение переменной n будет равно нулю или единице.
Значение ячейки (переменная n) округляется до целого и, если оно окажется больше единицы, вычисляется факториал с помощью цикла For… Next.
Пользовательская функция Factorial возвратит значение, присвоенное ей из переменной p.
Рекурсивная функция Factorial
Рекурсивной называется функция, которая вызывает сама себя.
Рекурсивная функция, вычисляющая факториал:
|
Function Factorial(n) If n <= 1 Then Factorial = 1 Else Factorial = Factorial(n — 1) * n End If End Function |
Как она работает, я не понимаю, но она работает!
Ограничение по типу данных
Максимальное значение пользовательской функции Factorial для ячеек с общим форматированием будет ограничено максимальным значением типа данных Double (1,79769313486232Е+308).
Максимально возможное значение будет превышено при вычислении факториала при n > 170. В этом случае, в ячейку с функцией Factorial, Excel возвратит сообщение об ошибке: #ЗНАЧ!.
При желании, можно в код функции Factorial добавить еще одно условие, проверяющее, не содержит ли переменная n значение больше 170. Если n > 170, тогда вывод сообщения об этом и выход из функции.
Попробуйте задать ячейке с функцией Factorial числовой тип без дробных значений. У меня в Excel 2016 x64 факториал от 146 отображается из 15 значащих цифр впереди и огромного количества нулей справа. Чтобы это увидеть, надо ячейку растянуть на всю ширину и уменьшить размер шрифта в ней. Значение факториала от 147 в ячейке с числовым форматом уже не отображается.