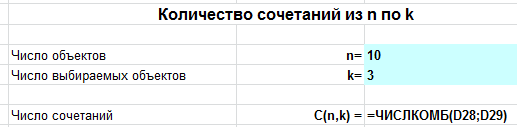
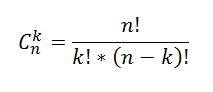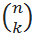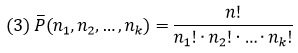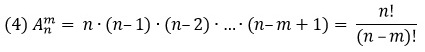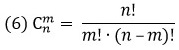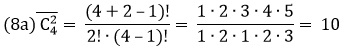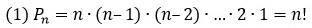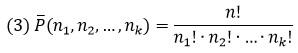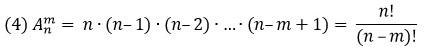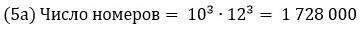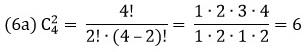Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).
Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:
(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)
Примечание
: Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье — плохая идея.
Отличие Сочетаний от Размещений
В отличие от
Размещений
следующие 3-х элементные комбинации (1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 1; 3); (3; 2; 1); (3; 1; 2) считаются одинаковыми, и в набор
Сочетаний
включается только одна из этих комбинаций. Очевидно, что для тех же n и k число
Сочетаний
всегда меньше чем число
Размещений
(так как при размещениях порядок важен, а для сочетаний — нет), причем в k! раз.
Подсчет количества Сочетаний
Число всех
Сочетаний
из n элементов по k можно вычислить по формуле:
Например, количество 4-х элементных комбинаций из 6 чисел {1; 2; 3; 4; 5; 6} равно 15=6!/(4!(6-4)!)
Примечание
: Для
Сочетаний
из n элементов по k также используется и другая запись:
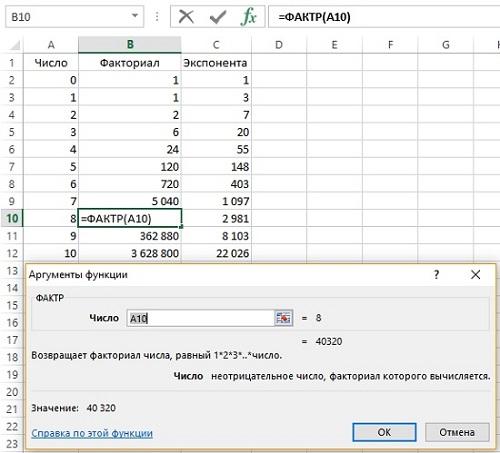
В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ() , английское название функции — COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4) , разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4) .
Очевидно, что k меньше или равно n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются). При k=n количество сочетаний всегда равно 1.
Примечание
: О Сочетаниях с повторениями (с возвращением элементов) можно прочитать в статье
Сочетания с повторениями: Комбинаторика в MS EXCEL
Вывод всех комбинаций Сочетаний
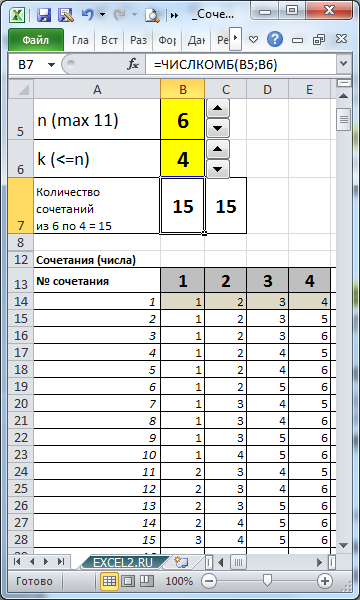
В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.
Задавая с помощью
элементов управления Счетчик
количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.
В файле примера не забывайте увеличивать количество строк с формулами, чтобы поместились все ваши комбинации. Для этого выделите последние ячейки с формулами (сочетание №330) и скопируйте их вниз на нужно количество строк. При увеличении строк с формулами размер файла быстро растет, а скорости пересчета листа падает. Если строк 4 тысячи, то размер файла составляет около 2 Мб.
Задача
Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.
Нам нужно определить число
Сочетаний
7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.
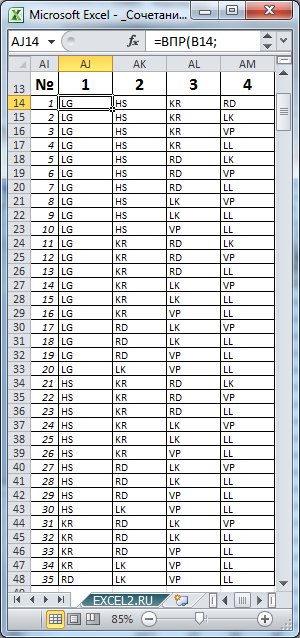
Воспользуемся файлом примера (ссылка внизу статьи) , чтобы наглядно убедиться, что мы решили задачу правильно.
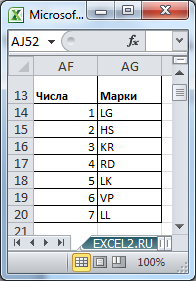
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …
Выставив в ячейках
В5
и
В6
значения 7 и 4 соответственно, определим все варианты размещений машин в автовозе (см. столбцы AJ:AM).
Примечание
: О Перестановках можно прочитать в статье
Перестановки без повторений: Комбинаторика в MS EXCEL
, а о Размещениях в статье
Размещения без повторений: Комбинаторика в MS EXCEL
.
Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.
Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!
Спасибо за ваши закладки и рекомендации
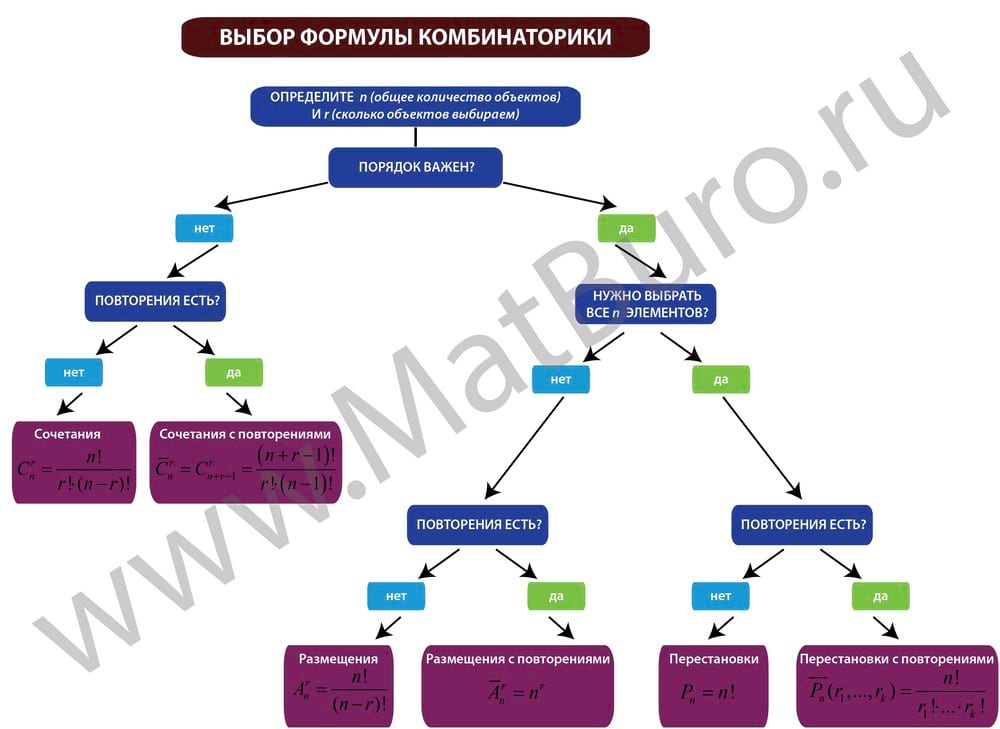
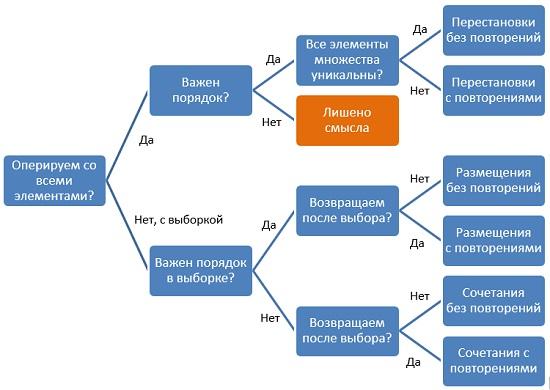
Как выбрать формулу комбинаторики?
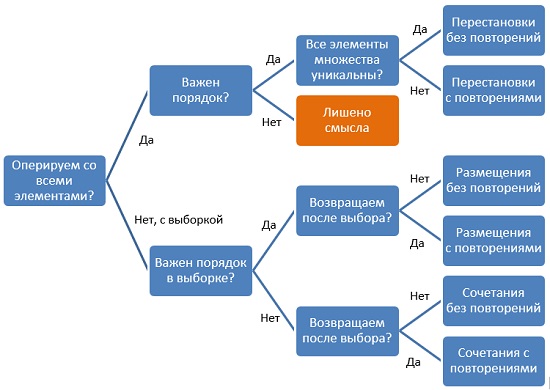
Нужно последовательно (см. схему выше) ответить на несколько вопросов:
- Сколько у нас есть объектов (число $n$)?
- Важен ли их порядок в комбинации?
- Могут ли встречаться повторяющиеся элементы?
- Нужно выбрать все элементы или только $klt n$?
Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:
Схема выбора формул с примерами задач
Консультируем по решению задач комбинаторики
Перестановки в Excel
Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно
$$P_n=n!=1cdot 2cdot 3 cdot … cdot (n-1) cdot n$$
Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.
Подробнее: факториал в эксель.
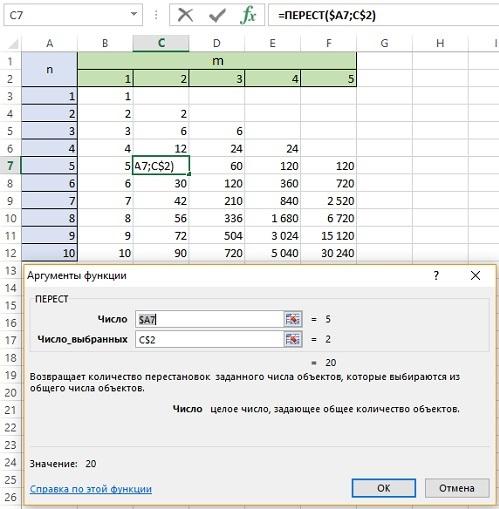
Для нахождения числа перестановок в Excel можно использовать одну из двух функций:
=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$), где $n$ — число переставляемых объектов.
Задача. Сколькими способами можно расставить 10 различных книг на одной полке?
Вводим число объектов 10 и получаем ответ: 3628800 способов.
В режиме формул это выглядит так:
Еще: онлайн калькулятор перестановок.
Перестановки с повторениями в Excel
Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа,… $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?
Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть
$$ P_n (n_1,n_2,…,n_k)=frac{n!}{n_1! cdot n_2!cdot … cdot n_k!}. $$
Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР(), которая находит факториал чисел и обычные действия (умножение, деление).
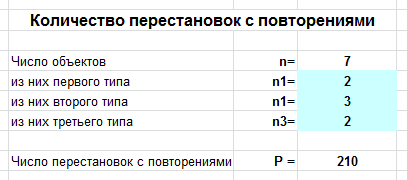
Задача. Сколько различных слов можно составить из букв слова «колокол»?
Вводим число букв $n=7$, а также $n_1=2$ (2 буквы «к»), $n_2=3$ (3 буквы «о»), $n_3=2$ (2 буквы «л»), и получаем ответ: 210 слов.
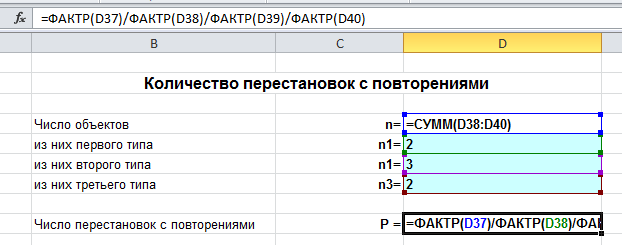
В режиме формул это выглядит так:
Еще: онлайн калькулятор перестановок c повторениями.
Размещения в Excel
Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно
$$A_n^k=frac{n!}{(n-k)!}=ncdot (n-1)cdot … cdot (n-k+1) $$
Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$).
Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?
Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.
В режиме формул это выглядит так:
Еще: онлайн калькулятор размещений.
Размещения с повторениями в Excel
Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле
$$overline{A}_n^k=ncdot ncdot … cdot n = n^k. $$
Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$).
Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?
Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.
В режиме формул это выглядит так:
Еще: онлайн калькулятор размещений с повторениями.
Сочетания в Excel
Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно
$$C_n^k=frac{n!}{(n-k)!cdot k!} $$
Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$).
Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?
Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.
В режиме формул это выглядит так:
Еще: онлайн калькулятор сочетаний.
Сочетания с повторениями в Excel
Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле
$$overline{C}_n^k=C_{k+n-1}^k=frac{(k+n-1)!}{(n-1)!cdot k!}$$
Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$).
Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?
Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.
В режиме формул это выглядит так:
Еще: онлайн калькулятор сочетаний с повторениями.
Полезные ссылки
Для собственных расчетов скачайте файл: Комбинаторика в Excel.
|
|
Решебник задач по комбинаторике
Комбинаторика в Excel
Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:
- Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
- Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
- Важен ли порядок элементов в выборке?
- После выбора элемента мы его возвращаем назад?
Рис. 1. Дерево решений, какую формулу комбинаторики использовать
Скачать заметку в формате Word или pdf, примеры в формате Excel
Перестановки без повторений
Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.
Рис. 2. Перестановки (картинка взята здесь)
Если все n элементы разные, то число перестановок обозначается Pn от perturbation.
С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!
Например
По определению: 1! = 1; 0! = 1.
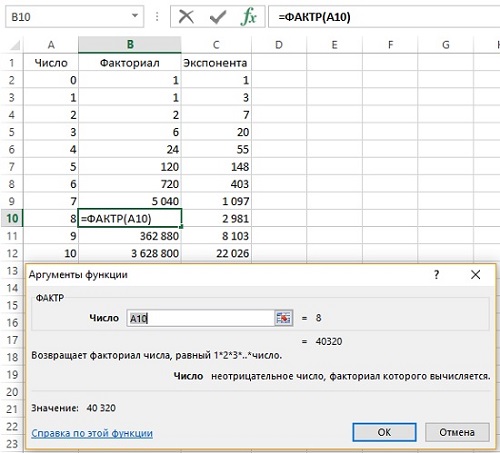
Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).
Рис. 3. Расчет числа перестановок без повторений с помощью факториала
Перестановки с повторениями
Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).
Рис. 4. Перестановки с повторениями (картинка найдена здесь)
В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n1 раз, второй – n2 раз, третий – n3 раз, …, k-й – nk раз (где n1 + n2 + … + nk = n) называется перестановкой с повторениями из n элементов.
Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?
Решение. Буквы а и н повторяются 2 раза, а буква м один раз.
Размещение без повторений
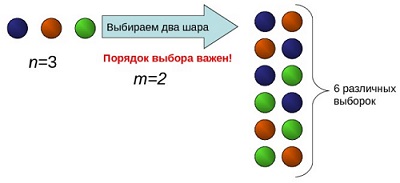
Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается от arrangement.
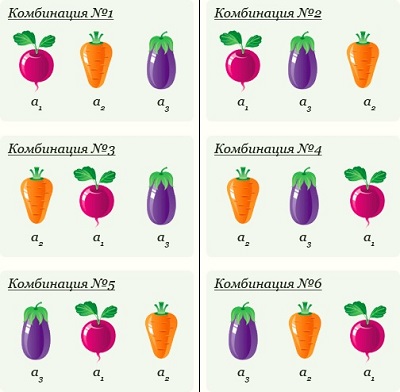
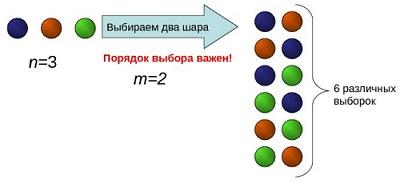
Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):
Рис. 5. Размещение без повторений (картинка из презентации)
Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).
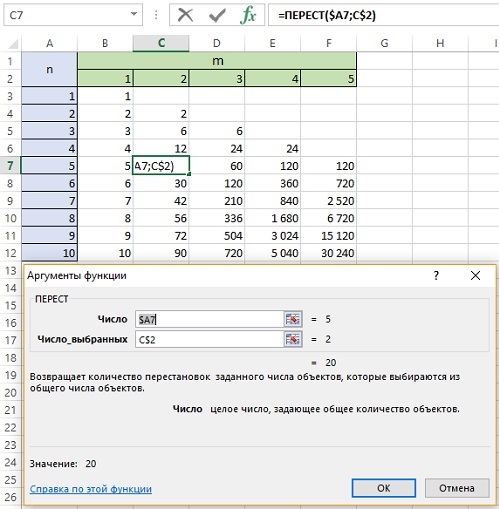
Название функции в Excel несколько обескураживает. Но… что поделаешь: =ПЕРЕСТ(n;m)
Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу
Размещение с повторениями
Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.
Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).
Рис. 7. Размещение с повторениями
В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:
В Excel используется функция ПЕРЕСТА(n;k).
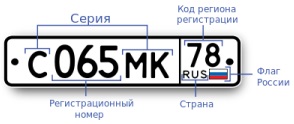
Задача. Сколько различных номеров можно составить в одном коде региона?
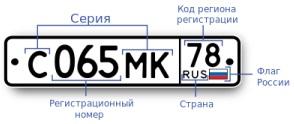
Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).
Рис. 8. Номер автомобиля
Решение. Можно воспользоваться формулой для размещения с повторениями:
Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.
Сочетания без повторений
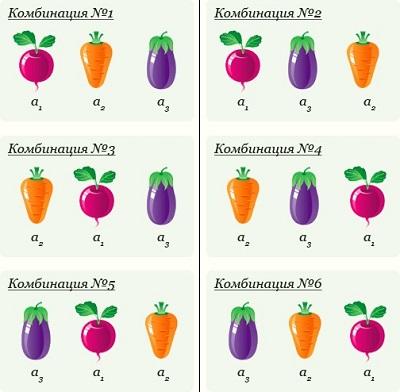
Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).
Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):
Рис. 9. Сочетания без повторений из 4 по 2
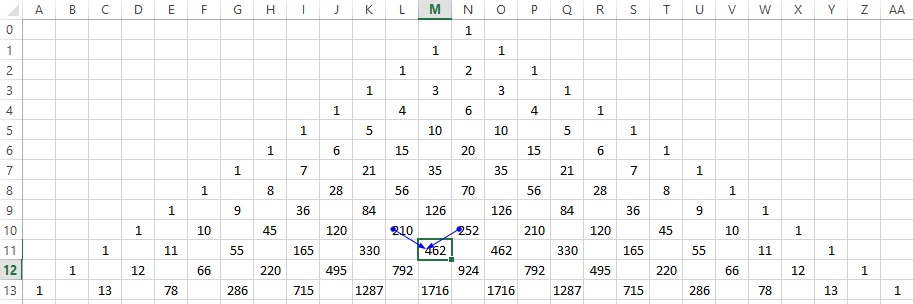
Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями
где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:
Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
В Excel используется функция =ЧИСЛКОМБ(n;m).
Сочетания с повторениями
Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.
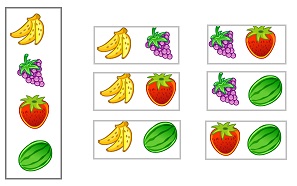
Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).
Рис. 11. Сочетания с повторениями
В общем случае, число сочетаний с повторениями:
Для нашего примера с фруктами
В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.
|
Cupon Пользователь Сообщений: 23 |
Помогите. Есть формулы, расчет комбинаций. Их слишком много. Необходимо заполнить таблицу например на миллион строк, затем продолжить расчет на новом листе с последний строки предыдущей таблицы. Если такое конечно возможно. Для примера кидаю файл. Изменено: Cupon — 04.09.2019 14:49:10 |
|
Dima S Пользователь Сообщений: 2063 |
а смысл? |
|
Cupon Пользователь Сообщений: 23 |
извините, делитант полный. что значит в массиве ? Изменено: Cupon — 04.09.2019 15:05:45 |
|
Cupon Пользователь Сообщений: 23 |
Может кто нибудь помочь ? Или подскажите, куда можно обратиться. Может это все-таки не в excel делать. Буду благодарен за любую подсказку |
|
Jack Famous Пользователь Сообщений: 10846 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
#5 05.09.2019 09:48:25
не совсем понятно, что именно вы хотите. Плодить миллионы данных нет никакого толку, т.к. вам же нужен анализ и результат. Так вот анализ нужно проводить в коде и полученный результат уже выводить на лист или в сообщении для пользователя Изменено: Jack Famous — 05.09.2019 09:51:05 Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
||
|
Cupon Пользователь Сообщений: 23 |
#6 05.09.2019 10:10:17 Jack Famous
мне как раз из полученных данных необходимо сделать выборку (привожу пример в новом файле). Мне нужна конечная цифра
можно подробнее, или хотя бы пример такого кода Прикрепленные файлы
Изменено: Cupon — 05.09.2019 10:14:09 |
||
|
Jack Famous Пользователь Сообщений: 10846 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
#7 05.09.2019 10:33:44
вы добавили 2 столбца. Что за конечная цифра (строго говоря, число тогда уж)? Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
||
|
Cupon Пользователь Сообщений: 23 |
да, верно — число |
|
Jack Famous Пользователь Сообщений: 10846 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
Cupon, вы не поняли — вы добавили 2 столбца, то есть 2*кол-во строк чисел. Вам их сумма нужна, среднее, минимум/максимум? Что в итоге-то нужно? Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
|
Cupon Пользователь Сообщений: 23 |
Идут 6 столбцов с числами. в 7 столбце высчитывается число из предыдущих шести. Именно оно мне нужно Изменено: Cupon — 05.09.2019 10:51:07 |
|
Jack Famous Пользователь Сообщений: 10846 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
Cupon, ещё раз: 7ой столбец это МИЛЛИОНЫ итоговых чисел (по количеству строк). Я понял, что вам нужно это число (+ округление), но их по-прежнему очень много и я пытаюсь выяснить, что вы с ними будете делать. Суммировать, сортировать… Неужели вы просто потом весь этот массив куда-то копируете? Изменено: Jack Famous — 05.09.2019 10:55:08 Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
|
Cupon Пользователь Сообщений: 23 |
аа) дальше что Изменено: Cupon — 05.09.2019 10:57:57 |
|
Jack Famous Пользователь Сообщений: 10846 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
Cupon, ну наконец-то)) тут пришёл главный по комбинаторике
не подскажу, потому что не вдупляю ваш алгоритм Название темы: «Комбинаторика. Перебор всех сочетаний с выводом списка повторений» Изменено: Jack Famous — 05.09.2019 11:10:17 Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
|
Cupon Пользователь Сообщений: 23 |
Jack Famous
спасибо большое. буду ждать) |
|
Jack Famous Пользователь Сообщений: 10846 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
#15 05.09.2019 11:11:30
поторопился я с обещаниями — прощу прощения…
это для модераторов — они меняют Изменено: Jack Famous — 05.09.2019 11:11:39 Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
||||
|
Cupon Пользователь Сообщений: 23 |
алгоритм там прост: количество сочетаний шести чисел без повтора из определенного числа |
|
MCH Пользователь Сообщений: 3875 |
#17 05.09.2019 11:23:40
Вам же не нужны все 13 миллионов чисел в итоге, скорее всего нужно найти оптимальное (максимальное или минимальное) перебирая все возможные сочетания чисел. http://www.excelworld.ru/forum/3-36449-1 Не все задачи можно решать простым перебором, количество комбинаций может быть очень большим, и не хватит времени найти решение перебором |
||
|
Jack Famous Пользователь Сообщений: 10846 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
#18 05.09.2019 11:25:01
ОК — скачайте файл отсюда и скажите, какой вариант ваш Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
||
|
MCH Пользователь Сообщений: 3875 |
#19 05.09.2019 11:26:54
Пока писал предыдущее сообщение, уже появилась конкретная задача, что нужно |
||
|
Jack Famous Пользователь Сообщений: 10846 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
Cupon, взял Combin за основу. Смотрите: для 6 понятно — сумму первых 3х делим на сумму остальных 3х и округляем до двух знаков. А если k<>6? Изменено: Jack Famous — 05.09.2019 11:56:51 Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
|
MCH Пользователь Сообщений: 3875 |
|
|
Cupon Пользователь Сообщений: 23 |
#22 05.09.2019 13:40:14
запутался ) у меня сочетание без повторений
вот тут я еще не продвинулся дальше. Я думаю методом подбора функций надо выйти на оптимальное решение. Пытался с пятью числами, но пока ерунда выходит
спасибо вам огромное. Я вторую неделю тут мучаюсь) но это естественно все от незнания. А можно сам алгоритм. В будущем хочу еще 5 из 50 Изменено: Cupon — 05.09.2019 13:40:58 |
||||||||
|
MCH Пользователь Сообщений: 3875 |
#23 05.09.2019 13:48:48
Какую функцию подбираем? какой результат нужен в итоге? для чего все это? |
||
|
PooHkrd Пользователь Сообщений: 6602 Excel x64 О365 / 2016 / Online / Power BI |
#24 05.09.2019 13:49:22
гм, а для нечетного количества как рассчитывать столбец с отношением суммы первых трех элементов к сумме последних трех? Вот горшок пустой, он предмет простой… |
||
|
Cupon Пользователь Сообщений: 23 |
#25 05.09.2019 14:01:15 тут уже надо искать другую формулу
да. Анализ всех вариантов и сравнение с уже имеющимися. функция (1+2+3)/(4+5+6) придумана чисто для удобства и более-менее выхода на красивую кривую можно ли увидеть из вашего итога, например какие варианты шести чисел содержит получившееся число 0,38 ? |
||
|
MCH Пользователь Сообщений: 3875 |
Посмотрите макрос, он небольшой (40 строчек кода), попробуйте разобраться самостоятельно. |
|
Cupon Пользователь Сообщений: 23 |
#27 05.09.2019 15:04:05 MCH
да, макрос уже посмотрел….буду разбираться MCH написал:
т.е. в этом же макросе внести изменения и выдаст результат ? |
||
|
Jack Famous Пользователь Сообщений: 10846 OS: Win 8.1 Корп. x64 | Excel 2016 x64: | Browser: Chrome |
#28 05.09.2019 15:34:33
да — всего пару-тройку строчек добавить, но вы это должны сами сделать, чтобы понять Во всех делах очень полезно периодически ставить знак вопроса к тому, что вы с давних пор считали не требующим доказательств (Бертран Рассел) ►Благодарности сюда◄ |
||
|
Cupon Пользователь Сообщений: 23 |
Изменено: Cupon — 05.09.2019 16:37:08 |
|
PooHkrd Пользователь Сообщений: 6602 Excel x64 О365 / 2016 / Online / Power BI |
#30 05.09.2019 16:28:42 Во вложении вариант на базе Power Query и Power Pivot.
Загружаем их в модель данных и в модели уже рисуем любую формулу, и её выводим в сводную в качестве агрегатора. Работает медленнее чем на VBA, но вдруг кому потребуется. Прикрепленные файлы
Изменено: PooHkrd — 10.09.2019 12:11:27 Вот горшок пустой, он предмет простой… |
|
Оглавление:
- 1 Как сделать комбинаторику в excel? — Разбираем подробно
- 1.1 Перестановки без повторений
- 1.2 Перестановки с повторениями
- 1.3 Размещение без повторений
- 1.4 Размещение с повторениями
- 1.5 Сочетания без повторений
- 1.6 Сочетания с повторениями
- 1.7 Алгоритм
Комбинаторика в Excel
Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:
- Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
- Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
- Важен ли порядок элементов в выборке?
- После выбора элемента мы его возвращаем назад?
Рис. 1. Дерево решений, какую формулу комбинаторики использовать
Скачать заметку в формате Word или pdf, примеры в формате Excel
Перестановки без повторений
Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.
Рис. 2. Перестановки (картинка взята здесь)
Если все n элементы разные, то число перестановок обозначается Pn от perturbation.
С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!
Например
По определению: 1! = 1; 0! = 1.
Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).
Рис. 3. Расчет числа перестановок без повторений с помощью факториала
Перестановки с повторениями
Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).
Рис. 4. Перестановки с повторениями (картинка найдена здесь)
В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n1 раз, второй – n2 раз, третий – n3 раз, …, k-й – nk раз (где n1 + n2 + … + nk = n) называется перестановкой с повторениями из n элементов.
Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?
Решение. Буквы а и н повторяются 2 раза, а буква м один раз.
Размещение без повторений
Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается от arrangement.
Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):
Рис. 5. Размещение без повторений (картинка из презентации)
Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).
Название функции в Excel несколько обескураживает. Но… что поделаешь: =ПЕРЕСТ(n;m)
Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу
Размещение с повторениями
Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.
Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).
Рис. 7. Размещение с повторениями
В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:
Задача. Сколько различных номеров можно составить в одном коде региона?
Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).
Рис. 8. Номер автомобиля
Решение. Можно воспользоваться формулой для размещения с повторениями:
Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.
Сочетания без повторений
Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).
Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):
Рис. 9. Сочетания без повторений из 4 по 2
Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями
где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:
Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
В Excel используется функция =ЧИСЛКОМБ(n;m).
Сочетания с повторениями
Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.
Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).
Рис. 11. Сочетания с повторениями
В общем случае, число сочетаний с повторениями:
Для нашего примера с фруктами
В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3 Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4 Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5 Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5 Затем — проверка для i = 2.
1 4 5 Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 52 4 53 4 5 — последнее сочетание, так как все его элементы равны n — m + i.
Did you find apk for android? You can find new Free Android Games and apps.
|
Поиск в «сочетании без повторений». |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
MulTEx »
10 Ноябрь 2017 6566 просмотров
Подбор вариантов
Данная функция является частью надстройки MulTEx
Вызов команды:
MulTEx -группа Специальные —Особые возможности —Подбор вариантов
Команда выводит все возможные варианты перестановок(комбинаций) заданных элементов. Элементами могут быть цифры, числа, буквы и целые слова. Комбинации генерируются без повторений, т.е. все подобранные комбинации уникальны:
Генерировать комбинации на основании:
выбирается один из двух вариантов
- Диапазона ячеек — указывается непрерывный диапазон из двух и более ячеек. Каждая ячейка будет считаться отдельным элементом. Пункт Разделитель игнорируется, даже если задан. Так, если указать диапазон A1:A3 и в этих ячейках записаны числа: 1, 2 и 3, то программа сгенерирует 6 комбинаций с различными перестановками значения каждой ячейки:
123
132
213
231
312
321 - Произвольного текста — указывается любой текст, который надо разбить на части(элементы) и сгенерировать комбинации перестановок элементов между собой. Если элементы необходимо разделять каким-то символом — необходимо задать этот символ в поле Разделитель. Если указать текст «1 2 3», а разделитель указать пробел, то получим 6 комбинаций:
123
132
213
231
312
321Если указать текст и не указывать разделитель, то каждый символ будет считаться отдельным элементом и будут выведены все возможные комбинации всех символов. Например, если указать «1 2 3», то будет создано 60 различных комбинаций(разъяснение почему комбинаций 60, а не 120 можно узнать далее. Причина — повторяется пробел ):
1 2 3
1 23
1 23
1 32
1 32
1 3 2
12 3
12 3
123
13 2
13 2
и т.д.
В обоих случаях (в ячейках или произвольном тексте) текст для обработки может быть любым, не только цифры. Например, если взять текст «мама мыла раму» и указать разделитель — » «(пробел), то получим все те же 6 комбинаций, но переставлены будут слова:
мама мыла раму
мама раму мыла
мыла мама раму
мыла раму мама
раму мама мыла
раму мыла мама
Записать результат, начиная с ячейки — указывается одна ячейка на листе, с которой начать записывать комбинации. В одну ячейку записывается одна комбинация. Если комбинаций получится больше, чем осталось строк на листе ниже указанной ячейки, то оставшиеся комбинации будут записаны в столбец правее и так до тех пор, пока не кончатся комбинации или столбцы листа.
В информационном поле ниже поле для ввода исходных данных отображается информация об общем количестве найденных комбинаций и о количестве уникальных комбинаций для вывода на лист. В чем отличие?
-
Всего количество допустимых комбинаций: это общее количество комбинаций, которые программе придется создать. Т.е. для трех разных элементов это будет 6. Но это число растет по экспоненте в зависимости от количества элементов. Например, для 4-х элементов это будет уже 24, для 5 — 120, а для 10 — 3 628 800.
Максимально возможное число неповторяющихся комбинаций: это максимальное количество комбинаций, которые будут выведены на лист. Это число может быть меньше или равно общему количеству комбинаций. Однако даже это число не всегда означает, что именно столько комбинаций будет выведено на лист. Например, возьмем числа: 1, 2, 3, 4 и 5. Всего комбинаций для них — 120. И столько же уникальных:

Однако, если хотя бы один элемент повторяется(возьмем числа 1,2, 2, 4 и 5) — то максимальное количество уникальных будет уже меньше — 60:
И чем больше повторяющихся элементов, тем меньше неповторяющихся комбинаций. Но эти числа программа рассчитывает формулами и иногда количество реально выведенных на лист комбинаций может быть меньше, т.к. для вывода на лист необходимо сгенерировать сначала все комбинации и убрать из них повторяющиеся.
Примечание: несмотря даже на возможно небольшое число итоговых комбинаций для вывода на лист, при большом количестве исходных элементов программа может выполняться значительное время и может возникнуть ощущение, что она «зависла», т.к. перебирать программе придется все равно ВСЕ возможные комбинации, а не только уникальные. Поэтому рекомендуется либо не задавать количество элементов более 12-ти или приготовиться ожидать завершения работы программы больше, чем хотелось бы. Хотя все это зависит от параметров компьютера и установленной оперативной памяти.
Расскажи друзьям, если статья оказалась полезной:
Видеоинструкции по использованию надстройки MulTEx

В Excel есть множество функций, позволяющих получить очень полезные результаты в математике и финансах, если назвать всего две категории. По этой причине мы рекомендуем вам установить Microsoft Office и прочтите эту статью, из которой вы узнаете чтобы перечислить все комбинации с функцией КОМБИНАТ в Excel
Что такое комбинация?
Вероятно, комбинация — это метод подсчета, используемый для получить количество групп элементов что можно взять из набора. Важно отметить, что элементы не повторяются, порядок не имеет значения, можно использовать числовые значения или символы, что выражается формулой C n, k = n! / (нк)! * к!
Функция COMBINATE в Excel
Функция КОМБИНАТ — это формула Excel, которая позволяет получить количество комбинаций для набора элементов. Таким образом, функция COMBINATE в Excel предоставляет общее количество групп, которые могут быть созданы из определенного количества элементов.
Функция COMBINAT в Excel поддерживает только числовые значения, и если некоторый текст включен в ячейки, которые будут аргументами формулы, будет получен усеченный результат, а на выходе #VALUE! Если один из аргументов содержит значение меньше 0, функция возвращает ошибку # ЧИСЛО!
Как перечислить все комбинации с функцией COMBINATE в Excel
Если вы хотите перечислить все комбинации с функцией COMBINATE в Excel, необходимо знать синтаксис требуется эту формулу и применить дополнительную процедуру в случае, если список групп включает текст вместо числовых значений.
Каков синтаксис функции КОМБИНАТ в Excel?
Синтаксис функции КОМБИНАТ в Excel имеет два аргумента. Первый аргумент относится к общему количеству элементов, а второй — к количеству элементов, разрешенных в каждой комбинации. Оба аргумента обязательны и выражаются так: = КОМБИНАТ (число, размер)
Перечислите количество возможных комбинаций с функцией КОМБИНАТ в Excel
Чтобы перечислить количество возможных комбинаций с помощью функции COMBINATE в Excel, вам необходимо вставить список предметов который будет использоваться как диапазон ячеек. Предположим, у вас есть список из восьми учеников, и вы хотите сгруппировать их в пары. Чтобы увидеть список всех возможных комбинаций, нам понадобится функция COMBINAT.
Напишите имя каждого ученика от A1 до A8. Для этого вы можете создать сводную таблицу . Перейдите к строке формул и выберите категорию «Математика и тригонометрия». Найдите функцию COMBINAT и нажмите «ОК». В «Число» нажмите значок красной стрелки, чтобы выбрать диапазон A1: A8, а в «Размер» введите 2 и нажмите «ОК».
Список всех комбинаций с функцией COMBINATE в Excel
Если вам нужно перечислить все комбинации с Функция COMBINATE в Excel, это необходимо создать макрос для выполнения процедуры. Для этого разделите имена на два столбца (A и B) и нажмите «Alt + F11». Таким образом вы получите доступ к редактору Visual Basic. Затем нажмите «Вставить» и «Модуль».
Вставьте следующие строки кода, чтобы вы могли видеть комбинации (вы должны помнить, что точки в начале каждой строки не входят в код):
- Под комбайном ()
- Dim i как целое, j как целое, LastRA как целое, LastRB как целое, Aux как целое
- Вспомогательный = 1
- LastRA = Диапазон («A4»). Конец (xlUp) .Row
- LastRB = Диапазон («B4»). Конец (xlUp) .Row
- Для i = 1 ТБ LastRA
- Для j = 1 ТБ LastRB
- Диапазон («C» & Aux) = Range («A» & i) & Range («B» & j)
- Вспомогательный = Вспомогательный + 1
- Следующий j
- Затем я
- End Sub
Как работает макрос для выполнения слияния
Чтобы комбинация была проведена, вы должны указать, что из всего «n» элементов (8 имен учащихся) возможно получить группы элементов без повторения и независимо от порядка, в котором они появляются.
При выборе диапазона или всех элементов столбец «C» получит возможные комбинации посредством поворота в два цикла для столбцов A и B. Удобно отметить, что если вы решите загрузите и установите LibreOffice на вашем компьютере вы не сможете разработать макрос, потому что это программное обеспечение несовместимо с приложениями Visual Basic.