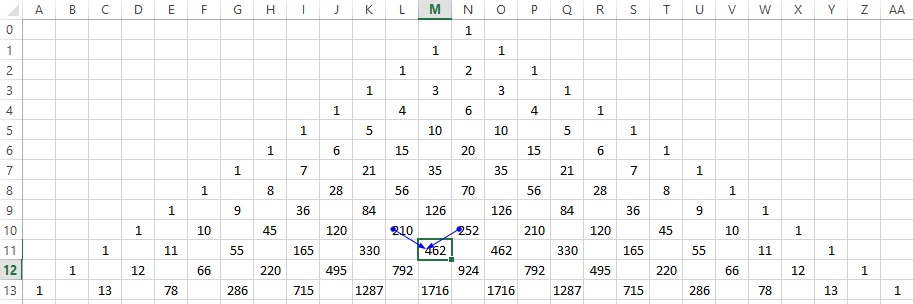
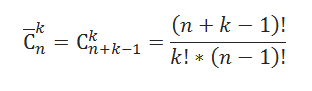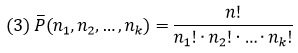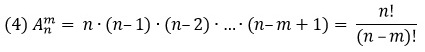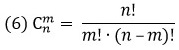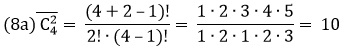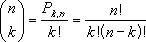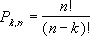Excel сочетания с повторениями - Word и Excel - помощь в работе с программами

Подсчитаем в MS EXCEL количество Сочетаний с повторениями из n по k (выборка с возвращением). Также с помощью формул выведем на лист соответствующие варианты Сочетаний (английский перевод термина: combinations with repetition).

Сочетания с повторениями (выборка с возвращением) — это Сочетание n объектов по k в предположении, что каждый объект может участвовать в сочетании несколько раз .

Примечание : О Сочетаниях без повторений (без возвращения элементов) можно прочитать в статье Сочетания без повторений: Комбинаторика в MS EXCEL

Например, из множества содержащего 3 (n) различных элемента ( a, b, c ) можно сформировать 6 =ФАКТР(3+2-1) / (ФАКТР (3-1) * ФАКТР (2)) упорядоченных наборов по 2 (k) элемента: аа, ab, ac, bb, bc, сс . В отличие от Сочетаний без повторений наборы аа, bb и сс допустимы. В отличие от Размещений наборы ac и ca считаются одинаковыми (порядок не важен).

В отличие от Сочетаний без повторений , k может быть меньше или больше n. Например, из множества содержащего 2 (n) различных элемента ( a, b ) можно сформировать 4 =ФАКТР(2+3-1) / (ФАКТР (2-1) * ФАКТР (3)) упорядоченных наборов по 3 (k) элемента (т.е. 4 сочетания с повторениями из 2 по 3): ааa, аab, abb, bbb.

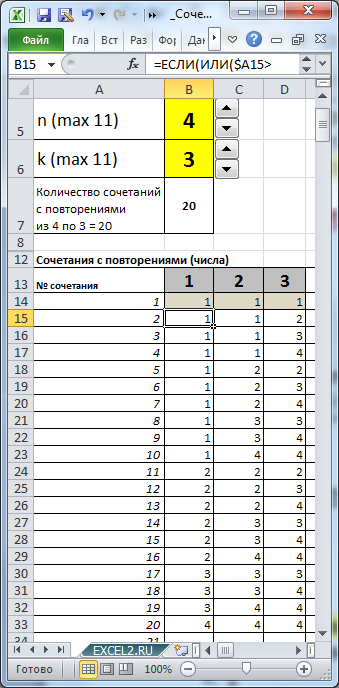
В файле примера MS EXCEL приведен подсчет количества Сочетаний с повторениями и созданы формулы для вывода всех Сочетаний для заданных n и k.

Задавая с помощью элементов управления Счетчик количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания с повторениями.

Задача

В магазине платки 4-х цветов продаются вперемешку в огромной корзине. Женщина не может определиться с выбором, и поэтому решается довериться случаю – выбрать не глядя 3 платка. Определить число различных вариантов покупки 3-х платков.

Так как не важно, в какой последовательности женщина будет выбирать платки, то нам нужно определить число Сочетаний с повторениями покупки 3-х платков 4-х возможных цветов. Т.е. n=4, а k=3. Оказывается, что таких вариантов =(4+3-1)!/(4-1)!/3! равно 20.

Воспользуемся файлом примера , чтобы убедиться, что мы решили задачу правильно.

По аналогии с решением задачи в статье Размещения без повторений сопоставим произвольным образом 4-м различным цветам числовые значения: 1; 2; 3; 4.

Выставив в ячейках В5 и В6 значения 4 и 3 соответственно, определим все варианты размещений.

Примечание : О Перестановках можно прочитать в статье Перестановки без повторений: Комбинаторика в MS EXCEL , а о Размещениях в статье Размещения без повторений: Комбинаторика в MS EXCEL .

Источник

Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.

Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!

Полезная страница? Сохрани или расскажи друзьям

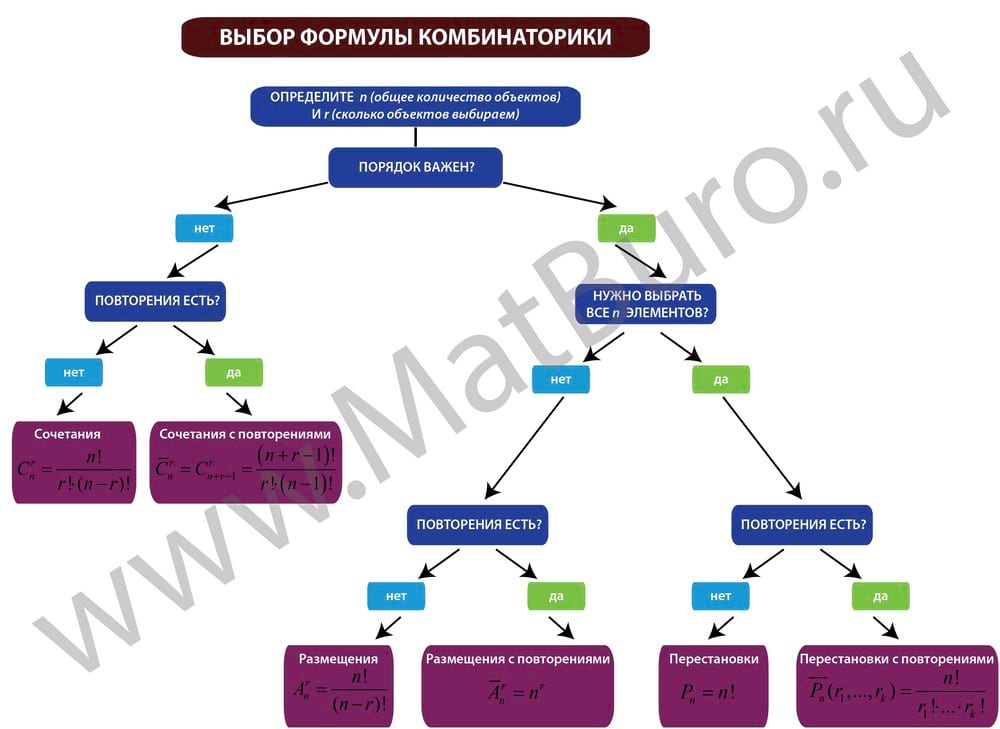
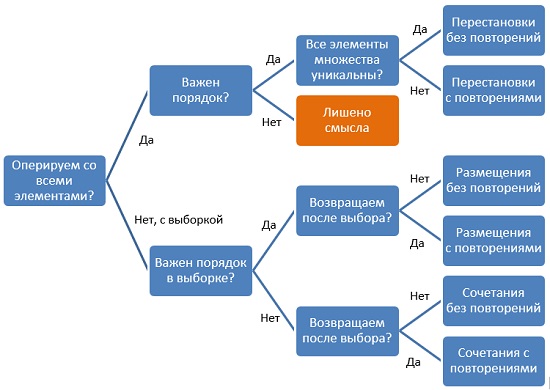
Как выбрать формулу комбинаторики?

Нужно последовательно (см. схему выше) ответить на несколько вопросов:

Сколько у нас есть объектов (число $n$)?
Важен ли их порядок в комбинации?
Могут ли встречаться повторяющиеся элементы?
Нужно выбрать все элементы или только $klt n$?

Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:

Схема выбора формул с примерами задач

Консультируем по решению задач комбинаторики

Перестановки в Excel

Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

$$P_n=n!=1cdot 2cdot 3 cdot … cdot (n-1) cdot n$$

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Подробнее: факториал в эксель.

Для нахождения числа перестановок в Excel можно использовать одну из двух функций:

=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$), где $n$ — число переставляемых объектов.

Задача. Сколькими способами можно расставить 10 различных книг на одной полке?

Вводим число объектов 10 и получаем ответ: 3628800 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок.

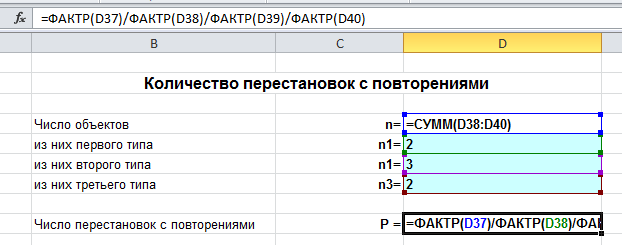
Перестановки с повторениями в Excel

Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа,… $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?

Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть

$$ P_n (n_1,n_2,…,n_k)=frac{n!}{n_1! cdot n_2!cdot … cdot n_k!}. $$

Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР(), которая находит факториал чисел и обычные действия (умножение, деление).

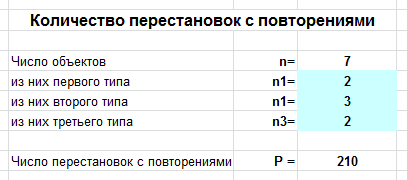
Задача. Сколько различных слов можно составить из букв слова «колокол»?

Вводим число букв $n=7$, а также $n_1=2$ (2 буквы «к»), $n_2=3$ (3 буквы «о»), $n_3=2$ (2 буквы «л»), и получаем ответ: 210 слов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок c повторениями.

Размещения в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно

$$A_n^k=frac{n!}{(n-k)!}=ncdot (n-1)cdot … cdot (n-k+1) $$

Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$).

Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений.

Размещения с повторениями в Excel

Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле

$$overline{A}_n^k=ncdot ncdot … cdot n = n^k. $$

Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$).

Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?

Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений с повторениями.

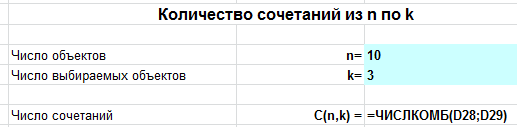
Сочетания в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно

$$C_n^k=frac{n!}{(n-k)!cdot k!} $$

Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$).

Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний.

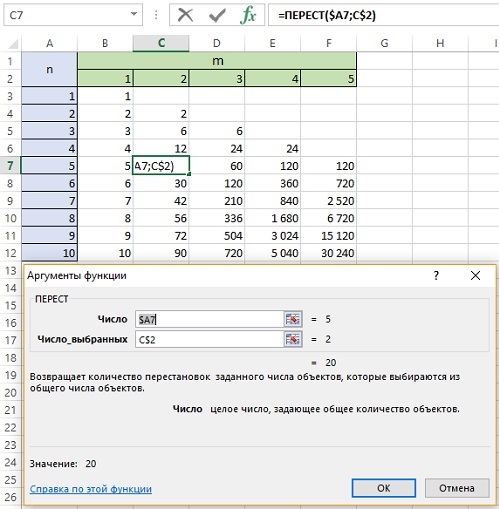
Сочетания с повторениями в Excel

Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле

$$overline{C}_n^k=C_{k+n-1}^k=frac{(k+n-1)!}{(n-1)!cdot k!}$$

Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$).

Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?

Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний с повторениями.

Полезные ссылки

Для собственных расчетов скачайте файл: Комбинаторика в Excel.

Онлайн калькуляторы
Онлайн учебник: Элементы комбинаторики
Примеры решений

Как решать задачи по комбинаторике?
Видеоуроки по комбинаторике
Решение на заказ

Решебник задач по комбинаторике

Источник

Комбинаторика в Excel

Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:

Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
Важен ли порядок элементов в выборке?
После выбора элемента мы его возвращаем назад?

Рис. 1. Дерево решений, какую формулу комбинаторики использовать

Скачать заметку в формате Word или pdf, примеры в формате Excel

Перестановки без повторений

Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.

Рис. 2. Перестановки (картинка взята здесь)

Если все n элементы разные, то число перестановок обозначается P_n от perturbation.

С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!

Например

По определению: 1! = 1; 0! = 1.

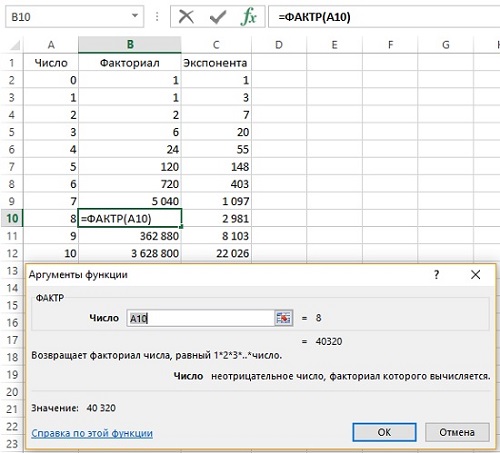
Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).

Рис. 3. Расчет числа перестановок без повторений с помощью факториала

Перестановки с повторениями

Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).

Рис. 4. Перестановки с повторениями (картинка найдена здесь)

В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n₁ раз, второй – n₂ раз, третий – n₃ раз, …, k-й – n_k раз (где n₁+ n₂+ … + n_k = n) называется перестановкой с повторениями из n элементов.

Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?

Решение. Буквы а и н повторяются 2 раза, а буква м один раз.

Размещение без повторений

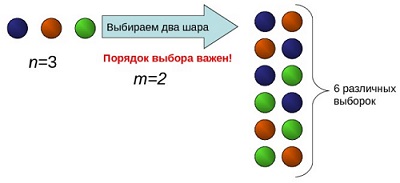
Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается от arrangement.

Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):

Рис. 5. Размещение без повторений (картинка из презентации)

Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).

Название функции в Excel несколько обескураживает. Но… что поделаешь: =ПЕРЕСТ(n;m)

Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу

Размещение с повторениями

Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.

Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).

Рис. 7. Размещение с повторениями

В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:

В Excel используется функция ПЕРЕСТА(n;k).

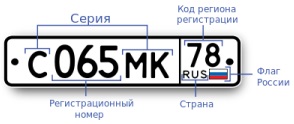
Задача. Сколько различных номеров можно составить в одном коде региона?

Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).

Рис. 8. Номер автомобиля

Решение. Можно воспользоваться формулой для размещения с повторениями:

Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.

Сочетания без повторений

Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).

Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):

Рис. 9. Сочетания без повторений из 4 по 2

Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями

где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:

Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке

В Excel используется функция =ЧИСЛКОМБ(n;m).

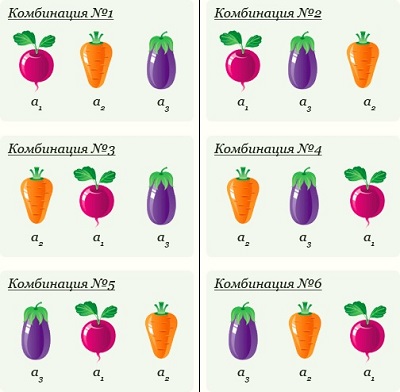
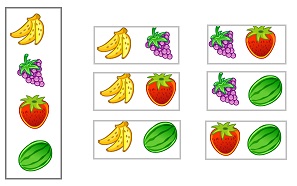
Сочетания с повторениями

Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.

Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).

Рис. 11. Сочетания с повторениями

В общем случае, число сочетаний с повторениями:

Для нашего примера с фруктами

В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.

Источник

В Excel есть множество функций, позволяющих получить очень полезные результаты в математике и финансах, если назвать всего две категории. По этой причине мы рекомендуем вам установить Microsoft Office и прочтите эту статью, из которой вы узнаете чтобы перечислить все комбинации с функцией КОМБИНАТ в Excel

Что такое комбинация?

Вероятно, комбинация — это метод подсчета, используемый для получить количество групп элементов что можно взять из набора. Важно отметить, что элементы не повторяются, порядок не имеет значения, можно использовать числовые значения или символы, что выражается формулой C n, k = n! / (нк)! * к!

Функция COMBINATE в Excel

Функция КОМБИНАТ — это формула Excel, которая позволяет получить количество комбинаций для набора элементов. Таким образом, функция COMBINATE в Excel предоставляет общее количество групп, которые могут быть созданы из определенного количества элементов.

Функция COMBINAT в Excel поддерживает только числовые значения, и если некоторый текст включен в ячейки, которые будут аргументами формулы, будет получен усеченный результат, а на выходе #VALUE! Если один из аргументов содержит значение меньше 0, функция возвращает ошибку # ЧИСЛО!

Как перечислить все комбинации с функцией COMBINATE в Excel

Если вы хотите перечислить все комбинации с функцией COMBINATE в Excel, необходимо знать синтаксис требуется эту формулу и применить дополнительную процедуру в случае, если список групп включает текст вместо числовых значений.

Каков синтаксис функции КОМБИНАТ в Excel?

Синтаксис функции КОМБИНАТ в Excel имеет два аргумента. Первый аргумент относится к общему количеству элементов, а второй — к количеству элементов, разрешенных в каждой комбинации. Оба аргумента обязательны и выражаются так: = КОМБИНАТ (число, размер)

Перечислите количество возможных комбинаций с функцией КОМБИНАТ в Excel

Чтобы перечислить количество возможных комбинаций с помощью функции COMBINATE в Excel, вам необходимо вставить список предметов который будет использоваться как диапазон ячеек. Предположим, у вас есть список из восьми учеников, и вы хотите сгруппировать их в пары. Чтобы увидеть список всех возможных комбинаций, нам понадобится функция COMBINAT.

Напишите имя каждого ученика от A1 до A8. Для этого вы можете создать сводную таблицу . Перейдите к строке формул и выберите категорию «Математика и тригонометрия». Найдите функцию COMBINAT и нажмите «ОК». В «Число» нажмите значок красной стрелки, чтобы выбрать диапазон A1: A8, а в «Размер» введите 2 и нажмите «ОК».

Список всех комбинаций с функцией COMBINATE в Excel

Если вам нужно перечислить все комбинации с Функция COMBINATE в Excel, это необходимо создать макрос для выполнения процедуры. Для этого разделите имена на два столбца (A и B) и нажмите «Alt + F11». Таким образом вы получите доступ к редактору Visual Basic. Затем нажмите «Вставить» и «Модуль».

Вставьте следующие строки кода, чтобы вы могли видеть комбинации (вы должны помнить, что точки в начале каждой строки не входят в код):

Под комбайном ()
Dim i как целое, j как целое, LastRA как целое, LastRB как целое, Aux как целое
Вспомогательный = 1
LastRA = Диапазон («A4»). Конец (xlUp) .Row
LastRB = Диапазон («B4»). Конец (xlUp) .Row
Для i = 1 ТБ LastRA
Для j = 1 ТБ LastRB
Диапазон («C» & Aux) = Range («A» & i) & Range («B» & j)
Вспомогательный = Вспомогательный + 1
Следующий j
Затем я
End Sub

Как работает макрос для выполнения слияния

Чтобы комбинация была проведена, вы должны указать, что из всего «n» элементов (8 имен учащихся) возможно получить группы элементов без повторения и независимо от порядка, в котором они появляются.

При выборе диапазона или всех элементов столбец «C» получит возможные комбинации посредством поворота в два цикла для столбцов A и B. Удобно отметить, что если вы решите загрузите и установите LibreOffice на вашем компьютере вы не сможете разработать макрос, потому что это программное обеспечение несовместимо с приложениями Visual Basic.

Ezoic

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции ЧИСЛКОМБ в Microsoft Excel.

Описание

Возвращает количество комбинаций для заданного числа элементов. Функция ЧИСЛКОМБ используется для определения общего числа всех групп, которые можно составить из элементов данного множества.

Синтаксис

ЧИСЛКОМБ(число;число_выбранных)

Аргументы функции ЧИСЛКОМБ описаны ниже.

Число — обязательный аргумент. Количество элементов.
Число_выбранных — обязательный аргумент. Количество элементов в каждой комбинации.

Замечания

Числовые аргументы усекаются до целых чисел.
Если хотя бы один из аргументов не является числом, то #VALUE! значение ошибки #ЗНАЧ!.
Если число < 0, number_chosen < 0 или < number_chosen, то #NUM! значение ошибки #ЗНАЧ!.
Комбинацией считается любое множество или подмножество элементов независимо от их внутреннего порядка. Комбинации отличаются от перестановок, для которых порядок существен.
Число комбинаций определяется по следующей формуле, где число = n, а число_выбранных = k:

где

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=ЧИСЛКОМБ(8;2)	Возможные команды по два человека, которые могут быть сформированы из восьми кандидатов.	28

Нужна дополнительная помощь?

Источник

In this guide, we’re going to show you how to find all combinations of two lists in Excel by using Power Query.

Download Workbook

In our example, we have two lists that contain Pokémon names and we want to see the combinations of matched Pokémon.

We can join these two tables to compare them by using Get & Transform Data. Get & Transform Data feature consists of tools, previously known as Power Query. You can get more information about this here: Power Query 101.

Creating queries from tables

First step is to convert the tables into Power Query structure.

Select one of your tables.
Open the Data tab and click the corresponding icon under the Get & Transform Data section to get data from your workbook.
1. (Microsoft 365 / Excel 2019) From Sheet
2. (Excel 2016) From Table/Range
3. (Excel 2010 / Excel 2013) Use Power Pivot tab instead of Data
Clicking the button opens the Power Query Editor.
Once you are done with the changes, click Custom Column in Add Column. We will add a helper column which will be a common point between the two tables.
Enter a friendly name for your new column and enter =1 into the formula section.
Click OK to save.
After adding the helper column, return to the Home tab and click Close & Load To item in Close & Load list to see options.
Make sure to select Only Create Connection in the Import Data This option will save the table as a connection rather that populating the queried data in the worksheet.
Apply the same steps to the other table. At the end you should have two queries corresponding with your tables. You can see these tables in Queries & Connections pane in Excel.

Joining queries to find all combinations of two lists

Next step is to join (merge) the queries on a new table which will allow us to see any differences between the tables.

Once the queries from the tables are ready, go to Data > Get Data > Combine Queries > Merge to open the Merge dialog of Power Query.
Select each table in the drop downs.
Click on the column for each table to select them.
Finally select Full Outer option for Join Kind to join by all rows from both tables.
Click OK to apply selections.
You will see three columns after merging. The first one is the items of the first list. Right-click on the column in the middle and select Remove to delete the helper column.
Click the button next to the column title.
Make sure that the Expand option is selected in the popup menu.
Uncheck the helper column.
Uncheck Use original column as prefix.
Click OK to populate the data of the second table.
You will see the combinations in Power Query. When you are OK with the outcome, click Close & Load, this time to populate the entire data into your worksheet.