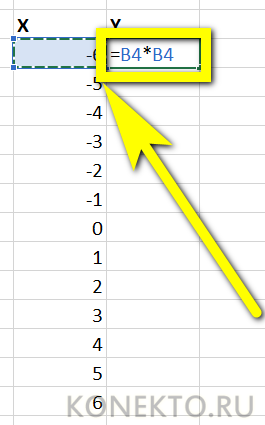Функция СТЕПЕНЬ в Excel используется для возведения чисел в степень, значение которой может являться сложным выражением, и возвращает полученное в результате числовое значение.
Функция СТЕПЕНЬ в Excel для возведения числа в указанную степень
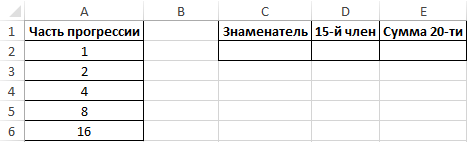
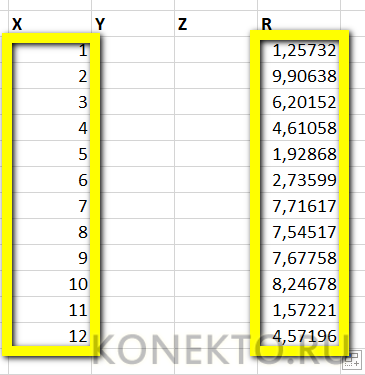
Пример 1. В таблице записана последовательность, которая представляет собой часть геометрической прогрессии. Необходимо определить: знаменатель геометрической прогрессии, значение 15-го ее члена, а также сумму первых 20 членов.
Таблица исходных данных:
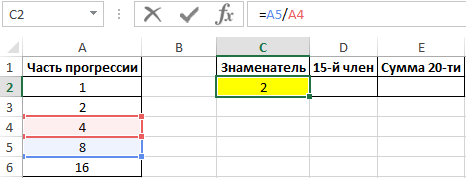
Определим знаменатель из условия, что он равен частному от деления любых последующего и предыдущего соседних членов:
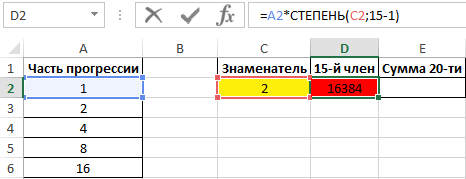
Для нахождения 15-го члена используем формулу:
=A2*СТЕПЕНЬ(C2;15-1)
Описание аргументов:
- A2 – ячейка, содержащая значение первого члена;
- СТЕПЕНЬ(C2;15-1) – формула, принимающая на вход значение знаменателя прогрессии, который возводится в степень, равную номеру позиции искомого члена -1.
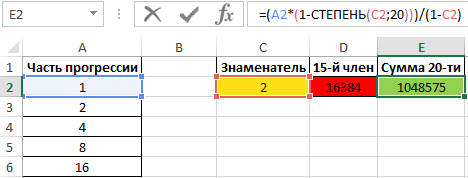
Для нахождения суммы первых 20 вхождений в последовательности введем формулу:
Примечание: в данном примере использовались известные из математики формулы, а применение функция СТЕПЕНЬ позволило упростить расчеты.
Как построить график функций используя СТЕПЕНЬ в Excel
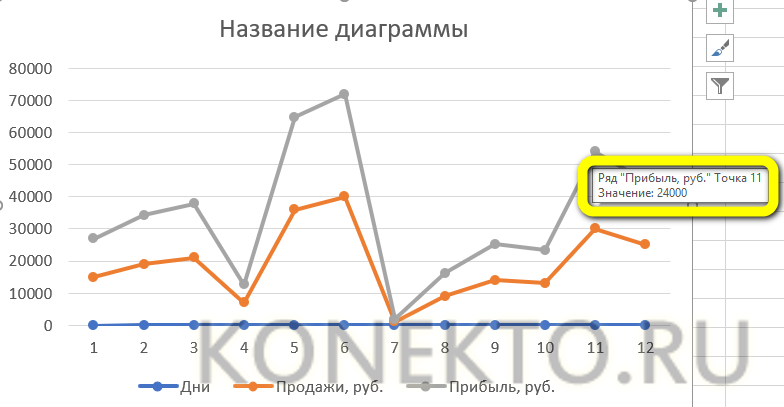
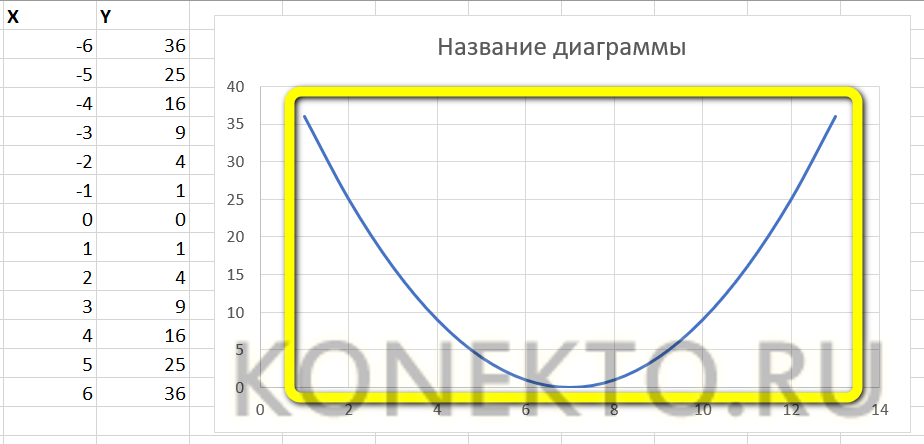
Пример 2. Построить график функции y=2^(x^2+2x).
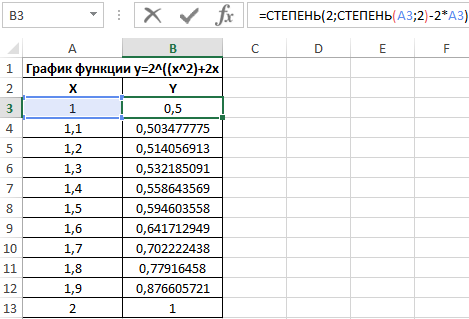
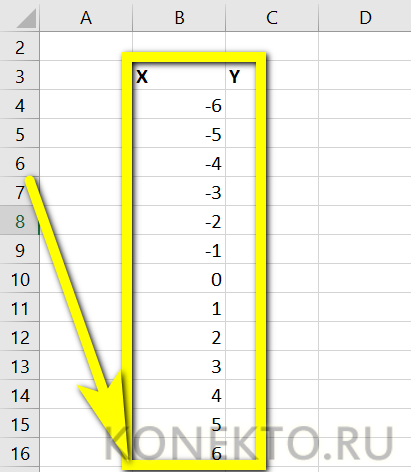
Для построения графика будем использовать несколько точек, полученных в результате расчета значения зависимой координаты y на основе известных произвольных значениях независимой координаты x. Внесем исходные данные в таблицу:
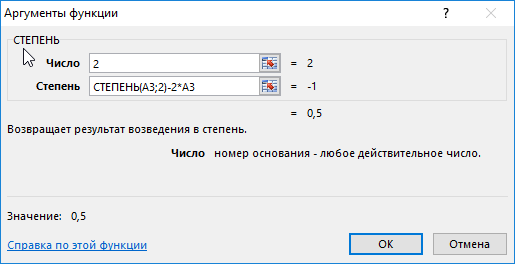
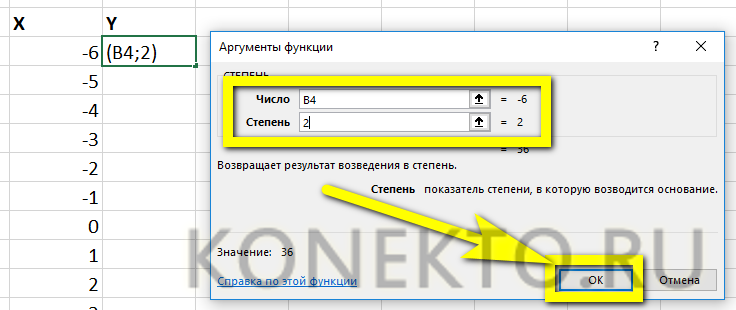
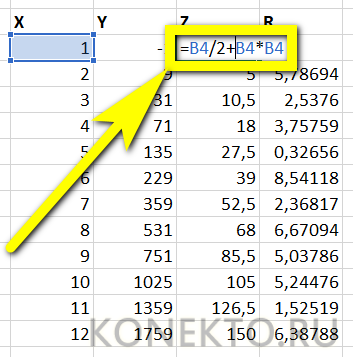
Определим первое значение зависимой переменной:
Описание аргументов:
- 2 – число, которое необходимо возвести в степень;
- СТЕПЕНЬ(A3;2)-2*A3 – степень, полученная в результате вычисления данного выражения.
Аналогично определим второе значение для Y, выделим ячейки B3 и B4, автоматически заполним остальные ячейки растягиванием выделенной области:
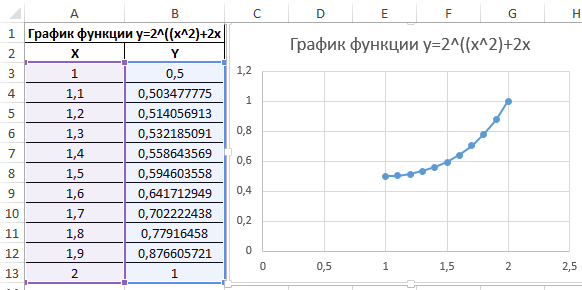
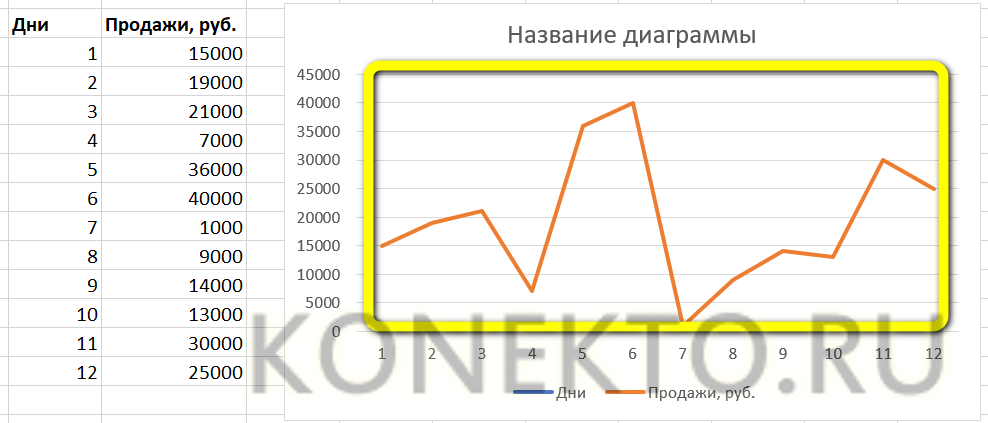
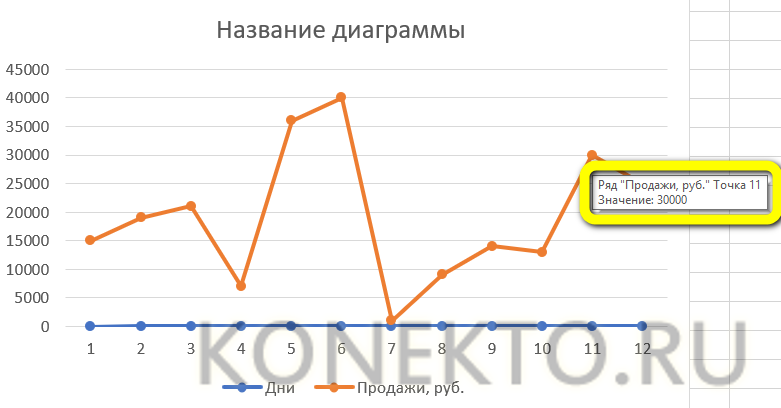
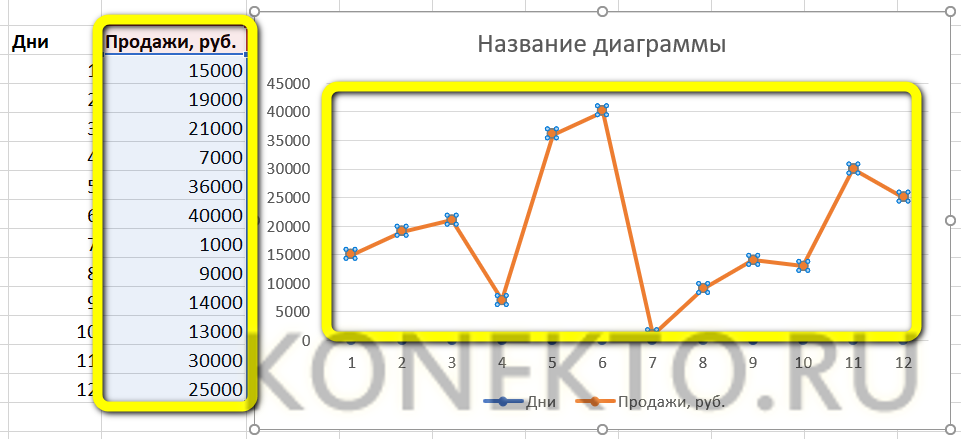
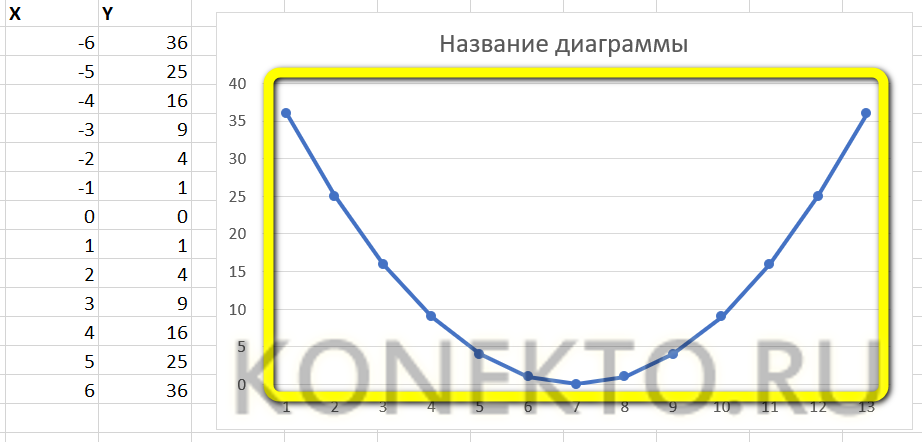
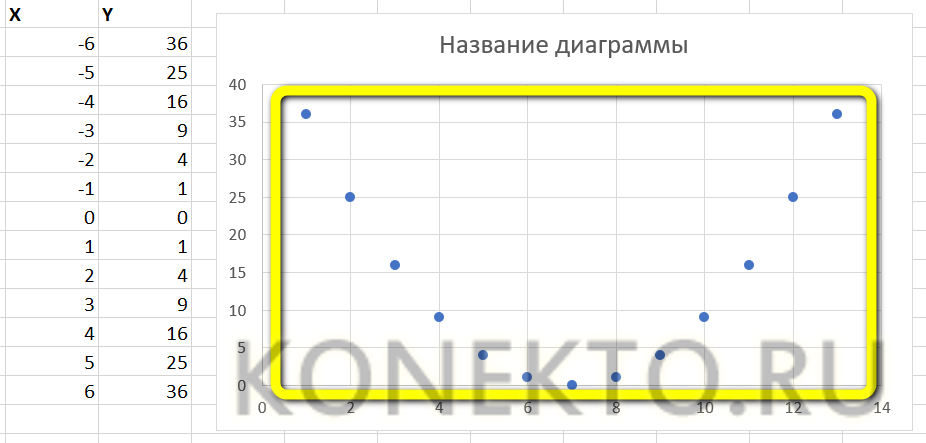
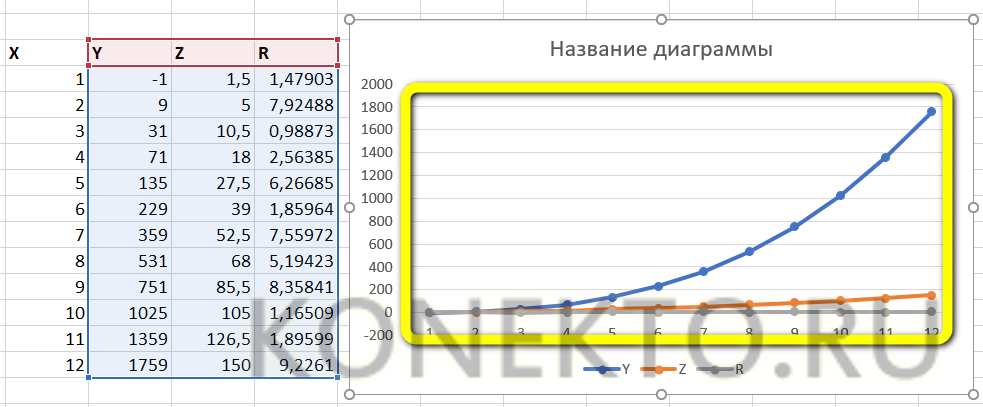
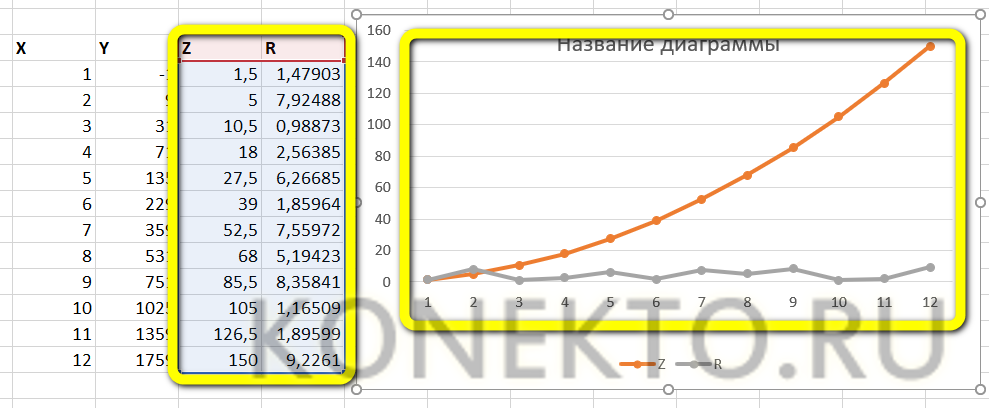
Для построения графика используем точечную диаграмму с маркерами. Готовый график функций имеет следующий вид:
Депозитный калькулятор в Excel
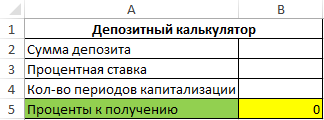
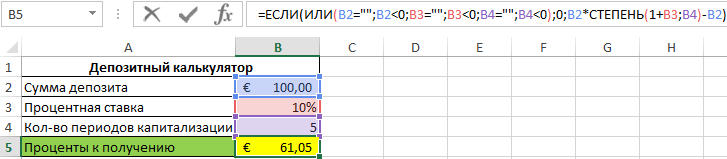
Пример 3. В таблице Excel создан калькулятор для расчета суммы процентов прибыли по депозитным вкладам в банковскую организацию. Рассмотрим его реализацию.
Калькулятор имеет следующий вид:
Заполним шаблон депозитного калькулятора исходными данными для расчетов:
В ячейке B5 содержится следующая формула:
Описание аргументов:
- ИЛИ(B2=»»;B2<0;B3=»»;B3<0;B4=»»;B4<0) – условия для проверки, чтобы в ячейке B5 не выводилась ошибка #ЗНАЧ!, если предыдущие ячейки не заполнены или введены неверные значения.
- 0 – значение, которое выводится по умолчанию, если расчет не производится.
- B2*СТЕПЕНЬ(1+B3;B4)-B2 – формула расчета суммы процентов. Для возведения в степень используется функция СТЕПЕНЬ.
Пример использования:
Примечание: для корректной работы данного калькулятора значение процентной ставки должно являться десятичной дробью (например, значение 10% — 0,1 указано в процентном формате ячеек).
Функция СТЕПЕНЬ в Excel и особенности ее использования
Рассматриваемая функция принадлежит к классу математических функций Excel и имеет следующую синтаксическую запись:
=СТЕПЕНЬ(число; степень)
Описание аргументов:
- число – обязательный аргумент, характеризующий число, которое необходимо возвести в степень.
- степень – обязательный аргумент, характеризующий степень, в которую требуется возвести число.
Примечания:
- Функция СТЕПЕНЬ вернет код ошибки #ЗНАЧ!, если один из параметров содержит текстовые данные.
- Записи типа =СТЕПЕНЬ(2;ЛОЖЬ) или =СТЕПЕНЬ(5;ИСТИНА) являются допустимыми, поскольку Excel выполняет автоматическое преобразование типов данных там, где это возможно. В первом случае будет возвращено значение 1 (ЛОЖЬ соответствует числовому значению 0), а во втором – 5 (ИСТИНА соответствует числовому значению 1).
- Запись типа =СТЕПЕНЬ(2;СТЕПЕНЬ(2;3)) является допустимой, в данном случае будет возвращено значение 256.
- Аргумент степень принимает также значения из диапазона отрицательных чисел. Запись типа =СТЕПЕНЬ(4;-2) эквивалентна записи =1/СТЕПЕНЬ(4;2).
- Для возведения чисел в степень можно также использовать запись типа «a^b», где a – число, возводимое в степень, b – степень, в которую требуется возвести значение, «^» — символ возведения в степень. Однако запись типа =СТЕПЕНЬ(a;b) является более наглядной.
- С помощью рассматриваемой функции можно извлечь корень любой степени из числа. Для реализации необходимо в качестве степени ввести выражение типа (1/b), где b – корень степени b.
Содержание
- Вычисление экспоненты в Эксель
- Способ 1: вычисление экспоненты при помощи ручного ввода функции
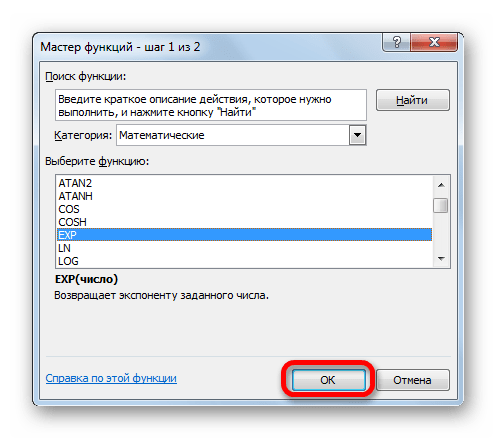
- Способ 2: использование Мастера функций
- Способ 3: построение графика
- Вопросы и ответы
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
f(x) = e^n,
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
=EXP(число)
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
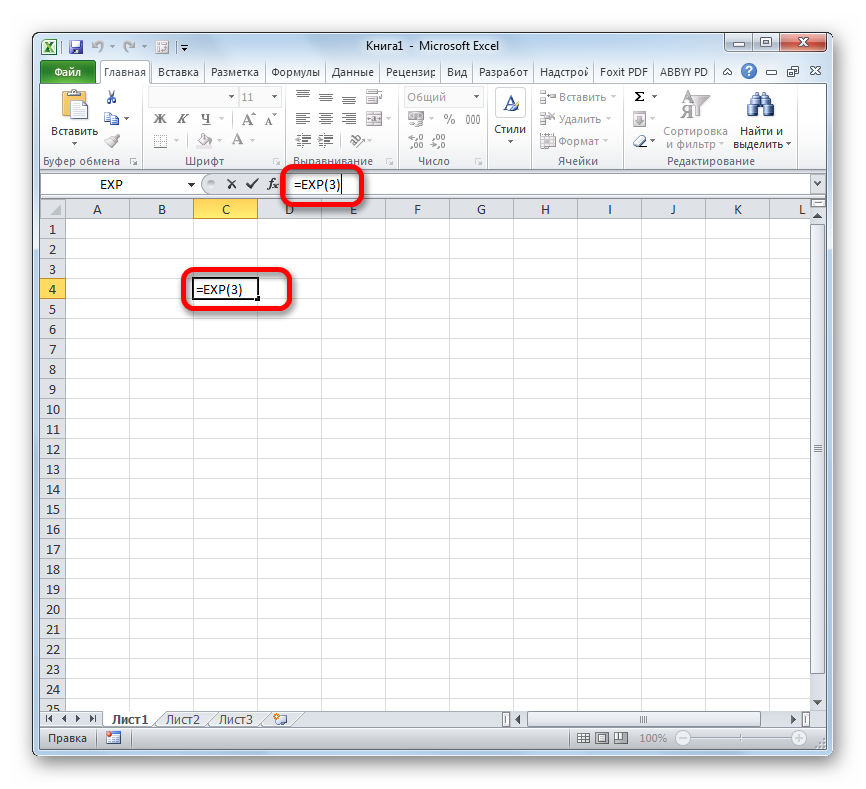
- Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:
=EXP(3) - Для выполнения расчета щелкаем по кнопке Enter. Итог выводится в заранее указанную ячейку.
Урок: Другие математические функции в Эксель
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.
- Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.
- Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».
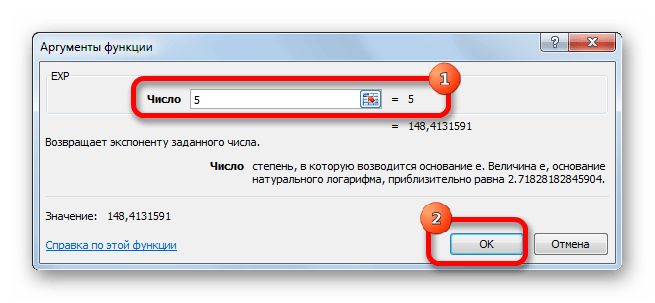
- Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».
- После вышеперечисленных действий результат расчета будет показан в той ячейке, которая была выделена в первом пункте данного способа.
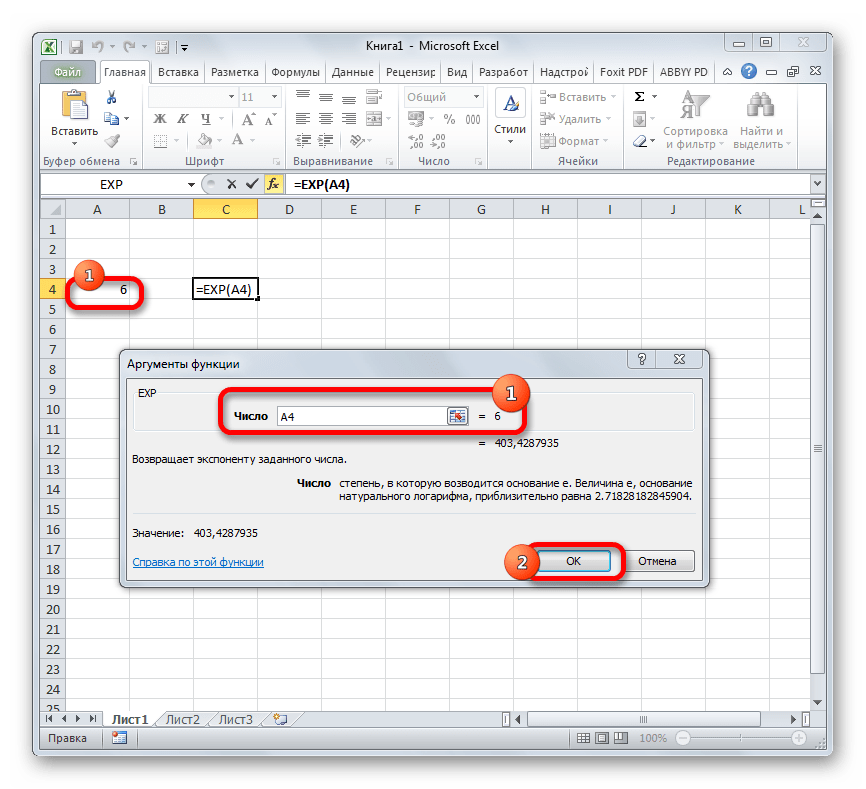
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».
Урок: Мастер функций в Microsoft Excel
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
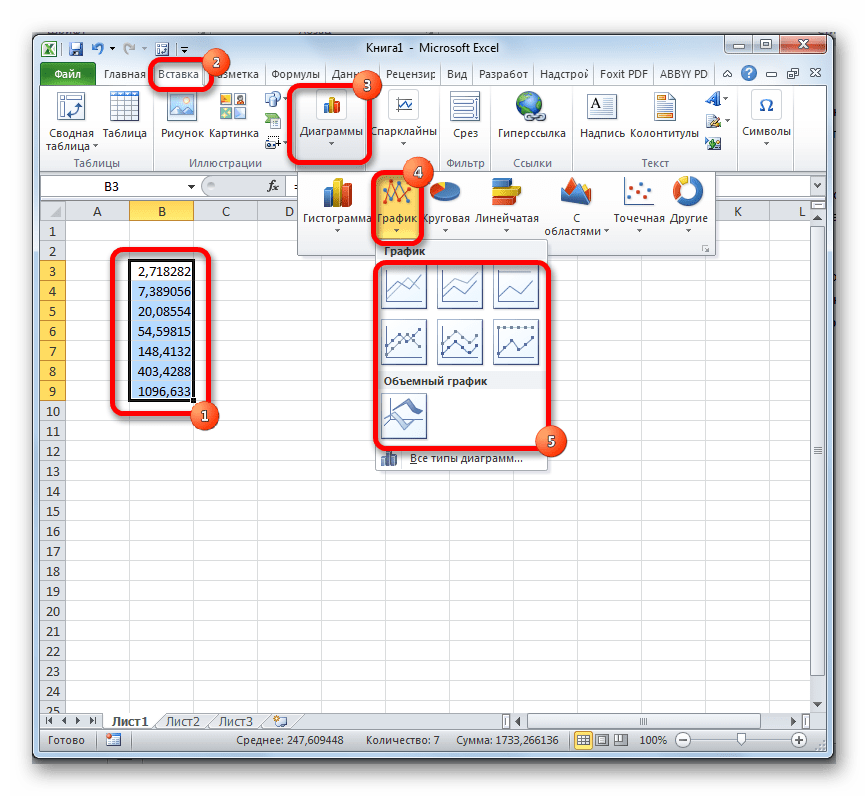
- Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.
- После того, как тип графика выбран, программа построит и отобразит его на том же листе, согласно указанным экспонентам. Далее его можно будет редактировать, как и любую другую диаграмму Экселя.
Урок: Как сделать график в Excel
Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.
Еще статьи по данной теме:
Помогла ли Вам статья?
|
0 / 0 / 0 Регистрация: 25.12.2014 Сообщений: 2 |
|
|
1 |
|
Построить график со степенными множителями21.06.2012, 23:15. Показов 7943. Ответов 1
подскажите пожалуйста, как в ексель ввести данные, число умноженное на 10 в стпени и построить с ними график, чтобы около оси надпись тоже от отображалась как числа умноженные на 10 в степени?
0 |
|
1300 / 402 / 22 Регистрация: 21.10.2011 Сообщений: 1,285 |
|
|
22.06.2012, 10:32 |
2 |
|
ID, Просто постройте график и автоматически ось будет подписана так, как надо.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
22.06.2012, 10:32 |
|
2 |
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
На чтение 11 мин Просмотров 3к. Опубликовано 04.07.2019
Содержание
- Вычисление экспоненты в Эксель
- Способ 1: вычисление экспоненты при помощи ручного ввода функции
- Способ 2: использование Мастера функций
- Способ 3: построение графика
- Excel works!
- Экспонента в Excel. Что такое экспонента и как применять?
- Экспонента. Что это такое?
- Принцип Парето и экспонента
- Экспонента в Excel
- Дополнение. Как запомнить 15 знаков числа е?
- Функция РОСТ()
- Функция ЛГРФПРИБЛ()
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
-
Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.
-
Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.
Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».
Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
-
Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.
Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Excel работает за вас
Excel works!
Thanks for Visiting
Экспонента в Excel. Что такое экспонента и как применять?
Мы немного затронули тему экспоненты в статье про округление больших чисел . В этой же статье мы обсудим, что же такое экспонента в Excel и, самое главное, для чего она может пригодиться в обычной жизни или в бизнесе.
В студенческие годы часто приходилось слышать, фразы типа: «Зачем мы вообще учим ‘это’, в жизни нам ‘это’ никогда не пригодиться». Одним из таких ‘это’ часто была экспонента или, например, факториал . У меня была слабая высшая математика при первом образовании, о чем я жалею. И вот сейчас приходиться догонять, темы что упустил раньше. Делюсь пересказом своих знаний.
Экспонента. Что это такое?
Мы знаем, что наш мир описан точными науками — т.е. набором правил и законов более-менее точно описывающих происходящее. Для этого в большинстве случаев помогают функции/формулы. В природе довольно часто встречаются экспоненциальные явления (описываем экспонентой) формулой с числом e, а у = e в степени x уже будет экспоненциальной функцией:
Число e — это т.н. число Эйлера, приблизительно равное 2,72. Примечательно оно тем, что производная от этой функции равна самой функции exp(x)` = exp(x).
Что это вообще такое, и что для нас означает?
Лучше всего, действие экспоненты показывают графики ниже:
Две функции: y = 2 в степени x и y = e в степени x , где x = время, к примеру. Мы видим, что скорость роста экспоненциального графика увеличивается быстрее. А все почему? Потому, что производная (скорость роста или уменьшения) функции равна самой функции, т.е. скорость увеличения функции равна значению функции.
Если грубо, то в природе, это действительно встречается часто — чем больше клеток делятся, тем быстрее их становиться больше. Чем больше у вас денег в банке, тем большую прибыль они приносят. Например:
Вы вложили 1 000 руб. в банк, через год они принесли свои 100 руб. процентами, еще через год на вас работают уже 2 работника 1 000 руб. и 100 руб. и так далее пока вы не заберете деньги или не случится банковский кризис.
Кстати население на планете Земля тоже растет по экспоненте;)
Принцип Парето и экспонента
Слышали о таком принципе? Думаю да. «20% усилий приносят 80% результата». Это он. Лучшее определение для запоминания, мне кажется:
20% любителей пива употребляют 80% всего пива
На принципе Парето построен и ABC анализ запасов, например.
Этот принцип Парето — еще один пример экспоненты.
Кстати очень справедливый закон в реальной жизни, подтверждаю своим опытом.Когда-то на первом своем проекте я заметил, что примерно за 20% времени ты создаешь 80% продукта (в количественном эквиваленте), далее работаешь на качество. Т.е. еще 80% времени допиливаешь, ищешь ошибки, настраиваешь. Я даже слышал, что говорят «разработка в стадии экспоненты» — т.е. в стадии приближения к идеалу.
При таком «допиливании» проекта важно вовремя остановиться, ведь продукт никогда не будет идеальным. Поэтому заранее определитесь какое качество вы хотели бы получить в конце. Если делаете не себе, обязательно соберите требования с заказчика. Принцип выглядит примерно так:
Экспонента в Excel
Когда по смыслу функции более-менее объяснил, напишу как считать ее и есть ли функция экспонента в Excel. Само собой есть.
В Эксель все посчитать несложно:
или можно число возвести в степень
Дополнение. Как запомнить 15 знаков числа е?
В качестве отвлечения привожу способ, как запомнить число e c точностью до 15 знаков
- запишите 2,7,
- затем дважды год рождения Льва Толстого – 1828,
- затем величины углов равнобедренного прямоугольного треугольника – 45°, 90°, 45°,
- в итоге получается: 2,718281828459045.
Как фанат Льва Николаевича, я не смог забыть этот способ 🙂 Кстати отличная книга о том как запоминать много информации и как работает память здесь .
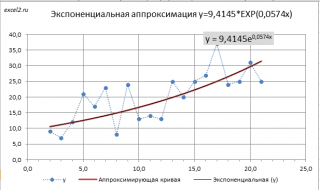
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.
Метод наименьших квадратов (англ. Ordinary Least Squares, OLS) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК — МНК: Метод Наименьших Квадратов в MS EXCEL.
В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:
y=a*m x =a*(e ln(m) ) x = a*e x*ln(m) =a*e bx , где b= ln(m))
В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).
После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента a необходимо выполнить обратное преобразование a= EXP(A) .
Примечание: Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы Линия тренда (Экспоненциальная линия тренда). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью Основы построения диаграмм в MS EXCEL.
Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больших по модулю отрицательных чисел) соответствующее значение y асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы Линия тренда. Если среди значений y есть отрицательные, то с помощью инструмента Линия тренда экспоненциальную линию тренда построить не удастся.
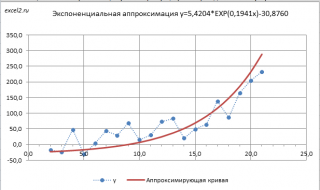
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте х значения y также будут увеличиваться. В качестве с можно взять некую заранее известную нижнюю границу для y, ниже которой у не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см. файл примера лист Экспонента2 ).
Если при росте х значения y уменьшаются по экспоненциальной кривой, т.е. a файл примера лист Экспонента3 ).
Функция РОСТ()
Еще одним способом построить линию экспоненциального тренда является использование функции РОСТ() , английское название GROWTH.
Синтаксис функции следующий:
РОСТ(известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст])
Для работы функции нужно просто ввести ссылки на массив значений переменной Y (аргумент известные_значения_y) и на массив значений переменной Х (аргумент известные_значения_x). Функция рассчитает прогнозные значения Y для Х, указанных в аргументе новые_значения_x. Если требуется, чтобы экспоненциальная кривая y=a*EXP(b*x) имела a=1, т.е. проходила бы через точку (0;1), то необязательный аргумент конст должен быть установлен равным ЛОЖЬ (или 0).
Если среди значений y есть отрицательные, то с помощью функции РОСТ() аппроксимирующую кривую построить не удастся.
Безусловно, использование функции РОСТ() часто удобно, т.к. не требуется делать замену переменных и сводить задачу к линейному случаю.
Наконец, покажем как с помощью функции РОСТ() вычислить коэффициенты уравнения y=a*EXP(b*x).
Примечание: В MS EXCEL имеется специальная функция ЛГРФПРИБЛ() , которая позволяет вычислить коэффициенты уравнения y=a*EXP(b*x). Об этой функции см. ниже.
Чтобы вычислить коэффициент a (значение Y в точке Х=0) используйте формулу =РОСТ(C26:C45;B26:B45;0) . В диапазонах C26:C45 и B26:B45 должны находиться массивы значений переменной Y и X соответственно.
Чтобы вычислить коэффициент b используйте формулу:
= LN(РОСТ(C26:C45;B26:B45;МИН(B26:B45))/
РОСТ(C26:C45;B26:B45;МАКС(B26:B45)))/
(МИН(B26:B45)-МАКС(B26:B45))
Функция ЛГРФПРИБЛ()
Функция ЛГРФПРИБЛ() на основе имеющихся значений переменных Х и Y подбирает методом наименьших квадратов коэффициенты а и m уравнения y=a*m^x.
Используя свойство степеней a mn =(a m ) n приведем уравнение экспоненциального тренда y=a*EXP(b*x)=a*e b *x = a*(e b ) x к виду y=a*m^x, сделав замену переменной m= e b =EXP(b).
Чтобы вычислить коэффициенты уравнения y=a*EXP(b*x) используйте следующие формулы:
= LN(ЛГРФПРИБЛ(C26:C45;B26:B45)) — коэффициент b
= ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2) — коэффициент a
Примечание: Функция ЛГРФПРИБЛ() , английское название LOGEST, является формулой массива, возвращающей несколько значений. Поэтому, например, для вывода коэффициентов уравнения необходимо выделить 2 ячейки в одной строке, в Строке формул ввести = ЛГРФПРИБЛ(C26:C45;B26:B45) , затем для ввода формулы вместо обычного ENTER нажать CTRL+SHIFT+ENTER.
Функция ЛГРФПРИБЛ() имеет линейный аналог – функцию ЛИНЕЙН() , которая рассмотрена в статье про простую линейную регрессию. Если 4-й аргумент этой функции (статистика) установлен ИСТИНА, то ЛГРФПРИБЛ() возвращает регрессионную статистику: стандартные ошибки для оценок коэффициентов регрессии, коэффициент детерминации, суммы квадратов: SSR, SSE и др.
Примечание: Особой нужды в функции ЛГРФПРИБЛ() нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y=a*m^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y=a*EXP(b*x).
Содержание
- 1 Как сделать график в Excel?
- 1.1 Простейший
- 1.2 С несколькими рядами данных
- 2 Как построить график функции в Экселе?
- 3 Как построить график зависимости в Excel?
- 4 Особенности оформления графиков в Excel
- 5 Вопросы от новичков
- 5.1 Какие виды графиков есть в Экселе?
- 5.2 Как добавить линию на существующий график?
- 6 Подводим итоги
Программы-редакторы электронных таблиц упрощают не только сбор и классификацию данных, но и обработку математических выражений; в частности, позволяют без лишних сложностей найти итоговую сумму или рассчитать значение по формуле. Пользователь, уже представляющий, как закрепить строку в Excel при прокрутке, сможет построить любой график. Как это сделать — попробуем разобраться.
Как сделать график в Excel?
Эксель позволяет начертить график или сделать диаграмму в несколько шагов, без предварительной обработки данных и в рамках основного пакета. Не нужно подключать дополнительные модули и устанавливать сторонние плагины — всё, что требуется, чтобы нарисовать зависимость, содержится в «ленте»; главное — правильно пользоваться предлагаемыми функциями.
Важно: работа в MS Excel мало отличается от пользования бесплатными редакторами. Посчитать проценты или создать график в любом из них можно, следуя приведённой далее инструкции — нужно лишь слегка адаптировать её под конкретный программный продукт.
Все приготовления, которые требуется сделать пользователю, заключаются в выяснении задачи и поиске исходных данных; как только всё будет готово, можно запускать Excel и приступать к делу.
Простейший
Самый простой график в Экселе — это зависимость одного ряда значений от другого. Рисовать её предельно просто: достаточно задать параметры и сделать несколько кликов мышью. Вполне естественно, на графике будет отображаться только одна линия; если их больше, необходимо вернуться к началу инструкции и проверить правильность совершённых действий.
Чтобы построить простой график в Excel, нужно:
- Составить таблицу исходных данных. Взаимозависимые значения для большего удобства следует располагать в столбцах с заголовками; чтобы получить на графика не только линию, но и автоматически подписанные оси, нужно выделить мышью не таблицу целиком.
- Перейти на вкладку «Вставка» и, отыскав в разделе «Диаграммы» подраздел «Вставить график», вызвать щелчком мыши выпадающее меню. Представленная рядом с «Диаграммами» функция «Спарклайн-график» для построения простой зависимости не подходит!
- В открывшемся списке выбрать самый первый пункт, так и называемый — «График».
- Построенная системой зависимость полностью соответствует введённым данным, однако не слишком хорошо оформлена; как исправить положение и сделать визуальное представление по-настоящему красивым, будет рассказано в соответствующем разделе нашего материала. Рисунок можно перемещать, копировать, вставить в текстовый документ и удалить, щёлкнув по нему и нажав на клавишу Delete.
- Если требуется построить простой график с точками, следует в том же выпадающем меню выбрать функцию «График с маркерами».
- Теперь, наводя указатель мыши на любую точку, пользователь сможет увидеть во всплывающей подсказке значение Y для отметки на оси X.
Важно: щёлкая по линии графика или оси, юзер увидит, к какому из рядов данных они относятся — будет подсвечен соответствующий столбец исходной таблицы.
С несколькими рядами данных
Можно начертить в Экселе и более сложную зависимость, включающую три, четыре и более рядов данных. В этом случае на простом графике будет столько линий, сколько в таблице столбцов (помимо основного, от которого зависят другие и который представляет собою ось X). Как и в предыдущем случае, график может быть «гладким» или с маркерами — это зависит только от потребностей и фантазии пользователя.
Чтобы нарисовать график с несколькими рядами значений, нужно:
- Подготовить и составить таблицу, как и прежде, размещая данные в подписанных столбцах, после чего выделить её целиком, включая заголовки.
- Перейти на вкладку «Вид» и выбрать в выпадающем меню соответственно функцию «График» или «График с маркерами» — в результате возле таблицы появится зависимость, содержащая уже две линии, для каждого ряда чисел.
- Если зависимые от первого столбца значения однородны (например, доходы от продажи товаров разных категорий), можно воспользоваться функцией «График с накоплением».
- Тогда на итоговом изображении можно будет посмотреть суммарные значения для каждой позиции по оси X.
Важно: применять эту опцию можно только в указанном случае — иначе построенный график будет некорректно отображать взаимозависимость данных.
- При этом на результирующей линии при наведении курсора будет показано значение для последнего ряда, а суммарное, без предварительной настройки, пользователь сможет посмотреть на оси Y.
Как построить график функции в Экселе?
Выше было рассказано, как нарисовать график в Excel, если все взаимозависимые данные уже известны; сделать это не сложнее, чем ускорить работу Windows 10 или разобраться в настройках видеоплеера. Чуть больше работы предстоит пользователю, если требуется построить график функции — придётся предварительно указать, по какой формуле программа должна вычислять значения.
Чтобы сделать простой график функции в Excel, нужно:
- Создать таблицу с заголовками типа X и Y или любыми другими, позволяющими проследить зависимость одного ряда значений от другого. Здесь же можно сразу задать несколько последовательных значений для оси X — самостоятельно или используя автоматическую нумерацию.
- Теперь следует переместиться в самую верхнюю ячейку под заголовком второго столбца, нажать на клавишу «Равно» и ввести нужную формулу. В примере будет построен график параболы, то есть любое значение Y равно соответствующему X, возведённому во вторую степень; для такой простой зависимости достаточно умножить соседнюю ячейку саму на себя, после чего нажать на клавишу Enter.
- В более сложных случаях имеет смысл перейти на вкладку «Формулы» и воспользоваться одной из функций, находящихся в разделе «Математические».
- Построить график параболы, как и любого другого возведения Y в степень от X, можно, выбрав в выпадающем списке функцию «Степень».
- Теперь остаётся указать исходное значение (соседнюю ячейку по оси X), вписать в нижнем текстовом поле требуемую степень и нажать на кнопку «ОК».
- Выделив ячейку с рассчитанным значением и потянув вниз за крестик, расположенный в правом нижнем её углу, пользователь наконец получит исходную таблицу соответствий.
- Чтобы сделать график более «масштабным», можно изменить несколько крайних исходных данных по оси X — значения по Y будут пересчитаны автоматически.
- Пытаясь рисовать график в Excel способом, описанным выше, пользователь столкнётся с неприятным сюрпризом: ось X будет «переползать» сверху вниз, не желая оставаться на одном уровне. Решить проблему можно, выделив для постройки зависимости только значения Y.
- Остальные манипуляции не отличаются от предыдущих: необходимо перейти на вкладку «Вставка» и выбрать в разделе «Диаграммы» функции «График» или «График с маркерами».
- Как можно заметить, линия, соединяющая точки, состоит из отдельных отрезков и для совершенно равномерной параболы смотрится неудовлетворительно. Чтобы придать графику привычный вид, нужно в том же разделе выбрать выпадающее меню «Вставить точечную…диаграмму» и в ней — функцию «Точечная с гладкими кривыми» или «Точечная с гладкими кривыми и маркерами».
- Получившийся график будет ровным, поскольку промежуточные прямые в нём преобразованы в кривые.
- Если заданных значений очень много или предполагается дополнить график пояснениями и рисунками, стоит выбрать в том же выпадающем списке функцию «Точечная» — тогда на графике функции будут отображены только соответствующие маркеры.
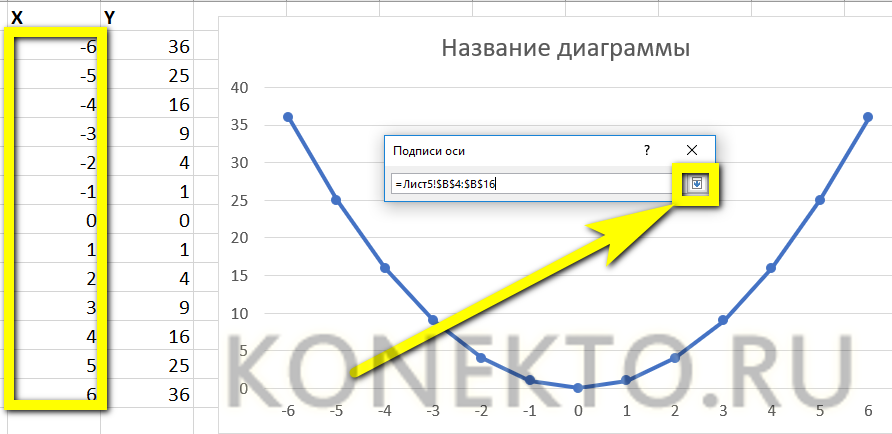
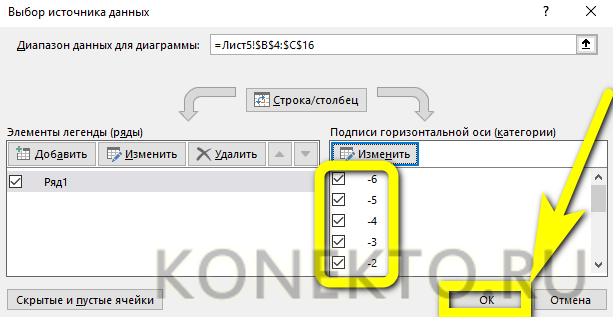
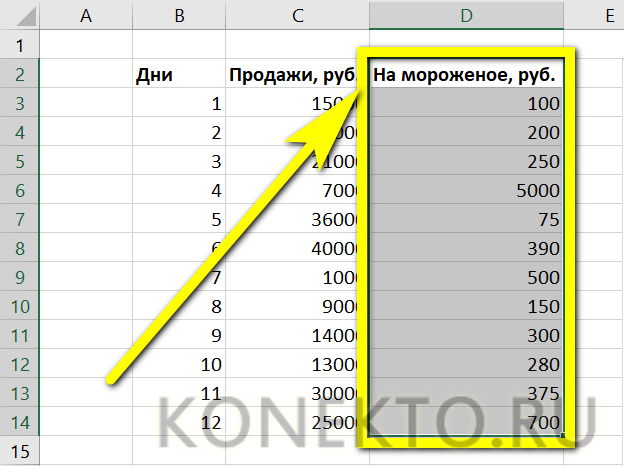
- Несложно заметить, что ось X на изображении подписана неправильно. Исправить это можно, выделив её (именно ось, не весь график) щелчком мыши и вызвав в контекстном меню команду «Выбрать данные».
- В открывшемся окне в графе «Подписи горизонтальной оси» нужно нажать на кнопку «Изменить».
- Теперь — нажать на расположенную в новом окошке обращённую вверх стрелочку.
- Выделив указателем мыши диапазон значений X, которые должны стать подписями для соответствующей оси, и нажав «ОК», пользователь увидит, что график уже претерпел изменения.
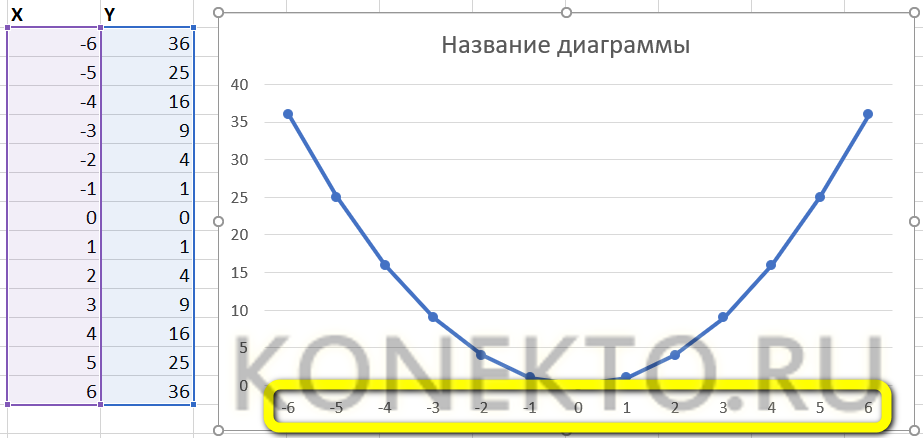
- Далее следует подтвердить правильность действий, снова нажав на кнопку «ОК».
- Посмотреть соответствия графика и осей можно, обратив внимание на выделенные столбцы исходной таблицы. При внесении изменений в ряд X значения Y автоматически пересчитываются, а график принимает новый вид.
Как построить график зависимости в Excel?
График зависимости по сути своей и есть график функции; речь может идти лишь о сложности математического выражения, в остальном порядок создания визуальных представлений остаётся тем же. Чтобы показать, как построить график сложной зависимости нескольких параметров от исходных значений, ниже будет приведён ещё один небольшой пример.
Пусть параметр Y зависит от X в виде y = x3 + 3x – 5; Z — в виде z = x/2 + x2; наконец, зависимость R — выражается в виде набора несистематизированных значений.
Тогда, чтобы построить сводный график зависимости, необходимо:
- Составить в Excel таблицу с заголовками, отображающими суть каждой зависимости. Пусть для примера это будут просто X, Y, Z и R. В этой таблице сразу можно задать значения оси абсцисс (X) и параметра R, не выражаемого известной функцией.
- Ввести в верхней ячейке столбца Y формулу, нажать клавишу Enter и «растянуть» значения на весь диапазон X.
- То же проделать для столбца Z. Как можно убедиться, при изменении любого параметра X будут меняться соответствующие значению Y и Z, в то время как R останется неизменным.
- Выделить три столбца производных от X и построить, как было рассказано раньше, график — гладкий, с маркерами или в виде точек.
- Если одна из функций мешает наблюдать за изменениями остальных, её можно удалить с графика, выделив щелчком мыши и нажав клавишу Delete.
Научившись строить графики в Экселе, пользователь может перейти к следующей важной задаче — попытаться сделать оформление каждой зависимости красивым и рациональным.
Особенности оформления графиков в Excel
Несколько советов по оформлению графиков в Excel:
- Первое, что следует сделать пользователю, — ввести правильно название зависимости. Для этого нужно выделить щелчком мыши блок «Название диаграммы», щёлкнуть по нему ещё раз и ввести требуемое наименование. При необходимости этот блок можно удалить, выделив его и нажав клавишу Delete.
- Если требуется изменить не только название, но и стиль написания, следует, снова выделив блок, вызвать контекстное меню и выбрать в нём раздел «Шрифт». Подобрав подходящий вариант, юзер может нажимать на «ОК» и переходить к дальнейшим действиям.
- Вызвав меню «Формат названия диаграммы», можно определить, в какой части рисунка будет располагаться наименование: в центре, в левом верхнем, нижнем правом углу и так далее.
- Чтобы добавить на график названия осей, следует щёлкнуть мышью по «плюсику» справа от рисунка и в выплывающем списке установить галочку в соответствующем чекбоксе.
- Если изначальное расположение названий не устраивает пользователя, он может свободно перетаскивать их по полю графика, а также менять их наименования описанным ранее способом.
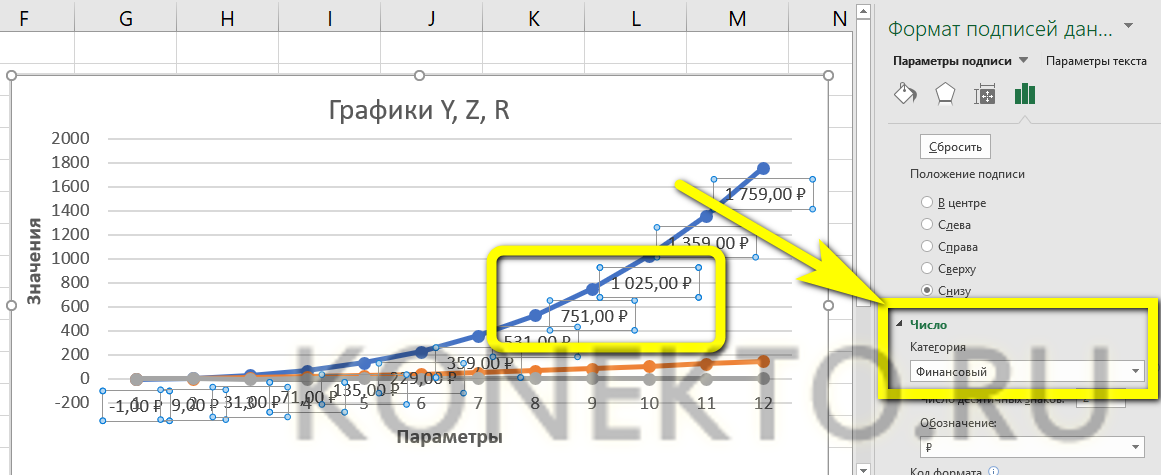
- Чтобы добавить на любую линию графика подписи (размещаются прямо на сетке) или выноски данных (в отдельных окошечках), нужно выделить её щелчком правой клавишей мыши и выбрать соответствующий параметр во вложенном меню «Добавить подписи данных».
- Юзер может свободно сочетать способы размещения подписей, выбирая любой из пунктов в расширенном меню окошка «Элементы диаграммы».
- Выбрав в том же меню «Дополнительные параметры», в боковом меню следует указать категорию представленных данных: простые числа, дроби, проценты, деньги и так далее.
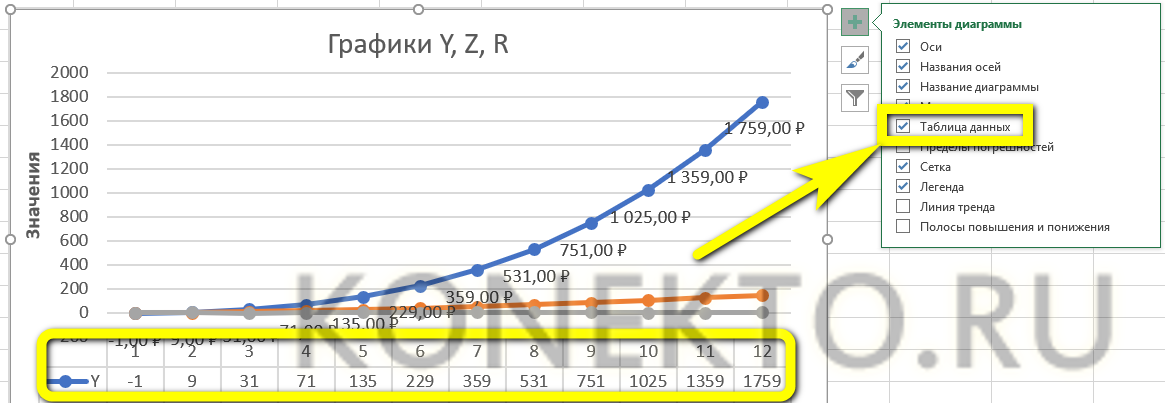
- Чтобы добавить таблицу с данными непосредственно на график, нужно вызвать нажатием на «плюсик» всё те же «Дополнительные параметры» и установить галочку в одноимённом чекбоксе.
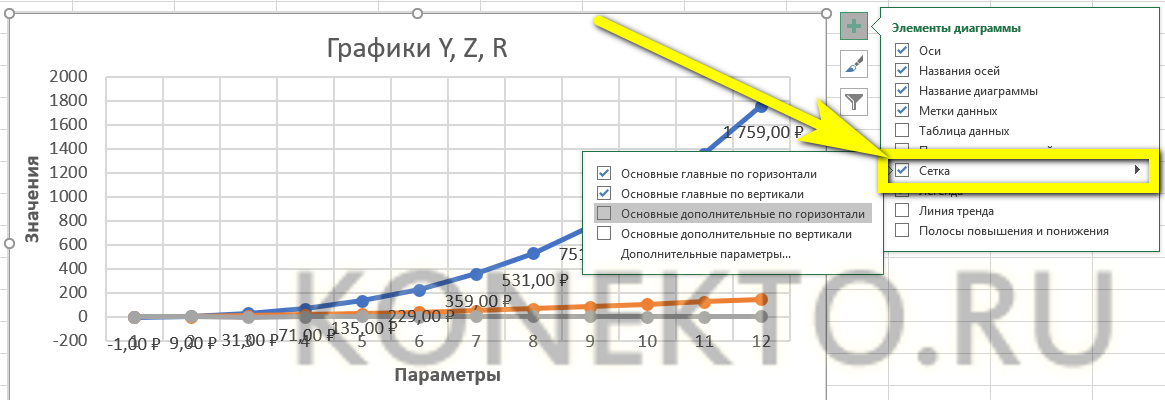
- Сетку, позволяющую найти значения графика в каждой точке, с помощью того же меню можно совсем убрать или добавить на неё основную и вспомогательную разметку.
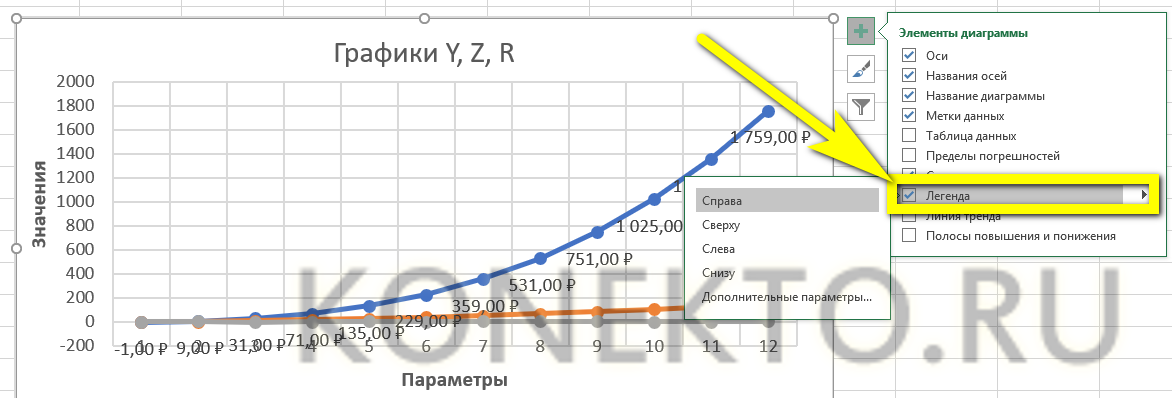
- «Легенда» — не самый полезный, но привычный блок графиков Excel. Убрать или перенести его можно, сняв галочку в окне «Дополнительные параметры» или вызвав вложенное меню. Более простой вариант — выделить блок щелчком мыши и нажать клавишу Delete или перетащить по полю графика.
- Понять общее направление движения графика поможет линия тренда; добавить её для каждого ряда значений можно в том же окне.
- Перейдя на вкладку «Конструктор», пользователь может кардинально изменить вид графика, выбрав один из стандартных шаблонов в разделе «Стили диаграмм».
- А вызвав находящееся там же меню «Изменить цвета» — подобрать палитру для каждой линии в отдельности или для всего графика в целом.
- Меню «Стили» вкладки «Формат» позволяет найти оптимальное представление для текстовых элементов графика.
- Изменить фон, оставив нетронутым тип диаграммы, можно с помощью раздела «Стили фигур».
- На этом настройку графика можно считать оконченной. Пользователь может в любой момент изменить тип диаграммы, перейдя в одноимённое меню и выбрав понравившийся вариант.
Вопросы от новичков
Ниже будут даны ответы на самые часто встречающиеся вопросы по построению графиков в Excel.
Какие виды графиков есть в Экселе?
Самые популярные виды графиков были перечислены ранее; всего их более полутора десятков:
- простой;
- с накоплением;
- нормированный;
- с маркерами;
- с маркерами и накоплением;
- нормированный с маркерами и накоплением;
- объёмный;
- с областями;
- с областями и накоплением;
- нормированный с областями и накоплением;
- объёмный с областями;
- объёмный с областями и накоплением;
- нормированный объёмный с областями и накоплением;
- точечный;
- точечный с гладкими кривыми;
- точечный с гладкими кривыми и маркёрами.
Совет: узнать о назначении каждой разновидности графиков Экселя юзер может, наведя указатель мыши на его пиктограмму и прочитав краткое пояснение.
Как добавить линию на существующий график?
Добавить новую последовательность данных в виде линии на график Excel следующим образом:
- Внести соответствующие правки в исходную таблицу.
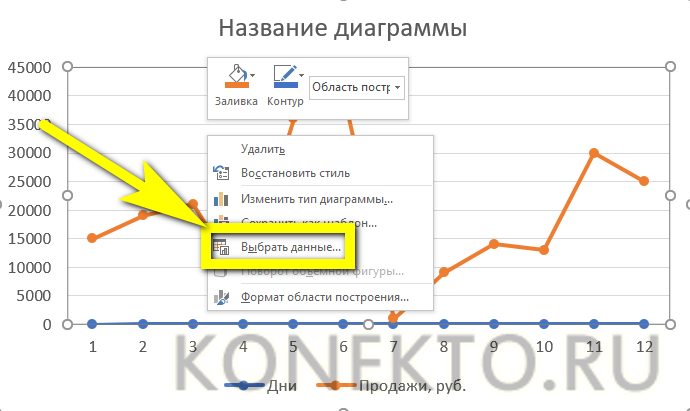
- Кликнуть правой клавишей по полю графика и вызвать в контекстном меню пункт «Выбрать данные».
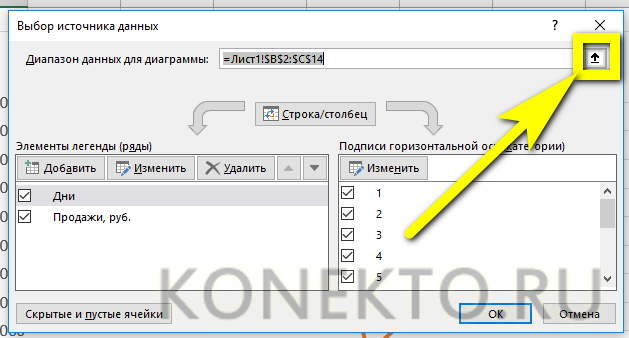
- Нажать на стрелочку возле поля «Диапазон данных для диаграммы».
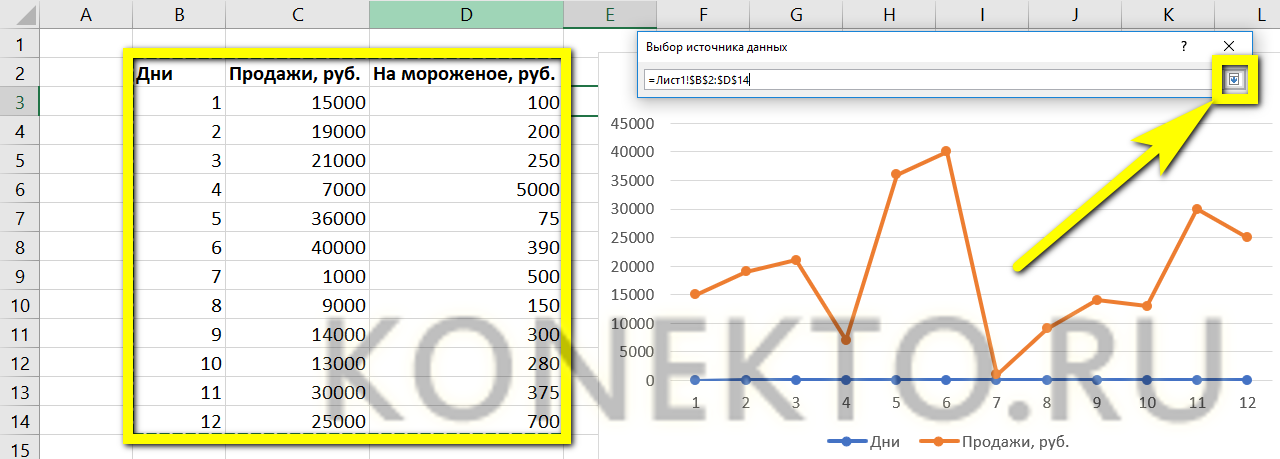
- Выделить мышью всю таблицу целиком, после чего вновь нажать на стрелочку в диалоговом окне.
- На графике появится новая линия; убрать её можно, выделив щелчком мыши и нажав клавишу Delete.
Подводим итоги
Построить график в Excel можно, создав таблицу значений, перейдя на вкладке «Вставка» в раздел «Диаграммы» и выбрав требуемый тип линии. Чтобы визуально представить функцию, необходимо задать её в исходной таблице, используя стандартные операции. Настройка графика осуществляется с помощью меню «Элементы диаграммы», а также на вкладках «Конструктор» и «Формат».
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке [-3;3]. Называем столбец «х», пишем первое значение «-3», второе – «-2,5». Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х», в другом – рассчитаны значения для заданной функции.
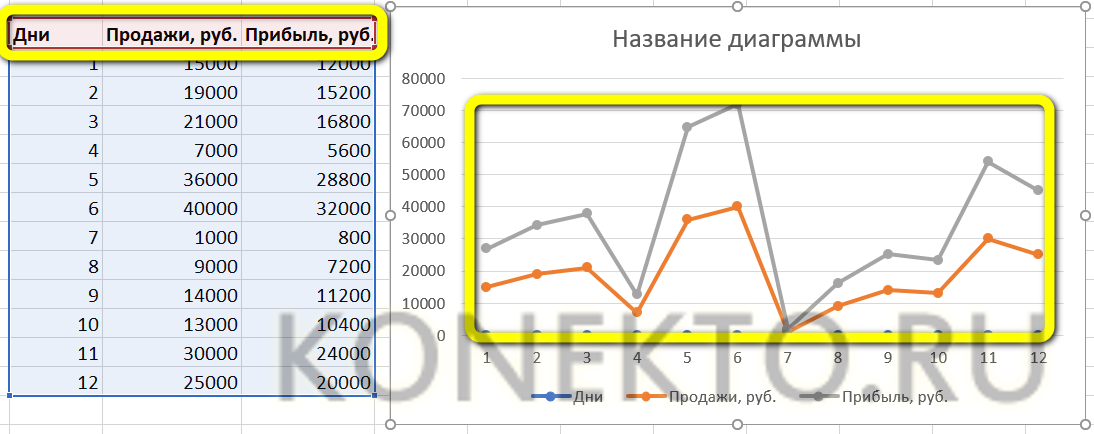
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у», переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная». Выберите одну из предложенных видов.
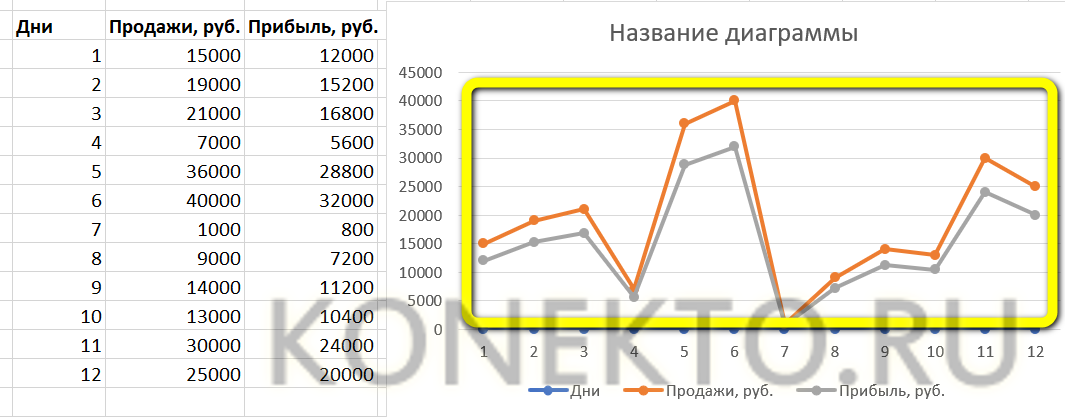
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси».
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений», поставьте маркер в пункте «фиксированное» и впишите значение «0,5».
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор», «Макет», «Формат».
Построить график функции в Эксель можно и с помощью «Графика». О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х».
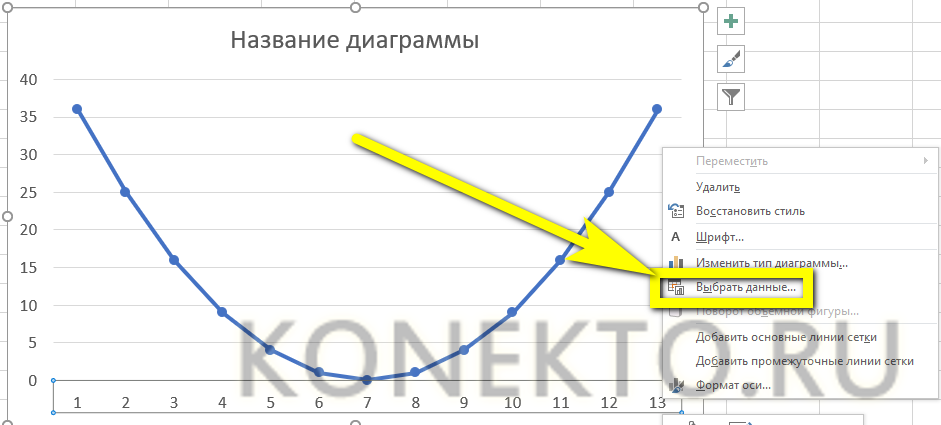
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные».
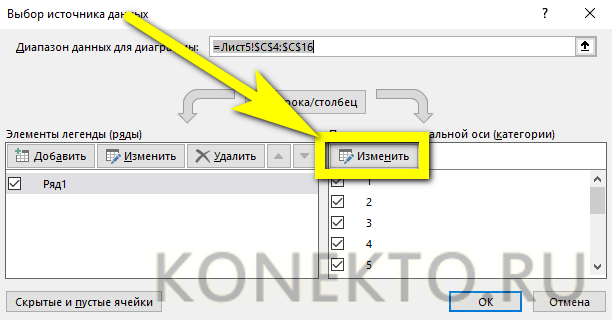
В поле «Элементы легенды» кликаем на кнопочку «Добавить».
Появится окно «Изменение ряда». Поставьте курсор в поле «Имя ряда» и выделите ячейку С1. Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК».
Чтобы для первого графика в Легенде не было написано «Ряд 1», выделите его и нажмите на кнопку «Изменить».
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК».
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1, подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1».
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Загрузка…
Об авторе: Олег Каминский
Вебмастер. Высшее образование по специальности «Защита информации». Создатель портала comp-profi.com. Автор большинства статей и уроков компьютерной грамотности