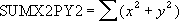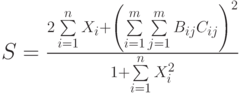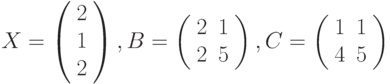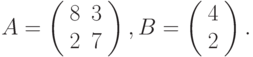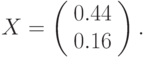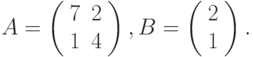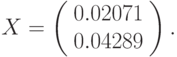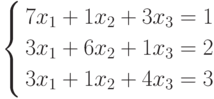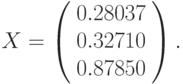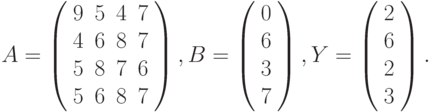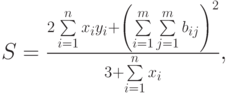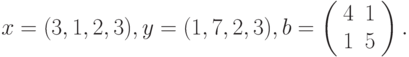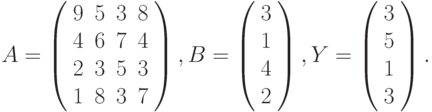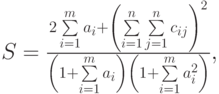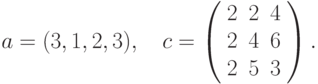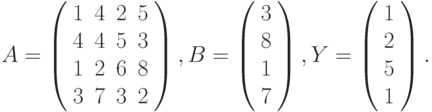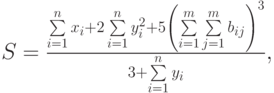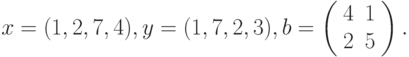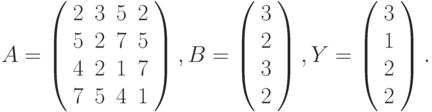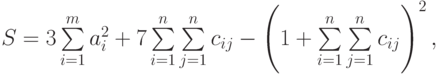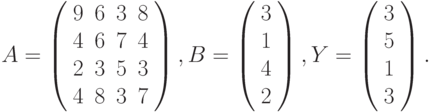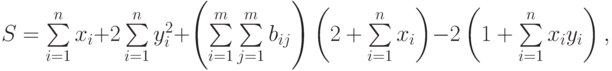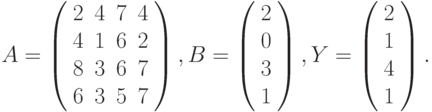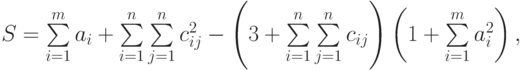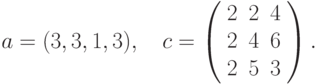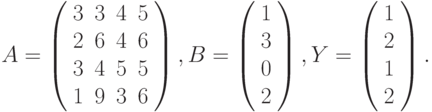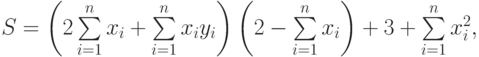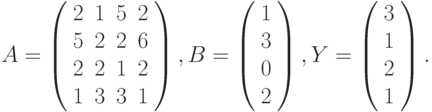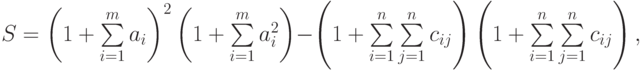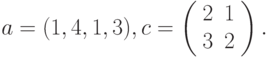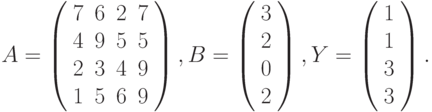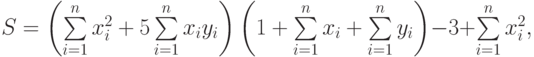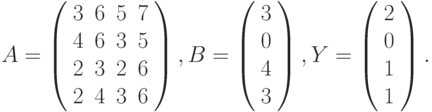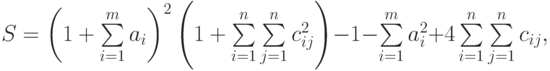Excel сумма двух массивов

Терминология

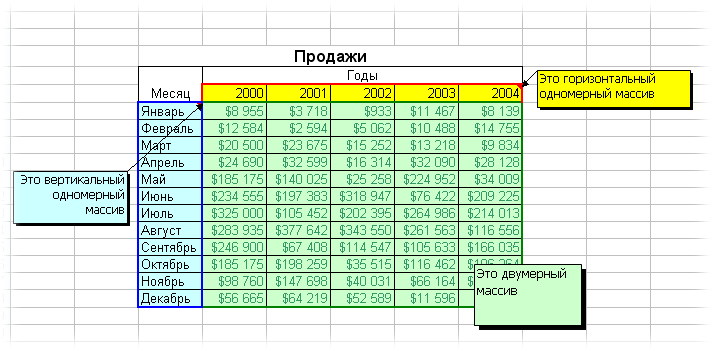
Под массивом обычно понимают набор данных, объединенных в группу. Массивы бывают одномерные (элементы массива образуют строку или столбец) или двумерные (матрица). Легко сообразить, что почти в любой таблице Excel при желании можно найти один или несколько таких массивов:

Формулы массива в Excel — это специальные формулы для обработки данных из таких массивов. Формулы массива делятся на две категории — те, что возвращают одно значение и те, что дают на выходе целый набор (массив) значений. Рассмотрим их на простых примерах…

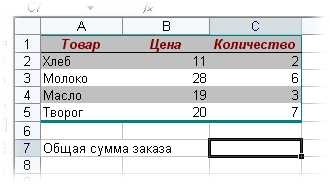
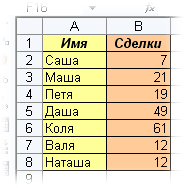
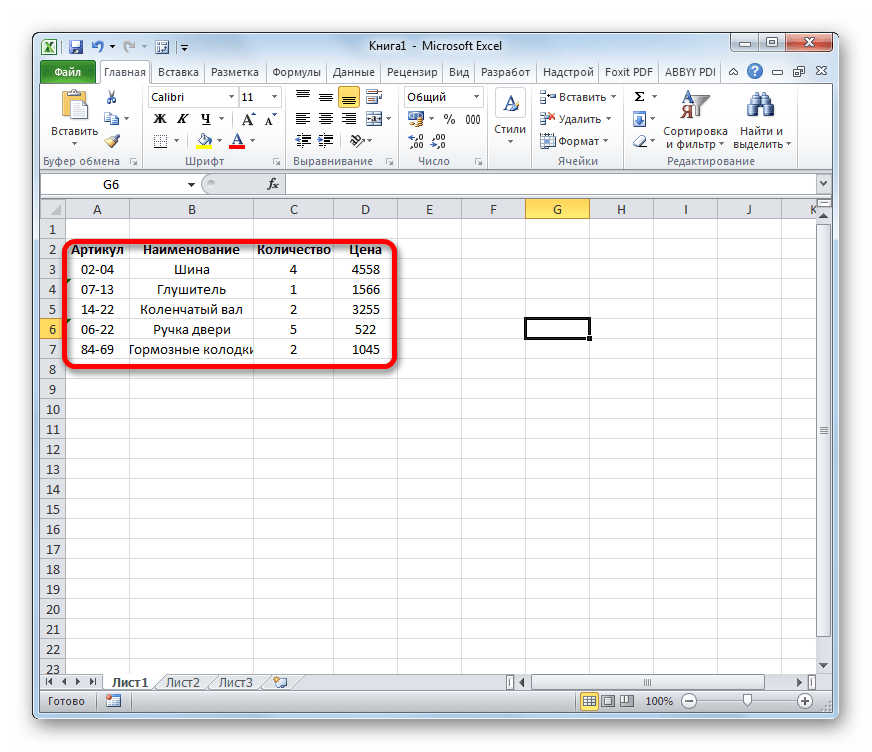
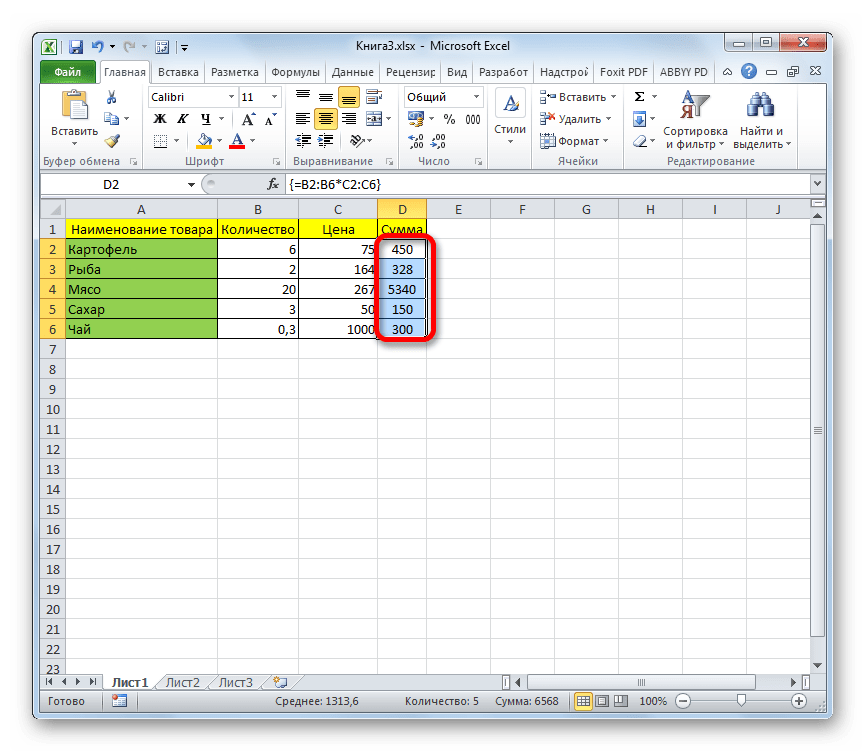
Пример 1. Классика жанра — товарный чек

Задача: рассчитать общую сумму заказа. Если идти классическим путем, то нужно будет добавить столбец, где перемножить цену и количество, а потом взять сумму по этому столбцу. Если же применить формулу массива, то все будет гораздо красивее:

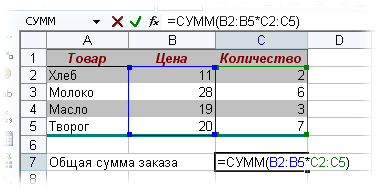
выделяем ячейку С7
вводим с клавиатуры =СУММ(
выделяем диапазон B2:B5
вводим знак умножения (звездочка)
выделяем диапазон C2:C5 и закрываем скобку функции СУММ — в итоге должно получиться так:
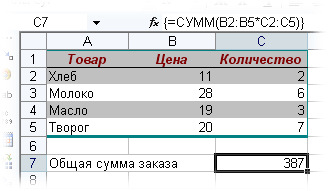
чтобы Excel воспринял нашу формулу как формулу массива жмем не Enter, как обычно, а Ctrl + Shift + Enter

Вуаля!

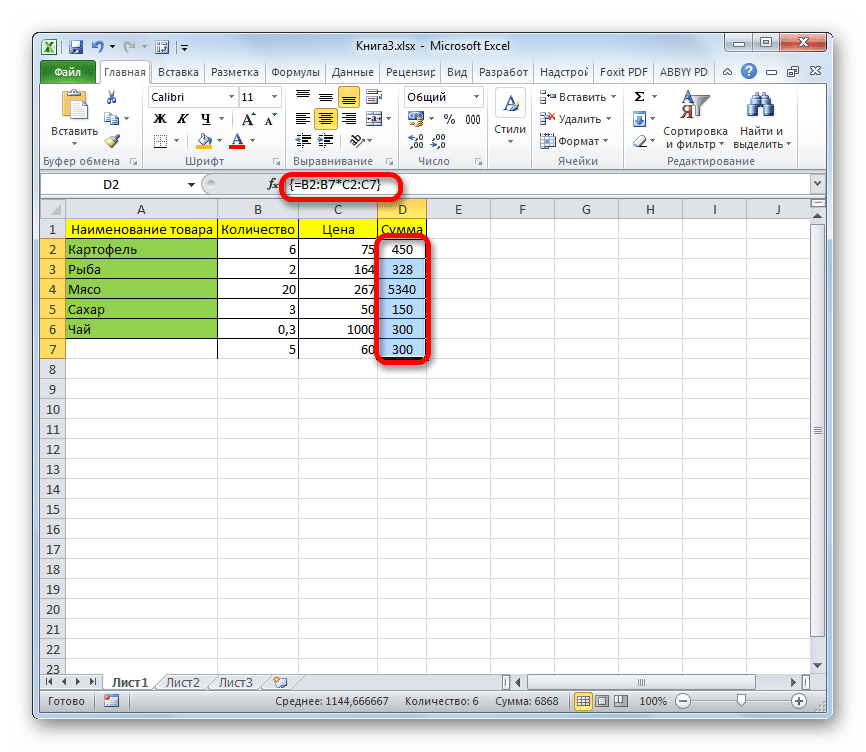
Т.е. Excel произвел попарное умножение элементов массивов B2:B5 и C2:C5 и образовал новый массив стоимостей (в памяти компьютера), а затем сложил все элементы этого нового массива.

Обратите внимание на фигурные скобки, появившиеся в формуле — отличительный признак формулы массива. Вводить их вручную с клавиатуры бесполезно — они автоматически появляются при нажатии Ctrl + Shift + Enter.

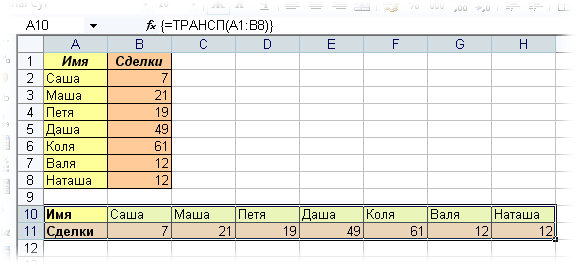
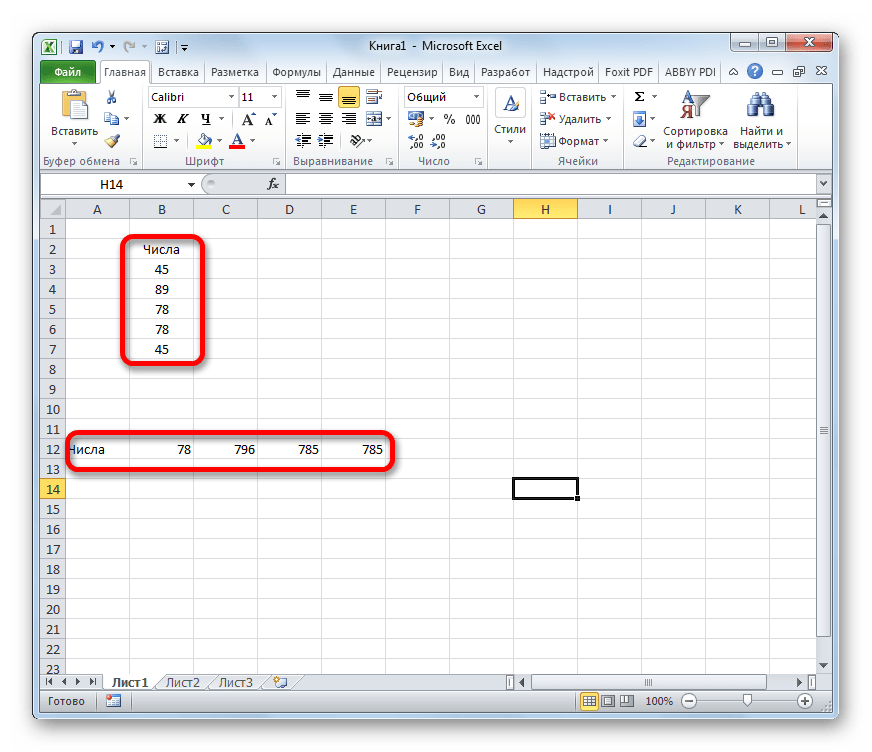
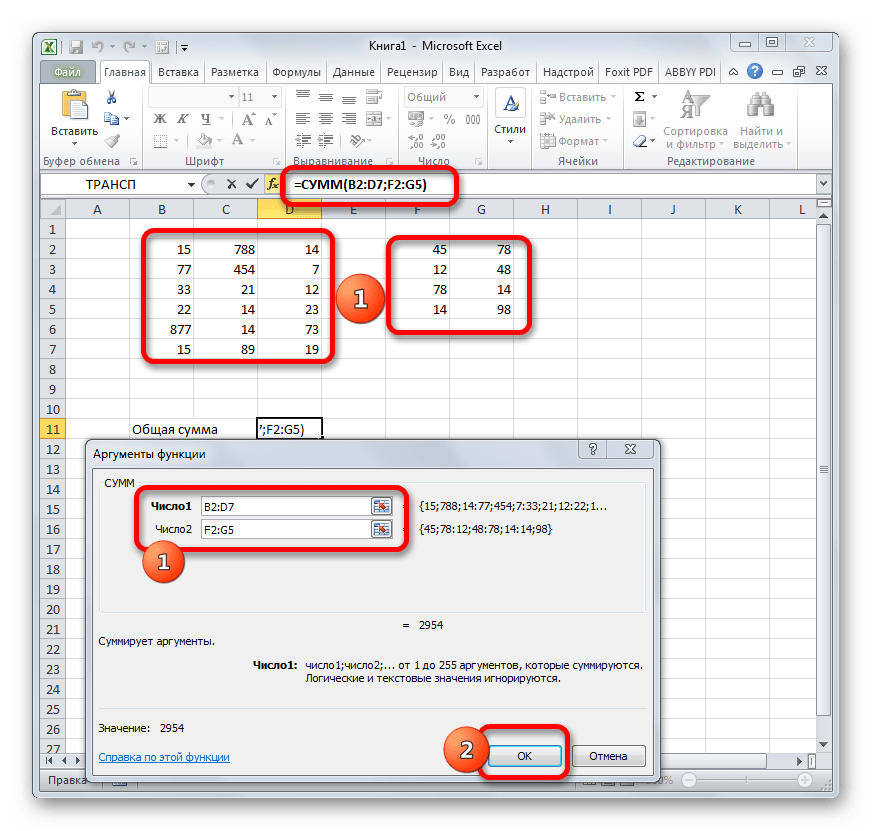
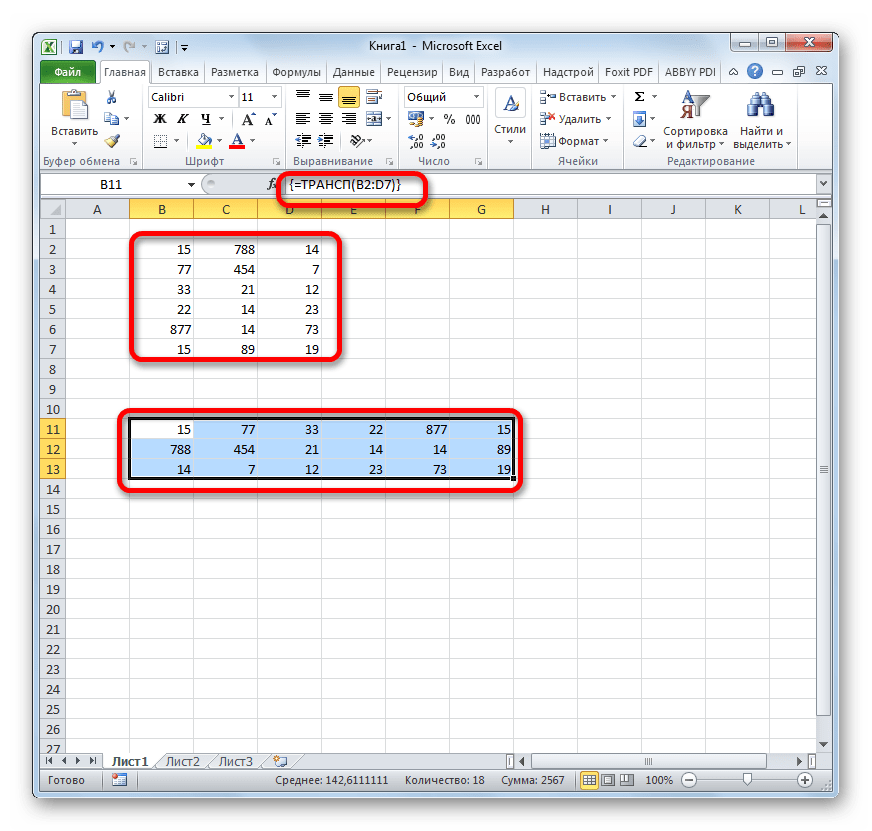
Пример 2. Разрешите Вас… транспонировать?

При работе с таблицами часто возникает необходимость поменять местами строки и столбцы, т.е. развернуть таблицу на бок, чтобы данные, которые раньше шли по строке, теперь располагались в столбцах и наоборот. В математике такая операция называется транспонированием. При помощи формулы массива и функции ТРАНСП (TRANSPOSE) это делается на раз.

Допустим, имеем двумерный массив ячеек, который хотим транспонировать.

Выделяем диапазон ячеек для размещения транспонированной таблицы. Поскольку исходный массив ячеек был 8 строк на 2 столбца, то надо выделить диапазон пустых ячеек размером 2 строки на 8 столбцов.
вводим функцию транспонирования =ТРАНСП(
в качестве аргумента функции выделяем наш массив ячеек A1:B8

жмем Ctrl + Shift + Enter и получаем «перевернутый массив» в качестве результата:

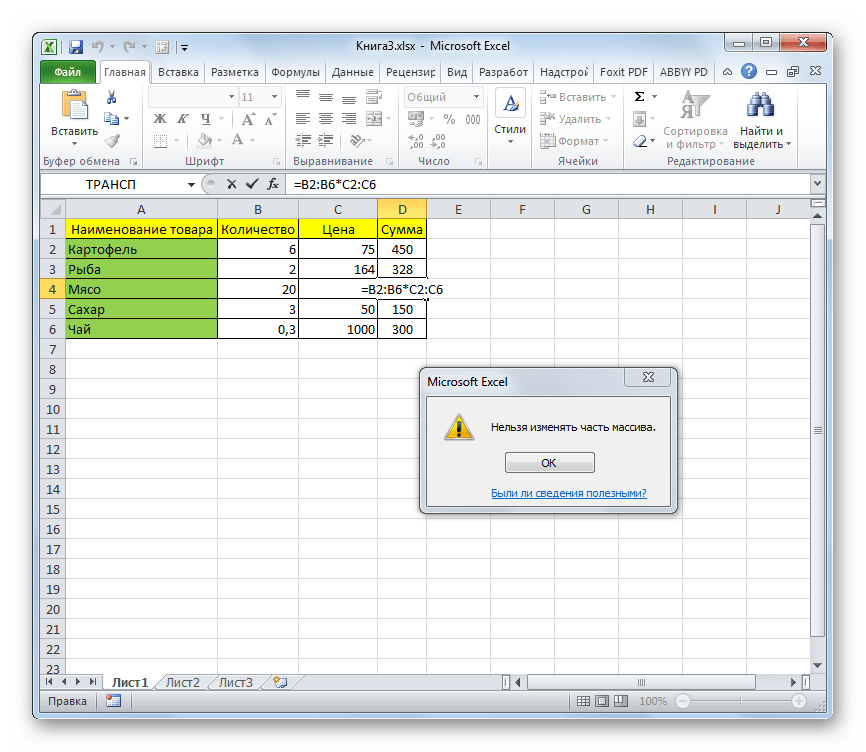
Редактирование формулы массива

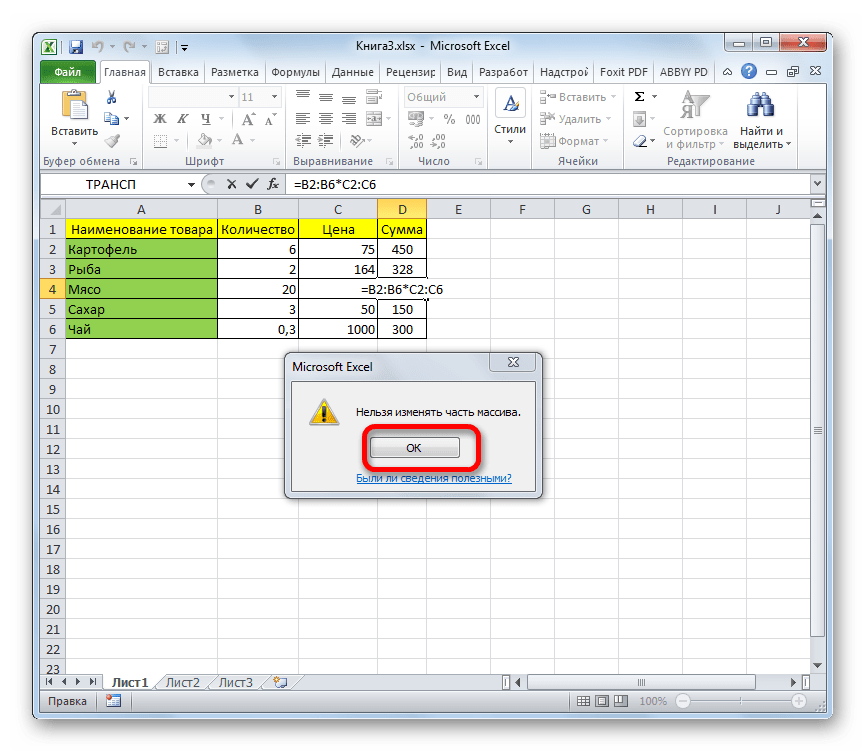
Если формула массива расположена не в одной ячейке (как в Примере 1), а в нескольких ячейках (как в Примере 2), то Excel не позволит редактировать или удалить одну отдельно взятую формулу (например в ячейке D10) и выдаст предупреждающее сообщение Невозможно изменить часть массива.

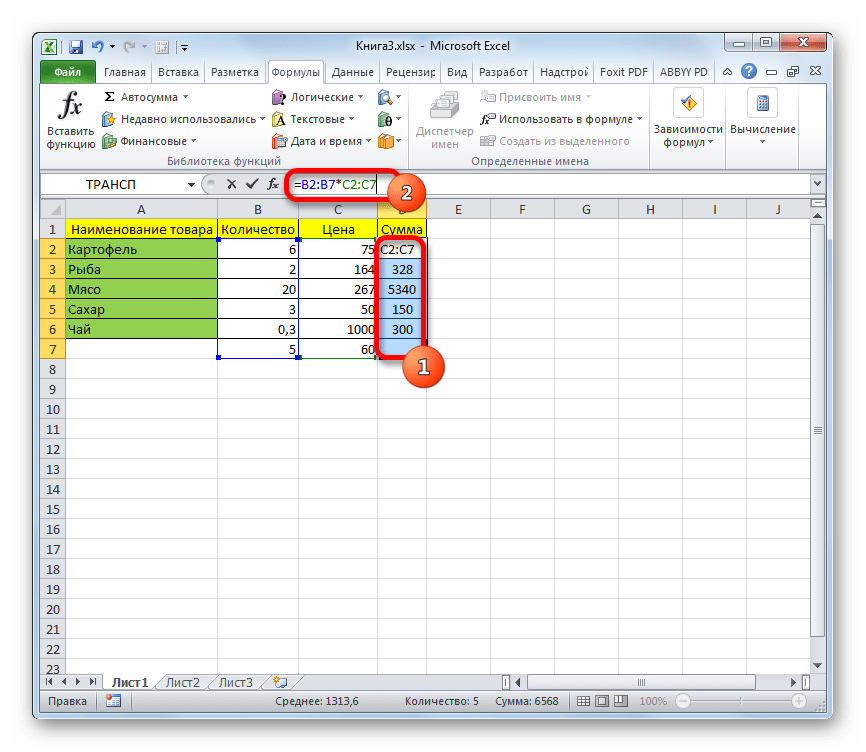
Для редактирования формулы массива необходимо выделить весь диапазон (A10:H11 в нашем случае) и изменить формулу в строке формул (или нажав F2). Затем необходимо повторить ввод измененной формулы массива, нажав сочетание клавиш Ctrl + Shift + Enter.

Excel также не позволит свободно перемещать ячейки, входящие в формулу массива или добавлять новые строки-столбцы-ячейки в диапазон формулы массива (т.е. в диапазон A10:H11 в нашем случае)

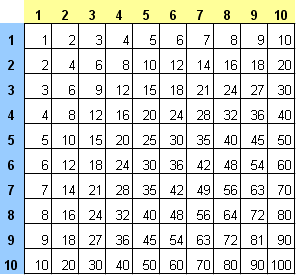
Пример 3. Таблица умножения

Вспомните детство, школу, свою тетрадку по математике… На обороте тетради на обложке было что? Таблица умножения вот такого вида:

При помощи формул массива она вся делается в одно движение:

выделяем диапазон B2:K11
вводим формулу =A2:A11*B1:K1
жмем Ctrl + Shift + Enter, чтобы Excel воспринял ее как формулу массива

и получаем результат:

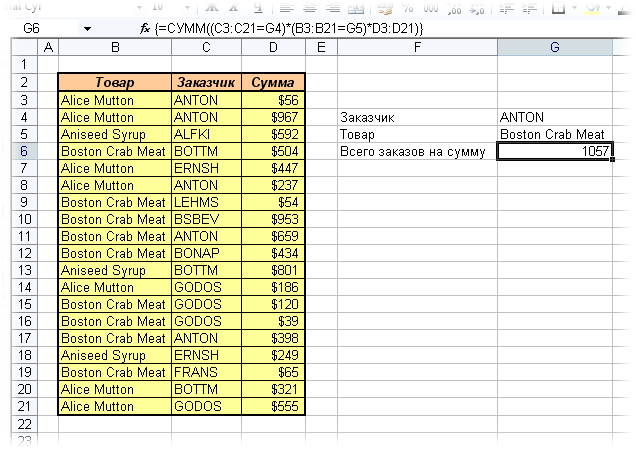
Пример 4. Выборочное суммирование

Посмотрите как при помощи одной формулы массива красиво и легко выбираются данные по определенному товару и заказчику:

В данном случае формула массива синхронно пробегает по всем элементам диапазонов C3:C21 и B3:B21, проверяя, совпадают ли они с заданными значениями из ячеек G4 и G5. Если совпадения нет, то результат равенства ноль, если совпадение есть, то единица. Таким образом суммы всех сделок, где заказчик не ANTON и товар не Boston Crab Meat умножаются на ноль и суммируются только нужные заказы.

Ссылки по теме

Формула массива для извлечения непустых ячеек из диапазона
Формула массива для извлечения уникальных ячеек из диапазона
Формула массива для извлечения данных из списка (многоразовый ВПР)

Источник

Содержание

Excel сумма двух массивов
SUMIF несколько столбцов с одним или несколькими критериями
Сумма Excel Если: несколько столбцов, один критерий
SUMIF несколько столбцов
СУММ как формула массива
формула СУММПРОИЗВ
Сумма Excel, если: несколько столбцов, несколько критериев
СУММЕСЛИМН + СУММЕСЛИМН для суммирования нескольких столбцов
Формула массива для условного суммирования нескольких столбцов
Формула СУММПРОИЗВ с несколькими критериями
Управление массивами в Microsoft Excel
Операции с массивами
Создание формулы
Изменение содержимого массива
Функции массивов
Оператор СУММ
Оператор ТРАНСП
Оператор МОБР

Добрый день. Есть два и более массивов состоящих всегда из двух столбцов и разного количества строк.
Необходимо создать итоговый массив в котором в первом столбце будут уникальные значения из первого столбца массивов, во втором столбце сумма из вторых столбцов массивов при совпадении значения.
То есть первая формула выводит уникальные имена из первых столбцов массивов в итоговый массив. Вторая формула при должна перебрать имена в первых столбцах массивов, при нахождении совпадений суммировать вторые столбцы напротив этих имен и сумму вывести напротив имени в итоговом массиве. Если имя уникально (не повторяется ни в одном массиве) то вывести значение напротив него. Файл «сумма массивов».

Если это невозможно то:
исходные массивы можно ручками объединить в один массив состоящий из двух столбцов. В первом столбце могут быть как уникальные так и повторяющиеся имена.
Вывод уникальных значений из первого столбца я сделал.
Нужна формула суммирования значений второго столбца при совпадении имен в первом столбце исходного и итогового массивов. Файл «сумма массива».

Сообщение Добрый день. Есть два и более массивов состоящих всегда из двух столбцов и разного количества строк.
Необходимо создать итоговый массив в котором в первом столбце будут уникальные значения из первого столбца массивов, во втором столбце сумма из вторых столбцов массивов при совпадении значения.
То есть первая формула выводит уникальные имена из первых столбцов массивов в итоговый массив. Вторая формула при должна перебрать имена в первых столбцах массивов, при нахождении совпадений суммировать вторые столбцы напротив этих имен и сумму вывести напротив имени в итоговом массиве. Если имя уникально (не повторяется ни в одном массиве) то вывести значение напротив него. Файл «сумма массивов».

Источник

SUMIF несколько столбцов с одним или несколькими критериями

Этот учебник научит вас нескольким простым способам суммирования нескольких столбцов в Excel на основе одного или нескольких критериев.

Выполнение условной суммы в Excel не составляет труда, если все значения, которые нужно суммировать, находятся в одном столбце. Суммирование нескольких столбцов представляет собой проблему, поскольку обе функции СУММЕСЛИ и СУММЕСЛИМН требуют, чтобы диапазон суммы и диапазон критериев были одинакового размера. К счастью, когда нет прямого способа что-то сделать, всегда есть обходной путь 🙂

Сумма Excel Если: несколько столбцов, один критерий

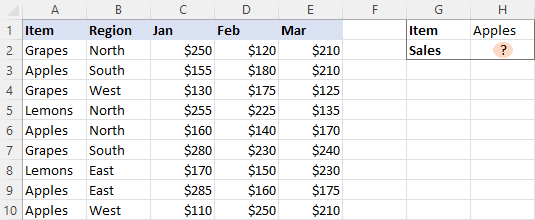
Прежде всего, давайте узнаем, какую именно проблему мы пытаемся решить. Предположим, у вас есть таблица ежемесячных продаж, как показано ниже. Поскольку он был объединен из нескольких региональных отчетов, для одного и того же продукта есть несколько записей:

Вопрос в том, как получить общий объем продаж определенного товара?

Первая идея, которая приходит на ум, — использовать формулу СУММЕСЛИ в чистом виде:

=СУММЕСЛИ(A2:A10, «яблоки», C2:E10)

К сожалению, это не сработает. Причина в том, что размеры сумма_диапазон определяются Excel автоматически на основе размеров диапазон аргумент. Поскольку диапазон наших критериев включает только один столбец (A2:A10), то же самое относится и к диапазону суммы (C2:C10). сумма_диапазон параметр, определенный в формуле (C2:E10), фактически определяет только верхнюю левую ячейку диапазона, который будет суммироваться. В результате приведенная выше формула суммирует продажи яблок только в столбце C. Не то, что мы ищем, а?

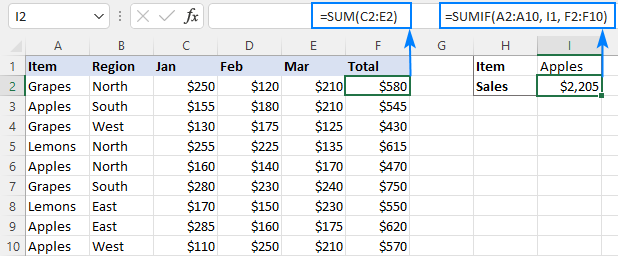
Самое простое рабочее решение, которое напрашивается само собой, — создать вспомогательный столбец, суммирующий числа для каждой отдельной строки, а затем использовать этот столбец для сумма_диапазон.

Итак, продолжайте и поместите формулу СУММ в F2, затем перетащите ее вниз на столько ячеек, сколько необходимо:

После этого можно быстро выполнить работу:

=СУММЕСЛИ(A2:A10, I1, F2:F10)

Где I1 представляет интерес.

В приведенной выше формуле сумма_диапазон имеет такой же размер, как диапазон (1 столбец и 9 строк), поэтому работает без сучка и задоринки:

Если в макете вашего рабочего листа нет места для дополнительных столбцов, примените одно из следующих решений.

SUMIF несколько столбцов

Идея состоит в том, чтобы написать отдельную формулу СУММЕСЛИ для каждого из столбцов, которые вы хотите суммировать, а затем сложить результаты:

СУММ(СУММЕСЛИ(…), СУММЕСЛИ(…), СУММЕСЛИ(…))

СУММЕСЛИ(…) + СУММЕСЛИ(…) + СУММЕСЛИ(…)

Практическая реализация выглядит следующим образом:

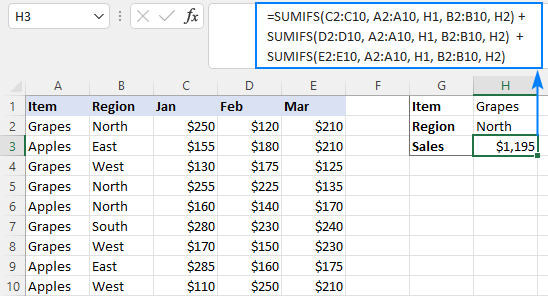
=СУММ(СУММЕСЛИ(A2:A10,H1,C2:C10), СУММЕСЛИ(A2:A10,H1,D2:D10), СУММЕСЛИ(A2:A10,H1,E2:E10))

=СУММЕСЛИ(A2:A10, H1, C2:C10) + СУММЕСЛИ(A2:A10, H1, D2:D10) + СУММЕСЛИ(A2:A10, H1, E2:E10)

Вы также можете «жестко закодировать» условие в формуле, если это необходимо:

=СУММЕСЛИ(A2:A10, «Яблоки», C2:C10) + СУММЕСЛИ(A2:A10, «Яблоки», D2:D10) + СУММЕСЛИСЛИ(A2:A10, «Яблоки», E2:E10)

Это прекрасно работает для разумного количества столбцов, но для большого набора данных формула становится слишком длинной и трудной для чтения. В этом случае нижеприведенные решения являются более подходящими.

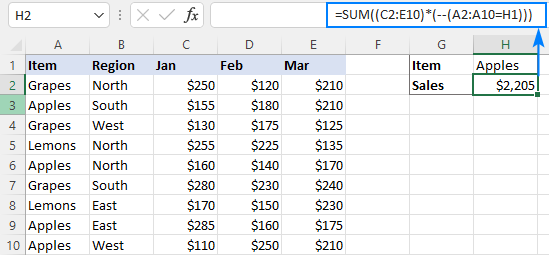
СУММ как формула массива

Другой способ сделать сумму, если в нескольких столбцах на основе одного критерия, состоит в том, чтобы построить формулу массива:

СУММА((сумма_диапазон) * (—(критерии_диапазонзнак равнокритерии)))

Для нашего примера набора данных формула принимает следующий вид:

В Excel 2019 и более ранних версиях вы должны нажать Ctrl + Shift + Enter, чтобы правильно завершить формулу. В Excel 365 и Excel 2021 это работает как обычная формула благодаря встроенной поддержке динамических массивов.

Как работает эта формула:

Основная концепция состоит в том, чтобы умножить элементы этих двух массивов:

(C2:E10) — все значения в диапазоне суммы. В нашем случае массив содержит 27 элементов (3 столбца и 9 строк:
(—(A2:A10=H1)) — сравнивает каждое значение в A2:A10 с целевым элементом в H1. Результатом является массив значений TRUE (условие выполнено) и FALSE (условие не выполнено), который затем преобразуется в массив из 1 и 0 с помощью двойного унарного оператора:

Обратите внимание, что первый массив двумерный (каждый столбец данных разделен запятой, а каждая строка — точкой с запятой), а второй — одномерный вертикальный массив (1 столбец данных, строки разделены точкой с запятой). ). Когда два массива умножаются, все элементы двумерного массива в данной строке умножаются на соответствующий элемент одномерного массива:

Поскольку умножение на ноль дает ноль, выживают только числа, для которых критерий ИСТИНА, и функция СУММ складывает их:

Чтобы упростить понимание логики формулы, вы можете написать первый множитель следующим образом:

=СУММ((C2:C10 + D2:D10 + E2:E10) * (—(A2:A10=H1)))

Это создаст массив сумм по строкам (как вспомогательный столбец в самом первом примере), который затем умножается на массив из 1 и 0:

Результат умножения подается в SUM:

Не нравится использовать формулы массивов на листе? Я тоже. Что ж, давайте проверим следующее решение 🙂

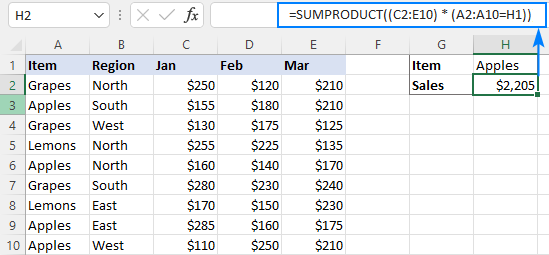
формула СУММПРОИЗВ

Стратегию, описанную в приведенном выше примере, также можно реализовать с помощью функции СУММПРОИЗВ.

СУММПРОИЗВ((сумма_диапазон) * (критерии_диапазонзнак равнокритерии))

Реальная формула выглядит следующим образом:

Логика формулы такая же, как и в предыдущем примере. Прелесть функции СУММПРОИЗВ заключается в том, что она изначально поддерживает массивы, поэтому она прекрасно работает как обычная формула во всех версиях Excel.

Сумма Excel, если: несколько столбцов, несколько критериев

Три подхода, которые мы использовали для сложения нескольких столбцов с одним критерием, также будут работать для условной суммы с несколькими критериями. Формулы просто станут немного сложнее.

СУММЕСЛИМН + СУММЕСЛИМН для суммирования нескольких столбцов

Для суммирования ячеек, соответствующих нескольким критериям, обычно используется функция СУММЕСЛИМН. Проблема в том, что, как и его аналог с одним критерием, СУММЕСЛИМН не поддерживает диапазон суммы из нескольких столбцов. Чтобы преодолеть это, мы пишем несколько СУММЕСЛИМН, по одному на каждый столбец в диапазоне сумм:

СУММ(СУММЕСЛИМН(…), СУММИММН(…), СУММИММН(…))

СУММЕСЛИМН(…) + СУММЕСЛИМН(…) + СУММЕСЛИМН(…)

Например, для суммирования продаж винограда (H1) в Северном регионе (H2) используется следующая формула:

=СУММЕСЛИМН(C2:C10, A2:A10, H1, B2:B10, H2) + СУММЕСЛИМН(D2:D10, A2:A10, H1, B2:B10, H2) + СУММЕСЛИМН(E2:E10, A2:A10, H1) , В2:В10, Н2)

Формула массива для условного суммирования нескольких столбцов

Формула СУММ для нескольких критериев очень похожа на формулу для одного критерия — вы просто включаете дополнительные пары критерии_диапазон=критерий:

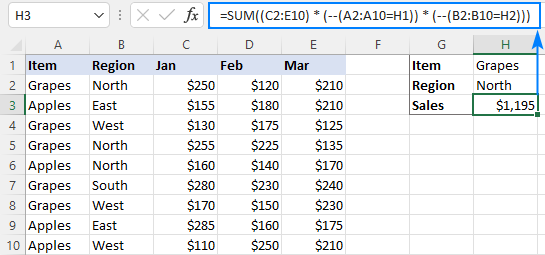
СУММА((сумма_диапазон) * (—(критерии_диапазон1знак равнокритерии1)) * (—(критерии_диапазон2знак равнокритерии2)))

Например, чтобы суммировать продажи товара в H1 и региона в H2, формула выглядит следующим образом:

=СУММ((C2:E10) * (—(A2:A10=H1)) * (—(B2:B10=H2)))

В Excel 2019 и более ранних версиях не забудьте нажать Ctrl + Shift + Enter, чтобы сделать формулу массива CSE. В динамических массивах Excel 365 и 2021 обычная формула будет работать нормально, как показано на снимке экрана:

Формула СУММПРОИЗВ с несколькими критериями

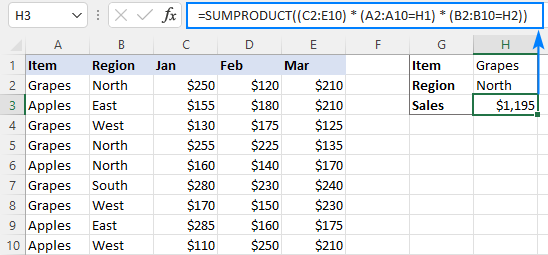
Самый простой способ суммировать несколько столбцов на основе нескольких критериев — это формула СУММПРОИЗВ:

СУММПРОИЗВ((сумма_диапазон) * (критерии_диапазон1знак равнокритерии1) * (критерии_диапазон2знак равнокритерии2))

Как видите, она очень похожа на формулу СУММ, но не требует дополнительных манипуляций с массивами.

Для суммирования нескольких столбцов с двумя критериями используется следующая формула:

=СУММПРОИЗВ((C2:E10) * (A2:A10=H1) * (B2:B10=H2))

Это 3 способа суммирования нескольких столбцов на основе одного или нескольких условий в Excel. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!

Источник

Управление массивами в Microsoft Excel

Во время работы с таблицами Excel довольно часто приходится оперировать с целыми диапазонами данных. При этом некоторые задачи подразумевают, что вся группа ячеек должна быть преобразована буквально в один клик. В Экселе имеются инструменты, которые позволяют проводить подобные операции. Давайте выясним, как можно управлять массивами данных в этой программе.

Операции с массивами

Массив – это группа данных, которая расположена на листе в смежных ячейках. По большому счету, любую таблицу можно считать массивом, но не каждый из них является таблицей, так как он может являться просто диапазоном. По своей сущности такие области могут быть одномерными или двумерными (матрицы). В первом случае все данные располагаются только в одном столбце или строке.

Во втором — в нескольких одновременно.

Кроме того, среди одномерных массивов выделяют горизонтальный и вертикальный тип, в зависимости от того, что они собой представляют – строку или столбец.

Нужно отметить, что алгоритм работы с подобными диапазонами несколько отличается от более привычных операций с одиночными ячейками, хотя и общего между ними тоже много. Давайте рассмотрим нюансы подобных операций.

Создание формулы

Формула массива – это выражение, с помощью которого производится обработка диапазона с целью получения итогового результата, отображаемого цельным массивом или в одной ячейке. Например, для того, чтобы умножить один диапазон на второй применяют формулу по следующему шаблону:

Над диапазонами данных можно также выполнять операции сложения, вычитания, деления и другие арифметические действия.

Координаты массива имеют вид адресов первой её ячейки и последней, разделенные двоеточием. Если диапазон двумерный, то первая и последняя ячейки расположены по диагонали друг от друга. Например, адрес одномерного массива может быть таким: A2:A7.

А пример адреса двумерного диапазона выглядит следующим образом: A2:D7.

Изменение содержимого массива

Если вы в дальнейшем попытаетесь удалить содержимое или изменить любую из ячеек, которая расположена в диапазоне, куда выводится результат, то ваше действие окончится неудачей. Также ничего не выйдет, если вы сделаете попытку отредактировать данные в строке функций. При этом появится информационное сообщение, в котором будет говориться, что нельзя изменять часть массива. Данное сообщение появится даже в том случае, если у вас не было цели производить какие-либо изменения, а вы просто случайно дважды щелкнули мышью по ячейке диапазона.

Если вы закроете, это сообщение, нажав на кнопку «OK», а потом попытаетесь переместить курсор с помощью мышки, или просто нажмете кнопку «Enter», то информационное сообщение появится опять. Не получится также закрыть окно программы или сохранить документ. Все время будет появляться это назойливое сообщение, которое блокирует любые действия. А выход из ситуации есть и он довольно прост

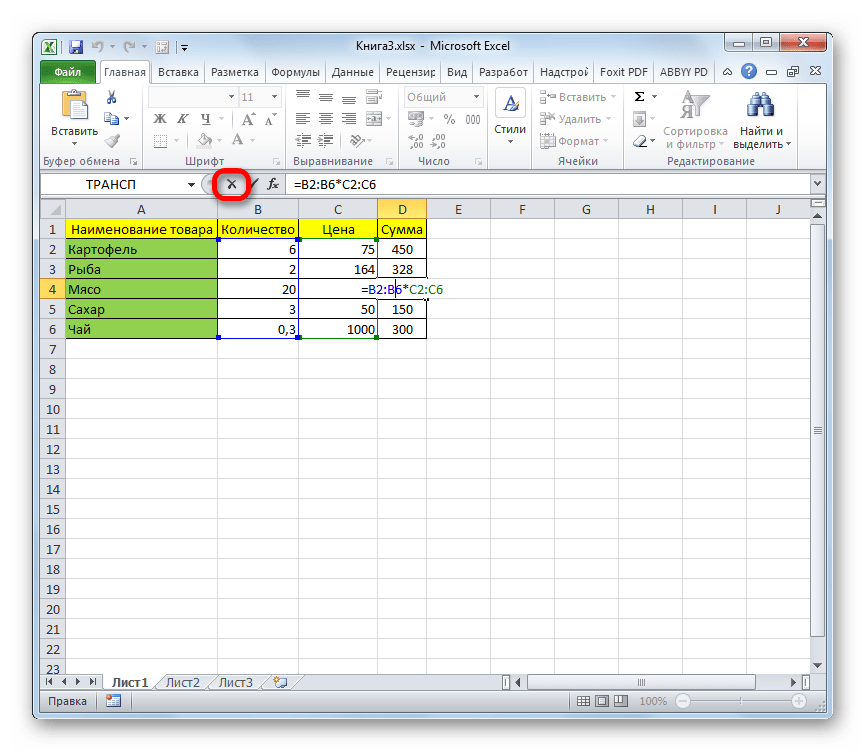
Закройте информационное окно, нажав на кнопку «OK».
Затем нажмете на кнопку «Отмена», которая расположена в группе значков слева от строки формул, и представляет собой пиктограмму в виде крестика. Также можно нажать на кнопку Esc на клавиатуре. После любой из этих операций произойдет отмена действия, и вы сможете работать с листом так, как и прежде.

Но что делать, если действительно нужно удалить или изменить формулу массива? В этом случае следует выполнить нижеуказанные действия.

Для изменения формулы выделите курсором, зажав левую кнопку мыши, весь диапазон на листе, куда выводится результат. Это очень важно, так как если вы выделите только одну ячейку массива, то ничего не получится. Затем в строке формул проведите необходимую корректировку.
После того, как изменения внесены, набираем комбинацию Ctrl+Shift+Esc. Формула будет изменена.

Для удаления формулы массива нужно точно так же, как и в предыдущем случае, выделить курсором весь диапазон ячеек, в котором она находится. Затем нажать на кнопку Delete на клавиатуре.
После этого формула будет удалена со всей области. Теперь в неё можно будет вводить любые данные.

Функции массивов

Наиболее удобно в качестве формул использовать уже готовые встроенные функции Excel. Доступ к ним можно получить через Мастер функций, нажав кнопку «Вставить функцию» слева от строки формул. Или же во вкладке «Формулы» на ленте можно выбрать одну из категорий, в которой находится интересующий вас оператор.

После того, как пользователь в Мастере функций или на ленте инструментов выберет наименование конкретного оператора, откроется окно аргументов функции, куда можно вводить исходные данные для расчета.

Правила ввода и редактирования функций, если они выводят результат сразу в несколько ячеек, те же самые, что и для обычных формул массива. То есть, после ввода значения обязательно нужно установить курсор в строку формул и набрать сочетание клавиш Ctrl+Shift+Enter.

Оператор СУММ

Одной из наиболее востребованных функций в Экселе является СУММ. Её можно применять, как для суммирования содержимого отдельных ячеек, так и для нахождения суммы целых массивов. Синтаксис этого оператора для массивов выглядит следующим образом:

Данный оператор выводит результат в одну ячейку, а поэтому для того, чтобы произвести подсчет, после внесения вводных данных достаточно нажать кнопку «OK» в окне аргументов функции или клавишу Enter, если ввод выполнялся вручную.

Оператор ТРАНСП

Функция ТРАНСП является типичным оператором массивов. Она позволяет переворачивать таблицы или матрицы, то есть, менять строки и столбцы местами. При этом она использует исключительно вывод результата в диапазон ячеек, поэтому после введения данного оператора обязательно нужно применять сочетание Ctrl+Shift+Enter. Также нужно отметить, что перед введением самого выражения нужно выделить на листе область, у которой количество ячеек в столбце будет равно числу ячеек в строке исходной таблицы (матрицы) и, наоборот, количество ячеек в строке должно равняться их числу в столбце исходника. Синтаксис оператора следующий:

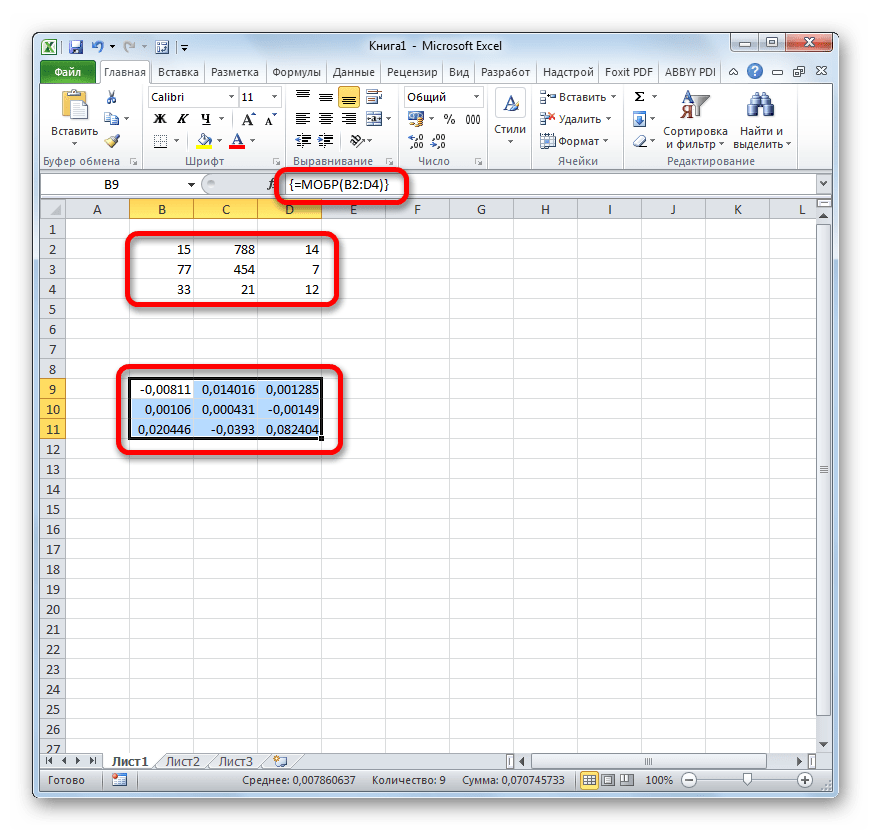
Оператор МОБР

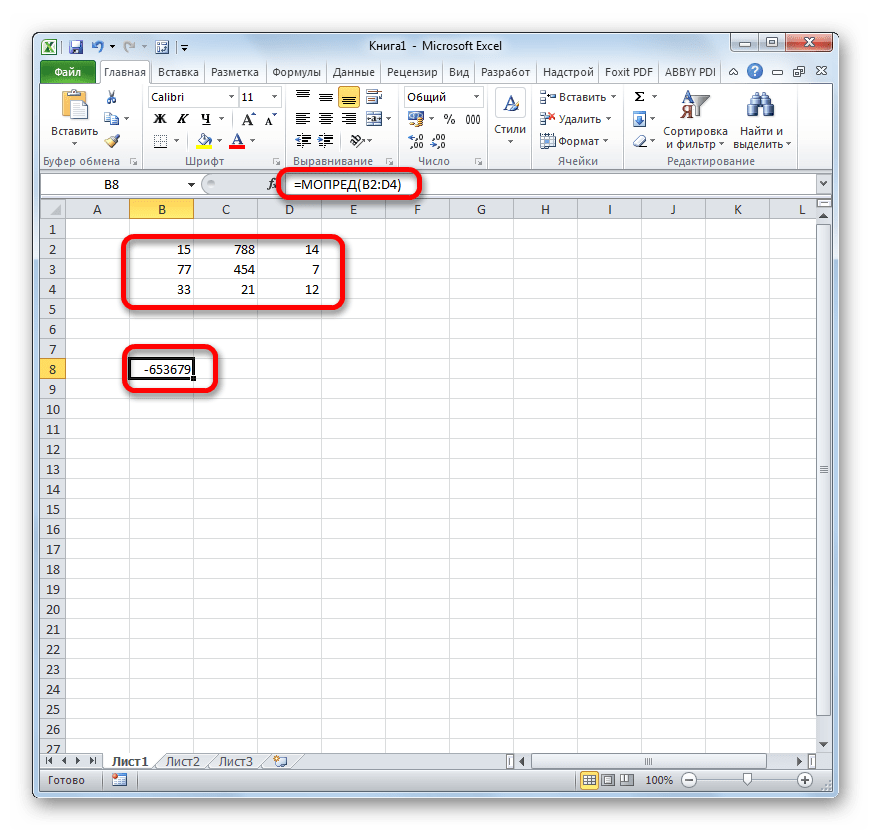
Функция МОБР позволяет производить вычисление обратной матрицы. Все правила ввода значений у этого оператора точно такие же, как и у предыдущего. Но важно знать, что вычисление обратной матрицы возможно исключительно в том случае, если она содержит равное количество строк и столбцов, и если её определитель не равен нулю. Если применять данную функцию к области с разным количеством строк и столбцов, то вместо корректного результата на выходе отобразится значение «#ЗНАЧ!». Синтаксис у этой формулы такой:

Для того чтобы рассчитать определитель, применяется функция со следующим синтаксисом:

Как видим, операции с диапазонами помогают сэкономить время при вычислениях, а также свободное пространство листа, ведь не нужно дополнительно суммировать данные, которые объединены в диапазон, для последующей работы с ними. Все это выполняется «на лету». А для преобразования таблиц и матриц только функции массивов и подходят, так как обычные формулы не в силах справиться с подобными задачами. Но в то же время нужно учесть, что к подобным выражениям применяются дополнительные правила ввода и редактирования.

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции СУММСУММКВ в Microsoft Excel.

Описание

Возвращает сумму сумм квадратов соответствующих элементов двух массивов. Сумма сумм квадратов — это распространенный термин во многих статистических вычислениях.

Синтаксис

СУММСУММКВ(массив_x;массив_y)

Аргументы функции СУММСУММКВ описаны ниже.

Массив_x Обязательный. Первый массив или диапазон значений.
Массив_y Обязательный. Второй массив или диапазон значений.

Замечания

Аргументы могут быть числами либо содержащими числа именами, массивами или ссылками.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
Если количество значений в аргументах «массив_x» и «массив_y» не совпадает, то функция СУММСУММКВ возвращает значение ошибки #Н/Д.
Уравнение для суммы сумм квадратов имеет следующий вид:

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
Первый массив	Второй массив
2	6
3	5
9	11
1	7
8	5
7	4
5	4
Формула	Описание (результат)	Результат
=СУММСУММКВ(A3:A9;B3:B9)	Сумма сумм квадратов двух приведенных выше массивов (521)	521
=СУММСУММКВ({2;3;9;1;8;7;5}; {6;5;11;7;5;4;4})	Сумма сумм квадратов двух констант массива (521)	521

Нужна дополнительная помощь?

Источник

Функция СУММПРОИЗВ с примерами формул

В статье объясняются основные и расширенные способы использования функции СУММПРОИЗВ в Excel. Вы найдете ряд примеров формул для сравнения массивов, условного суммирования и подсчета ячеек по нескольким условиям, расчета средневзвешенного значения и многое другое.

Когда вы впервые слышите название СУММПРОИЗВ, оно может звучать как какая-то бесполезная формула, выполняющая обычную операцию суммы произведений. Но это определение не показывает даже крошечной части того, на что способна функция Excel СУММПРОИЗВ (на английском – SUMPRODUCT).

На самом деле, СУММПРОИЗВ — это удивительно универсальная функция со множеством применений. Благодаря своей уникальной способности разумно и элегантно обрабатывать массивы, Она чрезвычайно полезна, если не незаменима, когда речь идет о сравнении данных в двух или более диапазонах и подсчёте данных с несколькими условиями. Следующие примеры раскроют всю мощь этой функции.

Функция СУММПРОИЗВ в Excel — синтаксис и использование
Логика работы СУММПРОИЗВ в Excel
Как работает СУММПРОИЗВ с несколькими условиями
Как работает формула СУММПРОИЗВ с одним условием
Как пересчитать, суммировать или найти среднее по нескольким условиям
1. Формула с логикой И
2. Формула с логикой ИЛИ
3. Формула с логикой И и ИЛИ
Формула СУММПРОИЗВ для средневзвешенного значения
СУММПРОИЗВ как альтернатива формулам массива
Excel СУММПРОИЗВ — примеры расширенных формул

Функция СУММПРОИЗВ в Excel — синтаксис и использование

Технически функция СУММПРОИЗВ в Excel перемножает числа в указанных диапазонах и возвращает сумму этих произведений.

Синтаксис функции СУММПРОИЗВ прост и понятен:

СУММПРОИЗВ(массив1; [массив2]; [массив3]; …)

Где массив1, массив2 и т. д. — это непрерывные диапазоны ячеек или массивов чисел, элементы которых вы хотите перемножить, а затем сложить.

Минимальное количество массивов равно 1. В этом случае формула СУММПРОИЗВ просто складывает все элементы и возвращает их сумму.

Максимальное количество массивов — 255 в Excel 365-2007 и 30 в более ранних версиях Excel.

Хотя СУММПРОИЗВ работает с массивами, она не требует использования формулы массива Ctrl + Shift + Enter. Вы вводите формулу обычным способом, нажимая клавишу Enter.

Примечания:

Все массивы в формуле СУММПРОИЗВ должны иметь одинаковое количество строк и столбцов, иначе вы получите ошибку #ЗНАЧ!.
Если какой-либо аргумент массива содержит нечисловые значения, они будут рассматриваться как нули.
Если массив является логическим тестом, он дает значения ИСТИНА и ЛОЖЬ. В большинстве случаев вам нужно преобразовать их в 1 и 0 с помощью двойного отрицания (—).
СУММПРОИЗВ не поддерживает подстановочные знаки * и ?.

Логика работы СУММПРОИЗВ в Excel

Чтобы получить общее представление о том, как работает функция СУММПРОИЗВ в Excel, рассмотрим следующий пример.

Предположим, у вас есть количество товаров в ячейках A2:A4, их цены в ячейках B2:B4, и вы хотите узнать их общую стоимость. Если бы вы делали школьный тест по математике, вы бы умножали количество на цену каждого предмета, а затем складывали промежуточные итоги. В Microsoft Excel вы можете получить сумму произведений с помощью одной формулы:

=СУММПРОИЗВ(B2:B5;C2:C5)

Следующий скриншот показывает ее в действии:

Вот что происходит «под капотом» с точки зрения математики:

Формула берет 1-е число из 1-го массива (цену) и умножает его на 1-е число из 2-го массива (количество), затем берет 2-е число из 1-го массива и умножает его на 2 е число из 2-го массива, и так далее.
Когда все элементы перемножаются, формула суммирует произведения и возвращает итоговую сумму.

Другими словами, наша формула СУММПРОИЗВ выполняет следующие математические операции:

=С2*B2 + С3*B3 + С4*B4 + С5*B5

Как использовать СУММПРОИЗВ в Excel с условиями – примеры формул

Только подумайте, сколько времени вы могли бы сэкономить, если бы ваша таблица содержала не 4 строки данных, а сотни или тысячи строк!

Перемножение соответствующих значений двух или более диапазонов, а затем нахождение суммы этих произведений — это самое простое и наиболее очевидное использование СУММПРОИЗВ в Excel, хотя далеко не единственное. Главное достоинство этой функции заключается в том, что она может делать гораздо больше, чем ее обычные заявленные возможности.

Далее в этом руководстве вы найдете несколько примеров формул, демонстрирующих более продвинутые и интересные способы использования, так что, пожалуйста, продолжайте читать.

Сумма произведений с несколькими условиями

Обычно в Microsoft Excel есть несколько способов выполнить одну и ту же задачу. Но когда дело доходит до сравнения двух или более массивов, особенно по нескольким условиям, СУММПРОИЗВ является наиболее эффективным, если не единственным решением. Ну, либо СУММПРОИЗВ, либо формула массива.

Предположим, что у вас есть список товаров в столбце A, запланированные данные о продажах в столбце B и фактические продажи в столбце C. Ваша цель — выяснить, сколько товаров из всего ассортимента продано меньше, чем планировалось. Для этого можно использовать один из следующих вариантов формулы СУММПРОИЗВ:

=СУММПРОИЗВ(—(C2:C10<B2:B10))

или

=СУММПРОИЗВ((C2:C10<B2:B10)*1)

Где C2:C10 — реальные продажи, а B2:B10 — запланированные продажи.

Но что, если у вас несколько условий? Допустим, вы хотите посчитать, сколько раз яблоки продавались хуже, чем планировалось. Решение состоит в том, чтобы добавить еще один критерий в формулу:

=СУММПРОИЗВ((C2:C10<B2:B10)*(A2:A10=»яблоки»))

Или вы можете использовать следующий синтаксис:

=СУММПРОИЗВ(—(C2:C10<B2:B10);—(A2:A10=»яблоки»))

А теперь давайте уделим минутку и разберёмся, что на самом деле делают приведенные выше формулы. Я считаю, что это достойное вложение времени, потому что многие другие формулы СУММПРОИЗВ работают с той же логикой.

Как работает формула СУММПРОИЗВ с одним условием

Для начала давайте разберем более простой случай. Нужно сравнить числа в двух столбцах построчно и сообщить, сколько раз числа колонки C меньше, чем B (то есть, план продаж не выполнен):

=СУММПРОИЗВ(—(C2:C10<B2:B10))

Если вы выделите часть (C2:C10<B2:B10) в строке формул и нажмете F9, чтобы просмотреть вычисленные значения, вы увидите следующую картину:

=СУММПРОИЗВ(—({ЛОЖЬ:ИСТИНА:ЛОЖЬ:ЛОЖЬ:ИСТИНА:ЛОЖЬ:ИСТИНА:ЛОЖЬ:ЛОЖЬ}))

Здесь мы имеем массив логических значений ИСТИНА и ЛОЖЬ, где ИСТИНА означает, что указанное условие выполнено (т. е. значение в столбце С меньше значения в колонке В в той же строке), а ЛОЖЬ указывает, что условие не выполнено.

Двойное отрицание (—) преобразует логические значения ИСТИНА и ЛОЖЬ в единицы и нули: {0:1:0:0:1:0:1:0:0}.

Другой способ преобразовать логические значения в числа — умножить массив на 1:

=СУММПРОИЗВ((C2:C10<B2:B10)*1)

В любом случае, поскольку в данном случае в формуле СУММПРОИЗВ использован только один массив, она просто складывает единицы в результирующем массиве, и мы получаем желаемое количество. Несложно, не так ли?

Как работает формула СУММПРОИЗВ с несколькими условиями

Когда формула СУММПРОИЗВ Excel содержит два или более массивов, она перемножает соответствующие элементы всех массивов, а затем находит сумму этих произведений.

Как вы помните, мы использовали следующие формулы, чтобы узнать, во сколько раз количество реальных продаж (столбец C) было меньше запланированных продаж (столбец B) яблок (столбец A):

=СУММПРОИЗВ((C2:C10<B2:B10)*(A2:A10=»яблоки»))

или:

=СУММПРОИЗВ(—(C2:C10<B2:B10);—(A2:A10=»яблоки»))

Единственное техническое различие между этими формулами заключается в способе преобразования ИСТИНА и ЛОЖЬ в 1 и 0 с помощью двойного отрицания или операции умножения. В результате получаем два массива единиц и нулей:

=СУММПРОИЗВ({0:1:0:0:1:0:1:0:0};{1:1:0:0:0:0:0:0:0})

Операция умножения, выполняемая СУММПРОИЗВ, объединяет эти числа в один массив. А поскольку умножение на ноль всегда дает 0, а 1 появляется только при выполнении обоих условий, то, следовательно, учитываются только строки, в которых выполнены оба условия:

Как пересчитать, суммировать или найти среднее по нескольким условиям

В Excel 2003 и более ранних версиях, в которых ещё не было функций ЕСЛИ с условиями, одним из наиболее распространенных применений функции СУММПРОИЗВ было условное суммирование или подсчет ячеек с несколькими критериями. Начиная с Excel 2007, Microsoft представила серию функций, специально разработанных для таких задач, — СУММЕСЛИМН, СЧЁТЕСЛИМН и СРЗНАЧЕСЛИ.

Но даже в современных версиях Excel формула СУММПРОИЗВ может быть достойной альтернативой, например, для условного суммирования и подсчета ячеек с логикой ИЛИ. Ниже вы найдете несколько примеров формул, демонстрирующих эту способность в действии.

Формула СУММПРОИЗВ с логикой И

Предположим, у вас есть следующий набор данных, где в столбце A перечислены регионы, в столбце B — товары, а в столбце C — данные о продажах:

Вам нужно получить количество, сумму и среднее значение продаж яблок в северном регионе.

В последних версиях Excel 2016, 2013, 2010 и 2007 задачу можно легко выполнить с помощью формул СУММЕСЛИМН, СЧЁТЕСЛИМН и СРЗНАЧЕСЛИ. Если вы не ищете легких путей или все еще используете Excel 2003 или более раннюю версию, вы можете получить желаемый результат с помощью СУММПРОИЗВ.

Чтобы сделать ваши формулы СУММПРОИЗВ более гибкими, мы указываем нужный регион и товар в отдельных ячейках, а затем ссылаемся на эти ячейки в своей формуле, как показано на скриншоте ниже:

Чтобы подсчитать количество продаж яблок для Севера :

=СУММПРОИЗВ(—(A3:A13=F2); —(B3:B13=F3))

Суммируем продажияблок для Севера:

=СУММПРОИЗВ(—(A3:A13=F2); —(B3:B13=F3); C3:C13)

Чтобы найти средний размер продажи яблок на Севере:

Чтобы вычислить среднее значение, мы просто делим сумму на количество следующим образом:

=СУММПРОИЗВ(—(A3:A13=F2); —(B3:B13=F3); C3:C13)/СУММПРОИЗВ(—(A3:A13=F2); —(B3:B13=F3))

Формула СУММПРОИЗВ с логикой ИЛИ

Напомним, что логика ИЛИ означает, что выполняется хотя бы одно из нескольких условий. Чтобы суммировать или подсчитывать ячейки с помощью логики ИЛИ, используйте знак плюс (+) между массивами.

В формулах СУММПРОИЗВ Excel, а также в формулах массива символ плюс действует как оператор ИЛИ, который указывает Excel вернуть ИСТИНА, если ЛЮБОЕ из условий в данном выражении оценивается как ИСТИНА.

На следующем скриншоте показана такая формула в действии:

Чтобы подсчитать количество всех продаж апельсинов и лимонов независимо от региона, использована следующая формула:

=СУММПРОИЗВ((B3:B13=F2)+(B3:B13=H2))

Она означает следующее: подсчитывать ячейки, если B3:B13=»апельсины» ИЛИ B3:B13=»лимоны».

Чтобы найти общие продажи апельсинов и лимонов , добавьте еще один аргумент, содержащий диапазон продаж :

=СУММПРОИЗВ((B3:B13=F2)+(B3:B13=H2); C3:C13)

Формула СУММПРОИЗВ с логикой И и ИЛИ

Во многих ситуациях вам может понадобиться условно подсчитать или суммировать ячейки с помощью логики И и ИЛИ одновременно. Даже в последних версиях Excel серия функций ЕСЛИ на это не способна.

Одним из возможных решений является объединение двух или более функций СУММЕСЛИМН+СУММЕСЛИМН или СЧЁТЕСЛИМН+СЧЁТЕСЛИМН .

Другой способ — использовать функцию СУММПРОИЗВ Excel, где:

Знак умножения (*) используется как оператор И.
Плюс (+) используется как оператор ИЛИ.

Для лучшего понимания, рассмотрим следующие примеры.

Чтобы сделать формулы немного более компактными, вы можете записать переменные в отдельные ячейки — «Регион» в F1 и «Товары» в F2 и H2 — и ссылаться на них в своей формуле:

Сосчитаем, сколько раз яблоки и лимоны были проданы в Северном регионе. Для этого составим формулу со следующей логикой:

=СУММПРОИЗВ((A3:A13=F2)*((B3:B13=F3)+(B3:B13=H3)))

Чтобы суммировать продажи яблок и лимонов в Северном регионе, возьмите приведенную выше формулу и добавьте массив Продажи с логикой «И»:

=СУММПРОИЗВ((A3:A13=F2)*((B3:B13=F3)+(B3:B13=H3))*C3:C13)

Формула СУММПРОИЗВ для средневзвешенного значения

Еще одним распространенным использованием СУММПРОИЗВ в Excel является вычисление средневзвешенного значения, где каждому числу присваивается определенный вес.

Общая формула СУММПРОИЗВ для средневзвешенного значения выглядит следующим образом:

СУММПРОИЗВ( значения ; веса )/СУММ( веса )

Если предположить, что значения находятся в ячейках B2:B7, а веса — в ячейке C2:C7, формула средневзвешенного СУММПРОИЗВ будет выглядеть следующим образом:

=СУММПРОИЗВ(B2:B7;C2:C7)/СУММ(C2:C7)

Думаю, на этом этапе у вас не возникнет трудностей с пониманием логики формулы. Находим сумму произведений процента выполнения на коэффициент важности и делим на сумму коэффициентов важности.

СУММПРОИЗВ как альтернатива формулам массива

Даже если вы читаете эту статью в ознакомительных целях и детали, скорее всего, потускнеют в вашей памяти, помните только один ключевой момент — функция СУММПРОИЗВ в Excel работает с массивами.

Какие преимущества это дает вам? По сути, вы сможете легко управлять своими формулами, не нажимая Ctrl + Shift + Enter каждый раз, когда вы вводите новую или редактируете существующую формулу массива.

В качестве примера мы можем взять простую формулу массива, которая подсчитывает все символы в заданном диапазоне ячеек. Более подробно этот пример рассмотрен в статье Как посчитать количество знаков в Excel.

=СУММПРОИЗВ(ДЛСТР( диапазон ))

или

=СУММПРОИЗВ(ДЛСТР(A2:A5))

Функция ДЛСТР в результате обработки диапазона ячеек возвращает массив значений – число символов в каждой из ячеек. Далее СУММПРОИЗВ складывает эти элементы массива и возвращает общее количество символов.

Excel СУММПРОИЗВ — примеры расширенных формул

Теперь, когда вы знаете синтаксис и логику функции СУММПРОИЗВ в Excel, вы можете изучить более сложные и более мощные формулы, в которых СУММПРОИЗВ используется совместно с другими функциями Excel.

Вот как мы это уже делали в более ранних публикациях на нашем сайте:

СУММПРОИЗВ для ВПР по нескольким критериям — как выполнять поиск по нескольким критериям и возвращать совпадающие числа.
«Левый» ВПР для числовых значений – извлекаем из столбца слева от столбца поиска числовые значения и суммируем их.
Как подсчитать символы в Excel — формулы для подсчета всего или только определенных символов в диапазоне.
СУММПРОИЗВ для подсчета слов в Excel — формулы для получения общего количества слов в определенном диапазоне или подсчета только определенных слов.
Как подсчитать различные значения — узнайте, сколько разных значений появляется в диапазоне (уникальных плюс первые повторяющиеся вхождения).
Подсчет дубликатов и уникальных значений — формула СУММПРОИЗВ / СЧЁТЕСЛИ для подсчета дубликатов и уникальных значений в столбце или между двумя столбцами.
Извлечение только чисел из буквенно-цифровых строк — СУММПРОИЗВ в сочетании с 7 другими функциями извлекает все числа из строки число-текст-число.

Источник

Аннотация:
Цель работы: научиться работать с функциями Excel для обработки массивов.
Содержание работы:
Поэлементное сложение, вычитание, умножение и деление двух массивов.
Вычисление функции, зависящей от элементов массива.
Вычисление сложных выражений.
Решение системы линейных уравнений с использованием функций для работы с матрицами.
Нахождение значения квадратичной формы.
Решение системы линейных уравнений методом Гаусса.
Порядок выполнения работы:
Изучить методические указания.
Выполнить задания.
Оформить отчет и ответить на контрольные вопросы.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Часто при работе с таблицами возникает необходимость применить одну и ту же операцию к целому диапазону ячеек или произвести расчеты по формулам, зависящим от большого массива данных.

Под массивом в MS Excel понимается прямоугольный диапазон формул или значений, которые программа обрабатывает как единую группу. MS Excel предоставляет простое и элегантное средство – формула массива – для решения подобных задач.

В качестве примера использования формулы массива приведем расчет цен группы товаров с учетом НДС. Например, в диапазоне В2:В4 даны цены группы товаров без учета НДС. Необходимо найти цену каждого товара с учетом НДС (который будем полагать равным 25%). Таким образом, необходимо умножить массив элементов В2:В4 на 125%. Результат надо разместить в ячейках диапазона С2:С4 (рис. 17.1
рис.
17.1). Для этого:

Выберите диапазон, например С2:С4, в котором будет размещен результат умножения первоначального массива на число. От диапазона, в котором будет находиться результат, требуется, чтобы он имел тот же размер, что и исходный диапазон (рис. 17.1
рис.
17.1).
Введите формулу

Завершите ввод формулы не нажатием клавиши <Enter>, а нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Таким образом, вы сообщите MS Excel, что необходимо выполнить операцию над массивом, т. е. создать формулу массива. В ответ MS Excel автоматически возьмет формулу в фигурные скобки (рис. 17.2
рис.
17.2):

Примечание. При выборе диапазона, в который будет введена формула массива, надо быть аккуратным. Если выбрать слишком маленький диапазон, то невозможно будет получить все результаты. Если диапазон выбрать слишком большим, то в неиспользуемых ячейках отобразится сообщение об ошибке #Н/Д.

Рис.
17.1.
Выделение диапазона для ввода результирующего массива

Рис.
17.2.
Умножение элементов массива на число

Исправление формулы массива

Формулы массивов действуют на все ячейки массива. Нельзя изменять отдельные ячейки в операндах формулы. Как же изменить формулу массива? Самый простой способ – выделить весь диапазон, в который введена формула массива, и удалить ее, нажав клавишу <Delete>. После чего ввести формулу массива корректно. Такой прямой способ хорош, когда формула простая. А если она сложная, а в ней просто требуется произвести какую-то небольшую коррекцию? В этом случае возможны две ситуации.

Формула массива введена в правильный диапазон. Тогда надо выделить этот диапазон. В строке формул произвести требуемые изменения и завершить ввод исправленной формулы нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
Формула массива введена в неправильный диапазон. В этом случае надо выделить этот диапазон, в строке формул выделить формулу и скопировать ее в буфер обмена. Затем повторно выбрать диапазон и удалить из него формулу массива. После этого надо выделить корректный диапазон, расположить в строке формул курсор и вставить в нее формулу из буфера обмена. Произвести, если требуется, необходимое исправление формулы и завершить ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.

Поэлементное сложение, вычитание, умножение и деление двух массивов

Продемонстрируем операцию поэлементного сложения двух массивов. Пусть, например слагаемыми будут массивы, содержащиеся в диапазонах А1:В2 и D1:E2 (рис. 17.3
рис.
17.3).

Рис.
17.3.
Сумма двух массивов

Выберите на рабочем листе диапазон, например Gl:H2, в который будет помещен результат поэлементного сложения двух массивов. От данного диапазона требуется, чтобы он имел тот же размер, что и массивы-слагаемые.
Введите формулу = A1:B2+D1:E2
Завершите ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. MS Excel возьмет формулу в строке формул в фигурные скобки (рис 17.3) и произведет требуемые вычисления {=A1:B2+D1:E2}

Примечание. Для избежания ошибок в формулу вводите ссылки на диапазоны ячеек не с клавиатуры, а путем выбора их на рабочем листе мышью. Тогда ссылка на диапазон ячеек в формулу будет вводиться автоматически.

Аналогично можно вычислить поэлементно разность, произведение и деление массивов.

Вычисление функции, зависящей от элементов массива

На рабочем листе допустимо создавать формулы массива, каждый элемент которого связан посредством некоторой функции с соответствующим элементом первоначального массива.

Например, пусть в диапазоне А1:В2 имеется некоторый массив данных. Требуется найти массив, элементы которого равны значениям функции SIN от соответствующих элементов искомого массива.

Для этого:

Выберите в рабочем листе диапазон, например D1:E2, в котором будет размещен результат. От данного диапазона требуется, чтобы он имел тот же размер, что и исходный диапазон.
Введите формулу =SIN(A1:B2)
Завершите ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива {=SIN(A1:B2)}

Вычисление сложных выражений

Приведем более сложный пример использования формул массива. А именно, попытаемся найти значение следующего выражения:

$S=frac{2sumlimits_{i=1}limits^{n}X_{i}+left(sumlimits_{i=1}limits^{m}sumlimits_{j=1}limits^{m}B_{ij}C_{ij}right)^{2}}{1+sumlimits_{i=1}limits^{n}X_{i}^{2}}$

где: X – вектор из n компонентов, B и C – матрицы размерности mxm, причем, n=3, m=2 и

$X=left(begin{array}{c} 2\ 1\ 2 end{array}right), B=left(begin{array}{cc} 2 &1\ 2 &5 end{array}right),C=left(begin{array}{cc} 1 &1\ 4 &5 end{array}right)$

Для решения этой задачи нам потребуется функция рабочего листа СУММ (SUM), которая суммирует все числа из диапазона ячеек.

Синтаксис:

СУММ{число1; число2; ...).

где: число1, число2, … – это от 1 до 30 аргументов, которые надо просуммировать. Аргументами могут быть либо ссылки на диапазоны ячеек, либо числа.

Например, СУММ(3;2) возвращает 5. Если в диапазоне ячеек А1:В2 содержатся числа 1, 2, 3, 4, то СУММ(А1:В2;15) возвращает 25.

Рис.
17.4.
Вычисление значения s

Теперь можно вернуться к вычислению значения s.

Введите в диапазон А2:А4 компоненты вектора X.
Введите в диапазон В2: С3 компоненты матрицы В.
Введите в диапазон D2:ЕЗ компоненты матрицы С.
Введите в ячейку В6 следующую формулу:

=(2*СУММ(А2:А4)+СУММ(В2:СЗ*D2:Е3) ^2) / (1+СУММ(А2 :А4^2))

Завершите ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления (рис. 17.4
рис.
17.4)

{=(2*СУММ(А2:А4)+СУММ(В2:СЗ*D2:ЕЗ) ^2) / (1+СУММ(А2 :А4^2))}

Примечание. Хотя в данном примере формула возвращает одно число, а не массив, тем не менее формула является формулой массива. Поэтому не забудьте ее ввод завершить нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Если вы это не сделаете, в ячейке В6 появится сообщение об ошибке #ЗНАЧ!.

Конечно, этот же результат можно было бы получить и без использования формул массивов, введя в ячейку В6 простую формулу

=(2*СУММ(А2:А4)+СУММПРОИЗВ(В2:СЗ;D2:ЕЗ)^2)/(1+СУММКВ(А2:А4))

В данной формуле используются функции рабочего листа СУММПРОИЗВ (SUMPRODUCT) и СУММКВ (SUMSQ).

Функция СУММПРОИЗВ возвращает сумму произведений соответствующих элементов массивов.

Синтаксис:

СУММПРОИЗВ (массив1; массив2; ...).

где: массив1, массив2, … – это от 2 до 30 массивов, чьи компоненты нужно перемножить, а затем сложить. Аргументы, которые являются массивами, должны иметь одинаковые размерности. Если это не так, то функция СУММПРОИЗВ возвращает значение ошибки #ЗНАЧ!.

Функция СУММКВ возвращает сумму квадратов аргументов.

Синтаксис:

СУММКВ (число1; число2; ...).

где: число1, число2, … – это от 1 до 30 аргументов, квадраты которых суммируются. Можно использовать отдельный массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

Функции рабочего листа для работы с матрицами

В MS Excel имеются функции рабочего листа для работы с матрицами, перечисленные в табл. 17.1
таблица
17.1.

Таблица
17.1.
Функции обработки матриц

Функция (рус.)	Функция (англ.)	Описание
МОБР (массив)	MINVERSE (array)	Возвращает обратную матрицу
МОПРЕД (массив)	MDETERM (array)	Возвращает определитель матрицы
МУМНОЖ (массив1; массив2)	MMULT (array1; array2)	Возвращает матричное произведение двух матриц
ТРАНСП (массив)	TRANSPOSE (array)	Возвращает транспонированную матрицу

Примечание 1. При работе с матрицами, перед вводом формулы, надо выделить область на рабочем листе, куда будет помещен результат вычислений, а ввод формулы завершать нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.

Примечание 2. Массивы в формулах могут быть заданы либо как диапазон ячеек, например А1:С3, либо как массив констант, например {1;2;3: 4;5;6: 7;8;9}, либо как имя диапазона или массива.

Решение системы линейных уравнений

Решим в качестве примера систему линейных уравнений с двумя неизвестными, матрица коэффициентов которой записана в ячейки А2:В3, а свободные члены – в ячейки D2:D3 (рис. 17.5
рис.
17.5).

Вспомним, что решение линейной системы АХ = В,

где: А – матрица коэффициентов,

В – столбец (вектор) свободных членов,

X– столбец (вектор) неизвестных, имеет вид X = А^-1В , где А^-1– обратная матрица к А.

В нашем случае

$A=left(begin{array}{cc} 8 &3\ 2 &7 end{array}right),B=left(begin{array}{c} 4\ 2 end{array}right).$

Поэтому, для решения системы уравнений

Выберите тот диапазон, в который будет введено решение. Например, F2: F3.
Введите в него формулу =МУМНОЖ(МОБР(А2:В3);D2:D3)
Завершите ввод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива (рис. 17.5
рис.
17.5).

{=МУМНОЖ(МОБР(А2:В3);D2:D3)}

Таким образом, решением системы уравнений является вектор

$X=left(begin{array}{c} 0.44\ 0.16 end{array}right).$

В качестве более сложного примера решим систему линейных уравнений А²Х = В, где

$A=left(begin{array}{cc} 7 &2\ 1 &4 end{array}right),B=left(begin{array}{c} 2\ 1 end{array}right).$

Рис.
17.5.
Решение системы линейных уравнений

Решением этой системы является вектор X = (А²)^-1В.

Для нахождения вектора X.

Введите элементы матрицы А в диапазон ячеек А2:В3.
Введите элементы вектора В в диапазон ячеек D2: D3.
Выберите диапазон F2:F3, куда поместим элементы вектора решения.
Введите в этот диапазон формулу:

=МУМНОЖ(МОБР(МУМНОЖ(А2:В3;А2:ВЗ));D2:D3)

Завершите ввод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+ +<Enter>. MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива.

{=МУМНОЖ(МОБР(МУМНОЖ(А2:В3;А2:ВЗ));D2:D3)}

В диапазоне ячеек F2:F3 будет найдено решение системы уравнений

$X=left(begin{array}{c} 0.02071\ 0.04289 end{array}right).$

Нахождение значения квадратичной формы

Рассмотрим пример вычисления квадратичной формы z = X^ТАХ, при этом

$A=left(begin{array}{cc} 8 &3\ 2 &7 end{array}right),B=left(begin{array}{c} 4\ 2 end{array}right).$

Для нахождения значения этой квадратичной формы:

Введите элементы матрицы А в диапазон ячеек А2:В3 (рис. 17.6
рис.
17.6).
Введите элементы вектора Х в диапазон ячеек D2:D3.
Выберите ячейку F2, куда необходимо поместить значение квадратичной формы.
Введите в эту ячейку формулу

=МУМНОЖ(МУМНОЖ(TPAHCП(D2:D3);A2:B3);D2:D3)

Завершите ввод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+ +<Enter>. MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массивов (рис. 17.6
рис.
17.6).

{=МУМНОЖ(МУМНОЖ(TPAHCП(D2:D3);A2:B3);D2:D3)}

Рис.
17.6.
Нахождение квадратичной формы

Примечание. Хотя в данном примере формула возвращает одно число, а не массив, тем не менее, она является формулой массива. Поэтому не забудьте ее ввод завершить нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Если вы это не сделаете, в ячейке F2 появится сообщение об ошибке #ЗНАЧ!.

Пошаговое решение системы линейных уравнений методом Гаусса

Хорошим упражнением по работе с массивами является пошаговое программирование на рабочем листе решения системы линейных уравнений методом Гаусса.

На рисунке 17.7
рис.
17.7 приведены результаты пошагового решения методом Гаусса следующей системы линейных уравнений:

$left{ begin{aligned} 7x_{1}+1x_{2}+3x_{3}=1\ 3x_{1}+6x_{2}+1x_{3}=2\ 3x_{1}+1x_{2}+4x_{3}=3 end{aligned} right.$

Рис.
17.7.
Пошаговое решение системы линейных уравнений методом Гаусса

Итак, для пошагового решения этой системы уравнений сначала введите на рабочем листе исходные данные. Для этого:

В ячейки диапазона А2:С4 введите коэффициенты системы, стоящие при неизвестных.
В ячейках диапазона D2: D4 задайте свободные члены.
Приступим к прямой прогонке метода Гаусса:
Через буфер обмена скопируйте диапазон А2:D2 на А6:D6.
Выберите диапазон А7:D7.
Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.

{=А3:D3-$A$2:$D$2*A3/$A$2}

Выберите диапазон A7:D7, расположите указатель мыши на маркере заполнения этого диапазона и пробуксируйте его вниз на одну строку.
Выделите диапазон А6: D7 и скопируйте его содержимое в буфер обмена.
Выберите ячейку А10.
Щелкните правой кнопкой мыши Специальная вставка. На экране отобразится диалоговое окно Специальная вставка (рис. 17.8
рис.
17.8). Выберите переключатель значения в группе Вставить и нажмите кнопку ОК. В результате в диапазон A10:D10 из диапазона А6:D7 будут скопированы только значения, а не формулы.
Выделите диапазон A12:D12.
Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.

Рис.
17.8.
Диалоговое окно Специальная вставка

Примечание. Команда Щелкните правой кнопкой мыши Специальная вставка удобна при копировании и вставке части атрибутов ячеек, таких как формат или значение. Команда позволяет комбинировать в одной ячейке атрибуты из разных ячеек, а также выполнять над ними арифметические операции. Кроме того, установка флажка транспонировать позволяет вставлять в рабочий лист данные из буфера обмена с одновременным их транспонированием. А установка флажка пропускать пустые ячейки разрешает игнорировать пустые ячейки при вставке в рабочий лист Данных из буфера обмена.

Прямая прогонка метода Гаусса закончилась. Переходим к обратной прогонке.

Выберите диапазон F8:I8.
Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.

Выделите диапазон F7:I7.
Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.

{=(А11:D11-F8:I8*C11)/B11}

Выберите диапазон F6:I6.
Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.

{=(А10:D10-F7:I7*B10-F8:I8*C10)/A10}

Итак, решением системы уравнений является следующий вектор

$X=left(begin{array}{c} 0.28037\ 0.32710\ 0.87850 end{array}right).$

Использование формулы массива для исключения промежуточной формулы

Использование формулы массива может избавить от необходимости вводить на рабочем листе промежуточные формулы. Продемонстрируем это на примере. На рисунке 17.9
рис.
17.9 приведена некоторая отчетная ведомость.

Необходимо найти:

суммарный прирост, скажем, по продажам в феврале по сравнению с январем. Для этого достаточно ввести в ячейку D7 формулу массивов:

максимальный квартальный прирост по продажам в феврале по сравнению с январем. Для этого достаточно ввести в ячейку D8 формулу массивов:

Примечание. Здесь используется формула рабочего листа МАКС (MAX), которая возвращает максимальное значение среди ее аргументов. Функция МИН (MIN) возвращает минимальное значение среди ее аргументов.

Рис.
17.9.
Исключение промежуточных формул

В случае если среди данных имеются как положительные, так и отрицательные значения, формулы массивов позволяют обработать только положительные или отрицательные данные без предварительной их сортировки или фильтрации. Например, пусть в диапазон А12:А16 введены как доходы, так и убытки за отчетный период. Тогда, для того чтобы найти:

суммарный доход, достаточно ввести в ячейку С12 формулу массивов:

{=СУММ(ЕСЛИ(А12:А16>0;А12:А16))}

суммарный убыток, достаточно ввести в ячейку С13 формулу массивов:

{=СУММ(ЕСЛИ(А12:А16<0;А12:А16))}

ЗАДАНИЯ

Вариант 1.

Решить системы линейных уравнений АХ = В, А³Х = В и вычислить значение квадратичной формы z=Y^TA^TA²Y , где

$A=left(begin{array}{cccc} 9 & 5 & 4 & 7\ 4 & 6 & 8 & 7\ 5 & 8 & 7 & 6\ 5 & 6 & 8 & 7 end{array}right),B=left(begin{array}{c} 0\ 6\ 3\ 7 end{array}right),Y=left(begin{array}{c} 2\ 6\ 2\ 3 end{array}right).$

Вычислить

$S=frac{2sumlimits_{i=1}limits^{n}x_{i}y_{i}+left(sumlimits_{i=1}limits^{m}sumlimits_{j=1}limits^{m}b_{ij}right)^{2}}{3+sumlimits_{i=1}limits^{n}x_{i}},$

где: х, у – векторы из n компонентов, b – матрица размерности mxm, причем n = 4, m = 2 и

$x=(3,1,2,3), y=(1,7,2,3), b=left(begin{array}{cc} 4 &1\ 1 &5 end{array}right).$

Вариант 2.

Решить системы линейных уравнений АХ = В, А²А^TХ = В и вычислить значение квадратичной формы z=Y^TA³Y , где

$A=left(begin{array}{cccc} 9 & 5 & 3 & 8\ 4 & 6 & 7 & 4\ 2 & 3 & 5 & 3\ 1 & 8 & 3 & 7 end{array}right),B=left(begin{array}{c} 3\ 1\ 4\ 2 end{array}right),Y=left(begin{array}{c} 3\ 5\ 1\ 3 end{array}right).$

Вычислить

$S=frac{2sumlimits_{i=1}limits^{m}a_{i}+left(sumlimits_{i=1}limits^{n}sumlimits_{j=1}limits^{n}c_{ij}right)^{2}}{left(1+sumlimits_{i=1}limits^{m}a_{i}right)left(1+sumlimits_{i=1}limits^{m}a_{i}^{2}right)},$

где: a – вектор из m компонентов, с – матрица размерности nxn, причем

n = 3, m = 4

$a=(3,1,2,3),quad c=left(begin{array}{ccc} 2 &2 &4\ 2 &4 &6\ 2 &5 &3 end{array}right).$

Вариант3.

Решить системы линейных уравнений АХ = В, АА^TАХ = В и вычислить значение квадратичной формы z=Y^TA^TA³Y, где

$A=left(begin{array}{cccc} 1 & 4 & 2 & 5\ 4 & 4 & 5 & 3\ 1 & 2 & 6 & 8\ 3 & 7 & 3 & 2 end{array}right),B=left(begin{array}{c} 3\ 8\ 1\ 7 end{array}right),Y=left(begin{array}{c} 1\ 2\ 5\ 1 end{array}right).$

Вычислить

$S=frac{sumlimits_{i=1}limits^{n}x_{i}+2sumlimits_{i=1}limits^{n}y_{i}^{2}+5left(sumlimits_{i=1}limits^{m}sumlimits_{j=1}limits^{m}b_{ij}right)^{3}}{3+sumlimits_{i=1}limits^{n}y_{i}},$

где: x, y – векторы из n компонентов, b – матрица размерности mxm, причем n = 4, m = 2 и

$x=(1,2,7,4), y=(1,7,2,3), b=left(begin{array}{cc} 4 &1\ 2 &5 end{array}right).$

Вариант4.

Решить системы линейных уравнений АХ = B, А²А^TАХ = В и вычислить значение квадратичной формы z=Y^TA^TAA^TY , где

$A=left(begin{array}{cccc} 2 & 3 & 5 & 2\ 5 & 2 & 7 & 5\ 4 & 2 & 1 & 7\ 7 & 5 & 4 & 1 end{array}right),B=left(begin{array}{c} 3\ 2\ 3\ 2 end{array}right),Y=left(begin{array}{c} 3\ 1\ 2\ 2 end{array}right).$

Вычислить

$S=3sumlimits_{i=1}limits^{m}a_{i}^{2}+7sumlimits_{i=1}limits^{n}sumlimits_{j=1}limits^{n}c_{ij}-left(1+sumlimits_{i=1}limits^{n}sumlimits_{j=1}limits^{n}c_{ij}right)^{2},$

где: а – вектор из m компонентов, с – матрица размерности nхn, причем

n = 3, m = 4 и

$a=(3,1,2,3),quad c=left(begin{array}{ccc} 2 &2 &4\ 2 &4 &6\ 2 &5 &3 end{array}right).$

Вариант5.

Решить системы линейных уравнений АХ = В, АА^TА²Х = B и вычислить значение квадратичной формы z=Y^TA³A^TY , где

$A=left(begin{array}{cccc} 9 & 6 & 3 & 8\ 4 & 6 & 7 & 4\ 2 & 3 & 5 & 3\ 4 & 8 & 3 & 7 end{array}right),B=left(begin{array}{c} 3\ 1\ 4\ 2 end{array}right),Y=left(begin{array}{c} 3\ 5\ 1\ 3 end{array}right).$

Вычислить

$S=sumlimits_{i=1}limits^{n}x_{i}+2sumlimits_{i=1}limits^{n}y_{i}^{2}+left(sumlimits_{i=1}limits^{m}sumlimits_{j=1}limits^{m}b_{ij}right)left(2+sumlimits_{i=1}limits^{n}x_{i}right)-2left(1+sumlimits_{i=1}limits^{n}x_{i}y_{i}right),$

где: х, у – векторы из n компонентов, b – матрица размерности mxm, причем n = 4, m = 2 и

$x=(1,2,7,4), y=(1,7,2,3), b=left(begin{array}{cc} 4 &1\ 2 &5 end{array}right).$

Вариант6.

Решить системы линейных уравнений АХ = В, А³А^TХ = В и вычислить значение квадратичной формы z=Y^TA²A^TAY , где

$A=left(begin{array}{cccc} 2 & 4 & 7 & 4\ 4 & 1 & 6 & 2\ 8 & 3 & 6 & 7\ 6 & 3 & 5 & 7 end{array}right),B=left(begin{array}{c} 2\ 0\ 3\ 1 end{array}right),Y=left(begin{array}{c} 2\ 1\ 4\ 1 end{array}right).$

Вычислить

$S=sumlimits_{i=1}limits^{m}a_{i}+sumlimits_{i=1}limits^{n}sumlimits_{j=1}limits^{n}c_{ij}^{2}-left(3+sumlimits_{i=1}limits^{n}sumlimits_{j=1}limits^{n}c_{ij}right)left(1+sumlimits_{i=1}limits^{m}a_{i}^{2}right),$

где: а – вектор из m компонентов, с – матрица размерности nxn, причем

n = 3, m = 4 и

$a=(3,3,1,3),quad c=left(begin{array}{ccc} 2 &2 &4\ 2 &4 &6\ 2 &5 &3 end{array}right).$

Вариант7.

Решить системы линейных уравнений АХ = В, А^TА³Х = В и вычислить значение квадратичной формы z=Y^TAA^TA²Y , где

$A=left(begin{array}{cccc} 3 & 3 & 4 & 5\ 2 & 6 & 4 & 6\ 3 & 4 & 5 & 5\ 1 & 9 & 3 & 6 end{array}right),B=left(begin{array}{c} 1\ 3\ 0\ 2 end{array}right),Y=left(begin{array}{c} 1\ 2\ 1\ 2 end{array}right).$

Вычислить

$S=left(2sumlimits_{i=1}limits^{n}x_{i}+sumlimits_{i=1}limits^{n}x_{i}y_{i}right)left(2-sumlimits_{i=1}limits^{n}x_{i}right)+3+sumlimits_{i=1}limits^{n}x_{i}^{2},$

где: х, y – векторы из n компонентов, причем n = 4 и x=(1, 2, 7, 4), y=(1, 7, 2, 3).

Вариант8.

Решить системы линейных уравнений АХ = В, АА^TА²Х = В и вычислить значение квадратичной формы z=Y^TA²A^TAY , где

$A=left(begin{array}{cccc} 2 & 1 & 5 & 2\ 5 & 2 & 2 & 6\ 2 & 2 & 1 & 2\ 1 & 3 & 3 & 1 end{array}right),B=left(begin{array}{c} 1\ 3\ 0\ 2 end{array}right),Y=left(begin{array}{c} 3\ 1\ 2\ 1 end{array}right).$

Вычислить

$S=left(1+sumlimits_{i=1}limits^{m}a_{i}right)^{2}left(1+sumlimits_{i=1}limits^{m}a_{i}^{2}right)-left(1+sumlimits_{i=1}limits^{n}sumlimits_{j=1}limits^{n}c_{ij}right)left(1+sumlimits_{i=1}limits^{n}sumlimits_{j=1}limits^{n}c_{ij}right),$

где: а – вектор из m компонентов, с – матрица размерности пxп, причем

n = 2, m = 4 и

$a=(1,4,1,3), c=left(begin{array}{cc} 2 &1\ 3 &2 end{array}right).$

Вариант9.

Решить системы линейных уравнений АХ = В, А^TАА^TX = В и вычислить значение квадратичной формы z=Y^TAA^TAA^TY , где

$A=left(begin{array}{cccc} 7 & 6 & 2 & 7\ 4 & 9 & 5 & 5\ 2 & 3 & 4 & 9\ 1 & 5 & 6 & 9 end{array}right),B=left(begin{array}{c} 3\ 2\ 0\ 2 end{array}right),Y=left(begin{array}{c} 1\ 1\ 3\ 3 end{array}right).$

Вычислить

$S=left(sumlimits_{i=1}limits^{n}x_{i}^{2}+5sumlimits_{i=1}limits^{n}x_{i}y_{i}right)left(1+sumlimits_{i=1}limits^{n}x_{i}+sumlimits_{i=1}limits^{n}y_{i}right)-3+sumlimits_{i=1}limits^{n}x_{i}^{2},$

где: x, y – векторы из n компонентов, причем n = 4 и х=(7, 5, 7, 4), у=(2, 4, 2, 3).

Вариант10.

Решить системы линейных уравнений АХ = В, A²A^TAX = B и вычислить значение квадратичной формы z=Y^TAA^TAA^TY , где

$A=left(begin{array}{cccc} 3 & 6 & 5 & 7\ 4 & 6 & 3 & 5\ 2 & 3 & 2 & 6\ 2 & 4 & 3 & 6 end{array}right),B=left(begin{array}{c} 3\ 0\ 4\ 3 end{array}right),Y=left(begin{array}{c} 2\ 0\ 1\ 1 end{array}right).$

Вычислить

$S=left(1+sumlimits_{i=1}limits^{m}a_{i}right)^{2}left(1+sumlimits_{i=1}limits^{n}sumlimits_{j=1}limits^{n}c_{ij}^{2}right)-1-sumlimits_{i=1}limits^{m}a_{i}^{2}+4sumlimits_{i=1}limits^{n}sumlimits_{j=1}limits^{n}c_{ij},$

где: а – вектор из m компонентов, с –матрица размерности nхn, причем

n = 3, m = 4

Источник

Терминология

Пример 1. Классика жанра — товарный чек

Пример 2. Разрешите Вас… транспонировать?

Редактирование формулы массива

Пример 3. Таблица умножения

Пример 4. Выборочное суммирование

Ссылки по теме