Перейти к содержанию
На чтение 2 мин Опубликовано 31.07.2015
- Функция ЧЁТН
- Функция НЕЧЁТ
- Чётное или нечётное?
На этом примере мы продемонстрируем работу функций EVEN (ЧЁТН) и ODD (НЕЧЁТ) в Excel. Также вы узнаете, как определить, является число чётным или нечётным.
Содержание
- ЧЁТН
- НЕЧЁТ
- Чётное или нечётное?
ЧЁТН
- Округлим положительное число до ближайшего четного целого.
=EVEN(A1)
=ЧЁТН(A1) - Округлим отрицательное число до ближайшего четного целого с помощью той же формулы.
НЕЧЁТ
- Округлим положительное число до ближайшего нечетного целого.
=ODD(A1)
=НЕЧЁТ(A1) - Округлим отрицательное число до ближайшего нечетного целого с помощью той же формулы.
Чётное или нечётное?
Один из способов определить, является число четным или нечетным, – использовать функцию MOD (ОСТАТ). Функция MOD (ОСТАТ) возвращает остаток от деления.
- Чётные целые числа, разделенные на 2, всегда дают в остатке 0. Например, 28 делится на 2 (ровно 14 раз) и даёт остаток 0. На примере функция IF (ЕСЛИ) возвращает «Even», т.е. «Чётное».
=IF(MOD(A2,2)=0,"Even","Odd")
=ЕСЛИ(ОСТАТ(А2;2)=0;"Четное";"Нечетное") - Нечетные целые числа, разделенные на 2, всегда дают остаток 1. Например, 29 делится на 2 (14 раз) и даёт остаток 1. На примере функция IF (ЕСЛИ) возвращает «Odd», т.е. «Нечётное».
Оцените качество статьи. Нам важно ваше мнение:
КАК НАЙТИ ЧЕТНЫЕ ЧИСЛА В EXCEL
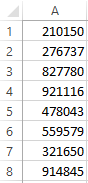
Набор четных и нечетных чисел, которые следует автоматически выделить разными цветами:
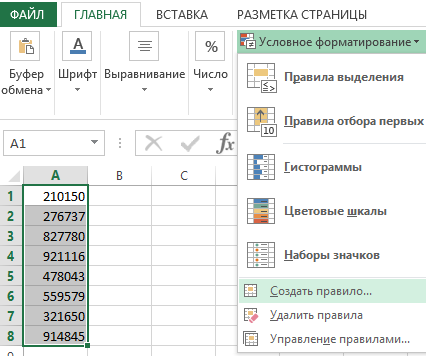
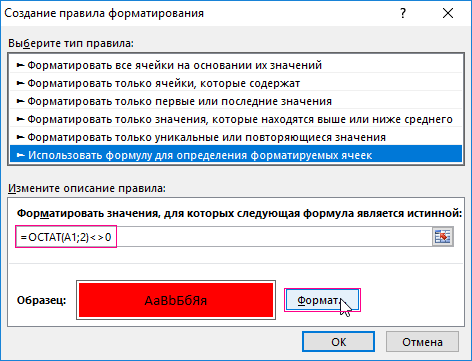
1. Выделите диапазон ячеек A1:A8 и выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило».
2. Ниже выберите: «Использовать формулу для определения форматируемых ячеек».
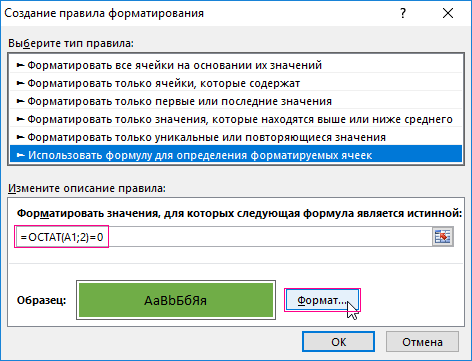
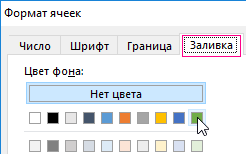
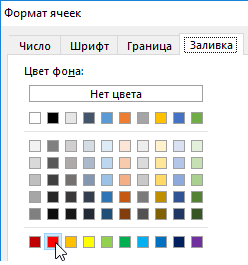
3. Чтобы найти четное число в Excel ниже введите формулу: =ОСТАТ(A1;2)=0 и нажмите на кнопку «Формат», чтобы задать зеленый цвет заливки ячеек. И нажмите ОК на всех открытых окнах.
4. Чтобы додать второе условие, не снимая выделения с диапазона A1:A8, снова выбираем инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило»-«Использовать формулу для определения форматируемых ячеек».
5. В поле ввода введите формулу: =ОСТАТ(A1;2)<>0 и нажмите на кнопку «Формат», чтобы задать синий цвет заливки ячеек. И нажмите ОК на всех открытых окнах.
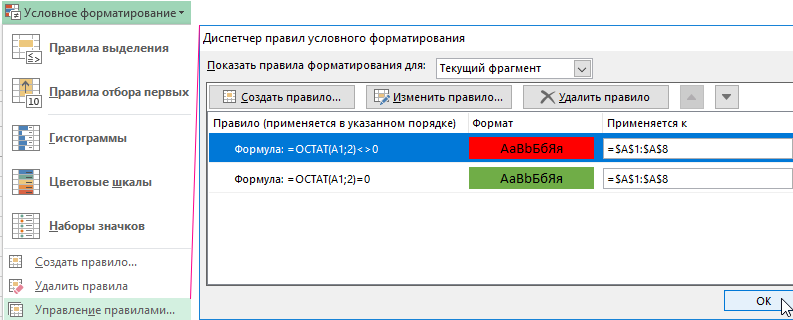
6. К одному и тому же диапазону должно быть применено 2 правила условного форматирования. Чтобы проверить выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Управление правилами».
|
Дан массив целых чисел. Определить количество чисел, которые имеют нечетные порядковые номера и которые являются четными. |
|
|
MCH Пользователь Сообщений: 3875 |
{quote}{login=Клара}{date=05.12.2010 07:26}{thema=Выбрать чётные числа в excel}{post}Дан массив целых чисел.{/post}{/quote} |
|
Serge Пользователь Сообщений: 11308 |
{quote}{login=Клара}{date=05.12.2010 07:26}{thema=Выбрать чётные числа в excel}{post}Определить количество чисел, которые имеют нечетные порядковые номера и которые являются четными.{/post}{/quote}Что есть «нечетные порядковые номера» и |
|
Serge Пользователь Сообщений: 11308 |
Хотя «количество чётных чисел» можно найти так: |
|
какую роль играют 2 дефиса после скобок в формуле? |
|
|
Юрий М Модератор Сообщений: 60585 Контакты см. в профиле |
Ищем по форуму «бинарное отрицание» или «двойное отрицание». |
|
Guest Гость |
#9 27.09.2012 21:38:38 ИСТИНУ конвертируют в 1 |
Когда нужно приготовить разного рода отчеты, иногда возникает потребность выделить все парные и непарные числа разными цветами. Для решения данной задачи наиболее рациональным способом является условное форматирование.
Набор четных и нечетных чисел, которые следует автоматически выделить разными цветами:
Допустим парные числа нам нужно выделит зеленым цветом, а непарные – синим.
Две формулы отличаются только операторами сравнения перед значением 0. Закройте окно диспетчера правил нажав на кнопку ОК.
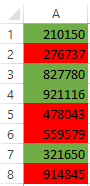
В результате у нас ячейки, которые содержат непарное число имеют синий цвет заливки, а ячейки с парными числами – зеленый.
Функция ОСТАТ в Excel для поиска четных и нечетных чисел
Функция =ОСТАТ() возвращает остаток от деления первого аргумента на второй. В первом аргументе мы указываем относительную ссылку, так как данные берутся из каждой ячейки выделенного диапазона. В первом правиле условного форматирования мы указываем оператор «равно» =0. Так как любое парное число, разделенное на 2 (второй оператор) имеет остаток от деления 0. Если в ячейке находится парное число формула возвращает значение ИСТИНА и присваивается соответствующий формат. В формуле второго правила мы используем оператор «неравно» 0. Таким образом выделяем синим цветом нечетные числа в Excel. То есть принцип работы второго правила действует обратно пропорционально первому правилу.
Немного теории
Среди олимпиадных задач для 5-6 классов обычно особую группу составляют такие, где требуется использовать свойства
чётности (нечётности) чисел. Простые и очевидные сами по себе эти свойства легко запоминаются или выводятся, и часто у школьников не возникает каких-либо сложностей при их изучении.
Но порой применить эти свойства и, главное, догадаться, что именно их надо применить для того или иного доказательства, бывает непросто. Перечислим здесь эти свойства.
Рассматривая с учениками задачи, в которых следует воспользоваться этими свойствами, нельзя не рассмотреть и такие, для решения
которых важно знать формулы чётного и нечётного чисел. Опыт преподавания этих формул пяти-шестиклассникам показывает, что многие из них даже не задумывались, что любое чётное число,
как и нечётное, можно выразить формулой. Методически бывает полезно озадачить ученика вопросом написать сначала формулу нечётного числа. Дело в том, что формула
чётного числа выглядит понятной и очевидной, а формула нечётного числа является своего рода следствием из формулы чётного числа. А если ученик в процессе изучения нового для себя материала задумался,
сделав паузу для этого, то он скорее запомнит обе формулы, чем если начинать с объяснение с формулы чётного числа. Так как чётное число — это то число, которое делится на 2, то его можно записать, как
2n, где n — целое число, а нечётное — соответственно как 2n+1.
Ниже приведены наиболее простые задачи на чётность/нечётность, которые бывает полезно рассматривать в виде лёгкой разминки.
Задачи
1) Докажите, что нельзя подобрать 5 нечётных чисел, сумма которых равна 100.
2) Имеется 9 листов бумаги. Некоторые из них разорвали на 3 или 5 частей. Некоторые из образовавшихся частей снова разорвали на 3 или 5 частей и так
несколько раз. Можно ли после нескольких шагов получить 100 частей?
3) Чётна или нечётна сумма всех натуральных чисел от 1 до 2019?
4) Докажите, что сумма двух последовательных нечетных чисел делится на 4.
5) Можно ли соединить 13 городов дорогами так, чтобы из каждого города выходило ровно 5 дорог?
6) Директор школы в своём отчёте написал, что в школе 788 учащихся, причём мальчиков на 225 больше, чем девочек. Но проверяющий инспектор сразу сообщил,
что в отчёте допущена ошибка. Как он рассуждал?
7) Записано четыре числа: 0; 0; 0; 1. За один ход разрешается прибавить 1 к любым двум из этих чисел. Можно ли за несколько
ходов получить 4 одинаковых числа?

9) Можно ли сложить замкнутую цепочку из 2017-ти квадратных плиток таким способом, как показано на рисунке?
10) Можно ли число 1 представить в виде суммы дробей
11) Докажите, что если сумма двух чисел есть число нечётное, то произведение этих чисел всегда будет числом чётным.
12) Числа a и b — целые. Известно, что a + b = 2018. Может ли сумма 7a + 5b равняться 7891?
13) В парламенте некоторой страны две палаты с равным количеством депутатов. В голосовании по важному вопросу приняли участие все
депутаты. По окончании голосования председатель парламента сказал, что предложение принято большинством в 23 голоса, причём воздержавшихся не было. После чего один из депутатов сказал, что результаты сфальсифицированы.
Как он догадался?
14) На прямой расположено несколько точек. Между двумя соседними точками поставили по точке. И так ставили точки дальше. После точки подсчитали.
Может ли количество точек быть равным 2018?
15) У Пети есть 100 рублей одной
купюрой, а у Андрея полные карманы монет по 2 и 5 рублей. Сколькими способами Андрей может
разменять купюру Пети?
16) Запишите в строчку пять чисел так, чтобы сумма любых двух соседних чисел была
нечётная, а сумма всех чисел была чётная.
17) Можно ли записать в строчку
шесть чисел так, чтобы сумма любых двух соседних чисел была чётная, а сумма всех чисел была бы нечёитная?
18) В секции фехтования мальчиков в 10 раз больше,
чем девочек, при этом всего в секции не более 20-ти человек. Смогут ли они разбиться на пары? Смогут ли они
разбиться на пары, если мальчиков будет в 9 раз больше, чем девочек? А если в 8 раз больше?
19) В десяти коробках лежат конфеты. В первой — 1, во второй — 2,
в третьей — 3, и т.д., в десятой — 10. Пете за один ход разрешается в любые две коробки добавлять по три конфеты.
Сможет ли Петя за несколько ходов уравнять количество конфет в коробках? Может ли Петя уравнять количество
конфет в коробках подкладывая в две коробки по три конфеты, если изначально коробок 11?
20) 25 мальчиков и 25 девочек сидят за круглым столом. Докажите, что
у кого-то из сидящих за столом оба соседа одного пола.
21) Маша и несколько пятиклассников
встали в круг, взявшись за руки. Оказалось, что каждый держит за руки либо двух мальчиков, либо двух девочек. Если в кругу стоит 10 мальчиков, то сколько там стоит девочек?
22) На плоскости расположено 11 шестеренок, соединенных по замкнутой цепочке, причём 11-я соединена с 1-й. Могут ли все шестеренки вращаться одновременно?
23) Докажите, что дробь
есть целое число при любом натуральном n.
24) На столе лежат 9 монет, причём одна
из них вверх олрлом, другие — вверх решкой. Можно ли все монеты положить вверх орлом, если разрешено одновременно
переворачивать две монеты?
25) Можно ли в таблице 5х5 расставить 25 натуральных чисел так,
чтобы во всех строках суммы были чётные, а во всех столбцах — нечётные?
26) Кузнечик прыгает по прямой: первый раз — на 1 см, второй раз на 2 см,
третий раз на 3 см и т.д. Может ли он через 25 прыжков вернуться на старое место?
27) Улитка ползает по плоскости с постоянной скоростью, каждые 15 минут поворачивая под прямым углом. Докажите, что вернуться
в исходную точку она сможет лишь через целое число часов.
28) В ряд выписаны числа от 1 до 2000. Можно ли меняя местами числа через одно, переставить их в обратном порядке?
29) На доске написаны 8 простых чисел, каждое из которых больше двух. Может ли их сумма равняться 79?
30) Маша и её друзья встали в круг. Оба соседа любого из детей — одного пола. Мальчиков 5, сколько девочек?
Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.
Например: -24, 0, 6, 38 — все это четные числа.
m = 2k — общая формула написания четных чисел, где k — целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.
Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.
Пример нечетных чисел: 3, 1, 7 и 35.
n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k — целое число.
Сложение и вычитание четных и нечетных чисел
В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.
|
Операция |
Результат |
Пример |
|
Четное + Четное |
||
|
Четное + Нечетное |
Нечетное |
|
|
Нечетное + Нечетное |
Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.
Умножение четных и нечетных чисел
При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.
|
Операция |
Результат |
Пример |
|
Четное * Четное |
||
|
Четное * Нечетное |
||
|
Нечетное * Нечетное |
Нечетное |
А теперь рассмотрим дробные числа.
Десятичная запись числа
Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.
Например: 3,14; 5,1; 6,789 — это все
С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.
Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.
Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.
А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом — дробную.
Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Стандартные функции
Первый способ возможен при использовании стандартных функций приложения. Для этого необходимо создать два дополнительных столбца с формулами:
- Четные числа – вставляем формулу «=
ЕСЛИ
(ОСТАТ(число;2)=0;число;0)», которая вернет число, в случае если оно делится на 2 без остатка.
- Нечетные числа – вставляем формулу «=
ЕСЛИ
(ОСТАТ(число;2)=1;число;0)», которая вернет число, в случае если оно не делится на 2 без остатка.
Затем необходимо определит сумму по двум столбцам с помощью функции «=СУММ()».
Плюсы данного способа в том, что он будет понятен даже тем пользователям, которые профессионально не владею приложением.
Минусы способа – приходится добавлять лишние столбцы, что не всегда удобно.
Пользовательская функция
Второй способ, является более удобным, чем первый, т.к. в нем применяется пользовательская функция, написанная на VBA – sum_num(). Функция возвращает сумму чисел в виде целого числа. Суммируются либо четные числа, либо нечетные, в зависимости от значения ее второго аргумента.
Синтаксис функции:
sum_num(rng;odd):
- Аргумент rng – принимает диапазон ячеек, по которым необходимо произвести суммирование.
- Аргумент odd – принимает логическое значение ИСТИНА для четных чисел или ЛОЖЬ для нечетных.
Важно:
Четными и нечетными числа могут являться только целые числа, поэтому числа, которые не соответствуют определению целого числа, игнорируются. Также, если значением ячейки является срока, то данная строка не участвует в расчете.
Плюсы: нет нужны добавлять новые столбцы; лучший контроль над данными.
Минусы заключаются в необходимости перевода файла в формат.xlsm для версий Excel, начиная с версии 2007. Также функция будет работать только в той книге, в которой она присутствует.
Использование массива
Последний способ является самым удобным, т.к. не требует создания дополнительных столбцов и программирования.
Его решение схоже с первым вариантом — они используют одни и те же формулы, но данный способ, благодаря использованию массивов, производит подсчет в одной ячейке:
- Для четных чисел — вставляем формулу «=СУММ
(ЕСЛИ
(ОСТАТ(диапазон_ячеек;2)
=0;диапазон_ячеек;0))». После ввода данных в строку формул нажимаем одновременно клавиши Ctrl + Shift + Enter, чем сообщаем приложению, что данные необходимо обрабатывать как массив, и оно заключит их в фигурные скобки;
- Для нечетных чисел — повторяем действия, но изменяем формулу «=СУММ
(ЕСЛИ
(ОСТАТ(диапазон_ячеек;2)
=1;диапазон_ячеек;0))».
Плюсом способа является то, что все рассчитывается в одной ячейке, без дополнительных столбцов и формул.
Минусом является лишь то, что неопытные пользователи могут не понять Ваших записей.
На рисунке видно,что все способы возвращают один и тот же результат, какой лучше, необходимо выбирать под конкретную задачу.
Скачать файл
с описанными варианта можно по данной ссылке.
·
Четные числа — это те, которые делятся на 2 без остатка (например, 2, 4, 6 и т.п.). Каждое такое число можно записать в виде 2K,
подобрав подходящее целое K (например, 4 = 2 х 2, 6 = 2 х 3, и т.д.).
·
Нечетные числа — это те, которые при делении на 2 дают в остатке 1 (например, 1, 3, 5 и т.п.). Каждое такое число можно записать в виде 2K + 1, подобрав подходящее целое K (например, 3 = 2 х 1 +
1, 5 = 2 х 2 + 1, и т.д.).
- Сложение и вычитание:
-
- Ч
ётное ±
Ч
ётное = Ч
ётное
- Ч
ётное ±
Н
ечётное = Н
ечётное
- Н
ечётное ±
Ч
ётное = Н
ечётное
- Н
ечётное ±
Н
ечётное = Ч
ётное
- Ч
ётное ±
- Умножение:
-
- Ч
ётное ×
Ч
ётное = Ч
ётное
- Ч
ётное ×
Н
ечётное = Ч
ётное
- Н
ечётное ×
Н
ечётное = Н
ечётное
- Ч
ётное ×
- Деление:
-
- Ч
ётное /
Ч
ётное — однозначно судить о чётности результата невозможно (если результат
целое число ,
то оно может быть как чётным, так и нечётным)
- Ч
ётное /
Н
ечётное -— если результат
целое число ,
то оно Ч
ётное
- Н
ечётное /
Ч
ётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Н
ечётное /
Н
ечётное —если результат
целое число ,
то оно Н
ечётное
- Ч
ётное /
Сумма любого числа четных чисел –
четно.
Сумма нечетного
числа нечетных чисел – нечетно.
Сумма четного
числа нечетных чисел – четно.
Разность двух
чисел имеет ту же
четность, что и их сумма
.
(напр. 2+3=5 и 2-3=-1 оба нечетные)
Алгебраическая
(со знаками + или -) сумма целых чисел
имеет ту же
четность, что и их сумма
.
(напр. 2-7+(-4)-(-3)=-6 и 2+7+(-4)+(-3)=2 оба четны)
Идея
четности имеет много разных применений. Самые простые из них:
1. Если в некоторой замкнутой цепочке чередуются объекты двух видов, то их четное число (и каждого вида поровну).
2. Если в некоторой цепочке чередуются объекты двух видов, а начало и конец цепочки разных видов, то в ней четное число объектов,
если начало и конец одного вида, то нечетное число. (четное число объектов соответствует нечетному числу
переходов
между ними и наоборот !!!
)
2″. Если у объекта чередуются два возможных состояния, а исходное и конечное состояния различны
, то периодов пребывания объекта в том или ином состоянии — четное
число, если исходное и конечное состояния совпадают — то нечетное
.
(переформулировка п.2)
3. Обратно: по четности длины чередующийся цепочке можно узнать, одного или разных видов ее начало и конец.
3″. Обратно: по числу периодов пребывания объекта в одном из двух возможных чередующихся состояний можно узнать, совпадает ли
начальное состояние с конечным. (переформулировка п.3)
4. Если предметы можно разбить на пары, то их количество четно.
5. Если нечетное число предметов почему-то удалось разбить на пары, то какой-то из них будет парой к самому себе, причем такой
предмет может быть не один (но их всегда нечетное число).
(!) Все эти соображения можно на олимпиаде
вставлять в текст решения задачи, как очевидные утверждения.
Примеры:
Задача 1.
На плоскости
расположено 9 шестеренок, соединенных по цепочке (первая со второй, вторая с третьей… 9-я с первой). Могут ли они вращаться одновременно?
Решение:
Нет, не могут. Если бы
они могли вращаться, то в замкнутой цепочке чередовалось бы два вида шестеренок: вращающиеся по часовой стрелке и против часовой стрелки (для решения задачи не имеет никакого значения, в
каком именно
направлении вращается первая шестеренка !
) Тогда всего должно быть
четное число шестеренок, а их 9 штук?! ч.и.т.д. (знак «?!» обозначает получение противоречия)
Задача 2.
В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки + и -, чтобы
получилось выражение, равное нулю?
Решение:
Нет, нельзя. Четность
полученного выражения всегда
будет совпадать с четностью суммы
1+2+…+10=55, т.е. сумма всегда будет нечетной
. А 0
— четное число?! ч.т.д.
Содержание
- КАК НАЙТИ ЧЕТНЫЕ ЧИСЛА В EXCEL
- Как четные и нечетные числа выделить разным цветом в Excel
- Как найти четные числа в Excel
- Функция ОСТАТ в Excel для поиска четных и нечетных чисел
- Сумма четных и нечетных чисел в Excel
- Стандартные функции
- Пользовательская функция
- Использование массива
- Функция ЕЧЁТН в Excel
- Синтаксис функции ЕЧЁТН
- Примеры использования ЕЧЁТН в Excel
- Функция ЕНЕЧЁТ в Excel
- Синтаксис функции ЕНЕЧЁТ
- Использование ЕНЕЧЁТ для определения нечётных чисел (примеры)
КАК НАЙТИ ЧЕТНЫЕ ЧИСЛА В EXCEL
КАК НАЙТИ ЧЕТНЫЕ ЧИСЛА В EXCEL
Набор четных и нечетных чисел, которые следует автоматически выделить разными цветами:
1. Выделите диапазон ячеек A1:A8 и выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило» .
2. Ниже выберите: «Использовать формулу для определения форматируемых ячеек» .
3. Чтобы найти четное число в Excel ниже введите формулу: =ОСТАТ(A1;2)=0 и нажмите на кнопку «Формат» , чтобы задать зеленый цвет заливки ячеек. И нажмите ОК на всех открытых окнах.
4. Чтобы додать второе условие, не снимая выделения с диапазона A1:A8 , снова выбираем инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило»-«Использовать формулу для определения форматируемых ячеек» .
5. В поле ввода введите формулу: =ОСТАТ(A1;2)<>0 и нажмите на кнопку «Формат», чтобы задать синий цвет заливки ячеек. И нажмите ОК на всех открытых окнах.
6. К одному и тому же диапазону должно быть применено 2 правила условного форматирования. Чтобы проверить выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Управление правилами» .
Источник
Как четные и нечетные числа выделить разным цветом в Excel
Когда нужно приготовить разного рода отчеты, иногда возникает потребность выделить все парные и непарные числа разными цветами. Для решения данной задачи наиболее рациональным способом является условное форматирование.
Как найти четные числа в Excel
Набор четных и нечетных чисел, которые следует автоматически выделить разными цветами:
Допустим парные числа нам нужно выделит зеленым цветом, а непарные – синим.
- Выделите диапазон ячеек A1:A8 и выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило».
- Ниже выберите: «Использовать формулу для определения форматируемых ячеек».
- Чтобы найти четное число в Excel ниже введите формулу: =ОСТАТ(A1;2)=0 и нажмите на кнопку «Формат», чтобы задать зеленый цвет заливки ячеек. И нажмите ОК на всех открытых окнах.
- Чтобы додать второе условие, не снимая выделения с диапазона A1:A8, снова выбираем инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Создать правило»-«Использовать формулу для определения форматируемых ячеек».
- В поле ввода введите формулу: =ОСТАТ(A1;2)<>0 и нажмите на кнопку «Формат», чтобы задать синий цвет заливки ячеек. И нажмите ОК на всех открытых окнах.
- К одному и тому же диапазону должно быть применено 2 правила условного форматирования. Чтобы проверить выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Управление правилами»
Две формулы отличаются только операторами сравнения перед значением 0. Закройте окно диспетчера правил нажав на кнопку ОК.
В результате у нас ячейки, которые содержат непарное число имеют синий цвет заливки, а ячейки с парными числами – зеленый.
Функция ОСТАТ в Excel для поиска четных и нечетных чисел
Функция =ОСТАТ() возвращает остаток от деления первого аргумента на второй. В первом аргументе мы указываем относительную ссылку, так как данные берутся из каждой ячейки выделенного диапазона. В первом правиле условного форматирования мы указываем оператор «равно» =0. Так как любое парное число, разделенное на 2 (второй оператор) имеет остаток от деления 0. Если в ячейке находится парное число формула возвращает значение ИСТИНА и присваивается соответствующий формат. В формуле второго правила мы используем оператор «неравно» <>0. Таким образом выделяем синим цветом нечетные числа в Excel. То есть принцип работы второго правила действует обратно пропорционально первому правилу.
Источник
Сумма четных и нечетных чисел в Excel
Высчитать сумму четных либо нечетных чисел в Excel можно несколькими способами:
Стандартные функции
Первый способ возможен при использовании стандартных функций приложения. Для этого необходимо создать два дополнительных столбца с формулами:
- Четные числа – вставляем формулу «= ЕСЛИ ( ОСТАТ(число;2) =0;число;0)», которая вернет число, в случае если оно делится на 2 без остатка.
- Нечетные числа – вставляем формулу «= ЕСЛИ ( ОСТАТ(число;2) =1;число;0)», которая вернет число, в случае если оно не делится на 2 без остатка.
Затем необходимо определит сумму по двум столбцам с помощью функции «=СУММ()».
Плюсы данного способа в том, что он будет понятен даже тем пользователям, которые профессионально не владею приложением.
Минусы способа – приходится добавлять лишние столбцы, что не всегда удобно.
Пользовательская функция
Второй способ, является более удобным, чем первый, т.к. в нем применяется пользовательская функция, написанная на VBA – sum_num(). Функция возвращает сумму чисел в виде целого числа. Суммируются либо четные числа, либо нечетные, в зависимости от значения ее второго аргумента.
Синтаксис функции: sum_num(rng;odd):
- Аргумент rng – принимает диапазон ячеек, по которым необходимо произвести суммирование.
- Аргумент odd – принимает логическое значение ИСТИНА для четных чисел или ЛОЖЬ для нечетных.
Важно: Четными и нечетными числа могут являться только целые числа, поэтому числа, которые не соответствуют определению целого числа, игнорируются. Также, если значением ячейки является срока, то данная строка не участвует в расчете.
Плюсы: нет нужны добавлять новые столбцы; лучший контроль над данными.
Минусы заключаются в необходимости перевода файла в формат .xlsm для версий Excel, начиная с версии 2007. Также функция будет работать только в той книге, в которой она присутствует.
Использование массива
Последний способ является самым удобным, т.к. не требует создания дополнительных столбцов и программирования.
Его решение схоже с первым вариантом — они используют одни и те же формулы, но данный способ, благодаря использованию массивов, производит подсчет в одной ячейке:
- Для четных чисел — вставляем формулу «=СУММ( ЕСЛИ ( ОСТАТ(диапазон_ячеек;2) =0;диапазон_ячеек;0))». После ввода данных в строку формул нажимаем одновременно клавиши Ctrl + Shift + Enter, чем сообщаем приложению, что данные необходимо обрабатывать как массив, и оно заключит их в фигурные скобки;
- Для нечетных чисел — повторяем действия, но изменяем формулу «=СУММ(ЕСЛИ( ОСТАТ(диапазон_ячеек;2) =1;диапазон_ячеек;0))».
Плюсом способа является то, что все рассчитывается в одной ячейке, без дополнительных столбцов и формул.
Минусом является лишь то, что неопытные пользователи могут не понять Ваших записей.
На рисунке видно,что все способы возвращают один и тот же результат, какой лучше, необходимо выбирать под конкретную задачу.
Источник
Функция ЕЧЁТН в Excel
Функция ЕЧЁТН в Excel проверяет является ли указанное число чётным. Формула ЕЧЁТН возвращает логическое значение результата проверки, которое можно использовать в других формулах или просто вывести в ячейку.
Рассмотрим синтаксис функции ЕЧЁТН и примеры её использования.
Синтаксис функции ЕЧЁТН
ЕЧЁТН(число)
Если в качестве аргумента передаётся дробное число, то оно усекается до целой части. Например, число 10,9 преобразуется в 10, а не в 11, то есть это не округление. Соответственно результат работы функции ЕЧЁТН будет одинаковым для всех чисел с одинаковой целой частью.
Если в формулу передать ноль, то получим значение ИСТИНА. Знак числа значения также не влияет на результат.
Других особенностей ЕЧЁТН не имеет.
Примеры использования ЕЧЁТН в Excel
Скачайте прикреплённый файл Excel после статьи. В нём рассмотрены несколько простых примеров применения ЕЧЁТН на практике, в том числе с передачей в функцию аргументов различного типа. Эти же примеры рассмотрены на видео.
Чтобы понять, как работает ЕЧЁТН, скопируйте в ячейку Excel следующее выражение: «=ЕЧЁТН(100)» (без кавычек). В результате мы получим число 100. Если передать в качестве аргумента 100,5 (через запятую), то получим то же самое из-за усечения значения аргумента до целого числа.
Попробуйте самостоятельно передать в формулу нечётные числа, ноль, а также дату или текст.
Вы можете просмотреть любой прикреплённый документ в виде PDF файла. Все документы открываются во всплывающем окне, поэтому для закрытия документа пожалуйста не используйте кнопку «Назад» браузера.
- Справка по функции ЕЧЁТН в Excel.pdf
Вы можете скачать прикреплённые ниже файлы для ознакомления. Обычно здесь размещаются различные документы, а также другие файлы, имеющие непосредственное отношение к данной публикации.
- Функция ЕЧЁТН в Excel (примеры).zip
Источник
Функция ЕНЕЧЁТ в Excel
Функция ЕНЕЧЁТ в Excel предназначена для определения нечётных чисел в ячейках. Возвращает логическое значение ИСТИНА, если в указанной ячейке находится нечётное число.
Функция ЕНЕЧЁТ относится к простейшим логическим функциям Excel и предназначается исключительно для работы с числами, то есть является узкоспециализированной. Если нужно определить, является ли число НЕчётным, то стоит воспользоваться именно этой формулой.
Посмотрим на синтаксис рассматриваемой формулы, а также её применение на примерах.
Синтаксис функции ЕНЕЧЁТ
Функция ЕНЕЧЁТ принимает единственный обязательный аргумент. Это может быть адрес ячейки или числовая константа. Если передаётся адрес ячейки, то в этой ячейке должно быть число.
Обобщённый синтаксис формулы выглядит следующим образом:
ЕНЕЧЁТ(число)
Стоит отметить одну особенность функции: если аргумент представляет собой дробное число, то оно усекается до целой части (не путайте с округлением). Таким образом, формула предназначается для работы только с целыми числами. Это может иметь значение при сложных вычислениях, когда аргумент функции ЕНЕЧЁТ формируется при помощи других формул.
Функция ЕНЕЧЁТ возвращает одно из двух логических значений:
- ИСТИНА — если аргумент передаёт нечётное число;
- ЛОЖЬ — если аргумент представляет собой чётное число;
Если в формулу ЕНЕЧЁТ передать ноль, то получим значение ЛОЖЬ. Также на результат не влияет знак числа.
Использование ЕНЕЧЁТ для определения нечётных чисел (примеры)
Скачайте файл с примерами после статьи. Эти и некоторые другие примеры также рассмотрены на видео. Все примеры использования функции ЕНЕЧЁТ простые, как и сама формула, так что разобраться с ними несложно.
Здесь же мы рассмотрим самый простой пример. Добавьте в ячейку выражение «=ЕНЕЧЁТ(33)» (без кавычек). После нажатия Enter в ячейке отобразится логическое значение «ИСТИНА». Если вместо 33 передать, например, число 10, то на выходе мы получим логическое значение «ЛОЖЬ».
Также попробуйте передать в формулу текстовое значение или дату, а также дробные числа (дробная часть отделяется запятой). Попробуйте самостоятельно перехватить вывод ошибки при передаче нечислового значения.
Вы можете просмотреть любой прикреплённый документ в виде PDF файла. Все документы открываются во всплывающем окне, поэтому для закрытия документа пожалуйста не используйте кнопку «Назад» браузера.
- Справка по функции ЕНЕЧЁТ в Excel.pdf
Вы можете скачать прикреплённые ниже файлы для ознакомления. Обычно здесь размещаются различные документы, а также другие файлы, имеющие непосредственное отношение к данной публикации.
- Функция ЕНЕЧЁТ в Excel (примеры).zip
Источник