Как рассчитать инфляцию в excel

Временная стоимость денег (Time Value of Money, TVM) – это важный показатель в бухгалтерской и финансовой отрасли. Идея заключается в том, что рубль сегодня стоит меньше чем тот же самый рубль завтра. Разница между этими двумя финансовыми значениями является прибыль, которую можно извлечь с одного рубля или убыток. Например, данная прибыль может быть получена с процентов, начисленных на банковском счете или в качестве дивидендов от инвестиций. Но также может быть убыток при оплате процентов за погашение кредитного долга.

Пример с расчетом текущей дисконтированной стоимости инвестиций в Excel

Программа Excel предлагает несколько финансовых функций для вычисления стоимости денег во времени. Например, функция ПС (приведенная стоимость) возвращает текущую стоимость инвестиций. Простыми словами, данная функция снижает сумму на размер процента дисконтирования и возвращает текущую стоимость для этой суммы. Если инвестиционный проект предполагает принести прибыль в размере 10 000 через год. Вопрос: какой максимальной суммой рационально рискнуть чтобы инвестировать в данных проект?

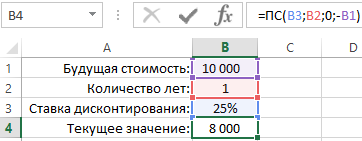
Например, в России розничный бизнес иногда делает прибыль до 35% годовых, а оптовый не более 15%. Учитывая небольшую сумму инвестиций предполагается, что инвестиционный объект не является оптовым бизнесом, а значит следует ожидать прибыль больше чем 15% годовых. Ниже на рисунке провиден пример формулы калькулятора доходности инвестиций в процентах:

Как мы видим на рисунке калькулятор нам отображает, чтобы получить сумму 10 000 за 1 год при доходности 25% нам необходимо вложить 8 000 финансовых средств. То есть если бы у нас была сумма 8 000 и мы вложили ее под 25% годовых через год мы заработали бы 10 000.

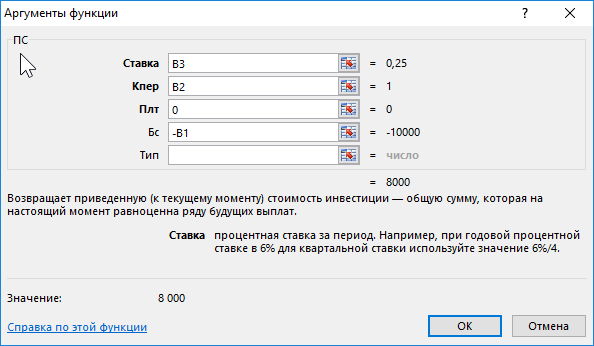
Функция ПС имеет 5 аргументов:

1. Ставка – процентная ставка дисконтирования. Это прибыль в процентах, на которую можно рассчитывать за период дисконтирования. Это значение имеет наибольшее влияние на вычисление текущей стоимости инвестиций, но его наиболее сложно точно определить. Осторожные инвесторы чаще всего занижают процентную ставку до максимально реально достижимого уровня при тех или иных условиях. Если же финансовые средства предназначены для погашения кредита, в таком случае данный аргумент определяется легко.
2. Количество периодов (Кпер) – период времени на протяжении которого дисконтируется будущая сумма. В данном примере указан 1 год (записанный в ячейке B2). Процентная ставка и количество лет должны быть выражены в соответственных единицах измерения. Это значит, что вы используете годовую ставку, тогда числовое значение в данном аргументе значит количество лет. Если указана процентная ставка в первом аргументе для месяцев (например, 2,5% ежемесячных), тогда число во втором аргументе значит количество месяцев.
3. Платеж (Плт) – сумма, которая периодически платится на протяжении периода дисконтирования. Если предусмотрен в условиях инвестирования только один платеж, как в выше приведенном примере, тогда данная сумма является будущей стоимостью денег, а сам платеж равен =0. Данный аргумент должен быть согласован со вторым аргументом количества периодов. Если количество периодов дисконтирования равно 10, а третий аргумент не равен <>0, тогда функция ПС посчитает как 10 платежей на сумму, указанную в третьем аргументе (Плт). Ниже на следующем примере изображено как вычисляется текущая стоимость денег при нескольких взносах отдельными платежами.
4. Будущая стоимость (БС) – это сумма, которую следует получить в конце периода дисконтирования. Финансовые функции Excel основаны на вычислениях наличного потока. Это значит, что будущая стоимость и текущая стоимость инвестиций имеют противоположные знаки чисел. В данном примере будущая стоимость является отрицательным числом, поэтому формула в результате вычислений возвращает положительное число.
5. Тип – данный аргумент должен иметь значение 0, если выплата итоговой суммы припадает на конец периода дисконтирования, или число 1 – если на его начало. В данном примере значение данного аргумента не имеет значения и никак не повлияет на итоговый результат вычисления. Так как платежный взнос равен нулю и аргумент определяющий тип может быть опущен. В таком случае функция по умолчанию присваивает данному аргументу значение 0.



Формула расчета текущей стоимости денег с учетом инфляции в Excel

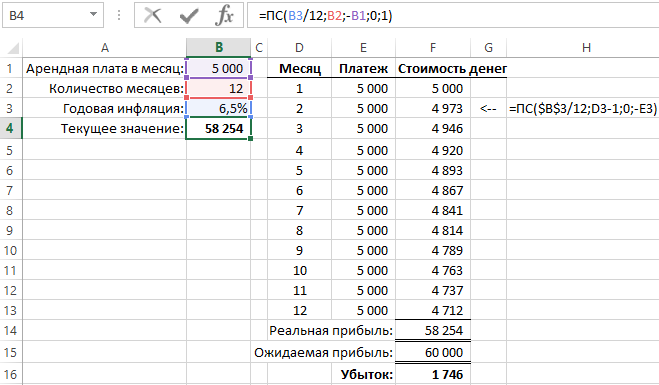
В другом примере применения функции ПС выполняется вычисление будущей стоимости денег сразу для целой серии будущих равных платежных взносов. Если, например, по договору аренды офиса арендатор должен платить по 5000 каждый месяц на протяжении одного года, тогда арендодатель с помощью функции ПС сможет посчитать сколько он потеряет дохода при учете 6,5% годовой инфляции:

В данном примере пятый аргумент «Тип» имеет числовое значение 1, так как оплата за аренду платится в начале каждого месяца.

В случае наличия суммы регулярных платежей функция ПС в реальности вычисляет текущую стоимость денег отдельно для каждого платежа и суммирует полученные результаты. На рисунке видны результаты вычисления стоимости для каждого платежа. Текущая стоимость первого платежа такая же, как и сумма платежа, так как платится сейчас по факту. Платеж в следующем месяце будет проплачен через месяц и уже уменьшается его текущая денежная стоимость (обесценивается). Он дисконтирован до суммы 4 973. Изменения не значительные, но последний платеж, который буде проплачен через 11 месяцев имеет стоимость уже существенно ниже – 4 712. Все результаты вычисления значений текущей стоимости инвестиций необходимо суммировать. Функция ПС выполняет всю эту работу автоматически без необходимости составления хронологического графика платежей за весь период.

В прошлой статье из курса «ФИНАНСОВАЯ МАТЕМАТИКА» мы рассмотрели понятие инфляции и статистические показатели для ее измерения, а сейчас закрепим полученные знания на практике.

Итак, убедившись, что с теорией у нас все ОК, учимся решать задачи: смотрим видеоурок и внимательно читаем примеры ниже.

Пример 1.

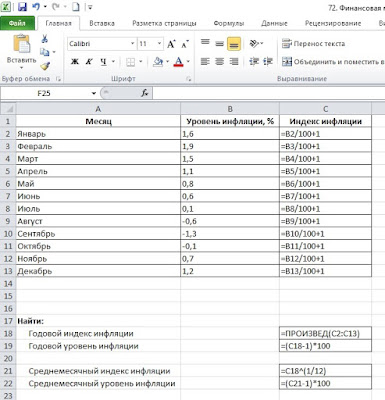
На рисунке 1 приведены исходные данные помесячных уровней инфляции на протяжении года (диапазон ячеек А1:В13 рабочего листа Excel). Например, за январь общий уровень повышения цен, или общий уровень инфляции составил 1,6%; в феврале — +1,9% и так далее. Вплоть до июля месяца мы видим ежемесячный рост цен. С августа по октябрь мы наблюдали снижение общего уровня цен, то есть, дефляцию. И в последние месяцы года инфляция вновь возобновилась. 

Рис. 1. Исходные данные

*Каждый рисунок можно увеличить щелчком левой кнопки мыши

Необходимо найти годовой индекс и годовой уровень инфляции, а также, среднемесячный индекс и среднемесячный уровень инфляции. 

Решение.

Для нахождения годовых и среднемесячных показателей, прежде всего, нам необходимо перейти от  исходных месячных уровней инфляции (колонка В) к соответствующим индексам инфляции (колонка С). Взаимосвязь между этими показателями демонстрирует первая формула, изображенная на рис. 1. Где лямбда — это уровень инфляции, %; І — индекс инфляции.

Выразив индекс инфляции через уровень инфляции, получим выражение: 

I = лямбда / 100% + 1.

Собственно, эту формулу и следует ввести в каждую из ячеек диапазона С2:С13.

Получив, таким образом, в ячейках С2:С13 месячные индексы инфляции, найдем в ячейке С18 годовой индекс инфляции с использованием второй формулы, рис. 1. То есть, общий индекс инфляции за весь период равен произведению частных индексов инфляции за все периоды, которые входят в его состав. В ячейку С18 введем формулу: 

=ПРОИЗВЕД(С2:С13).

Зная годовой индекс инфляции, рассчитаем в ячейке С19 годовой уровень инфляции с испоьзованием первой формулы, рис. 1. Для этого в ячейку С19 введем формулу: 

=(С18-1)*100.

Для нахождения среднемесячного индекса инфляции нам поможет третья формула, изображенная на рис. 1. То есть, зная общий индекс инфляции, мы должны найти корень n-ой степени из нее. Где n — количество рассчитанных месячных индексов инфляции, в нашем случае n=12. Итак, в ячейку С21 введем формулу: 

=С18^(1/12).

Теперь, зная среднемесячный индекс инфляции, переходим к среднемесячному уровню инфляции. В ячейку С22 вводим формулу: 

=(С21-1)*100.

Итак, все формулы, которые мы ввели на рабочий лист Excel показаны на рис. 2.

Рис. 2. Формулы для расчета требуемых показателей

Если теперь от формул перейти к результатам расчетов, то будем иметь, рис. 3.

Рис. 3. Результаты расчета годовых и среднемесячных показателей инфляции

По данным рисунка 3 можно сделать следующие выводы:

— в целом за год общий уровень цен в экономике вырос в 1,077 раза или на +7,71%;

— при этом, среднемесячный рост уровня цен составлял +0,621%.

Пример 2.

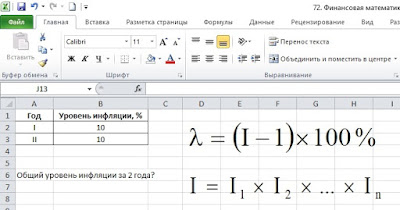
Уровень инфляции на протяжении двух лет составлял по 10% ежегодно. Найти общий уровень инфляции за эти два года. Условие задачи и необходимые для ее решения формулы приведены на рис. 4. 

Рис. 4. Исходные данные

Решение.

Распространенная ошибка при решении подобных задач: общий уровень инфляции за два года 10% + 10% = 20% — НЕПРАВИЛЬНО!

Общий уровень инфляции всегда находится только исходя из общего индекса инфляции, первая формула на рис. 4. Но для нахождения общего индекса инфляции, нам нужно знать частные индексы инфляции за каждый период, формула 2 на рис. 4.

Поэтому, в колонке С сначала найдем индексы инфляции для каждого года, используя формулу: I = лямбда / 100% + 1 = 10% / 100% + 1 = 1,1.

Далее, в ячейке С4 находим общий индекс инфляции за два года: 1,1 * 1,1 = 1,21. Ну и напоследок, в ячейке С7 найдем общий уровень инфляции за 2 года: (1,21 — 1) * 100% = 21%. Формулы для расчета требуемых показателей приведены на рис. 5.

Рис. 5. Формулы для расчета требуемых показателей

Таким образом, общий уровень инфляции за два года составил не 20%, как можно было подумать сначала, а ровно 21%.

Есть, со вторым примером разобрались. И еще один интересный и очень актуальный пример связанный с тем, что покупательная способность денег, вследствие инфляции, со временем падает.

Пример 3.

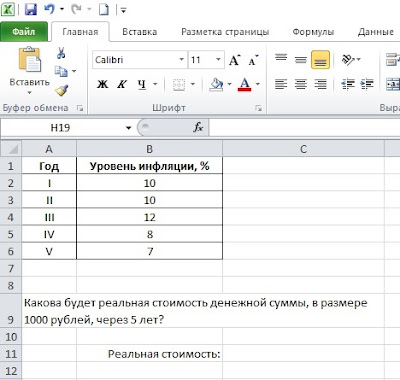
Имеются прогнозные данные о возможном уровне инфляции на протяжении следующих 5 лет. Необходимо определить, какова будет реальная стоимость денежной суммы, в размере 1000 руб. через 5 лет? Исходные данные приведены на рис. 6.

Рис. 6. Исходные данные

Решение.

Практическое решение данной задачи снова сводится к нахождению общего индекса инфляции.

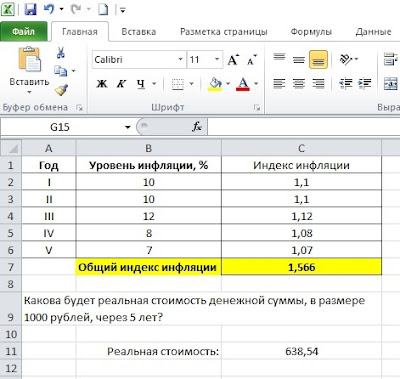
Сначала в колонке С находим индексы инфляции за каждый год. Далее в ячейке С7 рассчитываем общий индекс инфляции путем перемножения годовых индексов между собой. По результатам расчетов он будет равен 1,566. То есть, за 5 лет общий уровень цен в экономике вырастет в 1,566 раза. И ровно во столько же раз упадет покупательная способность наших 1000 руб.

В ячейке С11 рассчитываем реальную стоимость 1000 руб., как 1000 / 1,566 = 638,54 руб. Соответствующие результаты расчетов приведены на рис. 7.

Рис. 7. Результаты расчетов

Таким образом, через 5 лет за 1000 руб. мы сможем приобрести ровно такое же количество товаров и услуг, как и сегодня за 638,54 руб.

Все видеоуроки по курсу ФИНАНСОВОЙ МАТЕМАТИКИ вы можете найти на нашем Youtube-канале «Учите компьютер вместе с нами!»

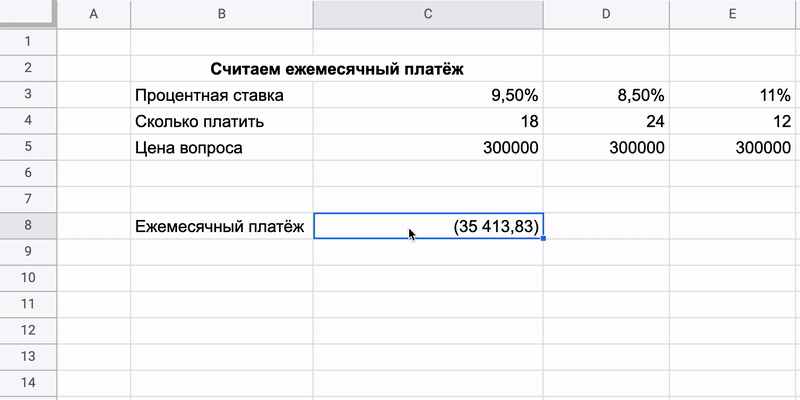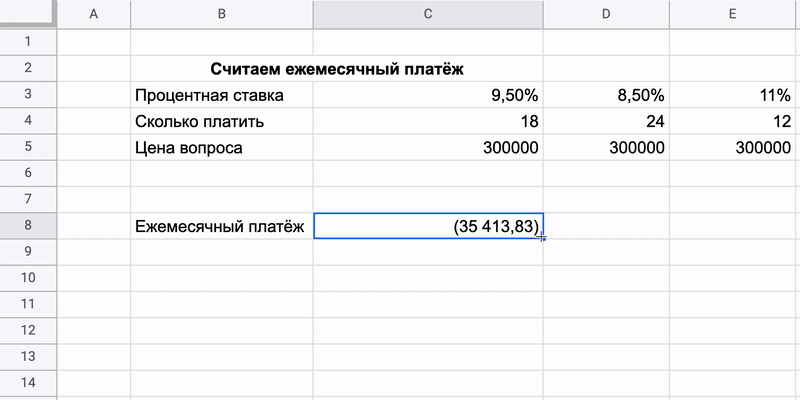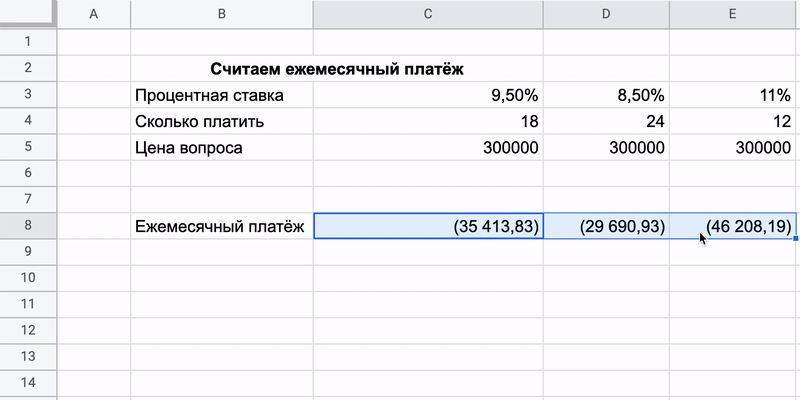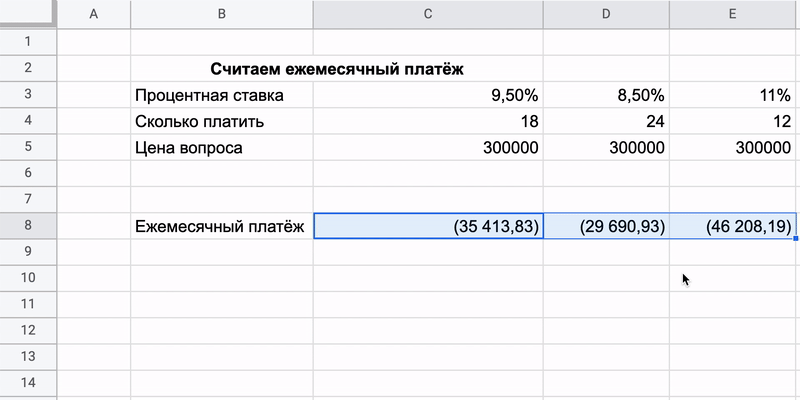
1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам

Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.

Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.

Какие данные нужны

Для начала надо правильно написать формулу — в любой свободной ячейке.

=ПЛТ(ставка;кпер;пс)

В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:

1. Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
2. Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
3. Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.

Как всё посчитать

Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.

Важно следить за оформлением: десятичные дроби отбиваются запятой, а не точкой. А ещё каждое значение в формуле нужно разделять точкой с запятой

Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.

Главное — не перепутать местоположение ячеек: все значения остаются в одних и тех же строках

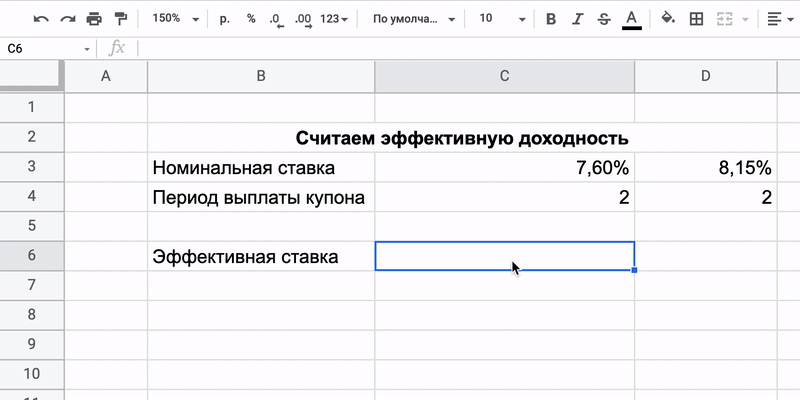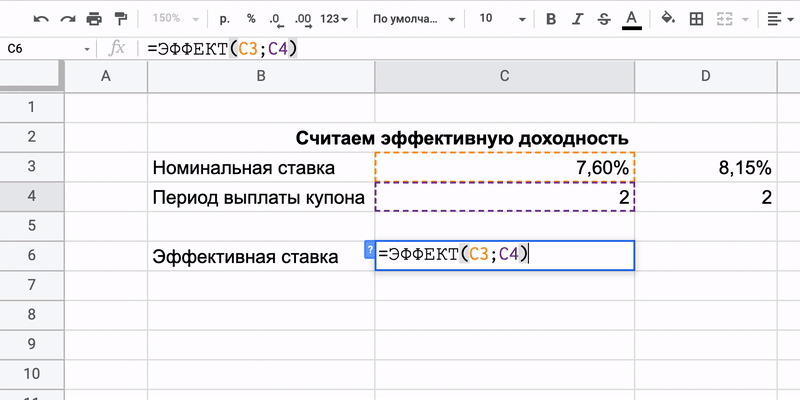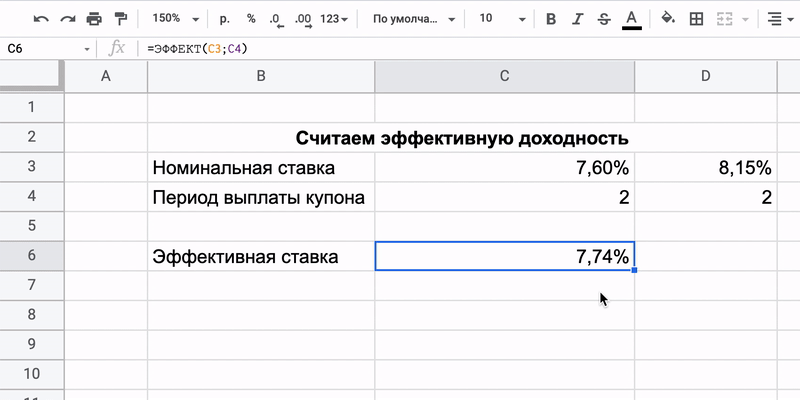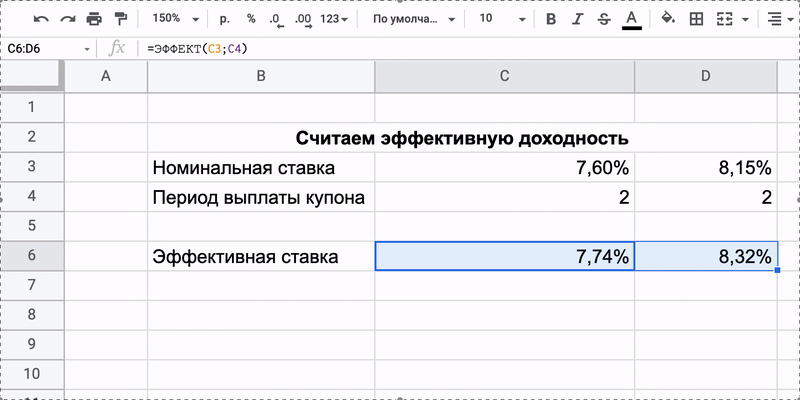
2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент

Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.

Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.

Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.

Какие данные нужны

Формула расчёта довольно простая:

=ЭФФЕКТ(номинальная_ставка;кол_пер)

В ней всего две переменные:

1. Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
2. Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).

Как всё посчитать

Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:

Чтобы было проще понимать результат, можно переключить отображение ячейки на проценты. А затем растянуть формулу дальше и сравнивать доходность

Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.

3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора

Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.

Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.

Какие данные нужны

Формула состоит из трёх компонентов:

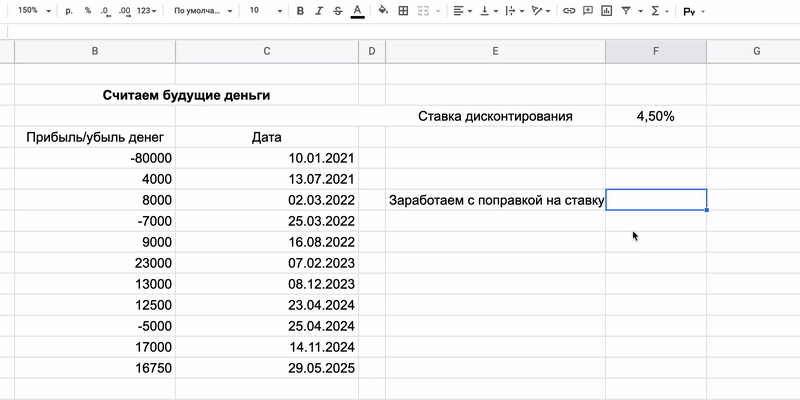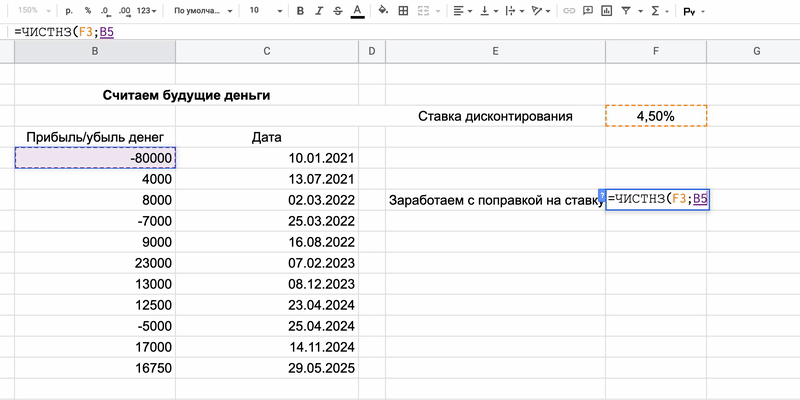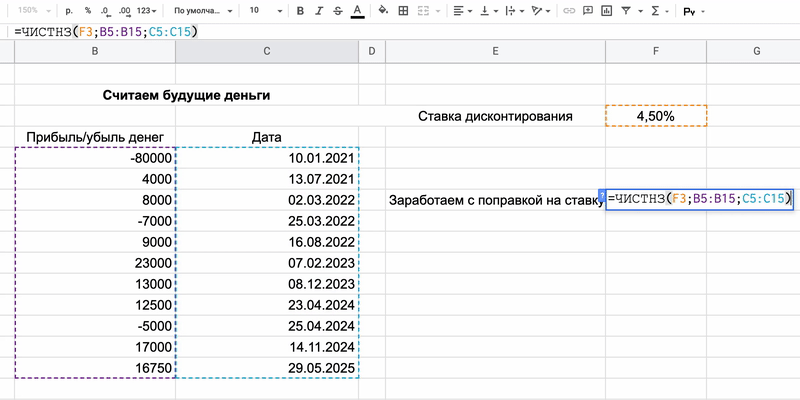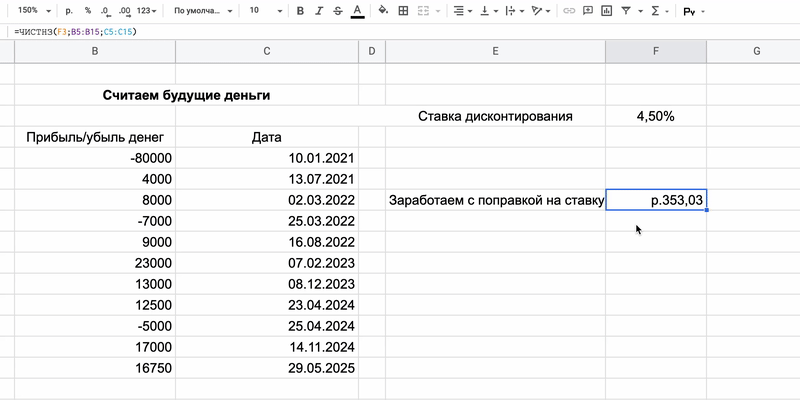
=ЧИСТНЗ(ставка;значения;даты)

Второй и третий достаточно ясны:

2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.

Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.

Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру , ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.

Как всё посчитать

Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.

Чтобы было проще осознавать результат, можно указать отображение «Валюта» для ячейки

Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.

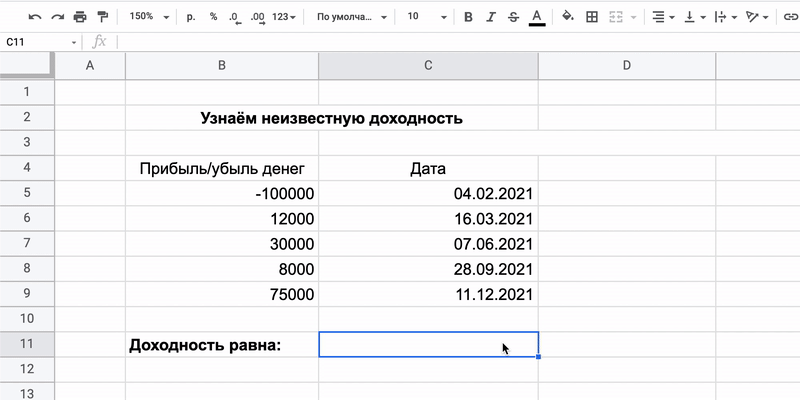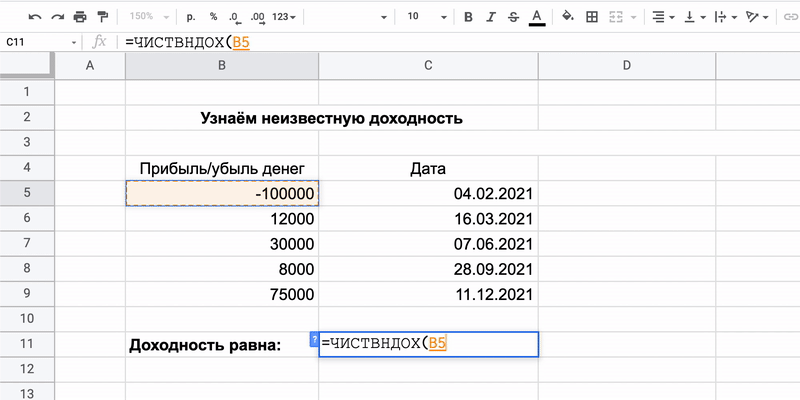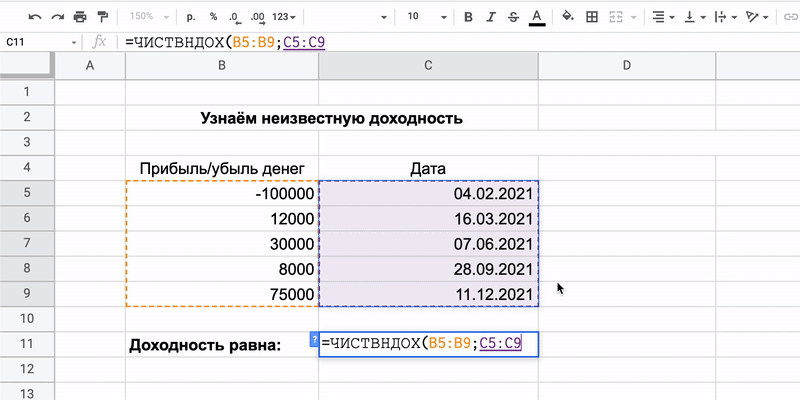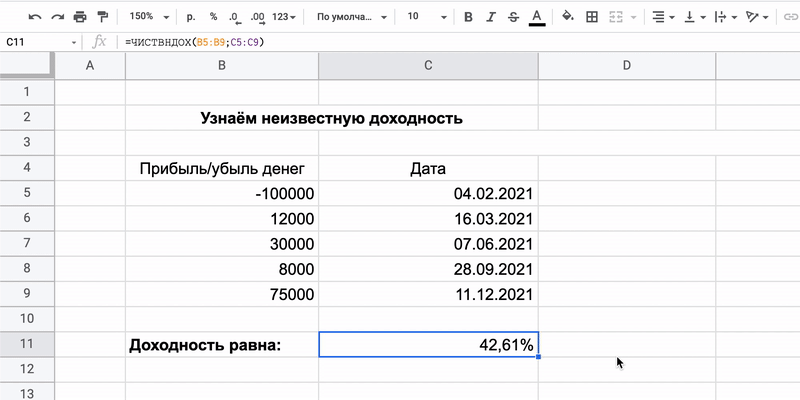
4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег

Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.

Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.

Какие данные нужны

Чтобы определить более выгодное предложение, применим формулу:

=ЧИСТВНДОХ(значения;даты)

Достаточно знать всего две переменные:

1. Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
2. Даты — график платежей, по которым будут выплачивать прибыль.

Как всё посчитать

Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.

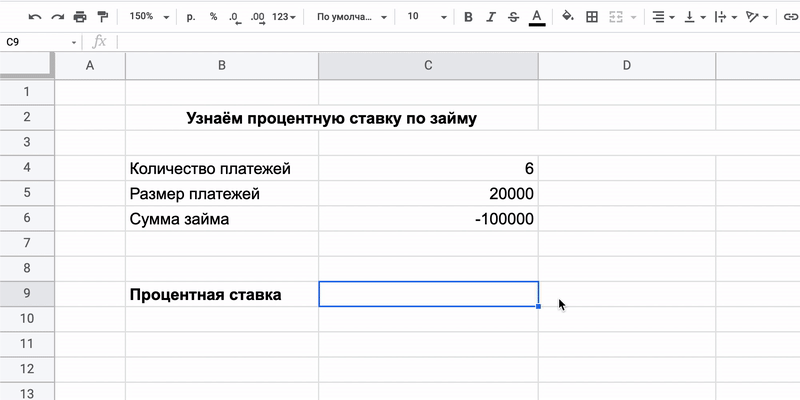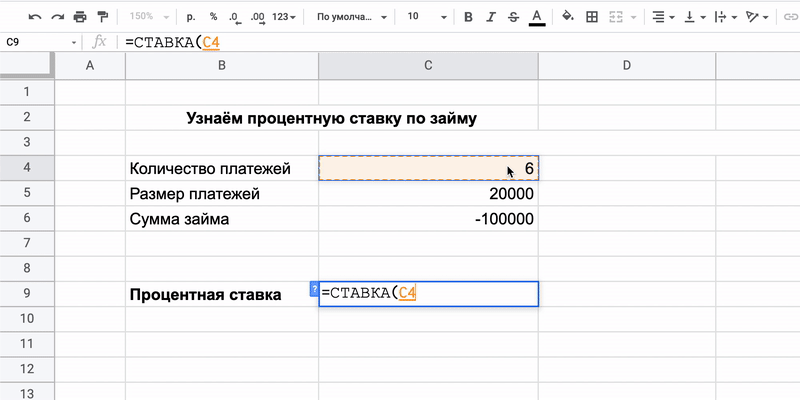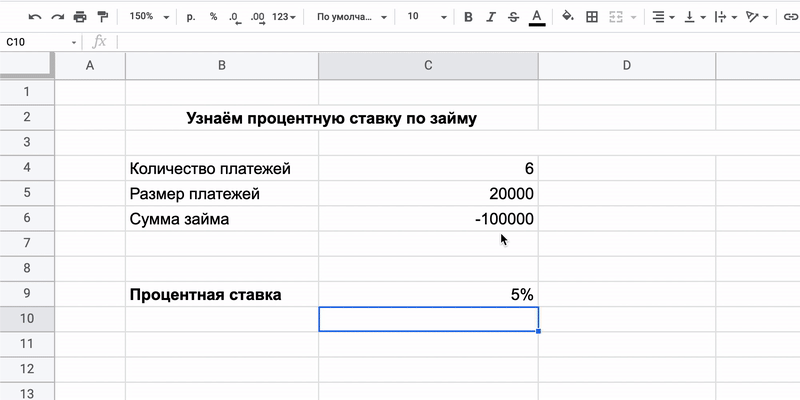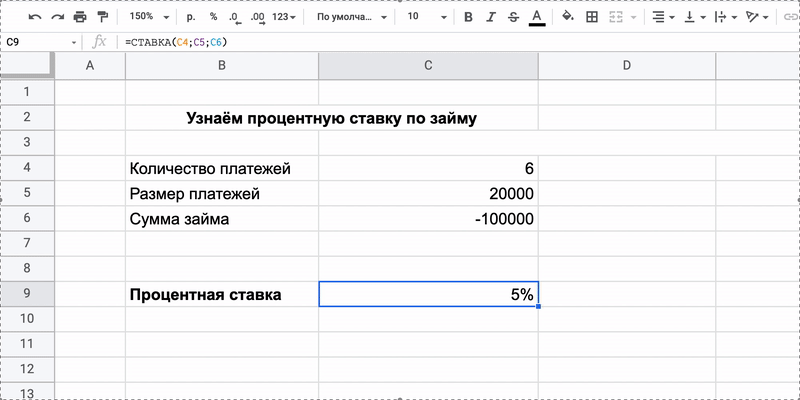
5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам

Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.

Какие данные нужны

Полезной будет эта формула:

=СТАВКА(кпер;плт;пс)

Три переменных в ней означают следующее:

1. Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
2. Плт — размер платежей. Считаются и основной долг, и проценты.
3. Пс — общая сумма займа. В нашем примере это 100 000 рублей.

Как всё посчитать

Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.

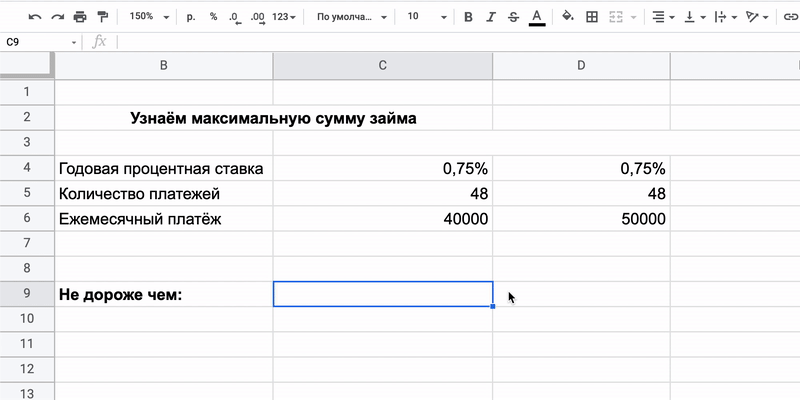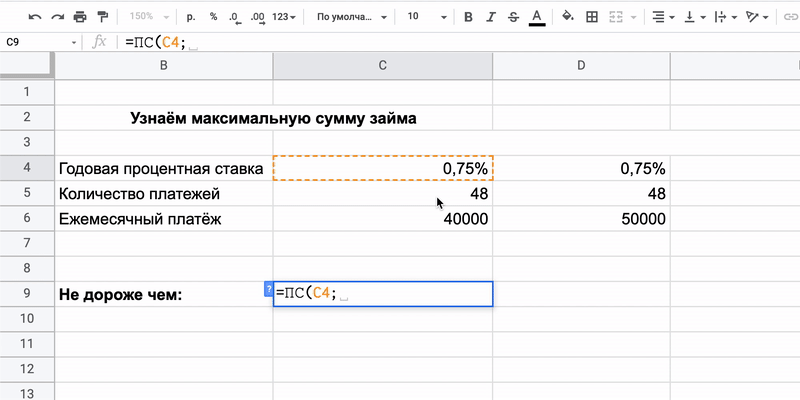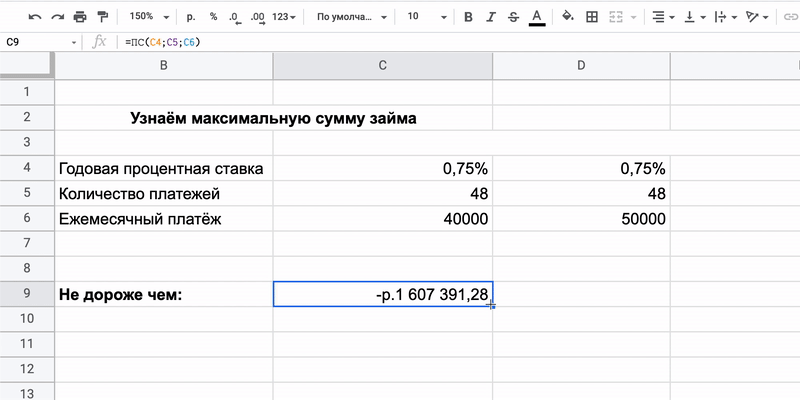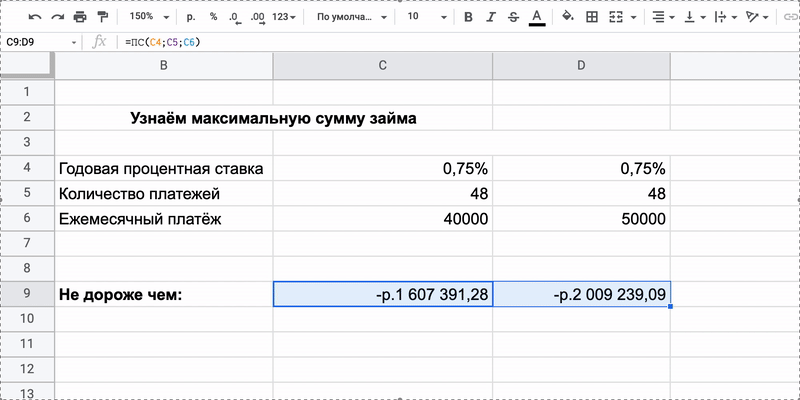
6. PV (ПС) — подсказывает, сколько денег можно взять в долг

Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.

Какие данные нужны

Пригодится формула расчёта текущей стоимости:

=ПС(ставка; кпер; плт)

Для этого потребуется информация, которая есть на сайте любого банка:

1. Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
2. Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
3. Плт — размер комфортного платежа.

Как всё посчитать

Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.

Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.

7. NPER (КПЕР) — помогает рассчитать время накоплений

Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.

Какие данные нужны

Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:

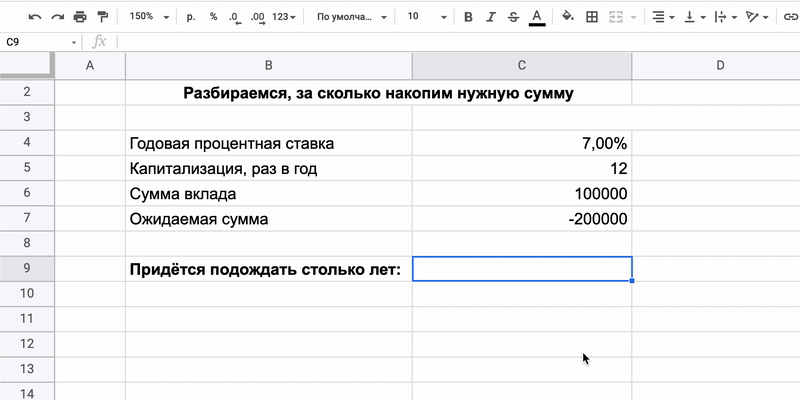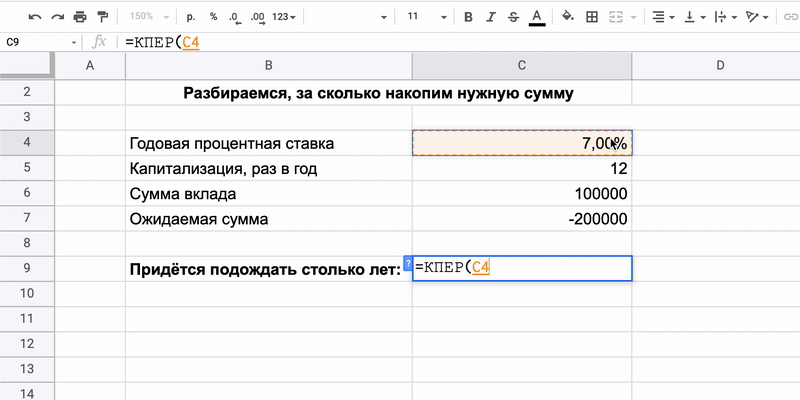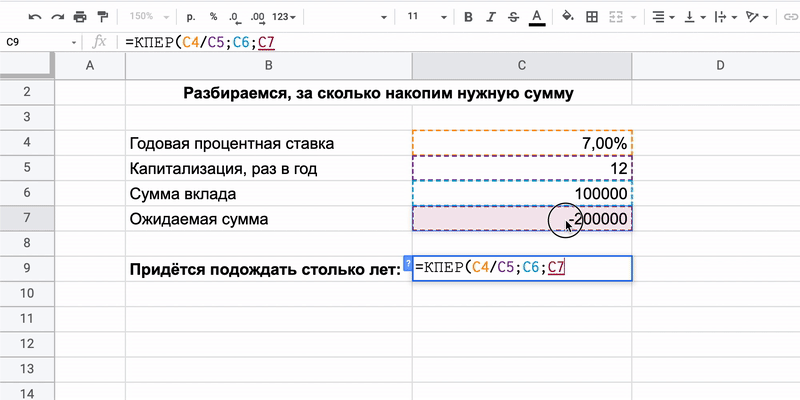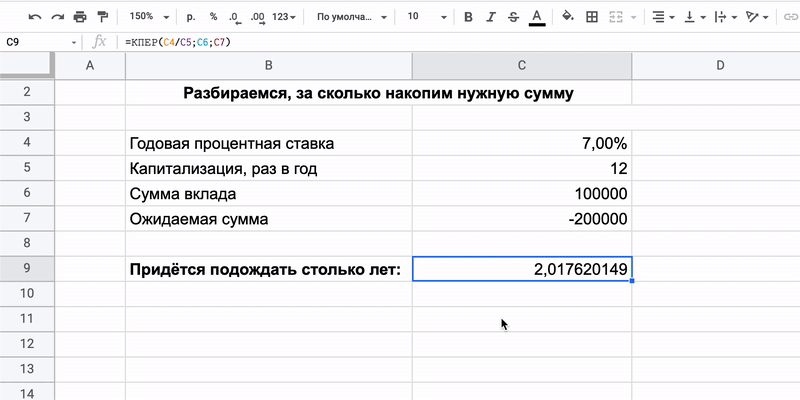
=КПЕР(ставка/периоды_капитализации;плт;пс;бс)

Она состоит из четырёх основных значений и одного дополнительного:

1. Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
2. Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
3. Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
4. Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
5. Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.

Как всё посчитать

Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.

Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.

Создание электронной таблицы для определения влияния инфляции на стоимость денег

Действительная
стоимость денег зависит от инфляции и
определяется по следующей формуле:

,
(2)

где

процент инфляции за период (например,
за год).

Задание 1.2

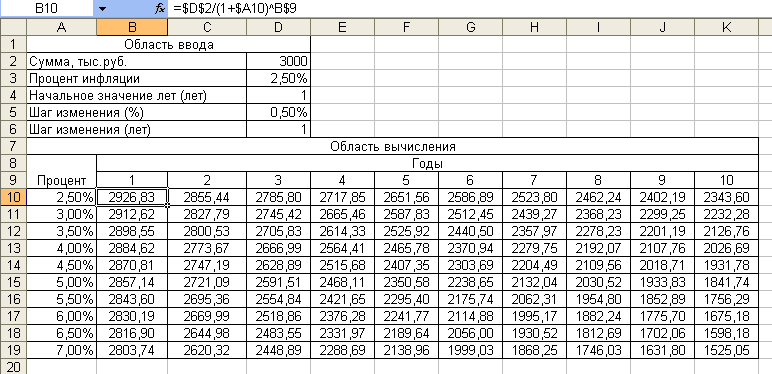
Аналогично
рассмотренному примеру создайте таблицу
для расчета реальной стоимости денег
с возможностью изменения суммы и процента
инфляции (рисунок 2).

Решение:

Рисунок
2 Таблица расчета реальной стоимости
денег с возможностью изменения суммы
и процента инфляции

Создание электронной таблицы для расчета процентов по остаткам на расчетном счете в банке

Задание 1.3

На конец каждого
операционного дня на расчетном счете
присутствуют остатки денежных средств:

Банк начисляет на
них проценты из расчета 3,0% годовых.
Датой поступления процентов на расчетный
счет является 26 число каждого месяца.
Выбран период с 27.09.2006г. по 26.10.2006 г.

Необходимо
произвести расчет суммы начисленных
процентов.

Решение:

Составим таблицу,
в которую внесем даты и суммы остатков
на расчетном счете на конец каждого
операционного дня.

Столбец А отведем
для дат, столбец В – для остатков на
расчетном счете, а столбец С – для
определения суммы ежедневно начисляемого
процента (рисунок 3).

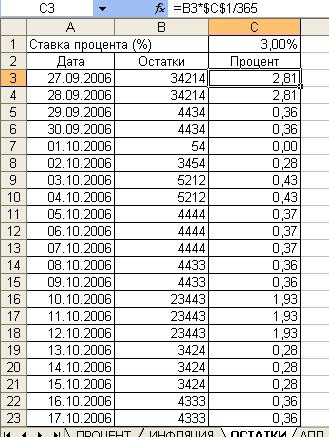
Рисунок
3 Таблица для расчета процентов по
остаткам

на
расчетном счете

В ячейку А3 введем
начальную дату 27.09.2006, а в ячейку А4
формулу:

=
А3 + 1. Для
заполнения
диапазона
А5:А32 применим метод автозаполнения.

Изменение даты в
ячейки А3 повлечет за собой соответствующее
изменение дат в области А4:А32. Это позволит
нам в следующем месяце, изменив дату в
ячейке А3, изменить весь временной
интервал.

В ячейку В4 введем
формулу: =
В3.

Таким образом,
сумма остатка на следующий день будет
равна сумме остатка предыдущего дня.
Это позволяет сэкономить время при
вводе данных в столбце остатков.
Аналогичным образом заполните все
пустые ячейки в столбце В.

Формула для
определения суммы процента (столбец С)
имеет следующий вид: =
B3*$C$1/365.

В данном случае
сумма денежных средств на расчетном
счете на каждую конкретную дату (ячейка
В3) умножается на процент банка (абсолютная
ссылка на ячейку С1) и делится на количество
дней в году (365).

2 Лабораторная работа №2. Обработка и анализ экономической информации с помощью финансовых функций ms Excel

Цель работы
−
формирование теоретических знаний и
практических навыков использования
финансовых
функций MS
Excel
для обработки, анализа экономической
информации и решения финансовых задач.

Задачи работы:

− уяснить сущность
и аргументы основных финансовых функций;

− определить
будущую стоимость на основе постоянной
и переменной процентных ставок;

− рассчитать
доходность ценных бумаг;

− определить
амортизационные отчисления;

− овладеть навыками
выбора финансовых функций для решения
экономических задач в зависимости от
исходных данных.

Теоретические
положения

В состав табличного
процессора Microsoft
Excel
входит более 300 встроенных функций,
дающих возможность выполнять самую
разнообразную обработку данных. Следует
различать понятия «встроенная функция»
(один из множества вычислительных
элементов Excel)
и «формула» (конкретное выражение,
возможно, включающее в себя более чем
одну функцию и выполняющее действия на
основе одного или нескольких значений).

Встроенные функции
MS
Excel
традиционно разделяются на следующие
категории:

− финансовые
функции;

− математические;

− функции для
работы с базами данных, массивами и
ссылками;

− функции работы
с датой и временем;

− логические
функции;

− статистические
функции и др.

Финансовые функции
применяются при планировании и анализе
финансово-хозяйственной деятельности
предприятия, а также при решении задач,
связанных с инвестированием средств.

В качестве
аргументов функций могут использоваться
константы, ссылки на ячейки, имена
диапазонов ячеек, а также другие функции
(вложенные функции). Рассмотрим основные
финансовые функции Microsoft
Excel.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #