Рассмотрим понятие процентиля, функцию
ПРОЦЕНТИЛЬ.ВКЛ()
, процентиль-ранг и построим кривую процентилей.
Сначала разберемся на примерах, что такое
процентиль
, затем рассмотрим соответствующие функции MS EXCEL.
Задача.
Проектируют койку на круизном лайнере. Необходимо, чтобы 95% пассажиров помещались на койке в полный рост. Как вычислить длину койки?
Для решения задачи потребуется найти рост, ниже которого 95% населения. Для этого нужно сделать
репрезентативную выборку
, скажем, из 2000 человек,
отсортировать значения выборки по возрастанию
, потом определить значение с позицией равной 1901 (2000*95%+1). Пусть найденный рост оказался равен 190 см.
Ответ
: Длина койки должна быть 190 см (+ запас для комфортного размещения на койке).
Значение 190 см называется 95%-й
процентилью
данной
выборки
, т.е. 95% опрошенных людей имеет рост <190 см.
Примечание
: Найденное значение (190см) является
оценкой
95%-й
процентили
всей
генеральной совокупности
, из которой взята
выборка
.
СОВЕТ
: Понятие
процентиля
связано с понятием
квантиля функции распределения
. Поэтому имеет смысл освежить в памяти понятия
функции распределения и обратной функции
.
На основании вышесказанного сформулируем определение для
процентили
:
K-й Процентиль представляет такое собой значение
Х
в наборе данных, которое разделяет набор на две части: одна часть содержит K процентов данных,
меньших Х
, а другая часть содержит все остальные значения набора (т.е. 1-
K
процентов данных б
о
льших Х).
Приведем алгоритм для нахождения
k
-й процентили выборки:
-
отсортировать значения
выборки
по возрастанию (пусть в
выборке
всего N значений); -
найти такую позицию в списке
, для которой k% значений оказалось бы меньше этого значения. Это можно сделать с помощью формулы N*k%+1 (затем,
округлить его до целого
);
-
значение, находящееся в этой позиции, и будет
k
-й процентилью
(примерно), т.к. k% значений массива данных будет меньше этого значения.
Примечание
: Более точный алгоритм расчета
процентилей
дан ниже в разделе про функцию
ПРОЦЕНТИЛЬ.ВКЛ()
.
Еще одна
задача
.
Зачет «автоматом» поставят только тем студентам, которые в течение семестра набрали в течение семестра больше баллов, чем 90%-я Процентиль (другими словами 10% лучшим студентам поставят зачет «автоматом»).
Так как порог установлен в
процентилях
, то заданному % студентов придется сдавать экзамен вне зависимости от набранных баллов (т.е. 90% студентов в любом случае будут сдавать экзамен). А вот если бы порог был установлен в абсолютных значениях, например, 380 баллов из 400, то вполне вероятна ситуация, когда половине студентов поставили бы «автоматом» (если бы они, конечно, набрали бы больше 380 баллов). Или наоборот, при общих слабых результатах ни один студент не получил бы зачет «автоматом». Установка порога в
процентилях
создает предпосылки здоровой конкуренции (или, наоборот, сговора: даже если никто особо не учился, то в любом случае 10% получат зачет «автоматом»).
Решим эту задачу, используя заданные значения
выборки
. Пусть всего 120 студентов, значения баллов за семестр разместим в диапазоне
A8:A127
(см.
Файл примера
, лист
Пример-Студенты
). Максимальный суммарный балл = 400. Порог получения зачета «автоматом» — больше баллов, чем 90%-я
Процентиль
.
Понятно, чтобы определить тех студентов, которые получат зачет «автоматом» нужно отсортировать их по набранным баллам и отобрать 10% (т.е. 12 студентов) с максимальными баллами. Но, чтобы студенты сами определились, начинать ли им готовиться к экзамену или нет, достаточно сообщить им проходной балл (90%-ю
процентиль
). Рассчитаем этот проходной балл.
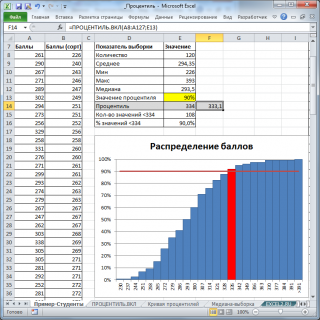
Для наглядности построим
Гистограмму распределения с накоплением
.
90%-ю
процентиль
можно найти с помощью формулы
=НАИМЕНЬШИЙ(A8:A127;ЦЕЛОЕ(120*0,9)+1)
Эта формула создана на основе алгоритма, приведенного выше. Результат формулы — 334 балла.
Как видно из рисунка выше, количество значений массива (студентов), у которых баллы хуже, действительно равно 108 (90% от 120). Следовательно, как и предполагалось, 12 студентов получат зачет «автоматом».
Примечание
:
Найденное значение
процентили
334 является приблизительным. Точное значение дает формула
=ПРОЦЕНТИЛЬ.ВКЛ(A8:A127;0,9)
, которое равно 331,4. О том как работает функция
ПРОЦЕНТИЛЬ.ВКЛ()
читайте ниже.
Как показывает опыт, для данных выборки
K
-я
процентиль
не всегда отделяет точно
К
процентов значений, которые меньше ее. Например, в нашем примере найдем 80%-ю
процентиль.
Оказывается, что только 79% значений меньше 80%-й
процентили
(318). Это происходит из-за округления. Для
выборок
с большим количеством значений (>100) обычно наблюдается хорошее соответствие. Повторы значений также могут привести к несоответствию значения
процентиля
и соответствующего % значений (см. ниже).
Примечание
:
Процентили
часто называют
перцентилями
(с этим соглашается и MS WORD) или
центилями
. В версии MS EXCEL 2007 и более ранних использовалась функция
ПЕРСЕНТИЛЬ()
, которая оставлена для совместимости. Но, начиная с версии EXCEL 2010, появились функции
ПРОЦЕНТИЛЬ.ВКЛ()
и
ПРОЦЕНТИЛЬ.ИСКЛ()
– английское название PERCENTILE.EXC(), а
Условное форматирование
предлагает настроить правило с использованием именно
процентилей
. В свою очередь,
надстройка Пакет Анализа
имеет инструмент
Ранг и Персентиль
.
Google также отдает предпочтение
процентилям
, выдавая гораздо больше результатов на запрос «процентиль», чем на запрос «перцентиль» (на начало 2016 года).
Таким образом, для
процентилей
используется 3 названия:
процентиль
(MS EXCEL, Google)
, персентиль
(MS EXCEL)
, перцентиль
(MS WORD)
.
Ниже детально рассмотрим как работает функция
ПРОЦЕНТИЛЬ.ВКЛ()
и создадим ее аналог с помощью альтернативной формулы. Также рассмотрим функцию
ПРОЦЕНТРАНГ.ВКЛ()
и
кривую процентилей
.
СОВЕТ
:
Нижеследующие разделы следует читать пользователям, владеющими базовыми понятиями
математической статистики (случайная величина, функция распределения)
.
Функция
ПРОЦЕНТИЛЬ.ВКЛ()
Начиная с версии MS EXCEL 2010 для расчета
процентилей
используется функция
ПРОЦЕНТИЛЬ.ВКЛ()
– английское название PERCENTILE.INC(). В более ранних версиях MS EXCEL использовался ее аналог — функция
ПЕРСЕНТИЛЬ()
.
Напомним определение
процентиля
, данное выше:
K-й Процентиль представляет такое собой значение
Х
в наборе данных, которое разделяет набор на две части: одна часть содержит K% данных,
меньших Х
, а другая часть содержит все остальные значения набора (т.е. 1-
K
% данных б
о
льших Х).
Разберем детально как работает функция
ПРОЦЕНТИЛЬ.ВКЛ()
.
Пусть имеется массив значений (
выборка
). В массиве 49 значений, массив расположен в диапазоне
B15:B63
, имеются
повторы значений
, массив для удобства
отсортирован по возрастанию
(см.
файл примера
, лист
ПРОЦЕНТИЛЬ.ВКЛ
).
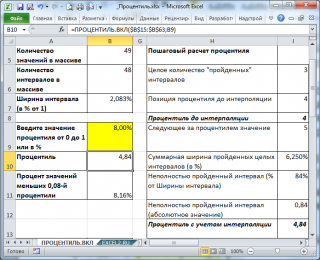
Рассчитаем 0,08-ю
процентиль
(
8%-процентиль
) с помощью формулы
=ПРОЦЕНТИЛЬ.ВКЛ(B15:B63; 0,08)
. Получим, что 0,08-я
процентиль
равна 4,84.
Проанализируем, что мы получили.
-
Во-первых, значения 4,84 нет в массиве (есть 4 и 5), т.е. функция
ПРОЦЕНТИЛЬ.ВКЛ()
интерполирует значения. -
Во-вторых, процент значений меньших 4,84 равен не точно 8%, а 8,16%=4/49*100% (т.к. всего 4 значения в массиве меньше 4,84). Это произошло, т.к. в
выборке
относительно мало значений. -
Другой причиной расхождения могут стать повторы. Например, заменив, первые 4 значения в массиве (т.е. 1; 2; 3; 4) числом 5, мы получим вместо 8,16% — 0%. Это произошло потому, что теперь 0,08-я
процентиль
равна 5, а в
выборке
нет ни одного значения меньше 5.
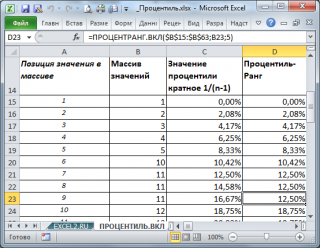
Как видно из рисунка ниже первое значение (
минимальное
, равное 1) является 0-й
процентилью
.
Соответственно, 1-й
процентилью
(100%
процентилью
), является
максимальное значение
равное 120 (см.
файл примера
лист ПРОЦЕНТИЛЬ.ВКЛ).
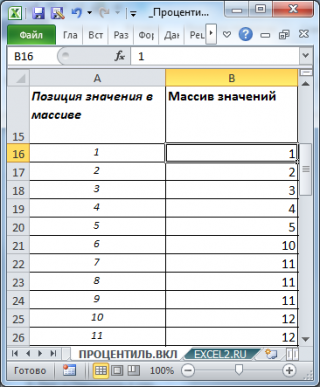
Как видно из рисунка, следующее за минимальным значением (т.е. число 2) является 0,0208-й
процентилью
. Значение 0,0208 или 2,08% — это (k-1)*1/(n-1), где n – это количество значений в массиве (в нашем массиве n=49), а k – это позиция числа в массиве (в данном случае k=2, где 2 – это позиция, а не само число).
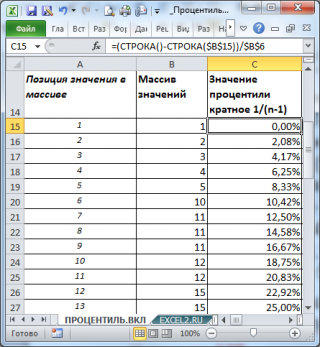
Поясним эту формулу. Для вычисления
процентили
принимается, что весь диапазон значений массива (от мин до макс) разбит n значениями на равные интервалы (их всего n-1). Соответственно, 1/(n-1), это «ширина» интервала (весь диапазон равен 1 или 100%). Обратите внимание, что «ширина» интервала не зависит от данных, а только от их количества. В нашем случае «ширина» интервала равна 0,0208 или 2,08%.
Приведем алгоритм расчета
12,50%-процентили
функцией
ПРОЦЕНТИЛЬ.ВКЛ()
(см. ячейку
С21
):
ПРОЦЕНТИЛЬ.ВКЛ()
определяет «ширину» интервала (в долях или процентах): =1/(49-1)=0,0208;-
подсчитывает
Количество интервалов
, которые были укладываются в 12,50%, т.е. =12,50%/2,08%=6 (значение
процентиля
кратно ширине интервала, т.е. делится нацело); - 6-й интервал располагается между числами массива 10 и 11. Верхняя граница последнего 6-го интервала равна 11;
-
Следовательно,
12,50%-я процентиль
равна 11 (см. ячейку
B
21
).
По аналогии с
непрерывной функцией распределения
(см.
статью про квантили
), получается, что 12,50% значений должно быть меньше полученного числа 11 (в соответствии с определением
процентиля
). Фактически получается, что таких значений 6 (1; 2; 3; 4; 5; 10) и процент значений меньших 11 равен 12,24%=6/49 (причины расхождения: повторы и небольшое количество значений).
Если значение
процентиля
не кратно ширине интервала (ширина интервала равна 1/(n-1)), то имеет место интерполирование. Например, вспомним результат вычисления
0,08-й процентили
равный 4,84. Значение
процентили
(т.е. не результат, а %) равно 0,08 (8%), что соответствует 3-м целым интервалам (8%/2,08%=
3
,84) и некой доли (0,84) от ширины следующего интервала. Границами этого «неполного» интервала являются значения 4 (
0,0625-я процентиль
) и 5 (
0,0833-я процентиль
). Т.к. разница между 5 и 4 равна 1, то умножая «пройденную» долю интервала (0,84) на длину интервала в абсолютных значениях (=5-4=1), получаем 0,84. В итоге получаем 4,84: 4 – левая граница интервала + часть следующего (5-4)*0,84.
Если бы в массиве вместо 5 было значение 6, то значение
0,08-й процентили
было бы равно 5,68 (4 – левая граница интервала + (6-4)*0,84=1,68).
Альтернативный расчет
процентили
с помощью формул приведен в
файле примера
.
Примечание
: Некоторые значения
процентилей
имеют специальные названия:
-
25-я
процентиль
называется 1-й квартилью; -
50-я
процентиль
называетсяМедианой
(2-я квартиль);
-
75-я
процентиль
называется 3-й квартилью.
Функция
ПРОЦЕНТРАНГ.ВКЛ()
и Кривая процентилей
Функция
ПРОЦЕНТРАНГ.ВКЛ()
используется для оценки относительного положения значения в массиве. Для заданного значения функция вычисляет сколько значений в массиве меньше или равно ему. Точнее — какой процент значений массива меньше или равен ему. Результат функции называется
процентиль-ранг (percentile rank)
. Понятно, что для максимального значения
процентиль-ранг
равен 0,00%, а для наименьшего — 100% (все значения массива меньше или равны ему).
Функция
ПРОЦЕНТРАНГ.ВКЛ()
, английская версия – PERCENTRANK(), является, в каком-то смысле, обратной функции
ПРОЦЕНТИЛЬ.ВКЛ()
: т.е. задавая в качестве аргумента значение из массива, функция
ПРОЦЕНТРАНГ.ВКЛ()
вернет
значение процентили
кратной 1/(n-1).
Как видно из рисунка выше, для повторяющихся значений функция
ПРОЦЕНТРАНГ.ВКЛ()
вернет, естественно, одинаковые значения. Также поступает функция
РАНГ.РВ()
или
РАНГ()
(см. статью
Функция РАНГ() в MS EXCEL
).
Действительно, функции
РАНГ.РВ()
и
ПРОЦЕНТРАНГ.ВКЛ()
очень похожи. Первая
возвращает позицию числа в массиве
в зависимости от его значения. Вторая, в принципе, делает тоже самое, но результат выводится в % от общего количества значений в массиве.
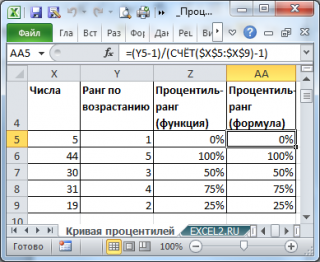
Как видно из картинки выше, чтобы получить
процентиль-ранг
необходимо значение ранга уменьшить на 1 и разделить на n-1. Значение
ранга
, естественно, должно быть
отсортировано по возрастанию
.
По
выборке
можно оценить
функцию распределения
Генеральной совокупности
, из которой взята данная
выборка.
Для этой цели построим
Кривую процентилей
(percentile curve или percentile rank plot).
Кривая
процентилей
представляет собой график зависимости
процентиль-ранга
от значений
выборки
.
Возьмем
выборку
состоящую из 100 значений (см.
файл примера
лист
Кривая процентилей
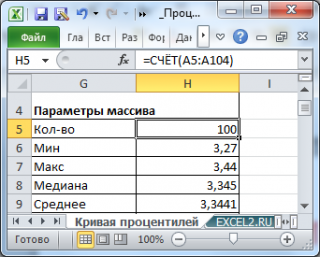
). Значения содержатся в диапазоне
А5:А104
.
Сначала построим
таблицу частот
для каждого из значений
выборки
.
Примечание
: В отличие от
Гистограммы
, где
кумулятивная
таблица частот
строится для интервалов значений,
таблицу частот
для
Кривой
процентилей
строят для
каждого
из значений
выборки
.
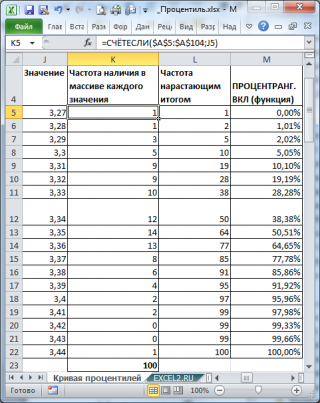
Из таблицы видно (столбец
Частота нарастающим итогом
), что
примерно
1 процент значений меньше или равен значения 3,27,
примерно
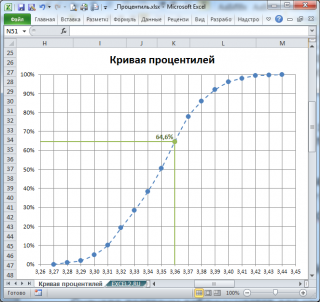
2 процента на уровне или ниже 3,28, 5 процентов на уровне или ниже 3,29, и так далее. График
Кривой
процентилей
для этих данных приведен на картинке ниже.
СОВЕТ
: Про построение графиков см. статью
Основные типы диаграмм
.
Следует отметить, что использование данных из таблицы приведет к точечному виду кривой (так как
процентиль-ранг
будет изменяться скачком для каждого значения
выборки
). Поэтому, сглаженная кривая, построенная на основе этих данных будет лучше представлять оцениваемую
функцию распределения
(пунктирная кривая).
Построив пунктирную кривую, становится ясно, зачем нам пришлось вводить понятие
процентиль-ранга: процентиль-ранг
– является приблизительной вероятностью выбрать случайную величину меньше или равную соответствующему значению (сравните с определением функции распределения). Это, в частности следует из расчета
процентиль-ранга
по формуле
=СЧЁТЕСЛИ($A$5:$A$104;»<«&A5)/ (СЧЁТ($A$5:$A$104)-1)
Обратите внимание, что при построении
Кривой процентилей
никакие значения из
выборки
не были удалены или сгруппированы. В этом смысле, построение
Кривой процентилей
это более точная процедура для оценки вида
функции распределения
, чем построение
Гистограммы данных
(так как информация не теряется в процессе построения). Правда, для этого требуется достаточно большая выборка (лучше >100 значений).
Примечание
: Формула
=(РАНГ.РВ(A5;$A$5:$A$104;1)-1)/ (СЧЁТ($A$5:$A$104)-1)
эквивалентна формуле
=ПРОЦЕНТРАНГ.ВКЛ($A$5:$A$104;A5;5)
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает k-ю процентиль для значений диапазона, где k — число от 0 и 1 (включая эти числа).
Эта функция используется для определения порога приемлемости. Например, можно принять решение экзаменовать только тех кандидатов, которые набрали большее количество баллов, чем 90-я персентиль.
Синтаксис
ПРОЦЕНТИЛЬ.ВКЛ(массив;k)
Аргументы функции ПРОЦЕНТИЛЬ.ВКЛ описаны ниже.
-
Массив — обязательный аргумент. Массив или диапазон данных, который определяет относительное положение.
-
k Обязательный. Значение процентили в интервале от 0 до 1, включая эти числа.
Замечания
-
Если массив пуст, процентиль. Inc возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если k не является числом, то процентиль. Inc возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если k < 0 или k > 1, процентиль. Inc возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если k не кратно 1/(n — 1), функция ПРОЦЕНТИЛЬ.ВКЛ производит интерполяцию для определения значения k-ой процентили.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
1 |
||
|
3 |
||
|
2 |
||
|
4 |
||
|
Формула |
Описание |
Результат |
|
=ПРОЦЕНТИЛЬ.ВКЛ(A2:A5;0.3) |
Тридцатая процентиль списка в диапазоне A2:A5. |
1,9 |
Нужна дополнительная помощь?
17 авг. 2022 г.
читать 2 мин
Вы можете использовать функцию ПРОЦЕНТРАНГ в Excel, чтобы вычислить ранг значения в наборе данных в процентах от общего набора данных.
Эта функция использует следующий базовый синтаксис:
=PERCENTRANK( A2:A16 , A2 )
В этом конкретном примере вычисляется процентильный ранг значения A2 в диапазоне A2:A16 .
В Excel также есть две другие функции процентиля:
- PERCENTRANK.INC : вычисляет процентильный ранг значения, включая наименьшее и наибольшее значения.
- PERCENTRANK.EXC : вычисляет процентильный ранг значения, исключая наименьшее и наибольшее значения.
В следующих примерах показано, как использовать эти функции на практике.
Пример: вычисление процентиля в Excel
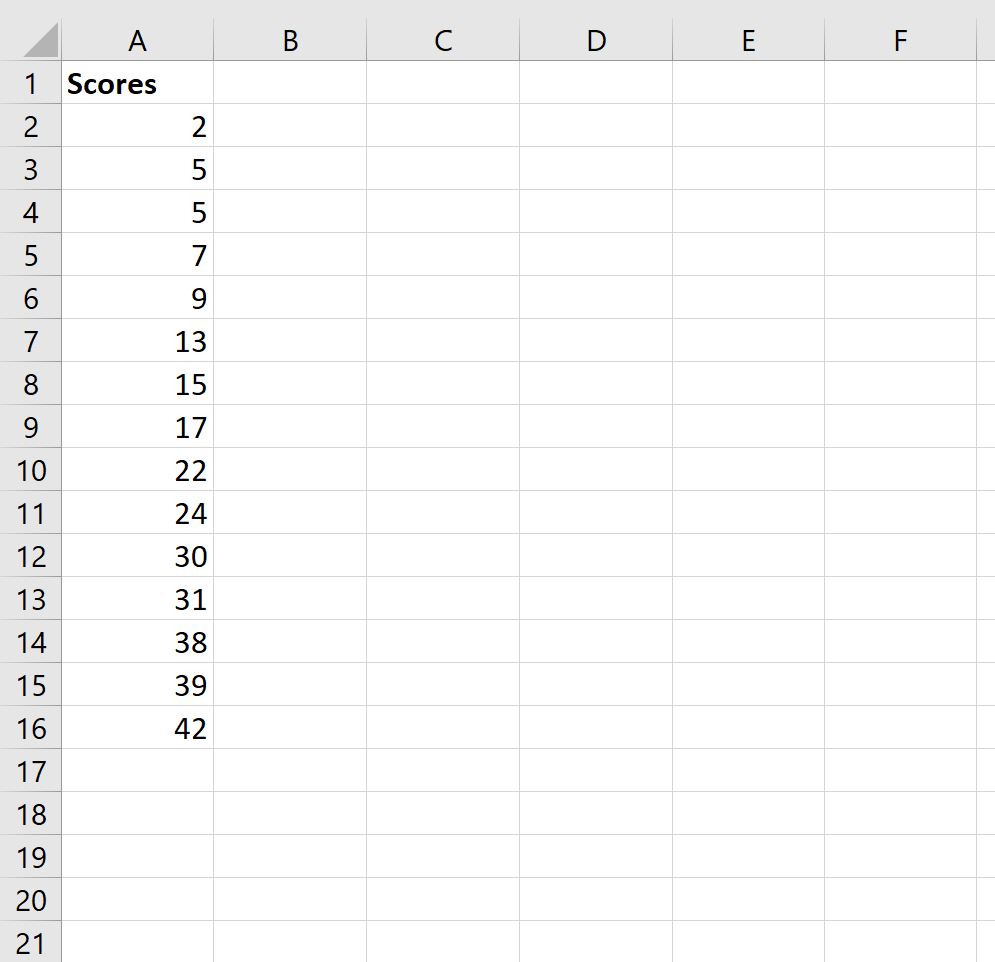
Предположим, у нас есть следующий набор данных, который показывает результаты экзаменов, полученные 15 учениками в определенном классе:
Теперь предположим, что мы хотели бы вычислить процентильный ранг оценки каждого учащегося.
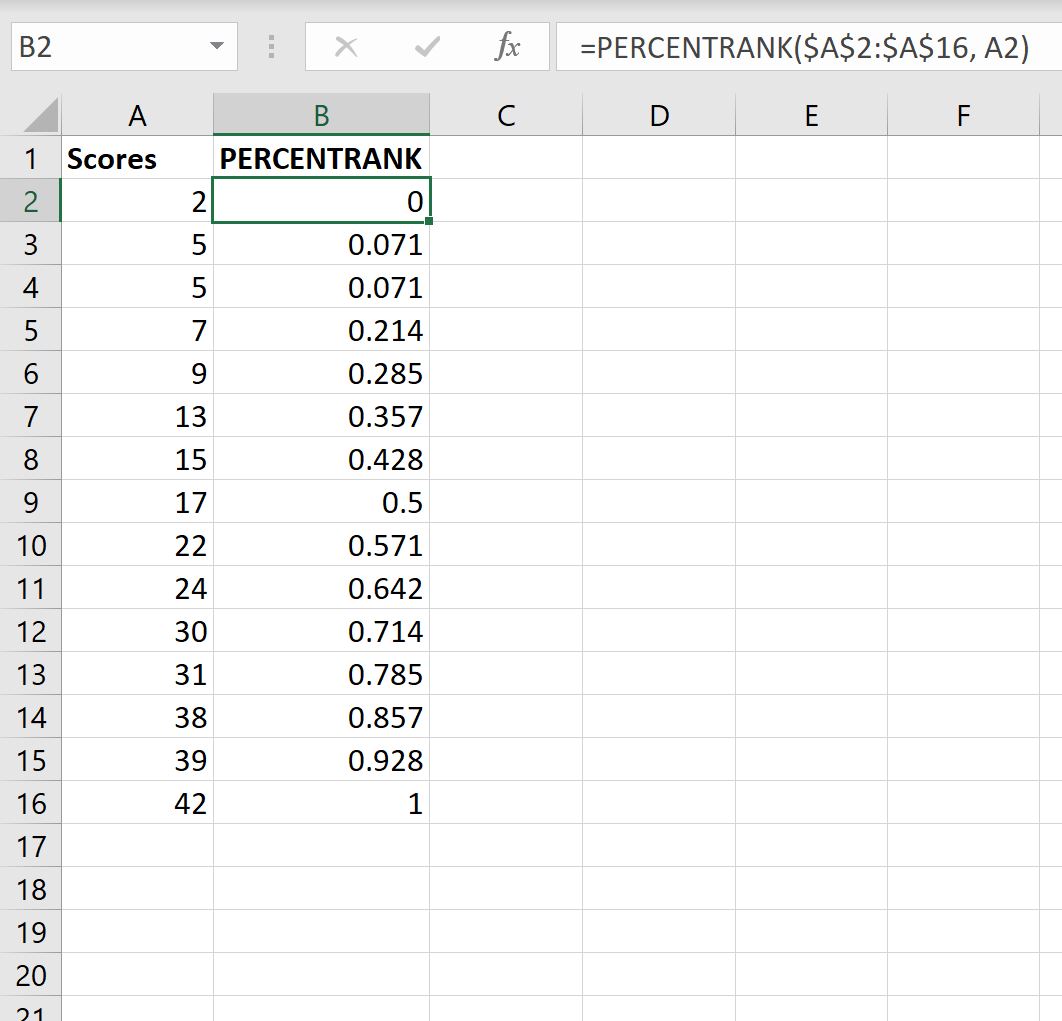
Мы можем ввести следующую формулу в ячейку B2:
=PERCENTRANK( $A$2:$A$16 , A2 )
Затем мы можем скопировать и вставить эту формулу в каждую оставшуюся ячейку в столбце B:
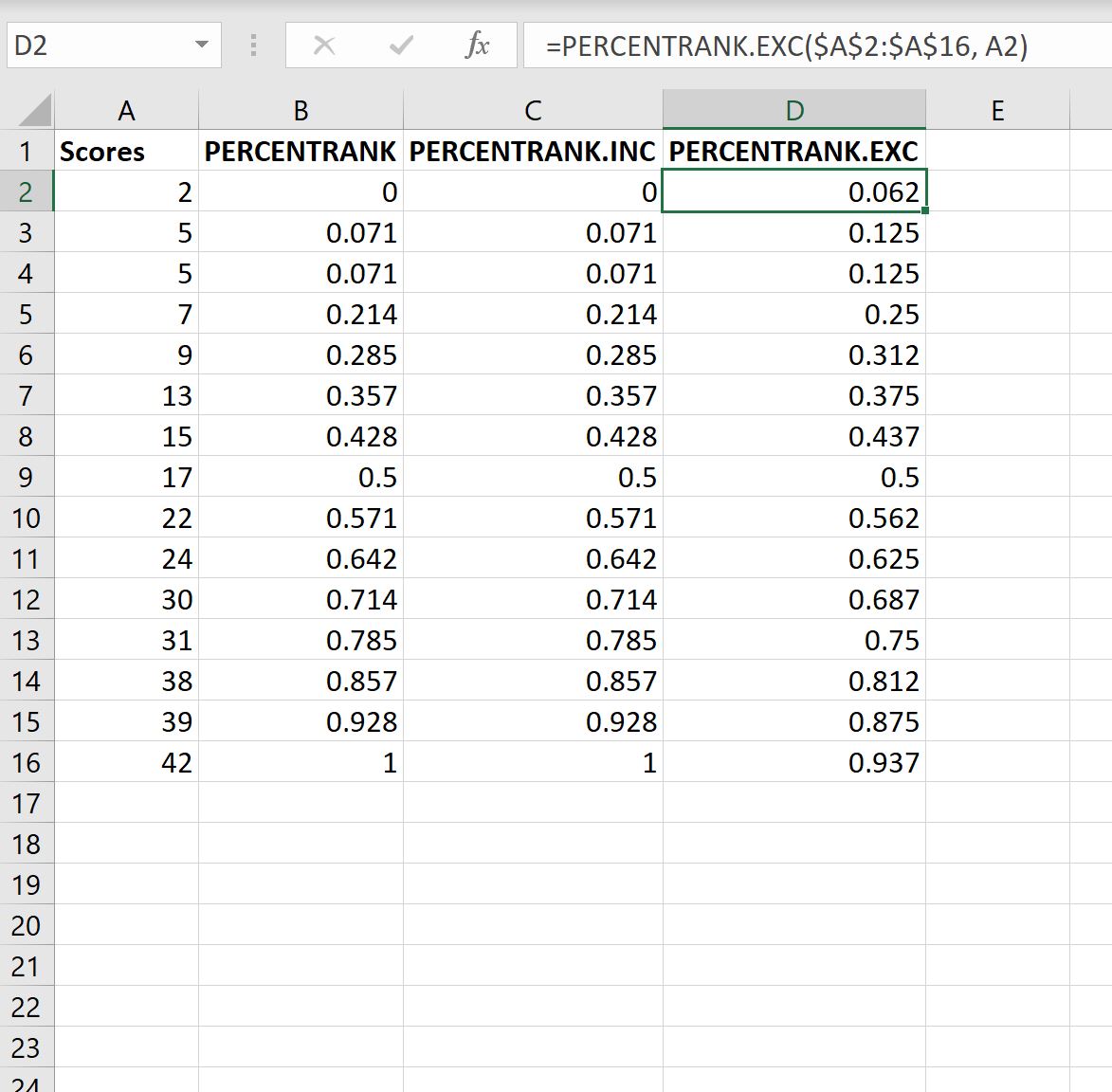
Вот как интерпретировать каждое значение процентного ранга:
- Учащийся, набравший 2 балла, занял 0 процентиль (или 0%) в классе.
- Учащиеся, набравшие 5 баллов, заняли процентиль 0,071 (или 7,1%) в классе.
- Учащийся, набравший 7 баллов, занял процентиль 0,214 (или 21,4%) в классе.
И так далее.
Обратите внимание, что когда мы используем функцию PERCENTRANK , наименьшее значение в наборе данных всегда будет иметь процентильный ранг 0, а самое большое значение в наборе данных всегда будет иметь процентильный ранг 1.
На следующем снимке экрана также показано, как использовать функции PERCENTRANK.INC и PERCENTRANK.EXC :
Здесь следует отметить две вещи:
1. Функция ПРОЦЕНТИЛЬ.ВКЛ возвращает точно такие же значения, что и функция ПРОЦЕНТИЛЬ .
2. Функция ПРОЦЕНТИЛЬ.ИСКЛ не возвращает значение 0 и 1 для наименьшего и наибольшего значений в наборе данных соответственно.
Полную документацию по функции ПРОЦЕНТРАНГ в Excel вы можете найти здесь .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как преобразовать Z-баллы в процентили в Excel
Как рассчитать среднее и стандартное отклонение в Excel
Как рассчитать межквартильный диапазон в Excel
Процентильная шкала определяет позицию определенного значения среди других данных в базе. Процентили в первую очередь используются для описания стандартных результатов тестов. Если же результат в стандартном тесте находится в 90-ом процентиле – это значит, что данный результат является выше чем 90% результатов показателей которые принимают участие в тесте. Другими словами, результат находится среди 10% самых высоких показателей, использованных в тесте.
Пример вычисления формулы процентиля в Excel
Перцентили (они же процентили или персентили) часто применяются в анализе данных. Они являются инструментом для оценки результатов на фоне целой группы данных. С их помощью можно, например, определить персентильную классификацию работника по его годовому обороту.
В программе Excel персентильную классификацию можно легко определить при использовании функции ПЕРСЕНТИЛЬ. Данная функция имеет 2 аргументы:
- Массив – диапазон исходных данных.
- К – значение найденного процентиля (чаще всего число в десятичной дроби диапазоном от 0 и до 1).
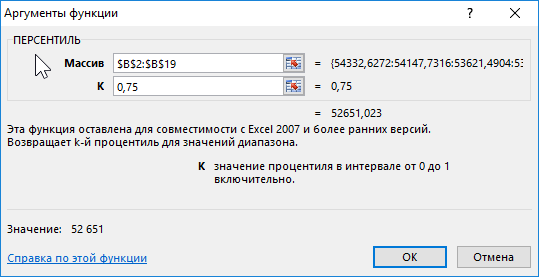
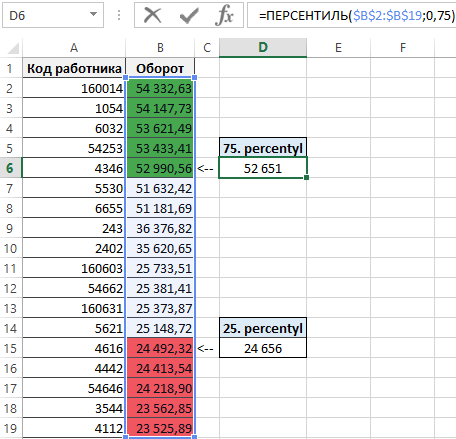
В примере, изображенном ниже на рисунке ячейка D6 содержит значение, которое является результатом вычисления ниже указанной формулы – число 0,75 процентиля данных диапазоне ячеек $B$2:$B$19:
Результат выше приведенной формулы указывает на то, что каждый работник, для которого годовые обороты превышают 52651 работает лучше, чем 75% всех остальных сотрудников.
Ячейка D15 содержит результат вычисления формулы, которая возвращает число 25 процентиля данных в диапазоне ячеек $B$2:$B$19.
Результат выше приведенной формулы указывает на то, что каждый работник, для которого годовой оборот не превышает 24656 находится среди 25% самых слабых сотрудников.
В данном примере используется условное форматирование использующие выше приведенные значения перцентилей. Значения больше чем 75 перцентиля выделены зеленым цветом, а значения меньше чем 25 перцентиля выделены красным цветом.
Два правила условного форматирования для одного диапазона ячеек в Excel
Чтобы создать описанную схему автоматического выделения ячеек по условию пользователя, выполните целый ряд следующих действий шаг за шагом:
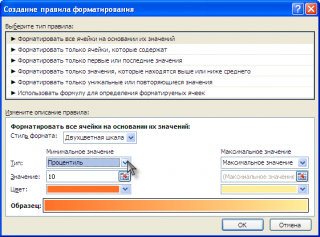
- Выделите диапазон ячеек B2:B19, которые будут автоматически выделятся цветом по условию формулы и выберите инструмент: «ГЛАВНАЯ»-«Условное форматирование»-«Создать правило». В результате чего высветится окно как ниже на рисунке:
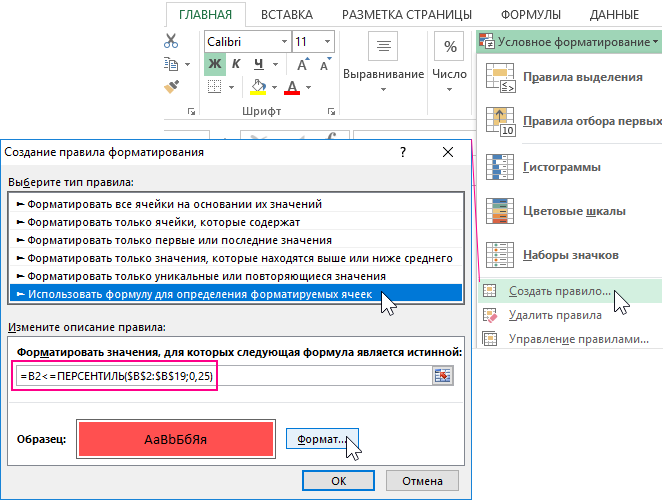
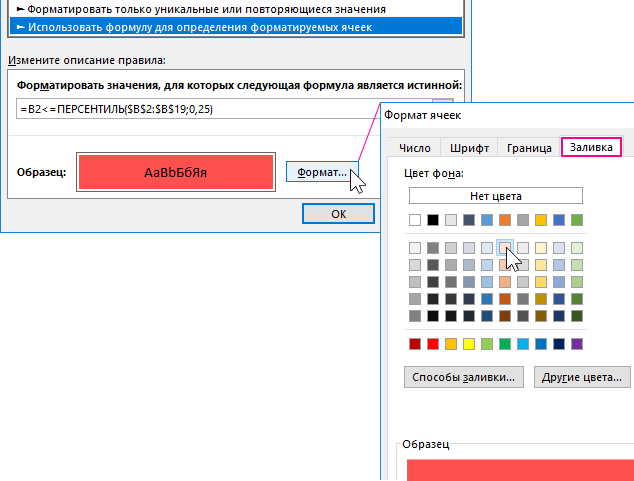
- В верхней части окна находится список опций. Выберите из него опцию «Использовать формулу для определения форматируемых ячеек». Данная опция служит для преобразования формата в ячейках в зависимости от их значений с помощью определенной формулы с логическим выражением. Если в результате вычисления формулы будет возвращено логическое значение ИСТИНА, тогда к текущей ячейке будет применено условное форматирование.
- В полю ввода введите формулу с логическим выражением, которая представлена ниже в этом разделе. Данная формула проверяет: если значение в целевой ячейке B2 меньше чем значение 25 перцентиля, тогда ей присваивается новый формат красного цвета фона для экспонирования.
=B2<=ПЕРСЕНТИЛЬ($B$2:$B$19;0,25)
- Нажмите на кнопку «Формат». Появится окно «Формат ячеек», в котором находятся все опции для форматирования шрифта, границы и фона ячеек. Главное укажите красный фон заливки. После указания своих пользовательских опций форматирования нажмите на кнопки ОК на все открытых окнах чтобы подтвердить и применить все изменения.
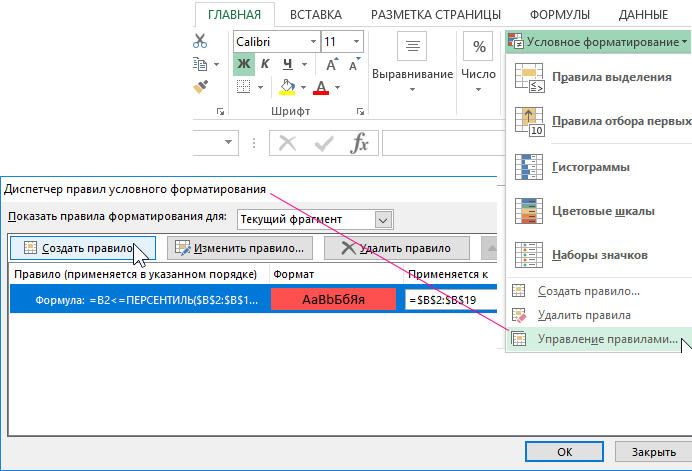
- Снова выделите диапазон ячеек B2:B19 и на этот раз уже выберите инструмент «ГЛАВНАЯ»-«Условное форматирование»-«Управление правилами». В результате появится окно «Диспетчер правил условного форматирования», где находится наше первое правило. Для создания второго правила в этом же окне нажмите на кнопку «Создать правило».
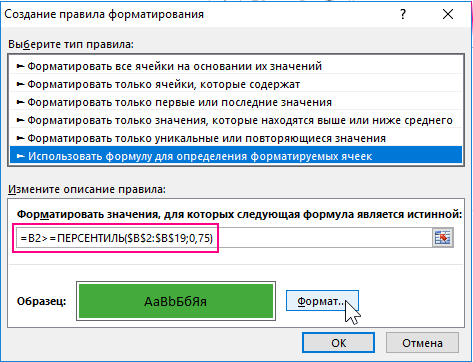
- И снова в появившемся окне «Создание правила форматирования» выберите опцию «Использовать формулу для определения форматируемых ячеек».
- В полю ввода формул на этот раз введите другую формул представленную на этом шаге. Данная формула проверяет: если значение в целевой ячейке B2 больше чем 75 персентиля, тогда применить для нее новый формат (зеленый фон).
- Снова нажмите на кнопку «Формат» где на этот раз следует указать зеленый фон заливки для ячеек. После чего нажмите на кнопку ОК для всех открытых окон.
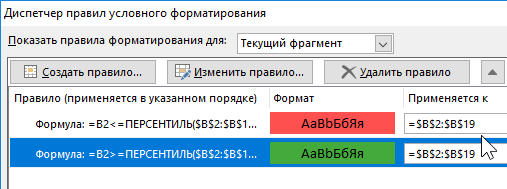
В результате к одному и тому же диапазону ячеек одновременно применяется 2 правила условного форматирования. В следствии чего одна группа значений выделена красным цветом значение которых меньше 25% показателей, а вторая группа – зеленым >75%.
Содержание
- ПРОЦЕНТИЛЬ Обзор функций
- Функция ПРОЦЕНТИЛЬ Синтаксис и входные данные:
- Что такое функция ПРОЦЕНТИЛЬ?
- ПРОЦЕНТИЛЬ — это функция «совместимости»
- Что такое процентиль?
- Как использовать функцию ПРОЦЕНТИЛЬ
- Два метода расчета процентилей
- PERCENTILE.INC
- Линейная интерполяция
- PERCENTILE.EXC
- PERCENTILE в Google Таблицах
- PERCENTILE примеров в VBA
Скачать пример рабочей книги
Загрузите образец книги
В этом руководстве показано, как использовать Функция ПРОЦЕНТИЛЬ в Excel в Excel для расчета процентиля.
ПРОЦЕНТИЛЬ Обзор функций
Функция PERCENTILE вычисляет k-й процентиль.
Чтобы использовать функцию PERCENTILE Excel Worksheet, выберите ячейку и введите:
(Обратите внимание, как появляются входные данные формулы)
Функция ПРОЦЕНТИЛЬ Синтаксис и входные данные:
| 1 | = ПРОЦЕНТИЛЬ (массив; k) |
множество — Массив чисел.
k — Значение процентиля от 0 до 1.
Что такое функция ПРОЦЕНТИЛЬ?
ПРОЦЕНТИЛЬ — одна из статистических функций Excel. Он возвращает k-й процентиль заданного диапазона данных.
ПРОЦЕНТИЛЬ — это функция «совместимости»
В Excel 2010 Microsoft заменила PERCENTILE двумя вариантами: PERCENTILE.INC и PERCENTILE. ИСКЛ.
PERCENTILE по-прежнему работает, поэтому старые таблицы, в которых он используется, будут работать в обычном режиме. Однако, если вам не требуется, чтобы таблица оставалась совместимой со старыми версиями Excel, следует использовать PERCENTILE.INC или PERCENTILE.EXC.
Мы обсудим все три, чтобы вы поняли все до мелочей.
Что такое процентиль?
Процентиль показывает, как значение сравнивается с другими значениями в заданном диапазоне. Когда значение находится на k-м процентиле, это означает, что оно выше, чем k% других значений в группе.
Например, если вы мужчина, живущий в США, и ваш рост 6 футов (180 см), вы находитесь в 71-м процентиле — вы выше 71% других мужчин в США. Если вы женщина и рост 180 см, то вы находитесь в группе 99th процентиль — вы выше 99% других женщин.
Когда вы имеете дело с процентилями, обратите внимание, что 50th процентиль равен медиане <> данных.
Функция Excel PERCENTILE сообщает вам, какова точка отсечения для данного процентиля, то есть, насколько высоким должно быть значение, чтобы оно попадало в k-й процентиль.
Как использовать функцию ПРОЦЕНТИЛЬ
Используйте PERCENTILE так:
| 1 | = ПРОЦЕНТИЛЬ (C4: C13; F3) |
Вот несколько друзей, которые решили вычислить 80th процентиль роста их группы, и мы видим результат — 183,4 см.
Первый аргумент функции — это диапазон данных — их высота, которую мы выложили в C4: C13.
Следующий аргумент — процентиль. В этом примере я поместил процентиль в ячейку F3, а затем указал на эту ячейку в функции. Таким образом, легко изменить процентиль и увидеть новые результаты.
Однако вы можете ввести процентиль непосредственно в формулу, если хотите. Вы можете определить его как десятичную дробь, например:
| 1 | = ПРОЦЕНТИЛЬ (C4: C13; .8) |
Или в процентах, например:
| 1 | = ПРОЦЕНТИЛЬ (C4: C13, 80%) |
И все они возвращают одно и то же значение.
Что нужно знать о PERCENTILE:
- Если определяемый вами процентиль не является числом, функция вернет #VALUE! ошибка
- Если процентиль меньше 0 или больше 1, вы получите # ЧИСЛО! ошибка
- Текст и пустые ячейки в диапазоне данных будут проигнорированы.
Два метода расчета процентилей
Давайте на секунду расставим наши данные по порядку:
Вы можете задаться вопросом, почему 80th процентиль не 183, так как Чендлер — 8th самый высокий человек в группе.
Что ж, на самом деле существует множество способов математического вычисления процентиля, но нет стандартизированного или предпочтительного метода для всех ситуаций. Это то, о чем статистики спорят в научных статьях.
Excel предлагает два способа сделать это, что приводит нас к PERCENTILE.INC и PERCENTILE.EXC.
Функция PERCENTILE.INC в Excel аналогична функции PERCENTILE. Часть «INC» — это сокращение от «включающий», потому что она может вычислять любой действительный процентиль (то есть что-либо от 0% до 100%).
Вы используете это так:
| 1 | = ПРОЦЕНТИЛЬ.INC (C4: C13; F3) |
Как видите, он возвращает тот же результат, что и ранее PERCENTILE.
Итак, возвращаясь к тому, почему 80th процентиль не в точности равен росту Чендлера. Помните, что здесь мы выполняем инклюзивный расчет, поэтому мы включаем все значения k от 0 до 1 (или от 0% до 100%).
Это означает, что наша самая короткая подруга Дженис находится на нулевой отметке.th процентиль, а Ричард, самый высокий, — это 100 человек.th процентиль. Все другие друзья имеют равные приращения между двумя, и это приращение равно 1 / (n-1), где n — количество точек данных в диапазоне.
В нашем случае это:
Это означает, что Чендлеру на самом деле не 80.th процентиль, он на 77,777th процентиль. Если мы подставим это число в PERCENTILE.INC, мы должны получить рост Чендлера …
… И мы делаем.
Линейная интерполяция
Теперь, когда указанное вами значение k не кратно 1 / (n-1), PERCENTILE.INC будет применять процесс, называемый линейной интерполяцией, для вычисления результата. Это звучит сложно, но в основном это означает, что Excel выберет одно из двух значений.
Так почему же мы получили 183,4, когда попросили 80?th процентиль раньше?
Расчет работает следующим образом:
- 80th процентиль падает между Чендлером и Россом, Чендлер на 77,777th процентиль и Росс на 88,888-м месте.
- 80th процентиль на 2,222% опережает рост Чендлера
- Мы знаем, что расстояние между высотами Чендлера и Росса составляет 11%.
- 222% / 11,111% = 20% после округления. Теперь мы знаем, что 80th процентиль — это 20% расстояния между высотами Росса и Чендлера.
- Разница между ростом Росса в 185 см и ростом Чендлера в 183 см составляет 2 см.
- 20% 2 см составляет 0,4 см
- Добавьте это к росту Чендлера, и мы получим 183,4 см.
PERCENTILE.EXC
Вы используете PERCENTILE.EXC практически таким же образом:
| 1 | = ПРОЦЕНТИЛЬ.ИСКЛ (C4: C13; F3) |
Итак, у нас одинаковые данные, нам нужен одинаковый процентиль, но мы получили разные результаты. Это почему?
Это связано с тем, что PERCENTILE.EXC исключает первое и последнее значения при вычислении интервалов процентилей. См. ниже:
Вместо того, чтобы интервал равнялся 1 / (n-1), с PERCENTILE.EXC интервал равен 1 / (n + 1), или в данном случае 9,091%.
Все остальное работает так же, как и с PERCENTILE.INC. Опять же, 80th процентиль находится между Чендлером и Россом, поэтому Excel применяет тот же метод линейной интерполяции:
- 80th процентиль падает между Чендлером и Россом, Чендлер на 72,727th процентиль и Росс на 81,818-м месте.
- 80th процентиль на 7,272% опережает рост Чендлера
- Мы знаем, что расстояние между высотами Чендлера и Росса составляет 9,091%.
- 272% / 9,091% = 80% после округления. Теперь мы знаем, что 80th процентиль — это 80% расстояния между высотами Росса и Чендлера.
- Разница между ростом Росса в 185 см и ростом Чендлера в 183 см составляет 2 см.
- 80% 2 см составляет 1,6 см
- Добавьте это к росту Чендлера, и мы получим 184,6 см.
PERCENTILE в Google Таблицах
Функция ПРОЦЕНТИЛЬ в Google Таблицах работает точно так же, как и в Excel:
PERCENTILE примеров в VBA
Вы также можете использовать функцию ПРОЦЕНТИЛЬ в VBA. Тип:application.worksheetfunction.percentile (массив, k)
Для аргументов функции (массив и т. Д.) Вы можете либо ввести их непосредственно в функцию, либо определить переменные, которые будут использоваться вместо них.
Вернуться к списку всех функций в Excel
Перейти к содержанию
На чтение 1 мин. Просмотров 8 Опубликовано 23.05.2021
Если вы обычно используете набор значков условного форматирования, вы должны знать, что набор значков основан на процентиле каждого значения. Однако знаете ли вы, как рассчитать процентиль ранга каждого значения в списке Excel?

Вычислить процентиль ранга в Excel
Вычислить процентиль ранга в Excel
Чтобы вычислить процентиль ранга данных списка, вы можете использовать формулу.
Выберите пустую ячейку, в которую вы поместите процентиль ранга в введите эту формулу = RANK.EQ (B2, $ B $ 2: $ B $ 9,1)/COUNT ($ B $ 2: $ B $ 9), нажмите клавишу Enter и перетащите маркер заполнения вниз, чтобы вычислить все процентили ранга.
В формуле B2 – это первая ячейка, которую вы используете в списке данных, B2: B9 – это список, который вы используете.

Примечание . Если результаты вычислений не отображаются в виде процентов, выберите эти вычисления. результатов, а затем нажмите Главная > Стиль в процентах . См. Снимок экрана:

Возможно, вы интересует эта утилита:
Преобразование числа в порядковый номер |
| Kutools for Excel ‘s Преобразовать число в порядковый номер для быстрого преобразования кардинальных чисел в порядковые. |
| Получить бесплатную пробную версию прямо сейчас! |
 |

Excel это наиболее часто используемая программа для работы с электронными таблицами и таблицами на персональных и настольных компьютерах. . Эта двусмысленность означает, что он простые в использовании функции и в то же время более сложные . Все они живут вместе по одной программе.
В этом смысле это Это нормально, что менее опытные специалисты не знают определенных инструментов. Однако Интернет предлагает нам окно в знания. В этой статье поэтому мы покажем вам, как пользоваться одной из самых популярных утилит государственных деятелей. .
Знать все о процентили и как это применяется в различных ситуациях , мы рекомендуем вам прочитать содержание следующего текста.
Что такое процентили и для чего эти данные используются в статистических операциях?

Процентиль — это используемый статистический показатель. определить проекцию популяции по характерным чертам ее поведения . Он широко используется в медицине для детей, потому что его можно установить в зависимости от их состояния. возраст и их Sexe , насколько они могут быть высокими, если у них есть определенное устройство, и как их текущий рост соотносится с общим числом детей их возраста.
Другими словами, берется население в целом, данные упорядочиваются от наименьшего к наибольшему, и анализируется их проекция. Затем он сравнивается со статистической стратой подлежат изучению и определяется процентное соотношение ниже или выше прогноза . Не следует забывать, что процентиль изучается в частотном распределении с база равна 1 .
«ОБНОВЛЕНИЕ ✅ Хотите узнать, как рассчитать процентили группы данных в электронной таблице Excel? ⭐ ВОЙДИТЕ СЮДА ⭐ и узнайте все С НУЛЯ! »
Таким образом, он может принимать значения от 1 до 99. и он представлен процентом, который находится под наблюдениями. Другими словами, если 35-й процентиль (P35) установлен , это интерпретируется как 35% наблюдения согласуются с характеристиками населения в целом. Пар Последовательные, 50-й процентиль будет равен медиане частотного распределения, которая может совпадать или не совпадать со средним значением . В свою очередь, P25 будет равняться первому квартилю, а P75 в третьем квартиле.
Какие аспекты следует учитывать при расчете процентилей?

При расчете процентилей необходимо учитывать следующие аспекты: работают с частотным распределением равным 1 и что для того, чтобы их можно было интерпретировать, они должны быть связаны с процентами. Они также связаны с квартилями и децилями. , так как нормальное распределение можно разделить на 4 или 10 частей. Это означает, что всякий раз, когда изучается процентиль, вы анализируете местоположение на Гауссовский колокол .
По этой причине для работы с процентилями данные должны быть ранжированы от самого низкого до самого высокого потому что иначе не было бы нормального распределения частот. Наконец, чтобы вы могли сравнивать дела, которые хотите проанализировать, два должен быть однородным . Под этим мы подразумеваем, что вы сможете сравнить, например, если вы используете его в детской медицине, с людьми того же возраста и пола.

Шаги для вычисления процентиля в электронной таблице Excel следующие:
- Введите данные группы, которая вы хотите проанализировать.
- Если вы хотите, вы можете представить графически с помощью гистограммы чтобы лучше понять распределение.
- Затем перейдите на вкладку формулы и выберите опцию Больше возможностей .
- Найдите функции статистики, затем нажмите PERCENTILE.EXC .
- Откроется окно, в котором вам нужно будет выбрать матрицу и количество процентилей . Вы должны иметь в виду что Excel работает в два этапа один , так что если вы ищете 5%, надо будет написать 0,05 .
- Наконец, вам нужно будет интерпретировать результат в соответствии с выбранным процентом для анализа.
Если у вас есть какие-либо вопросы, оставляйте их в комментариях, мы свяжемся с вами как можно скорее, и это будет большим подспорьем для большего числа участников сообщества. Je Vous remercie!
Что такое процентиль?
Термин ″процентиль″ (percentile) часто встречается в зарубежной литературе про инвестиции и вообще в статистических исследованиях – одно из таких исследований я упоминал в этой статье. Другими вариантами русских названий являются ″персентиль″ и ″перцентиль″. Думаю, что небольшая известность термина в России не вполне заслужена, поскольку нередко именно в процентилях удобно выразить полученные результаты.
Процентиль это определенная часть выборки данных
Возьмем простой пример. Группа студентов из 200 человек пишет тест, состоящий из 100 вопросов. Проходной порог, когда тест считается сданным, составляет 2/3 правильных ответов, т.е. не менее 66. Что получается с точки зрения отдельного студента?
Допустим, Иван правильно ответил на 70 вопросов. Задачу он выполнил — тест засчитан. Результат каждого участника теста также сравнивается с числом 66: если правильных ответов больше, тест сдан. В результате формируется список сдавших и не сдавших: каждый студент проходил через это. Пока ничего нового.
Но задачу можно поставить и по-другому: нужно сравнить результаты студентов не с проходным баллом в 66 пунктов, а между собой. Зачем это нужно? В данном случае, например, для объективной оценки сложность теста, что достигается группировкой результатов.
Вернемся к Ивану, который получил 70 правильных ответов. Много это или мало по сравнению с остальными? Это и покажет процентиль.
Процентили делят всю выборку на определенные части. Например, пятый процентиль охватывает 5% объема выборки. Предположим, показатель Ивана равен пятому процентилю. Это означает, что Иван написал тест лучше, чем 5% студентов (10 человек из 200 получили от нуля до 70 баллов). Не густо, поскольку в этом случае остальные 190 человек набрали больше, чем 70. Значит, тест был очень легкий и порог в 66 баллов можно и повысить.
Но в том же самом тесте может быть и обратная ситуация: результат Ивана равен 90-ому процентилю. Это значит, что Иван написал тест лучше, чем 90% студентов. Или по другому: только 10% (20 человек) набрали более 70 правильных ответов. Следовательно, тест был весьма трудным. Преимущество метода еще и в том, что разбивкой на процентили можно сравнивать тесты с разным числом участников.
Функция Гаусса
Процентиль можно пояснить и на примере симметричного распределения Гаусса, которое часто встречается в статистике для оценки веса, роста и т.п. На рисунке выше показаны 25, 50, 75 и 100 процентили. Случаи 25 и 75-ого процентиля, включающие четверть и три четверти выборки соответственно, называются квартилями.
Чем более высок процентиль, тем больше данных он включает
Расчет процентиля в Excel
Процентиль несложно вычислить по формуле:
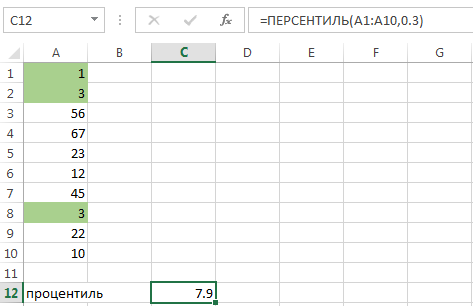
но проще обрабатывать массив данных одноименной функцией Excel. Для примера возьмем произвольную выборку полученных баллов и рассчитаем в ней процентили:
Функция PERCENTILE (ПЕРСЕНТИЛЬ) включает в себя ввод диапазона ячеек данных (А1:А10) и значения процентиля К, деленного на 100%. Т.е. в данном случае ввод 0.3 означает нахождение тридцатого процентиля. Смысл расчета: к 30-му процентилю будут относиться все результаты, меньше или равные 7.9.
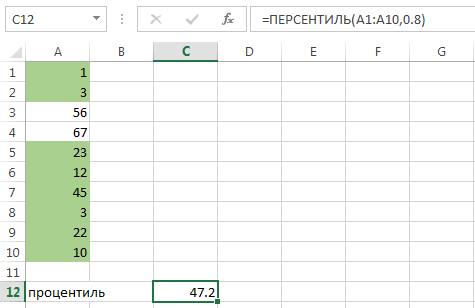
Если мы хотим узнать процентиль участника, получившего 10 баллов, то это несложно сделать, варьируя значение К до тех пор, пока значение в ячейке С12 не станет близким 10. Получится примерно 34-ый процентиль. При увеличении процентиля в выборку попадает больше табличных значений:
Итого, в 80-ый процентиль попадает уже 8 табличных значений из 10, которые меньше или равны 47.2. При этом подчеркнуть результат можно диапазоном процентилей — например, между восьмидесятым и сотым. В этом случае значения будут лежать между 47.2 и 67 (максимальным числом выборки).