Рассчитаем
Приведенную (к текущему моменту) стоимость
инвестиции при различных способах начисления процента: по формуле простых процентов, сложных процентов, аннуитете и в случае платежей произвольной величины.
Текущая стоимость (Present Value) рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Текущей стоимости, также как и
Будущей стоимости
важен, так как, платежи, осуществленные в различные моменты времени, можно сравнивать лишь после приведения их к одному временному моменту. Текущая стоимость получается как результат приведения Будущих доходов и расходов к начальному периоду времени и зависит от того, каким методом начисляются проценты:
простые проценты
,
сложные проценты
или
аннуитет
(в
файле примера
приведено решение задачи для каждого из методов).
Простые проценты
Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).
В MS EXCEL для обозначения Приведенной стоимости используется аббревиатура ПС (ПС фигурирует как аргумент в многочисленных финансовых функциях MS EXCEL).
Примечание
. В MS EXCEL нет отдельной функции для расчета Приведенной стоимости по методу Простых процентов. Функция
ПС()
используется для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить
ПС()
рассчитать Приведенную стоимость и по методу простых процентов (см.
файл примера
).
Для определения Приведенной стоимости при начислении простых процентов воспользуемся формулой для расчета
Будущей стоимости
(FV): FV = PV * (1+i*n) где PV — Приведенная стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка
за период
начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц); n – количество периодов времени, в течение которых начисляются проценты.
Из этой формулы получим, что:
PV = FV / (1+i*n)
Таким образом, процедура расчета Приведенной стоимости противоположна вычислению Будущей стоимости. Иными словами, с ее помощью мы можем выяснить, какую сумму нам необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Например, мы хотим знать, на какую сумму нам сегодня нужно открыть вклад, чтобы накопить через 3 года сумму 100 000р. Пусть в банке действует ставка по вкладам 15% годовых, а процент начисляется только основную сумму вклада (простые проценты). Для того чтобы найти ответ на этот вопрос, нам необходимо рассчитать Приведенную стоимость этой будущей суммы по формуле PV = FV / (1+i*n) = 100000 / (1+0,15*3) = 68 965,52р. Мы получили, что сегодняшняя (текущая, настоящая) сумма 68 965,52р. эквивалентна сумме через 3 года в размере 100 000,00р. (при действующей ставке 15% и начислении по методу простых процентов).
Конечно, метод Приведенной стоимости не учитывает инфляции, рисков банкротства банка и пр. Этот метод эффективно работает для сравнения сумм «при прочих равных условиях». Например, что с помощью него можно ответить на вопрос «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? Чтобы ответить на этот вопрос рассмотрим расчет Приведенной стоимости при начислении сложных процентов.
Сложные проценты
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования
простых процентов
изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».
Приведенную стоимость PV (или ПС) в этом случае можно рассчитать, используя
формулу наращения для сложных процентов
.
FV = РV*(1+i)^n где FV (или S) – будущая (или наращенная сумма), i — годовая ставка, n — срок ссуды в годах,
т.е. PV = FV / (1+i)^n
При капитализации m раз в год формула Приведенной стоимости выглядит так: PV = FV / (1+i/m)^(n*m) i/m – это ставка за период.
Например, сумма 100 000р. на расчетном счету через 3 года эквивалентна сегодняшней сумме 69 892,49р. при действующей процентной ставке 12% (начисление % ежемесячное; пополнения нет). Результат получен по формуле =100000 / (1+12%/12)^(3*12) или по формуле =ПС(12%/12;3*12;0;-100000).
Отвечая на вопрос из предыдущего раздела «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? нам нужно сравнить две Приведенные стоимости: 69 892,49р. (сложные проценты) и 68 965,52р. (простые проценты). Т.к. Приведенная стоимость, рассчитанная по предложению банка для вклада с простыми процентами, меньше, то это предложение выгоднее (сегодня нужно вложить денег меньше, чтобы через 3 года получить ту же сумму 100 000,00р.)
Сложные проценты (несколько сумм)
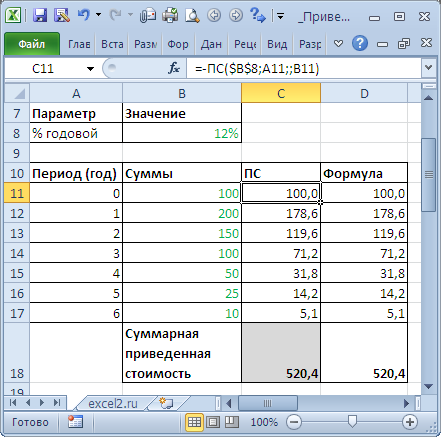
Определим приведенную стоимость нескольких сумм, которые принадлежат разным периодам. Это можно сделать с помощью функции
ПС()
или альтернативной формулы PV = FV / (1+i)^n
Установив значение ставки дисконтирования равной 0%, получим просто сумму денежных потоков (см.
файл примера
).
Аннуитет
Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Приведенной стоимости существенно усложняется (см. статью
Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость
, где приведен расчет с помощью функции
ПС()
, а также вывод альтернативной формулы).
Здесь разберем другую задачу (см.
файл примера
):
Клиент открыл вклад на срок 1 год под ставку 12% годовых с ежемесячным начислением процентов в конце месяца. Клиент также в конце каждого месяца вносит дополнительные взносы в размере 20000р. Стоимость вклада в конце срока достигла 1000000р. Какова первоначальная сумма вклада?
Решение может быть найдено с помощью функции
ПС()
:
=ПС(12%/12;12;20000;-1000000;0)
= 662 347,68р.
Аргумент
Ставка
указан за период начисления процентов (и, соответственно, дополнительных взносов), т.е. за месяц. Аргумент
Кпер
– это количество периодов, т.е. 12 (месяцев), т.к. клиент открыл вклад на 1 год. Аргумент
Плт
— это 20000р., т.е. величина дополнительных взносов. Аргумент
Бс
— это -1000000р., т.е. будущая стоимость вклада. Знак минус указывает на направление денежных потоков: дополнительные взносы и первоначальная сумма вклада одного знака, т.к. клиент
перечисляет
эти средства банку, а будущую сумму вклада клиент
получит
от банка. Это очень важное замечание касается всех
функций аннуитета
, т.к. в противном случае можно получить некорректный результат. Результат функции
ПС()
– это первоначальная сумма вклада, она не включает Приведенную стоимость всех дополнительных взносов по 20000р. В этом можно убедиться подсчитав Приведенную стоимость дополнительных взносов. Всего дополнительных взносов было 12, общая сумма 20000р.*12=240000р. Понятно, что при действующей ставке 12% их Приведенная стоимость будет меньше
=ПС(12%/12;12;20000)
= -225 101,55р. (с точностью до знака). Т.к. эти 12 платежей, сделанные в разные периоды времени, эквивалентны 225 101,55р. на момент открытия вклада, то их можно прибавить к рассчитанной нами первоначальной сумме вклада 662 347,68р. и подсчитать их общую Будущую стоимость
= БС(12%/12;12;; 225 101,55+662 347,68)
= -1000000,0р., что и требовалось доказать.
Определение Приведенной стоимости в случае платежей произвольной величины
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемые через равные промежутки времени, то для нахождения Текущей (приведенной) стоимости по методу сложных процентов используется функция
ЧПС()
. Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция
ЧИСТНЗ()
. Об этих расчетах читайте в статье
Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в MS EXCEL
.
Определение текущей стоимости
Согласно концепции временнoй ценности
денег, расходы и доходы, не относящиеся
к одному моменту времени, можно сопоставить
путем приведения их к одному сроку, т.е.
путем дисконтирования (см. выше).
В Excel имеется функцияПС,
позволяющая рассчитать текущую стоимость
единой суммы вклада (займа) и фиксированных
периодических платежей. Следует отметить,
что этот расчет является обратным к
определению будущей стоимости при
помощи функцииБС.
Общий синтаксис вызова функции ПС
имеет вид:
ПС(Ставка;Кпер;Плт;Бс;Тип)
Задача №6. Фирме потребуется 5
млн рублей через 12 лет. В настоящее время
фирма располагает деньгами и готова
положить их на депозит единым вкладом,
чтобы через 12 лет он достиг 5 млн рублей.
Определить необходимую сумму текущего
вклада, если годовая процентная ставка
по нему составляет 12%.
Решение. В данном случае используется
функцияПС следующего вида:
ПС(Ставка;Кпер; ;Бс;Тип).
Для конкретных значений, заданных в
условии задачи, соответствующая формула
имеет вид
=ПС(12%;12;;5000000)
Окончательное решение задачи представлено
на рис. 8. Чтобы проверить правильность
решения, необходимо использовать функцию
БС с аргументомПс, равным
-1283375,465.
Рис. 8 Расчет текущей величины вклада с
помощью функции ПС
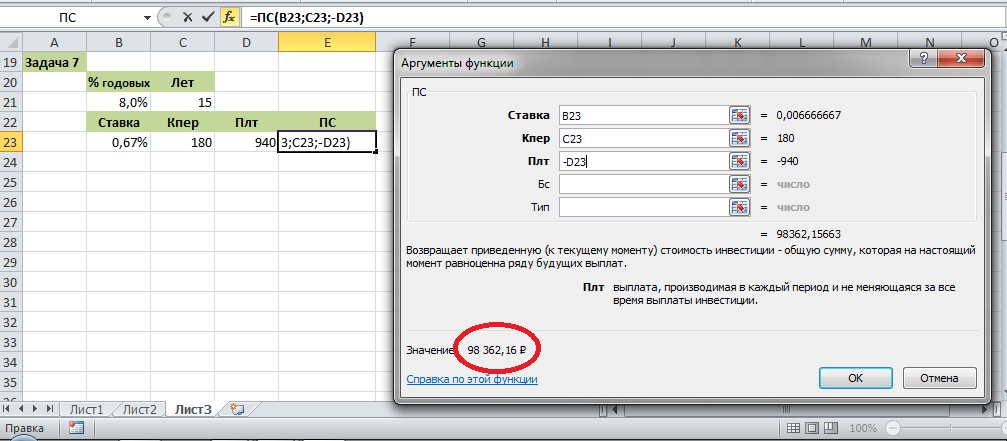
Задача №7. Предположим,
рассматриваются два варианта покупки
дома: заплатить сразу 99000 р. или в рассрочку
— по 940 р. ежемесячно в течение 15 лет.
Определить какой вариант предпочтительнее,
если годовая процентная ставка составляет
8%.
Решение. В данном случае используется
функцияПС следующего вида:
ПС(Ставка;Кпер;Плт)
Для конкретных значений, заданных в
условии задачи, соответствующая формула
имеет вид
=ПС(8%/12;15*12;-940)
Окончательное решение задачи представлено
на рис. 9. Полученное значение равно
98 362 руб 16 коп. Сравнивая полученное
значение с суммой, указанной в условии
задачи, делаем вывод о целесообразности
покупки дома в рассрочку.
Рис. 9 Расчет текущей стоимости постоянных
периодических выплат с помощью функции
ПС
Задача №8. Рассчитать текущую
стоимость вклада, который через 3 года
составит 15 тыс. рублей при начислении
20% в год.
Расчет срока платежа
Для вычисления общего количества
периодов выплат (как для единой суммы
вклада или займа, так и для постоянных
периодических выплат) используется
функция КПЕР, общий синтаксис которой
имеет вид
КПЕР(Норма;Выплата;Нз;Бс;Тип)
Задача №9. Через сколько лет вклад
размером 1000 р. достигнет величины
1 000 000 руб., если годовая процентная
ставка по вкладу составляет 16,79% и
начисление процентов производится
ежеквартально.
Решение. В данном случае используется
функцияКПЕР следующего вида:
КПЕР(Ставка; ;Пс;Бс)
Для конкретных значений, заданных в
условии задачи, соответствующая формула
имеет вид:
=КПЕР(16,79%/4;;-1000;1000000)/4.
Окончательное решение задачи представлено
на рис. 10. Следует отметить, что функция
КПЕР возвращает срок платежа в
периодах, поэтому его следует разделить
на 4 (количество периодов начисления
процентов в году).
Таким образом, чтобы вложенная 1000 р.
стала 1000000 р. при заданных в задаче
условиях, потребуется приблизительно
42 года.
Рис. 10 Расчет срока получения необходимой
суммы вклада с помощью функции КПЕР
Задача №10. Ожидается, что
ежегодные доходы от реализации проекта
составят 3 млн 300 тыс. р. Рассчитать срок
окупаемости проекта, если инвестиции
к началу поступления доходов составят
10 млн р., а процентная ставка 12,11%.
Задача №11. Ссуда размером 66000
р., выданная под 12% годовых, погашается
обычными ежемесячными платежами по
6630 р. Рассчитать срок погашения ссуды.
Задача №12. Сколько лет потребуется,
чтобы обязательные ежемесячные платежи
размером 15 тыс. р. начали приносить доход
в 1 млн р. при годовой процентной ставке
13,5%.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В предыдущем посте я обещала облегчить вашу учетную участь и рассказать вам о том, как обычный Excel может помочь с выбором депозита. Причем, выгодного вам, а не только банку. Обещала – выполняю. Следуя моей инструкции, вы легко сможете определить, какие условия по банковским вкладам принесут вам наибольший доход.
За расчет потенциальной доходности в Microsoft Excel отвечает специальная функция БС (Будущая Стоимость (Future Value (FV) – о ней мы говорили здесь). Для того, чтобы ее вызвать, нажмите на символ f x , слева от строки ввода значений и адресов ячеек.
В открывшемся Мастере функций в строке поиска функций введите БС и нажмите Ввод. Кликните мышью на подсвеченной синим цветом строке БС, как показано ниже.
Составляющим формулы расчета будущей стоимости FV = PV(1+r)n в Excel соответствуют следующие функции:
| Общее название | Функция в Excel | Краткое описание |
|---|---|---|
| FV (Future Value) | БС (Будущая Стоимость) | Будущая сумма вклада |
| PV (Present Value) | ПС (Текущая Стоимость) | Текущая стоимость вклада |
| n | КПЕР (Количество Периодов) | Число периодов начисления процентов по вкладу |
| r | СТАВКА | Процентная ставка по вкладу |
Заполняем (вручную или указав адреса соответствующих ячеек) поля данными из нашего примера. Напомню, что мы решили открыть депозит, разместив на нем 10 000 рублей сроком 5 лет и под 10% годовых.
Ставку по вкладу указываем в виде десятичной дроби, т.е. 10% превратятся в 0,1. В Кпер ставим количество лет – у нас вклад на 5 лет, значит 5. Поле Плт оставляем пустым. В поле ПС начальную сумму вклада указываем со знаком “минус”, т.к. мы эти деньги отдаем, а не получаем.
Поле Тип заполняем с учетом того, как производится выплата процентов по нашему вкладу:
- если в конце срока (на языке финансистов такой поток платежей называется постнумерандо), то ставим “0” или оставляем поле пустым;
- если в начале срока (на языке финансистов такой поток платежей называется пренумерандо), то ставим “1”.
В случае если проценты по вкладу начисляются ежемесячно или ежеквартально, то в поле Ставка годовую процентную ставку следует разделить на 12 или 4 соответственно в виде десятичной дроби. Вместе с этим нужно внести изменения в Кпер, пересчитав количество выплат: при ежемесячном начислении в течение 5 лет ставим 60 (12 мес. х 5 лет); при квартальном – 20 (4 кв. х 5 лет).
А теперь: внимание – вопрос. Как изменится доходность нашего вклада в случае начисления банком сложных процентов в конце каждого месяца, а не года, как мы считали до этого, на протяжении 5 лет? Давайте посмотрим. Напомню, до этого у нас получалась сумма в размере 16 105 руб. Заполняем поля и нажимаем “ОК”.
Получаем 16 453 рубля. Как видите, разница 343 рубля. А главное: чем больше сумма вашего вклада и время его размещения, тем ощутимей будет прибавка. Такова магия сложных процентов. Отсюда – вывод. Проценты по вашему вкладу должны:
- капитализироваться;
- капитализироваться ежемесячно.
Чем чаще начисляются проценты и добавляются к сумме вашего вклада, тем лучше работают ваши деньги. Кстати, хотите узнать, как скоро ваш вклад удвоится? Нет ничего проще. Воспользуйтесь правилом 72.
- Разделите число 72 на предлагаемую банком процентную ставку, и вы получите то число лет, которое нужно для увеличения ваших вложений в 2 раза.
А сейчас (барабанная дробь) испытайте чувство гордости за себя. Потому что теперь вы можете рассчитать это в Excel. Для этого вызовите функцию Кпер, заполните данные из нашего примера (10% годовых, 5 лет, выплата процентов в конце года) и добавьте в поле БС ожидаемую сумму вклада в размере 20 000 руб. (10 000 руб. х 2). Вуаля!
А еще есть правило волшебной двадцатки. Суть его в том, что для обеспечения завтра того уровня дохода, к которому вы привыкли сегодня, вам нужна сумма в 20 раз превышающая ваш годовой доход. Посчитайте и впечатлитесь полученной цифрой.
Но, как гласит народная мудрость, о деньгах и здоровье вспоминают тогда, когда они заканчиваются. И часто бывает так, что изменить что-либо уже поздно. Стоит ли рисковать? Когда все, что вам нужно сделать – это подумать о завтра сегодня.
- Если у вас есть вопросы, пишите их в комментариях ниже, я вам отвечу. Также вы всегда можете обратиться ко мне за консультацией, пройти мои курсы и вебинары.
Обучение торговле на бирже
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Mobile Еще…Меньше
Управление личными финансами может быть сложной задачей, особенно если вам нужно планировать свои платежи и сбережения. Excel формулы и шаблоны бюджетов помогут вам вычислить будущую стоимость своих задолженности и инвестиций, что упростит расчет времени, необходимого для достижения целей. Используйте следующие функции:
-
ПЛТ: возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и процентной ставки.
-
КПЕР: возвращает количество периодов выплаты для инвестиции на основе регулярных постоянных выплат и постоянной процентной ставки.
-
ПВ: возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на данный момент равноценна ряду будущих выплат.
-
БС: возвращает будущую стоимость инвестиции при условии периодических равных платежей и постоянной процентной ставки.
Расчет ежемесячных платежей для погашения задолженности по кредитной карте
Предположим, остаток к оплате составляет 5400 долларов США под 17% годовых. Пока задолженность не будет погашена полностью, вы не сможете рассчитываться картой за покупки.
С помощью функции ПЛТ(ставка;КПЕР;ПС)
=ПЛТ(17%/12;2*12;5400)
получаем ежемесячный платеж в размере 266,99 долларов США, который позволит погасить задолженность за два года.
-
Аргумент «ставка» — это процентная ставка на период погашения кредита. Например, в данной формуле ставка 17% годовых делится на 12 — количество месяцев в году.
-
Аргумент КПЕР 2*12 — это общее количество периодов выплат по кредиту.
-
Аргумент ПС или приведенной стоимости составляет 5400 долларов США.
Расчет ежемесячных платежей по ипотеке
Представьте дом стоимостью 180 000 долларов США под 5% годовых на 30 лет.
С помощью функции ПЛТ(ставка;КПЕР;ПС)
=ПЛТ(5%/12;30*12;180000)
получена сумма ежемесячного платежа (без учета страховки и налогов) в размере 966,28 долларов США.
-
Аргумент «ставка» составляет 5%, разделенных на 12 месяцев в году.
-
Аргумент КПЕР составляет 30*12 для ипотечного кредита сроком на 30 лет с 12 ежемесячными платежами, оплачиваемыми в течение года.
-
Аргумент ПС составляет 180 000 (нынешняя величина кредита).
Расчет суммы ежемесячных сбережений, необходимой для отпуска
Необходимо собрать деньги на отпуск стоимостью 8500 долларов США за три года. Процентная ставка сбережений составляет 1,5%.
С помощью функции ПЛТ(ставка;КПЕР;ПС;БС)
=ПЛТ(1,5%/12;3*12;0;8500)
получаем, что чтобы собрать 8500 долларов США за три года, необходимо откладывать по 230,99 долларов США ежемесячно.
-
Аргумент «ставка» составляет 1,5%, разделенных на 12 месяцев — количество месяцев в году.
-
Аргумент КПЕР составляет 3*12 для двенадцати ежемесячных платежей за три года.
-
Аргумент ПС (приведенная стоимость) составляет 0, поскольку отсчет начинается с нуля.
-
Аргумент БС (будущая стоимость), которую необходимо достичь, составляет 8500 долларов США.
Теперь допустим, вы хотите собрать 8500 долларов США на отпуск за три года, и вам интересно, какую сумму необходимо положить на счет, чтобы ежемесячный взнос составлял 175,00 долларов США. Функция ПС рассчитает размер начального депозита, который позволит собрать желаемую сумму.
С помощью функции ПС(ставка;КПЕР;ПЛТ;БС)
=ПС(1,5%/12;3*12;-175;8500)
мы узнаем, что необходим начальный депозит в размере 1969,62 долларов США, чтобы можно было откладывать по 175,00 долларов США в месяц и собрать 8500 долларов США за три года.
-
Аргумент «Ставка» составляет 1,5%/12.
-
Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).
-
Аргумент ПЛТ составляет -175 (необходимо откладывать по 175 долларов США в месяц).
-
Аргумент БС (будущая стоимость) составляет 8500.
Расчет срока погашения потребительского кредита
Представьте, что вы взяли потребительский кредит на сумму 2500 долларов США и согласились выплачивать по 150 долларов США ежемесячно под 3% годовых.
С помощью функции КПЕР(ставка;ПЛТ;ПС)
=КПЕР(3%/12;-150;2500)
выясняем, что для погашения кредита необходимо 17 месяцев и несколько дней.
-
Аргумент «Ставка» составляет 3%/12 ежемесячных платежей за год.
-
Аргумент ПЛТ составляет -150.
-
Аргумент ПС (приведенная стоимость) составляет 2500.
Расчет суммы первого взноса
Скажем, вы хотите приобрести автомобиль стоимостью 19 000 долларов США под 2,9 % годовых за три года. Вы хотите, чтобы ежемесячные платежи были на уровне 3500 долларов США в месяц, поэтому вам нужно выяснить сумму своего взноса. В этой формуле результатом функции ПС является сумма займа, которая затем вычитается из цены покупки, чтобы получить первый взнос.
С помощью функции ПС(ставка;КПЕР;ПЛТ)
= 19000-ПС(2,9%/12; 3*12;-350)
выясняем, что первый взнос должен составлять 6946,48 долларов США.
-
Сначала в формуле указывается цена покупки в размере 19 000 долларов США. Результат функции ПС будет вычтен из цены покупки.
-
Аргумент «Ставка» составляет 2,9%, разделенных на 12.
-
Аргумент КПЕР составляет 3*12 (или двенадцать ежемесячных платежей за три года).
-
Аргумент ПЛТ составляет -350 (необходимо будет выплачивать по 350 долларов США в месяц).
Оценка динамики увеличения сбережений
Начиная с 500 долларов США на счету, сколько можно собрать за 10 месяцев, если класть на депозит по 200 долларов США в месяц под 1,5% годовых?
С помощью функции БС(ставка;КПЕР;ПЛТ;ПС)
=БС(1,5%/12;10;-200;-500)
получаем, что за 10 месяцев выйдет сумма 2517,57 долларов США.
-
Аргумент «Ставка» составляет 1,5%/12.
-
Аргумент КПЕР составляет 10 (месяцев).
-
Аргумент ПЛТ составляет -200.
-
Аргумент ПС (приведенная стоимость) составляет -500.
См. также
ПЛТ
КПЕР
ПС
БС
Нужна дополнительная помощь?
Временная стоимость денег (Time Value of Money, TVM) – это важный показатель в бухгалтерской и финансовой отрасли. Идея заключается в том, что рубль сегодня стоит меньше чем тот же самый рубль завтра. Разница между этими двумя финансовыми значениями является прибыль, которую можно извлечь с одного рубля или убыток. Например, данная прибыль может быть получена с процентов, начисленных на банковском счете или в качестве дивидендов от инвестиций. Но также может быть убыток при оплате процентов за погашение кредитного долга.
Пример с расчетом текущей дисконтированной стоимости инвестиций в Excel
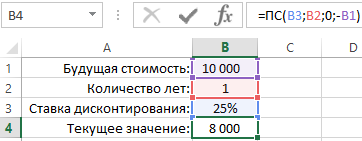
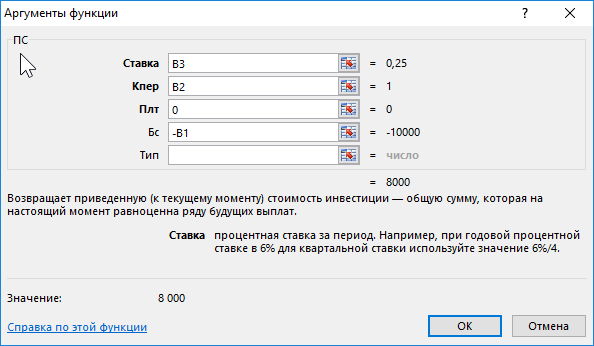
Программа Excel предлагает несколько финансовых функций для вычисления стоимости денег во времени. Например, функция ПС (приведенная стоимость) возвращает текущую стоимость инвестиций. Простыми словами, данная функция снижает сумму на размер процента дисконтирования и возвращает текущую стоимость для этой суммы. Если инвестиционный проект предполагает принести прибыль в размере 10 000 через год. Вопрос: какой максимальной суммой рационально рискнуть чтобы инвестировать в данных проект?
Например, в России розничный бизнес иногда делает прибыль до 35% годовых, а оптовый не более 15%. Учитывая небольшую сумму инвестиций предполагается, что инвестиционный объект не является оптовым бизнесом, а значит следует ожидать прибыль больше чем 15% годовых. Ниже на рисунке провиден пример формулы калькулятора доходности инвестиций в процентах:
Как мы видим на рисунке калькулятор нам отображает, чтобы получить сумму 10 000 за 1 год при доходности 25% нам необходимо вложить 8 000 финансовых средств. То есть если бы у нас была сумма 8 000 и мы вложили ее под 25% годовых через год мы заработали бы 10 000.
Функция ПС имеет 5 аргументов:
- Ставка – процентная ставка дисконтирования. Это прибыль в процентах, на которую можно рассчитывать за период дисконтирования. Это значение имеет наибольшее влияние на вычисление текущей стоимости инвестиций, но его наиболее сложно точно определить. Осторожные инвесторы чаще всего занижают процентную ставку до максимально реально достижимого уровня при тех или иных условиях. Если же финансовые средства предназначены для погашения кредита, в таком случае данный аргумент определяется легко.
- Количество периодов (Кпер) – период времени на протяжении которого дисконтируется будущая сумма. В данном примере указан 1 год (записанный в ячейке B2). Процентная ставка и количество лет должны быть выражены в соответственных единицах измерения. Это значит, что вы используете годовую ставку, тогда числовое значение в данном аргументе значит количество лет. Если указана процентная ставка в первом аргументе для месяцев (например, 2,5% ежемесячных), тогда число во втором аргументе значит количество месяцев.
- Платеж (Плт) – сумма, которая периодически платится на протяжении периода дисконтирования. Если предусмотрен в условиях инвестирования только один платеж, как в выше приведенном примере, тогда данная сумма является будущей стоимостью денег, а сам платеж равен =0. Данный аргумент должен быть согласован со вторым аргументом количества периодов. Если количество периодов дисконтирования равно 10, а третий аргумент не равен <>0, тогда функция ПС посчитает как 10 платежей на сумму, указанную в третьем аргументе (Плт). Ниже на следующем примере изображено как вычисляется текущая стоимость денег при нескольких взносах отдельными платежами.
- Будущая стоимость (БС) – это сумма, которую следует получить в конце периода дисконтирования. Финансовые функции Excel основаны на вычислениях наличного потока. Это значит, что будущая стоимость и текущая стоимость инвестиций имеют противоположные знаки чисел. В данном примере будущая стоимость является отрицательным числом, поэтому формула в результате вычислений возвращает положительное число.
- Тип – данный аргумент должен иметь значение 0, если выплата итоговой суммы припадает на конец периода дисконтирования, или число 1 – если на его начало. В данном примере значение данного аргумента не имеет значения и никак не повлияет на итоговый результат вычисления. Так как платежный взнос равен нулю и аргумент определяющий тип может быть опущен. В таком случае функция по умолчанию присваивает данному аргументу значение 0.
Формула расчета текущей стоимости денег с учетом инфляции в Excel
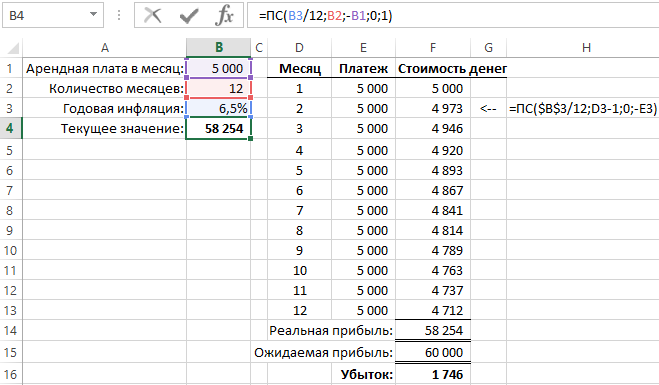
В другом примере применения функции ПС выполняется вычисление будущей стоимости денег сразу для целой серии будущих равных платежных взносов. Если, например, по договору аренды офиса арендатор должен платить по 5000 каждый месяц на протяжении одного года, тогда арендодатель с помощью функции ПС сможет посчитать сколько он потеряет дохода при учете 6,5% годовой инфляции:
В данном примере пятый аргумент «Тип» имеет числовое значение 1, так как оплата за аренду платится в начале каждого месяца.
В случае наличия суммы регулярных платежей функция ПС в реальности вычисляет текущую стоимость денег отдельно для каждого платежа и суммирует полученные результаты. На рисунке видны результаты вычисления стоимости для каждого платежа. Текущая стоимость первого платежа такая же, как и сумма платежа, так как платится сейчас по факту. Платеж в следующем месяце будет проплачен через месяц и уже уменьшается его текущая денежная стоимость (обесценивается). Он дисконтирован до суммы 4 973. Изменения не значительные, но последний платеж, который буде проплачен через 11 месяцев имеет стоимость уже существенно ниже – 4 712. Все результаты вычисления значений текущей стоимости инвестиций необходимо суммировать. Функция ПС выполняет всю эту работу автоматически без необходимости составления хронологического графика платежей за весь период.