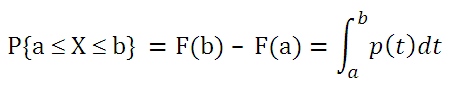Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
- ДИСП;
- ГИПЕРГЕОМ.РАСП;
- СРЗНАЧ и другие.
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
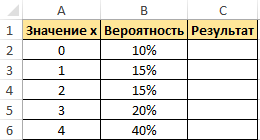
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
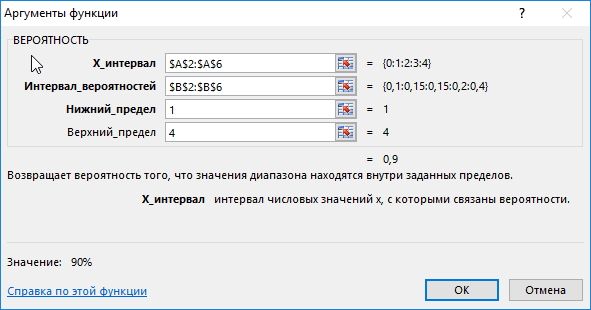
Для этого введем функцию со следующими аргументами:
тут:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
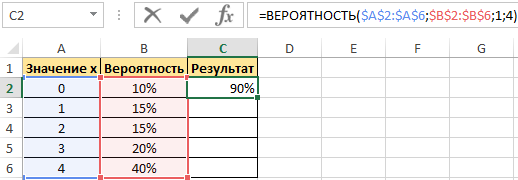
В результате выполненных вычислений получим:
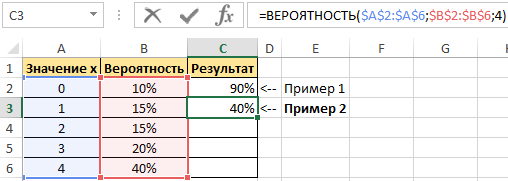
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
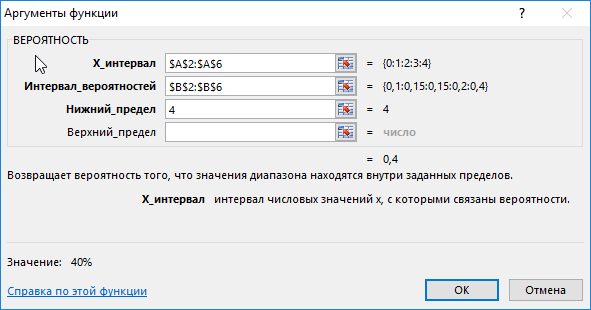
Введем в ячейку С3 введем функцию с такими аргументами:
тут:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Получим:
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Введем формулу:
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Скачать примеры функции ВЕРОЯТНОСТЬ в Excel
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование proB
Функция Microsoft Excel.
Описание
Возвращает вероятность того, что значение из интервала находится внутри заданных пределов. Если верхний_предел не задан, то возвращается вероятность того, что значения в аргументе x_интервал равняются значению аргумента нижний_предел.
Синтаксис
ВЕРОЯТНОСТЬ(x_интервал;интервал_вероятностей;[нижний_предел];[верхний_предел])
Аргументы функции ВЕРОЯТНОСТЬ описаны ниже.
-
x_интервал Обязательный. Диапазон числовых значений x, с которыми связаны вероятности.
-
Интервал_вероятностей Обязательный. Множество вероятностей, соответствующих значениям в аргументе «x_интервал».
-
Нижний_предел Необязательный. Нижняя граница значения, для которого вычисляется вероятность.
-
Верхний_предел Необязательный. Верхняя граница значения, для которого вычисляется вероятность.
Замечания
-
Если значение в prob_range ≤ 0 или любое значение в prob_range > 1, функция PROB возвращает #NUM! (значение ошибки).
-
Если сумма значений в prob_range не равна 1, функция PROB возвращает #NUM! (значение ошибки).
-
Если верхний_предел опущен, то функция ВЕРОЯТНОСТЬ возвращает вероятность равенства значению аргумента нижний_предел.
-
Если x_интервал и интервал_вероятностей содержат различное количество точек данных, то функция ВЕРОЯТНОСТЬ возвращает значение ошибки #Н/Д.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Значение x |
Вероятность |
|
|
0 |
0,2 |
|
|
1 |
0,3 |
|
|
2 |
0,1 |
|
|
3 |
0,4 |
|
|
Формула |
Описание |
Результат |
|
=ВЕРОЯТНОСТЬ(A3:A6;B3:B6;2) |
Вероятность того, что x является числом 2. |
0,1 |
|
=ВЕРОЯТНОСТЬ(A3:A6;B3:B6;1;3) |
Вероятность того, что x находится в интервале от 1 до 3. |
0,8 |
Нужна дополнительная помощь?
17 авг. 2022 г.
читать 2 мин
Вероятность описывает вероятность того, что некоторое событие произойдет.
Мы можем рассчитать вероятности в Excel, используя функцию PROB , которая использует следующий синтаксис:
ПРОБ(x_диапазон, вероятностный_диапазон, нижний_предел, [верхний_предел])
куда:
- x_range: диапазон числовых значений x.
- prob_range: диапазон вероятностей, связанных с каждым значением x.
- нижний_предел: нижний предел значения, для которого вы хотите получить вероятность.
- upper_limit: Верхний предел значения, для которого вы хотите получить вероятность. По желанию.
В этом руководстве представлено несколько примеров использования этой функции на практике.
Пример 1: Вероятность игры в кости
На следующем изображении показана вероятность выпадения кубика с определенным значением при данном броске:
Поскольку кости с одинаковой вероятностью выпадут на каждом значении, вероятность одинакова для каждого значения.
На следующем рисунке показано, как найти вероятность того, что кубик выпадет на число от 3 до 6:
Вероятность оказывается равной 0,5 .
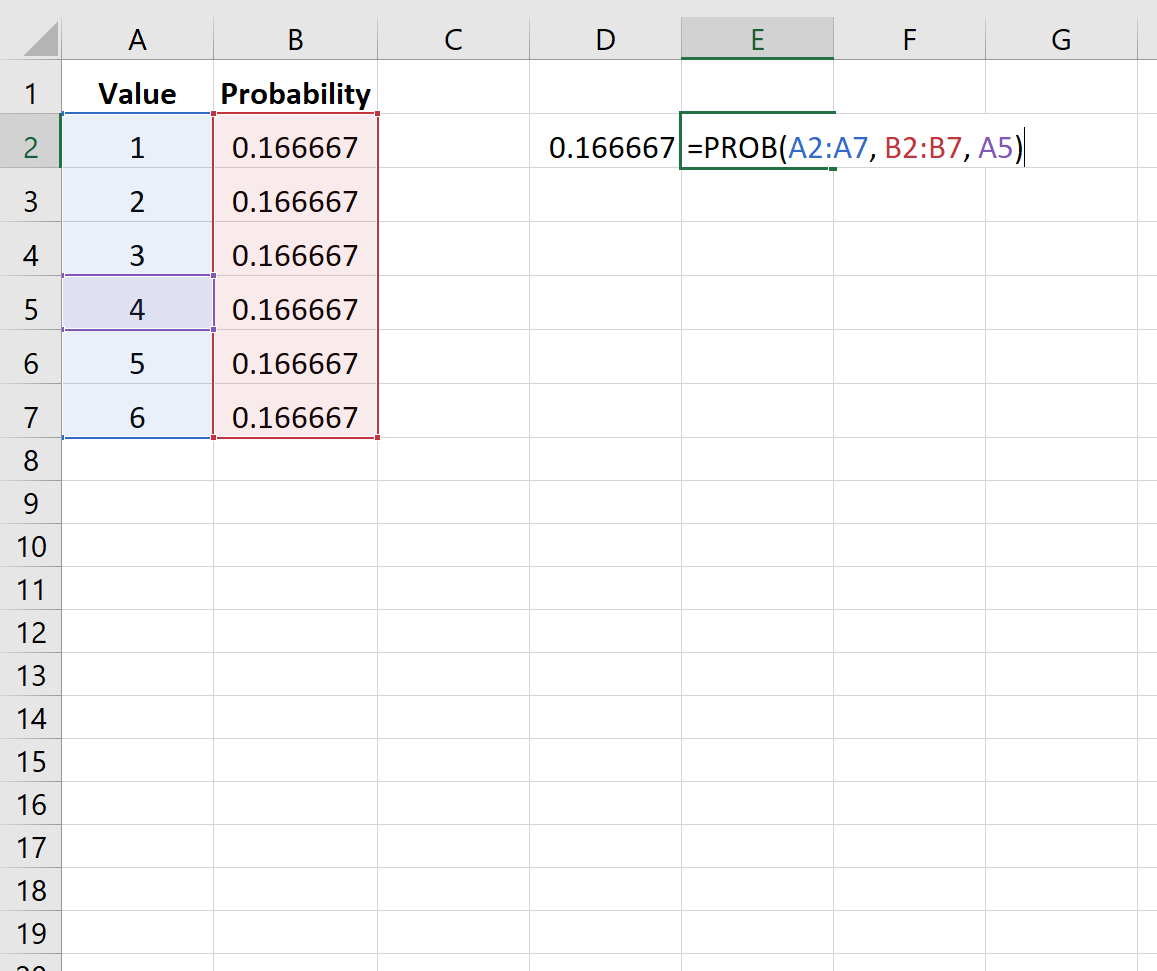
Обратите внимание, что аргумент верхнего предела является необязательным. Таким образом, мы могли бы использовать следующий синтаксис, чтобы найти вероятность того, что кости приземлятся только на 4:
Вероятность оказывается равной 0,166667 .
Пример 2: Вероятность продаж
На следующем изображении показана вероятность того, что компания продаст определенное количество товаров в предстоящем квартале:
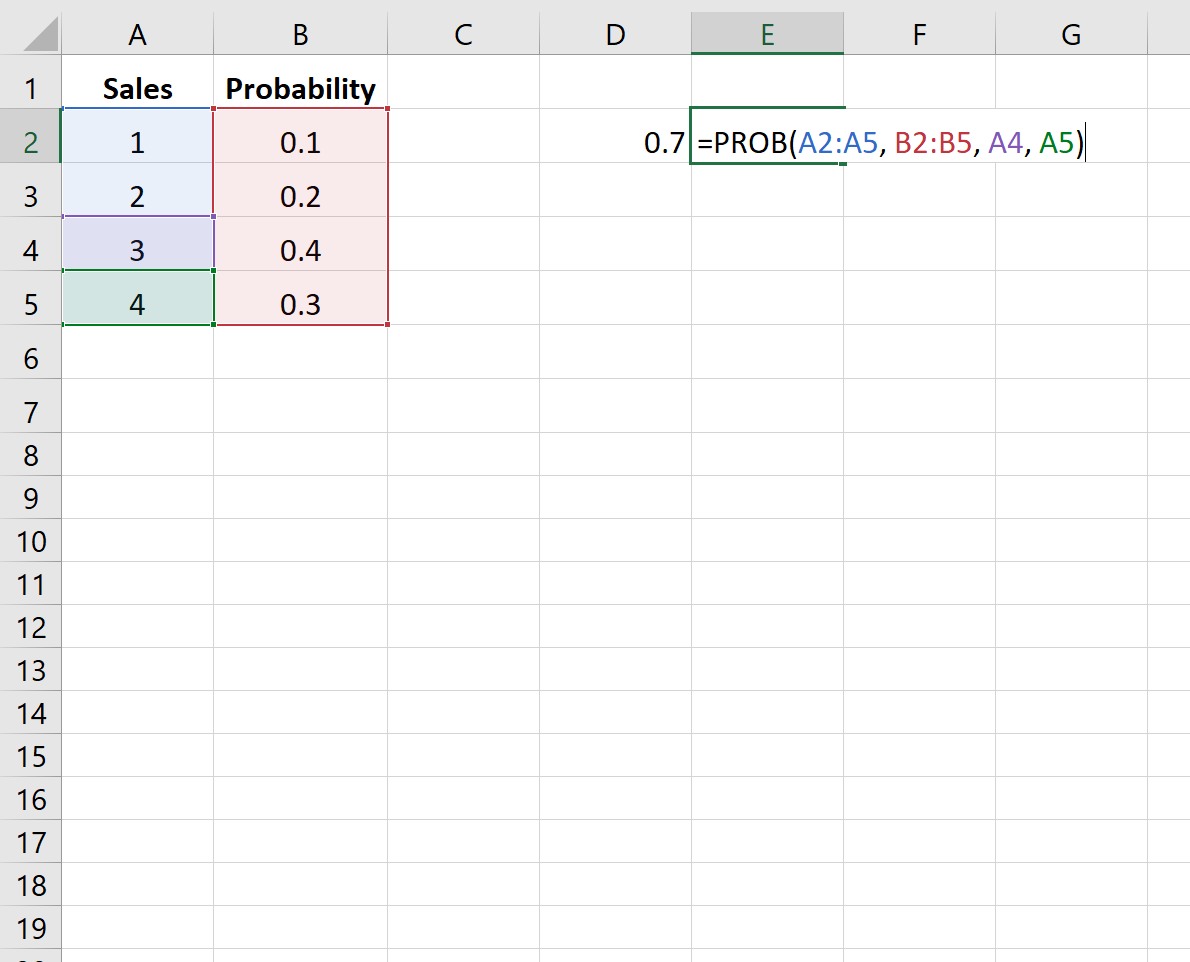
На следующем рисунке показано, как найти вероятность того, что компания совершит 3 или 4 продажи:
Вероятность оказывается равной 0,7 .
Дополнительные ресурсы
Как рассчитать относительную частоту в Excel
Как рассчитать кумулятивную частоту в Excel
Как создать частотное распределение в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Probability describes the likelihood that some event occurs.
We can calculate probabilities in Excel by using the PROB function, which uses the following syntax:
PROB(x_range, prob_range, lower_limit, [upper_limit])
where:
- x_range: The range of numeric x values.
- prob_range: The range of probabilities associated with each x value.
- lower_limit: The lower limit on the value for which you want a probability.
- upper_limit: The upper limit on the value for which you want a probability. Optional.
This tutorial provides several examples of how to use this function in practice.
Example 1: Dice Probabilities
The following image shows the probability of a dice landing on a certain value on a given roll:
Since the dice is equally likely to land on each value, the probability is the same for each value.
The following image shows how to find the probability that the dice lands on a number between 3 and 6:
The probability turns out to be 0.5.
Note that the upper limit argument is optional. So, we could use the following syntax to find the probability that the dice lands on just 4:
The probability turns out to be 0.166667.
Example 2: Sales Probabilities
The following image shows the probability of a company selling a certain number of products in the upcoming quarter:
The following image shows how to find the probability that the company makes either 3 or 4 sales:
The probability turns out to be 0.7.
Additional Resources
How to Calculate Relative Frequency in Excel
How to Calculate Cumulative Frequency in Excel
How to Create a Frequency Distribution in Excel
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта
www.excel2.ru
. Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL
.
Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.
Генеральная совокупность и случайная величина
Пусть у нас имеется
генеральная совокупность
(population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.
Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.
Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения
генеральная совокупность
представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.
В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.
Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является
случайной величиной
. По определению, любая
случайная величина
имеет
функцию распределения
, которая обычно обозначается F(x).
Функция распределения
Функцией распределения
вероятностей
случайной величины
Х называют функцию F(x), значение которой в точке х равно вероятности события X
F(x) = P(X
Поясним на примере нашего станка. Хотя предполагается, что наш станок производит только один тип деталей, но, очевидно, что вес изготовленных деталей будет слегка отличаться друг от друга. Это возможно из-за того, что при изготовлении мог быть использован разный материал, а условия обработки также могли слегка различаться и пр. Пусть самая тяжелая деталь, произведенная станком, весит 200 г, а самая легкая — 190 г. Вероятность того, что случайно выбранная деталь Х будет весить меньше 200 г равна 1. Вероятность того, что будет весить меньше 190 г равна 0. Промежуточные значения определяются формой Функции распределения. Например, если процесс настроен на изготовление деталей весом 195 г, то разумно предположить, что вероятность выбрать деталь легче 195 г равна 0,5.
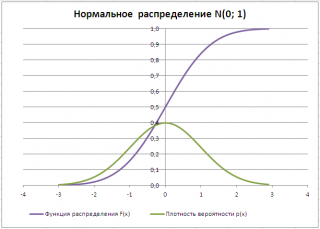
Типичный график
Функции распределения
для непрерывной случайной величины приведен на картинке ниже (фиолетовая кривая, см.
файл примера
):
В справке MS EXCEL
Функцию распределения
называют
Интегральной
функцией распределения
(
Cumulative
Distribution
Function
,
CDF
).
Приведем некоторые свойства
Функции распределения:
Функция распределения
F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
Функция распределения
– неубывающая функция;-
Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x
1
<=X
2)=F(x
2
)-F(x
1
).
Существует 2 типа распределений:
непрерывные распределения
и
дискретные распределения
.
Дискретные распределения
Если случайная величина может принимать только определенные значения и количество таких значений конечно, то соответствующее распределение называется
дискретным
. Например, при бросании монеты, имеется только 2 элементарных исхода, и, соответственно, случайная величина может принимать только 2 значения. Например, 0 (выпала решка) и 1 (не выпала решка) (см.
схему Бернулли
). Если монета симметричная, то вероятность каждого исхода равна 1/2. При бросании кубика случайная величина принимает значения от 1 до 6. Вероятность каждого исхода равна 1/6. Сумма вероятностей всех возможных значений случайной величины равна 1.
Примечание
: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье
Распределения случайной величины в MS EXCEL
.
Непрерывные распределения и плотность вероятности
В случае
непрерывного распределения
случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для
непрерывной случайной величины
равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой
функции плотности распределения p(x)
. Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение
функции распределения
на этом интервале:
Как видно из формулы выше
плотность распределения
р(х) представляет собой производную
функции распределения
F(x), т.е. р(х) = F’(x).
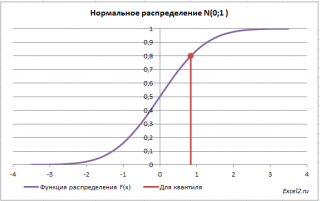
Типичный график
функции плотности распределения
для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):
Примечание
: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье
Распределения случайной величины в MS EXCEL
.
В литературе
Функция плотности распределения
непрерывной случайной величины может называться:
Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF)
.
Чтобы все усложнить, термин
Распределение
(в литературе на английском языке —
Probability
Distribution
Function
или просто
Distribution
)
в зависимости от контекста может относиться как
Интегральной
функции распределения,
так и кее
Плотности распределения.
Из определения
функции плотности распределения
следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от
Функции распределения,
больше 1. Например, для
непрерывной равномерной величины
, распределенной на интервале [0; 0,5]
плотность вероятности
равна 1/(0,5-0)=2. А для
экспоненциального распределения
с параметром
лямбда
=5, значение
плотности вероятности
в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.
Напомним, что
плотность распределения
является производной от
функции распределения
, т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что
плотность распределения
>1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере
экспоненциального распределения
).
Примечание
: Площадь, целиком заключенная под всей кривой, изображающей
плотность распределения
, равна 1.
Примечание
: Напомним, что функцию распределения F(x) называют в функциях MS EXCEL
интегральной функцией распределения
. Этот термин присутствует в параметрах функций, например в
НОРМ.РАСП
(x; среднее; стандартное_откл;
интегральная
). Если функция MS EXCEL должна вернуть
Функцию распределения,
то параметр
интегральная
, д.б. установлен ИСТИНА. Если требуется вычислить
плотность вероятности
, то параметр
интегральная
, д.б. ЛОЖЬ.
Примечание
: Для
дискретного распределения
вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL
плотность вероятности
может называть даже «функция вероятностной меры» (см. функцию
БИНОМ.РАСП()
).
Вычисление плотности вероятности с использованием функций MS EXCEL
Понятно, что чтобы вычислить
плотность вероятности
для определенного значения случайной величины, нужно знать ее распределение.
Найдем
плотность вероятности
для
стандартного нормального распределения
N(0;1) при x=2. Для этого необходимо записать формулу
=НОРМ.СТ.РАСП(2;ЛОЖЬ)
=0,054 или
=НОРМ.РАСП(2;0;1;ЛОЖЬ)
.
Напомним, что
вероятность
того, что
непрерывная случайная величина
примет конкретное значение x равна 0. Для
непрерывной случайной величины
Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).
Вычисление вероятностей с использованием функций MS EXCEL
1) Найдем вероятность, что случайная величина, распределенная по
стандартному нормальному распределению
(см. картинку выше), приняла положительное значение. Согласно свойству
Функции распределения
вероятность равна F(+∞)-F(0)=1-0,5=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу
=НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА)
=1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).
2) Найдем вероятность, что случайная величина, распределенная по
стандартному нормальному распределению
, приняла отрицательное значение. Согласно определения
Функции распределения,
вероятность равна F(0)=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу
=НОРМ.СТ.РАСП(0;ИСТИНА)
=0,5.
3) Найдем вероятность того, что случайная величина, распределенная по
стандартному нормальному распределению
, примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу
=НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА)
.
Все расчеты, приведенные выше, относятся к случайной величине, распределенной по
стандартному нормальному закону
N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье
Распределения случайной величины в MS EXCEL
приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.
Обратная функция распределения (Inverse Distribution Function)
Вспомним задачу из предыдущего раздела:
Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.
Вероятность этого события равна 0,5.
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение
медиану
или 50-ю
процентиль
).
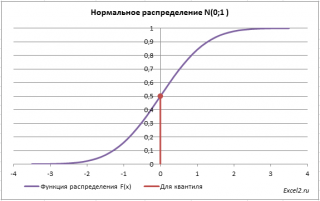
Для этого необходимо на графике
функции распределения
найти точку, для которой F(х)=0,5, а затем найти абсциссу этой точки. Абсцисса точки =0, т.е. вероятность, того что случайная величина Х примет значение <0, равна 0,5.
В MS EXCEL используйте формулу
=НОРМ.СТ.ОБР(0,5)
=0.
Однозначно вычислить значение
случайной величины
позволяет свойство монотонности
функции распределения.
Обратите внимание, что для вычисления обратной функции мы использовали именно
функцию распределения
, а не
плотность распределения
. Поэтому, в аргументах функции
НОРМ.СТ.ОБР()
отсутствует параметр
интегральная
, который подразумевается. Подробнее про функцию
НОРМ.СТ.ОБР()
см. статью про
нормальное распределение
.
Обратная функция распределения
вычисляет
квантили распределения
, которые используются, например, при
построении доверительных интервалов
. Т.е. в нашем случае число 0 является 0,5-квантилем
нормального распределения
. В
файле примера
можно вычислить и другой
квантиль
этого распределения. Например, 0,8-квантиль равен 0,84.
В англоязычной литературе
обратная функция распределения
часто называется как Percent Point Function (PPF).
Примечание
: При вычислении
квантилей
в MS EXCEL используются функции:
НОРМ.СТ.ОБР()
,
ЛОГНОРМ.ОБР()
,
ХИ2.ОБР(),
ГАММА.ОБР()
и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
A discrete distribution describes the probability of occurrence of a random variable that can take on only a certain number of values. Common examples for this are the probabilities in a dice roll or getting a certain card in a deck of regular cards. In this guide, we’re going to show you how to calculate discrete probability in Excel.
Download Workbook
What is probability?
Probability is a branch of mathematics that shows how likely an event is to occur. In a nutshell, it is the ratio of the number of occurrences of an event to the total number of occurrences.
Let’s look at rolling a dice. A standard dice has 6 sides and each side has an equal chance to be on top. Thus, we can say each number has 1/6 = 0.1667 probability.
If you want to calculate the probability of getting 1 or 2 or 3 on a dice roll, you can sum up the probability values or use the PROB function.
PROB function
The PROB function is a statistical function that can calculate the probability associated with a given range. The function allows you to set lower and upper limits to be able to calculate probability between.
PROB(x_range, prob_range, [lower_limit], [upper_limit])
| x_range | The range of numeric values which have associated probabilities. |
| prob_range | The range of probabilities associated with values in x_range. |
| lower_limit | The lower bound on the value for which you want to calculate the probability. |
| [upper_limit] | Optional. The lower bound on the value for which you want to calculate the probability. If this is omitted, the PROB function returns the probability for the x_range values equal to the lower_limit. |
How to calculate discrete probability with PROB function
The first argument of the PROB function, x_range, accepts events by numerical values. Events, in this example, are the numbers of a dice. The second argument, prob_range, is for the probabilities of occurrences of the corresponding events. The rest of the arguments are for the lower and upper limits, respectively.
To return the probability of getting 1 or 2 or 3 on a dice roll, the data and formula should be like the following:
The formula returns 0.5, which means you have a 50% chance to get 1 or 2 or 3 from a single roll. Let’s check a more complex example for calculating discrete probability with 2 dices.
When you roll two dices, you can get numbers between 2 and 12. However, the probabilities of numbers are not equal this time. The table of numbers and probability values are below.
If your aim is to find the probability of a single event, you can use the COUNTIF function to count values above, based on the event value and divide it by the total number of events. You can find total number by multiplying dice numbers (6 * 6) or counting them using the COUNT function.
You can see that the most likely result is the number 7 with a probability of 0.1667.
Лотерея — это не охота за удачей,
это охота за неудачниками.
С завидной регулярностью (а в последнее время — всё чаще) мне пишут люди с просьбами помочь в различных вычислениях, связанных с лотереями. Кто-то хочет реализовать в Excel свой секретный алгоритм подбора выигрышных чисел, кто-то — найти закономерности в выпавших номерах прошедших тиражей, кто-то — подловить организаторов лотереи на нечестной игре.
В этой статье мне хотелось бы ответить на часть этих вопросов. Благо, в Excel для решения таких задач достаточно инструментов, многие из которых, кстати, могут пригодиться и в более прозаических рабочих ситуациях.
Задача 1. Вероятность выигрыша
Возьмем для примера классическую лотерею «Столото 6 из 45». По правилам суперприз (10 млн. рублей или больше, если накопился остаток призового фонда с прошлых тиражей) получают только те, кто угадал все 6 чисел из 45. Если вы угадали 5, то получите 150 тыс. рублей, если 4 — 1500 р., если 3 числа из 6, то 150 р., если 2 числа — вернете 50 р., потраченных на билет. Угадаете только одно или ни одного — получите только эндорфины от процесса игры.
Математическую вероятность выигрыша можно легко рассчитать с помощью стандартной функции ЧИСЛКОМБ (COMBIN), которая имеется в Microsoft Excel на такой случай. Эта функция вычисляет количество комбинаций N чисел из M. Так для нашей лотереи «6 из 45» это будет:
=ЧИСЛКОМБ(45;6)
… что равно 8 145 060 — общее число всех возможных комбинаций в этой лотерее.
Если же хочется рассчитать вероятность для частичного выигрыша (2-5 чисел из 6), то придётся сначала вычислить количество таких вариантов, которое равно произведению числа комбинаций угаданных чисел из 6 на количество не угаданных чисел из оставшихся (45-6)=39 чисел. Затем общее количество всех возможных комбинаций (8 145 060) мы делим на полученное количество выигрышей по каждому варианту — и получим вероятности выигрыша для каждого случая:
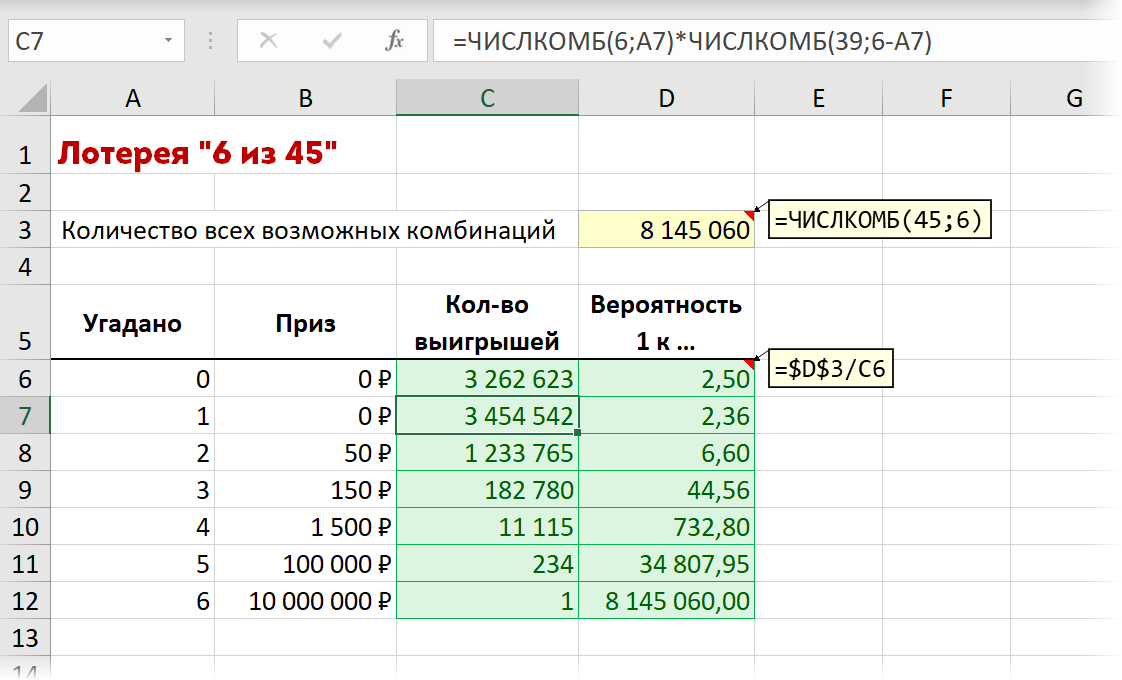
К слову, вероятность, например, погибнуть в авиакатастрофе в России оценивается примерно как 1 к миллиону. А вероятность выиграть в казино в рулетку, поставив всё на один номер — 1 к 37.
Если всё вышеперечисленное вас не остановило и вы по-прежнему готовы играть дальше — продолжаем.
Задача 2. Частота выпадения каждого числа
Для начала давайте определим с какой частотой выпадают те или иные числа. В идеальной лотерее, если брать для анализа достаточно большой временной интервал, у всех шаров должна быть одинаковая вероятность попадания в победную выборку. В реальности же особенности конструкции лототрона и вес-форма шаров могут вносить искажения в эту картину и для каких-то шаров вероятность выпадения вполне может оказаться выше/ниже, чем для других. Давайте проверим эту гипотезу на практике.
Возьмём для примера данные по всем прошедшим в 2020-21 году тиражам лотереи 6 из 45 с сайта их организатора Столото, оформленные в виде вот такой удобной для анализа «умной» таблицы с именем таблАрхивТиражей. Розыгрыши проходят два раза в день (в 11 утра и в 11 вечера), т.е. в этой таблице у нас полторы тысячи тиражей-строк — вполне достаточная для начала выборка для анализа:
Для подсчёта частоты выпадения каждого числа используем функцию СЧЁТЕСЛИ (COUNTIF) и дополнительно вложим в неё функцию ТЕКСТ (TEXT), чтобы добавить к одноразрядным числам начальные нули и звёздочки перед и после, чтобы СЧЁТЕСЛИ искала вхождение числа в любом месте комбинации в столбце В. Также для пущей наглядности построим диаграмму по результатам и отсортируем частоты по убыванию:
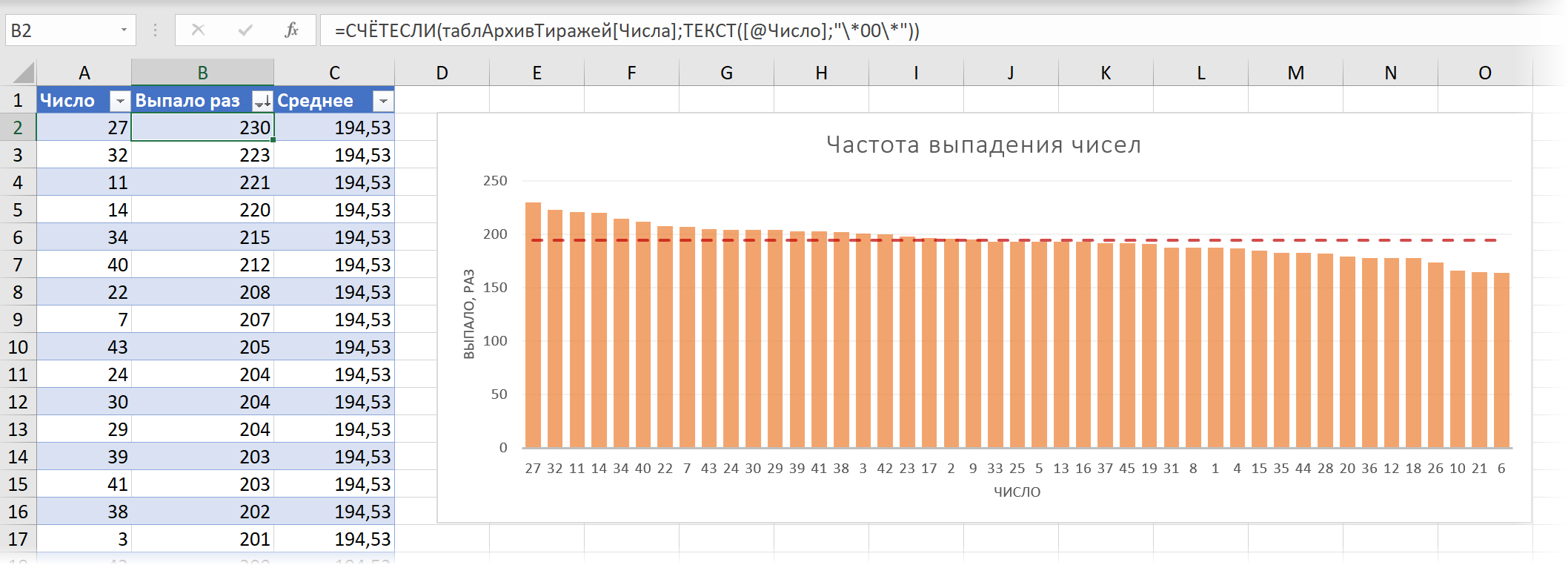
В среднем любой шар должен выпадать 1459 тиражей * 6 шаров / 45 номеров = 194,53 раз (это как раз то, что называется в статистике математическим ожиданием), но хорошо видно, что некоторые числа (27, 32, 11…) выпадали заметно чаще (+18%), а некоторые (10, 21, 6…) наоборот заметно реже (-15%), чем основная масса. Соответственно, можно попробовать использовать эту информацию для стратегии выигрыша, т.е. либо ставить на те шары, что выпадают чаще, либо наоборот — делать ставку на редко выпадающие шары в надежде, что они должны нагнать отставание.
Задача 3. Какие числа давно не выпадали?
Ещё одна стратегия базируется на идее, что при достаточно большом количестве тиражей рано или поздно должно выпасть каждое число из всех имеющихся от 1 до 45. Так что если какие-то числа давно не появлялись среди выигравших («холодные шары»), то логично попробовать сделать на них ставку в будущем.
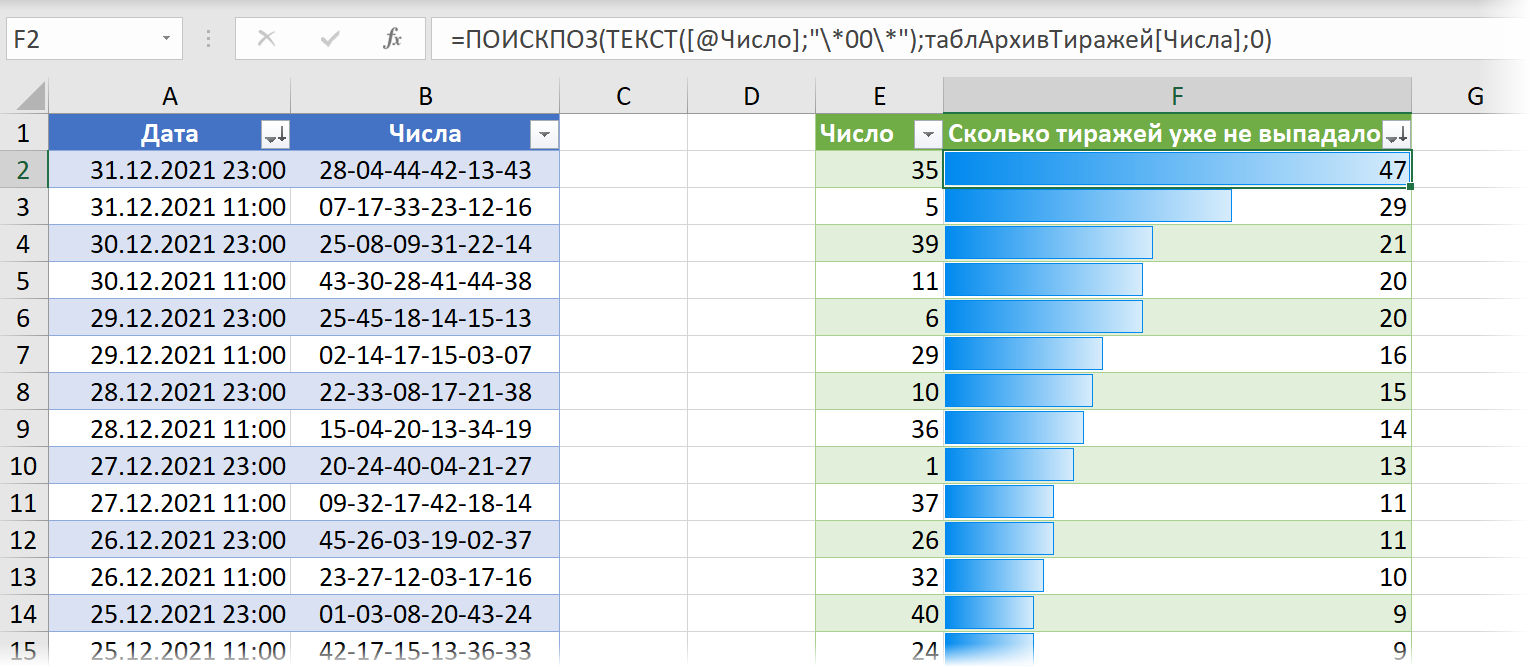
Можно легко найти все давно не выпадавшие номера, если отсортировать наш архив тиражей за 2020-21 год по убыванию даты и использовать функцию ПОИСКПОЗ (MATCH). Она будет сверху-вниз (т.е. от новых к старым тиражам) искать каждое число и выдавать порядковый номер тиража (считая от конца года к началу), где последний раз это число выпало:
Задача 4. Генератор случайных чисел
Ещё одна стратегия игры основана на том, чтобы исключить психологический фактор при угадывании номеров. Когда игрок выбирает числа, делая свою ставку, то подсознательно делает это не совсем рационально. По статистике, например, числа от 1 до 31 выбирают на 70 % чаще, чем остальные (любимые даты), реже выбирают 13 (чертова дюжина), чаще выбирают числа содержащие «счастливую» семерку и т.д. Но играем мы против машины (лототрона), для которой все числа одинаковы, так что имеет смысл выбирать их с такой же математической беспристрастностью, чтобы уравнять наши шансы. Для этого нам потребуется создать в Excel генератор случайных и — что особенно важно — неповторяющихся чисел:
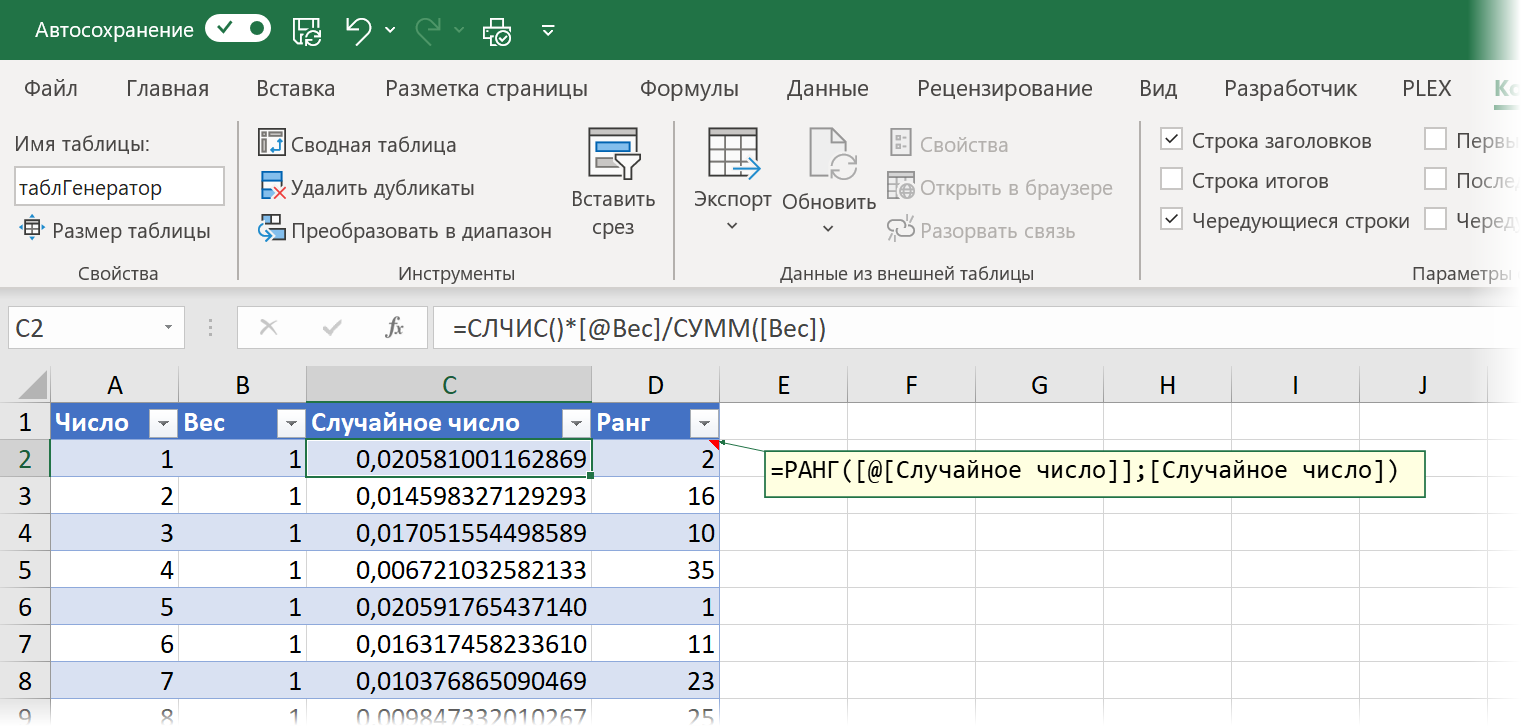
Для этого:
- Создадим «умную» таблицу с именем таблГенератор, где в первом столбце будут наши числа от 1 до 45.
- Во втором столбце введём вес для каждого числа (он потребуется нам чуть позднее). Если все числа для нас одинаково ценны и мы хотим выбирать их с равной вероятностью, то вес везде можно поставить равным 1.
- В третьем столбце используем функцию СЛЧИС (RAND), которая в Excel генерирует случайное дробное число от 0 до 1, добавив к нему вес из предыдущего столбца. Таким образом каждый раз при пересчёте листа (нажатии на клавишу F9) будет генерироваться новый набор из 45 случайных чисел с учётом веса для каждого из них.
- Добавим четвертый столбец, где с помощью функции РАНГ (RANK) вычислим ранг (позицию в топе) для каждого из чисел.
Теперь останется сделать выборку первых шести по рангу 6 чисел с помощью функции ПОИСКПОЗ (MATCH):
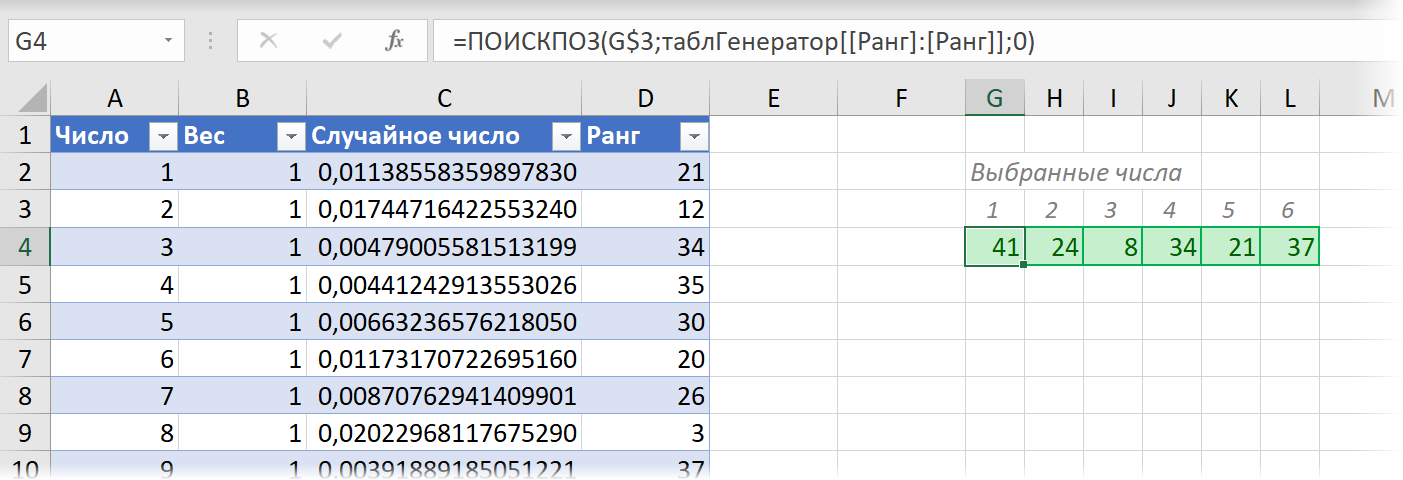
При нажатии на клавишу F9 формулы на листе Excel будут пересчитываться и мы будем каждый раз получать новый набор из 6 чисел в зеленых ячейках. Причём числа, для которых был задан в столбце B больший вес, будут получать пропорционально больший ранг и, таким образом, чаще оказываться в результатах нашей случайной выборки. Если же вес для всех чисел задать одинаковым, то все они будут выбираться с одинаковой вероятностью. Таким образом мы получаем справедливый и беспристрастный генератор случайных чисел 6 из 45, но с возможностью внести корректировки в случайность распределения при необходимости.
Если же мы решим играть в каждом тираже не одним, а, например, двумя билетами сразу, в каждом из которых будем выбирать неповторяющиеся числа, то можно просто добавить к зелёному диапазону дополнительные строки снизу, прибавив к рангу 6, 12, 18 и т.д. соответственно:
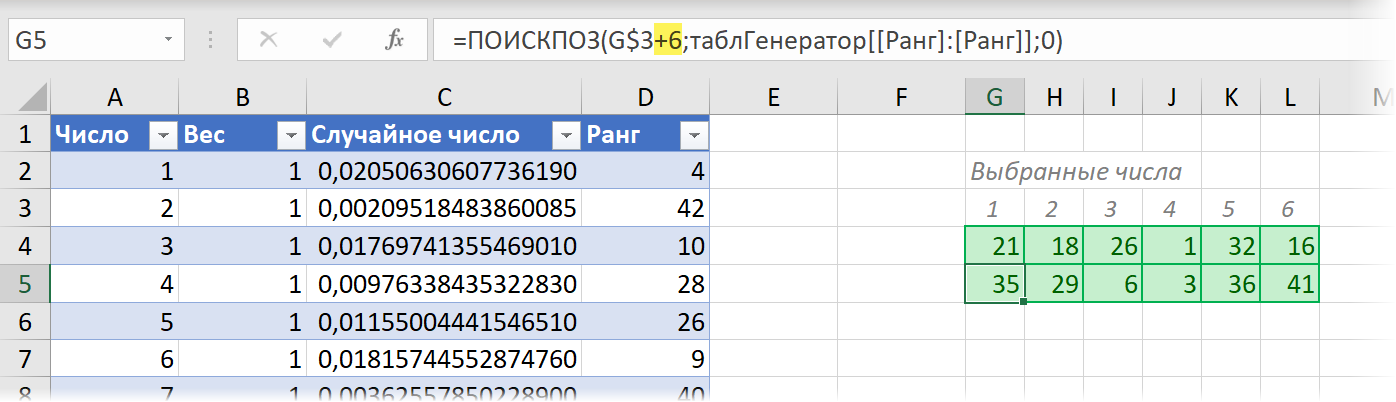
Задача 5. Симулятор лотереи в Excel
В качестве апофеоза всей этой темы давайте создадим в Excel полноценный симулятор лотереи, на котором можно будет опробовать любые стратегии и сравнить результаты (в теории оптимизации что-то похожее ещё называют методом Монте-Карло, но у нас будет попроще).
Чтобы все было максимально приближено к реальности, представим на минуту, что сейчас 1 января 2022 года и впереди у нас тиражи этого года, в которых мы планируем играть. Реальные выпавшие числа я занёс в таблицу таблТиражи2022, отделив дополнительно выпавшие числа друг от друга в отдельные столбцы для удобства последующих вычислений:
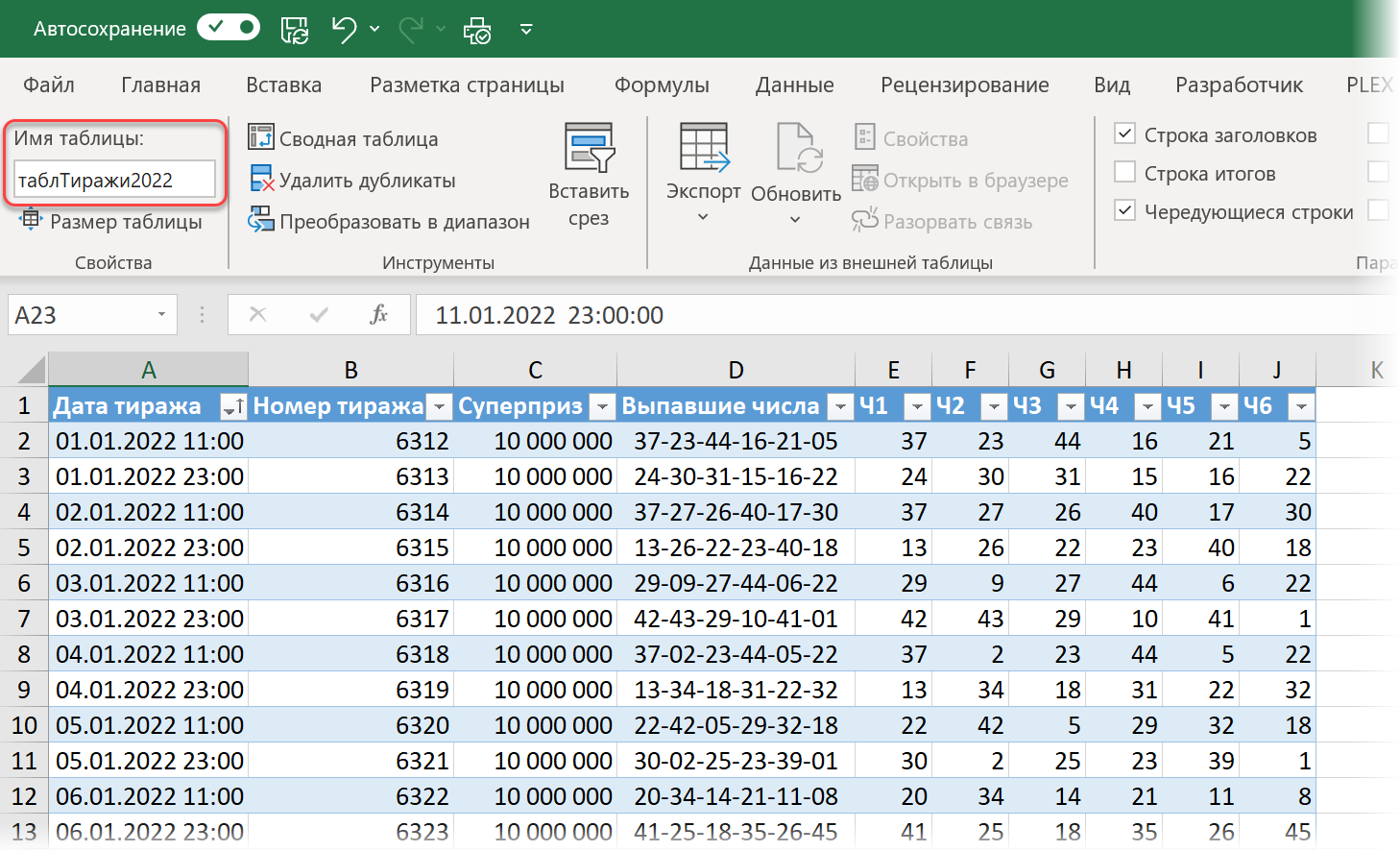
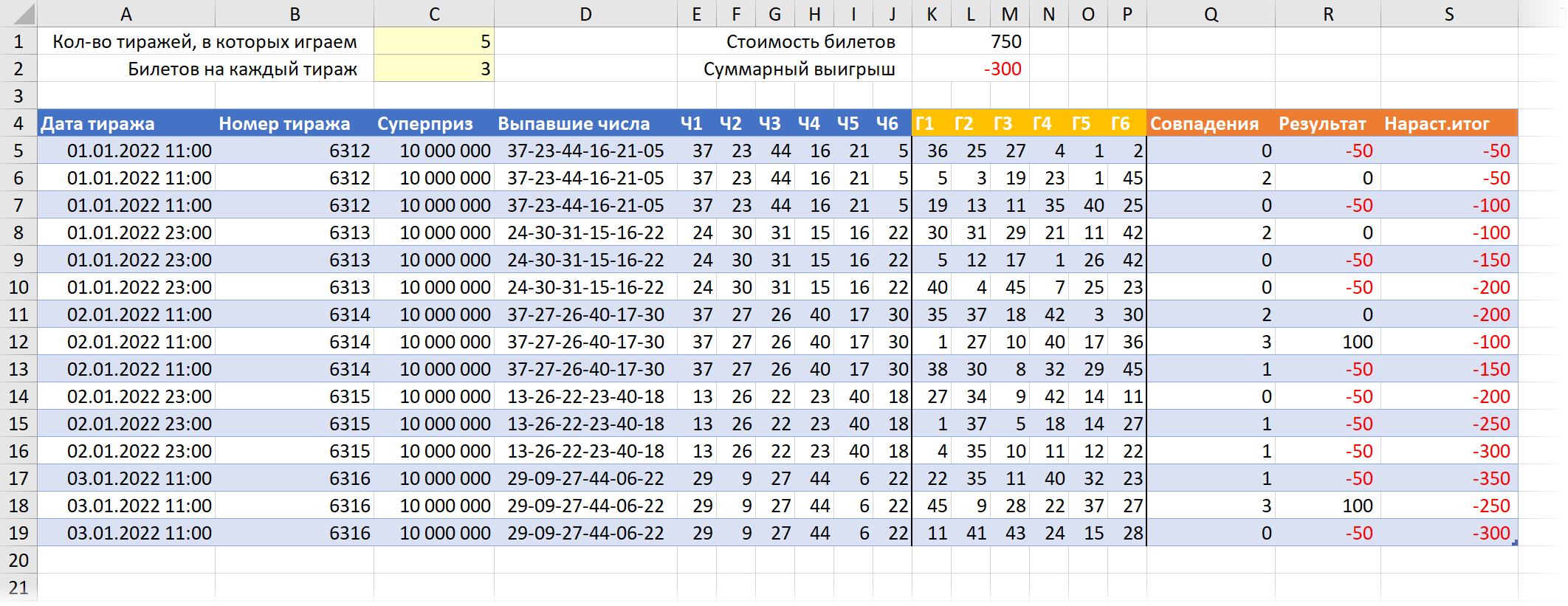
На отдельном листе Игра создадим заготовку для моделирования в виде «умной» таблицы с именем таблИгра следующего вида:
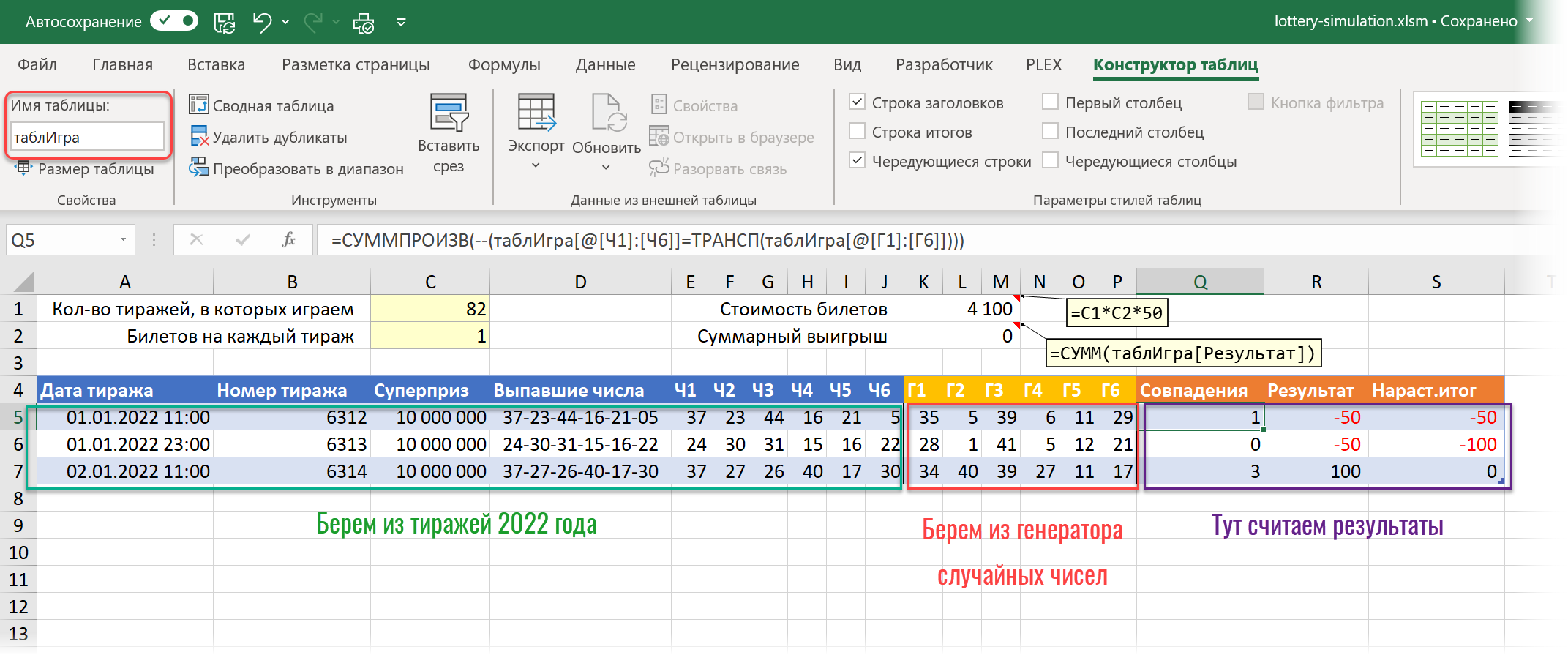
Здесь:
- В желтых ячейках сверху будем задавать для макроса количество тиражей 2022 года, в которых мы хотим участвовать (1-82) и количество билетов, которыми мы играем в каждом тираже.
- Данные для первых 11 столбцов (A-J) макрос будет копировать с листа тиражей 2022 года.
- Данные для следующих шести столбцов (K-P) макрос будет брать с листа Генератор, где мы реализовали генератор случайных чисел (см. задачу 4 выше).
- В столбце Q мы считаем количество совпадений выпавших чисел и сгенерированных с помощью функции СУММПРОИЗВ (SUMPRODUCT).
- В столбце R вычисляем финансовый результат (если не выиграли, то минус 50 рублей за билет, если выиграли, то приз — 50 р. за билет)
- В последнем столбце S считаем общий результат всей игры нарастающим итогом, чтобы видеть динамику в процессе.
И чтобы оживить всю эту конструкцию нам потребуется небольшой макрос. На вкладке Разработчик (Developer) выберем команду Visual Basic или воспользуемся сочетанием клавиш Alt+F11. Затем добавим новый пустой модуль через меню Insert — Module и введем туда следующий код:
Sub Lottery()
Dim iGames As Integer, iTickets As Integer, i As Long, t As Integer, b As Integer
'объявляем переменные для ссылки на листы
Set wsGame = Worksheets("Игра")
Set wsNumbers = Worksheets("Генератор")
Set wsArchive = Worksheets("Тиражи 2022")
iGames = wsGame.Range("C1") 'количество тиражей
iTickets = wsGame.Range("C2") 'количество билетов в каждом тираже
i = 5 'первая строка в таблице таблИгра
wsGame.Rows("6:1048576").Delete 'очищаем старые данные
For t = 1 To iGames
For b = 1 To iTickets
'копируем выигравшие номера с листа Тиражи 2022 и вставляем на лист Игра
wsArchive.Cells(t + 1, 1).Resize(1, 10).Copy Destination:=wsGame.Cells(i, 1)
'копируем и вставляем специальной вставкой значений сгенерированные номера с листа Генератор
wsNumbers.Range("G4:L4").Copy
wsGame.Cells(i, 11).PasteSpecial Paste:=xlPasteValues
i = i + 1
Next b
Next t
End Sub
Останется ввести желаемые исходные параметры в жёлтые ячейки и запустить макрос через Разработчик — Макросы (Developer — Macros) или сочетанием клавиш Alt+F8.
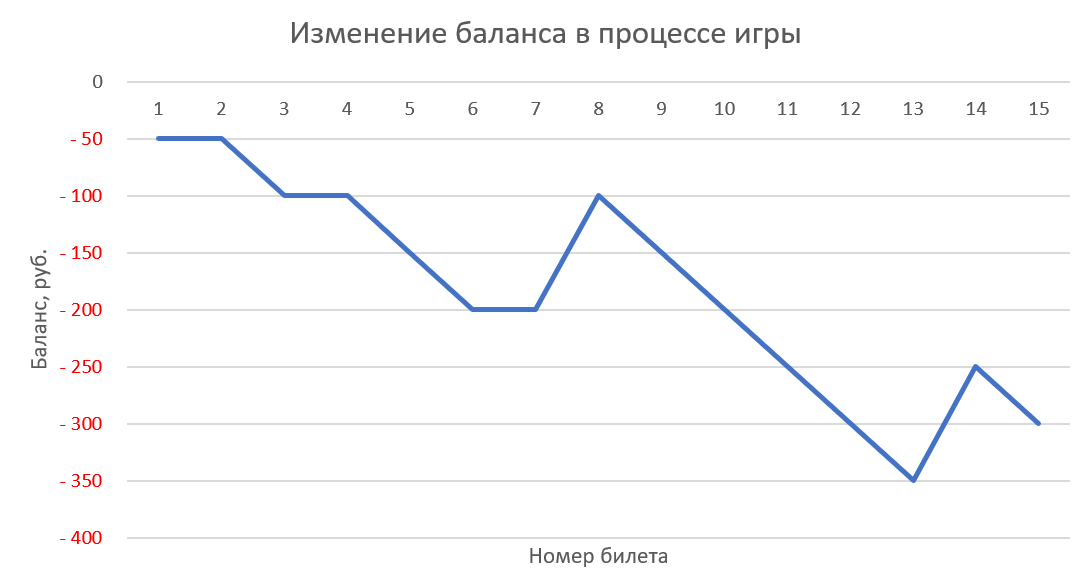
Для наглядности можно ещё построить диаграмму по последнему столбцу с нарастающим итогом, отражающую изменение денежного баланса в процессе игры:
Сравнение разных стратегий
Теперь, используя созданный симулятор, можно протестировать на реальных тиражах 2022 года любую стратегию игры и посмотреть на результаты, которые бы она принесла. Если играть 1 билетом в каждом тираже, то общая картина «слива» выглядит примерно так:
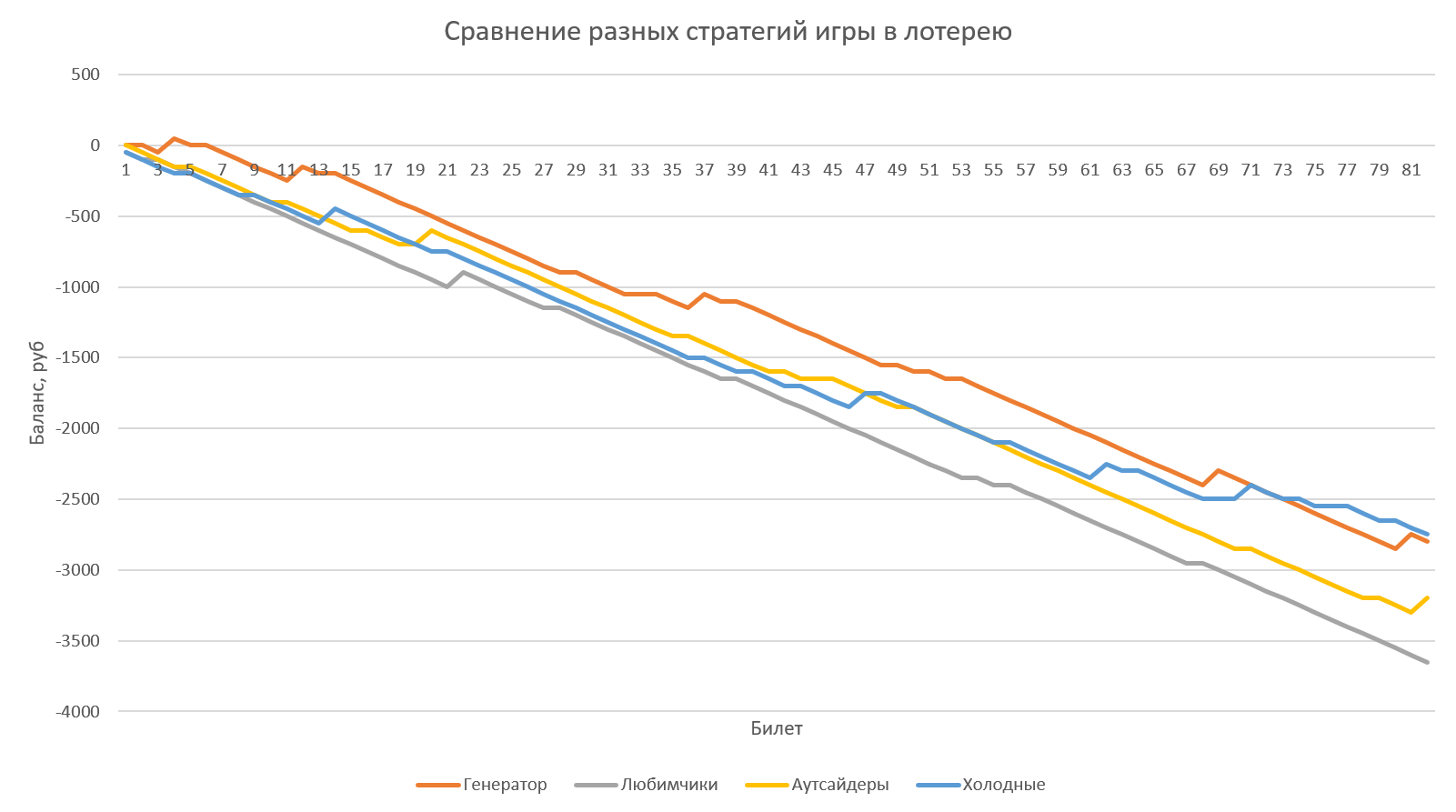
Здесь:
- Генератор — игра, где в каждом тираже мы выбираем случайные числа, созданные нашим генератором (с одинаковым весом).
- Любимчики — игра, где в каждом тираже мы используем одни и те же числа — те, что чаще всего выпадали в тиражах за последние два года (27, 32, 11, 14, 34, 40).
- Аутсайдеры — то же самое, но используем самые редко выпадающие числа (12, 18, 26, 10, 21, 6).
- Холодные — в всех тиражах используем числа, которые давно не выпадали (35, 5, 39, 11, 6, 29).
Как видите, разницы большой нет, но генератор случайных чисел ведёт себя чуть лучше остальных «стратегий».
Можно также попробовать играть большим количеством билетов в каждом тираже, чтобы перекрыть большее количество вариантов (иногда для этого несколько игроков объединяются в группу).
Игра в каждом тираже одним билетом со случайно сгенерированными числами (с одинаковым весом):
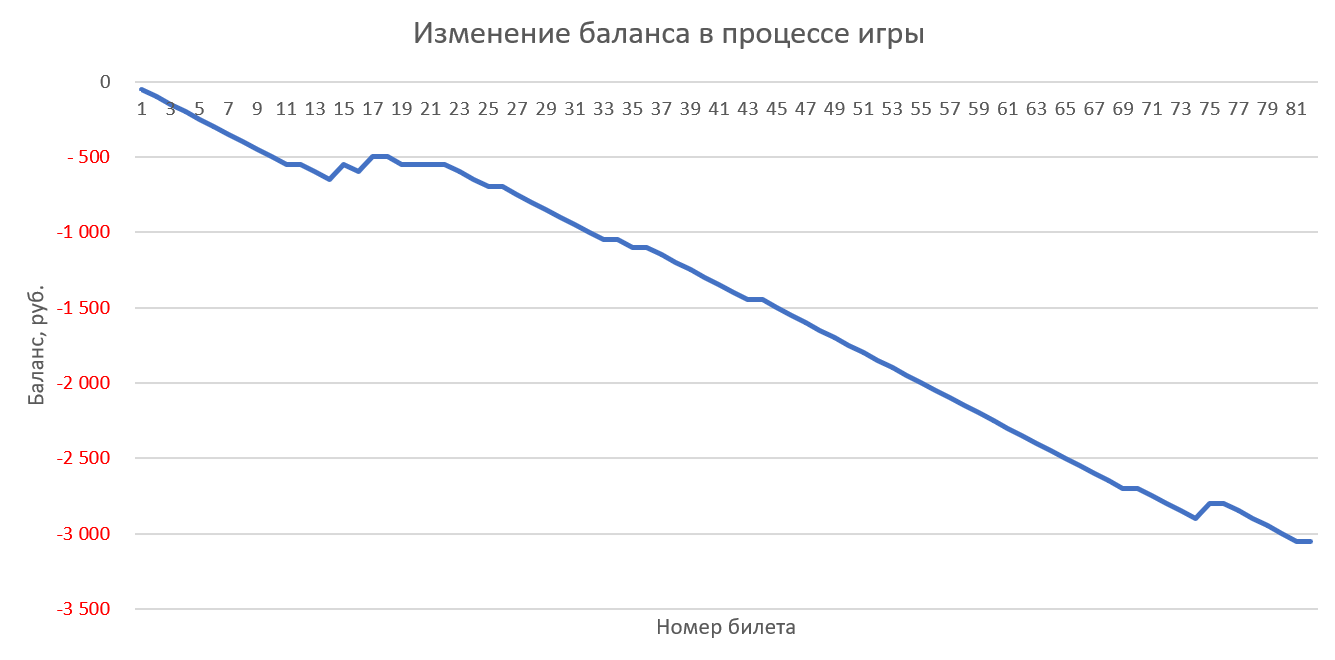
Игра 10 билетами в каждом тираже со случайно сгенерированными числами (с одинаковым весом):
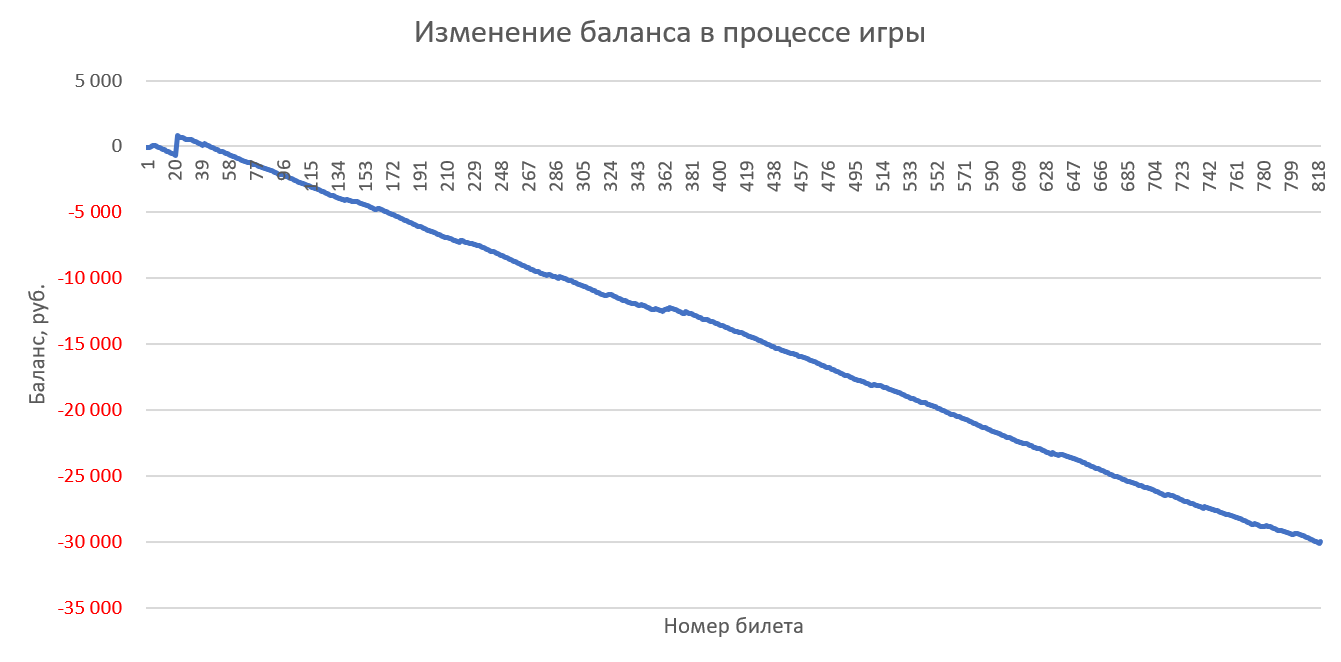
Игра 100 билетами в каждом тираже со случайными числами (с одинаковым весом):
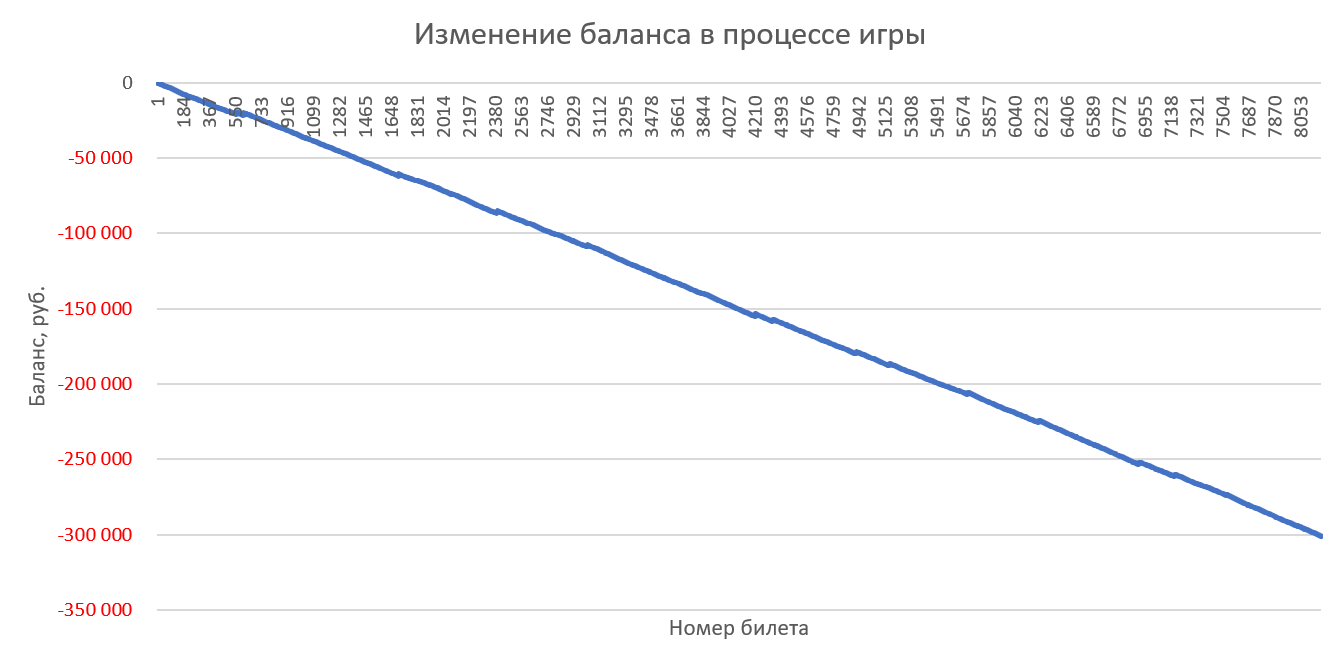
Комментарии, как говорится, излишни — слив депозита неизбежен во всех случаях