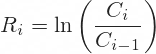12:57, 13.10.2018
Для новичков
Я получил вопрос от читателя, который спросил: «Можно ли рассчитать волатильность в Excel?» Ответ: Да, можно. Однако, есть несколько вещей, о которых вы должны знать. Не особо углубляясь в детали, скажу лишь, что есть много способов рассчитать волатильность. Два из наиболее распространенных способа касаются подразумеваемой и исторической (или статистической) волатильности. Историческая довольно-таки проста для расчета в Excel, и я покажу вам, как это делается в этом посте. Расчет подразумеваемой на порядок сложнее, и хотя вы можете посчитать её в Excel, но эту тему оставим на следующий раз, потому как она касается опционов, а это не простая тема.
Сегодня же давайте просто посмотрим, как рассчитать простую историческую волатильность в Excel.
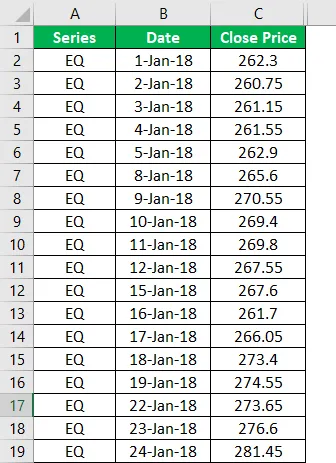
1. Соберите свои исходные данные в виде цены закрытия для каждого периода времени. Хотелось бы взять данные с сайта Московской биржи, но им похоже жалко, поэтому данная информация доступна только платным подписчикам. Что ж, на других рынках немного иначе, поэтому там получить данные проще. Возьмём к примеру информацию по Лукойлу с сайта Yahoo Finance за январь: https://finance.yahoo.com/quote/LKOD.IL/history?period1=1514754000&period2=1518469200&interval=1d&filter=history&frequency=1d (справа ссылка Download Data, ниже синей кнопки Apply). Открыв скачанный файл, мы увидем примерно следующее:

Данные в столбцах open, high, low, adj close, volume нам не нужны. Можете или скрыть столбцы или удалить их вовсе. Т.е. нас интересуют только колонки Date и Close. Немного навёл красоты:
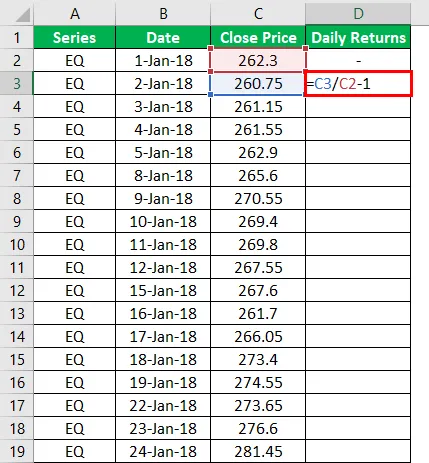
2. Данные собраны, теперь можно посчитать изменчивость каждого дня, т.е. насколько изменилась цена сегодня по отношению ко вчерашней. Делается это просто: данные дня делим на данные предыдущего, вычитаем единицу и преобразовываем формат ячейки в процентный. Аналогичную процедуру проделываем для всех строк. Т.е. вначале вот так:
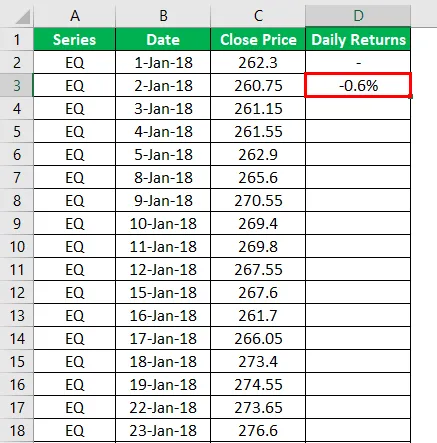
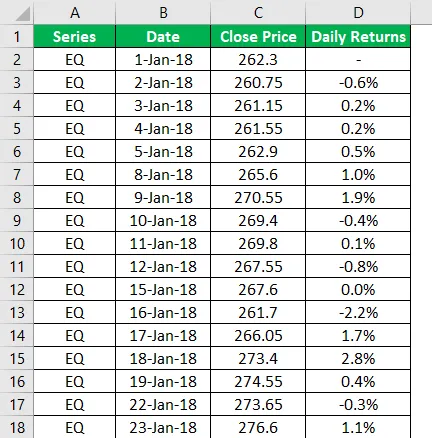
А затем это проделываем для каждой строки и получается вот так:
И преобразуем в процентный вид:
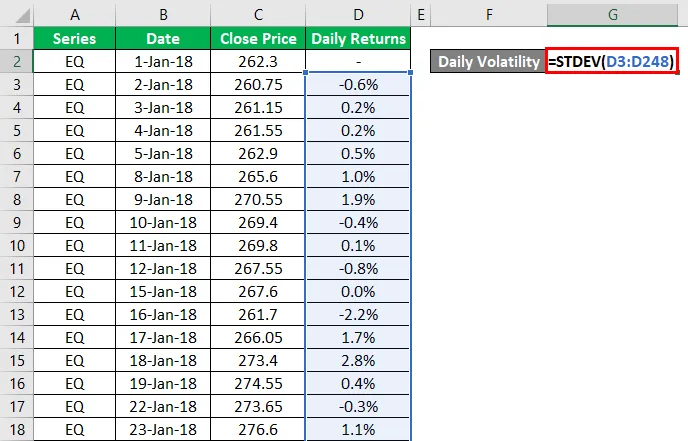
3. Теперь нам нужно посчитать стандартное отклонение. Если коротко, то это то, насколько что-то отклоняется от нормы. Ну примерно, если говорить простыми словами. Т.е. насколько сегодняшняя цена отличается от цен за какой-то период. Чтобы это посчитать, нужно воспользоваться соответсвующей формулой в Excel, называющейся STDEV или СТАНДОТКЛОН.В.
Как мы видим, здесь расчёт выбран за 10 дней, но это сделано только для иллюстрации. Вы можете выбрать любой период.
4. В заключении, нам нужно сделать одно — узнать, какова же историческая волатильность, а она — это по сути ежегодное стандартное отклонение. Для этого, мы возьмём волатильность за неделю, т.е. 5 дней, когда открыты рынки. Затем, умножим на корень из 52. Почему 52? Потому что в году 52 торговые недели. Таким образом получается:
Вот и всё. Получилось?
- Что такое формула волатильности?
Формула волатильности (Содержание)
- формула
- Примеры
- Калькулятор
Что такое формула волатильности?
Волатильность — это степень изменения доходности для данной ценной бумаги или рыночного индекса за определенный период времени. Это мера риска, а стандартное отклонение является типичной мерой, используемой для измерения волатильности любой данной акции, тогда как другим методом может быть просто отклонение между доходностью от той же ценной бумаги или рыночного индекса. Одной из общих мер волатильности данной ценной бумаги по отношению к рыночному индексу или эталону является его бета-версия.
В зависимости от использования может быть два типа волатильности — подразумеваемая волатильность, которая является прогнозной оценкой и используется в стратегии определения цены опциона. Другой является Регулярная Волатильность, которая более распространена и использует реальную фигуру, обращенную назад.
Степень волатильности
Высокая волатильность ценной бумаги будет означать, что при незначительном изменении факторов, влияющих на цену акций, цена ценной бумаги может резко измениться в любом направлении в течение короткого периода времени.
Более низкая волатильность означает, что ценность ценной бумаги не реагирует резко и имеет тенденцию быть более устойчивой.
Расчет волатильности ценной бумаги
Формула для годовой волатильности приведена ниже,
Annualized Volatility = Standard Deviation * √252
при условии, что в году 252 торговых дня. Стандартное отклонение — это степень, в которой цены отличаются от среднего за данный период времени.
Например: если ежедневное стандартное отклонение эталонного показателя S & P 500 в августе 2015 года составляет 1, 73%, его годовая волатильность будет:
1, 73 * √252 = 27, 4
Таким образом, годовая волатильность индекса S & P 500 в 2015 году составляет 27, 4% на основе дневной волатильности или дневных колебаний цен в августе 2015 года.
Как рассчитать стандартное отклонение
- Когда у вас есть ряд точек данных
- Рассчитать среднее значение набора данных.
- Вычтите среднее значение из фактического наблюдения, чтобы получить отклонение.
- Выровняйте все отклонения и сложите их, чтобы получить дисперсию.
- Рассчитайте квадратный корень из дисперсии, чтобы получить стандартное отклонение.
- Использование MS-Excel
- Скачать исторические цены данной ценной бумаги — до требуемого периода времени.
- Рассчитайте ежедневную прибыль, которая представляет собой процентное изменение каждый день по сравнению с предыдущим днем.
- Используйте функцию Excel STDEV ().
Пример формулы волатильности (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет волатильности.
Вы можете скачать этот шаблон формулы волатильности Excel здесь — Шаблон формулы волатильности Excel
Пример формулы волатильности
Рассмотрим расчет годовой волатильности данной акции, в этом случае ITC.
Ниже приведены данные ITC за период с января 2018 года по декабрь 2018 года. Рассчитайте дневную доходность, волатильность и годовую волатильность ITC.
Решение:
Мы рассчитываем дневную доходность (это столбец D здесь), используя цену закрытия, как указано в столбце C.
Таким образом, результат будет таким, как указано ниже.
Аналогичным образом рассчитайте ежедневную прибыль для всех оставшихся ячеек.
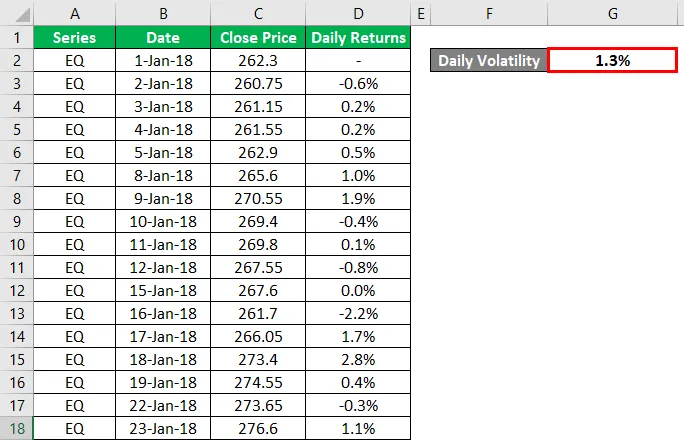
Дневная волатильность может быть рассчитана с использованием стандартного отклонения или формулы STDEV () в MS-Excel.
Выход будет таким, как указано ниже.
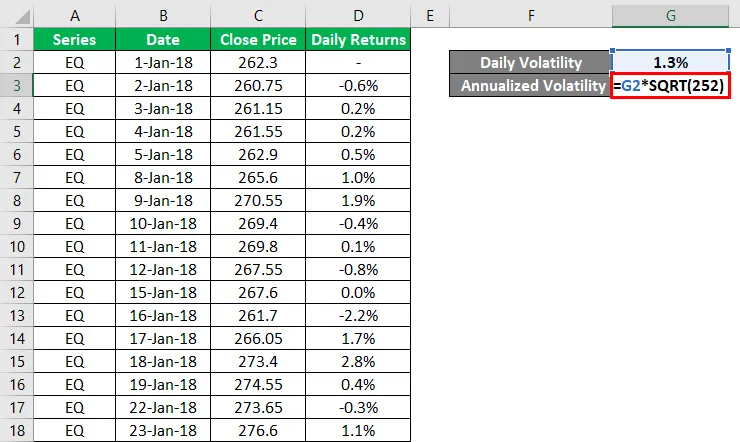
Годовая волатильность рассчитывается по формуле, приведенной ниже
Годовая волатильность = стандартное отклонение * √252
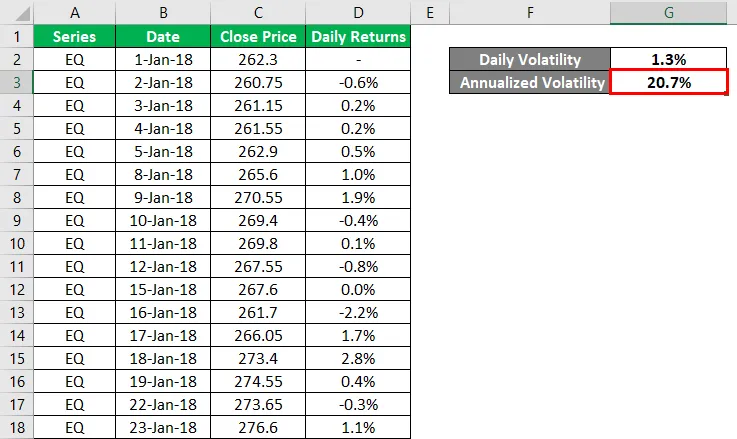
Вывод Годовой Волатильности будет таким, как показано ниже.
Актуальность и использование волатильности
Традиционно, это предположение или общее явление, что структуры риска, которые используют стандартное отклонение в качестве ключевого метода, предполагают, что доходность соответствует нормальному распределению в форме колокола. Это дает нам фиксированную структуру риска и доходности, и если доходности на кривой не показывают симметричное поведение, инвесторы склонны к панике.
Еще одно использование чисел волатильности — торговля на рынке и определение точки стоп-лосс. Знание запаса относительно того, сколько он будет перемещать в течение установленного времени, может помочь инвестору принять решение о стоп-лосс, а не столкнуться с убытками из-за случайных колебаний цены акций.
Понимание волатильности и знание ее применений могут действовать как обоюдоострый меч. Когда акции с высокой волатильностью могут привести к огромным убыткам, иногда, когда вы попадаете в правильные рыночные сроки, вы можете даже получить большую прибыль. Это, несомненно, снижает ожидаемый долгосрочный доход, но, безусловно, дает вам равные шансы получить несколько больших выгод.
Калькулятор формулы волатильности
Вы можете использовать следующий калькулятор волатильности
| Среднеквадратичное отклонение | |
| Годовая волатильность | |
| Годовая волатильность = | Стандартное отклонение х √252 |
| знак равно | 0 х √252 = 0 |
Рекомендуемые статьи
Это руководство по формуле волатильности. Здесь мы обсудим, как рассчитать волатильность вместе с практическими примерами. Мы также предоставляем Калькулятор волатильности с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —
- Калькулятор формулы возврата портфеля
- Примеры формулы процентного снижения
- Капитал Формула Модель ценообразования активов | Определение
- Коэффициент вариационной формулы (шаблон Excel)
The value of financial assets varies on a daily basis. Investors need an indicator to quantify these changes that are often difficult to predict. Supply and demand are the two principal factors that affect changes in asset prices. In return, price moves reflect an amplitude of fluctuations, which are the causes of proportional profits and losses. From an investor’s perspective, the uncertainty surrounding such influences and fluctuations is called risk.
The price of an option depends on its underlying ability to move, or in other words its ability to be volatile. The more likely it is to move, the more expensive its premium will be closer to expiration. Thus, computing the volatility of an underlying asset helps investors to price derivatives based on that asset.
Key Takeaways
- Pricing options contracts and other derivatives directly involves being able to compute an asset’s volatility, or the speed of price fluctuations.
- Volatility is derived from the variance of price movements on an annualized basis.
- This calculation can be complex and time-consuming, but using Excel calculating an asset’s historical volatility can be done quickly and accurately.
Measuring the Asset’s Variation
One way to measure an asset’s variation is to quantify the daily returns (percent move on a daily basis) of the asset. This brings us to the definition and concept of historical volatility. Historical volatility is based on historical prices and represents the degree of variability in the returns of an asset. This number is without a unit and is expressed as a percentage.
Computing Historical Volatility
If we call P (t) the price of a financial asset (foreign exchange asset, stocks, forex pair, etc.) at time t and P (t-1) the price of the financial asset at t-1, we define the daily return r (t) of the asset at time t by:
r (t) = ln (P (t) / P (t-1))
where Ln (x) = natural logarithm function.
The total return R at time t is:
R = r1 + r2 + r3 + 2 + … +rt-1+ rt,
which is equivalent to:
R = Ln (P1 / P0) + … Ln (Pt-1 / Pt-2) + Ln (Pt / Pt-1)
We have the following equality:
Ln (a) + Ln (b) = Ln (a*b)
So, this gives:
R = Ln [(P1 / P0* (P2 / P1)* … (Pt / Pt-1]
R = Ln [(P1. P2 … Pt-1. Pt) / (P0. P1. P2 … Pt-2. Pt-1)]
And, after simplification, we have:
R = Ln (Pt / P0).
The yield is usually computed as the difference in relative price changes. This means that if an asset has a price of P (t) at time t and P (t + h) at time t + h> t, the return (r) is:
r = (P (t + t) -P (t)) / P (t) = [P (t + h) / P (t)] – 1
When the return is small, such as just a few percent, we have:
r ≈ Ln (1 + r)
We can substitute r with the logarithm of the current price since:
r ≈ Ln (1 + r)
r ≈ Ln (1 + ([P (t + h) / P (t)] — 1))
r ≈ Ln (P (t + h) / P (t))
From a series of closing prices for instance, it is enough to take the logarithm of the ratio of two consecutive prices to compute daily returns r (t).
Thus, one can also compute the total return R by using only the initial and final prices.
Annualized Volatility
To fully appreciate the different volatilities over a period of a year, we multiply this volatility by a factor that accounts for the variability of the assets for one year.
To do this we use the variance. The variance is the square of the deviation from the average daily returns for one day.
To compute the square number of the deviations from the average daily returns for 365 days, we multiply the variance by the number of days (365). The annualized standard deviation is found by taking the square root of the result:
Variance = σ²daily = [Σ (r (t)) ² / (n — 1)]
For the annualized variance, if we assume that the year is 365 days, and every day has the same daily variance, σ²daily, we obtain:
Annualized Variance = 365. σ²daily
Annualized Variance = 365. [Σ (r (t)) ² / (n — 1)]
Finally, as the volatility is defined as the square root of variance:
Volatility = √ (variance annualized)
Volatility = √ (365. Σ²daily)
Volatility = √ (365 [Σ (r (t)) ² / (n — 1)].)
Simulation
The Data
We simulate from the Excel function =RANDBETWEEN a stock price that varies daily between values of 94 and 104.
Computing the Daily Returns
- In column E, we enter «Ln (P (t) / P (t-1)).»
Computing the Square of Daily Returns
- In column G, we enter «(Ln (P (t) / P (t-1)) ^2.”
Computing the Daily Variance
To compute the variance, we take the sum of the squares obtained and divide by the (number of days -1). So:
- In cell F25, we have «= sum (F6: F19).»
- In cell F26, we compute «= F25 / 18» since we have 19 -1 data points for this calculation.
Computing the Daily Standard Deviation
To compute the standard deviation on a daily basis, we compute the square root of the daily variance. So:
- In cell F28, we compute «= Square.Root(F26).»
- In cell G29, cell F28 is shown as a percentage.
Computing the Annualized Variance
To compute the annualized variance from the daily variance, we assume that each day has the same variance, and we multiply the daily variance by 365 with weekends included. So:
- In cell F30, we have «= F26* 365.»
Computing the Annualized Standard Deviation
To compute the annualized standard deviation, we only need to compute the square root of the annualized variance. So:
- In cell F32, we have «= ROOT (F30).»
- In cell G33, cell F32 is shown as a percentage.
This square root of the annualized variance gives us the historical volatility.
Although there are several ways to measure the volatility of a given security, analysts typically look at historical volatility. Historical volatility is a measure of past performance; it is a statistical measure of the dispersion of returns for a given security over a given period of time.
Because it allows for a more long-term assessment of risk, historical volatility is widely used by analysts and traders in the creation of investing strategies. For a given security, in general, the higher the historical volatility value, the riskier the security is. However, some traders and investors actually seek out higher volatility investments in order to find profit opportunities. You can calculate the historical volatility of a given security using Microsoft Excel.
Key Takeaways
- Analysts and traders can calculate the historical volatility of a stock using the Microsoft Excel spreadsheet tool.
- Historical volatility is a measure of past performance.
- It is a statistical measure of the dispersion of returns for a given security over a given period of time.
- For a given security, in general, the higher the historical volatility value, the riskier the security is.
- However, some traders and investors actually seek out higher volatility investments.
A Simplified Approach To Calculating Volatility
Calculating Historical Volatility in Excel
To calculate the volatility of a given security in a Microsoft Excel spreadsheet, first determine the time frame for which the metric will be computed.
Step 1: Timeframe
Volatility is a time-bound measurement, meaning that it measures the price swings of an asset or security over a particular period. Depending on the type of trader you are, different time periods would be more appropriate. A day trader, for instance, may only care about weekly volatility while a swing trader monthly. For the purposes of this article, a 10-day time period will be used in the example.
Step 2: Enter Price Information
After determining your timeframe, the next step is to enter all the closing stock prices for that timeframe into cells B2 through B12 in sequential order, with the newest price at the bottom. (Keep in mind that if you are doing a 10-day timeframe, you will need the data for 11 days to compute the returns for a 10-day period.)
Step 3: Compute Returns
In column C, calculate the inter-day returns by dividing each price by the closing price of the day before and subtracting one. For example, if McDonald’s (MCD) closed at $147.82 on the first day and at $149.50 on the second day, the return of the second day would be (149.50/147.82) — 1, or .011, indicating that the price on day two was 1.1% higher than the price on day one.
Step 4: Calculate Standard Deviations
Volatility is inherently related to variance, and by extension, to standard deviation, or the degree to which prices differ from their mean. In cell C13, enter the formula «=STDEV.S(C3:C12)» to compute the standard deviation for the period.
The link between standard deviation and volatility is evident in the types of technical indicators that investors use to chart a stock’s volatility, such as Bollinger Bands, which are based on a stock’s standard deviation and the simple moving average (SMA).
Step 5: Annualize the Period Volatility
Historical volatility is usually converted into an annualized figure, so to convert the daily standard deviation calculated above into a usable metric, it must be multiplied by an annualization factor based on the period used. The annualization factor is the square root of however many periods exist in a year.
The table below shows the volatility for McDonald’s within a 10-day timeframe:
The example above used daily closing prices, and there are 252 trading days per year, on average. Therefore, in cell C14, enter the formula «=SQRT(252)*C13» to convert the standard deviation for this 10-day period to annualized historical volatility.
Why Volatility Is Important for Investors
While volatility in a stock can sometimes have a bad connotation, many traders and investors actually seek out higher volatility investments. They do this in the hopes of eventually making higher profits. If a stock or other security does not move, it has low volatility. However, it also has a low potential to make capital gains.
On the other hand, a stock or other security with a very high volatility level can have tremendous profit potential. But by the same token, the risk of loss is quite high.
In order to be a trader or investor that capitalizes on volatility, the timing of any trades must be perfect. Even a correct market call could end up losing money if the security’s wide price swings trigger either a stop-loss order or a margin call.
Why Is Historical Volatility Important?
The volatility of a particular asset or security is thought to exhibit mean reversion over time. This means that if a security is uncharacteristically volatile, it should return eventually to its long-run average. Likewise, if it is subdued, its volatility should increase. Calculating historical volatility is how to arrive at this average or mean level.
What Does the Volatility of a Stock Mean?
Volatility describes the speed and magnitude of price swings over a given period of time (often on an annualized basis). Highly volatile stocks experience large and swift price swings, and they are often considered to be riskier than less volatile stocks.
Is High or Low Historical Volatility Better?
For day traders and options traders, high volatility can provide more opportunities to move and out of positions or profit from volatility spikes. For most long-term buy-and-hold investors, however, lower volatility is often preferred.
Содержание
- Стратегии исторической волатильности
- Ключевые выводы
- Упрощенный подход к расчету волатильности
- Почему волатильность важна для инвесторов
Хотя есть несколько способов измерить волатильность той или иной ценной бумаги, аналитики обычно обращают внимание на историческую волатильность. Историческая волатильность — это мера прошлых результатов; это статистическая мера разброса доходности для данной ценной бумаги за определенный период времени.
Историческая волатильность, поскольку она позволяет проводить более долгосрочную оценку риска, широко используется аналитиками и трейдерами при создании инвестиционных стратегий. Для данной ценной бумаги, как правило, чем выше историческое значение волатильности, тем более рискованной является ценная бумага. Однако некоторые трейдеры и инвесторы на самом деле ищут вложения с более высокой волатильностью. Вы можете рассчитать историческую волатильность
Стратегии исторической волатильности
Чтобы рассчитать волатильность данной ценной бумаги в электронной таблице Microsoft Excel, сначала определите временные рамки, для которых будет вычисляться метрика. Для целей этой статьи в примере будет использоваться 10-дневный период времени. После определения вашего таймфрейма следующий шаг — ввести все цены акций на момент закрытия для этого таймфрейма в ячейки с B2 по B12 в последовательном порядке, с самой новой ценой внизу. (Имейте в виду, что если вы используете 10-дневный таймфрейм, вам понадобятся данные за 11 дней, чтобы вычислить доходность за 10-дневный период.)
Ключевые выводы
- Аналитики и трейдеры могут рассчитать историческую волатильность акции с помощью инструмента электронных таблиц Microsoft Excel.
- Историческая волатильность — это показатель прошлых результатов; это статистическая мера разброса доходности для данной ценной бумаги за определенный период времени.
- Для данной ценной бумаги, как правило, чем выше историческое значение волатильности, тем более рискованной является ценная бумага.
- Однако некоторые трейдеры и инвесторы на самом деле ищут вложения с более высокой волатильностью.
В столбце C рассчитайте доходность за день, разделив каждую цену на цену закрытия предыдущего дня и вычтя единицу. Например, если McDonald’s (MCD) закрылся на уровне 147,82 доллара США в первый день и 149,50 доллара США во второй день, доходность второго дня будет равна (149,50 доллара США)./147,82) — 1, или 0,011, что указывает на то, что цена во второй день была на 1,1% выше, чем цена в первый день.
Волатильность по своей сути связана со стандартным отклонением или степенью, в которой цены отличаются от своего среднего значения. В ячейке C13 введите формулу «= СТАНДОТКЛОН.S (C3: C12)», чтобы вычислить стандартное отклонение для периода.
Как упоминалось выше, волатильность и отклонение тесно связаны. Это очевидно в типах технических индикаторов, которые инвесторы используют для составления графика волатильности акций, таких как полосы Боллинджера, которые основаны на стандартном отклонении акции и простой скользящей средней (SMA). Однако историческая волатильность — это годовой показатель, поэтому, чтобы преобразовать дневное стандартное отклонение, рассчитанное выше, в пригодную для использования метрику, его необходимо умножить на коэффициент годового использования, основанный на используемом периоде. Годовой коэффициент — это квадратный корень из числа периодов в году.
В таблице ниже показана волатильность McDonald’s за 10-дневный период:
В приведенном выше примере использовались дневные цены закрытия, а в году в среднем 252 торговых дня. Поэтому в ячейке C14 введите формулу «= КОРЕНЬ (252) * C13», чтобы преобразовать стандартное отклонение для этого 10-дневного периода в годовую историческую волатильность.
Упрощенный подход к расчету волатильности
Почему волатильность важна для инвесторов
Хотя волатильность акций иногда может иметь плохую коннотацию, многие трейдеры и инвесторы на самом деле ищут вложения с более высокой волатильностью. Они делают это в надежде в конечном итоге получить более высокую прибыль. Если акция или другая ценная бумага не движется, она имеет низкую волатильность. Однако он также имеет низкий потенциал для получения дохода от прироста капитала.
С другой стороны, акция или другая ценная бумага с очень высоким уровнем волатильности может иметь огромный потенциал прибыли. Но при этом риск проигрыша довольно высок.
Чтобы быть трейдером или инвестором, который извлекает выгоду из волатильности, время для любых сделок должно быть идеальным. Даже правильный рыночный запрос может закончиться потерей денег, если широкие колебания цены ценной бумаги вызовут либо стоп-лосс, либо маржевое требование.
С точки зрения математики, волатильность — это стандартное (среднеквадратичное) отклонение, которое показывает разброс величин относительно среднего значения за определённое время. Волатильность измеряется в процентах.
Для примера рассчитаем волатильность акций компании «Магнит» в октябре 2021 года c помощью Google Sheets:
1) пределяем период для расчёта и частоту данных, допустим, цены закрытия каждого торгового дня за месяц;
2) данные о ценах можно взять с сайта МосБиржи. Вбиваем в поиск название эмитента → итоги торгов. Для «Магнита» они доступны здесь;
3) заносим цены и даты в столбцы (см. рис. ниже);
4) в третьем столбце рассчитываем доходность: разницу между двумя соседними значениями цен в процентах или с помощью логарифма (функция LN от частного двух цен);
5) в свободной ячейке рассчитываем дневную волатильность по доходности. Для этого нажимаем на иконку fx (функции) на панели инструментов;
6) в списке категорий функций нажимаем на «Статистические» и выбираем функцию СТАНДОТКЛОН.В (или СТАНДОТКЛОН в Google Sheets);
7) в аргументе функции указываем диапазон ячеек — столбец с рассчитанной доходностью;

Вы можете сделать копию таблицы с расчётами и использовать её для своих подсчётов
Дневная волатильность составила 1,79%, а месячная — 8,22%. Чем больше значение, тем больше разброс цен и тем больше рисков. Для сравнения: волатильность индекса МосБиржи в октябре 2021 года была равна 4,59%, акций компании Virgin Galactic в рублях — 18,72%. Получается, что риск при покупке акций «Магнита» ниже, чем акций Virgin Galactic, которые сильно зависят от новостей, но выше среднего по рынку.
Непредсказуемые разовые события, влияющие на стоимость акции в течение нескольких дней, могут сильно влиять на показатель волатильности за месяц. Поэтому лучше учитывать его за более долгий срок или считать волатильность для классов активов, чтобы сгладить случайные колебания.
a:
Хотя есть несколько способов измерения волатильности данной безопасности, аналитики обычно смотрят на историческую волатильность. Историческая волатильность — это показатель прошлой работы. Поскольку он позволяет проводить более долгосрочную оценку риска, историческая волатильность широко используется аналитиками и трейдерами в создании стратегий инвестирования. ( Хотите улучшить свои навыки превосходства? Примите участие в экзамене Академии Investopedia. )
Чтобы вычислить волатильность данной безопасности в Microsoft Excel, сначала определите временной интервал, для которого будет вычисляться метрика. Для этого примера используется 10-дневный период. Затем введите все цены закрытия акций за этот период в ячейки B2 до B12 в последовательном порядке, с последней ценой внизу. Обратите внимание, что вам понадобятся данные в течение 11 дней для расчета доходности за 10-дневный период.
В столбце C вычислите среднедневную доходность, разделив каждую цену на цену закрытия предыдущего дня и вычитая ее. Например, если McDonald’s (MCD) закрывается на уровне 147 долларов. 82 в первый день и 149 долларов США. 50 на второй день, возвращение второго дня будет (149. 50 / 147, 82) — 1 или. 011, что указывает на то, что цена на второй день была на 1. 1% выше цены в первый день.
Волатильность по своей сути связана со стандартным отклонением или степенью, в которой цены отличаются от их среднего значения. В ячейке C13 введите формулу «= STDV (C3: C12)», чтобы вычислить стандартное отклонение за период.
Как упоминалось выше, волатильность и отклонения тесно связаны. Это видно из тех технических показателей, которые инвесторы используют для определения волатильности акций, таких как полосы Боллинджера, которые основаны на стандартном отклонении запаса и простой скользящей средней (SMA). Тем не менее, историческая волатильность представляет собой годовую цифру, поэтому для пересчета среднеквадратичного отклонения, вычисленного выше, в полезную метрику, она должна быть умножена на коэффициент годовой оценки на основе используемого периода. Годовой коэффициент является квадратным корнем, однако сколько-нибудь периодов существует через год.
В приведенной ниже таблице показана волатильность для McDonald’s в течение 10-дневного периода:
В приведенном выше примере использовались ежедневные цены закрытия, а в среднем 252 торговых дня в год. Поэтому в ячейке C14 введите формулу «= SQRT (252) * C13», чтобы преобразовать стандартное отклонение за этот 10-дневный период в годовую историческую волатильность.
This page explains how to calculate historical (realized) volatility from daily closing prices in Excel.
Things Needed for Calculating HV in Excel
- Historical data (daily closing prices of your stock or index) – there are many places on the internet where you can get it for free, such as Yahoo Finance or Alpha Vantage.
- Excel – this guide works for all Excel versions. There is one little difference for versions 2007 and older, which I will point out.
Excel Functions Used
Historical volatility calculation is not that complicated. We will only use the following Excel functions:
- LN = natural logarithm – to calculate daily logarithmic returns
- STDEV.S = sample standard deviation – to calculate standard deviation of these returns
- SQRT = square root – to annualize volatility
Don’t worry if you are not familiar with some of them. That’s what this page is for. Besides these functions it is only the very basics – multiplication, division, copying formulas etc.
So let’s get started. We’ll start from scratch – just open a new blank Excel worksheet.
Step 1: Put Historical Data in Spreadsheet
Historical volatility is calculated from daily historical closing prices. Therefore the first step is to put historical prices in our spreadsheet.
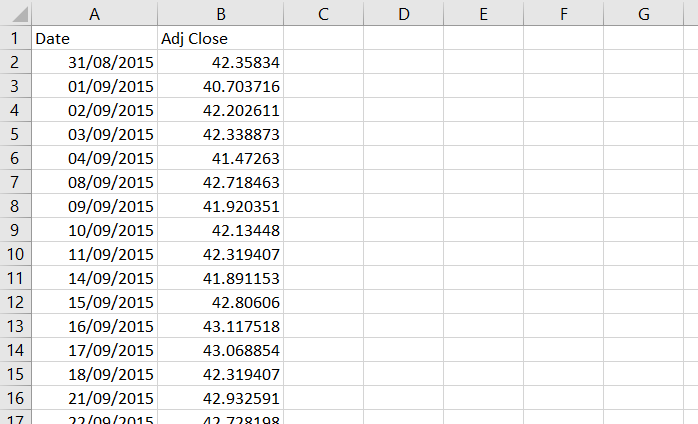
In this example I will be calculating historical volatility for Microsoft stock (symbol MSFT), using Yahoo Finance data from 31 August 2015 to 26 August 2016.
If you don’t have data, want to use Yahoo Finance and don’t know how to find and download data from there, I have created a detailed tutorial (using the same MSFT example).
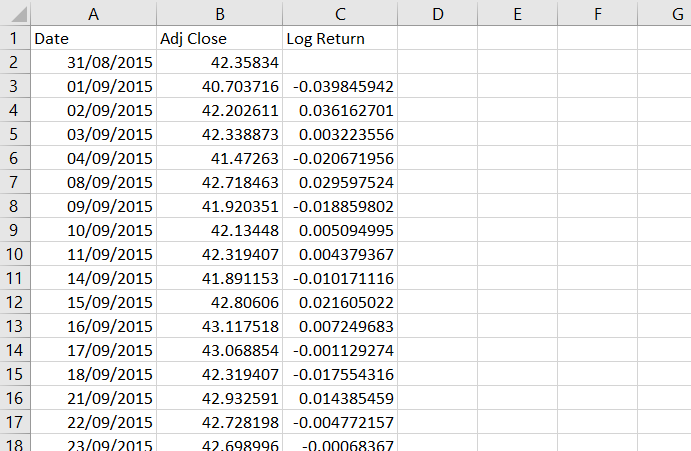
We will put the data in columns A (date) and B (closing price). Use row 1 for header, so we know which column does what later when we add more columns.
If your stock pays dividends or has history of splits or other actions affecting its price, it is better to use historical closing prices adjusted for these (usually called Adjusted Close), otherwise you will get misleading numbers. This is also what I will do with Microsoft stock.
Paste the data in rows 2 and below.
Now you should have historical data ready in columns A and B and you can start the actual historical volatility calculation.
Step 2: Calculate Logarithmic Returns
Historical volatility (at least the most common calculation method which we are using here) is calculated as standard deviation of logarithmic returns. Therefore we first need to calculate these logarithmic returns (also called continuously compounded returns) for every day (row) – we will do this in column C.
It is very simple: daily logarithmic return is the natural logarithm (ln) of the ratio of closing price and the closing price the day before. Mathematically:
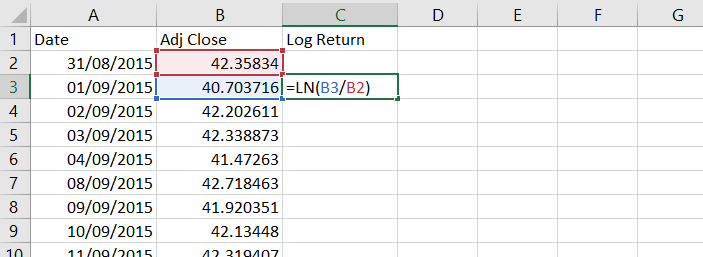
In Excel we will use the LN function, which has only one argument – the number x for which we want to find the natural logarithm ln(x). In our case the x is the ratio of closing prices. Therefore, the formula in cell C3 will be:
=LN(B3/B2)where cell B3 is the current day’s closing price and cell B2 the previous day’s closing price.
Copy the formula to the rest of column C. The return can’t be calculated for the first day, because we don’t know the previous day’s closing price, so we keep cell C2 empty.
We have now calculated daily logarithmic returns.
Step 3: Calculate Standard Deviation
The next step is to calculate standard deviation of these daily returns.
Standard deviation is the square root of variance, which is the average squared deviation from the mean. I have explained its calculation in detail on this page, but you don’t really need to worry about it, because Excel has a built-in function for standard deviation. Actually there are two functions, because there are two kinds of standard deviation: population standard deviation and sample standard deviation. The difference is explained here.
For historical volatility calculation we will use sample standard deviation and the Excel formula for that is STDEV.S (if you are using Excel 2007 or older, the formula is STDEV – without the «.S»; everything else is the same).
This formula takes only one argument and that is the reference to the cells for which we want to calculate standard deviation. It works with as little as two cells or with as much as your computer can handle. We will calculate standard deviation for each day, using a rolling window – a period of n consecutive days ending on the day for which we are calculating the standard deviation.
Which Period Length to Use?
What is n – how many days to include in our rolling window? That is the big decision that you must make when calculating historical volatility. It is often called historical volatility period and it is similarly used with moving averages and other technical analysis indicators.
If you choose a shorter period (small number of days), the resulting historical volatility will more closely reflect the most recent market action, but over time it will fluctuate more (will be more «volatile»). Conversely, if you choose a long period, it will be more stable, but perhaps it might not sufficiently reflect the most recent developments. There is a tradeoff.
If you have no idea, I recommend those I often use myself:
- 21 trading days = 1 calendar month
- 63 days = 3 months
- 252 days = 1 year
Occasionally I might also look at 10-day historical volatility if something interesting is happening in the market, but I wouldn’t go lower than that.
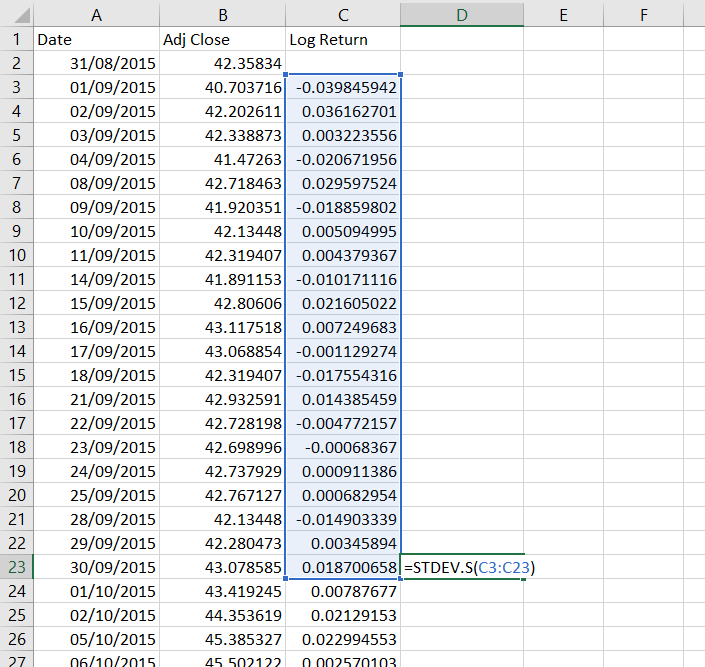
So let’s use 21 days for our example. We will calculate each standard deviation using the last 21 returns in column C. The first row where we can do this is row 23, where we will use the 21 returns in cells C3 to C23. The standard deviation formula in cell D23 will be:
=STDEV.S(C3:C23)If you are using Excel 2007 or older, the formula will be:
=STDEV(C3:C23)Copy the formula to all other cells below. Cells D2 to D22 remain empty, because we don’t have sufficient data to calculate them.
Step 4: Annualize Historical Volatility
Actually, we have already calculated a series of historical volatility values, because that’s what the standard deviations are. The only problem is that they represent 1-day historical volatility (because they have been calculated from daily returns). Therefore the final step in our calculation is to convert 1-day volatility to annualized volatility, which is much more common and much more useful.
To convert volatility from daily to annual you need to multiply it by the square root of the number of trading days per year.
Why trading days? Because we have been using a series of trading days (weekends and holidays not included).
Why square root? Because volatility (as we are using it now) is standard deviation and standard deviation is the square root of variance, where the number of days (items) actually enters the calculation. For more detailed explanation see why is volatility proportional to the square root of time.
How many trading days are there in a year? This depends on the market you are working with, as different countries and different exchanges observe different holidays. Furthermore, even for the same country and the same exchange the number of trading days varies from year to year. A good long-term average for US markets is 252 trading days per year, which I will use. If you have longer data history and want to be very precise, you can count the average number of trading days per year directly from your data. But for now let’s stick with 252.
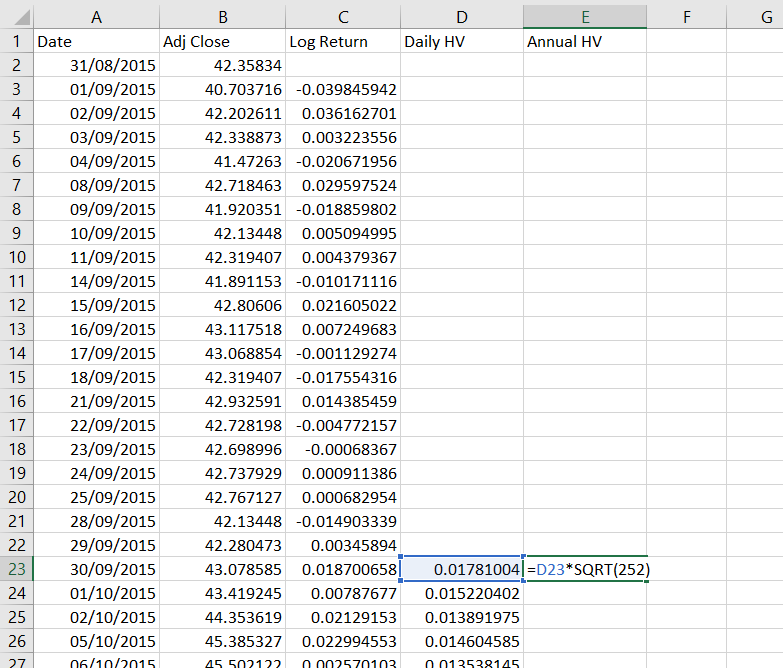
We will calculate the annualized historical volatility in column E, which will be equal to column D multiplied by the square root of 252. In Excel, the formula for square root is SQRT and our formula in cell E23 will be:
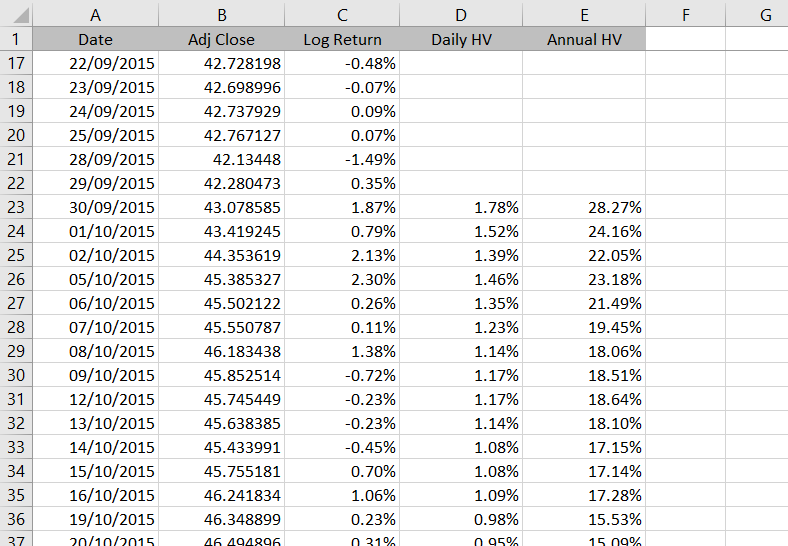
=D23*SQRT(252)We will again copy this formula to all the other cells below. We can also format columns C, D, E as percentages.
The series we have calculated in column E is historical volatility.
Possible Improvements
There are several ways how we can improve our spreadsheet to make it more useful. In particular:
We can make it support variable historical volatility period length, which the user would enter in some designated cell instead of changing all the standard deviation formulas. Hint: Use the OFFSET Excel function.
We can add a chart. This should be very easy.
You can find these and some more advanced features in the Historical Volatility Calculator.