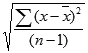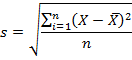Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции Функция СТАНДОТКЛОН.В.
Синтаксис
СТАНДОТКЛОН(число1;[число2];…)
Аргументы функции СТАНДОТКЛОН описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
-
Число2… Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
-
Функция СТАНДОТКЛОН предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП.
-
Стандартное отклонение вычисляется с использованием «n-1» метода.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОНА.
-
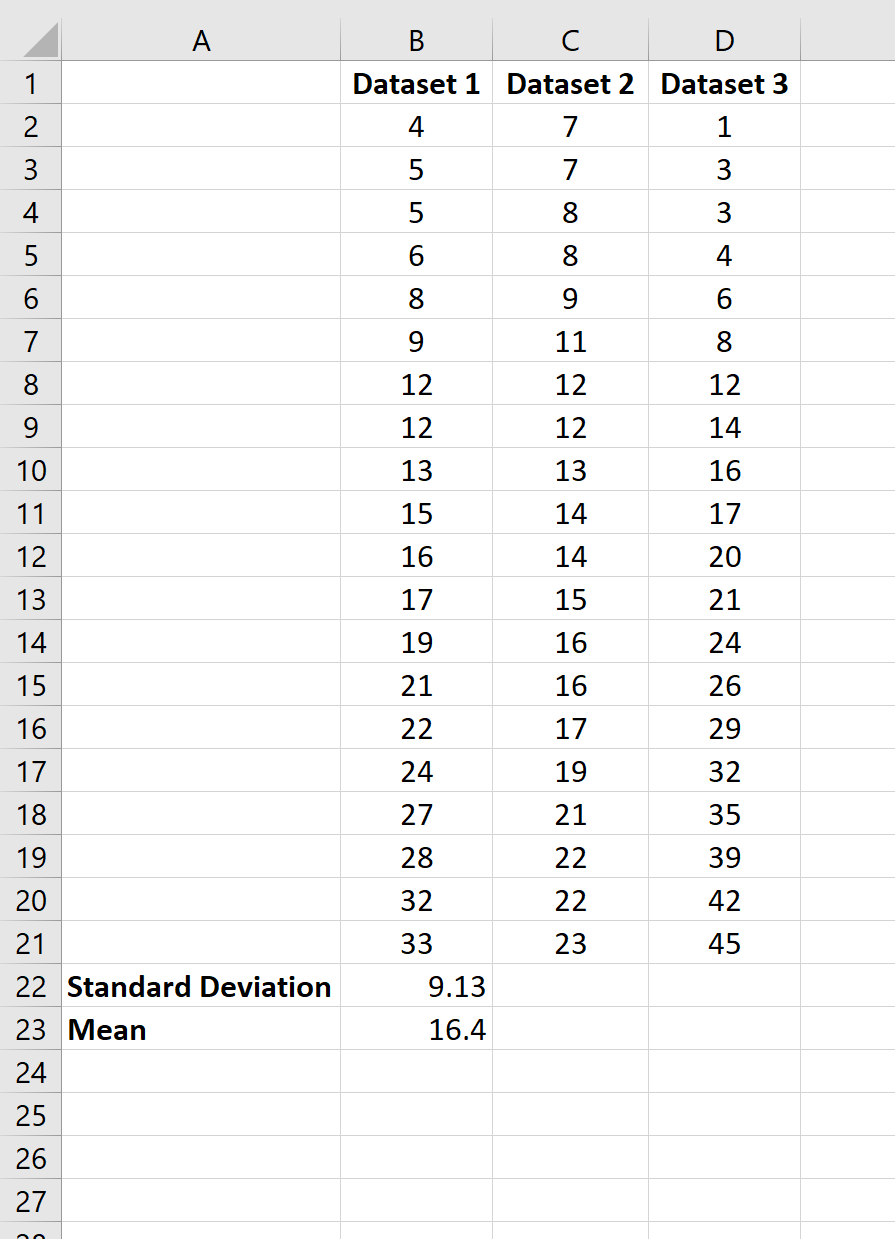
Функция СТАНДОТКЛОН вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание (результат) |
Результат |
|
=СТАНДОТКЛОН(A3:A12) |
Стандартное отклонение предела прочности (27,46392) |
27,46392 |
Нужна дополнительная помощь?
Шаги
-
1
Запустите Microsoft Excel. Дважды щелкните по значку в виде белой буквы «X» на зеленом фоне. Как правило, он находится на рабочем столе или на панели задач. Откроется начальная страница Excel.
- Если у вас есть готовая таблица Excel с нужными данными, дважды щелкните по файлу, чтобы открыть его в Excel, а затем перейдите к шагу «Щелкните по пустой ячейке».
-
2
Нажмите Новая книга. Эта опция находится в верхней левой части начальной страницы Excel.
-
3
Введите данные. Выберите столбец, а затем введите нужные данные в ячейки этого столбца.
- Например, если вы выбрали столбец «A», введите числа в ячейки «A1», «A2», «A3» и так далее.
-
4
Щелкните по пустой ячейке. Это ячейка, в которой отобразится значение стандартного отклонения. Так вы выберете ячейку.
-
5
Введите формулу для вычисления стандартного отклонения. В пустой ячейке введите =СТАНДОТКЛОН.Г(), где «Г» — генеральная совокупность. Стандартное отклонение по генеральной совокупности учитывает все данные (N).[1]
- Чтобы найти стандартное отклонение по выборке, введите =СТАНДОТКЛОН.В(). В этом случае учитывается (N-1) данных.
-
6
Введите диапазон значений. Внутри круглых скобок введите букву и номер ячейки с первым числом, потом введите двоеточие (:), а затем введите букву и номер ячейки с посленим числом.
- Например, если вы ввели числа в столбце «A» в строках с 1 по 10, формула должна выглядеть так: =СТАНДОТКЛОН.Г(A1:A10).
- Чтобы посчитать стандартное отклонение нескольких чисел, которые, например, находятся в ячейках A1, B3 и C5, введите адреса ячеек через запятые (например, =СТАНДОТКЛОН.В(A1,B3,C5)).
-
7
Нажмите ↵ Enter. Формула будет выполнена, а в ячейке с формулой отобразится стандартное отклонение выбранных данных.
Реклама
Советы
- В большинстве случаев вычисляется стандартное отклонение по генеральной совокупности, чтобы учесть все данные.
Реклама
Предупреждения
- Старая формула =СТАНДОТКЛОН() не работает в версиях Excel старше 2007 года.
Реклама
Об этой статье
Эту страницу просматривали 115 468 раз.
Была ли эта статья полезной?
17 авг. 2022 г.
читать 2 мин
Среднее значение представляет собой среднее значение в наборе данных. Это дает нам хорошее представление о том, где находится центр набора данных.
Стандартное отклонение показывает, насколько разбросаны значения в наборе данных. Это дает нам представление о том, насколько близко наблюдения сгруппированы вокруг среднего значения.
Используя только эти два значения, мы можем многое понять о распределении значений в наборе данных.
Чтобы вычислить среднее значение набора данных в Excel, мы можем использовать функцию = СРЗНАЧ (диапазон) , где диапазон — это диапазон значений.
Чтобы вычислить стандартное отклонение набора данных, мы можем использовать функцию =STDEV.S(Range) , где Range — это диапазон значений.
В этом руководстве объясняется, как использовать эти функции на практике.
Техническое примечание
Обе функции СТАНДОТКЛОН() и СТАНДОТКЛОН.С() вычисляют стандартное отклонение выборки .
Вы можете использовать функцию STDEV.P() для вычисления стандартного отклонения совокупности , если ваш набор данных представляет всю совокупность значений.
Однако в большинстве случаев мы работаем с выборочными данными, а не со всей совокупностью, поэтому мы используем функцию СТАНДОТКЛОН.С().
Пример 1: Среднее и стандартное отклонение одного набора данных
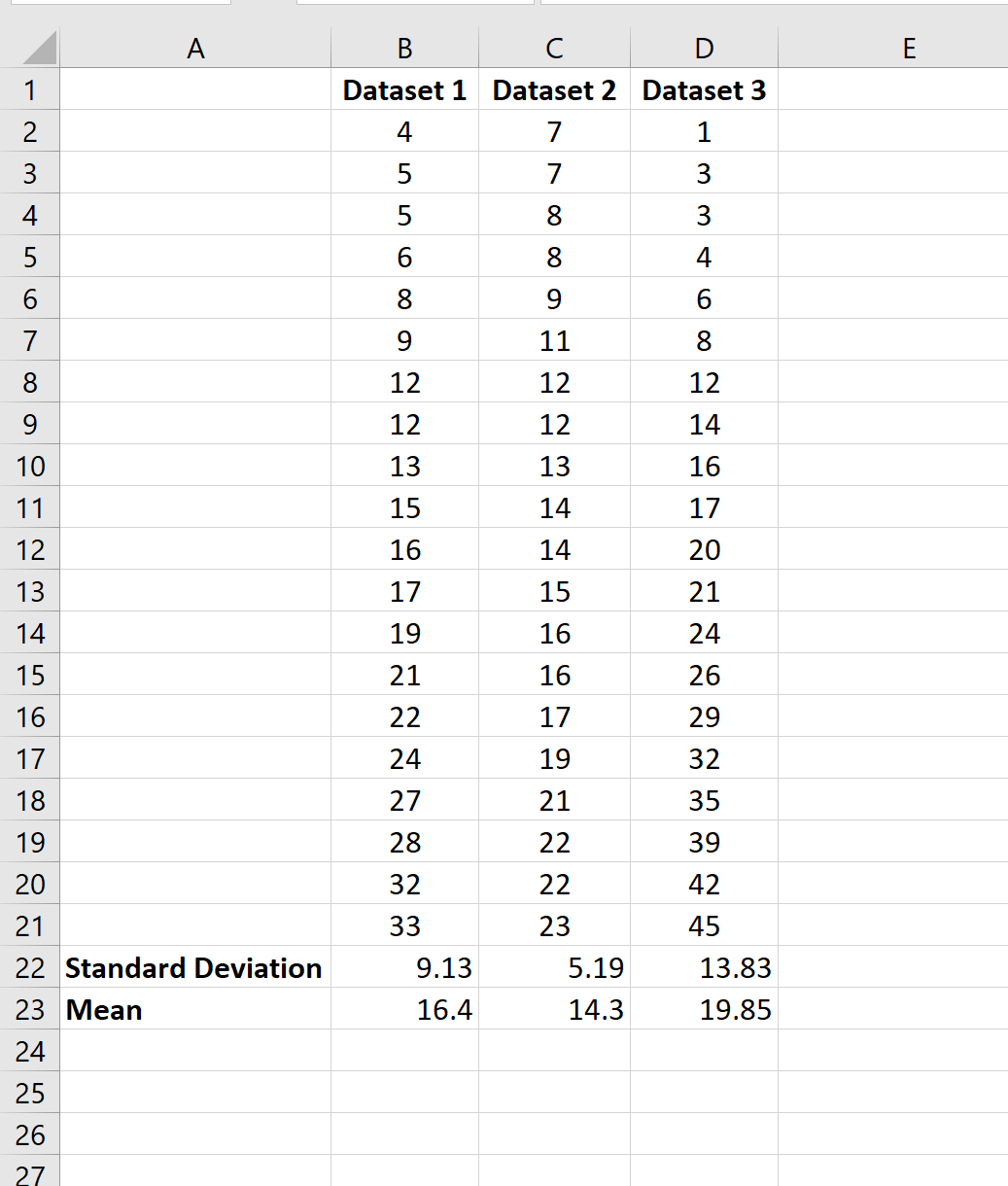
На следующем снимке экрана показано, как рассчитать среднее значение и стандартное отклонение одного набора данных в Excel:
Среднее значение набора данных составляет 16,4 , а стандартное отклонение — 9,13 .
Пример 2: Среднее и стандартное отклонение нескольких наборов данных
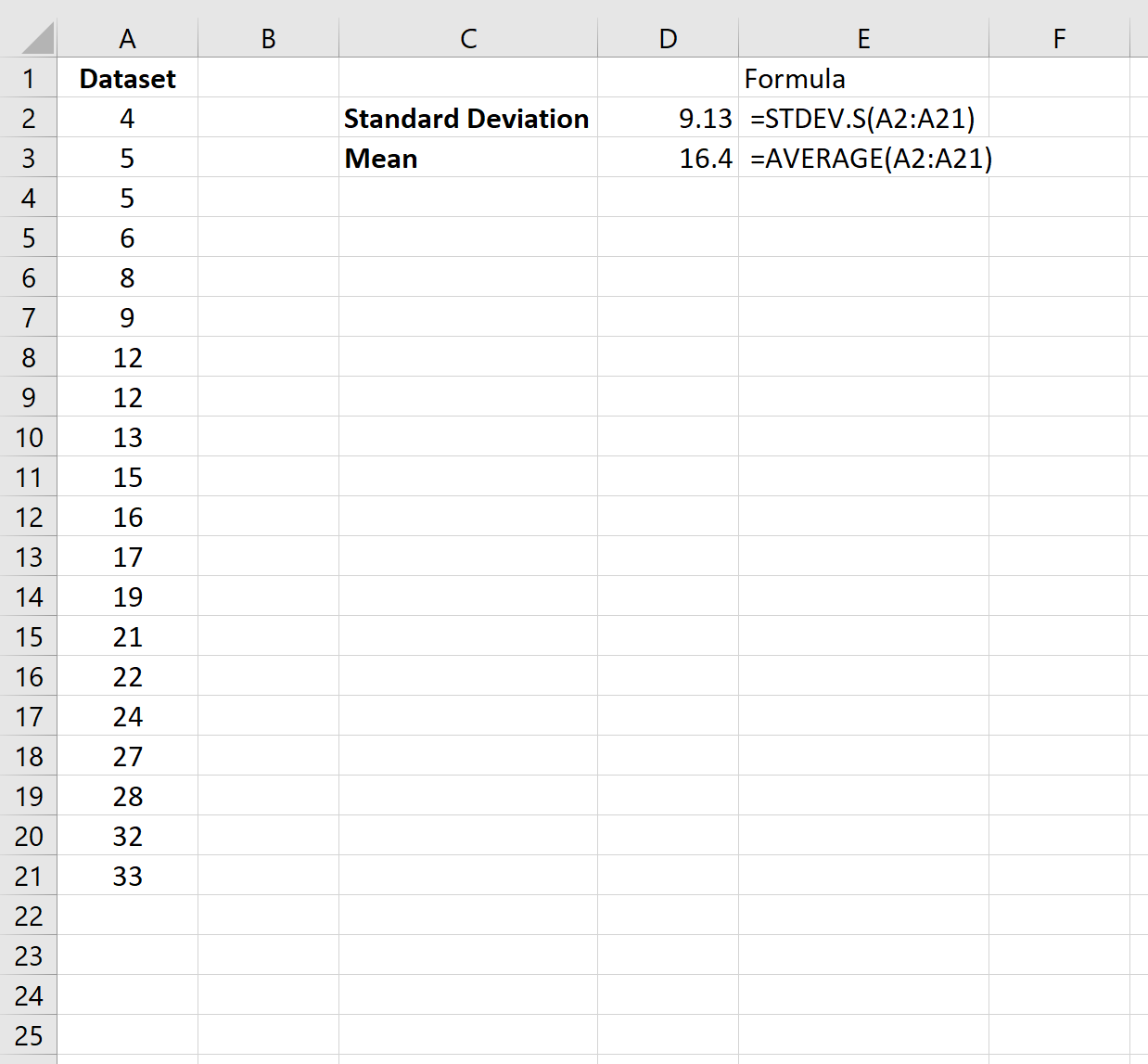
Предположим, у нас есть несколько наборов данных в Excel:
Чтобы вычислить среднее значение и стандартное отклонение первого набора данных, мы можем использовать следующие две формулы:
- Среднее значение: =СРЗНАЧ(B2:B21)
- Стандартное отклонение: =STDEV.S(B2:B21)
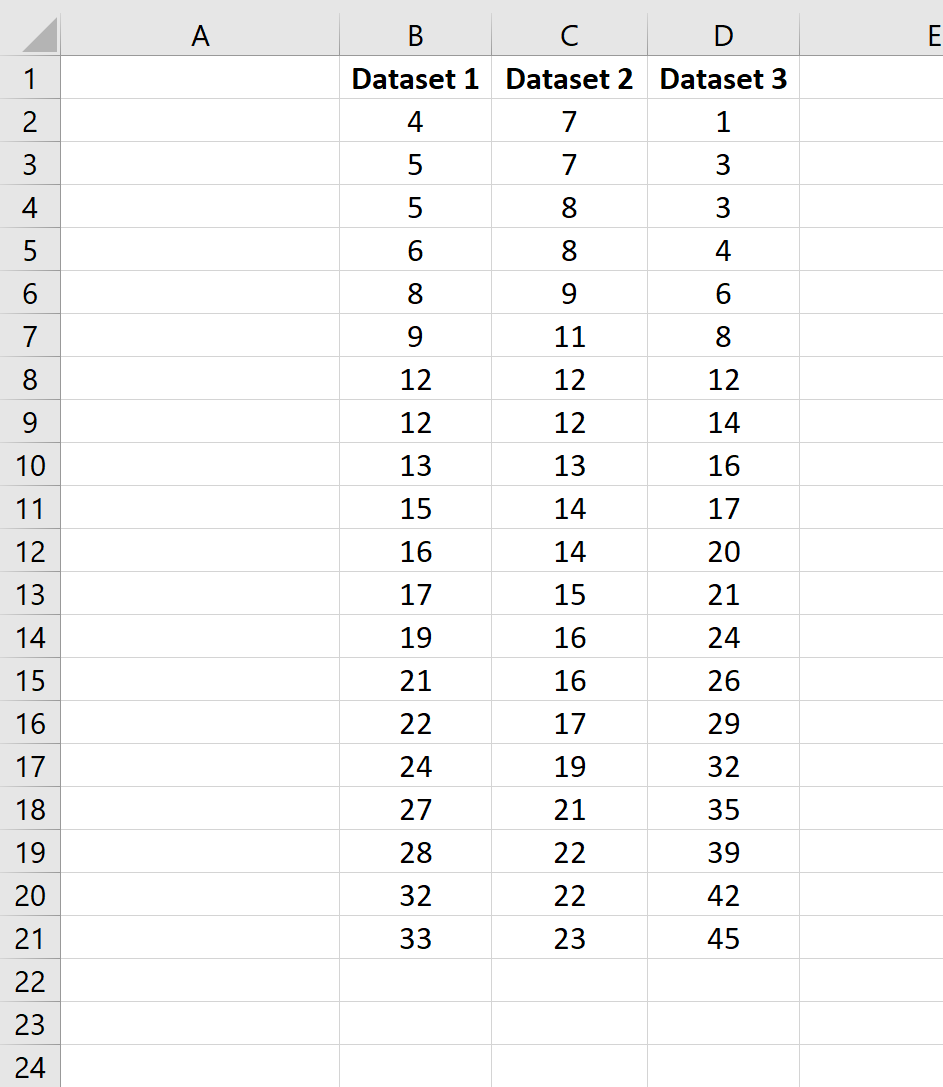
Затем мы можем выделить ячейки B22: B23 и навести указатель мыши на правый нижний угол ячейки B23, пока не появится крошечный +.Затем мы можем щелкнуть и перетащить формулы в следующие два столбца:
Дополнительные ресурсы
Как рассчитать сводку из пяти чисел в Excel
Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать стандартную ошибку среднего в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Download Article
Step-by-step tutorial for the STDEV functions
Download Article
This wikiHow shows you how to find the standard deviation of a dataset in Microsoft Excel. Whether you’re studying for statistics, analyzing data at work, or just researching something for fun, calculating a standard deviation is essential. And, it’s pretty easy to do in Excel! There are built-in functions for calculating the standard deviation.
Things You Should Know
- There are four functions for calculating standard deviation.
- STDEV.P and STDEV.S cover most situations. Use STDEV.P for populations and STDEV.S for samples.
- The function will calculate the standard deviation for a selected range of cells.
Steps
-
1
Enter the values you want to use. Pick a column in which you want to enter your data, then type each data value into individual cells in that column. Using Excel is a great way to organize and analyze your data.
- For example, if you select column «A» as the area in which to enter your data, you might type a number into cell A1, cell A2, cell A3, and so on.
- If needed, you can move columns in your spreadsheet to organize your data.
-
2
Note this information about the different functions. There are four functions in Excel for calculating standard deviation. The functions differ in two ways:[1]
- The selected function will either calculate the standard deviation for a sample (using n — 1) or a population (using n), where n is the sample size.
- The selected function will include or exclude logical values (TRUE and FALSE) and text (numbers represented as text). TRUE is interpreted as a 1, while FALSE is 0.
Advertisement
-
3
Choose a standard deviation function. Here are the four options for calculating standard deviation:
- STDEV.P — Finds the standard deviation of a population. This function doesn’t include logical values or text.[2]
- STDEV.S — Finds the standard deviation of a sample. This function doesn’t include logical values or text.[3]
- STDEVA — Finds the standard deviation of a sample. This function does include logical values or text.[4]
- STDEVPA — Finds the standard deviation of a population. This function does include logical values or text.[5]
- There are also two outdated functions that have been replaced by the above functions. They are still present in Excel for backward compatibility reasons, but may be phased out in future versions.
- STDEV — This function was replaced by STDEV.S. Finds the standard deviation of a sample. This function doesn’t include logical values or text.[6]
- STDEVP — This function was replaced by STDEV.P. Finds the standard deviation of a population. This function doesn’t include logical values or text.[7]
- STDEV — This function was replaced by STDEV.S. Finds the standard deviation of a sample. This function doesn’t include logical values or text.[6]
- STDEV.P — Finds the standard deviation of a population. This function doesn’t include logical values or text.[2]
-
4
Click a blank cell. This should be the cell in which you want to display the standard deviation value. Doing so selects the cell.
-
5
Type in the standard deviation function. In the cell you selected, enter the standard deviation function you want to use. Here is STDEV.S() as an example:
- =STDEV.S()
-
6
Add your value range. To do so:
- In between the parentheses, type the letter and number of the cell containing your first data value.
- Type a colon (:)
- Type the letter and number of the last cell.
- For example, if you entered your data in column «A» from rows 1 through 10, you would have =STDEV.S(A1:A10) typed here.
- If you just want to display the standard deviation of the value of a few scattered cells such as A1, B3, and C5, you can type the cell names separated by commas (e.g., =STDEV.S(A1,B3,C5)).
-
7
Press ↵ Enter. This will prompt Excel to run the formula, displaying the standard deviation of the selected cells in the formula’s cell.
- If you want to check your work, you can calculate the standard deviation by hand.
Advertisement
Add New Question
-
Question
How do I use Excel to calculate 2 standard deviations?
Use =STDEV(), and put your range of values in the parentheses. This can be 2 cells or 2 values (numbers).
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Advertisement
-
The old =STDEV( ) formula doesn’t work in versions of Excel older than 2007.
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 444,221 times.
Is this article up to date?
wikiHow Tech Help Pro:
Level up your tech skills and stay ahead of the curve
Let’s go!
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
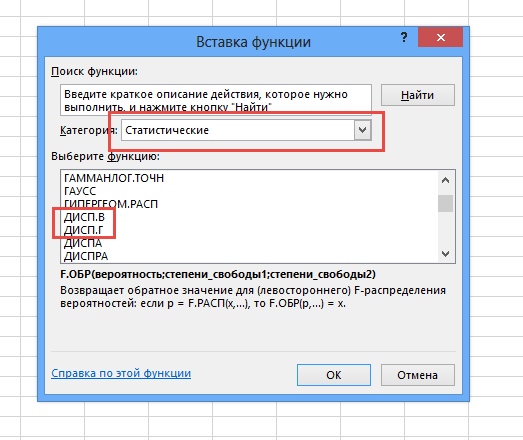
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
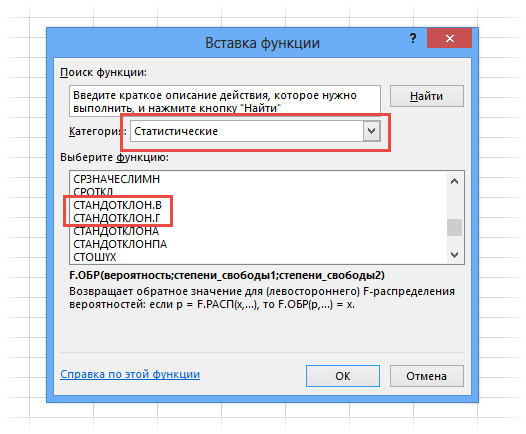
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
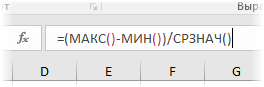
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях: