Как решать систему неравенств в excel - Word и Excel - помощь в работе с программами

Содержание

Решение системы уравнений в Microsoft Excel
Варианты решений
Способ 1: матричный метод
Способ 2: подбор параметров
Способ 3: метод Крамера
Способ 4: метод Гаусса

Решение системы уравнений в Microsoft Excel

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

f(x)

Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.

Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».

Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».

После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».

Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».

Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.

Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.

Аналогичным образом производим подсчет определителей для остальных трех таблиц.

На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

После этого копируем полученную строку и вставляем её в строчку ниже.

Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».

Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».

В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Источник

Дана система уравнений-x я уже нашла,не могу найти y(незнаю какие формулы применять.)Посоветуйте что-нибудь пожалуйста.

Эльфийка! Не у всех имеются последние версии Экселя.
Сохраните таблицу — Сохранить как 97-2003. И таблица будет доступна большей аудитории форумчан.

Может и я на что сгожусь … Если сгодился, можете меня по+благодарить+.

С помощью ЕСЛИ(abs(X)=<3,14/..;sin(…);ЕСЛИ(….;x*x+3.14/..;0)) только при подсчете sin разобраться с радиан или град.

Цитата: Wasilic от 14.05.2010, 14:51
Эльфийка! Не у всех имеются последние версии Экселя.
Сохраните таблицу — Сохранить как 97-2003. И таблица будет доступна большей аудитории форумчан.

Хорошо попробую сделать так как вы сказали…

Здесь просто суть, формулы лень было переписывать. Формула во вложении. Кстати формулу температуты завяжи с ячейками =B17+0,05*($D$8-$B$8), предварительно поправив числа (-3,838 4,433).

И до кучи — вместо 3,14 нужно писать функцию ПИ(), тогда начало формулы будет выглядеть так:
ЕСЛИ(abs(X)=<ПИ()/……

Скажи мне, кудесник, любимец ба’гов…

Яндекс-деньги: 41001632713405
Webmoney: R289877159277; Z102172301748; E177867141995

Источник

ЛР № 3. MS Excel. Построение графика функции, заданной системой неравенств

Лабораторная работа № 3 Построение графика функции, заданной системой неравенств

Цель:

Приобрести навыки использования логической функции ЕСЛИ при вычислении таблицы значений функции, заданной системой неравенств, и построения графика

данной функции

Методические указания:

При вычислении функции используйте логическую функцию ЕСЛИ.

Логическая функция ЕСЛИ возвращает одно значение, если заданное условие при вычислении дает значение ИСТИНА, и другое значение, если ЛОЖЬ. Синтаксис функции:

=ЕСЛИ(Лог_выражение;значение_если_истина;значение_если_ложь)

Лог_выражение — это любое значение или выражение, принимающее значения ИСТИНА или ЛОЖЬ.

Значение_если_истина — это значение, которое возвращается, если лог_выражение равно ИСТИНА.

Значение_если_ложь — это значение, которое возвращается, если лог_выражение равно ЛОЖЬ.

В MS Excel 2003 до 7 функций ЕСЛИ могут быть вложены друг в друга в качестве значений аргументов значение_если_истина и значение_если_ложь для конструирования более сложных проверок. В MS Excel 2007 до 64 функций.

Ход выполнения работы:

1.Из таблицы 1 выберите варианты индивидуальных заданий в соответствии с вашим номером в журнале.

2.Откройте Excel. Назовите первый лист книги 2_№ варианта.

3.Постройте на этом листе график (Точечную диаграмму со значениями, соединенными сглаживающими линиями без маркеров) функции, заданной системой двух неравенств (таблица 2). Ход выполнения работы описан в лекции.

4.Назовите второй лист книги 3_№ варианта.

5.Постройте на этом листе график функции, заданной системой трех неравенств (таблица 3). Ход выполнения работы описан в лекции.

6.Назовите третий лист книги 4_№ варианта.

7.Постройте на этом листе график функции, заданной системой четырех неравенств (таблица 4).

8.Сохраните вашу работу под именем ЛР_4_система неравенств в свою папку.

PDF created with pdfFactory Pro trial version www.pdffactory.com

ЛР № 3. MS Excel. Построение графика функции, заданной системой неравенств

Индивидуальные задания

								Таблица 1
	Выбор варианта индивидуального задания в соответствии с номером в журнале
Номер по		Задание	Задание	Задание	Номер по	Задание	Задание	Задание
списку		списку
	1	2	3	1	2		3
в журнале		в журнале

1.		1	5	10	16.	10	7	2
2.		2	6	11	17.	11	8	3
3.		3	7	12	18.	12	9	4
4.		4	8	13	19.	13	10	5
5.		5	9	14	20.	14	11	6
6.		6	10	15	21.	15	12	7
7.		7	11	1	22.	1	13	8
8.		8	13	2	23.	2	14	9
9.		9	12	3	24.	3	15	10
10.		10	14	4	25.	4	1	11
11.		11	15	5	26.	5	2	12
12.		12	1	6	27.	6	3	13
13.		13	2	7	28.	7	4	14
14.		14	3	8	29.	8	5	15
15.		15	4	9	30.	9	6	1

PDF created with pdfFactory Pro trial version www.pdffactory.com

ЛР № 3. MS Excel. Построение графика функции, заданной системой неравенств

Таблица 2

№ варианта

y(x)

y(x) =

ìx × ln x

x ³ 0.2

— 2

x < 0.2

îx2

y(x) =

ìx3

x ³ 1.0

x < 1.0

îx2 — 5

ìln x

x ³ 8,0

y(x) = í

x < 8,0

î x2

x ³ 5

y(x) =

— 2x

x < 5

îx

ln 3x

x ³ 0.5

y(x) = í

—10

x < 0.5

îx

x ³ 2

y(x) = í

îx

2 — 2

x < 2

y(x) =

ìx × lg x

x ³ 0.2

x < 0.2

îx

y(x) = íïe

x ³ 3

— 2

x < 3

îx

ì 4x +10

x ³ 0

y(x) = í0.5x2 — 2

x < 0

10.

x ³ 0.2

y(x) = í

x < 0.2

î— 4x2 — 2

11.

y(x) =

ì ln10x

x ³ 0.2

x < 0.2

î— ln 5x

12.

ì0.01x — 3

x ³ 4

y(x) = í

— 2

x < 4

îx

13.

y(x) = í3x

+ x x ³ 10

î— x2 — 2

x < 10

14.

y(x) =

íx

+ 4x x ³ 0

î x3 — 2

x < 0

15.

y(x) = í — x

+ 3x

x ³ 0

5x2 — 2x +10 x < 0

PDF created with pdfFactory Pro trial version www.pdffactory.com

ЛР № 3. MS Excel. Построение графика функции, заданной системой неравенств

Таблица 3

№

y(x)

№

y(x)

варианта

ì x + 4 x < —1

1— x

x £ 0

y(x) =

—1 £ x < 1

0 < x £ 2

íx2 + 2

y(x) = í0

x ³ 1

— 2

x > 2

x +1

x £ 0

10.

x £ 0

y(x) = í(x +1)

0 < x £ 2

x > 2

y(x) = íx

0 < x £ 1

î— x + 4

x > 1

î2 + x

11.

x £ π / 2

ì x + 2

x £ —1

ìcos x

y(x) =

ïx2 +1 —1 < x £ 1

y(x) = ï0

π / 2 < x < π

x > 1

x ³ π

î — x + 3

î 2

12.

ì — x

x £ 0

ì x —1

x £ 0

0 < x < 2

y(x) =

0 < x < 2

y(x) = í- (x —1)2

íx2

x — 3

x ³ 2

13.

ì- 2(x +1)

x £ —1

ì x +1

x < 0

+1)3

—1 < x < 0

y(x) =

y(x) = í

íx2 —1 0 £ x < 1

x ³ 0

x ³ 1

î — x

14.

ì — x

x £ 0

ì — x

x < 0

y(x) =

x2 0

< x £ 2

y(x) =

2 +1 0 £ x < 2

íx

x > 2

x ³ 2

îx +1

îx

15.

x2 +1

x £ 1

ì 2

x < —1

y(x) =

1 < x £ 3

y(x) =

— x

—1 £ x £ 1

í 2x

í1

x > 3

x > 1

îx + 2

î ln x

x — 3

x £ 0

y(x) =

0 < x £ 4

íx

+ x

x > 4

î 3

PDF created with pdfFactory Pro trial version www.pdffactory.com

ЛР № 3. MS Excel. Построение графика функции, заданной системой неравенств

Таблица 4

№

y(x)

№

y(x)

варианта

ìcos x

x < π

x < —1

p £ x < 2p

ïx

—1£ x < 0

ïcos5x

ïx3

Y (x) = í

2p £ x < 3p

Y (x) = í

0 £ x <1

ïsin 5x

ï— x3

ïsin2 x

x ³ 3p

x ³1

î(x +

x < —2

10.

ì2/ x

x < 4

ïx

— 2 £ x < —1

4 £ x < 6

ï(2x)2

ï5x

Y (x) = í

—1£ x <1

Y (x) = í

6 £ x < 8

ïsin8x

ïx

—1

x ³1

ï5 + x

x ³ 8

îx

ìsin x

x < π

11.

ìπ

x < π

p £ x < 2p

+ p/10

p £ x < 5

ïsin 5x

ïx

Y (x) = í

2p £ x < 3p

Y (x) = í

+ 15

5 £ x < 7.5

ïcos5x

ïx

x ³ 3p

—10

x ³ 7.5

îcos

îx

+ x

x < 0

12.

ì−1

x < −1

ïx

0 £ x < p/ 2

—1£ x <1

ïsin x

ïx

Y (x) = í

p/ 2 £ x < 3

Y (x) = í

1£ x < 2

ïcos x

ï1

x ³ 3

ï- x2

x ³ 2

î1/ x

ì2cos x

x < π

13.

+ 2

x < —2

ï— x

ïsin x

p £ x < 2p

ïcos x

— 2 £ x < 0

Y (x) = í

0 £ x < p

ï0.2 + sin 5x 2p £ x < 3p

ïsin x

ï1

x ³ 3p

x ³ p

îln x

ì− 2

x < −10

14.

ìtgx

x < π/3

—10 £ x < —9

p/3 £ x < p

ï- 0.5

ï3x

Y (x) = í

— 9 £ x < —8

Y (x) = í

p £ x <1.5p

ï1

ïsin x

x ³ —8

x ³1.5p

î2.5

îcos

ìx

x < −5

15.

ìsin x

x < −π

— 5 £ x < —3

+ 3

— p £ x < p

ï- x

Y (x) = í

— 3 £ x < —1

Y (x) = í

p £ x < 2p

ïx

ïcos 4x

x ³ —1

x ³ 2p

î— x

î3x

ì− cos x

x < π

p £ x < 2p

ï- cos2x

Y (x) = í

2p £ x < 3p

ï— cos3x

x ³ 3p

î— cos4x

PDF created with pdfFactory Pro trial version www.pdffactory.com

Соседние файлы в папке Kontrolnaya_TGz

#
18.05.2015432.96 Кб11Excel_Постр_графика функции_сист неравенств.ppsx
#
#
#
#
#
#

Источник

Решение систем уравнений с двумя
переменными с помощью надстройки Поиск решений

Пусть необходимо решить систему уравнений

Решение:

1.
Создать
книгу в MS Excel
и назвать его решение систем уравнений

2.
Лист1
назвать Решение систем уравнений

3.
В
ячейке A1 ввести X=, в ячейке B1 ввести 0, в ячейке A2 ввести Y=, в ячейке B2 ввести 0

4.
Далее
в ячейке A3 вводим левую часть
первого уравнения =5*В1*В1+В2

5.
В
ячейке A4 вводим левую часть
второго уравнения =В1+3*В2*В2

6.
В
ячейке В3 вводим 30 — правая часть первого уравнения

7.
В
ячейке В4 вводим 20 — правая часть второго уравнения

8.
Добавляем
на вкладку Данные надстройку Поиск решений. Для этого В меню Файл – Параметры –
Надстройки нажимаем перейти

В
данном окне ставим флажок Поиск решений

9.
Вызываем
диалоговое окно Параметры поиска решений

Параметр
«Оптимизировать целевую функцию» ссылка на левую часть первого уравнения — $A$4

До
выбираем Значение — вводим правую часть первого уравнения – 30

Изменяя
ячейки переменных – выбираем значения переменных X
и Y — $B$1;$B$2

В
соответствии с ограничениями

Нажимаем
Добавить ссылку на левую часть второго уравнения – А5 знак выбираем равно = и
ограничение – 20 – правая часть второго уравнения

Когда
все параметры введены то нажимаем кнопку Найти решение.

Получили
решение

Источник

17 авг. 2022 г.
читать 2 мин

Чтобы решить систему уравнений в Excel, мы можем использовать функции МУМНОЖ и МИНВЕРС .

В следующих примерах показано, как использовать эти функции для решения нескольких различных систем уравнений в Excel.

Пример 1. Решение системы уравнений с двумя переменными

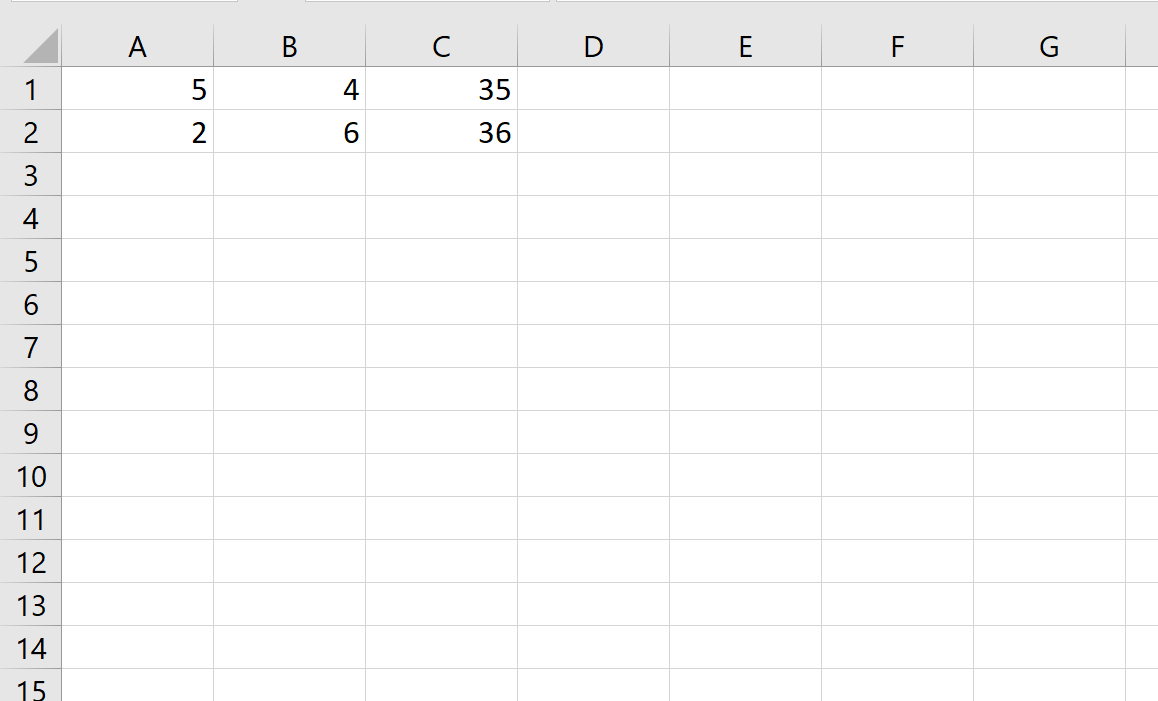
Предположим, у нас есть следующая система уравнений, и мы хотели бы найти значения x и y:

5х + 4у = 35

2х + 6у = 36

Чтобы решить эту систему уравнений, мы можем сначала ввести следующие значения в Excel:

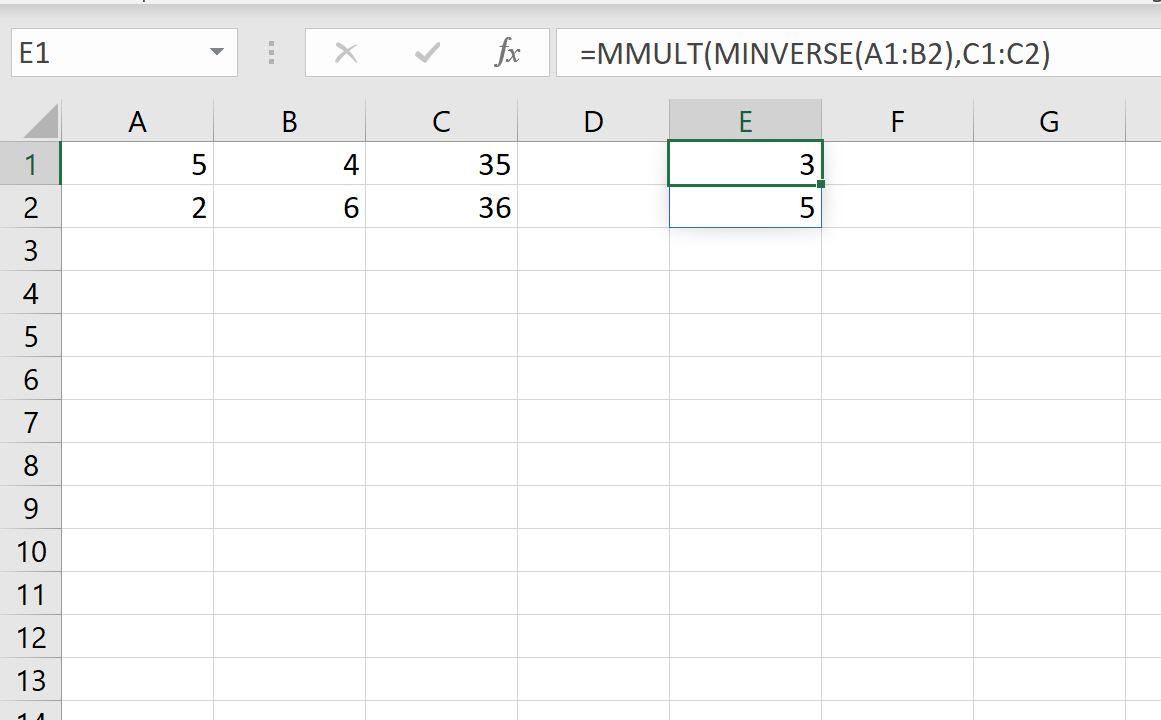
Затем мы можем использовать следующую формулу для определения значений x и y:

=MMULT(MINVERSE( A1:B2 ), C1:C2 )

Мы можем ввести эту формулу в ячейку E1, а затем нажать CTRL + SHIFT + ENTER:

Это говорит нам о том, что значение x равно 3 , а значение y равно 5 .

Пример 2. Решение системы уравнений с тремя переменными

Предположим, у нас есть следующая система уравнений, и мы хотели бы найти значения x, y и z:

4х + 2у + 1з = 34

3x + 5y – 2z = 41

2х + 2у + 4з = 30

Чтобы решить эту систему уравнений, мы можем сначала ввести следующие значения в Excel:

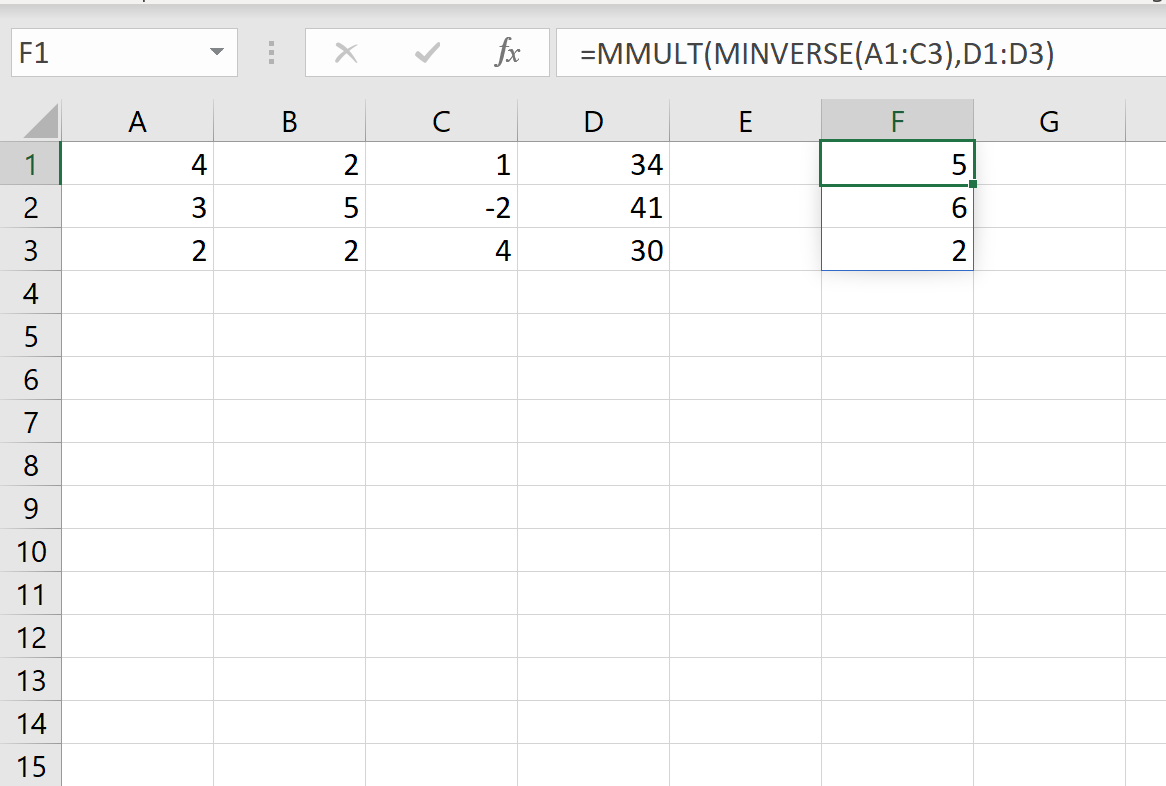
Затем мы можем использовать следующую формулу для определения значений x, y и z:

=MMULT(MINVERSE( A1:C3 ), D1:D3 )

Мы можем ввести эту формулу в ячейку F1, а затем нажать CTRL + SHIFT + ENTER:

Это говорит нам о том, что значение x равно 5 , значение y равно 6 , а значение z равно 2 .

Пример 3. Решение системы уравнений с четырьмя переменными

Предположим, у нас есть следующая система уравнений, и мы хотели бы найти значения w, x, y и z:

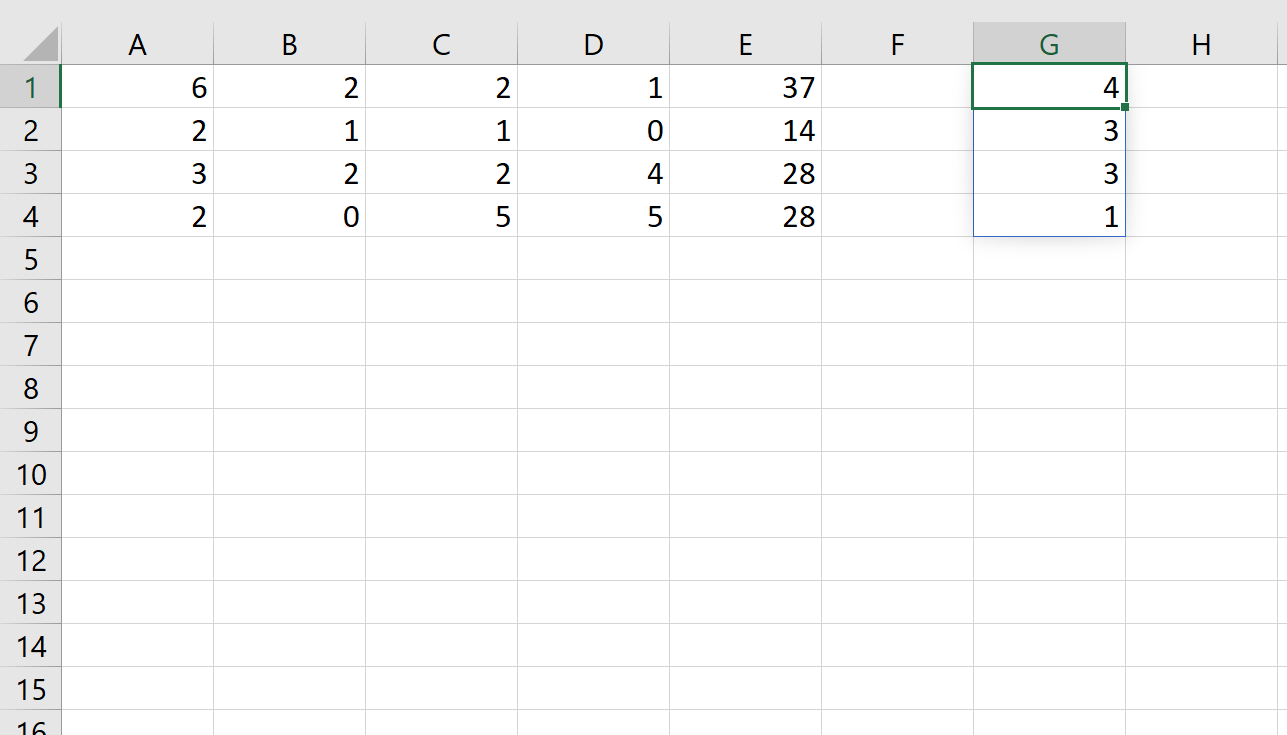
6ш + 2х + 2у + 1з = 37

2ш + 1х + 1у + 0з = 14

3ш + 2х + 2у + 4з = 28

2ш + 0х + 5у + 5з = 28

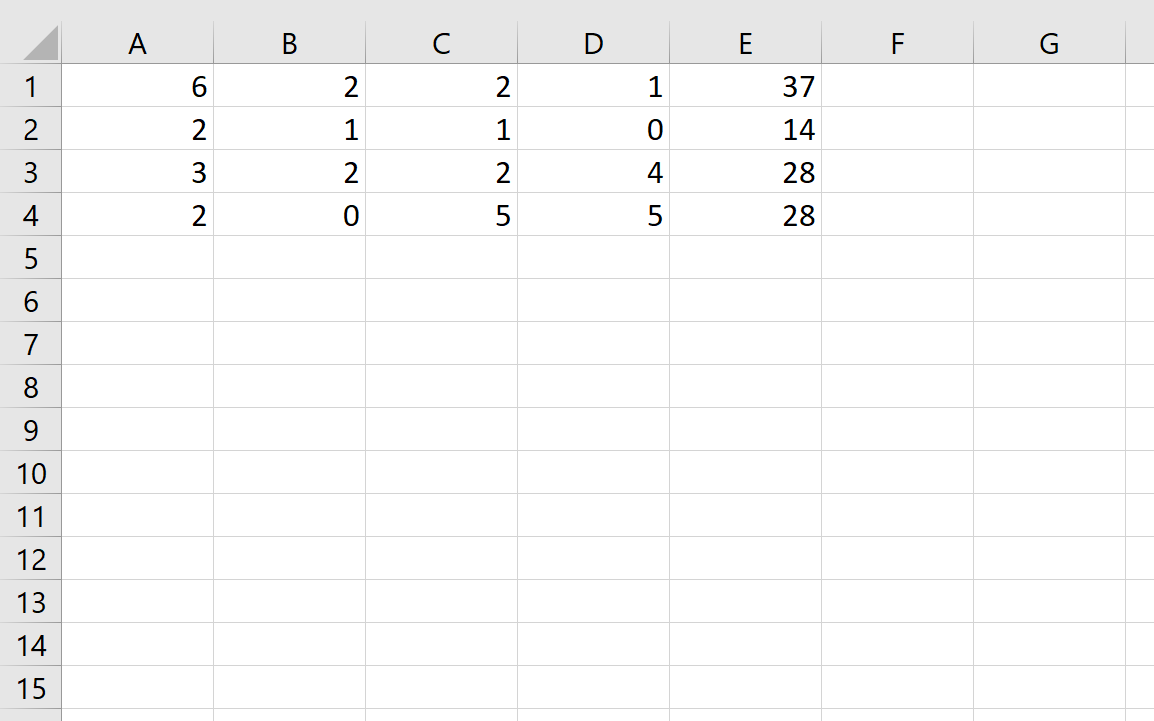
Чтобы решить эту систему уравнений, мы можем сначала ввести следующие значения в Excel:

Затем мы можем использовать следующую формулу для определения значений w, x, y и z:

=MMULT(MINVERSE( A1:D4 ), E1:E4 )

Мы можем ввести эту формулу в ячейку G1, а затем нажать CTRL + SHIFT + ENTER:

Это говорит нам о том, что значение w равно 4 , x равно 3 , y равно 3 и z равно 1 .

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные операции в Excel:

Как построить уравнение в Excel
Как нормализовать данные в Excel
Как подогнать кривую в Excel

Источник

Многие задачи математики и статистики приходится решать электронно. В этом уроке мы подробно разберем, как без сложностей решить систему уравнений в Excel. Используя предложенные методики, вы сможете быстро и правильно справится даже с самыми сложными уравнениями.

Метод Гаусса для простых уравнений

Для простых уравнений, где три или меньше неизвестных, можно воспользоваться методом Гаусса. Вы можете решить одно уравнение или несколько одновременно. Будем решать по следующим данным:
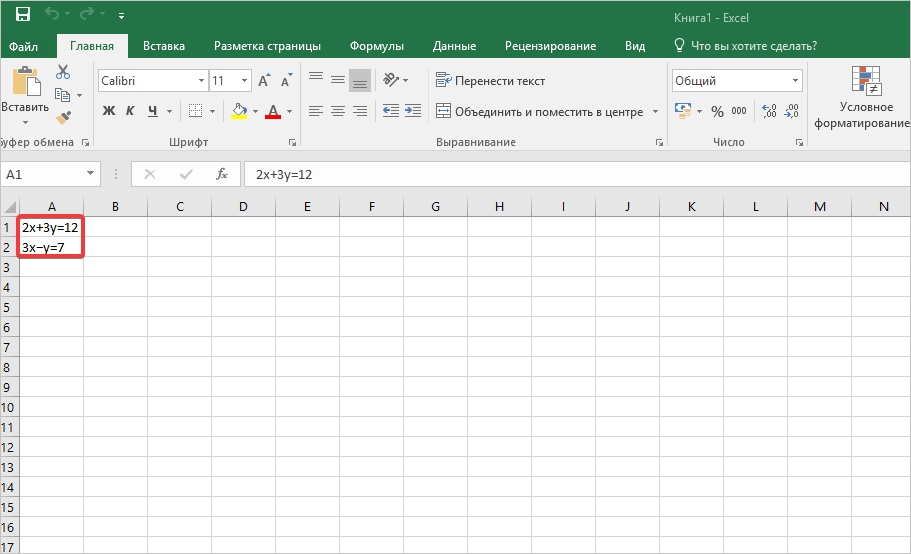
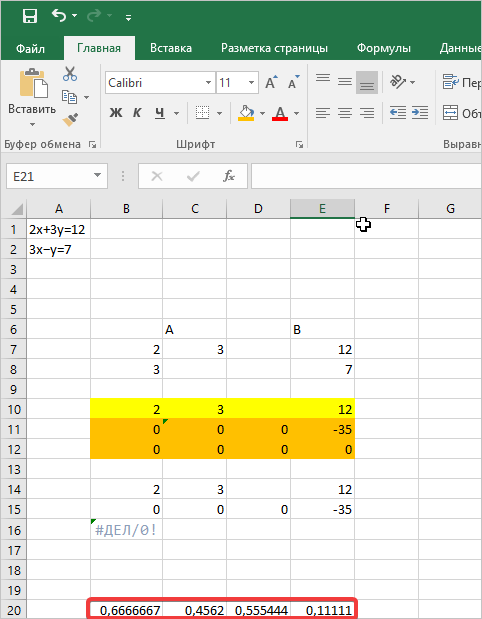
2x+3y=12
3x−y=7.

Вставим наши уравнения в ячейки (желательно их оформить у самого края электронной книги).

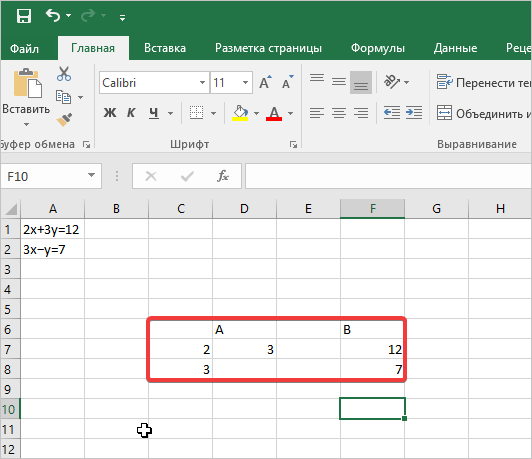
Чуть ниже на этой странице делаем две небольшие таблицы, куда будут вноситься коэффициенты и свободные члены. Для этого оформим несколько ячеек со значением А (для коэффициентов) и несколько с шапкой В (для свободных членов)

Важно!

Будьте внимательны при внесении записей, все значения, которые расположены после знака равно, записываются в табличку В.

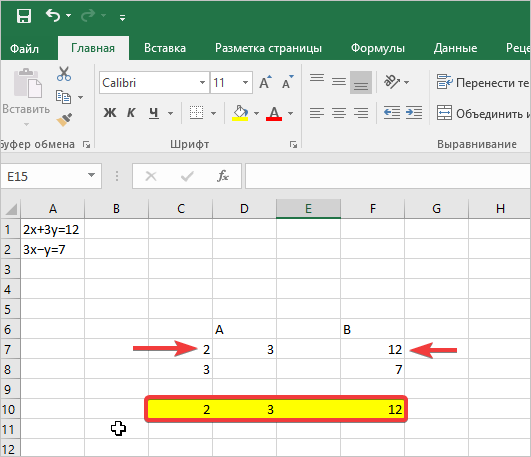
Теперь занимаемся первым уравнением. Для этого скопируем первую матрицу вместе со значением после знака равно. Размещаем ее ниже наших табличек на одну строчку.

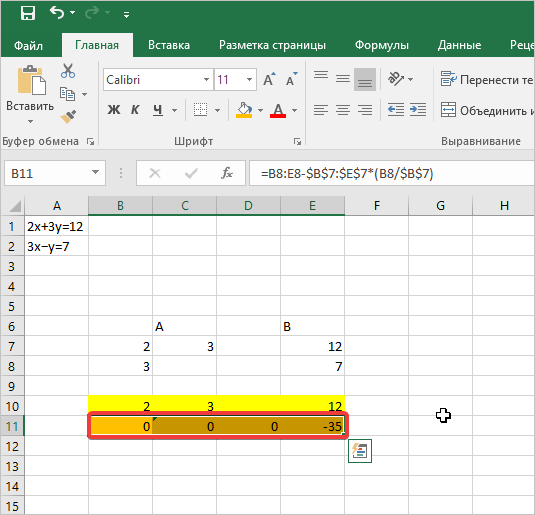
Далее в ячейку ниже вводим подготовленную формулу: =B8:E8-$B7:7:E7∗(B8/7*(B8/B$7). Затем нажимаете комбинацию клавиш CTRL+SHIFT+ENTER. Во всей строке проставятся точные значения.

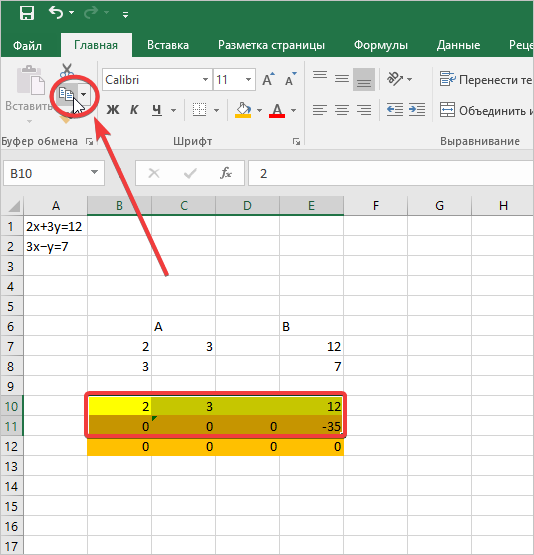
Далее вам нужно скопировать эту строку и продублировать ее на ячейку ниже. Теперь скопируем две первые строчки после пустующей строки. Для этого выделим их и нажмем комбинацию CTRL+C или при помощи встроенного инструмента «Копировать» на панели управления.

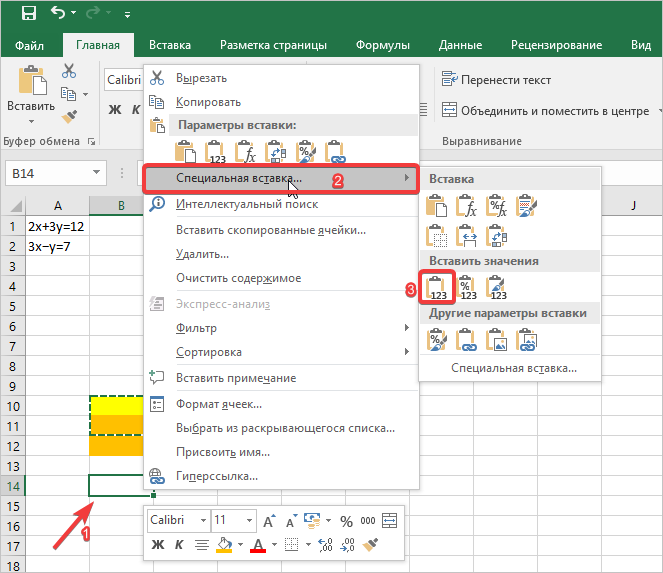
Отступаем одну строчку и на следующей делаем выделение пустой ячейки курсором мыши. Затем вызываем выпадающий список путем нажатия на правую кнопку мыши. Теперь выбираем пункт «Специальная вставка», появится дополнительный список, в котором необходимо отметить «Вставить значения».

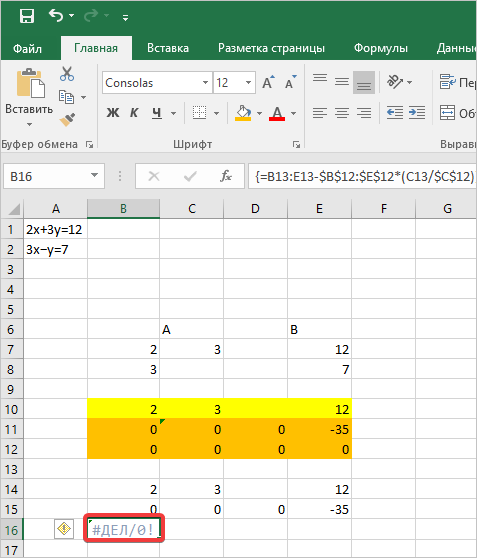
Как видим, в нашем случае высвечивается ошибка о запрете деления на «0». В вашем случае, это будут другие значения.

В дальнейшем вам необходимо сделать обратную прогонку. Для этого отступим три пустые строки на странице, а в четвертую вставим формулу: =B17:E17/D17. Затем выделяем строчку и жмем все ту же комбинацию клавиш CTRL+SHIFT+ENTER.

В результате, при проведении правильных расчетов вы должны получить ответы на буквенные символы. Однако, этот метод требует внимательности и точного ввода формул, с чем не каждый пользователь справляется, поэтому рассмотрим другой вариант для решения.

Полезно знать!

Аналогичным способом проводим вычисление неизвестных аргументов для второго и третьего уравнений, если они присутствуют, и представляют собой целую систему.

Решение квадратного уравнения с подбором параметров

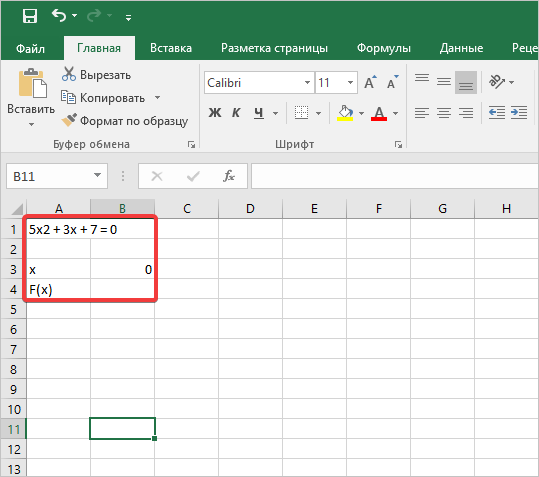
Предположим, есть буквенное выражение 5×2 + 3x + 7 = 0. Чтобы его решить вручную, придется тратить время на каждое действие. При помощи Excel, а именно подбора параметров, сделать это можно в считанные минуты.

Открываем новый лист Excel и вносим уравнение в первую ячейку. Отступим одну строку вниз и пропишем значение для Х=0. Далее будем высчитывать его через строку формул F(х), обязательно прописываем выражение в отдельной ячейке.

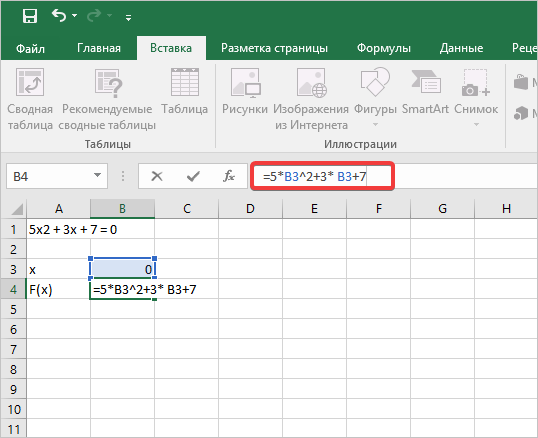
После этого заносим следующую формулу после знака равно в строке формул. Обязательно учитывайте, что ваши значения будут другими. Делайте на примере нашего выражения. Итак, вставляем =5x^2+3 x+7, при этом вместо значения X вы должны вставить адрес ячейки, в которой обозначено, за какое число принято неизвестное, то есть «0». Затем нажимаем кнопку ENTER.

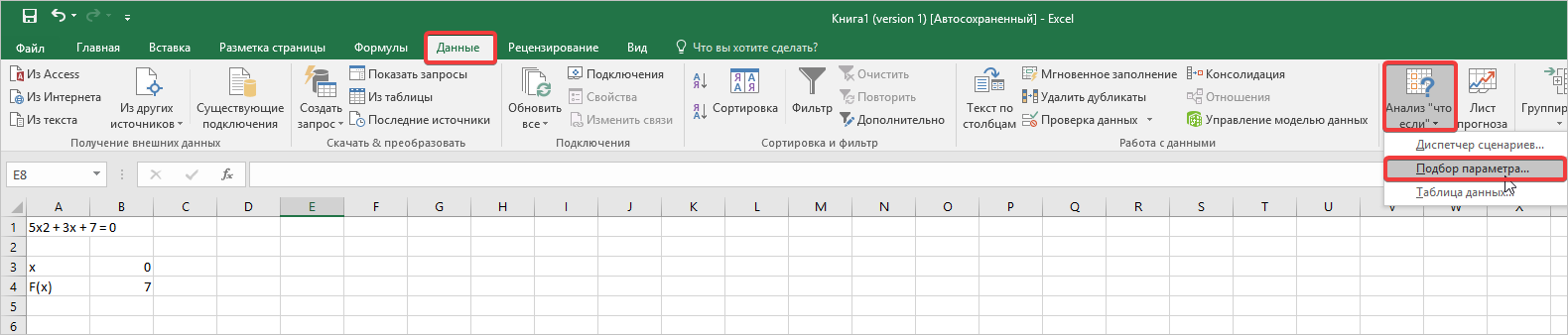
В ячейке, отвечающей за значение в строке формулы, вы получаете конкретное число. Теперь заходим во вкладку «Данные», переходим к пункту «Анализ «что, если»». Нажимаем на него и открываем дополнительный список, в котором кликаем по записи «Подбор параметра».

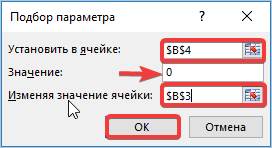
Перед вами открывается окно с ячейками для заполнения. Нам необходимо прописать значения во всех трех ячейках. Давайте сделаем все по порядку. В поле «Установить в ячейке» прописываем адрес ячейки с найденным числом. Следующее поле «Значение» ставим «0», а в ячейке «Изменяя значение», указываем адрес значения X, то есть ту графу, где прописан «0». После проделанных манипуляций нажимаем кнопку «Ок».

Важно!

Обратите внимание, при правильном вводе всех данных начнется автоматический расчет с посекундным изменением чисел в ячейках. Поэтому дождитесь остановки и внесите подтверждение для всплывшего окна.

Теперь в появившемся окне нажимаем кнопку «ОК» для сохранения. Мы видим, что программа нашла ответ на наше уравнение, это будет «-1». Таким образом мы разобрали самые простые способы решения уравнений, с которыми разберётся даже начинающий пользователь офисной программы Microsoft Excel.

Источник

Решение системы уравнений в Microsoft Excel

Варианты решений

Способ 1: матричный метод

Способ 2: подбор параметров

Способ 3: метод Крамера

Способ 4: метод Гаусса

Пример 1. Решение системы уравнений с двумя переменными

Пример 2. Решение системы уравнений с тремя переменными

Пример 3. Решение системы уравнений с четырьмя переменными

Дополнительные ресурсы

Метод Гаусса для простых уравнений

Решение квадратного уравнения с подбором параметров

А вот еще интересные статьи: