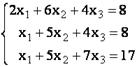Недаром программа Microsoft Excel пользуется колоссальной популярностью как среди рядовых пользователей ПК, так и среди специалистов в разных отраслях. Все дело в том, что данное приложение содержит огромное количество интегрированных формул, называемых функциями. Восемь основных категорий позволяют создать практически любое уравнение и сложную структуру, вплоть до взаимодействия нескольких отдельных документов.
Понятие встроенных функций
Что же такое эти встроенные функции в Excel? Это специальные тематические формулы, дающие возможность быстро и качественно выполнить любое вычисление.
К слову, если самые простые из функций можно выполнить альтернативным (ручным) способом, то такие действия, как логические или ссылочные, — только с использованием меню «Вставка функции».
Таких функций в Excel очень много, знать их все невозможно. Поэтому компанией Microsoft разработан детальный справочник, к которому можно обратиться при возникновении затруднений.
Сама функция состоит из двух компонентов:
- имя функции (например, СУММ, ЕСЛИ, ИЛИ), которое указывает на то, что делает данная операция;
- аргумент функции — он заключен в скобках и указывает, в каком диапазоне действует формула, и какие действия будут выполнены.
Кстати, не все основные встроенные функции Excel имеют аргументы. Но в любом случае должен быть соблюден порядок, и символы «()» обязательно должны присутствовать в формуле.
Еще для встроенных функций в Excel предусмотрена система комбинирования. Это значит, что одновременно в одной ячейке может быть использовано несколько формул, связанных между собой.
Аргументы функций
Детально стоит остановиться на понятии аргумента функции, так как на них опирается работа со встроенными функциями Excel.
Аргумент функции – это заданное значение, при котором функция будет выполняться, и выдавать нужный результат.
Обычно в качестве аргумента используются:
- числа;
- текст;
- массивы;
- ошибки;
- диапазоны;
- логические выражения.
Как вводить функции в Excel
Создавать формулы достаточно просто. Сделать это можно, вводя на клавиатуре нужные встроенные функции MS-Excel. Это, конечно, при условии, что пользователь достаточно хорошо владеет Excel, и знает на память, как правильно пишется та или иная функция.
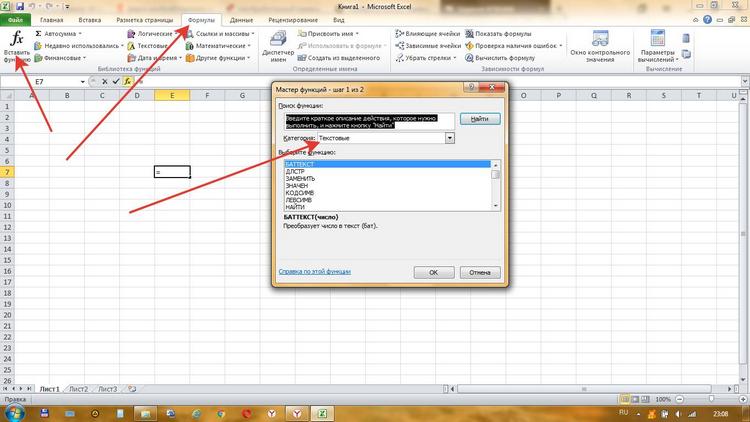
Второй вариант более подходит для всех категорий пользователей – использование команды «Функция», которая находится в меню «Вставка».
После запуска данной команды откроется мастер создания функций – небольшое окно по центру рабочего листа.
Там можно сразу выбрать категорию функции или открыть полный перечень формул. После того как искомая функция найдена, по ней нужно кликнуть и нажать «ОК». В выбранной ячейке появится знак «=» и имя функции.
Теперь можно переходить ко второму этапу создания формулы – введению аргумента функции. Мастер функций любезно открывает еще одно окно, в котором пользователю предлагается выбрать нужные ячейки, диапазоны или другие опции, в зависимости от названия функции.
Ну и в конце, когда аргумент уже выбран, в строке формул должно появиться полное название функции.
Виды основных функций
Теперь стоит более детально рассмотреть, какие же есть в Microsoft Excel встроенные функции.
Всего 8 категорий:
- математические (50 формул);
- текстовые (23 формулы);
- логические (6 формул);
- дата и время (14 формул);
- статистические (80 формул) – выполняют анализ целых массивов и диапазонов значений;
- финансовые (53 формулы) – незаменимая вещь при расчетах и вычислениях;
- работа с базами данных (12 формул) – обрабатывает и выполняет операции с базами данных;
- ссылки и массивы (17 формул) – прорабатывает массивы и индексы.
Как видно, все категории охватывают достаточно широкий спектр возможностей.
Математические функции
Данная категория является наиболее распространенной, так как математические встроенные функции в Excel можно применять для любого типа расчетов. Более того, эти формулы можно использовать в качестве альтернативы калькулятору.
Но это далеко не все достоинства данной категории функций. Большой перечень формул – 50, дает возможность создавать многоуровневые формулы для сложных научно-проектных вычислений, и для расчета систем планирования.
Самая популярная функция из этого радела – СУММ (сумма).
Она рассчитывает сумму нескольких значений, вплоть до целого диапазона. Кроме того, с ней очень удобно подсчитывать итог и выводить общую сумму в разных колонках чисел.
Еще один лидер категории – ПРОМЕЖУТОЧНЫЕ.ИТОГИ. Позволяет считать итоговую сумму с нарастающим итогом.
Функции ПРОИЗВЕД (произведение), СТЕПЕНЬ (возведение чисел в степень), SIN, COS, TAN (тригонометрические функции) также очень популярны, и, что самое важное, не требуют дополнительных знаний для их введения.
Функции дата и время
Данная категория нельзя сказать, что уж очень распространена. Но использование встроенных функций Excel «Дата и время» дают возможность преобразовывать и манипулировать данные, связанные с временными параметрами. Если документ Microsoft Excel является структурным и сложноподчиненным, то применение временных формул обязательно имеет место.
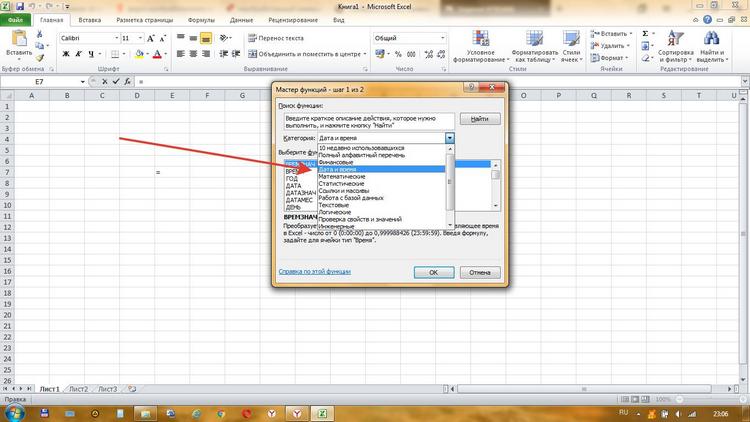
Формула ДАТА указывает в выбранной ячейке листа текущее время. Аналогично работает и функция ТДАТА – она указывает текущую дату, преобразовывая ячейку во временной формат.
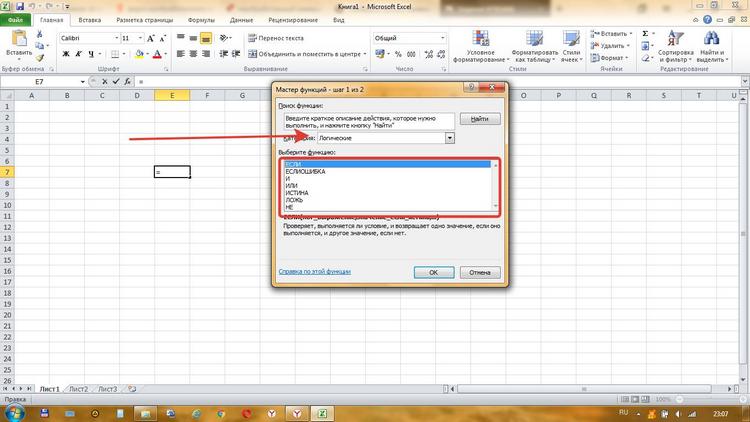
Логические функции
Отдельного внимания заслуживает категория функций «Логические». Работа со встроенными функциями Excel предписывает соблюдение и выполнение заданных условий, по результатам которых будет произведено вычисление. Собственно, условия могут задаваться абсолютно любые. Но результат имеет лишь два варианта выбора – Истина или Ложь. Ну или альтернативные интерпретации данных функций – будет отображена ячейка или нет.
Самая популярная команда – ЕСЛИ – предписывает указание в заданной ячейке значения являющего истиной (если данный параметр задан формулой) и ложью (аналогично). Очень удобна для работы с большими массивами, в которых требуется исключить определенные параметры.
Еще две неразлучные команды – ИСТИНА и ЛОЖЬ, позволяют отображать только те значения, которые были выбраны в качестве исходных. Все отличные от них данные отображаться не будут.
Формулы И и ИЛИ – дают возможность создания выбора определенных значений, с допустимыми отклонениями или без них. Вторая функция дает возможность выбора (истина или ложь), но допускает вывод лишь одного значения.
Текстовые функции
В данной категории встроенных функций Excel — большое количество формул, которые позволяют работать с текстом и числами. Очень удобно, так как Excel является табличным редактором, и вставка в него текста может быть выполнена некорректно. Но использование функций из данного раздела устраняет возможные несоответствия.
Так, формула БАТТЕКСТ преобразовывает любое число в каллиграфический текст. ДЛСТР подсчитывает количество символов в выбранном тексте.
Функция ЗАМЕНИТЬ находит и заменяет часть текста другим. Для этого нужно ввести заменяемый текст, искомый диапазон, количество заменяемых символов, а также новый текст.
Статистические функции
Пожалуй, самая серьезная и нужная категория встроенных функций в Microsoft Excel. Ведь известный факт, что аналитическая обработка данных, а именно сортировка, группировка, вычисление общих параметров и поиск данных, необходима для осуществления планирования и прогнозирования. И статистические встроенные функции в Excel в полной мере помогают реализовать задуманное. Более того, умение пользоваться данными формулами с лихвой компенсирует отсутствие специализированного софта, за счет большого количества функций и точности анализа.
Так, функция СРЗНАЧ позволяет рассчитать среднее арифметическое выбранного диапазона значений. Может работать даже с несмежными диапазонами.
Еще одна хорошая функция — СРЗНАЧЕСЛИ(). Она подсчитывает среднее арифметическое только тех значений массива, которые удовлетворяют требованиям.
Формулы МАКС() и МИН() отображают соответственно максимальное и минимальное значение в диапазоне.
Финансовые функции
Как уже упоминалось выше, редактор Excel пользуется очень большой популярностью не только среди рядовых обывателей, но и у специалистов. Особенно у тех, что очень часто используют расчеты – бухгалтеров, аналитиков, финансистов. За счет этого применение встроенных функций Excel финансовой категории позволяет выполнить фактически любой расчет, связанный с денежными операциями.
Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.
Функции работы с базами данных
Еще одна важная категория, в которую входят встроенные функции в Excel для работы с базами данных. Собственно, они очень удобны для быстрого анализа и проверок больших списков и баз с данными. Все формулы имеют общее название – БДФункция, но в качестве аргументов используются три параметра:
- база данных;
- критерий отбора;
- рабочее поле.
Все они заполняются в соответствии с потребностью пользователя.
База данных, по сути, это диапазон ячеек, которые объединены в общую базу. Исходя из выбранных интервалов, строки преобразовываются в записи, а столбцы – в поля.
Рабочее поле – в нем находится столбец, который используется формулой для определения искомых значений.
Критерий отбора – это интервал выбираемых ячеек, в котором находятся условия функции. Т. е. если в данном интервале имеется хотя бы одно сходное значение, то он подходит под критерий.
Наиболее популярной в данной категории функций является СЧЕТЕСЛИ. Она позволяет выполнить подсчет ячеек, попадающих под критерий, в выбранном диапазоне значений.
Еще одна популярная формула – СУММЕСЛИ. Она подсчитывает сумму всех значений в выбранных ячейках, которые были отфильтрованы критерием.
Функции ссылки и массивы
А вот данная категория популярна благодаря тому, что в нее вошли встроенные функции VBA Excel, т. е. формулы, написанные на языке программирования VBA. Собственно, работа с активными ссылками и массивами данных с помощью данных формул очень легка, настолько они понятны и просты.
Основная задача этих функций – вычленение из массива значений нужного элемента. Для этого задаются критерии отбора.
Таким образом, набор встроенных функций в Microsoft Excel делает данную программу очень популярной. Тем более что сфера применения таблиц этого редактора весьма разнообразна.
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
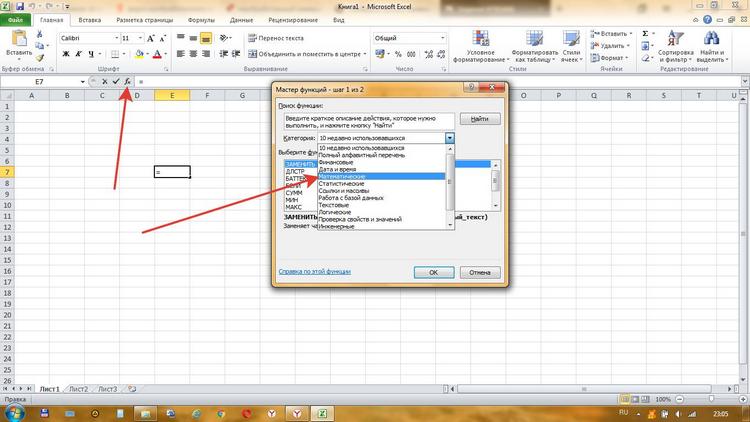
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12793 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в EXCEL
history 12 ноября 2015 г.
-
Группы статей
- Системы линейных уравнений
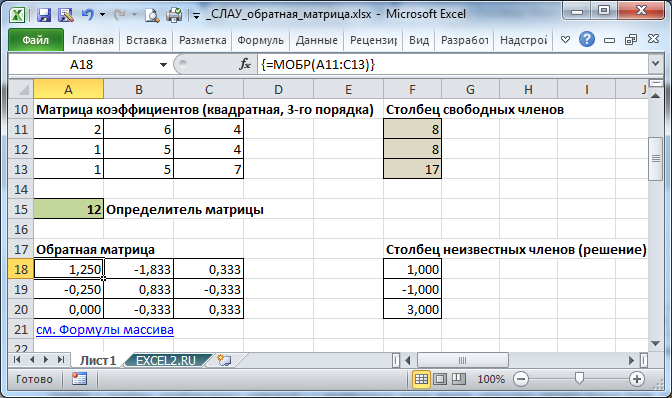
Решим Систему Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL. В этой статье нет теории, объяснено только как выполнить расчеты, используя MS EXCEL.
Решим систему из 3-х линейных алгебраических уравнений с помощью обратной матрицы (матричным методом).
Запишем в ячейки основную матрицу системы и столбец свободных членов.
Систему n линейных алгебраических уравнений с n неизвестными можно решать матричным методом только тогда, когда определитель основной матрицы системы отличен от нуля (в противном случае мы имеем линейно зависимые уравнения и соответственно решение систем не единственное). В нашем случае определитель =12.
Для этого выделите ячейки A18:C20 , а в Строке формул введите =МОБР(A11:C13) , затем нажмите CTRL+SHIFT+ENTER .
Решение системы уравнений получим умножением обратной матрицы и столбца свободных членов. Перемножить матрицы можно с помощью формулы массива =МУМНОЖ() .
Для этого выделите ячейки F18:F20 , а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13) , затем нажмите CTRL+SHIFT+ENTER .
В файле примера также приведено решение системы 4-х и 5-и уравнений.
Ваш браузер не поддерживается
Рнтернет-сервис Студворк построен РЅР° передовых, современных технологиях Рё РЅРµ поддерживает старые браузеры. Для просмотра сайта загрузите Рё установите любой РёР· следующих браузеров:
Решение систем уравнений в среде Microsoft Excel
обучающие:
- повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
- повторение алгоритма решения систем уравнений;
- формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;
развивающие:
- формирование умений анализировать, выделять главное, сравнивать, строить аналогии;
воспитывающие:
- осуществление эстетического воспитания;
- воспитание аккуратности, добросовестности.
Тип урока: урок закрепления изученного материала и объяснения нового.
ХОД УРОКА
I. Организационная часть.
Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!
Ответ: “Знание – сила!”
Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)
Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).
II. Повторение пройденного материала.
Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)
Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.
III. Объяснение нового.
А. Решим систему 

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.
Запишем алгоритм решения систем уравнений графическим способом:
1. Преобразовать систему уравнений, если это необходимо.
2. Задать начальные значения для Х.
3. Найти значение первой функции при заданных Х.
4. Найти значение второй функции при тех же Х.
5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.
6. Решение системы — точка пересечения графиков функций.
7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.
Б. Решить систему уравнений 
Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:
При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.
Запишем примерный алгоритм решения системы уравнений, используя Поиск решения
1. Преобразовать систему уравнений, если это необходимо
2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.
3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.
4. Выбрать команду Сервис – Поиск решения.
5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения
6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)
7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК
8. Решить систему уравнений, щелкнув кнопкой Выполнить
IV. Практическая работа на компьютере.
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
V. Подведение итогов.
Повторить алгоритмы решения систем уравнений
Выставить оценки за тестирование в журнал
VI. Домашнее задание.
Решить рациональным способом системы уравнений:

источники:
http://excel2.ru/articles/reshenie-sistemy-lineynyh-algebraicheskih-uravneniy-slau-metodom-obratnoy-matricy-v-ms-excel
http://studwork.org/spravochnik/informatika/excel/reshenie-slau-v-ms-excel
http://urok.1sept.ru/articles/510787

•данные по строке “Производственная прибыль” рассчитайте как разность между валовой прибылью и общими затратами;
•данные по строке “Удельная валовая прибыль” рассчитайте как результат деления производственной прибыли на торговые доходы;
•данные в колонке “Итого за год” рассчитайте суммированием квартальных данных.
8.Задайте для строки “Удельная валовая прибыль” Процентный формат, а для всех остальных строк – Формат с разделителями.
9.На строке 1 (при необходимости вставьте строку) введите заголовок, задав для него более крупный жирный шрифт и расположение по центру всей таблицы.
10.На листе с таблицей по данным Торговых расходов фирмы за первые три квартала постройте разрезанную круговую диаграмму (при выделении данных для построения диаграммы используйте и названия кварталов).
11.Добавьте на диаграмму данные по 4 кварталу.
12.По данным Валовой прибыли постройте гистограмму. Оформите заголовки и легенды диаграмм, расположите диаграммы рядом под таблицей.
13.Измените числовое значение за 4 квартал по Торговым расходам фирмы. Проследите зависимость графических данных в диаграммах от числовых в таблице.
14. На отдельном листе постройте нормированную гистограмму со столбцами в виде цилиндров по данным всей таблицы (исключая графу Итого за год).
Тема III. Основные правила работы со встроенными функциями
Встроенные в Excel функции призваны значительно облегчить работу пользователя, поскольку сокращают написание формул. Функции – подпрограммы, выполняющие вычисления и возвращающие единственное значение. Все функции имеют уникальные имена (идентификаторы). Функции имеют параметры, посредством которых передаются значения аргументов — исходных данных для вычислений. Синтаксис функции имеет вид:
ИМЯ_ФУНКЦИИ(список параметров)
Список параметров может задаваться адресными ссылками или ссылками посредством имен на ячейки или диапазоны, в виде имен функций, а также литералами, отделенными друг от друга символом ; (точка с запятой).
Примеры функций:
СУММ(А2:A10) – суммируются значения всех ячеек диапазона. СУММ(СуммаКредита) – суммируются значения всех ячеек диапазона с
именем СуммаКредита
СУММ(12; 10; 13) – суммируются значения, заданные списком числовых литералов.
Список параметров, заключенный в круглые скобки следует после имени функции безо всяких интервалов. Даже если список параметров пуст (как у функции СЕГОДНЯ() ), круглые скобки должны присутствовать.
Для задания функции используют следующие правила.
40

Прежде всего, следует установить курсор в ячейку, которая должна содержать результат выполнения функции. Далее можно выполнить одно из следующих действий:
•нажать клавиши <Shift>-<F3>;
•задать команду ФУНКЦИЯ из меню ВСТАВКА;
•нажать кнопку ВСТАВКА ФУНКЦИИ [fx] на стандартной панели.
Далее следует выбрать категорию функции и саму функцию в правой части окна Мастера функций. Для выполнения пошаговой подстановки аргументов с помощью Мастера функций нажать кнопку ОК. На следующих шагах следует указать адреса (имена) ячеек, значения которых будут использованы в качестве аргументов функции.
Примечание: При использовании в качестве аргумента вводимой функции другой какой-либо функции следует выбрать имя требуемой функции из списка функций в строке формул слева и произвести требуемые шаги Мастера функций. После завершения ввода аргументов вложенной функции щелкните указателем мыши в строке формул (в конце вводимой формулы).
1.1. Суммирование ячеек, удовлетворяющих определенному критерию
СУММЕСЛИ(ДИАПАЗОН;УСЛОВИЕ;ДИАПАЗОН_СУММИРОВАНИЯ) — группа
математических функций.
Функция предназначена для суммирования только ячеек, удовлетворяющих некому критерию.
•диапазон — это диапазон, в котором определяется критерий;
•условие — указывается в форме числа, выражения или текста;
•диапазон_суммирования — это диапазон суммируемых ячеек.
Пример III.1. В ячейки A1,A2,A3,A4,A5 введена информация:
A1=1000, A2=2000, A3=900, A4=800, A5=1500.
Требуется подсчитать сумму чисел, значение которых больше или равно 1000. Результат должен быть получен в ячейке А6. Пошаговыми действиями Мастера функций в ячейку А6 следует ввести формулу:
=СУММЕСЛИ (А1:А5;’’>=1000’’).
В ячейке А6 получится число 4500.
Измените значение ячейки А3 на любое большее 1000. Проследите изменение результата вычислений.
1.2. Подсчет количества значений в диапазоне
Для подсчета количества числовых значений в диапазоне:
СЧЕТ (ЗНАЧЕНИЕ1;ЗНАЧЕНИЕ2;…) — группа статистических функций.
Пример III.2. В ячейки В1,В2,В3,В4,В5 введена информация:
В1=’’Текст’’, В2=2000, В3= , В4=800, В5=1500.
Требуется подсчитать количество ячеек c числовыми значениями в диапазоне В1:В5. Результат должен быть получен в ячейке В6.
Пошаговыми действиями Мастера функций в ячейку В6 следует ввести формулу:
=СЧЕТ (В1:В5)
В ячейке В6 получится число 3.
Для подсчета количества всех значений в списке аргументов и непустых ячеек: СЧЕТЗ(ЗНАЧЕНИЕ1;ЗНАЧЕНИЕ2;…) — группа статистических функций.
41
Если эта функция будет введена в примере 2 в ячейку В7, то результат в ячейке В7 будет равен 4.
1.3. Подсчет количества пустых ячеек в диапазоне
СЧИТАТЬПУСТОТЫ(ДИАПАЗОН) — группа статистических функций.
Пример III.3. В ячейки С1,С2,С3,С4,С5 скопируйте информацию из соответствующих ячеек столбца А, оставив пустой ячейку С3:
С1=1000, С2=2000, С3= , С4=800, С5=1500.
Требуется подсчитать количество пустых ячеек в диапазоне С1:С5. Результат должен быть получен в ячейке С6.
Пошаговыми действиями Мастера функций в ячейку С6 следует ввести формулу:
=СЧИТАТЬПУСТОТЫ(С1:С5) .
Вячейке С6 получится число 1.
1.4.Подсчет количества непустых ячеек в диапазоне, удовлетворяющих
заданному условию
СЧЕТЕСЛИ(ДИАПАЗОН; УСЛОВИЕ) — группа статистических функций.
•диапазон — это диапазон, в котором определяется критерий;
•условие — указывается в виде числа, выражения или текста и определяет какие ячейки надо подсчитывать.
Пример III.4. Подсчитать количество непустых ячеек в диапазоне С1:С5, значение которых больше или равно 1000.
Результат должен быть получен в ячейке С7. Пошаговыми действиями Мастера функций в ячейку С7 следует ввести формулу:
=СЧЕТЕСЛИ(С1:С5;’’>=1000’’).
В ячейке С7 получится число 3.
Измените значение ячейки С1 на любое, меньшее 1000. Проследите изменение результата вычислений.
1.5. Расчет среднего значения
СРЗНАЧ(ДИАПАЗОН1; ДИАПАЗОН2;…) — группа статистических функций.
В текущую ячейку возвращается среднее значение для чисел указанного диапазона.
Пример III.5. В диапазоне ячеек A1:A5 из примера 1 определить среднее значение.
Результат должен быть получен в ячейке А7.
Пошаговыми действиями Мастера функций в ячейку А7 следует ввести формулу:
=СРЗНАЧ(А1:А5).
1.6. Определение максимального значения
МАКС(ДИАПАЗОН1; ДИАПАЗОН2;…) — группа статистических функций.
В текущую ячейку возвращается максимальное число из данного диапазона.
Пример III.6. В диапазоне ячеек A1:A5 из примера 1 определить максимальное значение.
Результат должен быть получен в ячейке А8.
Пошаговыми действиями Мастера функций в ячейку А8 следует ввести формулу:
=МАКС(А1:А5).
Вячейке А8 получится число 2000.
1.7.Определение минимального значения
МИН(ДИАПАЗОН1; ДИАПАЗОН2;…) — группа статистических функций.
42
В текущую ячейку возвращается минимальное число из данного диапазона.
Пример III.7. В диапазоне ячеек В1:В5 из примера 2 определить минимальное значение.
Результат должен быть получен в ячейке В8.
Пошаговыми действиями Мастера функций в ячейку В8 следует ввести формулу:
=МИН(В1:В5).
Вячейке В8 получится число 800.
1.8.Генерация случайного числа
СЛЧИС() — группа математических функций.
В текущую ячейку возвращается равномерно распределенное случайное число большее либо равное 0 и меньшее 1. Чтобы получить случайное вещественное число между a и b, можно использовать следующую формулу: СЛЧИС()*(b-a)+a.
Новое случайное число возвращается каждый раз, когда рабочий лист вычисляется повторно. Чтобы число, полученное случайным образом не менялось в дальнейшем, можно ввести =СЛЧИС() в строку формул и нажать F9.
Пример III.8. Для генерации случайного числа большего или равного 0, но меньшего 50 можно использовать формулу: СЛЧИС()*50.
Самостоятельно получите случайным образом последовательность чисел от 100 до 200.
1.9. Функции прогнозирования
ТЕНДЕНЦИЯ(ИЗВЕСТНЫЕ ЗНАЧЕНИЯ_Х; ИЗВЕСТНЫЕ ЗНАЧЕНИЯ_У; НОВОЕ
ЗНАЧЕНИЕ_У) — группа статистических функций В текущую ячейку возвращается новое значение_Х, рассчитанное на основании
известных значений.
Пример III.9. Ввести таблицу, начиная с ячейки G1:
Годы Цена
2000 450
2001 380
2002 600
2003
Результат прогнозирования должен быть получен в ячейке H5. Пошаговыми действиями Мастера функций в ячейку H5 вводим формулу:
=ТЕНДЕНЦИЯ (H2:H4;G2:G4;G5).
Вячейке H5 получится число 626.66671.
Самостоятельно рассчитайте тенденцию для 2004 и 2005 годов.
1.10. Определение ранга числа
РАНГ(АДРЕС ЯЧЕЙКИ; ДИАПАЗОН) — группа статистических функций.
В текущую ячейку возвращается величина, соответствующая положению (рангу) числа, заданного адресом ячейки, в указанном диапазоне.
Пример III.10. В ячейки D1,D2,D3,D4,D5 скопируйте информацию из соответствующих ячеек столбца А. Для каждой ячейки из диапазона D1:D5 определить ранг числа.
Результат должен быть получен в ячейках E1:E5. Функция ранга вводится сначала в ячейку E1, затем копируется для всех ячеек до E5.
Пошаговыми действиями Мастера функций в ячейку E1 вводим формулу:
1 Результат прогнозирования может быть получен и другим способом: выделить диапазон ячеек с известными значениями цен и растянуть этот диапазон за правый нижний угол на одну ячейку вниз.
43
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мы уже пользовались встроенными функциями СУММ и СЧЕТ, когда подсчитывали сумму значений в ячейках и количество ячеек с числами. Готовые функции значительно облегчают составление формул. Как увидеть доступные встроенные функции?
Щелкните мышью на значке fx. Появится окно, подобное представленному на рис. 3.6. В этом окне сначала выберите категорию, к которой относится нужная вам функция (если выберете не ту, ничего страшного, можно поискать и в других категориях), как показано на рис. 3.7. На этом рисунке выбрана категория Математические.
Рис. 3.6. Выбор функции
Рис. 3.7. Выбор категории
При этом отобразится список функций, входящих в выбранную категорию. Выберите нужную функцию и щелкните на ней мышью. Например, на рис. 3.8 выбрана функция КОРЕНЬ (она позволяет извлечь квадратный корень из указанного числа). Затем щелкните на кнопке OK.
Рис. 3.8. Выбор функции КОРЕНЬ
Для всех функций нужно указывать один или несколько аргументов. Аргумент — это значение, которое нужно указать функции, чтобы функция выполнила подсчет. В случае с функцией КОРЕНЬ аргументом является число, из которого нужно извлечь квадратный корень. Мы можем указать этот аргумент в виде числа или ввести адрес ячейки, из которой функция должна взять значение. Как только мы выберем нужную нам функцию и щелкнем мышью на кнопке OK, тут же откроется окно, показанное на рис. 3.9, где можно ввести требуемые аргументы.
Рис. 3.9. Ввод аргументов функции
Для случая, показанного на рис. 3.10, мы можем либо вручную ввести в поле Число адрес ячейки C4, откуда нужно брать число, либо щелкнуть мышью на ячейке C4 в таблице (тогда значение из ячейки C4 само подставится в поле Число). Бывают случаи, когда нужно для выбора ячейки щелкнуть на ней мышью, но большое окно с аргументами функции закрывает таблицу. В этом случае можно щелкнуть мышью на кнопке в правой части соответствующего поля (в которое требуется ввести значение). Окно с аргументами скроется, а на экране останется только небольшая панель с полем ввода и кнопкой , как показано на рис. 3.11.
Рис. 3.10. Выбор ячейки в качестве аргумента
Щелкайте мышью на нужной ячейке или ячейкам — их адреса будут появляться в поле ввода на панели. Когда закончите выбор, щелкните мышью на кнопке. В результате снова появится окно с аргументами функции, где нужное поле будет заполнено выбранными вами значениями.
Рис. 3.11. Панель аргументов функции
данные по строке “Производственная прибыль” рассчитайте как разность между валовой прибылью и общими затратами;
данные по строке “Удельная валовая прибыль” рассчитайте как результат деления производственной прибыли на торговые доходы;
данные в колонке “Итого за год” рассчитайте суммированием квартальных данных.
8.
Задайте для строки “Удельная валовая прибыль” Процентный формат, а для всех остальных строк – Формат с разделителями.
9.
На строке 1 (при необходимости вставьте строку) введите заголовок, задав для него более крупный жирный шрифт и расположение по центру всей таблицы.
10.На листе с таблицей по данным Торговых расходов фирмы за первые три квартала постройте разрезанную круговую диаграмму
(при выделении данных для построения диаграммы используйте и названия кварталов).
11.Добавьте на диаграмму данные по 4 кварталу.
12.По данным Валовой прибыли постройте гистограмму
. Оформите заголовки и легенды диаграмм, расположите диаграммы рядом под таблицей.
13.Измените числовое значение за 4 квартал по Торговым расходам фирмы. Проследите зависимость графических данных в диаграммах от числовых в таблице.
14. На отдельном листе
постройте нормированную гистограмму со столбцами в виде цилиндров по данным всей таблицы (исключая графу Итого за год).
Тема III. Основные правила работы со встроенными функциями
1. Использование встроенных функций Excel
Встроенные в Excel функции призваны значительно облегчить работу пользователя, поскольку сокращают написание формул. Функции –
подпрограммы, выполняющие вычисления и возвращающие единственное значение. Все функции имеют уникальные имена (идентификаторы). Функции имеют параметры, посредством которых передаются значения аргументов — исходных данных для вычислений. Синтаксис функции имеет вид:
ИМЯ_ФУНКЦИИ(список параметров)
Список параметров может задаваться адресными ссылками или ссылками посредством имен на ячейки или диапазоны, в виде имен функций, а также литералами, отделенными друг от друга символом ;
(точка с запятой).
Примеры функций:
СУММ(А2:A10) – суммируются значения всех ячеек диапазона. СУММ(СуммаКредита) – суммируются значения всех ячеек диапазона с
именем
СуммаКредита
СУММ(12; 10; 13) – суммируются значения, заданные списком числовых литералов.
Список параметров, заключенный в круглые скобки следует после имени функции
безо всяких интервалов. Даже если список параметров пуст (как у функции СЕГОДНЯ
()
), круглые скобки должны присутствовать.
Для задания функции используют следующие правила
.
Прежде всего, следует установить курсор в ячейку
, которая должна содержать результат выполнения функции
. Далее можно выполнить одно из следующих действий:
нажать клавиши
-;
задать команду
ФУНКЦИЯ
из меню ВСТАВКА
;
нажать кнопку
ВСТАВКА ФУНКЦИИ
[
f
x
]
на стандартной панели.
Далее следует выбрать категорию функции
и саму функцию
в правой части окна Мастера функций. Для выполнения пошаговой подстановки аргументов с помощью Мастера функций нажать кнопку ОК
.
На следующих шагах следует указать адреса (имена) ячеек, значения которых будут использованы в качестве аргументов функции.
Примечание
: При использовании
в качестве аргумента
вводимой функции другой
какой-либо
функции
следует выбрать имя требуемой функции из списка функций в строке формул слева и произвести требуемые шаги Мастера функций. После завершения ввода аргументов
вложенной функции щелкните указателем мыши в строке формул (в конце вводимой формулы).
1.1. Суммирование ячеек, удовлетворяющих определенному критерию
СУММЕСЛИ(ДИАПАЗОН;
УСЛОВИЕ;
ДИАПАЗОН_
СУММИРОВАНИЯ)
— группа
математических функций.
Функция предназначена для суммирования только ячеек, удовлетворяющих некому критерию.
условие — указывается в форме числа, выражения или текста;
диапазон_суммирования — это диапазон суммируемых ячеек.
Пример III.1.
В ячейки A1,A2,A3,A4,A5 введена информация:
A1=1000, A2=2000, A3=900, A4=800, A5=1500.
СУММЕСЛИ
(А1:А5;’’>=1000’’).
В ячейке А6 получится число 4500.
Измените значение ячейки А3 на любое большее 1000. Проследите изменение результата вычислений.
1.2. Подсчет количества значений в диапазоне
Для подсчета количества числовых
значений в диапазоне:
СЧЕТ
(ЗНАЧЕНИЕ
1;
ЗНАЧЕНИЕ
2;…)
— группа статистических функций.
Пример III.2.
В ячейки В1,В2,В3,В4,В5 введена информация:
В1=’’Текст’’, В2=2000, В3= , В4=800, В5=1500.
Пошаговыми действиями Мастера функций
в ячейку В6 следует ввести формулу:
СЧЕТ
(В1:В5)
В ячейке В6 получится число 3.
Для подсчета количества всех значений
в списке аргументов и непустых ячеек: СЧЕТЗ
(ЗНАЧЕНИЕ
1;
ЗНАЧЕНИЕ
2;…)
— группа статистических функций.
Если эта функция будет введена в примере 2
в ячейку В7, то результат в ячейке В7 будет равен 4.
1.3. Подсчет количества пустых ячеек в диапазоне
Пример III.3.
В ячейки С1,С2,С3,С4,С5 скопируйте информацию из соответствующих ячеек столбца А, оставив пустой ячейку С3:
С1=1000, С2=2000, С3= , С4=800, С5=1500.
Пошаговыми действиями Мастера функций
в ячейку С6 следует ввести формулу:
В
ячейке С6 получится число 1.
1.4.
Подсчет количества непустых ячеек в диапазоне, удовлетворяющих
заданному условию
СЧЕТЕСЛИ
(ДИАПАЗОН
;
УСЛОВИЕ
)
— группа статистических функций.
диапазон — это диапазон, в котором определяется критерий;
условие — указывается в виде числа, выражения или текста и определяет какие ячейки надо подсчитывать.
Результат должен быть получен в ячейке С7. Пошаговыми действиями Мастера функций
в ячейку С7 следует ввести формулу:
СЧЕТЕСЛИ
(С1:С5;’’>=1000’’).
В ячейке С7 получится число 3.
Измените значение ячейки С1 на любое, меньшее 1000. Проследите изменение результата вычислений.
1.5. Расчет среднего значения
СРЗНАЧ
(ДИАПАЗОН
1;
ДИАПАЗОН
2;…)
— группа статистических функций.
В текущую ячейку возвращается среднее значение для чисел указанного диапазона.
Пример III.5.
В диапазоне ячеек A1:A5 из примера 1
определить среднее значение.
Результат должен быть получен в ячейке А7.
Пошаговыми действиями Мастера функций
в ячейку А7 следует ввести формулу:
СРЗНАЧ
(А1:А5).
1.6. Определение максимального значения
МАКС
(ДИАПАЗОН
1;
ДИАПАЗОН
2;…)
— группа статистических функций.
В текущую ячейку возвращается максимальное число из данного диапазона.
Пример III.6.
В диапазоне ячеек A1:A5 из примера 1
определить максимальное значение.
Результат должен быть получен в ячейке А8.
Пошаговыми действиями Мастера функций
в ячейку А8 следует ввести формулу:
МАКС
(А1:А5).
В
ячейке А8 получится число 2000.
1.7.
Определение минимального значения
МИН
(ДИАПАЗОН
1;
ДИАПАЗОН
2;…)
— группа статистических функций.
В текущую ячейку возвращается минимальное число из данного диапазона.
Пример III.7.
В диапазоне ячеек В1:В5 из примера 2
определить минимальное значение.
Результат должен быть получен в ячейке В8.
Пошаговыми действиями Мастера функций
в ячейку В8 следует ввести формулу:
МИН
(В1:В5).
В
ячейке В8 получится число 800.
1.8.
Генерация случайного числа
СЛЧИС
()
— группа математических функций.
В текущую ячейку возвращается равномерно распределенное случайное число большее либо равное 0 и меньшее 1. Чтобы получить случайное вещественное число между a и b, можно использовать следующую формулу: СЛЧИС()*(b-a)+a.
Новое случайное число возвращается каждый раз, когда рабочий лист вычисляется повторно. Чтобы число, полученное случайным образом не менялось в дальнейшем, можно ввести =СЛЧИС() в строку формул и нажать F9.
Пример III.8.
Для генерации случайного числа большего или равного 0, но меньшего 50 можно использовать формулу: СЛЧИС()*50.
Самостоятельно получите случайным образом последовательность чисел от 100 до 200.
1.9. Функции прогнозирования
ТЕНДЕНЦИЯ(ИЗВЕСТНЫЕ ЗНАЧЕНИЯ_
Х;
ИЗВЕСТНЫЕ ЗНАЧЕНИЯ_
У;
НОВОЕ
ЗНАЧЕНИЕ
_
У
) —
группа статистических функций В текущую ячейку возвращается новое значение_Х, рассчитанное на основании
известных значений.
Пример III.9.
Ввести таблицу, начиная с ячейки G1:
Годы Цена
Результат прогнозирования должен быть получен в ячейке H5. Пошаговыми действиями Мастера функций
в ячейку H5 вводим формулу:
ТЕНДЕНЦИЯ
(H2:H4;G2:G4;G5).
В
ячейке H5 получится число 626.6667
1
.
Самостоятельно рассчитайте тенденцию для 2004 и 2005 годов.
1.10. Определение ранга числа
РАНГ
(АДРЕС ЯЧЕЙКИ
;
ДИАПАЗОН
)
— группа статистических функций.
В текущую ячейку возвращается величина, соответствующая положению (рангу) числа, заданного адресом ячейки, в указанном диапазоне.
Пример III.10.
В ячейки D1,D2,D3,D4,D5 скопируйте информацию из соответствующих ячеек столбца А. Для каждой ячейки из диапазона D1:D5 определить ранг числа.
Результат должен быть получен в ячейках E1:E5. Функция ранга вводится сначала в ячейку E1, затем копируется для всех ячеек до E5.
Пошаговыми действиями Мастера функций
в ячейку E1 вводим формулу:
1
Результат прогнозирования может быть получен и другим способом: выделить диапазон ячеек с известными значениями цен и растянуть этот диапазон за правый нижний угол на одну ячейку вниз.
Встроенные функции
|
Наименование параметра |
Значение |
| Тема статьи: | Встроенные функции |
|
Рубрика (тематическая категория) |
Программирование |
Типы данных
Современные СУБД позволяют обрабатывать данные разнообразных типов, среди которых наиболее распространенными можно назвать следующие.
Целые числа (INT, SMALLINT). В столбцах, имеющих такой тип данных, обычно хранятся данные о количестве и возрасте сотрудников, идентификаторы.
Десятичные числа (NUMERIC, DECIMAL). В столбцах данного типа хранятся числа, имеющие дробную часть с фиксированным количеством знаков после запятой, к примеру, курсы валют и проценты.
Числа с плавающей запятой (REAL, FLOAT). Числа с плавающей запятой представляют больший диапазон действительных значений, чем десятичные числа.
Строки символов постоянной длины (CHAR). В столбцах, имеющих данный тип данных, хранятся имена и фамилии, географические названия, адреса и т.п.
Строки символов переменной длины (VARCHAR). Столбцы этого типа позволяют хранить символьные строки, длина которых изменяется в заданном диапазоне.
Денежные величины (MONEY, SMALLMONEY). Наличие отдельного типа данных для хранения денежных величин позволяет правильно форматировать их и снабжать признаком валюты перед выводом на экран.
Дата и время (DATATIME, SMALLDATETIME). Поддержка особого типа данных для значений дата/время широко распространена в различных СУБД. Как правило, с этим типом данных связаны особые операции и процедуры обработки.
Булевы величины (BIT). Столбцы такого типа данных позволяют хранить логические значения True (1) и False (0).
Длинный текст (TEXT). Многие СУБД поддерживают хранение в столбцах текстовых строк длиной до 32 КБ или 64 КБ символов, а в некоторых случаях и больше. Это позволяет хранить в базе данных целые документы.
Неструктурированные потоки битов (BINARY, VARBINARY, IMAGE). Такой тип данных позволяет хранить графические файлы и видеоизображения, исполняемые файлы и другие неструктурированные данные.
Встроенные функции, доступные при работе при работе с SQL, можно разделить на следующие группы:
§ математические функции;
§ строковые функции;
§ функции для работы с величинами типа дата-время;
§ функции конфигурирования;
§ системные функции:
§ функции системы безопасности;
§ функции управления метаданными;
§ статистические функции.
| ФУНКЦИЯ | НАЗНАЧЕНИЕ |
| ABS(число) | Вычисляет абсолютную величину числа |
| ISNUMERIC(выражение) | Определяет, имеет ли выражение числовой тип данных |
| SING(число) | Определяет знак числа |
| RAND(целое число) | Вычисляет случайное число с плавающей запятой в интервале от 0 до 1 |
| ROUND(число, точность) | Выполняет округление числа с указанной точностью |
| POWER(число, степень) | Возводит число в степень |
| SQRT(число) | Извлекает квадратный корень из числа |
| SIN(число) | Вычисляет синус угла, указанного в радианах |
| COS(число) | Вычисляет косинус угла, указанного в радианах |
| EXP(число) | Вычисляет экспоненту числа |
| LOG(число) | Вычисляет натуральный логарифм |
| LEN(строка) | Вычисляет длину строки в символах |
| LTRIM(строка) | Удаляет пробелы в начале строки |
| RTRIM(строка) | Удаляет пробелы в конце строки |
| LEFT(строка, количество) | Возвращает указанное количество символов строки, начиная с самого левого символа |
| RIGHT(строка, количество) | Возвращает указанное количество символов строки, начиная с самого правого символа |
| LOWER(строка) | Приводит символы строки к нижнему регистру |
| UPPER(строка) | Приводит символы строки к верхнему регистру |
| STR(число) | Выполняет конвертирование числового значения в символьный формат |
| SUBSTRING(строка, индекс, длина) | Возвращает для строки подстроку заданной длины, начиная с символа заданного индекса |
| GETDATE | Возвращает текущую системную дату |
| ISDATE(строка) | Проверяет строку на соответствие одному из форматов даты и времени |
| DAY(дата) | Возвращает число указанной даты |
| MONTH(дата) | Возвращает месяц указанной даты |
| YEAR(дата) | Возвращает год указанной даты |
| DATEADD(тип, число, дата) | Прибавляет к дате указанное число единиц заданного типа (год, месяц, день, час и т.п.) |
Встроенные функции — понятие и виды. Классификация и особенности категории «Встроенные функции» 2017, 2018.
Приоритет операций
При вычислении значений выражений следует учитывать, что операторы имеют разный приоритет.
В Object Pascal определены следующие операции:
Ø унарные not, @ ;
Ø мультипликативные *, /, div, mod, and, shi, shr;
Ø аддитивные +, -, or, xor;
Ø отношения =,… .
Встроенные функции — это основной набор функций, который поставляется вместе с MathCad. Сюда относятся функции sin(x), cos(x), ln(x) и т.д. Их список можно просмотреть в окне «Choose Function» после выбора команды меню Math/Choose Function (Математика/Выбор функции).
Для вставки встроенной функции… .
Функции – это специальные, заранее созданные формулы, которые позволяют легко и быстро выполнять сложные вычисления. Microsoft Excel имеет более 300 встроенных функций, которые выполняют широкий спектр различных вычислений.
Полное описание всех функций изложено в справочной… .
Excel используется как делопроизводителями, например, для оформления сложных по структуре таблиц без вычислений, так и экономистами, финансистами для ведения учета или табличных расчетов со сложными формулами. Такие формулы включены в справочник функций. Всем, кто хочет научиться делать оптимальный выбор функции и правильно указывать ее параметры, адресована эта статья.
Поскольку функций в Excel более 300, их выбор является сложной задачей. Для облегчения работы программистами Microsoft создан Мастер функций. Его можно вызвать кнопкойfx
, расположенной на одном уровне со строкой ввода данных, или одновременным нажатием клавиш SHIFT
и F
3
. В нем пользователю предлагается сузить область поиска за счет выбора категории, затем выбрать из списка функций, упорядоченных по алфавиту и относящихся именно к этой категории. При выборе имени функции внизу окна появляется подсказка о том, что она вычисляет (возвращает).
Остается только указать аргумент в окне функции (лучше это делать щелчком мыши, так как при вводе вручную необходимо следить, чтобы был включен английский язык, при использовании русского результатом будет сообщение об ошибке).
Кажется, все просто, но есть нюансы. Рассмотрим их на примерах. Во-первых, у функции может не быть аргументов. Пример на рисунке.
Во-вторых, аргументом не обязательно должна быть одна ячейка. Например, необходимо подсчитать среднее для нескольких чисел. Тогда:
вызовите Мастер функций
;
среди функций выберите СРЗНАЧ
;
выделите все ячейки, среди которых определяется среднее значение (обратите внимание, что в поле они оказались перечисленными через двоеточие);
подтвердите действия кнопкой ОК
.
Кстати, если вы знаете имя функции и правила указания аргументов, то часто удобнее вводить все вручную (без Мастера функций), особенно при использовании вложенных функций.
В-третьих, аргументов может быть больше одного. Можно рассмотреть пример перемножения двух массивов:
щелкните по ячейке с будущим результатом;
вызовите Мастер функций
;
из имен функций выберите СУММПРОИЗВ
;
для поля первого массива укажите мышкой ячейки с числовыми значениями первой таблицы, для поля второго массива — ячейки с числовыми значениями второй таблицы (обратите внимание на то, что в строке ввода аргументы разделены точкой с запятой);
подтвердите действия кнопкой ОК
.
В-четвертых, не всегда вставка функции подтверждается клавишей ENTER. Некоторые функции являются блочными. Например, нужно определить место каждого спортсмена в соревновании, то есть ранжировать их результаты:
выделите все ячейки, в которых должны отобразиться места;
вызовите Мастер функций
;
из имен функций выберите РАНГ.РВ
;
подтвердите свои действия нажатием клавиш CTRL
,
SHIFT
и ENTER
одновременно (после этого формула в строке ввода данных будет заключена в фигурные скобки).
Использование встроенных функций, предусмотренное всеми версиями Excel, позволит вам заметно повысить эффективность работы, а сведения из этой статьи обеспечат безошибочное указание аргументов.
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
КУРСОВАЯ РАБОТА
по дисциплине «Информатика»
Введение
С каждым годом резко сокращается число предприятий и организаций, не имеющих компьютерной базы. Современные руководители, менеджеры и экономисты уже не представляют, как можно выполнять работу, не имея в своем распоряжении пакета офисных программ, электронной почты и Интернета. И это не случайно. Ведь в условиях конкуренции только эффективное ведение бизнеса позволяет выжить на рынке и добиться успеха.
Одной из таких необходимых и труднозаменимых программ является офисная программа MS Excel.
MS Excel имеет много функциональных возможностей. На ней можно создавать как простейшей таблицы, например таблицы умножения, так и разрабатывать более сложные, в которых производится расчет НДС, простых и сложных процентов по вкладу, генерируется написание дат и сумм прописью. MS Excel помогает формировать и анализировать различные списки (например, с данными о сотрудниках, должностных окладах и т. д.), а также выполнять с их элементами разные операции: изменять должностные оклады, начислять премии, рассчитывать выплаты, связанные с временной нетрудоспособностью. Знание приемов работы со списками позволит проводить маркетинговые исследования, в частности анализировать объемы продаж товаров как отдельным клиентам, так и по регионам.
Но в своей курсовой работе я рассмотрю встроенные функции MS Excel. Эти функции помогают легко и быстро заполнять таблицы. Расскажу о возможностях каждой категории этих функций.
В практической части я решу ряд задач: создам и заполню таблицы, наглядно продемонстрирую действие одной из встроенных функций MS Excel, построю график.
Курсовая работа выполнена с использованием офисных программ MS Word 2003 и MS Excel 2003.
Теоретическая часть
Excel, как и любая электронная таблица, представляет собой инструмент для вычислений. Каждая ячейка в Excel может содержать данные одного из трех типов: текст, число или формула.
Формула
— выражение, состоящее из операндов, которое используется для выполнения вычислений над имеющимися данными. Каждая формула начинается с символа «равно» (=). В качестве операндов могут быть: числа, логические значения, ссылки на адреса ячеек (диапазон ячеек), встроенные функции, которые соединяются с помощью символов операций — сложения, вычитания, умножения.
Excel выполняет вычисления последовательно, но некоторые операции имеют более высокий приоритет и выполняются раньше других:
1. Возведение в степень и выражения в круглых скобках.
2. Умножение и деление.
3. Сложение и вычитание.
Ввод формул
Адрес ячейки можно включить в формулу одним щелчком мыши. Например, вместо того, чтобы «вручную» набирать =C6+C7+…, можно сделать следующее:
§ ввести «=»;
§ щелкнуть мышью на ячейке C6 (ее адрес появится в формуле);
§ ввести «+»;
§ щелкнуть на C7 и т. д.
Копирование формул
В учебной задаче мы вставляли суммы отдельно в каждую ячейку по строке 10 и по столбцу F. Однако Excel позволяет скопировать готовую формулу в смежные ячейки; при этом адреса ячеек будут изменены автоматически.
Выделите ячейку С10. Установите указатель мыши на черный квадратик в правом нижнем углу курсорной рамки (указатель примет форму черного крестика). Нажмите левую кнопку и смещайте указатель вправо по горизонтали, — так, чтобы смежные ячейки D10 и E10 были выделены пунктирной рамкой. Отпустите кнопку мыши.
Копировать формулу, записанную в выделенной ячейке, можно только по горизонтали или вертикали. При этом:
§ при копировании влево (вправо) по горизонтали смещение на одну ячейку уменьшает (увеличивает) каждый номер столбца в формуле на единицу.
§ при копировании вверх (вниз) по вертикали смещение на одну ячейку уменьшает (увеличивает) каждый номер строки в формуле на единицу.
Этим же способом можно копировать в смежные ячейки числа и тексты.
Абсолютные адреса
Чтобы запретить программе Excel механически изменять адрес ячейки, достаточно перед номером столбца и номером строки записать символ «$», т.е. вместо относительного указать абсолютный адрес (например, $F$10). Знак «$», указанный перед номером столбца, означает, что этот номер не будет изменяться при операциях копирования формул, вставки и удаления строк и столбцов. Знак «$», указанный перед номером строки, означает, что этот номер не будет изменяться при операциях копирования формул, вставки и удаления строк и столбцов.
Для быстрого изменения типа адресации используется функциональная клавиша F4.
Вместо абсолютной адресации мы можем воспользоваться именем ячейки. Например, если присвоить ячейке F10 имя Всего, вместо адреса F$10 можно указать: Всего.
При присвоении имен нужно учитывать следующее:
§ имена должны состоять из букв, цифр, точек и символов подчеркивания;
§ пробелы не допускаются;
§ прописные и строчные буквы воспринимаются одинаково;
§ можно использовать как латинский, так и русский регистр.
Пример применения абсолютной адресации — задача расчета заработной платы, где при расчете суммы налога применяется абсолютная ссылка на ячейку со ставкой налогообложения.
Проценты
В столбце G мы записали формулы для расчета долей округов города в общей сумме выручки. Очень часто нам необходимо показать эти доли в процентах (т. е. просто умножить каждую долю на 100). Excel позволяет сделать это одним щелчком мыши.
Выделите столбец G и щелкните мышью на кнопке панели «Форматирование» с изображением %. Все доли будут умножены на 100 и помечены знаком «%».
Возможности Excel позволяют создавать сложные формулы. Но длинная мощь Excel как программного средства реализуется через широкий набор встроенных функций, предназначенных для выполнения различных вычислительных и логических процедур.
Функция
В общем случае — это переменная величина, значение которой зависит от значений других величин (аргументов). Функция имеет имя (например, КОРЕНЬ) и, как правило, аргументы, которые записываются в круглых скобках следом за именем функции. Скобки — обязательная принадлежность функции, даже если у нее нет аргументов. Если аргументов несколько, один аргумент отделяется от другого запятой. В качестве аргументов функции могут использоваться числа, адреса ячеек, диапазоны ячеек, арифметические выражения и функции. Смысл и порядок следования аргументов однозначно определен описанием функции, составленным ее автором. Например, если в ячейке G6 записана формула с функцией возведения в степень =СТЕПЕНЬ(A4,2.3), значением этой ячейки будет значение A4, возведенное в степень 2.3.
В процессе конструирования выражений, содержащих формулы, существенную помощь пользователю оказывает Мастер функций. Вызов Мастера функций осуществляется либо из меню Вставка —> Функции, либо с помощью одноименной кнопки на панели инструментов Стандартная. Далее в появившемся окне диалога необходимо выбрать категорию функций и далее — нужную функцию из категории (рис. 1). Использование окна Мастер функций оказывает помощь при задании аргументов функций. В качестве аргументов функции могут использоваться другие функции и адреса ячеек.
Рис. 1.Мастер функций
Работая с функциями, помните:
1. функция, записанная в формуле, как правило, возвращает уникальное значение: арифметическое, символьное или логическое;
2. существуют функции, которые не возвращают значение, а выполняют некоторые операции (например, объединяют текстовые строки);
3. существуют функции без аргументов (например, функция ПИ() возвращает число П = 3.1415…).
В программе Excel можно использовать свыше400 функций, которые разделены на категории (тематические группы): математические, финансовые, статистические, ссылки и массивы, работа с базой данных, текстовые, логические, дата и временя, проверка свойств и значений.
Для того, чтобы воспользоваться перечисленными или другими функциями Excel, вам необязательно читать толстые книги по этому продукту. Полное описание всех функций имеется в справочной системе Excel. Правда, к справочной системе Excel следует относиться критически: в ней имеются неточности и даже ошибки (особенно в описании логических операций).
Теперь рассмотрим, что представляет из себя каждая из этих категорий.
Финансовые функции
По типу решаемых задач финансовые функции Excel делятся на следующие условные группы:
* для анализа аннуитетов и инвестиционных проектов;
* для анализа ценных бумаг;
* для расчета амортизационных платежей;
* вспомогательные.
Функции каждой группы имеют практически одинаковый набор обязательных и дополнительных (необязательных) аргументов.
Например, функция ДДОБ (рис. 2).
ДДОБ(нач_стоимость,ост_стоимость,время_эксплуатации,период,
коэфициент)
Результат: Величина амортизации имущества для указанного периода при использовании метода двухкратного учета амортизации или иного явно указанного метода.
Аргументы:
нач_стоимость — начальная стоимость имущества;
ост_стоимость — остаточная стоимость имущества;
время_эксплуатации — количество периодов, охватывающих промежуток времени, в течение которого имущество амортизируется (период амортизации);
период — период, для которого требуется вычислить амортизацию (аргументы период и время_эксплуатации должны быть выражены в одинаковых единицах измерения);
коэффициент — норма снижения балансовой стоимости (амортизации); если коэффициент опущен, то предполагается, что он равен 2 (метод двухкратного учета амортизации).
Все пять аргументов должны принимать только положительные значения.
Рис. 2. Диалоговое окно ввода аргументов функции ДДОБ
Текстовые функции
Большое количество функций предназначено для обработки текстов. С помощью этих функций пользователь может преобразовывать прописные литеры в строчные, текстовые значения в числовые и обратно, а также выполнять целый ряд других операций. В качестве аргументов текстовых функций используются, как правило, цепочки символов.
Например, функция ДЛСТР
ДЛСТР(текст)
Результат: Количество символов в текстовом аргументе текст.
Аргументы:
текст — текст, длину которого нужно определить. При вычислении длины текста учитываются пробелы.
Логические функции
Логические выражения используются для записи условий, в которых сравниваются числа, функции, формулы, текстовые или логические значения. Любое логическое выражение должно содержать, по крайней мере, один оператор сравнения, который определяет отношение между элементами логического выражения.
Результатом логического выражения является логическое значение ИСТИНА (1) или логическое значение ЛОЖЬ (0).
Например, функция ИЛИ
ИЛИ(логическое_значение1,логическое значение2,…)
Результат: Возвращает значение ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА; возвращает значение ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ.
Аргументы:
логическое_значение1, логическое_значение2,… — от 1 до 30 проверяемых условий, которые могут иметь значение либо ИСТИНА, либо ЛОЖЬ. Можно использовать функцию ИЛИ как формулу массива, чтобы проверить, имеются ли значения в массиве. Для того чтобы ввести функцию ИЛИ как формулу массива, нажмите клавиши .
Статистические функции
Применение статистических функций облегчает пользователю статистический анализ данных. Количество доступных статистических функций в седьмой версии программы увеличилось, и можно утверждать, что по спектру доступных функций Excel сегодня почти не уступает специальным программам обработки статистических данных. Для того чтобы иметь возможность использовать все статистические функции, следует загрузить надстройку Пакет анализа.
Основу статистического анализа составляет исследование совокупностей и выборок. Выборка представляет собой подмножество совокупности. В качестве примера выборки можно привести опросы общественного мнения. Исследуя выборки с помощью вычисления отклонений и отслеживания взаимосвязей с генеральной совокупностью, можно проследить, насколько репрезентативна выборка.
Целый ряд статистических функций Excel предназначен для анализа вероятностей.
Например, функция ДИСП
ДИСП(число1,число2, …)
Результат: Дисперсия выборки. Аргументы рассматриваются как выборка из генеральной совокупности.
Аргументы:
число1, число2,… — не более 30 аргументов; текстовые, логические и пустые поля приводят к ошибке.
Математические функции
Среди функций рабочего листа одну из наиболее многочисленных категорий образуют математические функции. Применение этих функций позволяет значительно ускорить и упростить процесс вычислений. В качестве аргументов математических функций выступают, как правило, числовые значения.
Например, функция КОРЕНЬ
КОРЕНЬ(число)
Результат: Корень квадратный числа.
Аргументы:
число — число, для которого вычисляется квадратный корень (если число отрицательное, то функция КОРЕНЬ возвращает значение ошибки #ЧИСЛО!).
Ф
ункции этой категории используются в первую очередь при работе со ссылками. Сюда относится определение адресов ячеек, размеров диапазонов ячеек и т. п.
Например, функция ВПР
ВПР(искомое_значение,инфо_таблица,номер_столбца,интервальный
Просмотр)
Результат: В матрице инфо_таблица ищется строка, первая колонка которой содержит величину искомое_значение. В найденной строке из колонки номер_столбца извлекается значение и возвращается функцией.
Аргументы:
искомое_значение — задает значение, которое функция ищет в первой колонке матрицы (если это значение не будет найдено, будет взято ближайшее меньшее; если меньшего не существует, возникнет ошибка #Н/Д);
инфо_таблица — таблица, содержащая искомые данные;
номер_столбца — колонка в найденной строке, из которой должно быть взято значение;
интервальный_просмотр — логическое значение, которое определяет характер поиска: точное или приближенное соответствие. Если этот аргумент имеет значение ИСТИНА или опущен, то возвращается приблизительно соответствующее значение. Если этот аргумент имеет значение ЛОЖЬ, то функция ВПР ищет точное соответствие. Если таковое не найдено, то возвращается значение ошибки #Н/Д.
Дата и время
Excel хранит дату в виде последовательных чисел (сериальных чисел), а время в виде десятичной части этого значения (время является частью даты). Значения даты и времени представляются числами, поэтому их можно использовать в вычислениях. Например, чтобы определить длительность промежутка времени, можно вычесть из конечного начальный момент времени. При использовании основного формата для ячеек, содержащих дату и время, можно отобразить дату в виде числа или время в виде дробной части числа с десятичной точкой.
Например, функция ВРЕМЯ
ВРЕМЯ(часы,минуты,секунды)
Результат: Значение времени в числовом формате, соответствующее введенным аргументам. Это десятичная дробь в интервале от 0 до 0,99999999, представляющая время суток от 0:00:00 (12:00:00 ночи) до 23:59:59 (11:59:59 вечера).
Аргументы:
часы — число от 1 до 24 (количество часов);
минуты — число от 1 до 59 (количество минут);
секунды — число от 1 до 59 (количество секунд).
Проверка свойств и значений
В рабочих листах эти функции используются главным образом вместе с функцией ЕСЛИ в случае, если результаты вычислений зависят от содержимого ячейки. Девять функций этой категории используются для проверки типа значения или ссылки. Каждая из этих функций проверяет тип значения и возвращает значение ИСТИНА или ЛОЖЬ.
Например, функция ЕПУСТО
ЕПУСТО(значение)
Результат: Возвращает значение ИСТИНА в случае, если значение ссылается на пустую ячейку.
Аргументы:
значение — проверяемое значение. (Значение может быть пустой ячейкой, значением ошибки, логическим значением, текстом, числом, ссылкой или именем объекта любого из перечисленных типов.)
Работа с базой данных
Наряду с возможностями использования автофильтров для управления базами данных и списками Excel дополнительно предлагает пользователю функции, с помощью которых можно, например, выполнить статистический анализ данных в базе данных.
Например, функция БДДИСП
БДДИСП(база_данных,поле,критерий)
Результат: Дисперсия [рассеяние] генеральной совокупности, определенная путем оценки выборки относительно всех выбранных значений.
Аргументы:
база_данных — интервал ячеек, формирующих базу данных;
поле — аргумент типа Text, который должен содержать имя столбца (поля) базы данных;
критерий — интервал ячеек, который содержит критерий поиска.
электронный таблица функция формула
Практическая часть
1. Запустить табличный процессор MS Excel.
2. Создать книгу с именем «Летучий голландец».
3. Лист 1 переименовать в лист с названием .
4. На рабочем листе Сведения о выполненных маршрутах
MS Excel создать таблицу данных о выполненных маршрутах.
5. Заполнить таблицу данных о выполненных маршрутах исходными данными (рис. 1)
Рис. 1. Таблица «Данные о выполненных маршрутах»
6. Лист 2 переименовать в лист с названием Автомобили
.
7. На рабочем листе Автомобили
MS Excel создать таблицу, в которой будут содержаться технические характеристики автомобилей.
8. Заполнить таблицу с техническими характеристиками автомобилей исходными данными (рис. 2).
Рис. 2. Таблица «Технические характеристики автомобилей»
9. Лист 3 переименовать в лист с названием Рейсы
.
10. На рабочем листе Рейсы
MS Excel создать таблицу, в которой будут содержаться данные о протяженности рейсов.
11. Заполнить таблицу «Протяженность рейса»
исходными данными (рис. 3).
Рис. 3. Таблица «Протяженность рейсов»
12. Выделить ячейки
A2:C5 в таблице «Протяженность рейсов
», находящейся на листе Рейсы
, и присвоить им имя Рейсы
.
13. Заполнить графу Протяженность рейса
таблицы «», находящейся на листе Сведения о выполненных маршрутах
следующим образом:
Занести в ячейку F2 формулу:
ВПР(D2;Рейсы;2;1).
Размножить введенную в ячейку F2 формулу для остальных ячеек (с F3 по F8) данной графы (Рис. 4).
Рис. 4. Заполнение графы Протяженность рейса
14. Выделить ячейки B2:C4 в таблице «Технические характеристики автомобилей», находящейся на листе Автомобили
, и присвоить им имя Автомобили
.
15. Заполнить графу Расход топлива на 100 км
таблицы «Данные о выполненных маршрутах
», находящейся на листе Сведения о выполненных маршрутах
следующим образом:
Занести в ячейку G2 формулу:
ВПР(C2;Автомобили;2;1).
Размножить введенную в ячейку G2 формулу для остальных ячеек данной графы (с G3 по G8) (рис. 5).
Рис. 5. Заполнение графы Расход топлива на 100 км
16. Заполнить графу Израсходовано топлива
таблицы «Данные о выполненных маршрутах
», находящейся на листе Сведения о выполненных маршрутах
следующим образом:
Занести в ячейку H2 формулу:
=(G2/100)*(E2*F2).
Размножить введенную в ячейку H2 формулу для остальных ячеек (с H3 по H8) (рис. 6).
17. Заполнить графу Грузоподъемность
таблицы «Данные о выполненных маршрутах
», находящейся на листе Сведения о выполненных маршрутах
следующим образом:
Рис. 6. Заполнение графы Израсходовано топлива
Занести в ячейку I2 формулу:
ВПР(C2;Автомобили;3;1).
Размножить введенную в ячейку I2 формулу для остальных ячеек (с I3 по I8) (рис. 7).
Рис. 7. Заполнение графы Грузоподъемность
18. Заполнить графу
Вес перевезенного груза
таблицы «Данные о выполненных маршрутах
», находящейся на листе Сведения о выполненных маршрутах
следующим образом:
Занести в ячейку J2 формулу:
Размножить введенную в ячейку J2 формулу для остальных ячеек (с J3 по J8) (рис. 8).
Рис. 8. Заполнение графы Вес перевезенного груза
19. Заполним графу ИТОГО
таблицы «Данные о выполненных маршрутах
», находящейся на листе Сведения о выполненных маршрутах
следующим образом:
Занести в ячейку F9 формулу:
СУММ(F2:F8).
Размножить введенную в ячейку F9 формулу для остальных ячеек (с G9 по J9) (рис. 9).
Рис. 9. Заполнение графы ИТОГО
20. Заполним графу В СРЕДНЕМ
таблицы «Данные о выполненных маршрутах
», находящейся на листе Сведения о выполненных маршрутах
следующим образом:
Занести в ячейку F10 формулу:
СРЗНАЧ(F2:F8).
Рис. 10. Заполнение графы В СРЕДНЕМ
Размножить введенную в ячейку
F10 формулу для остальных ячеек (с G10 по J10) (рис. 10).
21. Ячейки F10:J10 с помощью Формата ячеек перевести в числовой формат, сократив число десятичных знаков до 2 (рис. 10).
22. Лист 4 переименовать в лист с названием Ведомость
.
23. На рабочем листе Ведомость
MS Excel создать ведомость расхода горючего каждым водителем за неделю (рис. 11).
24. Путем создания межтабличных связей заполнить созданную форму полученными данными из таблицы «Данные о выполненных маршрутах
».
Рис. 11. Ведомость расхода горючего
25. Для начала в таблице «Данные о выполненных маршрутах
», находящейся на листе Сведения о выполненных маршрутах
, расположить данные графы ФИО водителей
в алфавитном порядке.
26. В этой же таблице выделить ячейки B2:J10 и присвоить им имя Маршруты
.
27. Заполнить графу № рейса
Ведомость
, следующим образом:
Занести в ячейку D11 формулу:
ВПР(C11;Маршруты;3;1).
Размножить введенную в ячейку D11 формулу для остальных ячеек (с D12 по D17) (рис. 12).
Рис. 12. Заполнение графы № рейса
28. Заполнить графу Выполнено рейсов
ведомости расхода горючего, находящейся на листе Ведомость
, следующим образом:
Занести в ячейку E11 формулу:
ВПР(C11;Маршруты;4;1).
Размножить введенную в ячейку E11 формулу для остальных ячеек (с E12 по E17) (рис. 13).
Рис. 13. Заполнение графы Выполнено рейсов
29. Заполнить графу Израсходовано топлива
ведомости расхода горючего, находящейся на листе Ведомость
, следующим образом:
Занести в ячейку F11 формулу:
ВПР(C11;Маршруты;7;1).
Рис. 14. Заполнение графы Израсходовано топлива
Размножить введенную в ячейку F11 формулу для остальных ячеек (с F12 по F17) (рис. 14).
30. Заполнить графу ИТОГО
ведомости расхода горючего, находящейся на листе Ведомость
, следующим образом:
Занести в ячейку E18 формулу:
СУММ(E11:E17).
Размножить введенную в ячейку E18 формулу для ячейки F18 (рис. 15).
Рис. 15. Заполнение графы ИТОГО
31. Результаты расчета количества израсходованного топлива за неделю представить в графическом виде.
Рис. 16. Диаграмма результатов вычислений количества израсходованного топлива за неделю
Заключение
В курсовой работе я рассказала как можно легко и быстро выполнять вычисления, используя встроенные функции MS Excel. Мастер функций еще больше упростит нам эту работу.
Рассмотрев эти функции и оценив их возможности и возможности MS Excel в целом, мы можем с уверенностью сказать, что эта программа необходима в современном мире для получения быстрых и продуктивных результатов труда, для эффективного ведения бизнеса.
Список использованной литературы
1. Информатика в экономике: Учеб. Пособие / Под ред. проф. Б.Е. Одинцова, проф. А.Н. Романова. — М.: Вузовский учебник, 2008. — 478 с.
2. Компьютерные системы и сети: Учеб. Пособие / В.П. Косарева и др. / Под ред. В.П. Косарева и Л.В. Еремина. — М.: Финансы и статистика, 2009. — 464 с.: ил.
3. Шафрин Ю.А. Информационные технологии. — М.: Лаборатория Базовых Знаний, 2008 г. — 704 с.
4. Сайт Интернета — http://www.taurion.ru/excel/10 — Самоучитель MS Excel.
Размещено на Allbest.ru
Подобные документы
Формулы. Использование ссылок и имен. Перемещение и копирование формул. Относительные и абсолютные ссылки. Понятие функции. Типы функций. Основным достоинством электронной таблицы Excel является наличие мощного аппарата формул и функций.
реферат , добавлен 15.02.2003
Вычисления в Excel. Формулы и функции: Использование ссылок и имен, перемещение и копирование формул. Относительные и абсолютные ссылки. Понятиеи и типы функций. Рабочая книга Excel. Связь между рабочими листами. Построение диаграмм в EXCEL.
лабораторная работа , добавлен 28.09.2007
Ввод, редактирование и форматирование данных в табличном редакторе Microsoft Excel, форматирование содержимого ячеек. Вычисления в таблицах Excel при помощи формул, абсолютные и относительные ссылки. Использование стандартных функций при создании формул.
контрольная работа , добавлен 05.07.2010
Создание таблицы «Покупка товаров с предпраздничной скидкой». Понятие формулы и ссылки в Excel. Структура и категории функций, обращение к ним. Копирование, перемещение и редактирование формул, автозаполнение ячеек. Формирование текста функции в диалоге.
лабораторная работа , добавлен 15.11.2010
Создание электронных таблиц в MS Excel, ввод формул при помощи мастера функций. Использование относительной и абсолютной ссылок в формулах. Логические функции в MS Excel. Построение диаграмм, графиков и поверхностей. Сортировка и фильтрация данных.
контрольная работа , добавлен 01.10.2011
Средства создания и форматирования электронных таблиц MS Excel. Условное форматирование с использованием инструмента. Анализ функции Excel следующих категорий: математические, статистические, условные, ссылки и массивы. Механизм создания сводных таблиц.
контрольная работа , добавлен 02.02.2015
Табличный процессор Microsoft Excel — программа управления электронными таблицами общего назначения; встроенные функции: математические, текстовые, логические. Расчет выполненных маршрутов по перевозке грузов, формирование ведомости расхода горючего.
курсовая работа , добавлен 07.07.2013
Основные приемы работы в Excel. Селекция блока ячеек, ввод данных. Копирование формул, установка границ ячеек. Изменение ширины столбца. Решение транспортной задачи: ввод исходных данных, формирование элементов математической модели и целевой функции.
курсовая работа , добавлен 30.01.2012
Расчет и построение таблицы значений функции (протабулирование функции) при различных значениях аргумента. Нахождение наибольшего и наименьшего значений функции на отрезке и построение графика. Рабочий лист Excel в режимах отображения значений и формул.
контрольная работа , добавлен 27.05.2010
Краткая история табличных процессоров. Интерфейс Microsoft Excel-2010. Документ Excel 2010. Типы данных в ячейках Excel. Диапазоны (массивы, блоки) в Excel. Текстовые и числовые данные. Формулы и ссылки на ячейки. Форматы представления числовых данных.
MS
Excel 2003 содержит 320 встроенных функций.
Для удобства функции в Excel 2003 разбиты
по категориям (матем, финансовые,
статистические и т.д.).
Обращение
к каждой функции состоит из двух частей:
имени функции и аргументов в круглых
скобках.
Встроенные
функции
Математические:
КОРЕНЬ(…)
Вычисление квадратного корня
ABS(…)
Вычисление абсолютного значения
(модуля) числа
ЦЕЛОЕ(…)
Округление числа или результата
выражения, указанного в скобках, до
ближайшего меньшего (!) целого
ПИ() * Значение математической константы
«ПИ» (3,1415926…)
НОД(…)
Наибольший общий делитель нескольких
чисел
НОК(…)
Наименьшее общее кратное нескольких
чисел
СЛЧИС() * Вычисление случайного числа в
промежутке между 0 и 1
Статистические
МИН(…)
Определение минимального из указанных
чисел
МАКС(…)
Определение максимального из указанных
чисел
СРЕДНЕЕ(…)
Определение среднего значения указанных
чисел
СУММ(…)
Определение суммы указанных чисел
Дата
и время
СЕГОДНЯ
() * Значение сегодняшней даты в виде
даты в числовом формате
МЕСЯЦ(дата)
Вычисление порядкового номера месяца
в году по указанной дате
ДЕНЬ(дата)
Вычисление порядкового номера дня в
месяце по указанной дате
ГОД(дата)
Вычисление года по указанной дате
Логические
И(условие1;
условие2;…)
Вычисление
значения (ИСТИНА, ЛОЖЬ) логической
операции И
ИЛИ
(условие1;
условие2;…)
Вычисление
значения (ИСТИНА, ЛОЖЬ) логической
операции ИЛИ
ЕСЛИ
(условие;
знач_ИСТИНА; знач_ЛОЖЬ)
Вычисление
значения в зависимости от выполнения
условия.
Виды
ссылок:
Относительная
(С3)
При
копировании: Меняется в соответствии
с новым положением ячейки
Технология
ввода: Щелкнуть в ячейке
Абсолютная
($C$3)
При
копировании: Не меняется
Технология
ввода: Щелкнуть в ячейке и нажимать F4
до преобразования адреса к нужному
виду
Смешанная
При
копировании: (С$3) Не меняется номер
строки
При
копировании: ($C3) Не меняется имя столбца
Использование
относительных ссылок в Excel аналогично
указанию направления движения по улице
— «идти три квартала на север, затем
два квартала на запад». Следование
этим инструкциям из различных начальных
мест будет приводить в разные места
назначения.
Например,
формула, которая суммирует числа в
столбце или строке, затем часто копируется
для других номеров строк или столбцов.
В таких формулах используются
относительные ссылки.
В
Excel абсолютная ссылка на ячейку или
область ячеек будет всегда ссылаться
на один и тот же адрес строки и столбца.
При сравнении с направлениями улиц это
будет примерно следующее: «Идите на
пересечение Арбата и Бульварного
кольца». Вне зависимости от места
старта это будет приводить к одному и
тому же месту. Если формула требует,
чтобы адрес ячейки оставался неизменным
при копировании, то должна использоваться
абсолютная ссылка (формат записи $А$1).
Например, когда формула вычисляет доли
от общей суммы, ссылка на ячейку,
содержащую общую сумму, не должна
изменяться при копировании.