Как решить математическую модель в excel

Цели урока:

1. Обучающие: Повторить и закрепить навыки
   работы в MS Excel; научить применять современное
   программное обеспечение в решении
   математических задач, строить математические
   модели в среде MS Excel.




2. Развивающие: Развивать: практические и
   исследовательские навыки по составлению моделей
   в электронных таблицах, научное мировоззрение
   через связь информационных технологий с другими
   школьными предметами, логическое и
   алгоритмическое мышление, аналитические
   способности, внимание, память.




3. Воспитательные: Воспитание общей и
   информационной культуры, творческого подхода к
   работе, желания экспериментировать,
   самостоятельности в учебном труде.

• компьютеры с ОС MS Windows XP;

• пакет Microsoft Office;

• мультимедийный проектор

Время проведения урока: один из
последних уроков в разделе «Информационное
моделирование».

План урока: (40 минут)

1. Орг. момент. (1 мин)
2. Проверка и актуализация знаний. / Тестирование
   по теме (4 мин)./ Разминка (5 мин)
3. Теоретическая часть. (10 мин)
4. Практическая часть. (10 мин)
5. Самостоятельная работа. (8 мин)
6. Подведение итогов. Д/з (2 мин)

1. Организационный момент.

Приветствие, проверка присутствующих.

С помощью проектора демонстрируется
на экране первый слайд презентации. Приложение 1

Сообщается тема урока: «Математическое
моделирование в среде электронных таблиц MS Excel
«.Озвучить цели и план урока.

2. Актуализация опорных знаний.

Пройденная нами тема «Электронные
таблицы»– одна из наиболее практически
значимых, востребованных, после текстового
редактора Word и его возможностей. Но электронные
таблицы не только позволяют автоматизировать
расчеты, но и являются эффективным средством
моделирования различных вариантов и ситуаций.
Меняя значения исходных данных, можно проследить
за изменением получаемых результатов и из
множества вариантов решения задачи выбрать
наиболее подходящий.

Перечислите, что вы научились делать,
изучая табличный процессор MS Excel?

– выполнять вычислительные операции
при помощи формул;

Тестирование по теме «Электронные
таблицы».

Домашним заданием было повторить весь
изученный материал по теме «Электронные
таблицы». Чтобы проверить домашнее задание, я
предлагаю Вам ответить на вопросы электронного
теста. (Дети уже знакомы с работой системы
дистанционного обучения MyTestServer 1.1) Приложение 2

Перед началом работы учащиеся
прослушивают инструкцию по выполнению теста.

Тест состоит из 5 вопросов. Дается
только одна попытка, будьте внимательны, не
торопитесь. Время на тест 3 минуты.

После завершения тестирования каждому
ученику системой выставляется оценка, которую он
видит на экране своего монитора.

Сегодня на уроке мы будем использовать
электронные таблицы с их мощным вычислительным
потенциалом для решения математических задач –
построим математическую модель в среде MS Excel и
проведем небольшое исследование.

А для этого вспомним основные понятия
по теме “моделирование” (проводим устную разминку).

Вопросы разминки: Приложение 1

Приведите пример знаковой
информационной модели, рассматриваемой на
уроках математики.

Основным языком информационного
моделирования в науке является язык математики.

Какую бы жизненную задачу ни взялся
решать человек, первым делом он строит модель
заданного объекта. Очень часто задачи связаны с
потребностями человека.

Сегодня нам предстоит решить
следующую задачу:

Задача 1: Приложение
1

У маленького Васи есть небольшой
бассейн во дворе. Иногда Вася ходит к речке и
приносит воду в бассейн в небольшой цистерне
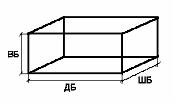
цилиндрической формы. Известны ширина ШБ, высота
ВБ, ДБ бассейна и объем цистерны Об Ц. Сколько раз
Васе нужно сходить к речке за водой, чтобы
наполнить бассейн наполовину?

Этот текст можно рассматривать как
словесную модель бассейна.

Постановка задачи: выяснение
условий

Какую форму может иметь бассейн?
(ответы детей).

А какой формы он в нашей задаче?– В
форме куба или параллелепипеда, потому, что даны
его параметры: ширина, высота, длина. А что еще нам
известно?

– объем цистерны.

Давайте попробуем решить задачу:
узнаем сколько раз (N) Васе нужно сходить к речке
за водой, чтобы наполнить бассейн наполовину.

Что для этого нужно знать?

– сколько цистерн воды помещается в
бассейн.

А как это узнать?

– определить объем бассейна (Об Б)

– сравнить половину объема бассейна и
объем цистерны (Об Б / Об Ц / 2).

Карточка – задание №1 Приложение 3

Задание для практической работы: Скопировать
в свою папку файл – шаблон Excel Приложение 4

Назвать лист номером задачи «Задача
1» (редактирование названия – двойной щелчок
мыши на «Лист 1»).

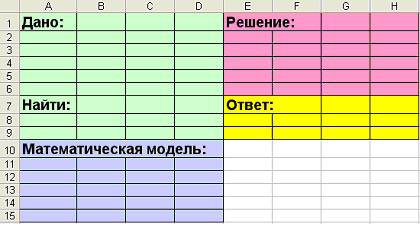
Оформить на листе решения разделы «Дано«,
«Найти«, «Математическая модель«,
«Решение«, «Ответ» (по образцу):

В ячейках А1и А7 напечатать
слова «Дано» и «Найти«.

Объединить ячейки А10, В10 и С10,
ввести текст: «Математическая модель«

Объединить ячейки Е1 и F1,
напечатать слово «Решение«.

В ячейку Е7 – «Ответ«.

 Заполнить таблицу начальными
данными.

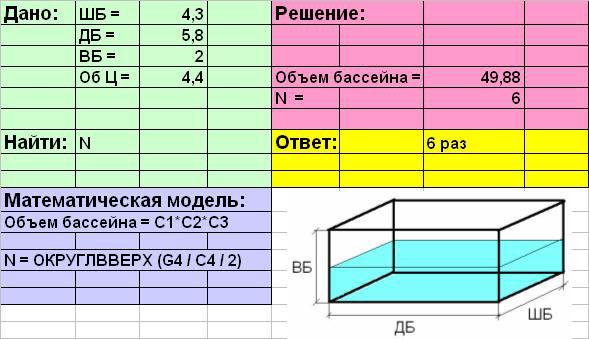
В ячейки В1:В4 ввести текст: ШБ=;
ДБ=; ВБ=; Об Ц=.

В ячейки С1:С4; ввести
соответствующие значения параметров: 4,3; 5,8; 2; 4,5.

Для наглядности, если есть
возможность, можно построить графическую модель
(рисунок задаче) в Painte и скопировать ее в
электронную таблицу или нарисовать бассейн
непосредственно в Excel.

Далее заполнить раздел таблицы
«Математическая модель».

Объединить ячейки А11, В11 и С11,
ввести формулы (тип данных – текст) в раздел
(пробел перед знаком «=»). «Объем бассейна
=С1*С2*С3«

Объединить ячейки А13, В13 и С13
и ввести текст «N = ОКРУГЛВВЕРХ(G4 / C4 / 2)«.
(для получения целого числа используем функцию
округления ОКРУГЛВВЕРХ)

В разделе «Решение»
создать сетку вычислений:

– Обозначить искомые и промежуточные
величины.

– Объединить ячейки Е4 и F4,
ввести текст: «Объем бассейна =«. В ячейку
Е5 – «N =«(тип данных – текст).

В ячейки G4 и G5; ввести
соответствующие формулы (тип данных – формулы):
=С1*С2*С3;

Используем функцию округления
дробного числа до целого:

Вставка-функция – математические –
ОКРУГЛВВЕРХ – число разрядов выбираем «0«.

=ОКРУГЛВВЕРХ(G4 / C4 / 2)

В разделе «Ответ» запишем
искомый результат в ячейку G7 (тип данных –
текст).

 Проведем небольшое исследование:

Вопрос: Сколько раз Васе нужно будет
сходить к речке за водой, если он возьмет
цистерну емкостью 5,6 литров; 4 литра; 3,3
литра?

Меняем в ячейке С4 значение на 5,6
и электронные таблицы автоматически производят
пересчет.

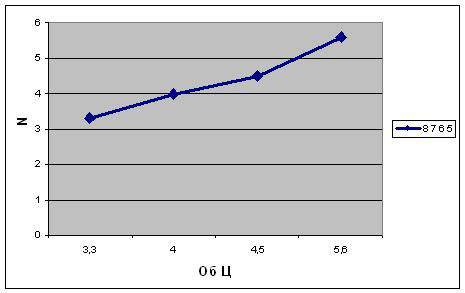
Создадим таблицу значений Об Ц и
будем заносить в нее результаты вычислений N.

Введем в ячейку А20 и В2 текст
«Об Ц» и » N«. Заполним таблицу
данными.

Для графического представления
результатов выделить диапазон А21: В24,
построить график функции, отредактировать его.

 Анализ полученных результатов.

Задача 2. Пешеход начал движение из
начала координат со скоростью V=0,6 м/с.
Найдите, какой путь S прошел пешеход за одну
минуту t после начала движения, если он
двигался равномерно.

Постановка задачи: выяснение
условий

Скажите, что мы будем моделировать? –

– движение

Какие виды движения вы знаете? (ответы
детей)

Какое движение рассматривается в
нашей задаче?

– равномерное. Приложение 1

Давайте вспомним формулу расчета
скорости: V=s/t– отсюда s=V*t

Технология моделирования:

1. Назвать лист номером задачи «Задача 2»
   (редактирование названия – двойной щелчок мыши
   на «Лист 2»).
2. Выделить расчетную таблицу на листе «Задача1»
   и скопировать ее на лист «Задача 2«.
3. Заполнить таблицу новыми начальными данными.
4. Ввести формулу (тип данных – текст) в раздел
   «Математическая модель» (пробел перед
   знаком «=»).
5. Ввести фоpмулу (тип данных – формулы) в
   раздел «Решение«.
6. В разделе «Ответ» записать искомый
   результат (тип данных – текст).




7. Создать таблицу значений t и занести в нее
   результаты вычислений S. Заполнить таблицу
   данными.
8. Для графического представления результатов
   выделить область аргументов и функций, построить
   график зависимости пути S от времени при t=40;60;90,
   отредактировать график.

Сегодня на уроке мы узнали, как можно
использовать электронные таблицы в решении
математических задач, научились строить
математические модели в. среде MS Excel

Домашним заданием будет: самим
придумать задачу, разработать ее математическую
модель.

У кого есть вопросы по пройденному материалу?

Спасибо за работу. Вы сегодня молодцы. Можете
быть свободны.

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.



Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Министерство
здравоохранения Саратовской области

Государственное автономное
профессиональное

образовательное учреждение

«Балаковский медицинский
колледж»

МЕТОДИЧЕСКОЕ
ПОСОБИЕ

ПРАКТИЧЕСКОГО 
ЗАНЯТИЯ ДЛЯ СТУДЕНТОВ

по
разделу: «Организация
профессиональной

деятельности
с помощью средств Microsoft Office»

на 4 час.

Тема:
«Применение математической модели в  Excel
для вычислений определённых величин»

Учебная
дисциплина: «Информатика»

ПМ
06 Организационно-аналитическая деятельность

                 
Специальность: 31.02.01 «лечебное дело»

Курс
4

Балаково

2017
г.

 Методическое
пособие   по учебной дисциплине  Информатика по разделу: «Организация
профессиональной деятельности  с помощью средств Microsoft Office»
на тему: «Применение математической модели в  Excel
для вычислений определённых величин» .

Автор:
Шаныгина Людмила  Григорьевна  Балаково, 2017 г. —  
страниц — 21

Рецензент:
 преподаватель высшей квалификационной категории  

Балаковского
медицинского колледжа: Ростовская Т.А.

Содержание

1.Пояснительная записка

2.Технологическая
карта практического занятия

3.Распределение
рабочего времени на учебном занятии:

4.Методические указания для студентов к практическому
занятию дисциплина: «Информатика»

5.Контролирующие задания

Вариант 1. Знакомство с электронными таблицами

Вариант 2. Ввод информации в электронные таблицы

Вариант3. Фрагменты таблицы. Относительная и
абсолютная адресация

6.Список рекомендуемой литературы

1.Пояснительная записка

Цель данной работы:  Понимание особенностей
использования математической модели в Excel  для вычислений и построения диаграмм .

Актуальность темы: Будущему медику необходимо обладать
основными навыками работы с компьютером и с программами пакета MS Office. Пособие  составлено  для
совершенствования учебного процесса, более эффективного усвоения знаний
студентами и формирования у них профессиональных компетенций.

Методическое  пособие практического
занятия предназначено для студентов дисциплины Информационные технологии в
профессиональной деятельности по специальности «Лечебное дело». Материалы
разработаны  в соответствии с требованиями ФГОС СПО по специальности  «Лечебное
дело».

Занятие проводится в кабинете
Информатики. Бюджет времени на указанную тему составляет практическая часть –
180 минут.  В методических рекомендациях  отражены учебные, воспитательные и
развивающие цели, осуществляются межмодульные и внутридисциплинарные связи. Для
лучшего усвоения материала являются необходимыми знания и умения, полученные на
предшествующих и сопутствующих дисциплинах. 

На занятии предполагается проверка
знаний студентов, которые они получили на теоретических занятиях и при
самостоятельной работе с учебной литературой. Практическая часть занятия дает
возможность закрепить, систематизировать знания и применять их  в дальнейшем
процессе обучения.

Для преподавателей данное  методическое
пособие  поможет правильно организовать и на доступном современном уровне провести
практическое  занятие,  заинтересовать студентов в необходимости теоретических
знаний специальных дисциплин.

2.Технологическая карта практического занятия

Цели занятия:                               

1)   
Знакомство  с  текстовым процессором Excel.

2)    Создание
таблицы в Microsoft Excel.
Осуществлять ввод и редактирование данных.  Производить форматирование таблицы.

3)     Использовать
формулы и функции.

4)    Построить
диаграмму с помощью Мастера диаграмм. Редактировать диаграмму. Осуществлять
сортировку и поиск данных в таблице.

5)   
Совершенствование  приобретенного
практического опыта    с целью формирования  профессиональных компетенций 
фельдшера.

6)   
Применение умений и знаний  в
самостоятельном решении  поставленных задач  в различных ситуациях.

Развивающие:

1)   
Развитие умения оперировать полученными
знаниями,  делать самостоятельные выводы по полученной информации.

2)   
Развитие навыков концентрации внимания,
мыслительных способностей студентов при решении  поставленных задач..

3)   
Развитие у студентов интереса к новейшим
медицинским технологиям.

Воспитательные:

1)   
Побуждение студентов к активности через
включение в процесс.  

2)   
Формирование профессиональных качеств
медицинского работника:  

   
ответственность, доброжелательность, бережное отношение к аппаратуре и умение
выполнять сложные задачи.

3)   
Воспитание в себе стремления быть образованным и
эрудированным человеком.

    
Знать:

1.     Методы
создания таблиц в Microsoft Excel.

2.     Способы ввода
и редактирования данных.

3.     Производить
форматирование таблицы.

4.    
Методы
ввода данных в таблицы;

Уметь:

1)    Использовать
формулы и функции.

2)    Строить
диаграмму с помощью Мастера диаграмм.

3)    Редактировать
диаграмму.

4)     Осуществлять
сортировку и поиск данных в таблице.

Место
проведения: кабинет
информатики. Время: 180 минут

Освоение общих
компетенций:

ОК 1.
Понимать
сущность и социальную значимость своей будущей профессии, проявлять к ней
устойчивый интерес.

ОК 2.
Организовывать
собственную деятельность, выбирать типовые методы и способы выполнения
профессиональных задач, оценивать их выполнение и качество.

ОК 4.
Осуществлять
поиск и использование информации, необходимой для эффективного выполнения 
возложенных на него профессиональных задач, а также для своего 
профессионального и личностного развития.

ОК 5.  Использовать
информационно-коммуникационные технологии в профессиональной деятельности.

ОК 8.
Самостоятельно
определять задачи профессионального и личностного развития, заниматься
самообразованием, осознанно планировать и осуществлять повышение своей
квалификации.

ОК 9.  Ориентироваться
в условиях частой смены технологий в профессиональной деятельности.

Фельдшер должен обладать профессиональными компетенциями:

ПМ 06
«Организационно-аналитическая деятельность»:

ПК 6.1. Рационально организовывать деятельность персонала с
соблюдением психологических и этических аспектов работы в команде.

ПК 6.2. Планировать свою деятельность на ФАПе, в здравпункте
промышленных предприятий, детских дошкольных учреждениях, центрах общей
врачебной (семейной) практики и анализировать ее эффективность.

ПК 6.3. Вести медицинскую документацию.

ПК 6.4. Организовывать и контролировать выполнение
требований противопожарной безопасности, техники безопасности и охраны труда на
ФАПе, в здравпункте промышленных предприятий, детских дошкольных учреждениях,
центрах офисе общей врачебной (семейной) практики.

ПК 6.5. Повышать профессиональную квалификацию и внедрять
новые современные формы работы.

Материальное
обеспечение учебного занятия:

Оснащение:

Технологическая
карта занятия, персональные компьютеры, методические пособия для  студентов на
каждом задействованном в занятии ПК.

Методические
приемы:

1.     Проверка
самостоятельной внеаудиторной работы.

2.     Рецензирование
ответов студентов.

3.     Работа
по алгоритму.

3.Распределение рабочего времени на учебном занятии:

4.Методические указания для студентов к практическому занятию
дисциплина: «Информатика»

Специальность
Лечебное дело

ПМ
06 Организационно-аналитическая деятельность

Тема:
«Применение математической модели в  Excel
для вычислений определённых величин» .

Цель работы: Использование
математической модели  в Excel

 при решении задач.

Работа состоит из 4  заданий
рассчитанных на выполнение в течение 180 минут.

Задание  №1

Задача №1 Определение рабочего диаметра аорты с использованием математической
модели

Технология выполнения:

Произведите последовательность действий:

1.           
Запустите программу Excel (Пуск => Программы Microsoft Excel).

2.              
Заполните электронную таблицу: в ячейки B₁ и С₁
введите условные сокращения УОС и АДп. Далее в ячейки B₁ и С₁
введите соответствующие значения гемодинамических показателей пациента (таблица
№1)

Таблица №1.

Значения гемодинамических показателей пациентов, необходимые для расчета
рабочего диаметра аорты  внесите в таблицу.

3.                                  
В ячейку D₂ введите
формулу. Для этого поставьте  в ячейку знак равенства.

Затем нажмите кнопку со стрелкой для выбора функции в
панели для ввода и изменения формул. Выберите сначала «Другие функции», затем
категорию функций «Математические» и функцию «Корень». В строке формул появится
запись =  КОРЕНЬ(). В скобках введите подкоренное выражение 2,81(*)В₂/С₂.

При этом
арифметический оператор умножения вводят с клавиатуры знаком *, арифметический
оператор деления обозначают косой чертой (/). Нажмите «Enter». Произойдет автоматический расчет рабочего диаметра
аорты по введенной формуле. Полученное значение диаметра аорты занесите в
таблицу в тетради. Дополните таблицу до 10 пациентов и введите новые значения в
таблицу №1 для всех пациентов. Ввод каждой цифры заканчивайте нажатием клавиши «Enter». В ячейке D₃ появится новое
автоматически рассчитываемое значение рабочего диаметра аорты у очередного пациента.

4.                                  
По результатам вычислений постройте диаграмму,
отражающею диаметр аорты разных пациентов.

Задание
2

Задача
№ 2. Определение остаточного объема левого желудочка с  использованием
математической модели.

Известен способ
определения остаточного объема левого желудочка, согласно которому в качестве
геометрической модели левого желудочка используют трехмерный эллипсоид, имеющий
две одинаковые малые и одну большую оси, соотношение которых в систоле и
диастоле принимается постоянным — 1:1:2. Объем эллипсоида описывается формулой:

V
= 4/ЗπА.В.С где V — объем
эллипсоида, А, В, С — полуоси эллипсоида. Подставляя вместо А, В, С
соответствующие эхокардиографические размеры полости левого желудочка в конце
систолы, вычисляют остаточный объем.

Voct
= АДд*t*К/Vуд*АДп

где Vуд.
в мл — ударный объем сердца, t
— время изгнания крови в сек., АДд — диастолическое артериальное давление, АДп
пульсовое артериальное давление, К — коэффициент, равный для мужчин 9284, для
женщин — 5732.

Технология
выполнения:

1.Откройте лист 2 
и заполните электронную таблицу: в ячейки В введите соответственно пол:
муж./жен. В ячейки C₁ D₁ Е₁
F₁ и т.д.
введите условные сокращения АДд, t, К, Vуд, АДп, Vосt Да ячейки
В2, С2, D2, Е2, F2 введите
соответствующие значения гемодинамических показателей пациента А.

2.    В ячейку
для расчёта объёма сердца введите формулу =, используя арифметические операторы
умножения и деления. Для правильной последовательности действий произведение в
знаменателе необходимо взять в скобки. Voct.= АДд* t*K/( Vуд* АДп)

3.    Дополните
таблицу показателями для 3 мужчин и 4 женщинs и рассчитайте остаточный объём
сердца.

 Таблица
2

                                                                                                          
 ^58,6

Постройте
диаграмму по результатам вычислений остаточного объема левого желудочка.

Задание
3

Задача 3  Рассчитайте
конечнодиастолический объем сердца оцените диастолическую функцию левого
желудочка.

Для
решения этой задачи необходимо продолжить  заполнение ячеек  предыдущей таблицы
2 и  введите сокращения КДО и ДФ. В ячейку I₂ введите формулу
= (сумма ударного и остаточного объемов сердца), нажмите «Enter». В
ячейку J₂ введите
формулу = Vост/КДО(%),
нажмите «Enter».

Таблица 3.

Задание
4

Задача
№ 4. Исследование показателей системной гемодинамики у здоровых людей,
пациентов с пограничной артериальной гипертензией и больных гипертонической
болезнью I стадии.

Для определения
важнейшего параметра системной гемодинамики среднего динамического
артериального давления возможно использование усовершенствованной модели В.А.
Лишука. Конечное выражение модели указанных показателей системы кровообращения
имеет вид:

Адср= Vн*ОПС(Св + ОПС*Са)^-1

где Адср — среднее
артериальное давление, Vh — напряженный объем крови, 1/β —
насосный коэффициент сердца, Св — эластичность венозных сосудов, Са — эластичность
артериальных сосудов, ОПС — общее периферическое сопротивление.

 Технология
выполнения:

Откройте лист 3 и заполните
электронную таблицу: в ячейки Al, Bl,
Cl, Dl, Е1
введите условные сокращения Vh, Св,
ОПС, Са, АДср. Далее в ячейки В₂, С₂, D₂ введите
соответствующие значения гемодинамических показателей пациентов из таблицы 4.

3. В ячейку F₂ введите формулу = B₂*D₂*1/(C₂+(D₂*E₂) используя арифметические операторы умножения,
деления и сложен — *, / и +. Для правильной последовательности действий в
знаменателе используйте скобки. Нажмите «Enter».

В ячейке F₂ будет появляться новое
автоматически рассчитываемое значение АД. Входные параметры для расчета
среднего артериального давления (АДер) у здоровых людей, больных с пограничной
артериальной гипертензией (ПАГ) и больных с гипертонической болезнью (ГБ) 1
стадии.

Таблица 4     

По 
результатам вычислений постройте  диаграмму.

Работу  распечатать и сдать на проверку
преподавателю.

В заключении ответить на тесты по теме: MS Excel.

ПРИЛОЖЕНИЯ

5.Контролирующие задания

Вариант 1. Знакомство с
электронными таблицами

1. Электронная таблица – это:

1) приложение,
хранящее и обрабатывающее данные в прямоугольных таблицах и предназначенное для
автоматизации расчетов

2) программные
средства, осуществляющие поиск информации

3) приложение,
предназначенное для сбора, хранения, обработки и передачи информации

4) приложение,
предназначенное для набора и печати таблиц

2. Независимые поля:

1) содержат
исходные данные для расчетов

2) вычисляются
через значения других столбцов

3. Дана таблица:

Определите, какие столбцы будут
вычисляемыми:

1) 5, 6

2) 2, 3, 4

3) 1, 2, 3, 4

4) нет вычисляемых
столбцов

4. Документ в электронной таблице
называется:

1) рабочая книга

2) рабочий лист

3) таблица

4) ячейка

5. Рабочая книга состоит из:

1) строк и
столбцов

2) рабочих листов

3) таблиц

4) ячеек

 6. В электронной таблице буквами A,
B,
… обозначаются:

1) строки

2) столбцы

3) ячейки

4) нет таких
обозначений

7. В электронной таблице числами 1, 2, …
обозначаются:

1) строки

2) столбцы

3) ячейки

4) нет таких
обозначений

8. В электронной таблице А1, В4 – это
обозначения:

1) строк

2) столбцов

3) ячеек

4) нет таких
обозначений

9. Данные в электронных таблицах – это 
только:

1) текст, число и
формула

2) текст и число

3) формула

4) число и формула

Вариант 2. Ввод информации в
электронные таблицы

Вариант3. Фрагменты таблицы.
Относительная и абсолютная адресация

1.     Адрес
какой ячейки является относительным?

1)    3S

2)    F$9

3)    D4

4)    $B$7

2.     Адрес
какой ячейки является абсолютным?

1)    $A:$3

2)    $F$3

3)    $8$D

4)    A6

3.     В каком
адресе не может меняться номер строки при копировании?

1)    F17

2)    D$9

3)    $A15

4)    13B

4.     Сколько
ячеек содержит выделенная область А2:С4?

1)    8

2)    6

3)    7

4)    9

5.     В ячейки D5, D6, E5, E6 введены
соответственно числа: 8, 3, 5, 2. В ячейке G3 введена формула =СУММ(D5:E6). Какое
число будет в ячейке G3?

1)    16

2)    4

3)    24

4)    18

6.     В ячейку
Е4 введена формула =$C2+D3.
Содержимое Е4 скопировали в ячейку G4. Какая формула будет в G4?

1)    =$C2+D3

2)    =C3+$F3

3)    =$C2+F3

4)    =$C2+E3

7.     В ячейку D3 введена
формула =В1*С2. Содержимое D3 скопировали в ячейку D7. Какая формула
будет в D7?

1)    =В4*С6

2)    =В5*С6

3)    =В4*С5

4)    =В6*С7

8.     В ячейки
С4, С5, D4, D5 введены
соответственно числа: 5, 3, 4, 8. В ячейке Е9 введена формула =СРЗНАЧ(С4:D5). Какое
число будет в ячейке Е9?

1)    20

2)    5

3)    13

Оценка практических умений

«5» – четкое грамотное выполнение лабораторной работы с
теоретическим обоснованием, стремление познать новое, использовать
дополнительный материал.

4» – менее свободное выполнение лабораторной работы, с
незначительной помощью преподавателя при теоретическом обосновании, стремление
и активность в улучшении результата.

«3» – недостаточно четкое выполнение лабораторной работы,
слабое овладение техникой, затруднения при теоретическом обосновании материала,
отсутствие стремления к самостоятельности в работе.

«2» – неумение
самостоятельно выполнить  лабораторную  работу, полное отсутствие знаний и
интереса к работе.

   Тест – контроль

   «5» – 91%
от количества заданий и выше.

   «4» – 81%
— 90% от количества заданий.

   «3» – 71% 
— 80% от количества заданий.

  «2» – 70% и меньше от количества заданий.

Ответы к тестам

Вариант1.

Вариант 2.

Вариант 3.

6.Список рекомендуемой литературы

Основная литература

1. Информационные технологии
в профессиональной деятельности: учеб. пособие для студ. сред. проф.
образования / Е.В. Михеева. – М.: Издательский центр «Академия», 2012г.

Дополнительная литература:

2.                
Омельченко В.П., Демидова А.А. Практикум
по медицинской информатике, «Феникс», Ростов-на-Дону, 2011

3.                
Информационные технологии. (Учебное
пособие для ссузов.) Румянцева Е.Л., Слюсарь В.В. (2012, 256с.)

Электронное информационное
обеспечение и Интернет-ресурсы:

Электронная
библиотека медицинского вуза «Консультант студента»

Консультант Студента. Электронная библиотека медицинского
вуза. . www.studmedlib.ru/ Информатика для
медиков: учебное пособие / Г. А. Хай. — СПб. : СпецЛит, 2009. — 223 с.

Поиск решения — это надстройка Microsoft Excel, с помощью которой  можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.

Поиск решения будем рассматривать в

MS EXCEL 2010

(эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в

MS EXCEL 2007)

. В этой статье рассмотрим:

• создание оптимизационной модели на листе MS EXCEL
• настройку
  
  Поиска решения;
  
• простой пример (линейная модель).

Установка Поиска решения

Команда

Поиск решения

находится в группе

Анализ

на вкладке

Данные

.

Если команда

Поиск решения

в группе

Анализ

недоступна, то необходимо включить одноименную надстройку. Для этого:

• На вкладке
  
  Файл
  
  выберите команду
  
  Параметры
  
  , а затем — категорию
  
  Надстройки
  
  ;
• В поле
  
  Управление
  
  выберите значение
  
  Надстройки Excel
  
  и нажмите кнопку
  
  Перейти;
  
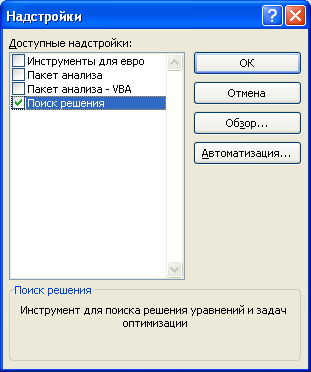
• В поле
  
  Доступные надстройки
  
  установите флажок рядом с пунктом
  
  Поиск решения
  
  и нажмите кнопку ОК.

Примечание

. Окно

Надстройки

также доступно на вкладке

Разработчик

. Как включить эту вкладку

читайте здесь

.

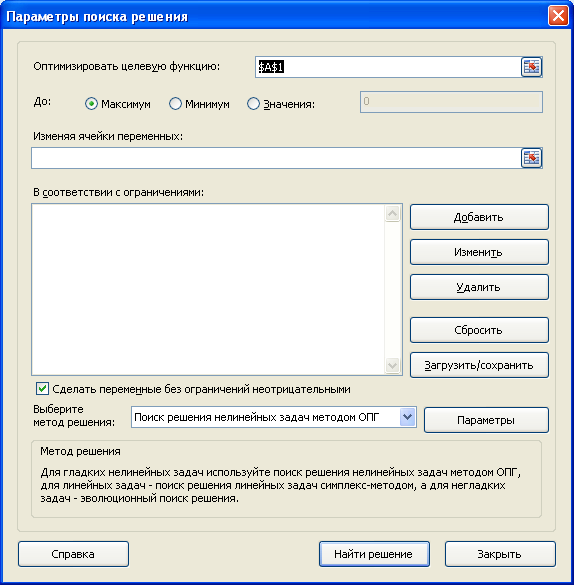
После нажатия кнопки

Поиск решения

в группе

Анализ,

откроется его диалоговое окно

.

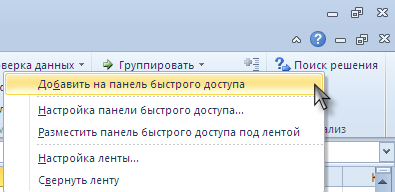
При частом использовании

Поиска решения

его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт

Добавить на панель быстрого доступа

.

О моделях

Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.

Совет

. Перед использованием

Поиска решения

настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.

Ниже приведен небольшой ликбез по этой теме.

Надстройка

Поиск решения

помогает определить

лучший способ

сделать

что-то

:

• «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
• «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.

Вот некоторые типичные примеры оптимизационных задач:

• Определить

  план производства

  , при котором доход от реализации произведенной продукции максимальный;

• Определить

  схему перевозок

  , при которой общие затраты на перевозку были бы минимальными;

• Найти

  распределение нескольких станков по разным видам работ

  , чтобы общие затраты на производство продукции были бы минимальными;

• Определить минимальный срок исполнения всех работ проекта (критический путь).

Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется

Поиском решения

только по одному показателю

(этот оптимизируемый показатель называется

целевой функцией

). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.

Поиск решения

подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.

Примечание

. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента

Подбор параметра

. Перед первым знакомством с

Поиском решения

имеет смысл сначала детально разобраться с родственным ему инструментом

Подбор параметра

. Основные отличия

Подбора параметра

от

Поиска решения

:

• 
  Подбор параметра
  
  работает только с моделями с одной переменной;
• в нем невозможно задать ограничения для переменных;
• определяется не максимум или минимум целевой функции, а ее равенство некому значению;
• эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).

Подготовка оптимизационной модели в MS EXCEL

Поиск решения

оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне

Поиска решения

возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.

Совет

. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки

Поиска решения

(см. ниже).

Приведем алгоритм работы с

Поиском решения

, который советуют сами разработчики (

]]>
www.solver.com

]]> ):

• Определите ячейки с переменными модели (decision variables);
• Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
• Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
• С помощью диалогового окна
  
  Поиск решения
  
  введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений;
• Запустите
  
  Поиск решения
  
  для нахождения оптимального решения.

Проделаем все эти шаги на простом примере.

Простой пример использования

Поиска решения

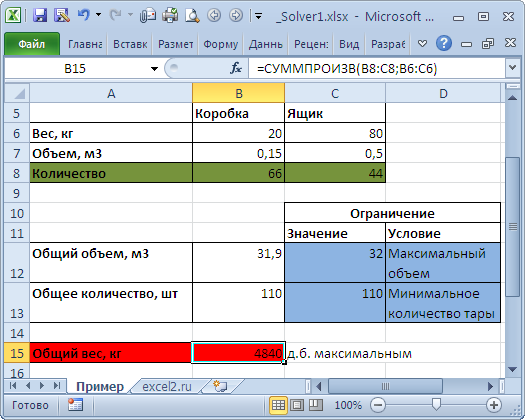
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.

Данные модели организуем следующим образом (см.

файл примера

).

Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему (<=32) – синим. Целевая функция рассчитывается по формуле

=СУММПРОИЗВ(B8:C8;B6:C6)

– это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем —

=СУММПРОИЗВ(B7:C7;B8:C8)

. Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков (<=32). Также для задания ограничения модели рассчитаем общее количество тары

=СУММ(B8:C8)

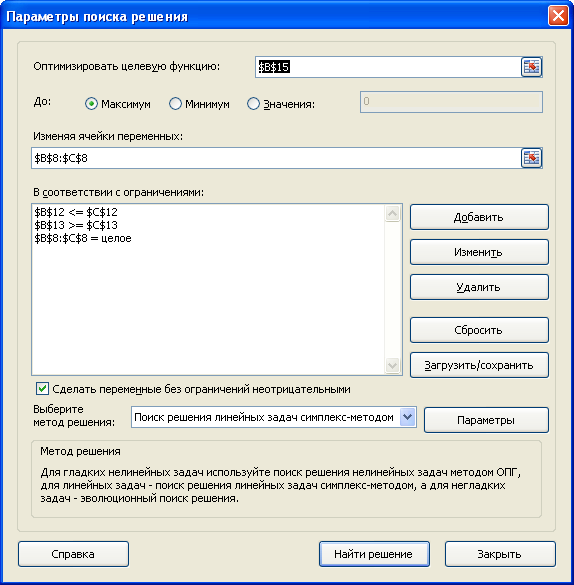
. Теперь с помощью диалогового окна

Поиск решения

введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.

После нажатия кнопки

Найти решение

будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.

Совет

: в статье »

Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями

» показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.

Резюме

На самом деле, основной проблемой при решении оптимизационных задач с помощью

Поиска решения

является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью

Поиска решения

. Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью

Поиска решения

рассмотрено

в этом разделе

.

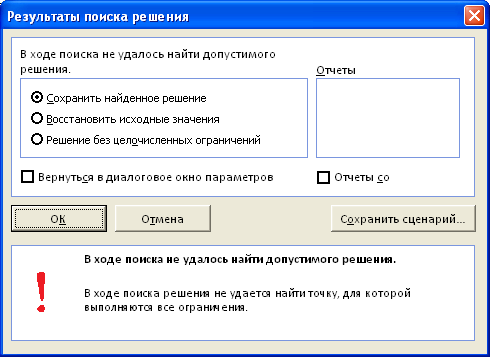
Поиску решения не удалось найти решения (Solver could not find a feasible solution)

Это сообщение появляется, когда

Поиск решения

не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете

Симплекс метод решения линейных задач

, то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите

Поиск решения

с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и

Поиск решения

не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае,

Поиск решения

может найти решение (если оно действительно существует).

Примечание

. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи

Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства

.

В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, <= вместо >=) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3,

Поиск решения

не найдет решения.

При ограничении 17 м3

Поиск решения

найдет решение.

Некоторые настройки

Поиска решения

Метод решения

Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
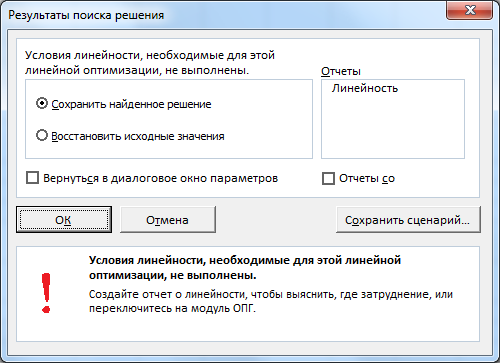
Поиска решения

можно также проверить на линейность саму модель. В случае нелинейной модели Вы получите следующее сообщение:

В этом случае необходимо выбрать метод для решения нелинейной задачи. Примеры нелинейных зависимостей: V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2, где x – переменная, а V – целевая функция.

Кнопки Добавить, Изменить, Удалить

Эти кнопки позволяют добавлять, изменять и удалять ограничения модели.

Кнопка Сбросить

Чтобы удалить все настройки

Поиска решения

нажмите кнопку

Сбросить

– диалоговое окно очистится.

Сохранение и загрузка модели

Эта опция удобна при использовании разных вариантов ограничений. При сохранении параметров модели (кнопка

Загрузить/ Сохранить,

далее нажмите кнопку

Сохранить

) предлагается выбрать верхнюю ячейку диапазона (столбца), в который будут помещены: ссылка на целевую функцию, ссылки на ячейки с переменными, ограничения и параметры методов решения (доступные через кнопку

Параметры

). Перед сохранением убедитесь в том, что этот диапазон не содержит данных модели. Для загрузки сохраненных параметров нажмите сначала кнопку

Загрузить/ Сохранить

, затем, в появившемся диалоговом окне кнопку

Загрузить

, после чего задайте диапазон ячеек, содержащих сохраненные ранее настройки (нельзя указывать только одну верхнюю ячейку). Нажмите кнопку OK. Подтвердите сброс текущих значений параметров задачи и их замену на новые.

Точность

При создании модели исследователь изначально имеет некую оценку диапазонов варьирования целевой функции и переменных. Принимая во внимание

ограниченную точность

вычислений в MS EXCEL, рекомендуется, чтобы эти диапазоны варьирования были значительно выше точности вычисления (она обычно устанавливается от 0,001 до 0,000001). Как правило, данные в модели нормируют так, чтобы диапазоны варьирования целевой функции и переменных были в пределах 0,1 – 100 000. Конечно, все зависит от конкретной модели, но если ваши переменные изменяются более чем на 5-6 порядков, то возможно следует «загрубить» модель, например, с помощью операции логарифмирования.