Математические и тригонометрические функции (справочник)
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
Возвращает модуль (абсолютную величину) числа.
Возвращает арккосинус числа.
Возвращает гиперболический арккосинус числа.
ACOT
Возвращает арккотангенс числа.
ACOTH
Возвращает гиперболический арккотангенс числа.
Возвращает агрегат для списка или базы данных.
АРАБСКОЕ
Преобразует римские числа в арабские в виде числа.
Возвращает арксинус числа.
Возвращает гиперболический арксинус числа.
Возвращает арктангенс числа.
Возвращает арктангенс для заданных координат x и y.
Возвращает гиперболический арктангенс числа.
ОСНОВАНИЕ
Преобразует число в текстовое представление с данным основанием (базой).
Округляет число до ближайшего целого или кратного.
ОКРВВЕРХ.МАТ
Округляет число в большую сторону до ближайшего целого или кратного.
Округляет число до ближайшего целого или кратного. Число округляется до большего значения вне зависимости от его знака.
Возвращает количество комбинаций для заданного числа объектов.
ЧИСЛКОМБА
Возвращает количество комбинаций с повторами для заданного числа элементов.
Возвращает косинус числа.
Возвращает гиперболический косинус числа.
COT
Возвращает котангенс угла.
COTH
Возвращает гиперболический котангенс числа.
CSC
Возвращает косеканс угла.
CSCH
Возвращает гиперболический косеканс угла.
ДЕС
Преобразует текстовое представление числа в заданном основании в десятичное число.
Преобразует радианы в градусы.
Округляет число до ближайшего четного целого.
Возвращает число e, возведенное в указанную степень.
Возвращает факториал числа.
Возвращает двойной факториал числа.
Округляет число до ближайшего меньшего по модулю значения.
ОКРВНИЗ.МАТ
Округляет число в меньшую сторону до ближайшего целого или кратного.
Округляет число в меньшую сторону до ближайшего целого или кратного. Число округляется в меньшую сторону независимо от знака.
Возвращает наибольший общий делитель.
Округляет число до ближайшего меньшего целого.
ISO.ОКРВВЕРХ
Округляет число в большую сторону до ближайшего целого или кратного.
Возвращает наименьшее общее кратное.
Возвращает натуральный логарифм числа.
Возвращает логарифм числа по заданному основанию.
Возвращает десятичный логарифм числа.
Возвращает определитель матрицы массива.
Возвращает обратную матрицу массива.
Возвращает матричное произведение двух массивов.
Возвращает остаток от деления.
Возвращает число, округленное с требуемой точностью.
Возвращает мультиномиальный коэффициент множества чисел.
МЕДИН
Возвращает матрицу единицы или заданный размер.
Округляет число до ближайшего нечетного целого.
Возвращает число пи.
Возвращает результат возведения числа в степень.
Возвращает произведение аргументов.
Возвращает целую часть частного при делении.
Преобразует градусы в радианы.
Возвращает случайное число в интервале от 0 до 1.
Возвращает массив случайных чисел в интервале от 0 до 1. Но вы можете указать количество заполняемых строк и столбцов, минимальное и максимальное значения, а также какие значения необходимо возвращать: целые или десятичные.
Возвращает случайное число в интервале между двумя заданными числами.
Преобразует арабские числа в римские в виде текста.
Округляет число до указанного количества десятичных разрядов.
Округляет число до ближайшего меньшего по модулю значения.
Округляет число до ближайшего большего по модулю значения.
SEC
Возвращает секанс угла.
SECH
Возвращает гиперболический секанс угла.
Возвращает сумму степенного ряда, вычисленную по формуле.
Возвращает знак числа.
Возвращает синус заданного угла.
Возвращает гиперболический синус числа.
Возвращает положительное значение квадратного корня.
Возвращает квадратный корень из значения выражения (число * пи).
Возвращает промежуточный итог в списке или базе данных.
Суммирует ячейки, удовлетворяющие заданному условию.
Суммирует ячейки в диапазоне, удовлетворяющие нескольким условиям.
Возвращает сумму произведений соответствующих элементов массивов.
Возвращает сумму квадратов аргументов.
Возвращает сумму разностей квадратов соответствующих значений в двух массивах.
Возвращает сумму сумм квадратов соответствующих элементов двух массивов.
Возвращает сумму квадратов разностей соответствующих значений в двух массивах.
Возвращает тангенс числа.
Возвращает гиперболический тангенс числа.
Отбрасывает дробную часть числа.
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Тригонометрические функции SIN COS в Excel для синуса и косинуса
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
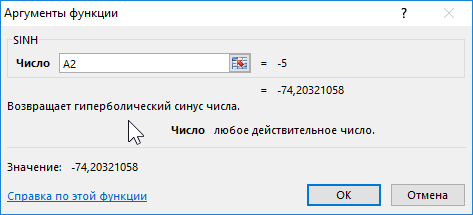
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
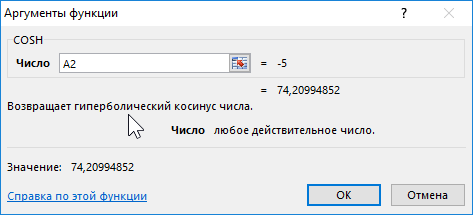
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
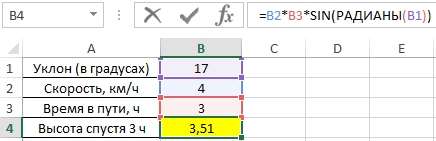
Для решения используем формулу:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
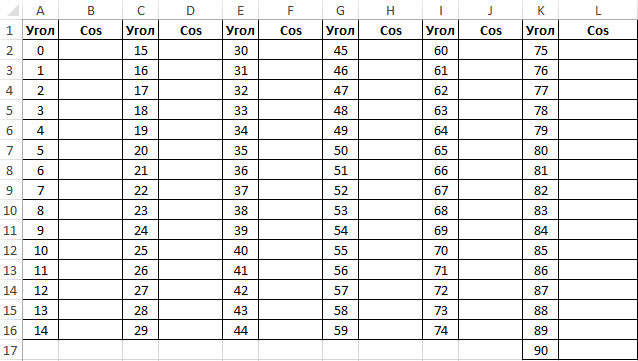
Заполним столбцы значениями углов в градусах:
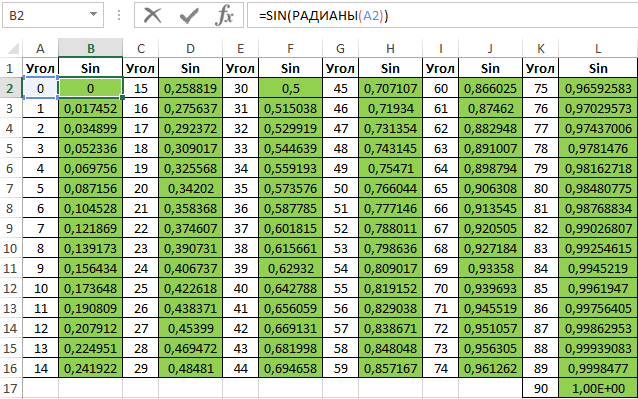
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
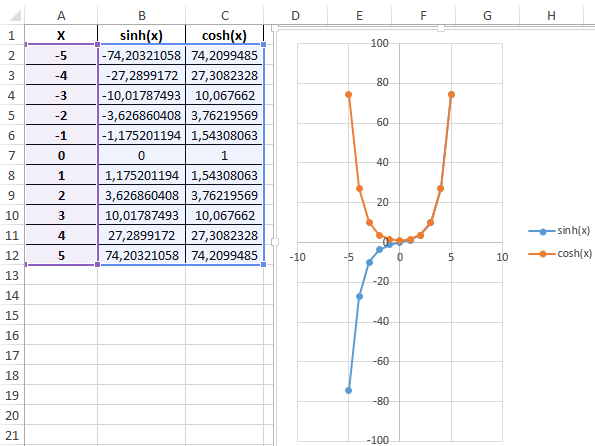
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Формула для нахождения синусов гиперболических:
Формула для нахождения косинусов гиперболических:
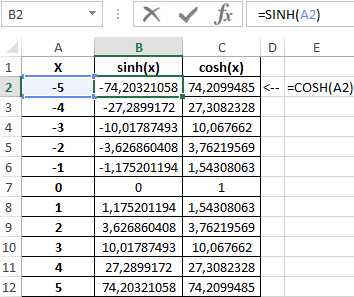
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
Синтаксис функции SINH:
Синтаксис функции COS:
Синтаксис функции COSH:
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://exceltable.com/funkcii-excel/primery-funkciy-sin-sinh-cos-cosh
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
Want to graph trigonometric equations, but don’t know where to start? Here’s how to do it in Excel like a pro.
Visualizing trigonometric equations is an important step in understanding the relationship between the X and Y axis. Without a graph, guessing a complex trigonometric equation’s behavior can become quite a challenge. Fortunately, Microsoft Excel is an excellent tool for graphing and visualizing data, including trigonometric equations.
Visualizing an equation makes it easier to grasp, and once you’ve got the hang of graphing trigonometric equations with Excel, you’ll have a better time understanding trigonometry. In this article, we’ll explain how to use Excel to graph trigonometric equations and provide a step-by-step example to help you get started.
How to Graph Trigonometric Equations With Excel
To graph an equation with Excel, you’ll need to create a chart for the X and Y values. The good news is that you don’t have to manually calculate the Y values, as Excel has an arsenal of trigonometric functions built into it.
All you need to do is create a data table with the X values, and then write an Excel formula to automatically calculate the Y values. With your data table ready, you can create an Excel chart to graph the equation.
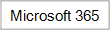
Now let’s put this outline to use and graph the y = (x.cos(x).sin(x))² equation. This equation is tough to imagine just by looking at it, but you can save yourself the burden by quickly graphing the equation with Excel.
1. Input the X Values
A graph needs X and Y values. You can enter the domain you want to graph in the X values, and then calculate the Y values with a formula in the next step. It’s a good idea to create a table for your data, as it will enable Excel’s autofill feature.
The smaller the increment between your X values is, the more accurate your graph will be. We’re going to have each X value increase by 1/4 in this table. Here’s how you can automatically input the X values:
- Type in the first value in a cell. In this example, we’re going to type -3 in cell A3.
- Select the cell below. That’s A4 in our case.
- In the formula bar, enter the formula below:
=A3+1/4 - Press Enter.
- Grab the fill handle and drop it into the cells below.
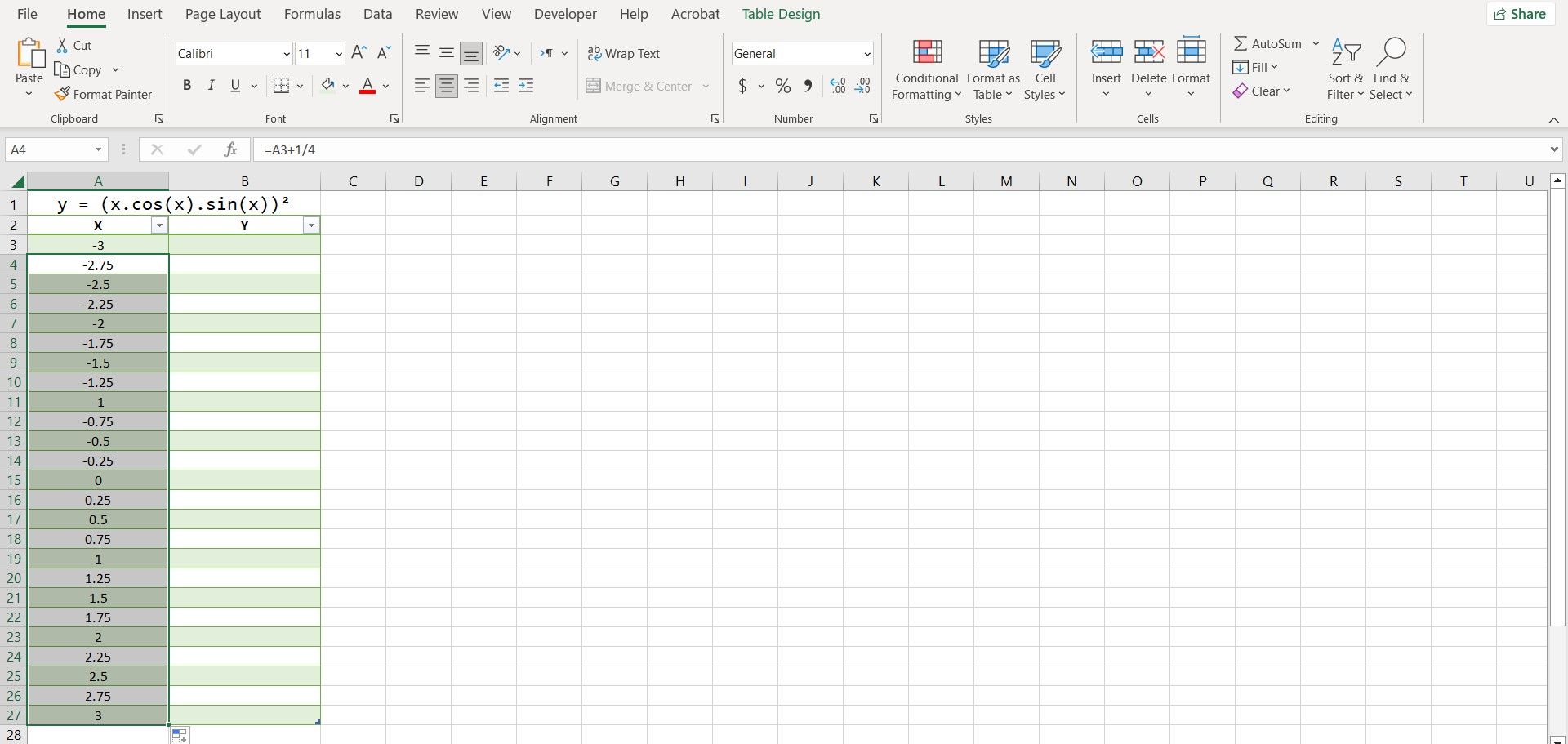
Excel will now fill in all the other X values. The advantage of using a formula to input the values is that you can now quickly change the values by editing the first value or altering the formula.
2. Create a Formula to Calculate the Y Values
With the X values in place, it’s time to calculate the Y values. You can calculate the Y values by translating the trigonometric equation into Excel’s language. It’s essential that you have an understanding of the trigonometric functions in Excel to proceed with this step.
When creating your formula, you can use a circumflex (^) to specify the power. Use parentheses where needed to indicate the order of operations.
- Select the first cell where you want to calculate the Y value. That’s B3 in our case.
- Go to the formula bar and enter the formula below:
=(A3*COS(A3)*SIN(A3))^2 - Press Enter.
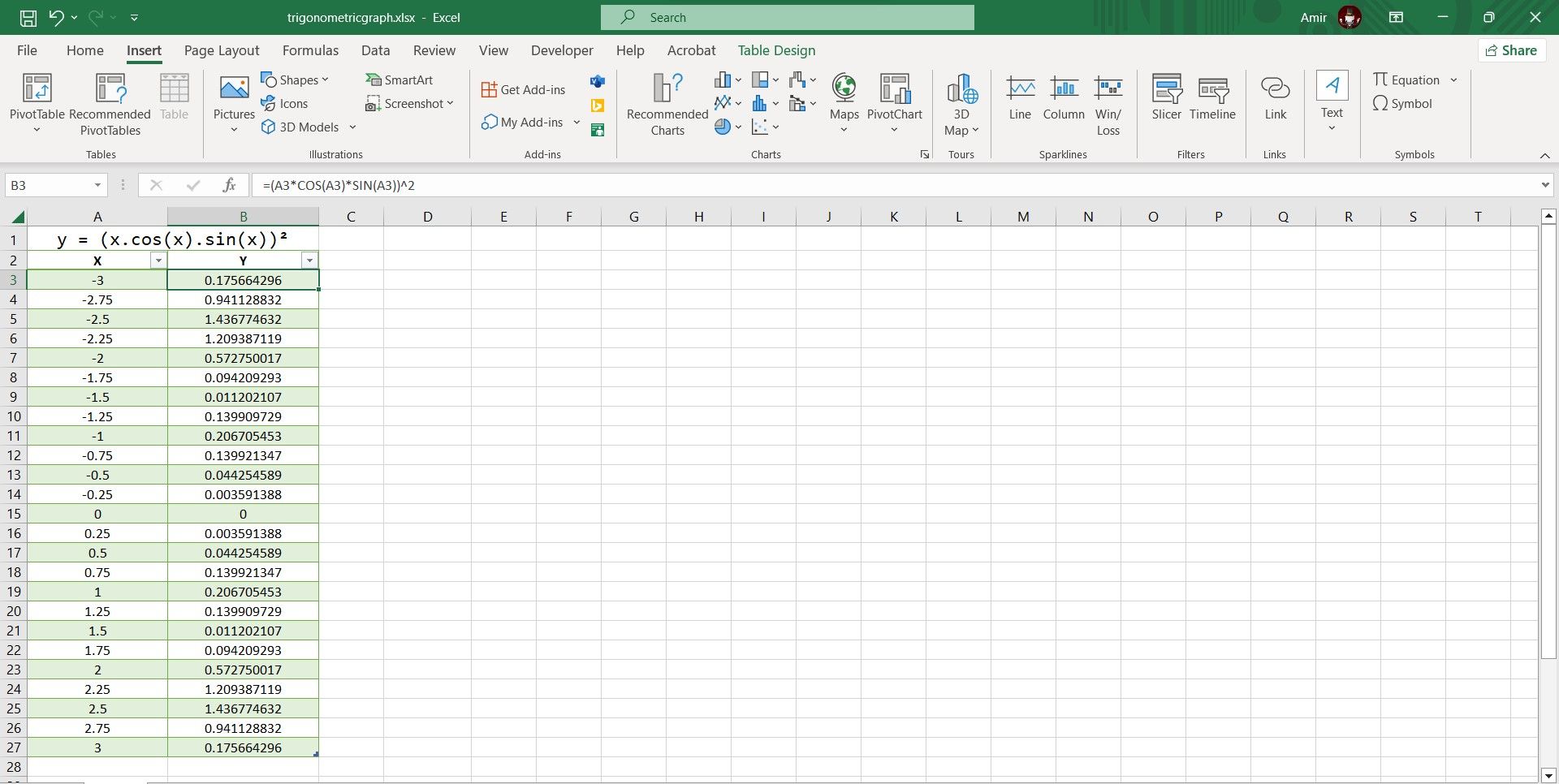
Excel will now calculate all Y values in the table. Excel’s trigonometric functions use radians, so this formula will perceive the X values as radians as well. If you want your X-axis to be on a pi-radian scale rather than a radian scale, you can multiply the cell reference by pi using the PI function in Excel.
=(A3*PI()*COS(A3*PI())*SIN(A3*PI()))^2
The formula above will output the Y values for the same trigonometric equation, but the values will be on a pi-radian scale instead.
3. Create a Scatter Plot Chart
A scatter plot is the best way to graph a trigonometric equation in Excel. Since you’ve got your X and Y values ready, you can graph your equation with a single click:
- Select the table containing the X and Y values.
- Go to the Insert tab.
- In the Charts section, click on Scatter and then select Scatter with Smooth Lines.
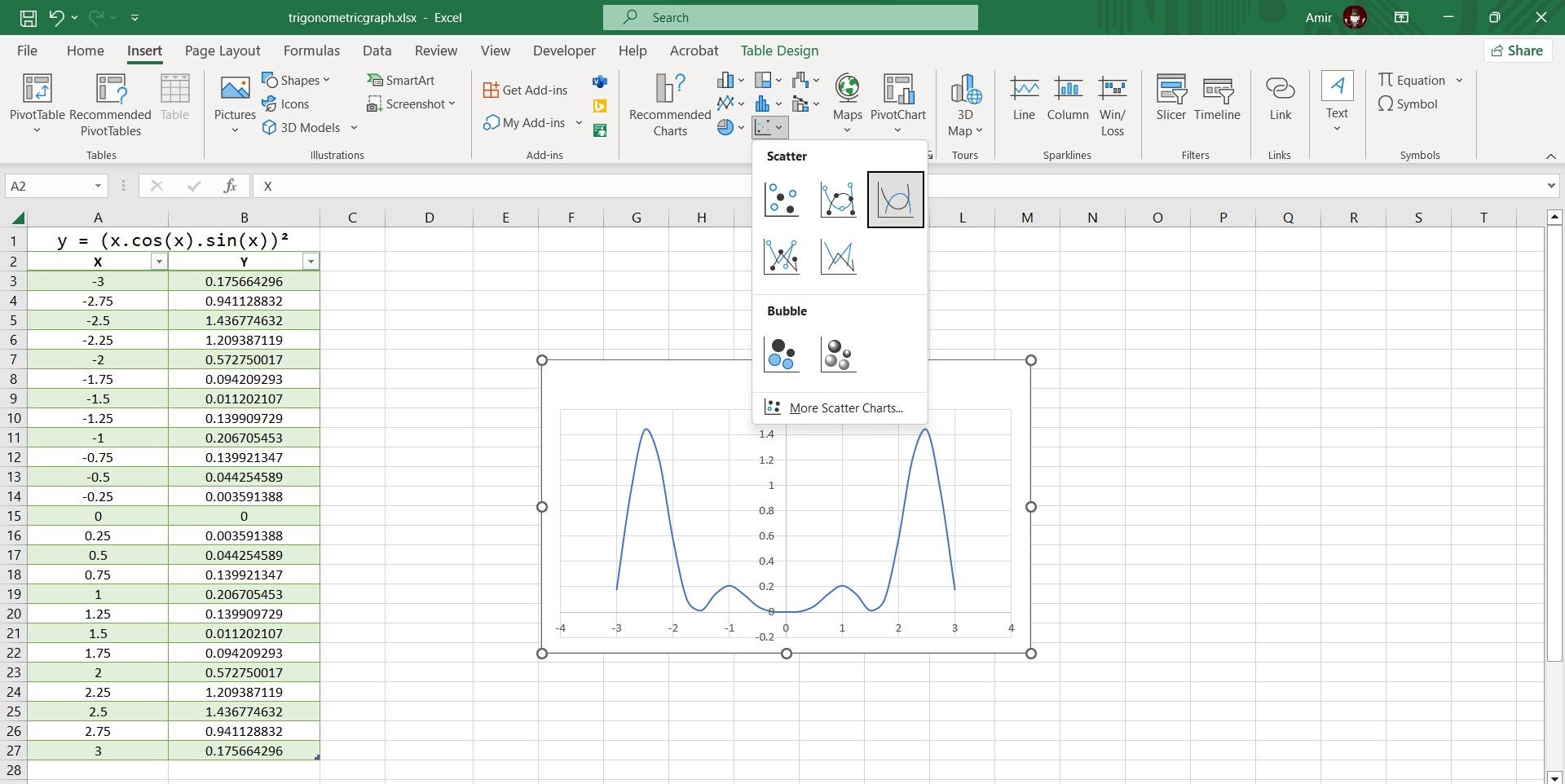
There you have it! You can now inspect the graph to better understand the equation’s behavior. This is the last step if you’re looking for a quick visualization, but if you want to present the graph, you can fully customize the Excel chart to properly graph the trigonometric equation.
4. Modify the Excel Chart
Although the chart does display the graph, you can make some changes to improve the chart’s readability and make it more presentable. There are lots of things you can customize to improve the chart, and in the end, it’s a matter of personal preference. Still, here are some adjustments that can always improve your trigonometric graph.
I. Set the Axis Units and Add Tick Marks
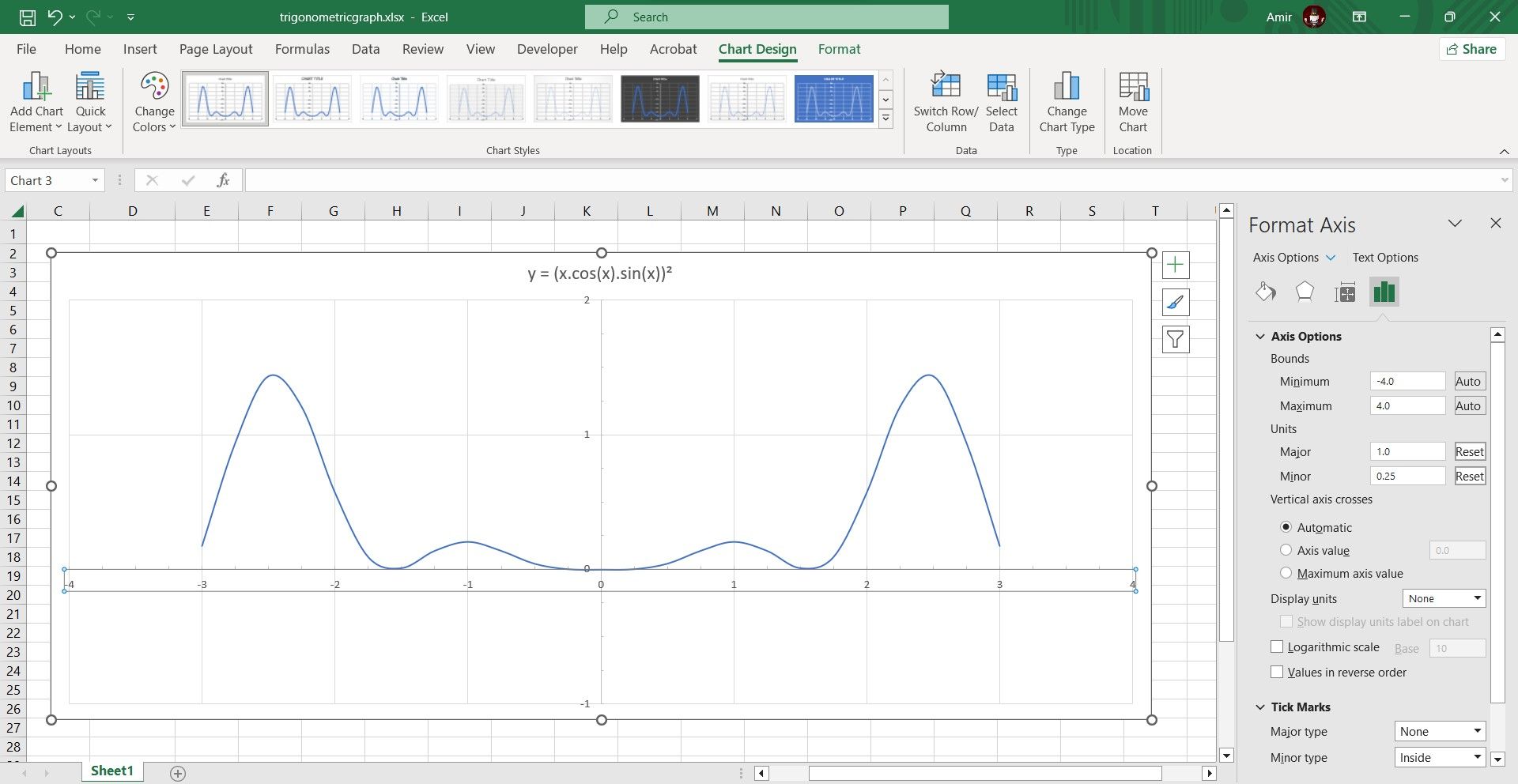
If you take a closer look at your chart, you’ll see that the horizontal and vertical grid lines aren’t the same unit. Here’s how you can fix that:
- Click on the chart to select it.
- Double-click the axis. This will bring up Format Axis on the right.
- In Format Axis, find Units under Axis Options and change Major and Minor.
- Go to Tick Marks and change Minor type to what you want.
Repeat the same process for the other axis, and make sure that you use the same major and minor units for both. Your graph should look tidier now.
II. Add Minor Gridlines
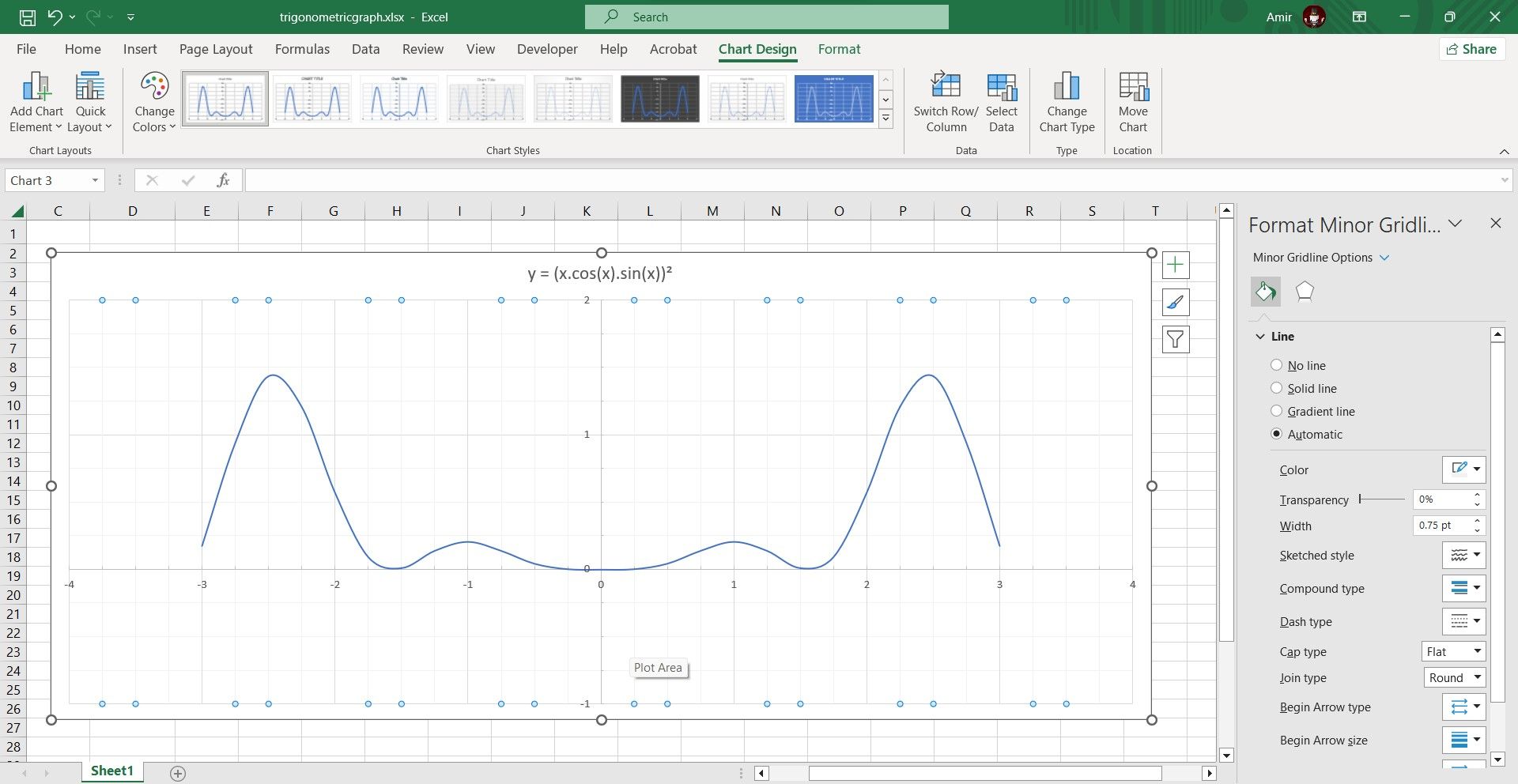
You can add minor gridlines to make the graph easier to read. To do this, simply right-click on the axis and then select Add Minor Gridlines. Repeat the process for the other axis to add gridlines there as well. You can then right-click the axis and select Format Minor Gridlines to change their appearance.
III. Add Axis Titles
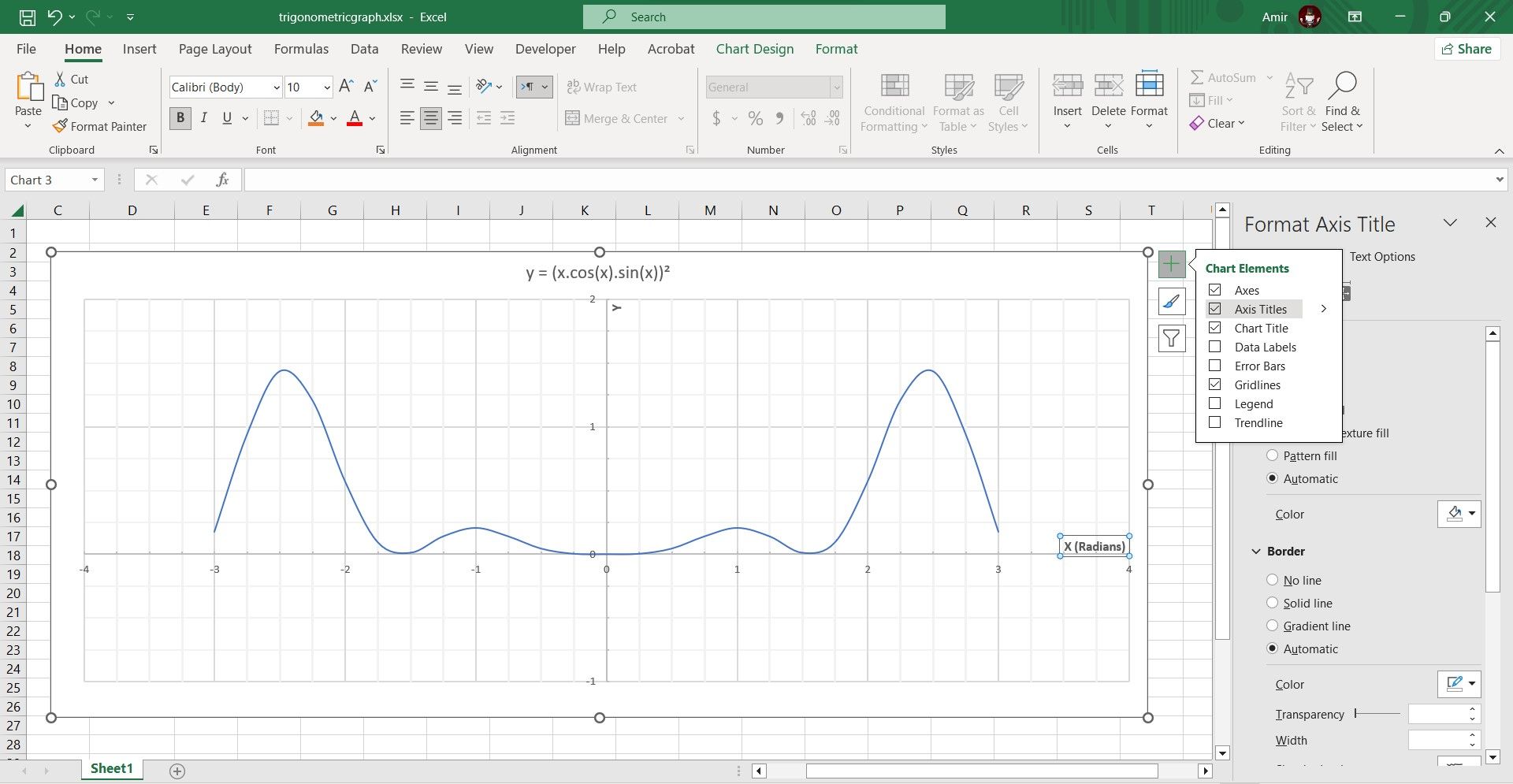
Although it’s obvious that the horizontal axis is displaying the X values, you can add a title to specify that the values are in radians. This prevents confusion with pi-radians.
- Select the chart.
- Click on Chart Elements on the top right. This is marked with a + sign.
- Select Axis Titles.
- Double-click the axis titles and edit the text.
IV. Add Data Callouts
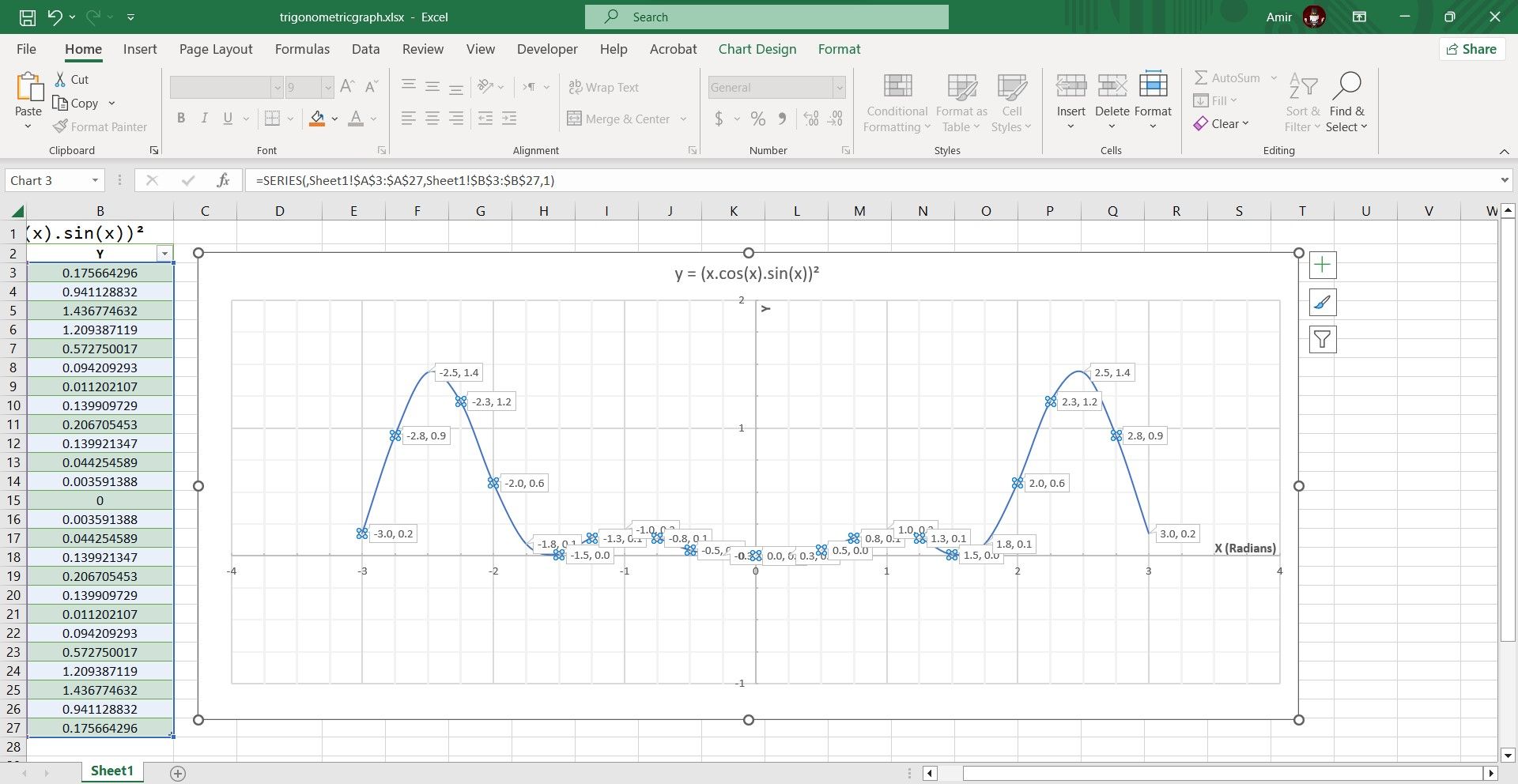
Finally, you can add callouts to identify the minimum and maximum points on your graph. Here’s how you can do that:
- Select the chart.
- Right-click the series line.
- Go to Add Data Labels and then select Add Data Callouts.
If some of the callouts seem unnecessary to you, you can individually select them and then press Del on your keyboard to delete the callout.
Graph It Properly With Excel
Visualizing an equation is vital to understanding it. This is especially true when you’re dealing with complex trigonometric equations and can’t quickly guess the values. Well, there’s no need to tax your brain to get a mental image of an equation. You can use Excel to efficiently graph a trigonometric function.
The only elements that you need to manually input are the starting X value and the increment. From there, you can have Excel automatically fill in the X values. Thanks to its array of trigonometric functions, you can easily turn your equation into an Excel formula and calculate the Y values as well.
With both the X and Y values set out in a table, graphing the equation is only a matter of selecting the data and creating a scatter plot to visualize it.
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Таблица данных:
Для решения используем формулу:
=B2*B3*SIN(РАДИАНЫ(B1))
Описание аргументов:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
=COS(РАДИАНЫ(A2:A16))
Вычислим значения для всех значений углов. Полученный результат:
Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.
Аналогичным способом создадим таблицу синусов в Excel:
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Исходные данные:
Формула для нахождения синусов гиперболических:
=SINH(A2:A12)
Формула для нахождения косинусов гиперболических:
=COSH(A2:A12)
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
=SIN(число)
Синтаксис функции SINH:
=SINH(число)
Синтаксис функции COS:
=COS(число)
Синтаксис функции COSH:
>=COSH(число)
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
Примечания 1:
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
Примечения 2:
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
Скачать примеры тригонометрических функций SIN и COS
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Пахомов Н.А. 1Селищев Д.В. 1
1МБОУ «СОШ №12»
Утяганова З.З. 1
1МБОУ «СОШ № 12»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Постановка проблемы и актуальность исследования. Школьный курс математики, начиная с начальной ступени и до 11 класса, включает в себя большое количество способов решения различных видов уравнений и систем уравнений. Некоторые уравнения решаются нестандартными методами, которые применить может небольшая часть выпускников школ. Анализ изученной литературы показал, что уравнения и системы уравнений встречаются в различных отраслях промышленности и экономики. И как правило, эти уравнения выглядят не так привлекательно, как школьные, и имеют нецелые решения. Чтобы автоматизировать процесс решения уравнений и систем уравнений, мы решили найти способы с помощью электронных таблиц. Электронные таблицы широко используются в профессиональной деятельности специалистов самых разных областей науки, производства и сферы услуг, в различных государственных и коммерческих организациях и фирмах. Кроме того, электронные таблицы могут быть использованы при решении бытовых задач, таких, как создание домашней картотеки книг или компакт-дисков, ведение учета коммунальных платежей или домашнего бюджета и т.п.
К настоящему времени существует достаточное количество различных учебных материалов, где подробно раскрываются способы решения производственных задач с помощью уравнений и систем уравнений [1, 3, 7, 8, 9], а также методы их решения с помощью электронных таблиц [2, 4, 5, 7-9].
Тем не менее, в ходе исследования было обнаружено, что недостаточно исследованы способы решения уравнений высших степеней, а также уравнений, имеющих бесконечное множество решений (например, тригонометрических).
Актуальность обозначенной проблемы определила выбор темы исследования: «Решение уравнений средствами приложения Microsoft Excel».
Цель работы: исследовать инструменты приложения Microsoft Excel для решения уравнений разного порядка.
Объект исследования: приложение Microsoft Excel.
Предмет исследования: применение инструментов ПОДБОР ПАРАМЕТРА и ПОИСК РЕШЕНИЯ приложения Microsoft Excel при решении уравнений.
Гипотеза исследования: использование инструментов приложения MS Excel ПОДБОР ПАРАМЕТРА и ПОИСК РЕШЕНИЯ значительно упрощает процесс решения уравнений различного вида.
Задачи исследования:
Изучить литературу по применению уравнений при решении производственных задач.
Изучить литературу по использованию приложения Microsoft Excel в практической деятельности.
Рассмотреть способы решения уравнений с помощью инструментов ПОДБОР ПАРАМЕТРА и ПОИСК РЕШЕНИЯ приложения Microsoft Excel.
Создать видеокурсы по решению различных видов уравнений.
Теоретическая значимость: проведен анализ ряда источников по возможностям приложения Microsoft Excel при решении уравнений разного порядка.
Практическая значимость: предложены способы решения уравнений высших порядков и тригонометрических уравнений с помощью приложения MS Excel, систематизирован и обобщен материал в форме видеокурсов.
Методы исследования: теоретический анализ и обобщение научной литературы и материалов сети Интернет; проведение экспериментов по решению уравнений различного вида с помощью инструментов Подбор параметра и Поиск решения; создание видеокурсов по использованию инструментов Подбор параметра и Поиск решения при решении различных уравнений.
УРАВНЕНИЯ В РАЗЛИЧНЫХ ОТРАСЛЯХ
В современном обществе уравнения нашли свое применение во многих отраслях хозяйства и производства, а также практически во всех новейших технологиях. Конечно, математика, как и любая другая наука, не стоит на месте. Уже выработано достаточно способов решения различных видов уравнений различных степеней. Появление компьютеров и стремительное развитие информационных технологий позволило в несколько раз упростить задачи нахождения корней различных уравнений. В данной главе, в качестве примеров, нами представлены виды уравнений, решаемых в некоторых отраслях хозяйства и производства.
1.1. Уравнения при решении экономических задач
Пример 1.1.1. Рассчитать, с какого возраста необходимо уплачивать по 1000 рублей в качестве дополнительных страховых взносов, чтобы получить прибавку к пенсии в 2000 рублей за счет участия в государственной программе софинансирования?
Входные данные:
ежемесячные отчисления – 1000 руб.;
период уплаты дополнительных страховых взносов – расчетная величина (пенсионный возраст (в примере – для мужчины) минус возраст участника программы на момент вступления);
пенсионные накопления – расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза;
ожидаемый период выплаты трудовой пенсии – 228 мес. (19 лет);
желаемая прибавка к пенсии – 2000 руб.
пенсионные накопления – расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза).
Пусть х – возраст, с которого необходимо производить отчисления. Тогда прибавка к пенсии (в размере 2000 рублей) будет рассчитана по формуле:
Получили линейное уравнение, в котором необходимо найти параметр x.
Пример 1.1.2. Пусть дана структура цены договора: собственные расходы, прибыль, НДС. Известно, что собственные расходы составляют 150 000,00 руб., НДС 18%, а целевая стоимость договора 200 000,00 руб. Необходимо подобрать такое значение прибыли, при которой стоимость договора равна Целевой (то есть Расхождение должно равняться нулю) [8].
Пусть х – прибыль. Тогда цену продукции будем рассчитывать как сумму Собственных расходов и Прибыли: 150000+х. НДС от цены продукции будет равен (150000+х)*0,18. Стоимость договора вычислим как сумму Цены продукции и НДС: (150000+х)+ (150000+х)*0,18=(150000+х)*1,18.
Итак, получили уравнение (150000+х)*1,18=2000.
Пример 1.1.3., решение которого также сводится к линейному уравнению. Определить максимальную сумму кредита, которую мы можем себе позволить взять в банке, если известно, что ежемесячно мы можем выплачивать сумму в размере 1 800,00 руб. Известны также процентная ставка по кредиту и срок, на который мы хотим взять кредит (количество месяцев) [8].
Пример 1.1.4, решение которого сводится к системе линейных уравнений. Предприятию для изготовления наборов елочных украшений необходимо изготовить их составные части — шар, колокольчик, мишура [9].
В свою очередь для изготовления этих составных частей необходимы три вида сырья — стекло (в г), папье-маше (в г), фольга (в г), потребности в котором отражены в таблице.
Требуется:
1) определить потребности в сырье для выполнения плана по изготовлению комплектов первого, второго, третьего и четвертого вида в количестве соответственно x1, x2, x3 и x4 штук;
2) провести подсчеты для значений x1 = 500, x2 = 400, x3 = 300 и x4=200.
Для решения данной задачи необходимо найти корни системы линейных уравнений:
y1 = 5· (5x1 + 6x2 + 8x3 + 10x4) = 25x1 + 30x2 + 40x3 + 50x4
y2 = 4· (3x1 + 4x2 + 6x3) = 12x1 + 16x2 + 24x3
y3 = 3· (5x1 + 6x2 + 8x3 + 10x4) + 75· (3x2 + 5x3 + 8x4) = 15x1 + 243x2 + 399x3 + 630x4
Уравнения в электроэнергетике
Рассмотрим применение уравнений в электроэнергетике [3, С. 11].
Пример 1.2.1. Приведена схема электрической цепи постоянного тока. Найти токи в ветвях цепи.
Для решения данной задачи необходимо составить и решить систему линейных уравнений на основе законов Кирхгофа (здесь не рассматривается процесс составления системы уравнений):
Уравнения в транспортной отрасли
Пример 1.3.1. Для решения задач проектирования транспортных сооружений и принятия обоснованных решений при планировании, контроле и управлении технологическими процессами дорожного строительства необходимо выявлять взаимосвязи между параметрами, определяющими ход этих процессов, и представлять их в количественной форме – в виде математических моделей. В связи с этим на практике часто применяется регрессионный анализ.
Регрессионный анализ – метод моделирования измеряемых данных и исследования их свойств путем выявления взаимосвязи между зависимой переменной y и одной или несколькими независимыми переменными x1, x2, …, xn.
Независимые переменные иначе называют факторами, аргументами, или регрессорами, а зависимые переменные – функциями, откликами, результирующими, объясняемыми.
На практике уравнение регрессии чаще всего подбирается в виде линейной и нелинейной функции (наиболее простые – гипербола, экспонента и парабола) [1, С.7-8].
Пример 1.3.2. Транспортная задача
Требуется составить план перевозок, при котором все запасы (строительных материалов или конструкций) поставщиков (АБЗ, ЦБЗ, карьеры) будут вывезены, спрос потребителей (объекты дорожных работ, участки) полностью удовлетворен, и при этом суммарные транспортные издержки будут минимальными (стоимость перевозок, сроки, другие ресурсы).
При решении данной задачи составляется система линейных уравнений относительно xij – количества груза (материалов), перевозимого из пункта i в пункт j [1, С. 14].
Уравнения в строительной отрасли
Пример 1.4.1. Вычислить стрелу прогиба ( в середине) прямоугольной пластины. Прямоугольная пластина загружена равномерно распределенной нагрузкой интенсивностью q. Пластина защемлена по контуру, края неподвижны [7].
Стрела прогиба вычисляется как корень нелинейного уравнения на интервале [0; 0,05]:
Пример 1.4.2. Определить критическую силу для стальной колонны двутаврового сечения, если известны длина колонны L, модуль упругости стали Е, коэффициент жесткости упругой опоры С, момент инерции I.
Критическая сила вычисляется по формуле:
где – коэффициент приведения длины колонны, который определяется по формуле
Параметр находится из решения уравнения
на интервале [3,2; 4,6].
ИСПОЛЬЗОВАНИЕ ИНСТРУМЕНТА ПОДБОР ПАРАМЕТРА ПРИ РЕШЕНИИ УРАВНЕНИЙ
При решении производственных задач достаточно часто возникает проблема подбора параметра. Например, в экономических расчётах применяются алгоритмы расчёта стоимости товара, расчёта фонда заработной платы, прибыли от деятельности предприятия, которые, в свою очередь, зависят от множества изменяемых и неизменяемых факторов [4, 5].
Пример 2.1. Итак, сначала, с целью изучения принципа работы надстройки ПОДБОР ПАРАМЕТРА, рассмотрим решение линейного уравнения вида Ах+В=С с помощью приложения Microsoft Excel.
В ячейку В3 введем любое первоначальное значение переменной x, например, 0, а в ячейку С1 введем левую часть уравнения в виде формулы: =B1*B3+B2. Вызовем диалоговое окно ПОДБОР ПАРАМЕТРА с помощью команд Данные – Анализ «что-если» — Подбор параметра. В этом окне в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение – ожидаемый результат (т.е. 7), в поле Изменяя значение в ячейке – ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
Рисунок 1 – Диалоговое окно ПОДБОР ПАРМЕТРА
После нажатия кнопки ОК, получим результат.
Рисунок 2 – Решение линейного уравнения с помощью диалогового окна ПОДБОР ПАРАМЕТРА
Известно, что инструмент Подбор параметра в основном используется при решении линейного уравнения. Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (которое имеет два корня), то инструмент найдет решение, но только одно, то, которое ближе к начальному значению.
Пример 2.2. Рассмотрим пример решения квадратного уравнения. Найдем корни квадратного уравнения . Сначала создадим первоначальную таблицу.
Рисунок 3 – Первоначальные данные квадратного уравнения
Зададим любое первоначальное значение х, например, 0. Далее воспользуемся инструментом ПОДБОР ПАРАМЕТРА.
Получили результат: 2.
Второй корень найдем, задав другое начальное значение, например, 5. И проделаем те же действия.
ИСПОЛЬЗОВАНИЕ НАДСТРОЙКИ ПОИСК РЕШЕНИЯ ПРИ РЕШЕНИИ УРАВНЕНИЙ
Пример 3.1. Рассмотрим решение квадратного уравнения (с предыдущей главы) с помощью инструмента ПОИСК РЕШЕНИЯ.
Введем начальные данные
Рисунок 4 – Первоначальные данные квадратного уравнения
Вызываем инструмент ПОИК РЕШЕНИЯ, выбрав команду ДАННЫЕ.
Рисунок 5 – Надстройка ПОИСК РЕШЕНИЯ при решении квадратного уравнения
В поле «Установить целевую ячейку» выбираем ячейку с формулой квадратного уравнения С1. Далее установим переключатель в положение «Равной значению 0». В поле «Изменяя ячейки» добавим ячейку В4. Нажмем кнопку «Выполнить». Получили решение.
Рисунок 6 – Решение квадратного уравнения, найденного с помощью надстройки ПОИСК РЕШЕНИЯ
При решении данным способом также получили только один корень.
Для нахождения второго корня зададим другое начальное значение переменной х, например, равно 1.
Однако, на любом производстве чаще всего приходится сталкиваться с уравнениями высших степеней.
Пример 3.2. Рассмотрим уравнение пятой степени –3x5+x3+2x2–3x–3=0.
Прежде чем находить корни уравнения (а у этого уравнения должно быть максимум 5 корней), выясним, в каких интервалах содержатся эти корни. Воспользуемся графиком функции, с помощью которого мы наглядно увидим промежутки расположения корней уравнения.
Построим график функции. Для этого в ячейке А1 введем «х», в ячейке В1 введем «у». Значения х внесем в ячейки А2:А22, значения у будем рассчитывать в ячейках В2:В22 соответственно.
Рисунок 7 – Формула уравнения пятой степени
Известно, что корень уравнения (уравнение записано в виде f(x)=0) – это такое значение аргумента, при котором значение функции равно нулю. В графическом представлении – это может быть точка пересечения или касания графика функции с осью абсцисс.
Построим график функции.
Рисунок 8 – График функции на промежутке [–10; 10] с шагом 1
График функции показывает, что уравнение, имеет единственный действительный корень (остальные – комплексные), который находится в промежутке [–1; 0].
Найдем его с помощью инструмента ПОИСК РЕШЕНИЯ. Для этого в таблице выберем точку, близкую к решению уравнения, например, –0,7.
Рисунок 9 – Нахождение корня уравнения с помощью надстройки
ПОИСК РЕШЕНИЯ
Установим с помощью команды «Формат ячеек» относительную погрешность 0,0001.
Итак, решением уравнения является х≈ –0,668.
Таким образом, получили алгоритм решения уравнения высшей степени:
поиск интервалов, в которых содержится только по одному корню;
уточнение корня в выбранном интервале (определением значения корня с заданной точностью).
Тригонометрические уравнения
Особенность тригонометрических уравнений заключается в том, что они имеют бесконечно много решений, и все решения отличаются между собой на определенный период.
Пример решения одного из тригонометрических уравнений подробно рассмотрен в Приложении 1.
В Приложении 2 также рассмотрен пример нахождения решений системы линейных уравнений.
ЗАКЛЮЧЕНИЕ
В результате проведенной исследовательской работы было выявлено, что решение различных уравнений и систем уравнений применяется во многих отраслях экономики и промышленности.
В ходе исследований мы научились находить корни уравнений и систем линейных уравнений с помощью инструментов ПОИСК РЕШЕНИЯ и ПОДБОР ПАРАМЕТРА приложения Microsoft Excel, создали видеокурсы по решению уравнений с помощью приложения Microsoft Excel.
Таким образом, поставленные цель и задачи данного исследования были выполнены.
Кроме того, экспериментальным путём, было выявлено, что использование инструментов ПОИСК РЕШЕНИЯ и ПОДБОР ПАРАМЕТРА приложения Microsoft Excel значительно упрощает процесс нахождения корней уравнений и систем уравнений. Таким образом, поставленная в начале исследования гипотеза подтвердилась.
Результаты выполненной работы позволят использовать возможности изученных инструментов в будущей профессиональной деятельности, особенно если выполнение задания будет содержать сложные расчеты.
Исследование может быть полезно не только учащимся в учебной деятельности, но и специалистам различных отраслей экономики и промышленности, занимающимся проектированием объектов.
Результаты проведенной работы могут быть использованы при изучении других возможностей приложения Microsoft Excel.
На этом исследование не закончено. Мы планируем продолжить рассмотреть способы решения систем нелинейных уравнений с помощью Microsoft Excel.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ:
Богомолов, С.В. Экономико-математические методы проектирования транспортных сооружений [Электронный ресурс] : методические указания к практическим занятиям и самостоятельной работе для студентов специальности 270205 «Автомобильные дороги и аэродромы» всех форм обучения / С.В. Богомолов. – Электрон. дан. – Кемерово: КуГТУ, 2013. – 30 с.
Информатика для экономистов. Практикум: учебное пособие для бакалавров / под ред. В.П. Полякова, В.П. Косарева. – М.: Издательство Юрайт, 2013. – 343 с.
Митрофанов, С.В. Использование системы MathCAD при решении задач электротехники и электромеханики : методические указания к выполнению РГЗ по дисциплине «Прикладные задачи программирования» / С.В. Митрофанов, А.С. Падеев. – Оренбург: ГОУ ОГУ, 2005. – 40 с.
Репкин, Д.А. Применение MS EXCEL для решения прикладных задач в экономике: учебное пособие для студентов направления 080100 «Экономика» всех профилей подготовки, всех форм обучения / Д.А. Репкин. — Киров: ПРИП ФГБОУ ВПО «ВятГУ», 2012. [Электронный ресурс]
Федулов, С.В. Использование MS Excel в финансовых вычислениях : учеб.-метод. пособие / С.В. Федулов. – Екатеринбург: Изд-во УрГУПС, 2013. – 94 с.
Численные методы. Часть 1: Методические указания к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика» / Сост. Ф.Г. Ахмадиев, Ф.Г. Габбасов, Р.Ф. Гизяятов, И.В. Маланичев. – Казань: Изд-во казан. гос. архитект-строит. ун-та, 2013 – 34 с.
Решение нелинейных уравнений в Excel https://www.altstu.ru/media/f/lr3nelin-uravn.pdf – сайт Алтайского государственного технического университета им. И.И. Ползунова
http://excel2.ru/articles/podbor-parametra-v-ms-excel – сайт Excel2.ru
https://knowledge.allbest.ru/mathematics/3c0b65625b3ad68b4c43a89421306d37_0.html – сайт allbest
Приложение 1
Решение тригонометрического уравнения с помощью инструмента ПОИСК РЕШЕНИЯ
Найдем решения уравнения .
Решать данное уравнение будем аналогично примеру 3.1. То есть:
Протабулируем функцию и построим ее график;
Уточним корни уравнения.
Протабулируем функцию на промежутке [-10; 10]. Сначала в ячейках А2:А22 зададим значения аргумента x и найдем значения функции в данных точках, которые запишем в ячейки В2:В22.
В ячейке В2 укажем формулу: =A2*TAN(A2)-1
Рисунок 1 – Таблица значений аргумента и функции
на отрезке [-10; 10] с шагом 1
Построим график функции на данном отрезке.
Рисунок 2 – График заданной тригонометрической фнкции
Проанализировав график и таблицу значений функции, видим, что корни уравнения расположены в промежутках (–10; –9), (–7; –6); (–4; –3) и т.п., то есть на тех промежутках, где функция меняет знак и пересекает ось Ох.
Уточним первый корень уравнения. Для этого установим курсор в ячейке В2 и вызовем инструмент ПОИСК РЕШЕНИЯ.
Рисунок 3 – Надстройка ПОИСК РЕШЕНИЯ
Итак, первый корень получен.
Рисунок 4 – Решение тригонометрического уравнения
Аналогично, найдем корень уравнения, задав начальное значение х=–7 и х= –4.
Рисунок 5 – Три корня тригонометрического уравнения
Учитывая, что период функции тангенса равен π, найдем разницу между корнями уравнения: получили 3,04 и 3,01. Итак, разность между корнями равна примерно 3. Следовательно, следующие корни уравнения: – 0,4; 2,6; и т.п.
Таким образом, для нахождения корней тригонометрического уравнения, необходимо проделать те же действия, что и при решении уравнений высших степеней.
Приложение 2
Использование инструмента ПОИСК РЕШЕНИЯ при решении систем линейных уравнений
С помощью инструмента ПОИСК РЕШЕНИЯ можно решить и систему линейных уравнений [6, С. 31].
Пример 4.1. Решим следующую систему линейных уравнений
Для этого зададим ячейки, где будут записаны решения системы уравнений. Пусть это будут ячейки A2:D2.
Рисунок 1 – Создание таблицы для решения системы линейных уравнений
Введем в ячейки, предназначенные для решения (А2:D2) произвольные величины, лежащие в области определения (начальные значения).
В ячейки (А3:D3) внесем формулы, по которым должны вычисляться правые части уравнений: (=8*A2+4*B2-6*C2; =–2*А2–4*С2–6*D2; =6*А2+4*В2+4*С2+6*D2; = 4*А2+6*В2+8*С2+8*D2)
Рисунок 2 – Первоначальная таблица для решения системы линейных уравнений
Запустим ПОИСК РЕШЕНИЯ из меню ДАННЫЕ. Выберем одну из ячеек, содержащих формулы, в качестве целевой ячейки (например, А3), сделаем её равной –18.
В поле ИЗМЕНЯЯ ЯЧЕЙКИ вставим ячейки А2:D2. Добавим ограничения, нажимая на кнопку ДОБАВИТЬ: В3=–2; С3=–14; D3=–6.
Рисунок 3 – Диалоговое окно надстройки ПОИСК РЕШЕНИЯ
Рисунок 4 – Диалоговое окно ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ
Нажмем на кнопку ВЫПОЛНИТЬ. Получим решение:
Рисунок 5 – Решение системы линейных уравнений
Таким образом, решение системы линейных уравнений найдено. Если проверить решение (х1=–5, х2=1, х3=–3, х4=4) подстановкой, то получим верные равенства.
Просмотров работы: 2160
Электронные таблицы EXCEL можно
использовать при изучении многих разделов
физики, математики и других предметов. Одной из
тем, является математическая тема: «Анализ
тригонометрических функций». Данная работа
будет посвящена использованию электронных
таблиц EXCEL в анализе тригонометрических функций.
В ней, используя знания и навыки работы с
мастером функций и диаграмм Excel, будет проведен
анализ тригонометрических функций с проведением
расчетов по формулам и с построением графиков,
используя ссылки.
Для анализа элементарных функций необходимо
уметь решать следующие задачи:
- определение возрастания или убывания функции
на заданном интервале, - определение максимума (минимума) данной функции
на заданном интервале, - определение четности данной функции на
заданном интервале, - определение периодичности данной функции на
заданном интервале,
Каждая из этих задач может быть решена разным
способом. В данной работе рассмотрен один из
вариантов их решения.
ЗАДАЧА №1. ИССЛЕДОВАНИЕ ФУНКЦИИ НА
ВОЗРАСТАНИЕ.
Признаком возрастания или убывания заданной
функции на заданном отрезке можно предложить
результат действия функции EXCEL – ЗНАК(…) –,
определяющей знак числа: =ЗНАК(f(x2) – f(x1)),
где
x1, x2 – значения концов заданного интервала,
f(x2) – последующее значение функции,
f(x1) – предыдущее значение функции.
При результате действия функции ЗНАК(…) равном 1
функция возрастает; а если результат равен (–1),
то функция убывает на заданном отрезке.
ЗАДАЧА №2. ИССЛЕДОВАНИЕ ФУНКЦИИ НА
МАКСИМУМ И МИНИМУМ.
Исследования поведения любой функции Y=f(X)
проводится в определенном интервале [A,B]. Для
этого в EXCEL имеются соответствующие функции.
Для этого воспользуемся следующим алгоритмом:
- выделить ячейку для результата,
- задать соответствующую функцию в мастере
функций, - замаркировать диапазон значений, для которых
определяем максимальное или минимальное
значение, - запустить на выполнение.
ЗАДАЧА №3. ИССЛЕДОВАНИЕ ФУНКЦИИ НА
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ.
Предлагается определение четности или
нечетности данной функции в EXCEL проводится в два
этапа:
- проверка равенства модулей f(x) и f(–x) для всех
значений аргумента, - определение четности или нечетности заданной
функции.
Проверку равенства модулей можно проводить на
основе следующей формулы: ABS(ABS(f(x)) – ABS( f(–x)))
Значение данной сумы для всех без исключения
строк должно быть равно «0», в противном случае не
может быть речи о четности или нечетности
заданной функции.
Очевидно, что для четной или нечетной функции
автосумма столбца значений данной функции равна
«0».
Для определения четности заданной функции
воспользуемся формулой:
ABS (f(x) – f(–x))
И определим для полученных по этой формуле
значений автосумму. Если автосумма равна нулю, то
заданная функция – четная, иначе – не четная.
Просматривая результаты расчетов, можно сделать
вывод, что функция Y=SIN(X) НЕЧЕТНАЯ.
ЗАДАЧА №4. ИССЛЕДОВАНИЕ ФУНКЦИИ НА
ПЕРИОДИЧНОСТЬ.
Для полученных значений определяем для каждого
значения аргумента значение формулы: =ABS(Sin(x) –
Sin(x+Pi))
И для всех, полученных по данной формуле
значений, определяем автосумму. Если автосумма
равна нулю, то данная функция действительно
имеет период равный 2*Pi.
Просматривая результаты расчетов, можно сделать
вывод, что функция Y=SIN(X) ПЕРИОДИЧЕСКАЯ, период
этой функции T=2*PI .
Практические задания для выполнения в
электронных таблицах
ЗАДАНИЕ N 1: «АНАЛИЗ ФУНКЦИИ Y=SIN(X)
НА МАКСИМУМ, МИНИМУМ»
Фамилия
Класс
Написать на 1 листе, начиная в ячейке A1, А2
тему урока, A3 задание, в А4 фамилию, класс.
В пятой строке сделать надписи:Номер; Угол X; SIN(X).
С помощью автозаполнения с шестой строки ввести
в столбец A номера точек (17) от 0 до 16, в столбец B
значение углов X от –360 градусов до +360 через 45
градусов, по которым будут рассчитаны значения
функции в этих точках и построен график функции
Y=SIN(X).
В ячейке E24 сделать надпись: Конст. ПИ, в F24 ввести
значение константы ПИ, выбрав его с помощью
мастера функций из категории
«Математические».
В столбце С посчитать значения функции Y=SIN(X) ,
задав относительные ссылки (B6, B7,…, B22) на значения
угла в градусах для столбца В, и абсолютную
ссылку $F$24 на ячейку F24,при
переводе значений углов из градусов в радианы.
Пример формулы расчета в ячейке С6:
=SIN(B6*$F$24/180)
В ячейке B23 сделать надпись МАКС=, в C23 определить
значение максимума для функции SIN(X) по столбцу С
от C6 до C22.
В ячейке B24 сделать надпись МИН=, в C24 определить
значение минимума для функции SIN(X) по столбцу С
от C6 до C22.
Внизу под
вычислениями построить
точечный график функции Y=SIN(X) по диапазону
B6:C22.
| А | B | C | D | E | |
| Номер Nн– |
X | SIN(X) | |||
| 0 | –360 | 2,4503E–16 | |||
| 1 | –315 | 0,707106781 | |||
| 2 | –270 | 1 | |||
| 3 | –225 | 0,707106781 | |||
| 4 | –180 | –1,2251E–16 | |||
| 5 | –135 | –0,70710678 | |||
| 6 | –90 | –1 | |||
| 7 | –45 | –0,70710678 | |||
| 8 | 0 | 0 | |||
| 9 | 45 | 0,707106781 | |||
| 10 | 90 | 1 | |||
| 11 | 135 | 0,707106781 | |||
| 12 | 180 | 1,22515E–16 | |||
| 13 | 225 | –0,70710678 | |||
| 14 | 270 | –1 | |||
| 15 | 315 | –0,70710678 | |||
| 16 | 360 | –2,4503E–16 | |||
|
МАКСИМУМ |
1 | ||||
|
МИНИМУМ |
–1 | КОНС.PI | 3,141593 |
ЗАДАНИЕ N 2: « АНАЛИЗ ФУНКЦИИ Y=SIN(X) НА
ПЕРИОДИЧНОСТЬ».
Фамилия
Класс
Скопировать с 1 листа на 2 лист,начиная с A1 тему
урока, задание, фамилию,класс.В задании исправить
МАКСИМУМ, МИНИМУМ на ПЕРИОДИЧНОСТЬ
В пятой строке сделать надписи:
Номер; Угол X; SIN(X); SIN(X+2*ПИ); SIN(X)–SIN(X+2*ПИ)
Скопировать с 1 листа на 2 лист значения, формулы,
расчеты для диапазона A6:C24 c помощью команды
«Специальная вставка»,опция «ВСЕ».
Удалить на листе 2 надписи и значения для расчета
максимума и минимума в B23:C24.
В столбце D посчитать значения функции Y=SIN(X+2*ПИ),
скопировав формулу из С6 в D6, и добавив в скобках к
аргументу X значение +2*ПИ. Формула расчета в
ячейке D6: =SIN(B6*$F$24/180+2*ПИ)
В столбце E посчитать значения разности по модулю
двух функций SIN(X) и SIN(X+2*ПИ). Формула расчета
в ячейке E6: =ABS(C6–D6) .
В ячейке D23 сделать надпись:»Сумма
разностей»,в E23 сосчитать сумму разностей по
столбцу E в диапазоне E6:E22.Формула =СУММ(E6:E22)
Внизу под вычислениями построить совместный
точечный график функции Y=SIN(X) и график функции
Y=SIN(X+2*ПИ) по диапазону B6:D22.
| X | SIN(X) | Sin(X+2*ПИ) | Sin(X)–Sin(X+2*ПИ) | |
| –360 | 2,4503E–16 | 4,90059E–16 | 2,4503E–16 | |
| –315 | 0,707106781 | 0,707106781 | 7,77156E–16 | |
| –270 | 1 | 1 | 0 | |
| –225 | 0,707106781 | 0,707106781 | 4,44089E–16 | |
| –180 | –1,22515E–16 | –3,67545E–16 | 2,4503E–16 | |
| –135 | –0,707106781 | –0,707106781 | 7,77156E–16 | |
| –90 | –1 | –1 | 0 | |
| –45 | –0,707106781 | –0,707106781 | 1,11022E–16 | |
| 0 | 0 | 2,4503E–16 | 2,4503E–16 | |
| 45 | 0,707106781 | 0,707106781 | 2,22045E–16 | |
| 90 | 1 | 1 | 0 | |
| 135 | 0,707106781 | 0,707106781 | 1,11022E–16 | |
| 180 | 1,22515E–16 | –1,22515E–16 | 2,4503E–16 | |
| 225 | –0,707106781 | –0,707106781 | 1,11022E–16 | |
| 270 | –1 | –1 | 0 | |
| 315 | –0,707106781 | –0,707106781 | 2,22045E–16 | |
| 360 | –2,4503E–16 | 0 | 2,4503E–16 | |
| Сумма разностей | 4,00071E–15 | |||
| КОНС.PI | 3,14159265 |
ЗАДАНИЕ N 3: «АНАЛИЗ ФУНКЦИИ Y=SIN(X) НА
ВОЗРАСТАНИЕ И УБЫВАНИЕ».
Фамилия
Класс
Скопировать с 1 листа на 3 лист,начиная с A1 тему
урока, задание, фамилию,класс.В задании исправить
МАКСИМУМ, МИНИМУМ на ВОЗРАСТАНИЕ И УБЫВАНИЕ.
В пятой строке сделать надписи:
Номер; Угол X; SIN(X); ЗНАК РАЗНОСТИ; ВОЗРАСТАНИЕ ИЛИ
УБЫВАНИЕ
Скопировать с 1 листа на 3 лист
значения,формулы,расчеты для диапазона A6:C24 c
помощью команды «Специальная вставка»,опция
«ВСЕ». Удалить на листе 3 надписи и значения
для расчета максимума и минимума в B23:C24.
В столбце D посчитать значения функции ЗНАК
,начиная со второй ячейке столбца функций D7,
вычитая из предыдущего значения
функции последующее значение функции.Формула
расчета в ячейке D7:=ЗНАК(C7–C6) Если значение
разности>0,то результат вычисления 1,
если значение разности<0,то результат
вычисления –1.
В столбце E написать слово возрастает,если
результат вычисления 1, в соответствующей ячейки
столбца D, иначе написать слово убывает, если
результат вычисления –1 .
Внизу под вычислениями построить точечный
график функции Y=SIN(X) и график функции ЗНАК по
диапазону B6:D22.
| N | X | SIN(X) | знак разности | ||
| 0 | –360 | 2,4503E–16 | |||
| 1 | –315 | 0,70710678 | 1 | возрастает | |
| 2 | –270 | 1 | 1 | экстремум | |
| 3 | –225 | 0,70710678 | –1 | убывает | |
| 4 | –180 | –1,225E–16 | –1 | убывает | |
| 5 | –135 | –0,7071068 | –1 | убывает | |
| 6 | –90 | –1 | –1 | экстремум | |
| 7 | –45 | –0,7071068 | 1 | возрастает | |
| 8 | 0 | 0 | 1 | возрастает | |
| 9 | 45 | 0,70710678 | 1 | возрастает | |
| 10 | 90 | 1 | 1 | экстремум | |
| 11 | 135 | 0,70710678 | –1 | убывает | |
| 12 | 180 | 1,2251E–16 | –1 | убывает | |
| 13 | 225 | –0,7071068 | –1 | убывает | |
| 14 | 270 | –1 | –1 | экстремум | |
| 15 | 315 | –0,7071068 | 1 | возрастает | |
| 16 | 360 | –2,45E–16 | 1 | возрастает | |
| КОНС.PI | 3,141593 |
ЗАДАНИЕ N 4: «АНАЛИЗ ФУНКЦИИ Y=SIN(X) НА
ЧЕТНОСТЬ».
Фамилия
Класс
Скопировать с 1 листа на 3 лист,начиная с A1 тему
урока, задание, фамилию,класс.В задании исправить
МАКСИМУМ, МИНИМУМ на НА ЧЕТНОСТЬ
В пятой строке сделать надписи: Номер; Угол X; SIN(X);
SIN(–X); ABS(SIN(X)–SIN(–X));ABS(SIN(X))–ABS(SIN(–X))
Скопировать с 1 листа на 3 лист
значения,формулы,расчеты для диапазона A6:C24 c
помощью команды «Специальная вставка»,опция
«ВСЕ». Удалить на листе 3 надписи и значения
для расчета максимума и минимума в B23:C24.
В столбце D посчитать значения функции Y=SIN(–X),
скопировав формулу из С6 в D6, и добавив в скобках к
аргументу X ЗНАК – . Формула расчета в ячейке D6:
=SIN(–B6*$F$24/180)
В столбце E посчитать значения функции
Y=ABS(SIN(X)–SIN(–X)) , т.е. модуль разности функции Y=SIN(X)
и функции Y=SIN(–X).
Формула расчета в ячейке E6: =ABS(C6–D6) .
В столбце F посчитать значения функции
Y=ABS(SIN(X))–ABS(SIN(–X)) т.е. разность модулей
функции Y=SIN(X) и функции Y=SIN(–X). Формула
расчета в ячейке E6: =ABS(C6)–ABS(D6) .
В ячейке С23 сделать надпись:»Контрольные
суммы»,в E23 сосчитать сумму по столбцу E в
диапазоне E6:E22.Формула =СУММ(E6:E22), в F23 сосчитать
сумму по столбцу F в диапазоне F6:F22.Формула
=СУММ(F6:F22).
Внизу под вычислениями построить точечный
график функции Y=SIN(X) и график функции Y=SIN(–X) по
диапазону B6:D22.
| N | X | SIN(X) | SIN(–X) | ABS(SIN(X)–SIN(–X)) | ABS(SIN(X))– ABS(SIN(–X)) |
| 0 | –360 | 2,4503E–16 | –2,4503E–16 | 0 | |
| 1 | –315 | 0,70710678 | –0,707106781 | 1,414213562 | 0 |
| 2 | –270 | 1 | –1 | 2 | 0 |
| 3 | –225 | 0,70710678 | –0,707106781 | 1,414213562 | 0 |
| 4 | –180 | –1,225E–16 | 1,22515E–16 | 2,4503E–16 | 0 |
| 5 | –135 | –0,7071068 | 0,707106781 | 1,414213562 | 0 |
| 6 | –90 | –1 | 1 | 2 | 0 |
| 7 | –45 | –0,7071068 | 0,707106781 | 1,414213562 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 |
| 9 | 45 | 0,70710678 | –0,707106781 | 1,414213562 | 0 |
| 10 | 90 | 1 | –1 | 2 | 0 |
| 11 | 135 | 0,70710678 | –0,707106781 | 1,414213562 | 0 |
| 12 | 180 | 1,2251E–16 | –1,22515E–16 | 2,4503E–16 | 0 |
| 13 | 225 | –0,7071068 | 0,707106781 | 1,414213562 | 0 |
| 14 | 270 | –1 | 1 | 2 | 0 |
| 15 | 315 | –0,7071068 | 0,707106781 | 1,414213562 | 0 |
| 16 | 360 | –2,45E–16 | 2,4503E–16 | 4,90059E–16 | 0 |
| Контрольные суммы | 19,3137085 | 0 | |||
| КОНС.PI | 3,141592654 |
Данная работа посвящена исследованию
тригонометрических функций. Именно на примере
функции SIN(X) продемонстрированы возможности
электронных таблиц Excel для анализа функций. Было
показано, как можно определить участки
возрастания или убывания функции, как определить
их максимальное и минимальное значения на
заданном интервале аргумента, как можно
определить периодичность функции, ее четность
или нечетность.
В школе был проведен открытый
интегрированный урок: Информатика – Математика
по теме: «Исследование тригонометрических
функций с помощью электронных таблиц». На этом
уроке участники каждой группы с помощью
демонстрационной презентации рассказали о
постановке своих задач, а в Excel показали, как они
решаются.
Данная работа может использоваться в школах, как
дополнительное пособие при изучении
соответствующих разделов математики и
информатики.