Модуль (или абсолютная величина) – это неотрицательное значение любого числа. То есть, например, для отрицательного числа -32 он равняется 32, в то время, как для любого положительного числа равен этому же числу.
Давайте посмотрим, как найти модуль числа в Эксель.
Использование функции ABS
В программе Excel для нахождения модуля числа предусмотрена специальная функция ABS, формула которой в общем виде может выглядеть так:
- ABS(число)
- ABS(адрес_ячейки_с_числом)
Допустим, нам нужно найти модуль числа -27. Для этого в любой свободной ячейке пишем выражение: =ABS(-27).
Нажав клавишу Enter получаем результат в выбранной ячейке.
Некоторые пользователи по привычке пишут в ячейке математическое выражение, а именно, |-27|.
В данном случае после нажатия Enter программа выдаст ошибку.
Вместо того, чтобы вручную прописывать формулы, можно использовать Мастер функций.
- Выбрав ячейку, куда мы планируем добавить функцию и провести расчеты, кликаем по кнопке “Вставить функцию” (fx) слева от строки формул.
- В открывшемся окне вставки функций выбираем категорию “Математические”, в предложенном списке кликаем по оператору “ABS” и жмем OK.
- На экране отобразится окно для заполнения аргумента функции – “Число”. Адрес ячейки с числовыми значением, модуль которого нужно посчитать, можно указать вручную, либо просто кликнуть по ней в самой таблице. Курсор при этом должен находиться в поле для ввода значения аргумента. По готовности жмем кнопку OK.
- В ячейке с функцией появится результат вычислений.
- Если нужно посчитать модули по всему столбцу, можно растянуть формулу на другие строки. Для этого наводим указатель мыши на ячейку с результатом, когда появится небольшой черный плюсик, зажав левую кнопку мыши тянем его вниз до последней ячейки столбца (или до той ячейки, для которой нужно посчитать аналогичный результат).
- Все готово, мы получили модули всех значений в исходном столбце.
Заключение
Таким образом, в Эксель можно легко и быстро посчитать модуль числа с помощью специально предназначенной для этого функции. Причем ввиду того, что формула достаточно проста и содержит всего один аргумент, ее можно сразу писать в ячейке таблицы. Или же можно воспользоваться мастером функций, который позволит безошибочно выполнить расчет.
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12683 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Решение систем уравнений в среде Microsoft Excel
обучающие:
- повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
- повторение алгоритма решения систем уравнений;
- формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;
развивающие:
- формирование умений анализировать, выделять главное, сравнивать, строить аналогии;
воспитывающие:
- осуществление эстетического воспитания;
- воспитание аккуратности, добросовестности.
Тип урока: урок закрепления изученного материала и объяснения нового.
ХОД УРОКА
I. Организационная часть.
Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!
Ответ: “Знание – сила!”
Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)
Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).
II. Повторение пройденного материала.
Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)
Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.
III. Объяснение нового.
А. Решим систему 

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.
Запишем алгоритм решения систем уравнений графическим способом:
1. Преобразовать систему уравнений, если это необходимо.
2. Задать начальные значения для Х.
3. Найти значение первой функции при заданных Х.
4. Найти значение второй функции при тех же Х.
5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.
6. Решение системы — точка пересечения графиков функций.
7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.
Б. Решить систему уравнений 
Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:
При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.
Запишем примерный алгоритм решения системы уравнений, используя Поиск решения
1. Преобразовать систему уравнений, если это необходимо
2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.
3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.
4. Выбрать команду Сервис – Поиск решения.
5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения
6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)
7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК
8. Решить систему уравнений, щелкнув кнопкой Выполнить
IV. Практическая работа на компьютере.
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
V. Подведение итогов.
Повторить алгоритмы решения систем уравнений
Выставить оценки за тестирование в журнал
VI. Домашнее задание.
Решить рациональным способом системы уравнений:

источники:
http://exceltable.com/otchety/reshenie-uravneniy
http://urok.1sept.ru/articles/510787
Модуль – это абсолютная положительная величина любого числа. Даже у отрицательного числа модуль будет всегда положительным. Давайте выясним, как рассчитать величину модуля в Microsoft Excel.
Функция ABS
Для расчета величины модуля в Excel существует специальная функция под названием «ABS». Синтаксис этой функции очень простой: ABS(число). Либо формула может принимать такой вид: ABS(адрес_ячейки_с_числом). Чтобы рассчитать, например, модуль от числа -8, нужно вбить в строку формул или в любую ячейку на листе следующую формулу: «=ABS(-8)».
Для выполнения расчета жмем на Enter — программа выдает в ответ положительное значение.
Существует еще один способ расчета модуля. Он подойдет для тех пользователей, которые не привыкли держать в голове различные формулы.
- Кликаем по ячейке, в которой хотим, чтобы хранился результат. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
- Запускается окно «Мастера функций». В списке, который расположен в нем, найдите функцию ABS и выделите ее. Подтверждаем на «OK».
- Открывается окно аргументов функции. ABS имеет всего один аргумент — число, поэтому вводим его. Если же вы хотите взять число из данных, которые хранятся в какой-либо ячейке документа, нажмите на кнопку, размещенную справа от формы ввода.
- Окно свернется, а вам нужно кликнуть по ячейке, где содержится число, от которого хотите рассчитать модуль. После его добавления опять жмите на кнопку справа от поля ввода.
- Опять откроется окно с аргументами функции, где поле «Число» уже будет заполнено значением. Нажмите «OK».
- Вслед за этим в ранее указанной вами ячейке выводится значение модуля того числа, которое вы выбрали.
- Если значение расположено в таблице, формулу модуля можно скопировать и на другие ячейки. Для этого надо навести курсор нижний левый угол ячейки, в которой уже есть формула, зажать кнопку мыши и провести ею вниз до конца таблицы. Таким образом, в ячейках данного столбца появятся значение по модулю исходных данных.
Важно заметить, что некоторые пользователи пытаются записать модуль, как это принято в математике, то есть |(число)|, например |-48|. Но в такой ситуации вместо ответа появится лишь ошибка, так как Excel не понимает подобный синтаксис.
В расчете модуля из числа через Microsoft Excel нет ничего сложного, так как данное действие выполняется с помощью простой функции. Единственное условие состоит в том, что данную функцию нужно просто знать.
Еще статьи по данной теме:
Помогла ли Вам статья?
Цели:
- актуализировать знания обучающихся о
геометрических преобразованиях; - формировать умения применять эти
геометрические преобразования к построению
графиков, содержащих модуль; - закрепить знания и умения по построению
графиков в практической ситуации при решении
уравнений; - отрабатывать навыки построения графиков с
использованием компьютера в среде MS Office Excel; - вовлекать учащихся в творческую и
коммуникативную деятельность через проектную
работу.
Оборудование:
- Компьютерный класс, мультимедийный проектор и
экран. - Раздаточный материал (инструкционная карта по
построению графиков в Excel, карточки
трехуровневые, презентация к уроку, презентации
с проектами детей, презентация для релаксации)
ХОД УРОКА
I. Организационный этап
– Приветствие учащихся;
– Целеполагание.
II. Актуализация знаний
1. Актуализация знаний по математике
– Что называется графиком функции? (Графиком
называется множество точек координатной
плоскости, у которых значения х и у связаны
некоторой зависимостью и каждому значению х
соответствует единственное значение у).
– Графический способ – один из самых удобных
и наглядных способов представления и анализа
информации.
– Например, метеорологическая служба фиксирует
изменения температуры, строя с помощью
термографа (специального прибора, отмечающего
температуру на движущейся ленте или экране
дисплея) график температуры.
– Используя показания сейсмографов (приборов,
непрерывно фиксирующих колебания почвы и
строящих специальные графики – сейсмограммы)
геологи могут предсказывать приближение
землетрясения или цунами.
– Врачи выявляют болезни сердца, изучая графики,
полученные с помощью кардиографа, их называют
кардиограммами.
– Широко применяются графики в экономике, в
частности кривая спроса и предложения, линия
производственных возможностей.
– Таким образом, видим, что графики с нами на
протяжении всей жизни и их необходимо уметь
строить и читать.
– Мы с Вами начали изучать модуль и его
применение. Скажите классическое определение
модуля (ответы детей).
– Давайте повторим основные геометрические
преобразования, которые мы используем при
построении графиков. На слайде примеры,
учащиеся озвучивают их и рассказывают о том или
ином преобразовании.
– А сейчас вспомним построение графика.
Предлагаю построить график функции (слайд).
Работа с классом над построением графика.
Находим нули функции: х1 = 2, х2
= 0
1) х < 0
у = х – х + 2 + х = х + 2
2) 0 < х < 2
у = х – х + 2 – х = – х + 2
3) х > 2
у = х + х – 2 – х = х – 2
Получаем график:
(График построен на доске, а также представлен
на слайде).
2. Актуализация знаний по информатике
– Какая программа поможет нам в построении
графиков? (Excel)
– Что является минимальным элементом Excel? (Ячейка)
– Что имеет каждая ячейка? (Имя)
– Как называется группа ячеек? (Диапазон)
– С чего начинаются вычисления в Excel? (Со знака
равенства)
– Для построения графика, что в Excel нам
необходимо (Точки)
– Что имеет каждая точка? (Координаты)
– Значение какой координаты мы выбираем сами? (Х)
– Как находим У? (Записываем формулу и
протягиваем ее для всех введенных значений Х)
– У Вас на парте инструкционная карта по
построению графика в Excel, который Вы только что
построили в тетрадях. Давайте вспомним, как это
делается в Excel (Работа с инструкционной картой,
учитель показывает на компьютере каждый шаг, все
действия отражаются на экране, учащиеся помогают
учителю).
Инструкционная карта <Приложение
1>
II. Практическая часть урока
У учащихся на партах карточки (трехуровневые –
распределены с учетом индивидуальных
особенностей учащихся) разного цвета: зеленые и
красные. Цвет карточки показывает деление ребят
на группы для работы за компьютером. На карточках
два задания: задание на построение графика
ребята выполняют за компьютером, второе задание
на решение уравнения с модулем выполняют в
тетрадях.
Карточки:
№1, уровень 1
1. –
построить графики в Excel
2. – решить
графически уравнение
№2, уровень 1
1. – построить
графики в Excel
2. – решить
графически уравнение
№ 3, уровень 1
1. – построить
графики в Excel
2. – решить
графически уравнение
№ 4, уровень 1
1. 
графики в Excel
2. – решить
графически уравнение
№ 5, уровень 1
1. 
графики в Excel
2. – решить
графически уравнение
№ 6, уровень 2
1. – построить
графики в Excel
2. – решить
графически уравнение
№7, уровень 2
1. – построить
графики в Excel
2. – решить
графически уравнение
№8, уровень 2
1. – построить
графики в Excel
2. – решить
графически уравнение
№9, уровень 2
1. – построить
графики в Excel
2. – решить
графически уравнение
№10, уровень 3
1. – построить
графики в Excel
2. – решить
графически уравнение
№11, уровень 3
1. – построить
графики в Excel
2. – решить
графически уравнение
№12, уровень 3
1. – построить
графики в Excel
2. – решить
графически уравнение
№13, уровень 3
1. – построить
графики в Excel
2. – решить
графически уравнение
– Сейчас мы переходим к практической части
урока. У вас на партах карточки. В карточке два
задания. Первое задание на построение графика вы
выполняете за компьютером, второе задание на
решение уравнения вы выполняете в тетрадях.
– К работе за компьютером приступают ребята, у
которых карточка зеленого цвета.
– Работу за компьютером предлагаю оценить Вам в
листе самооценки.
III. Релаксация
Предлагаем Вам немного отдохнуть,
расслабиться, послушать музыку и постараться
представить себя внутри каждой картины,
насладиться красивой природой.
(Просмотр презентации – Релаксация). <Приложение 2>
После одного задания карточки учащиеся меняются.
К работе за компьютерами приступают учащиеся с
карточками красного цвета.
IV. Защита проектов
Учащиеся представляют выполненные ими проекты
по построению графиков (презентации):
Проект «Тюльпан» <Приложение 3>
Проект «Аусеклис» <Приложение
4>
Проект «Ракета» <Приложение 5>
V. Итог урока
Учитель математики озвучивает оценки за
решение уравнений.
Учитель информатики подводит итог по листам
самооценки.
Стаья
на тему: «Графическая интерпретация
решения линейных уравнений и неравенств, содержащих знак модуля»
Учитель математики Супрягина И.И.,
Учитель информатики Волкова Т.И.
Современное общество ставит перед педагогами задачу
организовать подготовку школьников, таким образом, чтобы они были готовы
осмысленно и творчески использовать знания и умения, полученные в процессе
обучения в школе, в будущем, в профессиональной деятельности.
Развитие современной системы образования тесно связано
с активным внедрением достижений информационных технологий в процесс обучения.
Интегрированные уроки позволяют использовать знания,
полученные на уроках одного учебного предмета, например, информатики на уроках
другого учебного предмета, например, математики и наоборот.
Разработан курс интегрированных уроков по теме:
«Графическая иллюстрация решений задач по математике с использованием
электронных таблиц» (7-9 классы).
Курс будет способствовать повышению качества и
результативности учебного процесса. Это позволит добиться не только успешного
усвоения методов решения уравнений, неравенств, построения графиков функций, но
и дальнейшего использования полученных навыков при решении любых типов уравнений
и неравенств графическим методом.
Содержание курса предполагает:
1.
Развитие графической грамотности необходимой для свободного владения методами
решения задач;
2.
Позволяет осуществить углубленное изучение математики:
§
Совершенствовать
навыки анализа решения уравнений и неравенств;
§
Научить
применять наиболее рациональные методы их решения;
§
Повысить
наглядность взаимосвязи графического отображения свойств функций, содержащих
знак модуля.
В этой статье предлагается разработка интегрированного
урока (математика и информатика) на тему: «Графическая интерпретация решения
линейных уравнений и неравенств, содержащих знак модуля».
Цель урока: Показать
и научить учащихся применять современные компьютерные программы для решения
уранений и неравенств, содержащих знак модуля. Показать возможности
использования программы Excel для решения
задач по математике.
Задачи
урока:
Образовательная –
знакомство учащихся с основными приемами построения графиков функций,
содержащих знак модуля, в программе Excel;
Развивающая
–
формирование у учащихся логического и алгоритмического мышления; развитие
познавательного интереса к предмету; развитие умения оперировать ранее
полученными знаниями; развитие умения планировать свою деятельность;
анализировать полученные результаты; повысить его интеллектуальную активность;
Воспитательная –
умение самостоятельно мыслить; ответственность за выполняемую работу; расширить
кругозор; аккуратность при выполнении работы.
Технические
и программные средства:
·
Персональные
компьютеры;
·
Приложение
Windows – электронные таблицы Excel;
·
Принтер.
Ход урока
I. Раздел
урока «Математика»
Определение.
Модулем
действительного числа называется само число, если оно неотрицательное, и
противоположное ему число, если данное число отрицательное.
Так как по
определению │х│≥ 0, то уравнение │х│= a, имеет решение при а ≥ 0, х=а или
х= -а.
Решить
уравнение: │2х+4│= 3х — 4


= 8.
Для того,
чтобы графически решить данное уравнение надо построить графики функций
у=│2х+4│; у = 3х – 4 и найти абсциссу точки их пересечения. Графики функций
учащиеся строят с помощью программы Excel. Построение графика функции,
содержащий знак модуля, разбирается в разделе «Информатика». Результат работы показан
на рис.1. На графике учащиеся находят точку пересечения графиков функций и
сравнивают графическое и аналитическое решение.
С помощью
построенных графиков функций можно проверить и решение линейных неравенств,
содержащих знак модуля.
Решить
неравенство: │2х+4│> 3х – 4.

Полученное решение учащиеся
проверяют по графикам (рис.2).
Далее, учащиеся получают карточки с
индивидуальным заданием: решить линейные уравнение и неравенство, содержащие
знак модуля. Правильность своего аналитического решения они проверяют
графическим решением, используя программу Excel.
II Раздел
урока «Информатика»
На уроках
информатики учащиеся освоили основные приемы работы с программой Excel.
Перед
объяснением нового материала повторяем основные понятия по работе с
электронными таблицами (фронтальный опрос):
·
Что
является основным элементом таблицы;
·
Какую
информацию может содержать ячейка;
·
Как
автоматически заполнить данными таблицу (столбец/строку), для которой известен
закон изменения;
·
Как
занести формулу в ячейку;
·
Что
такое маркер заполнения и для чего он нужен?
·
Что
такое относительная адресация ячеек?
·
Что
такое абсолютная адресация ячеек? Как она задается?
Новый
материал:
Прежде,
чем построить график функции, нам необходимо ее вычислить, т.е. занести формулу
расчета в ячейки таблицы. На предыдущих уроках учащиеся уже рассчитывали и
строили график линейной функции.
В формуле второй
функции, которую мы должны рассчитать, появился знак модуля, поэтому ее
значение будет вычисляться по разным формулам в зависимости от значения аргумента.
Рассмотрим
на данном примере правила ввода формулы расчеты функции. Эта функция относится
к логическому типу и имеет следующий общий вид записи:
ЕСЛИ
(условие; действие1; действие2)
Где:
Условие – это
любое условное выражение, которое может при вычислении иметь значение ИСТИНА
или ЛОЖЬ
Действие1 – это
формула, по которой вычисляется значение функции, если заданное условие имеет
значение истина;
Действие2 – это
формула, по которой вычисляется значение функции, если заданное условие имеет
значение ложь;
Рассмотрим
задачу: y=2x +4, если
х ³ -2
y=-2x— 4, если
х < -2
В качестве
условия будем использовать условное логическое выражение со связкой ИЛИ и оно
будет выглядеть следующим образом: ИЛИ(х> -2; x = -2). Мы
знаем, что числовое значение аргумента занесено в ячейку В3, тогда формула
расчета функции будет иметь вид:
ЕСЛИ (ИЛИ(В3
> -2; В3 = -2); 2*В3+4; -2*В3 -4)
После
ввода формулы в первую ячейку столбца, мы ее копируем по всему столбцу. Теперь
остается только построить график функции, оформить его и проанализировать.
Рис 1
Графическая
иллюстрация решения неравенства │2х+4│> 3х – 4
Рис 2
Подведение итогов урока
В конце урока учащиеся демонстрируют
графическое решение индивидуальной задачи. Учитель оценивает их работу.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12694 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
источники:
http://lumpics.ru/how-solve-system-equations-excel/
http://exceltable.com/otchety/reshenie-uravneniy
В Excel есть множество формул и операторов, облегчающих расчеты. Одной из востребованных функций является вычисление модуля числа в Экселе.
Причины применения функции
В математике модуль числа показывает его абсолютное значение, знак величины не учитывается. С помощью формулы определение записывается так: I-aI = IaI = a. Все значения по модулю являются положительными.
Программа Excel оперирует числами, под которыми часто «скрываются» не абстрактные математические действия, а реальные предметы или бухгалтерские расчеты. Поэтому полученные результаты не могут быть отрицательными.
Например, какие-то товары были проданы сверх плана, другие, наоборот, остались на складе. Тогда реализованные изделия будут иметь положительное значения, а не проданные — отрицательные. Если понадобится сложить все отклонения от плана, то результатом может стать отрицательное значение или ноль. Применение модуля покажет абсолютную сумму отклонений.
Оператор также находит применение при подсчете векторных величин, которые могут иметь отрицательное значение, сравнении двух элементов таблицы, расчете процентов по кредиту.
Поставить модуль числа в Excel можно функцией ABS, аббревиатура образовалась от английского слова Absolute, что означает «абсолютный».
Стандартный вариант
Правильное написание выглядит так: «ABS(X)» или «ABS(адрес_ячейки_с_числом)». Здесь «X» — число, модуль которого нужно найти, «адрес ячейки с числом» — элемент таблицы, в котором будет указано абсолютное значение. Вставить формулу можно двумя способами. Простой вариант:
- Вписать в ячейку или в строку формул значение, для которого нужно найти модуль. Пусть это будет -8. Тогда надпись будет такова: «=ABS(-8)».
- Нажать ввод и получить результат.
Второй вариант:
- Выделить необходимую ячейку и кликнуть по опции «Вставить формулу», обозначенной символом fx.
- В появившемся списке найти надпись «ABS», выделить ее и подтвердить.
- Откроется меню «Аргументы функции». Здесь нужно ввести необходимую цифру в функцию модуля. Можно указать адрес ячейки, в которой находится необходимое значение. Для этого нажать на иконку, находящуюся справа от строки «Число».
- Окно аргументов свернется, в рабочей таблице нужно будет кликнуть по нужному элементу и снова нажать на иконку.
- Опять появится меню с аргументами, где в строке значений будет стоять адрес выбранной ячейки. Подтвердить операцию.
- Функция сработает в указанном месте.
- Можно распространить действие формулы на другие ячейки. Для этого в ячейке с примененной функцией ABS нажать на правый нижний угол мышкой и не отпуская кнопку «потянуть» мышку вниз, выделяя нужные элементы. К ним будет применена функция.
ABS в формулах
Наряду с простым приведением к модулю, функция может использоваться в связке с формулами и решать комплексные задачи. Например, определить на сколько минимальное отрицательное число меньше минимального положительного можно так:
- Имеется массив, в котором нужно решить поставленную задачу.
- В строку формул нужно вписать следующую композицию: {МИН(ABS(B3:B12))}.Здесь фигурные скобки показывают, что расчеты ведутся с массивом данных. Вводятся такие скобки не с клавиатуры, а нажатием клавиш Ctrl+Shift+Enter в конце написания формулы.
Программа в этом случае рассчитывает модуль в каждой из ячеек между B3 и B12. Без применения массивов ABS выдала бы сообщение об ошибке при такой записи. - Результат применения:
Примеры расчетов
Ниже приведены возможные случаи использования функции модуля ABS, как отдельно, так и в составе формулы.
Задача по математике на определение проекции отрезка на ось абсцисс (X) и ось ординат(Y). По условиям задания отрезок имеет координаты начала A(-17; -14) и конца B(-39;-56). Решение в Excel:
- Ввести в таблицу известные данные.
- Рассчитывается проекция на ось X с помощью ABS.
- Аналогично находится проекция на ось ординат. В строке «Число» нужно указать B5-B3.
- Результат появится в таблице.
Подсчет расходов компании — здесь нужно сложить отрицательные значения по модулю.
Имеется набор финансовых операции компании за отчетный период. Нужно определить сумму трат предприятия. По условию расходы указываются со знаком минус:
- Составить массив в Excel.
- Написать формулу: {=СУММ(ЕСЛИ(В3:В12<0;ABS(В3:В12);0))}
В конце нажать Ctrl+Shift+Enter для указания того, что используются массивы данных. - Программа анализирует данные ячеек B3-B12 и если имеются отрицательные числа, то берется их модуль. После проверки всех элементов, отрицательные значения складываются. Положительные данные не учитываются в расчетах. Итоговый результат имеет следующий вид:
Другие варианты получения абсолютного значения
Кроме ABS возможны и другие способы получения модуля числа в Эксель при помощи альтернативных функций.
ЗНАК
Принцип основан на том, что отрицательные числа умножаются на -1, а положительные на 1. Выглядит это так:
На картинке действие производится над ячейкой A4.
КОРЕНЬ
Квадратный корень величины не может быть отрицательным. Поэтому исходное число возводится в квадрат, а потом извлекается корень.
ЕСЛИ
Удобный способ. Если значение отрицательное, то оно умножается на -1, в противном случае ничего не происходит. Вот как это выглядит для ячейки A1:
Язык VBA
Во многих языках программирования модуль находится через ABS. В VBA команда будет выглядеть следующим образом: A=Abs(-7). Здесь Abs — команда для получения абсолютного значения. В данном случае объекту A будет присвоено число 7.
ABS и альтернативные варианты просты в исполнении. Умение применять их, облегчит работу и сэкономит время.
17 авг. 2022 г.
читать 3 мин
Часто вас может заинтересовать построение уравнения или функции в Excel. К счастью, это легко сделать с помощью встроенных формул Excel.
В этом руководстве представлено несколько примеров того, как строить уравнения/функции в Excel.
Пример 1: построение линейного уравнения
Предположим, вы хотите построить следующее уравнение:
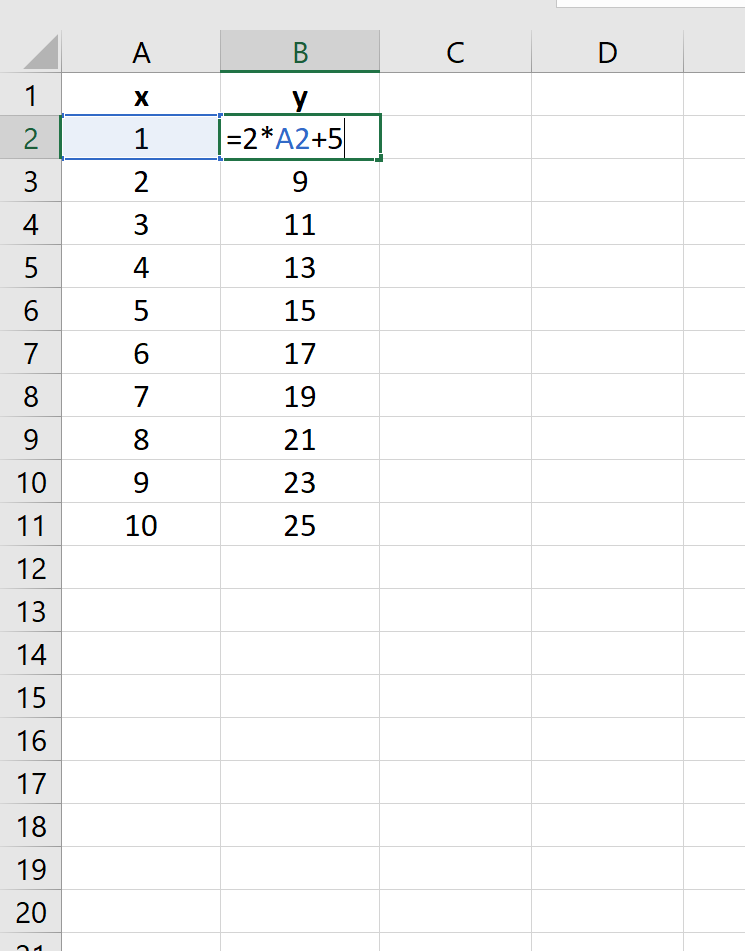
у = 2х + 5
На следующем изображении показано, как создать значения y для этого линейного уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
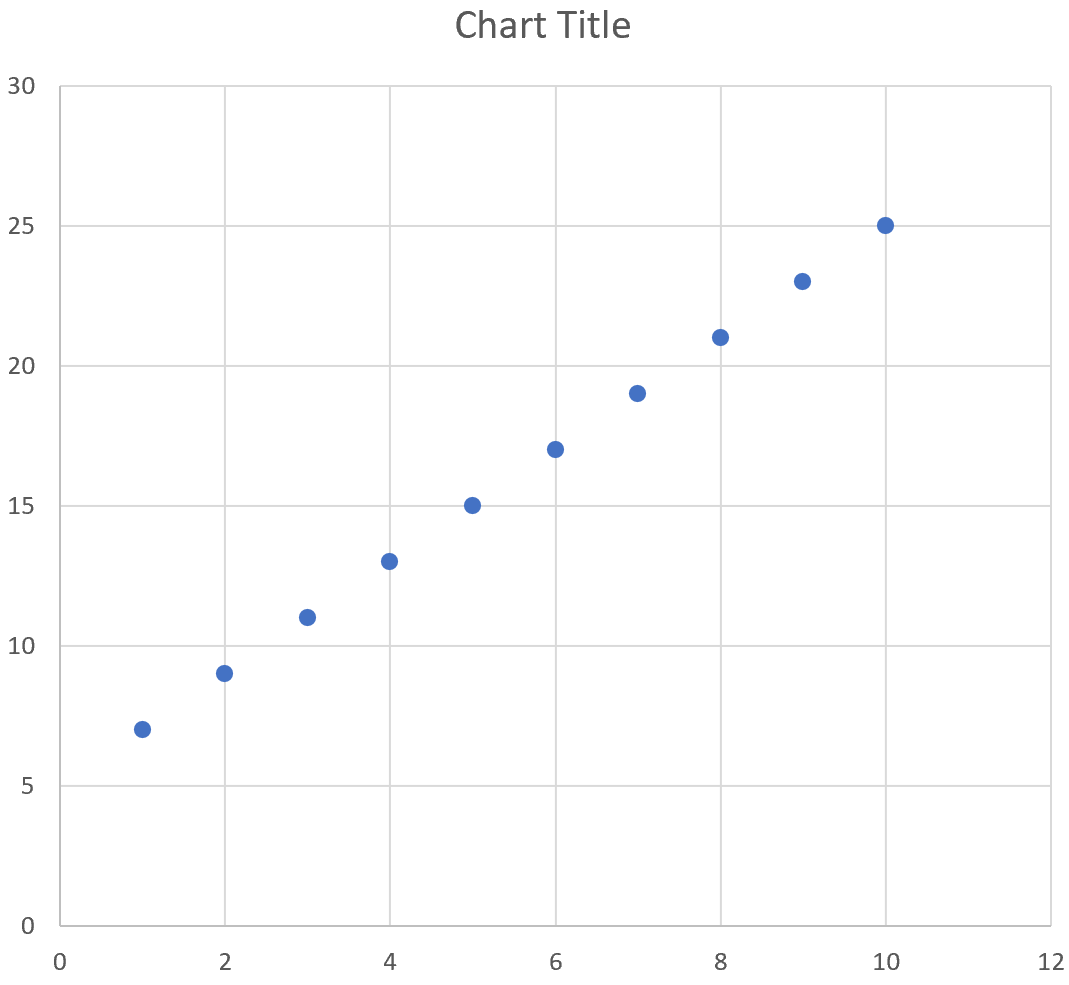
Автоматически появится следующий график:
Мы видим, что график следует прямой линии, поскольку уравнение, которое мы использовали, было линейным по своей природе.
Пример 2. Построение квадратного уравнения
Предположим, вы хотите построить следующее уравнение:
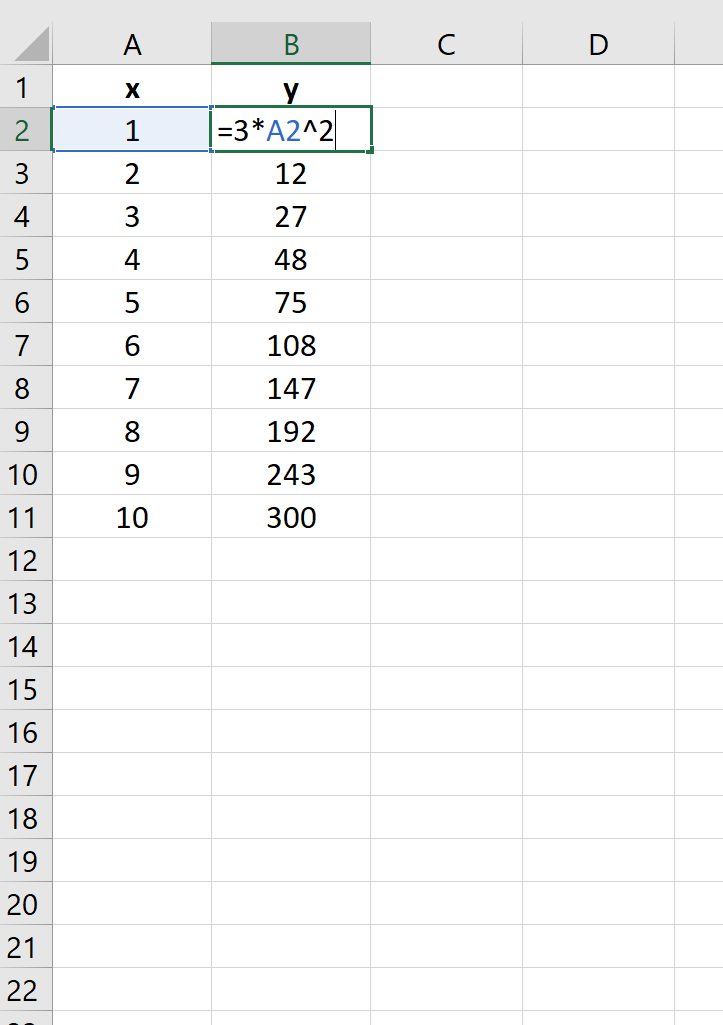
у = 3x 2
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
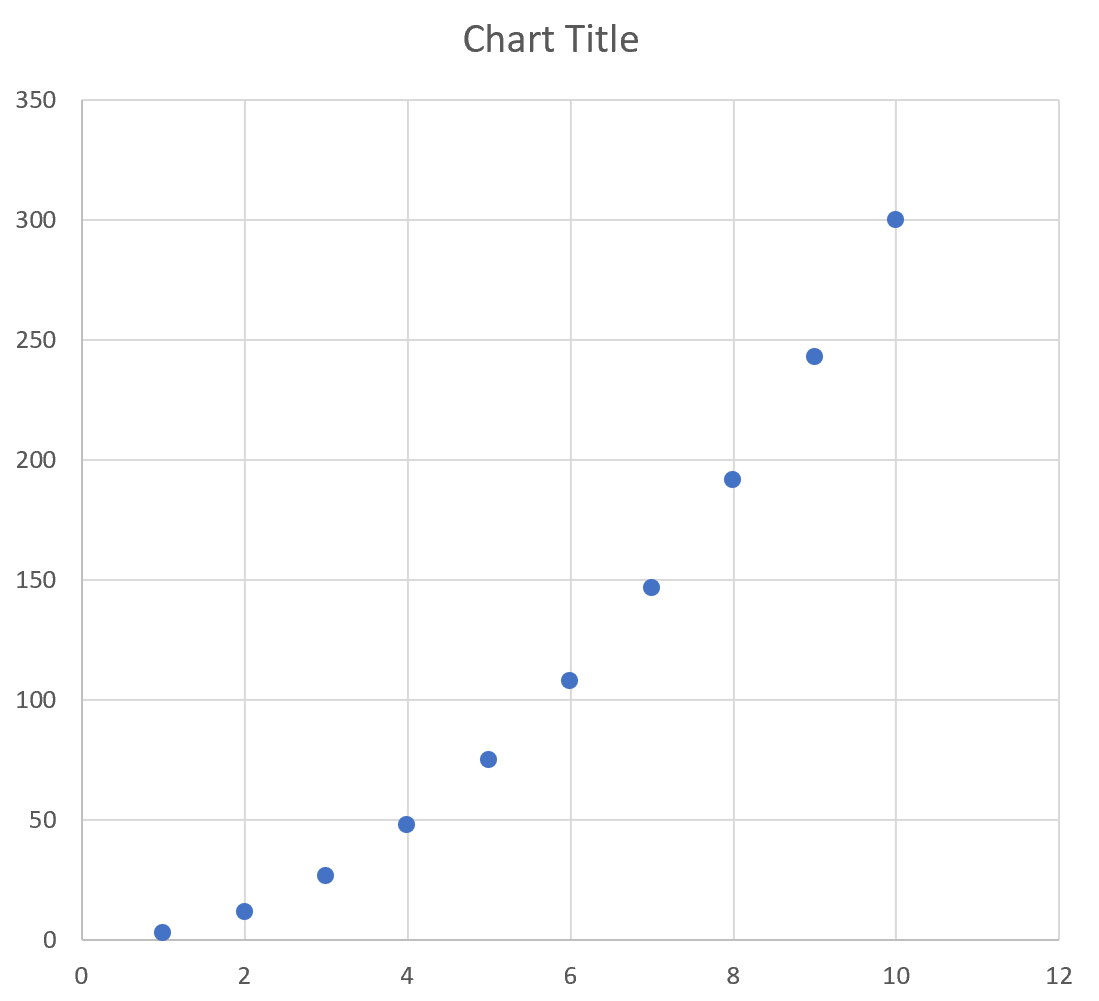
Автоматически появится следующий график:
Мы видим, что график следует изогнутой линии, поскольку уравнение, которое мы использовали, было квадратным.
Пример 3: построение уравнения обратной связи
Предположим, вы хотите построить следующее уравнение:
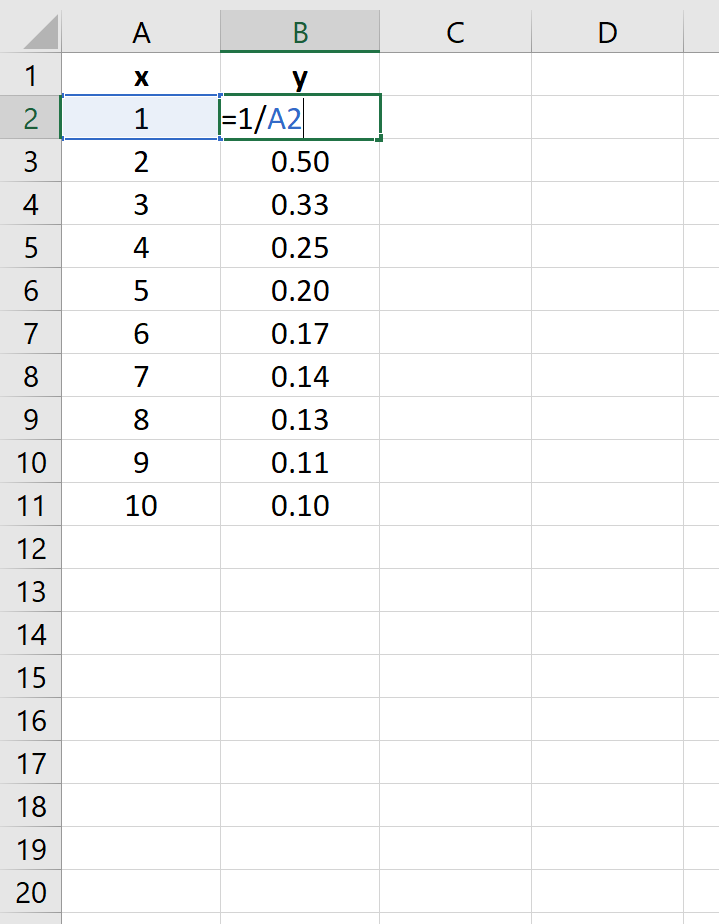
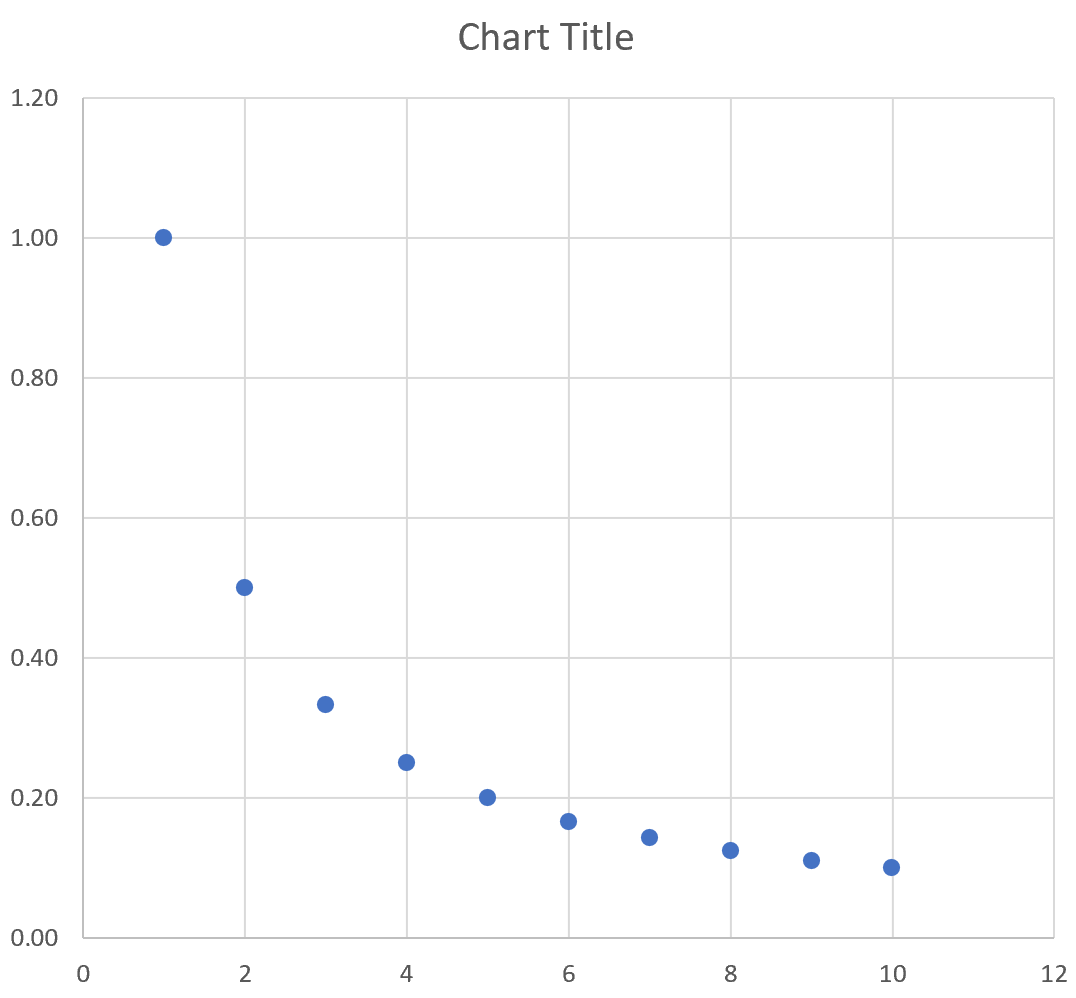
у = 1/х
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует по изогнутой линии вниз, поскольку это представляет уравнение y = 1/x.
Пример 4. Построение уравнения синуса
Предположим, вы хотите построить следующее уравнение:
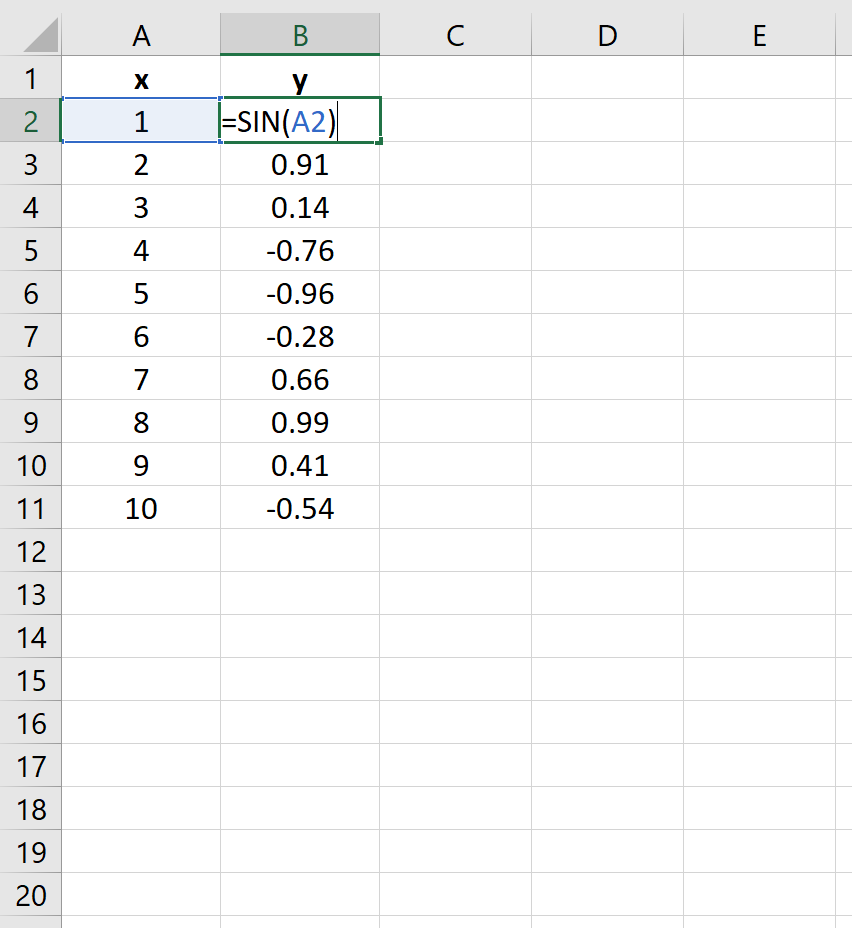
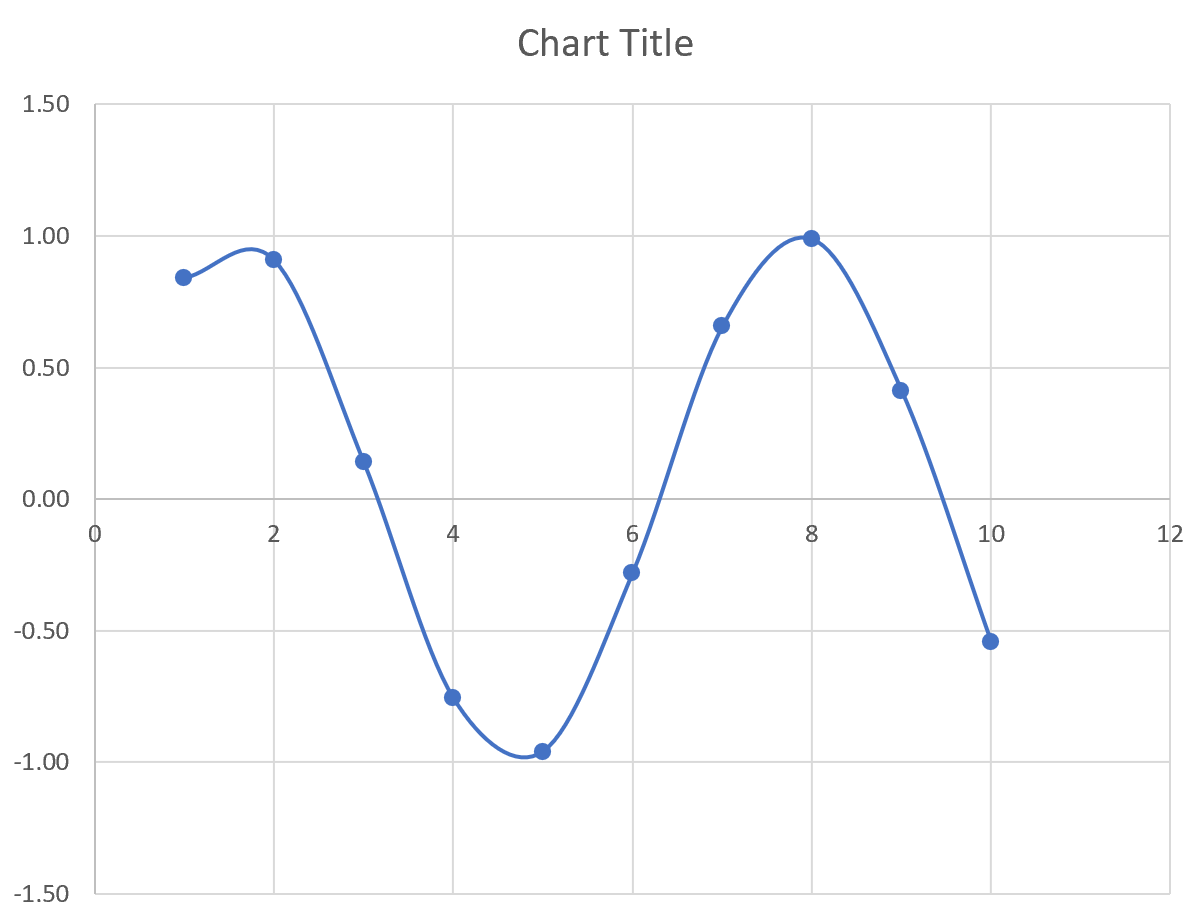
у = грех (х)
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика « Разброс с плавными линиями и маркерами» .
Автоматически появится следующий график:
Вывод
Вы можете использовать аналогичную технику для построения графика любой функции или уравнения в Excel. Просто выберите диапазон значений x для использования в одном столбце, затем используйте уравнение в отдельном столбце, чтобы определить значения y на основе значений x.