Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
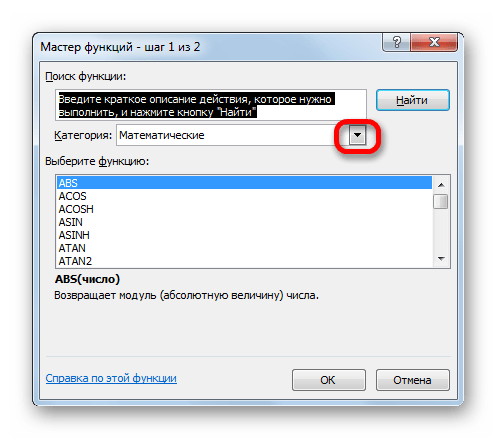
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
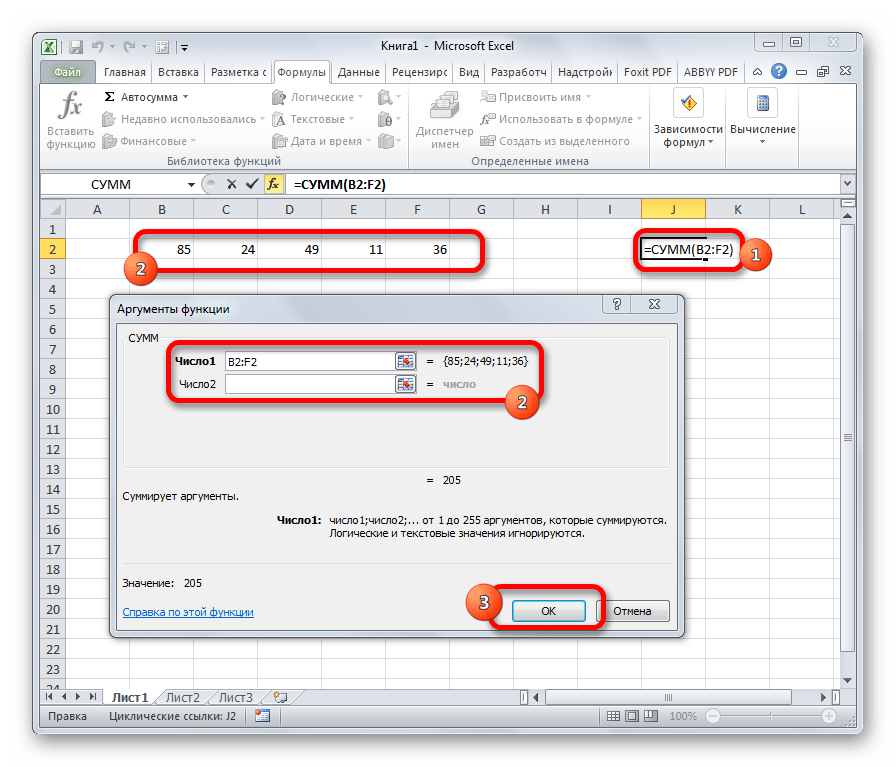
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
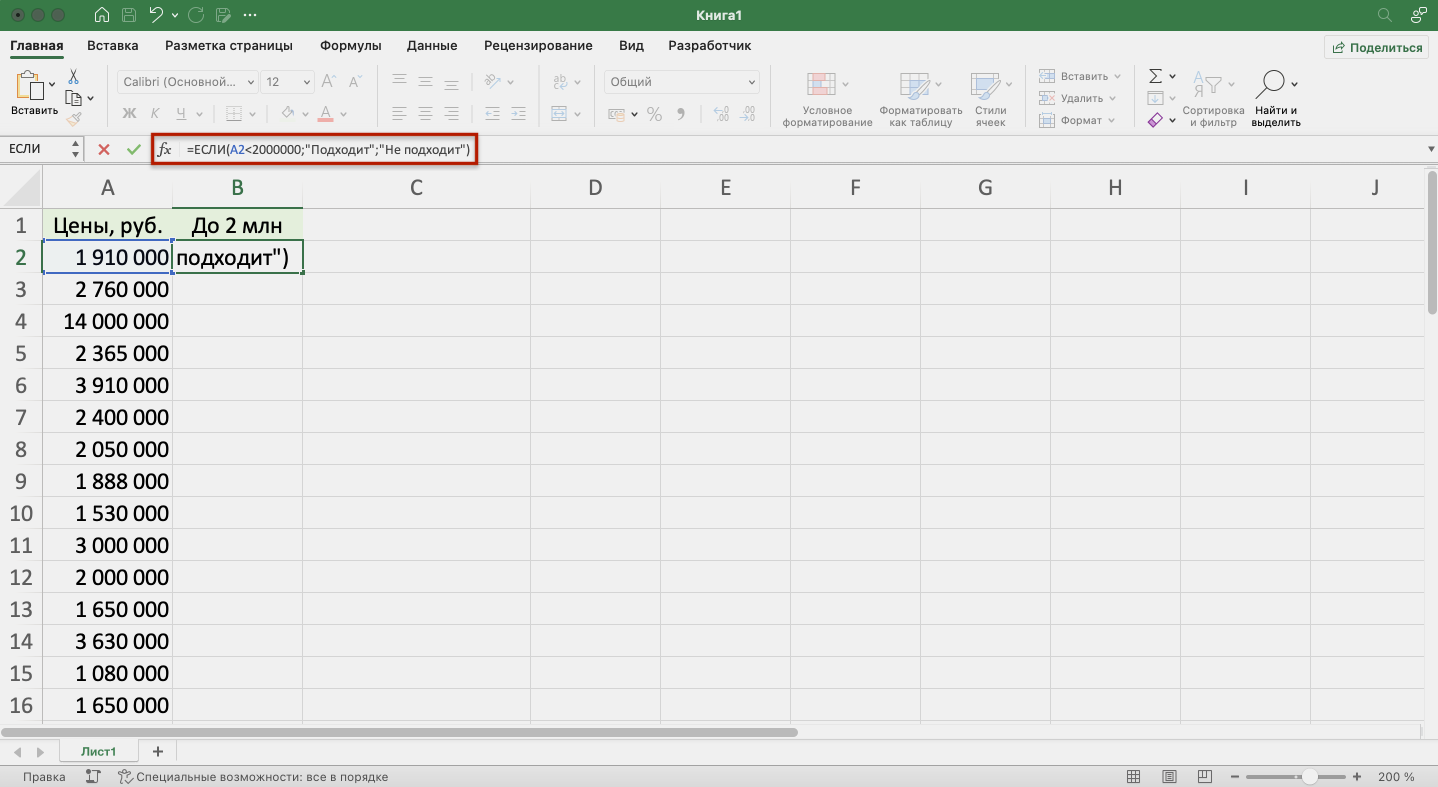
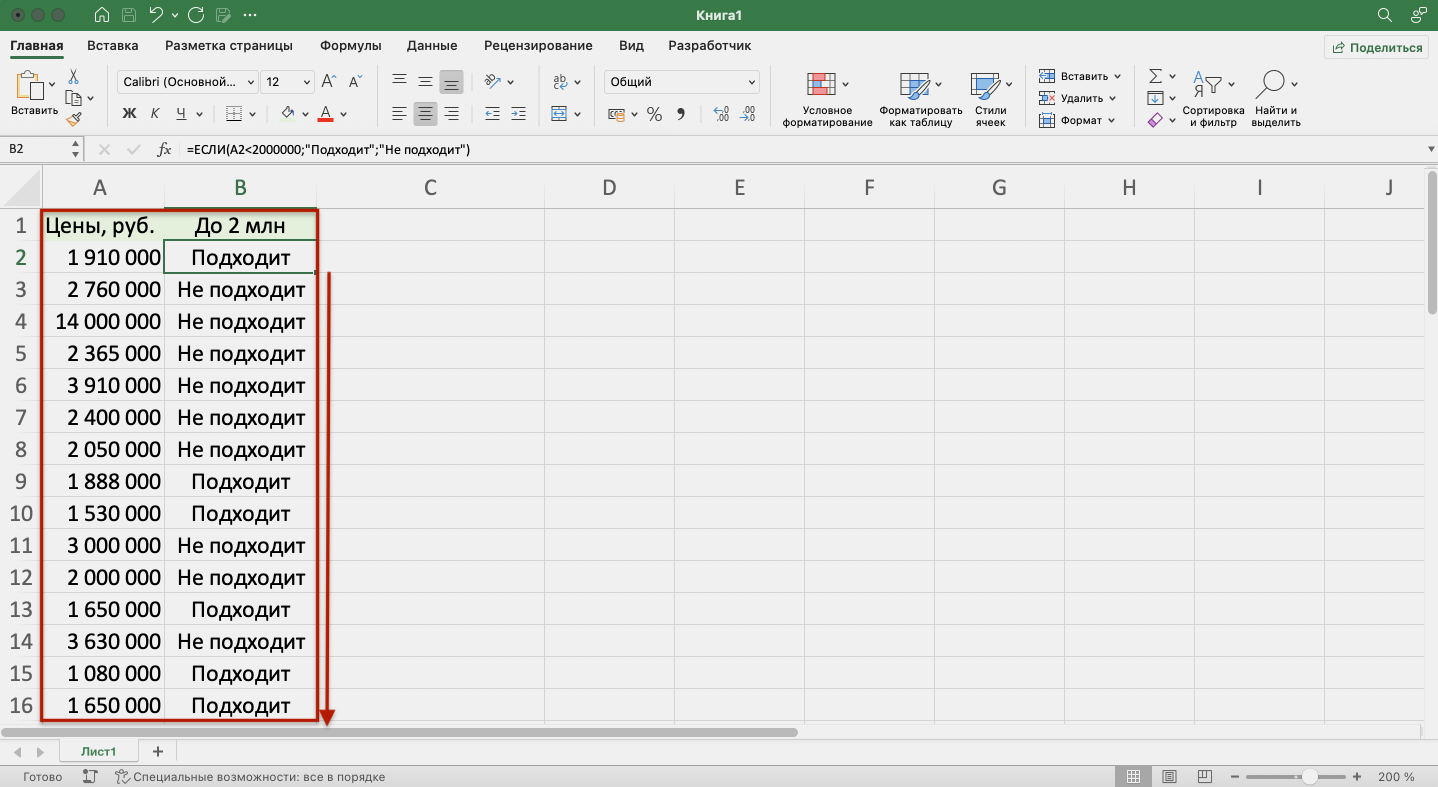
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
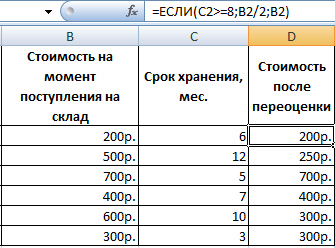
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
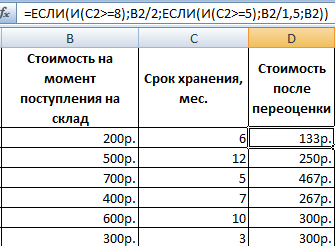
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
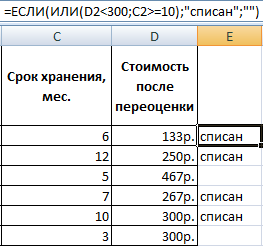
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12686 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение систем уравнений в среде Microsoft Excel
обучающие:
- повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
- повторение алгоритма решения систем уравнений;
- формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;
развивающие:
- формирование умений анализировать, выделять главное, сравнивать, строить аналогии;
воспитывающие:
- осуществление эстетического воспитания;
- воспитание аккуратности, добросовестности.
Тип урока: урок закрепления изученного материала и объяснения нового.
ХОД УРОКА
I. Организационная часть.
Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!
Ответ: “Знание – сила!”
Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)
Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).
II. Повторение пройденного материала.
Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)
Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.
III. Объяснение нового.
А. Решим систему 

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.
Запишем алгоритм решения систем уравнений графическим способом:
1. Преобразовать систему уравнений, если это необходимо.
2. Задать начальные значения для Х.
3. Найти значение первой функции при заданных Х.
4. Найти значение второй функции при тех же Х.
5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.
6. Решение системы — точка пересечения графиков функций.
7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.
Б. Решить систему уравнений 
Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:
При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.
Запишем примерный алгоритм решения системы уравнений, используя Поиск решения
1. Преобразовать систему уравнений, если это необходимо
2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.
3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.
4. Выбрать команду Сервис – Поиск решения.
5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения
6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)
7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК
8. Решить систему уравнений, щелкнув кнопкой Выполнить
IV. Практическая работа на компьютере.
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
V. Подведение итогов.
Повторить алгоритмы решения систем уравнений
Выставить оценки за тестирование в журнал
VI. Домашнее задание.
Решить рациональным способом системы уравнений:

Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://urok.1sept.ru/articles/510787
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
Содержание
- Применение математических функций
- СУММ
- СУММЕСЛИ
- ОКРУГЛ
- ПРОИЗВЕД
- ABS
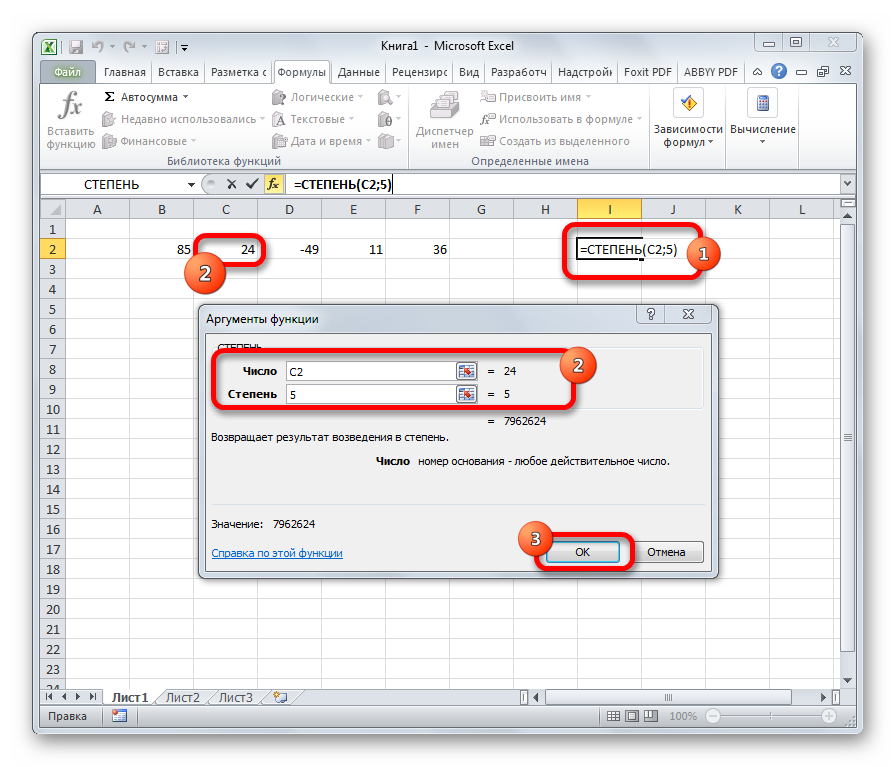
- СТЕПЕНЬ
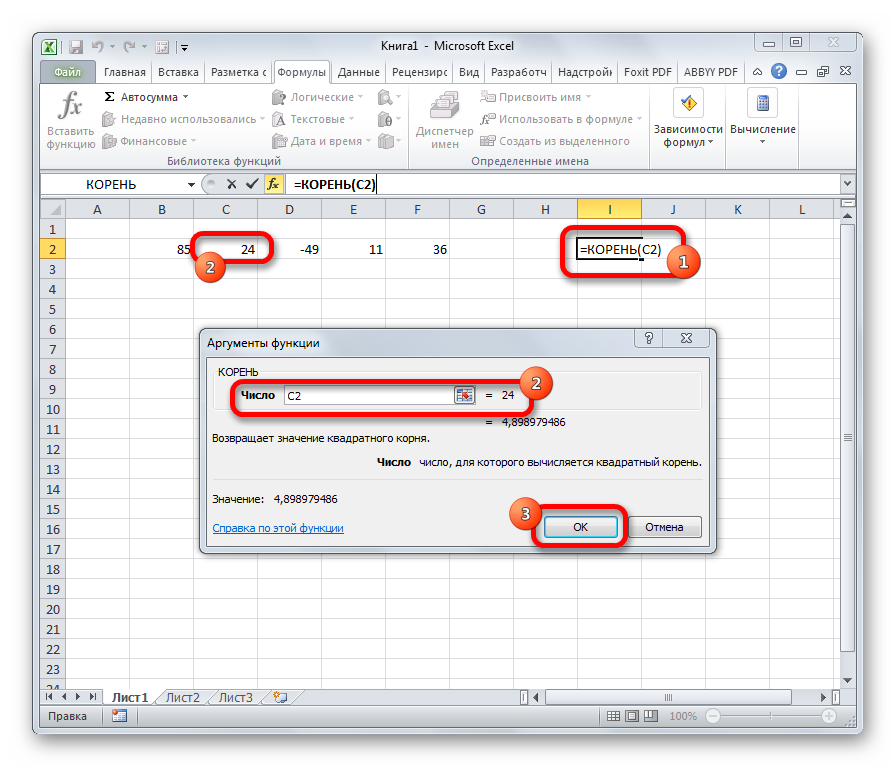
- КОРЕНЬ
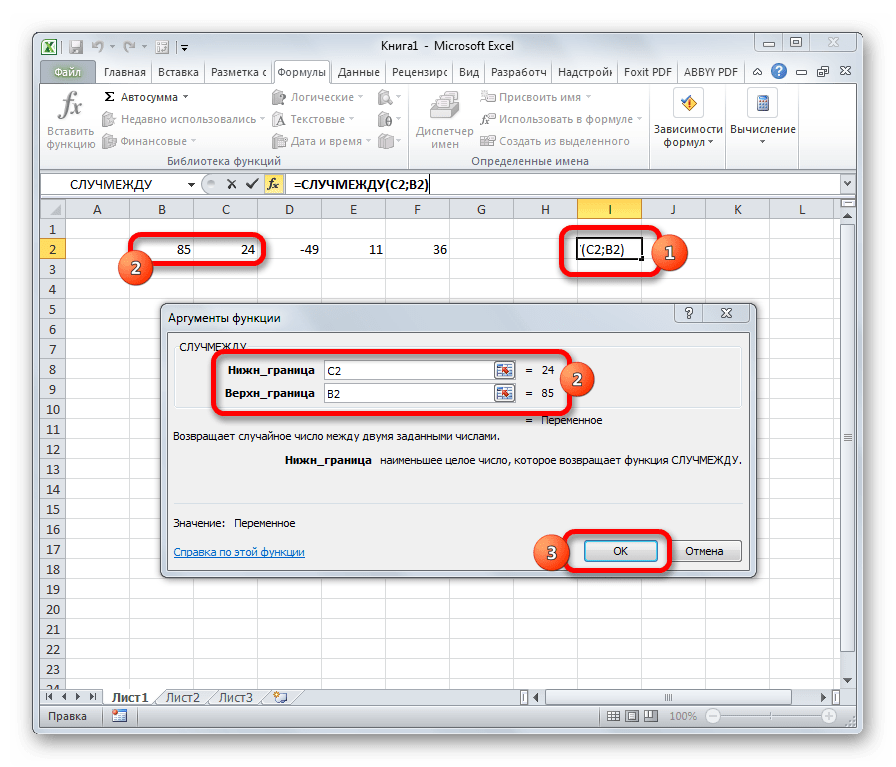
- СЛУЧМЕЖДУ
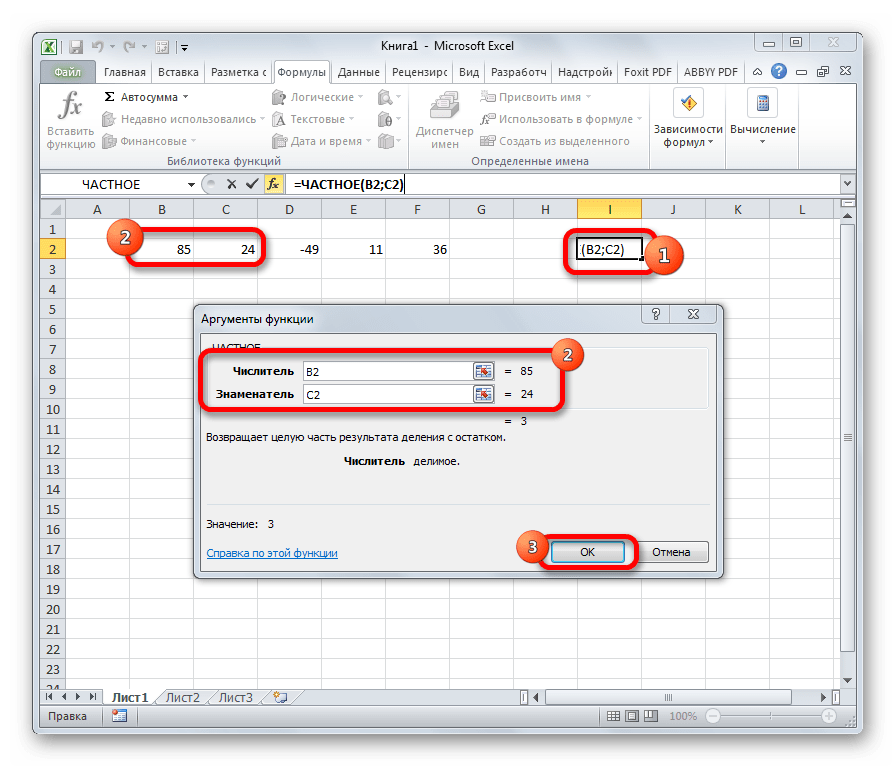
- ЧАСТНОЕ
- РИМСКОЕ
- Вопросы и ответы
Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.
Применение математических функций
С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.
Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.
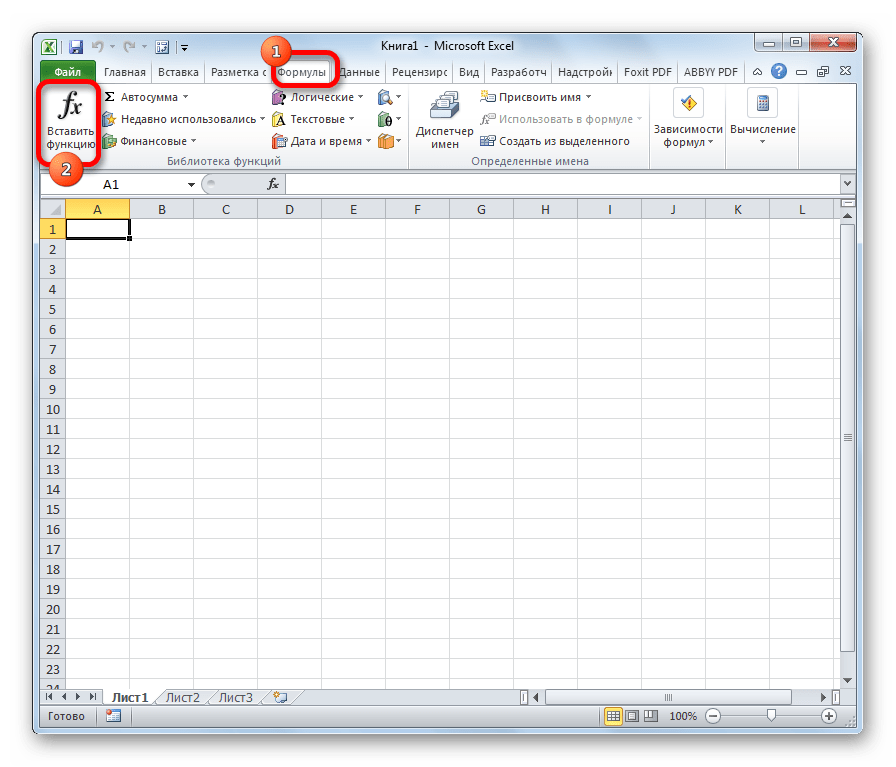
Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».
Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».
Открывается выпадающий список. Выбираем в нем позицию «Математические».
После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.
Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.
Урок: Мастер функций в Excel
СУММ
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:
=СУММ(число1;число2;…)
В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.
Урок: Как посчитать сумму в Экселе
СУММЕСЛИ
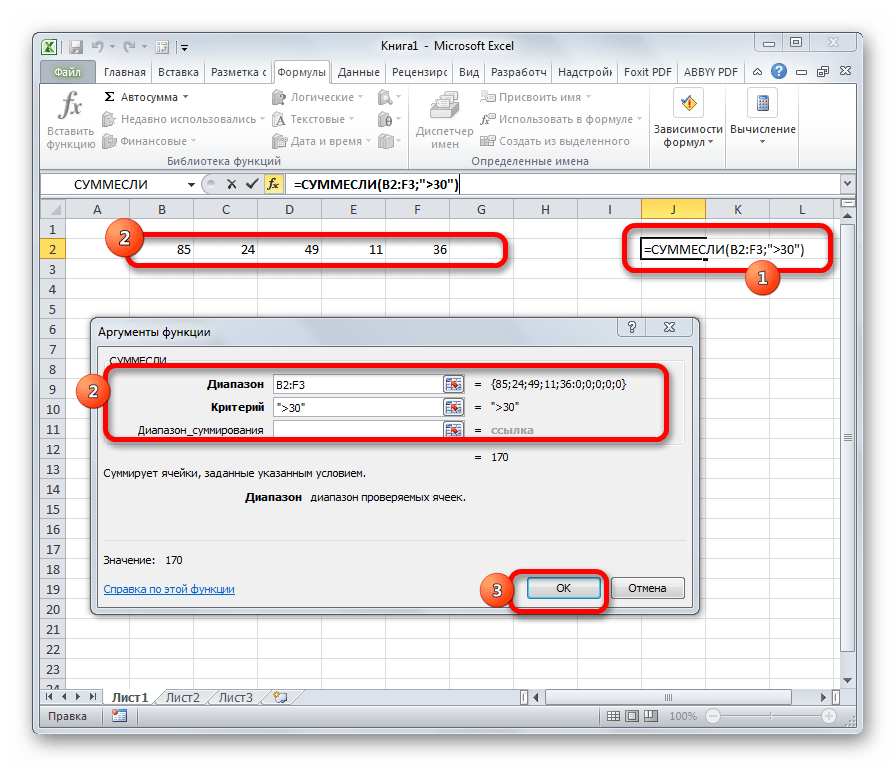
Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
ОКРУГЛ
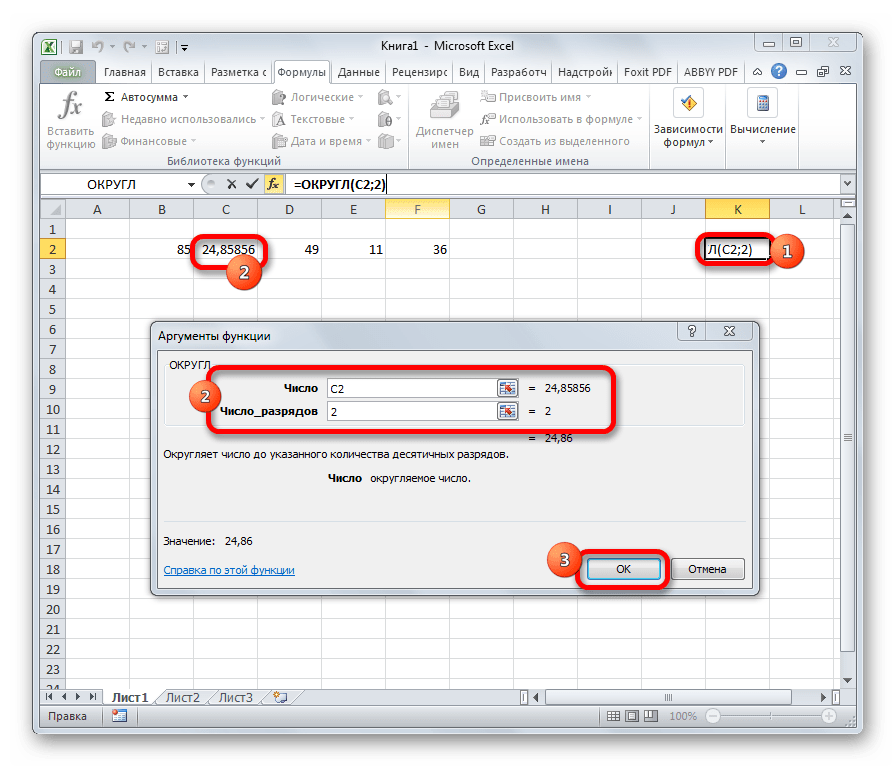
Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:
=ОКРУГЛ(число;число_разрядов)
Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.
Урок: Округление чисел в Excel
ПРОИЗВЕД
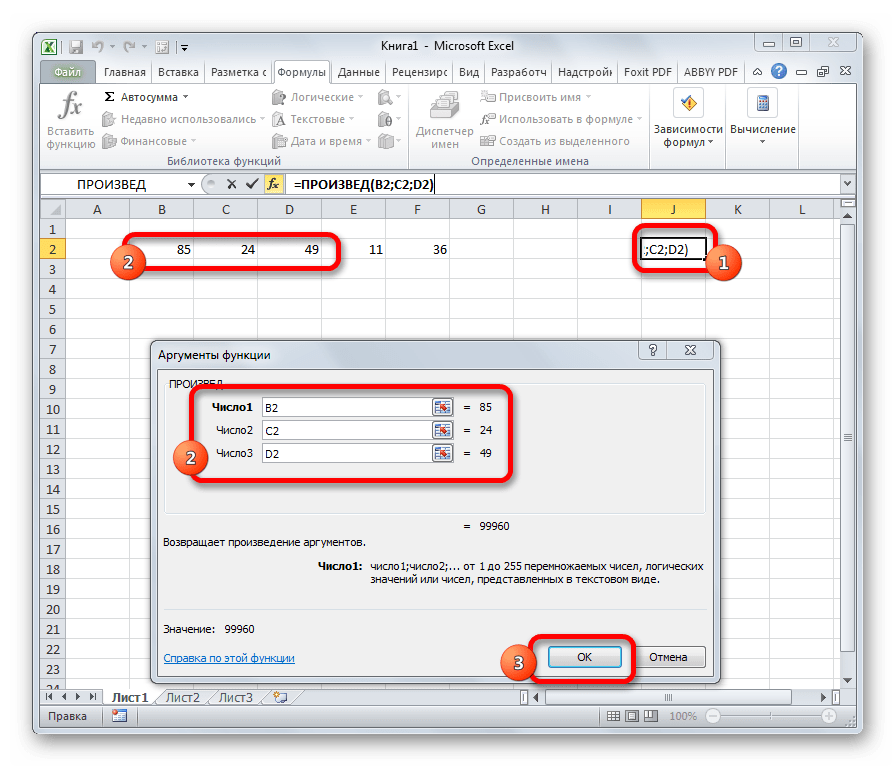
Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:
=ПРОИЗВЕД(число;число;…)
Урок: Как правильно умножать в Excel
ABS
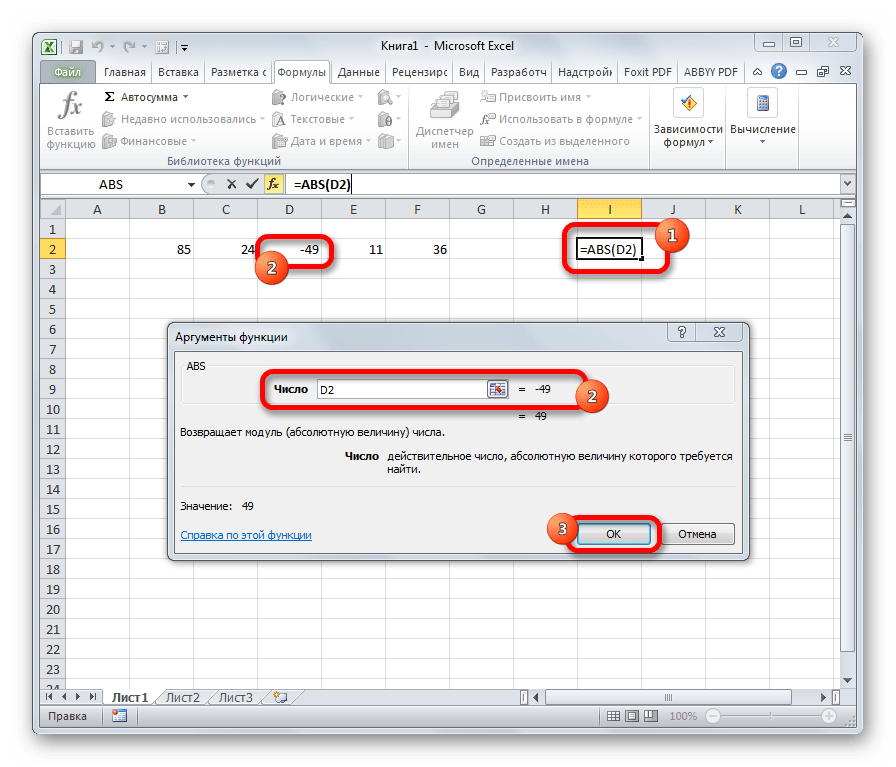
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:
=ABS(число)
Урок: Функция модуля в Excel
СТЕПЕНЬ
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
=СТЕПЕНЬ(число;степень)
Урок: Как возводить в степень в Экселе
КОРЕНЬ
Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:
=КОРЕНЬ(число)
Урок: Как посчитать корень в Экселе
СЛУЧМЕЖДУ
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:
=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)
ЧАСТНОЕ
Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:
=ЧАСТНОЕ(Числитель;Знаменатель)
Урок: Формула деления в Экселе
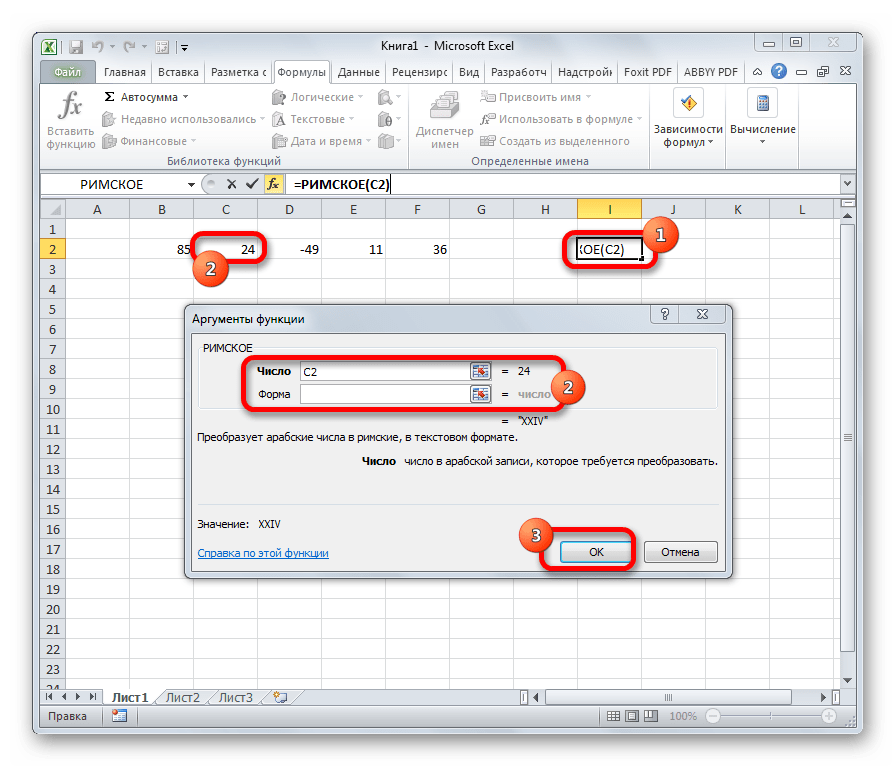
РИМСКОЕ
Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:
=РИМСКОЕ(Число;Форма)
Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.
Если вы не знакомы с Excel в Интернете, скоро вы обнаружите, что это не просто сетка, в которую вы вводите числа в столбцах или строках. Да, можно использовать Excel в Интернете для поиска итогов по столбцу или строке чисел, но можно также вычислить платеж по кредиту, решить математические или технические задачи или найти оптимальный сценарий на основе переменных чисел, которые вы подключали.
Excel в Интернете делает это с помощью формул в ячейках. Формула выполняет вычисления или другие действия с данными на листе. Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак «плюс» или «минус») и функции, которые значительно расширяют возможности формулы.
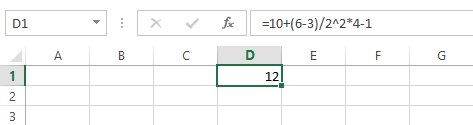
Ниже приведен пример формулы, умножающей 2 на 3 и прибавляющей к результату 5, чтобы получить 11.
=2*3+5
Следующая формула использует функцию ПЛТ для вычисления платежа по ипотеке (1 073,64 долларов США) с 5% ставкой (5% разделить на 12 месяцев равняется ежемесячному проценту) на период в 30 лет (360 месяцев) с займом на сумму 200 000 долларов:
=ПЛТ(0,05/12;360;200000)
Ниже приведены примеры формул, которые можно использовать на листах.
-
=A1+A2+A3 Вычисляет сумму значений в ячейках A1, A2 и A3.
-
=КОРЕНЬ(A1) Использует функцию КОРЕНЬ для возврата значения квадратного корня числа в ячейке A1.
-
=СЕГОДНЯ() Возвращает текущую дату.
-
=ПРОПИСН(«привет») Преобразует текст «привет» в «ПРИВЕТ» с помощью функции ПРОПИСН.
-
=ЕСЛИ(A1>0) Анализирует ячейку A1 и проверяет, превышает ли значение в ней нуль.
Элементы формулы
Формула также может содержать один или несколько из таких элементов: функции, ссылки, операторы и константы.
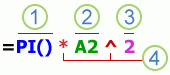
1. Функции. Функция ПИ() возвращает значение числа Пи: 3,142…
2. Ссылки. A2 возвращает значение ячейки A2.
3. Константы. Числа или текстовые значения, введенные непосредственно в формулу, например 2.
4. Операторы. Оператор ^ («крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.
Использование констант в формулах
Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, но не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после изменения формулы.
Использование операторов в формулах
Операторы определяют операции, которые необходимо выполнить над элементами формулы. Вычисления выполняются в стандартном порядке (соответствующем основным правилам арифметики), однако его можно изменить с помощью скобок.
Типы операторов
Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.
Арифметические операторы
Арифметические операторы служат для выполнения базовых арифметических операций, таких как сложение, вычитание, умножение, деление или объединение чисел. Результатом операций являются числа. Арифметические операторы приведены ниже.
|
Арифметический оператор |
Значение |
Пример |
|
+ (знак «плюс») |
Сложение |
3+3 |
|
– (знак «минус») |
Вычитание |
3–1 |
|
* (звездочка) |
Умножение |
3*3 |
|
/ (косая черта) |
Деление |
3/3 |
|
% (знак процента) |
Доля |
20% |
|
^ (крышка) |
Возведение в степень |
3^2 |
Операторы сравнения
Операторы сравнения используются для сравнения двух значений. Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
|
Оператор сравнения |
Значение |
Пример |
|
= (знак равенства) |
Равно |
A1=B1 |
|
> (знак «больше») |
Больше |
A1>B1 |
|
< (знак «меньше») |
Меньше |
A1<B1 |
|
>= (знак «больше или равно») |
Больше или равно |
A1>=B1 |
|
<= (знак «меньше или равно») |
Меньше или равно |
A1<=B1 |
|
<> (знак «не равно») |
Не равно |
A1<>B1 |
Текстовый оператор конкатенации
Амперсанд (&) используется для объединения (соединения) одной или нескольких текстовых строк в одну.
|
Текстовый оператор |
Значение |
Пример |
|
& (амперсанд) |
Соединение или объединение последовательностей знаков в одну последовательность |
Выражение «Северный»&«ветер» дает результат «Северный ветер». |
Операторы ссылок
Для определения ссылок на диапазоны ячеек можно использовать операторы, указанные ниже.
|
Оператор ссылки |
Значение |
Пример |
|
: (двоеточие) |
Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки. |
B5:B15 |
|
; (точка с запятой) |
Оператор объединения. Объединяет несколько ссылок в одну ссылку. |
СУММ(B5:B15,D5:D15) |
|
(пробел) |
Оператор пересечения множеств, используется для ссылки на общие ячейки двух диапазонов. |
B7:D7 C6:C8 |
Порядок выполнения Excel в Интернете в формулах
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.
Порядок вычислений
Формулы вычисляют значения в определенном порядке. Формула всегда начинается со знака равенства (=). Excel в Интернете интерпретирует символы, которые следуют знаку равенства, как формулу. После знака равенства вычисляются элементы (операнды), такие как константы или ссылки на ячейки. Они разделяются операторами вычислений. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Приоритет операторов
Если объединить несколько операторов в одну формулу, Excel в Интернете выполняет операции в порядке, показанном в следующей таблице. Если формула содержит операторы с одинаковым приоритетом (например, если формула содержит оператор умножения и деления), Excel в Интернете вычисляет операторы слева направо.
|
Оператор |
Описание |
|
: (двоеточие) (один пробел) , (запятая) |
Операторы ссылок |
|
– |
Знак «минус» |
|
% |
Процент |
|
^ |
Возведение в степень |
|
* и / |
Умножение и деление |
|
+ и — |
Сложение и вычитание |
|
& |
Объединение двух текстовых строк в одну |
|
= |
Сравнение |
Использование круглых скобок
Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, приведенная ниже формула возвращает значение 11, так как Excel в Интернете выполняет умножение перед добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
=5+2*3
В отличие от этого, если для изменения синтаксиса используются круглые скобки, Excel в Интернете 5 и 2, а затем умножает результат на 3, чтобы получить 21.
=(5+2)*3
В следующем примере скобки, которые заключают первую часть формулы, принудительно Excel в Интернете сначала вычислить B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Использование функций и вложенных функций в формулах
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления.
Синтаксис функций
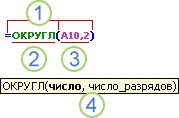
Приведенный ниже пример функции ОКРУГЛ, округляющей число в ячейке A10, демонстрирует синтаксис функции.
1. Структура. Структура функции начинается со знака равенства (=), за которым следует имя функции, открывающая скобка, аргументы функции, разделенные запятыми, и закрывающая скобка.
2. Имя функции. Чтобы отобразить список доступных функций, щелкните любую ячейку и нажмите клавиши SHIFT+F3.
3. Аргументы. Существуют различные типы аргументов: числа, текст, логические значения (ИСТИНА и ЛОЖЬ), массивы, значения ошибок (например #Н/Д) или ссылки на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
4. Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Ввод функций
Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. При вводе функции в формулу в диалоговом окне Вставить функцию отображаются имя функции, все ее аргументы, описание функции и каждого из аргументов, текущий результат функции и всей формулы.
Чтобы упростить создание и редактирование формул и свести к минимуму количество опечаток и синтаксических ошибок, пользуйтесь автозавершением формул. После ввода знака = (знак равенства) и начальных букв или триггера отображения Excel в Интернете под ячейкой отображается динамический раскрывающийся список допустимых функций, аргументов и имен, соответствующих буквам или триггеру. После этого элемент из раскрывающегося списка можно вставить в формулу.
Вложенные функции
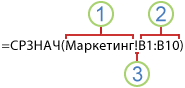
В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в приведенной ниже формуле для сравнения результата со значением 50 используется вложенная функция СРЗНАЧ.
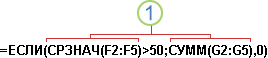
1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. Если это не так, Excel в Интернете отображает #VALUE! В противном случае TE102825393 выдаст ошибку «#ЗНАЧ!».
<c0>Предельное количество уровней вложенности функций</c0>. В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
Использование ссылок в формулах
Ссылка определяет ячейку или диапазон ячеек на листе и сообщает Excel в Интернете где искать значения или данные, которые нужно использовать в формуле. С помощью ссылок можно использовать в одной формуле данные, находящиеся в разных частях листа, а также использовать значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.
Стиль ссылок A1
Стиль ссылок по умолчанию По умолчанию в Excel в Интернете используется ссылочный стиль A1, который ссылается на столбцы с буквами (A–XFD, всего 16 384 столбца) и ссылается на строки с числами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.
|
Ячейка или диапазон |
Использование |
|
Ячейка на пересечении столбца A и строки 10 |
A10 |
|
Диапазон ячеек: столбец А, строки 10-20. |
A10:A20 |
|
Диапазон ячеек: строка 15, столбцы B-E |
B15:E15 |
|
Все ячейки в строке 5 |
5:5 |
|
Все ячейки в строках с 5 по 10 |
5:10 |
|
Все ячейки в столбце H |
H:H |
|
Все ячейки в столбцах с H по J |
H:J |
|
Диапазон ячеек: столбцы А-E, строки 10-20 |
A10:E20 |
<c0>Ссылка на другой лист</c0>. В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
1. Ссылка на лист «Маркетинг».
2. Ссылка на диапазон ячеек с B1 по B10 включительно.
3. Ссылка на лист, отделенная от ссылки на диапазон значений.
Различия между абсолютными, относительными и смешанными ссылками
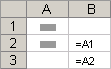
Относительные ссылки . Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.
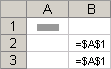
Абсолютные ссылки . Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.
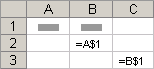
Смешанные ссылки . Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец имеет вид $A1, $B1 и т. д. Абсолютная ссылка на строку имеет вид A$1, B$1 и т. д. Если положение ячейки с формулой изменяется, относительная ссылка меняется, а абсолютная — нет. При копировании или заполнении формулы по строкам и столбцам относительная ссылка автоматически изменяется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в ячейку B3 она автоматически изменяется с =A$1 на =B$1.
Стиль трехмерных ссылок
Удобный способ для ссылки на несколько листов . Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. Excel в Интернете использует все листы, хранящиеся между начальным и конечным именами ссылки. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от Лист2 до Лист13 включительно.
-
При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
-
Трехмерные ссылки нельзя использовать в формулах массива.
-
Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.
Что происходит при перемещении, копировании, вставке или удалении листов . Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.
-
Вставка или копирование . Если вставить или скопировать листы между листами 2 и 6 (в этом примере это конечные точки), Excel в Интернете содержит все значения в ячейках A2–A5 из добавленных листов в вычислениях.
-
Удаление . При удалении листов между листами 2 и 6 Excel в Интернете удаляет их значения из вычисления.
-
Перемещение . При перемещении листов между листами 2 и 6 в расположение за пределами указанного диапазона листов Excel в Интернете удаляет их значения из вычисления.
-
Перемещение конечного листа . При перемещении листа 2 или листа 6 в другое место в той же книге Excel в Интернете корректирует вычисление в соответствии с новым диапазоном листов между ними.
-
Удаление конечного листа . При удалении sheet2 или Sheet6 Excel в Интернете корректирует вычисление в соответствии с диапазоном листов между ними.
Стиль ссылок R1C1
Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы. Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает расположение ячейки с «R», за которым следует номер строки и «C», за которым следует номер столбца.
|
Ссылка |
Значение |
|
R[-2]C |
относительная ссылка на ячейку, расположенную на две строки выше в том же столбце |
|
R[2]C[2] |
Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее |
|
R2C2 |
Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца |
|
R[-1] |
Относительная ссылка на строку, расположенную выше текущей ячейки |
|
R |
Абсолютная ссылка на текущую строку |
При записи макроса Excel в Интернете некоторые команды с помощью ссылочного стиля R1C1. Например, если вы записываете команду, например нажатие кнопки « Автосчет», чтобы вставить формулу, которая добавляет диапазон ячеек, Excel в Интернете формулу с помощью стиля R1C1, а не стиля A1, ссылок.
Использование имен в формулах
Можно создать определенные имена для представления ячеек, диапазонов ячеек, формул, констант или Excel в Интернете таблиц. Имя — это значимое краткое обозначение, поясняющее предназначение ссылки на ячейку, константы, формулы или таблицы, так как понять их суть с первого взгляда бывает непросто. Ниже приведены примеры имен и показано, как их использование упрощает понимание формул.
|
Тип примера |
Пример использования диапазонов вместо имен |
Пример с использованием имен |
|
Ссылка |
=СУММ(A16:A20) |
=СУММ(Продажи) |
|
Константа |
=ПРОИЗВЕД(A12,9.5%) |
=ПРОИЗВЕД(Цена,НСП) |
|
Формула |
=ТЕКСТ(ВПР(MAX(A16,A20),A16:B20,2,FALSE),»дд.мм.гггг») |
=ТЕКСТ(ВПР(МАКС(Продажи),ИнформацияОПродажах,2,ЛОЖЬ),»дд.мм.гггг») |
|
Таблица |
A22:B25 |
=ПРОИЗВЕД(Price,Table1[@Tax Rate]) |
Типы имен
Существует несколько типов имен, которые можно создавать и использовать.
Определенное имя Имя, используемое для представления ячейки, диапазона ячеек, формулы или константы. Вы можете создавать собственные определенные имена. Кроме того, Excel в Интернете иногда создает определенное имя, например при настройке области печати.
Имя таблицы Имя таблицы Excel в Интернете, которая представляет собой коллекцию данных об определенной теме, которая хранится в записях (строках) и полях (столбцах). Excel в Интернете создает имя таблицы Excel в Интернете «Table1», «Table2» и т. д. при каждой вставке таблицы Excel в Интернете, но вы можете изменить эти имена, чтобы сделать их более значимыми.
Создание и ввод имен
Имя создается с помощью команды «Создать имя» из выделенного фрагмента. Можно удобно создавать имена из существующих имен строк и столбцов с помощью фрагмента, выделенного на листе.
Примечание: По умолчанию в именах используются абсолютные ссылки на ячейки.
Имя можно ввести указанными ниже способами.
-
Ввода Введите имя, например, в качестве аргумента формулы.
-
<c0>Автозавершение формул</c0>. Используйте раскрывающийся список автозавершения формул, в котором автоматически выводятся допустимые имена.
Использование формул массива и констант массива
Excel в Интернете не поддерживает создание формул массива. Вы можете просматривать результаты формул массива, созданных в классическом приложении Excel, но не сможете изменить или пересчитать их. Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.
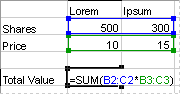
В примере формулы массива ниже вычисляется итоговое значение цен на акции; строки ячеек не используются при вычислении и отображении отдельных значений для каждой акции.
При вводе формулы «={СУММ(B2:D2*B3:D3)}» в качестве формулы массива сначала вычисляется значение «Акции» и «Цена» для каждой биржи, а затем — сумма всех результатов.
<c0>Вычисление нескольких значений</c0>. Некоторые функции возвращают массивы значений или требуют массив значений в качестве аргумента. Для вычисления нескольких значений с помощью формулы массива необходимо ввести массив в диапазон ячеек, состоящий из того же числа строк или столбцов, что и аргументы массива.
Например, по заданному ряду из трех значений продаж (в столбце B) для трех месяцев (в столбце A) функция ТЕНДЕНЦИЯ определяет продолжение линейного ряда объемов продаж. Чтобы можно было отобразить все результаты формулы, она вводится в три ячейки столбца C (C1:C3).
Формула «=ТЕНДЕНЦИЯ(B1:B3;A1:A3)», введенная как формула массива, возвращает три значения (22 196, 17 079 и 11 962), вычисленные по трем объемам продаж за три месяца.
Использование констант массива
В обычную формулу можно ввести ссылку на ячейку со значением или на само значение, также называемое константой. Подобным образом в формулу массива можно ввести ссылку на массив либо массив значений, содержащихся в ячейках (его иногда называют константой массива). Формулы массива принимают константы так же, как и другие формулы, однако константы массива необходимо вводить в определенном формате.
Константы массива могут содержать числа, текст, логические значения, например ИСТИНА или ЛОЖЬ, либо значения ошибок, такие как «#Н/Д». В одной константе массива могут присутствовать значения различных типов, например {1,3,4;ИСТИНА,ЛОЖЬ,ИСТИНА}. Числа в константах массива могут быть целыми, десятичными или иметь экспоненциальный формат. Текст должен быть заключен в двойные кавычки, например «Вторник».
Константы массива не могут содержать ссылки на ячейку, столбцы или строки разной длины, формулы и специальные знаки: $ (знак доллара), круглые скобки или % (знак процента).
При форматировании констант массива убедитесь, что выполняются указанные ниже требования.
-
Константы заключены в фигурные скобки ( { } ).
-
Столбцы разделены запятыми (,). Например, чтобы представить значения 10, 20, 30 и 40, введите {10,20,30,40}. Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца.
-
Значения ячеек из разных строк разделены точками с запятой (;). Например, чтобы представить значения 10, 20, 30, 40 и 50, 60, 70, 80, находящиеся в расположенных друг под другом ячейках, можно создать константу массива с размерностью 2 на 4: {10,20,30,40;50,60,70,80}.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12694 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
источники:
http://lumpics.ru/how-solve-system-equations-excel/
http://exceltable.com/otchety/reshenie-uravneniy
В программе Excel разработчиками заложено огромное количество различных функций, но, пользователи чаще всего пользуются математическими. Давайте рассмотрим их и подробнее остановимся на самых популярных.
-
Использование математических функций в программе
- СУММ
- СУММЕСЛИ
- ПРОИЗВЕД
- ЧАСТНОЕ
- СТЕПЕНЬ
- КОРЕНЬ
- ОКРУГЛ
- ABS
- LOG
- ОСТАТОК
- Заключение
Использование математических функций в программе
В категорию математических функций входит более 60 различных операторов, которые позволяют выполнять различные вычисления.
Вставить функцию в свободную ячейку таблицы можно по-разному:
- Жмем кнопку “Вставить функцию” (fx) слева от строки формул. Выполнить данное действие можно, находясь в любой вкладке.
- Переключаемся во вкладку “Формулы”. Здесь также представлена кнопка “Вставить функцию” – в левом углу ленты инструментов.
- Нажимаем комбинацию клавиш Shift+F3, чтобы вызвать Мастер функций.
Результатом любого из вышеописанных способов будет открытие окна вставки функции. Здесь мы выбираем категорию “Математические”.
Теперь, когда категория выбрана, в поле ниже отмечаем требуемую функцию и щелкаем OK.
После этого откроется окно с аргументами для заполнения.
Примечание: Если мы, находясь во вкладке “Формулы”, в группе инструментов “Библиотека функций” нажмем по значку математических функций, сразу откроется список операторов, которые мы можем выбрать, минуя окно вставки функции.
Стоит учитывать, что в предлагаемом перечне присутствуют не все операторы, но самые необходимые здесь все же есть, и в большинстве случаев их достаточно.
Теперь перейдем к детальному рассмотрению самых популярных функций.
СУММ
Пожалуй, это самая популярная функция, которая используется в Эксель. С помощью нее выполняется суммирование числовых данных. Формула функции:
=СУММ(число1;число2;...)
В аргументах можно указать как конкретные числа, так и ссылки на ячейки, содержащие числовые значения. Причем указать координаты можно вручную (с помощью клавиш клавиатуры) или методом клика/выделения непосредственно в самой таблице.
Для перехода к заполнению следующего аргумента достаточно кликнуть по полю напротив него или нажать клавишу Tab.
СУММЕСЛИ
Данная функция позволяет считать сумму чисел с заданным условиями, с помощью которых будет выполняться отбор значений, учитывающихся в суммировании. Формула выглядит следующим образом:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
В аргументах функции указывается диапазон ячеек (вручную или путем выделения в таблице), значения которых нужно просуммировать. В качестве критерия можно задать следующие условия (в кавычках):
- больше (“>”)
- меньше (“<“)
- не равно (“<>”)
Аргумент “Диапазон_сумирования” заполнять не обязательно.
ПРОИЗВЕД
С помощью данного оператора выполняется умножение чисел. Синтаксис выглядит следующим образом:
=ПРОИЗВЕД(число;число;…)
В аргументах функции, как и в СУММ, можно указывать как конкретные числа, так и адреса ячеек (диапазоны ячеек), которые содержат числовые значения.
ЧАСТНОЕ
Чаще всего для деления используется формула со знаком “/” между делимым и делителем: =Число1/Число2.
Однако в программе также есть отдельная функция для выполнения деления, синтаксис которой представлен ниже:
=ЧАСТНОЕ(Числитель;Знаменатель)
Заполнить нужно два аргумента: Числитель (Делимое) и Знаменатель (Делитель).
СТЕПЕНЬ
Оператор позволяет возвести число в указанную степень. Формула выглядит так:
=СТЕПЕНЬ(число;степень)
В аргументах функции указывается само число, а также, степень, в которую нужно его возвести.
КОРЕНЬ
С помощью данного оператора можно извлечь квадратный корень из числа. Синтаксис выглядит следующим образом:
=КОРЕНЬ(число)
Заполнить требуется только один аргумент – “Число”.
ОКРУГЛ
Функция применяется для выполнения еще одного распространенного математического действия – округления чисел (по общематематическим правилам, т.е., к ближайшему по модулю значению). Синтаксис функции представлен ниже:
=ОКРУГЛ(число;число_разрядов)
В аргументе “Число” указывается значение, которое требуется округлить. В числе разрядов, соответственно, пишем количество цифр, которые хотим оставить после запятой.
Также, в Excel доступны операторы ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые, как следует из их названий, используются для округления до ближайшего верхнего и нижнего числа, соответственно (по модулю).
ABS
Позволяет получить модуль числа. Формула функции представлена ниже:
=ABS(число)
Заполнить нужно всего один аргумент – “Число”, модуль которого требуется найти.
LOG
С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:
=LOG(Число;Основание)
Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).
Также для десятичного логарифма предусмотрена отдельная функция – LOG10.
ОСТАТОК
Применяется для получения остатка от деления чисел. Формула оператора выглядит следующим образом:
=ОСТАТ(чило;делитель)
Для того, чтобы получить результат, требуется заполнить значения двух аргументов: Число и Делитель.
Заключение
Таким образом, мы разобрали самые популярные математические функции, которые используются в Excel. Однако возможности программы гораздо шире, и в ее инструментарии можно найти функцию для успешного выполнения практически любой задачи.
Логические функции в Excel проверяют данные и возвращают результат «ИСТИНА», если условие выполняется, и «ЛОЖЬ», если нет.
Рассмотрим синтаксис логических функций и примеры применения их в процессе работы с программой Excel.
Использование логических функций в Excel
| Название функции | Значение | Синтаксис | Примечание |
| ИСТИНА | Не имеет аргументов, возвращает логическое значение «ИСТИНА». | =ИСТИНА () | Редко используется в качестве самостоятельной функции. |
| ЛОЖЬ | Не имеет аргументов, возвращает логическое выражение «ЛОЖЬ». | =ЛОЖЬ () | ——-//——- |
| И | Если все заданные аргументы возвращают истинный результат, то функция выдает логическое выражение «ИСТИНА». В случае хотя бы одного ложного логического значения вся функция выдает результат «ЛОЖЬ». | =И (Лог_знач. 1; Лог_знач. 2;…) | Принимает до 255 аргументов в виде условий или ссылок. Обязательным является первый. |
| ИЛИ | Показывает результат «ИСТИНА», если хотя бы один из аргументов является истинным. | =ИЛИ (Лог_знач.1; Лог_знач. 2;…) | ——-//——- |
| НЕ | Меняет логическое значение «ИСТИНА» на противоположное – «ЛОЖЬ». И наоборот. | #ИМЯ? | Обычно сочетается с другими операторами. |
| ЕСЛИ | Проверяет истинность логического выражения и возвращает соответствующий результат. | #ИМЯ? | «Логическое_выражение» при вычислении должно иметь результат «ИСТИНА» или «ЛОЖЬ». |
| ЕСЛИОШИБКА | Если значение первого аргумента истинно, то возвращает сам аргумент. В противном случае – значение второго аргумента. | #ИМЯ? | Оба аргумента обязательны. |
Логические функции в Excel и примеры решения задач
Задача 1. Необходимо переоценить товарные остатки. Если продукт хранится на складе дольше 8 месяцев, уменьшить его цену в 2 раза.
Сформируем таблицу с исходными параметрами:
Чтобы решить поставленную задачу, воспользуемся логической функцией ЕСЛИ. Формула будет выглядеть так: =ЕСЛИ(C2>=8;B2/2;B2).
Логическое выражение «С2>=8» построено с помощью операторов отношения «>» и «=». Результат его вычисления – логическая величина «ИСТИНА» или «ЛОЖЬ». В первом случае функция возвращает значение «В2/2». Во втором – «В2».
Усложним задачу – задействуем логическую функцию И. Теперь условие такое: если товар хранится дольше 8 месяцев, то его стоимость уменьшается в 2 раза. Если дольше 5 месяцев, но меньше 8 – в 1,5 раза.
Формула приобретает следующий вид: .
В функции ЕСЛИ можно использовать в качестве аргументов текстовые значения.
Задача 2. Если стоимость товара на складе после уценки стала меньше 300 р. или продукт хранится дольше 10 месяцев, его списывают.
Для решения используем логические функции ЕСЛИ и ИЛИ: . Условие, записанное с помощью логической операции ИЛИ, расшифровывается так: товар списывается, если число в ячейке D2 = 10.
При невыполнении условия функция ЕСЛИ возвращает пустую ячейку.
В качестве аргументов можно использовать другие функции. К примеру, математические.
Задача 3. Ученики перед поступлением в гимназию сдают математику, русский и английский языки. Проходной балл – 12. По математике для поступления нужно получить не менее 4 баллов. Составить отчет о поступлении.
Составим таблицу с исходными данными:
Нужно общее количество баллов сравнить с проходным баллом. И проверить, чтобы по математике оценка была не ниже «4». В графе «Результат» поставить «принят» или «нет».
Введем формулу вида: . Логический оператор «И» заставляет функцию проверять истинность двух условий. Математическая функция «СУММ» используется для подсчета итогового балла.
Функция ЕСЛИ позволяет решать многочисленные задачи, поэтому используется чаще всего.
Статистические и логические функции в Excel
Задача 1. Проанализировать стоимость товарных остатков после уценки. Если цена продукта после переоценки ниже средних значений, то списать со склада этот продукт.
Работаем с таблицей из предыдущего раздела:
Для решения задачи используем формулу вида: . В логическом выражении «D2<СРЗНАЧ(D2:D7)» применена статистическая функция СРЗНАЧ. Она возвращает среднее арифметическое в диапазоне D2:D7.
Задача 2. Найти средние продажи в магазинах сети.
Составим таблицу с исходными данными:
Необходимо найти среднее арифметическое для ячеек, значение которых отвечает заданному условию. То есть совместить логическое и статистическое решение.
Чуть ниже таблицы с условием составим табличку для отображения результатов:
Решим задачу с помощью одной функции: . Первый аргумент – $B$2:$B$7 – диапазон ячеек для проверки. Второй аргумент – В9 – условие. Третий аргумент – $C$2:$C$7 – диапазон усреднения; числовые значения, которые берутся для расчета среднего арифметического.
Функция СРЗНАЧЕСЛИ сопоставляет значение ячейки В9 (№1) со значениями в диапазоне В2:В7 (номера магазинов в таблице продаж). Для совпадающих данных считает среднее арифметическое, используя числа из диапазона С2:С7.
Задача 3. Найти средние продажи в магазине №1 г. Москва.
Видоизменим таблицу из предыдущего примера:
Нужно выполнить два условия – воспользуемся функцией вида: .
Функция СРЗНАЧЕСЛИМН позволяет применять более одного условия. Первый аргумент – $D$2:$D$7 – диапазон усреднения (откуда берутся цифры для нахождения среднего арифметического). Второй аргумент – $B$2:$B$7 – диапазон для проверки первого условия.
Скачать примеры логических функций
Третий аргумент – В9 – первое условие. Четвертый и пятый аргумент – диапазон для проверки и второе условие, соответственно.
Функция учитывает только те значения, которые соответствуют всем заданным условиям.
#Руководства
- 18 янв 2023
-
0
Показали, как работать с логическими функциями Excel: ИСТИНА, ЛОЖЬ, И, ИЛИ, НЕ, ЕСЛИ, ЕСЛИОШИБКА, ЕОШИБКА, ЕПУСТО.
Иллюстрация: Merry Mary для Skillbox Media
Рассказывает просто о сложных вещах из мира бизнеса и управления. До редактуры — пять лет в банке и три — в оценке имущества. Разбирается в Excel, финансах и корпоративной жизни.
Логические функции в Excel проверяют, выполняются ли заданные условия в выбранном диапазоне. Пользователь указывает критерии, соответствие которым нужно проверить, — функции проверяют и выдают результат: ИСТИНА или ЛОЖЬ.
Также логические функции используют в сложных расчётах для того, чтобы убрать промежуточные шаги вычисления и объединить несколько действий в одной ячейке. Это значительно сокращает время обработки данных.
В статье рассмотрим основные логические функции Excel — расскажем, для чего они нужны, и на примерах покажем, как они работают.
- Функции ИСТИНА и ЛОЖЬ
- Функции И и ИЛИ
- Функция НЕ
- Функция ЕСЛИ
- Функция ЕСЛИОШИБКА
- Функция ЕОШИБКА
- Функция ЕПУСТО
В конце расскажем, как узнать больше о работе в Excel.
Функции ИСТИНА и ЛОЖЬ не используют самостоятельно — только внутри других логических функций. Они нужны, чтобы отмечать значения как истинные или ложные.
Функция ИСТИНА возвращает только истинные значения. Её синтаксис: =ИСТИНА().
Функция ЛОЖЬ возвращает только ложные значения. Её синтаксис: =ЛОЖЬ().
Функции И и ИЛИ нужны для того, чтобы показать связь между условиями пользователя. Они определяют, будут соблюдены все условия или только некоторые из них.
Функция И. Её используют, чтобы показать, что указанные число или текст должны соответствовать одновременно всем критериям. В этом случае функция возвращает значение ИСТИНА. Если один из критериев не соблюдается, функция И возвращает значение ЛОЖЬ.
Синтаксис функции И такой: =И(логическое_значение1;логическое_значение2;…), где логическое_значение — условия, которые функция будет проверять. Задано может быть до 255 условий.
Пример работы функции И. Проверим, соблюдены ли два условия:
- число 662 больше 300;
- число 8626 больше 9000.
Для этого выберем любую ячейку и в строке формул введём: =И(A1>300;A2>9000), где А1 — ячейка с числом 662, А2 — ячейка с числом 8626.
Нажмём Enter. Функция возвращает значение ЛОЖЬ — одно из условий не соблюдено (число 8626 < 9000).
Скриншот: Excel / Skillbox Media
Проверим другие условия:
- число 662 меньше 666;
- число 8626 больше 5000.
Снова выберем любую ячейку и в строке формул введём: =И(A1<666;A2>5000).
Функция возвращает значение ИСТИНА — оба условия соблюдены.
Скриншот: Excel / Skillbox Media
Функция ИЛИ. Её используют, чтобы показать, что указанные число или текст должны соответствовать одному из условий. Если хотя бы одно условие соблюдено, функция возвращает значение ИСТИНА. Если все условия не соблюдены, функция ИЛИ возвращает значение ЛОЖЬ.
Синтаксис функции ИЛИ: =ИЛИ(логическое_значение1;логическое_значение2;…).
Максимальное количество логических значений (условий) — тоже 255.
Пример работы функции ИЛИ. Проверим три условия:
- число 662 меньше 666;
- число 8626 больше 5000;
- число 567 больше 786.
В строке формул введём: =ИЛИ(A1<666;A2>5000;A3>786).
Функция возвращает значение ИСТИНА, несмотря на то, что одно условие не соблюдено (число 567 < 786).
Скриншот: Excel / Skillbox Media
Проверим другие условия:
- число 662 меньше 500;
- число 8626 больше 9000;
- число 567 больше 600.
В строке формул введём: =ИЛИ(A1<500;A2>9000;A3>600).
Функция возвращает значение ЛОЖЬ, так как ни одно из условий не соблюдено.
Скриншот: Excel / Skillbox Media
С помощью этой функции возвращают значения, которые противоположны по отношению к заданному параметру.
Если в качестве параметра функции НЕ указать ложное значение — она вернёт значение ИСТИНА. Наоборот, если указать истинное значение, функция вернёт ЛОЖЬ.
Синтаксис функции НЕ: =НЕ(логическое_значение), где «логическое_значение» — выражение, которое нужно проверить на соответствие значениям ИСТИНА или ЛОЖЬ. В этой функции можно использовать только одно такое выражение.
Пример работы функции НЕ. Проверим выражение «662 меньше 500». Выберем любую ячейку и в строке формул введём: =НЕ(A1<500), где А1 — ячейка с числом 662.
Нажмём Enter.
Выражение «662 меньше 500» ложное. Но функция НЕ поменяла значение на противоположное и вернула значение ИСТИНА.
Скриншот: Excel / Skillbox Media
Функцию ЕСЛИ используют, когда нужно сравнить данные таблицы с условиями, заданными пользователем.
У этой функции также два результата: ИСТИНА и ЛОЖЬ. Первый результат функция выдаёт, когда значение ячейки совпадает с заданным условием, второй — когда значение условию не соответствует.
Например, если нужно определить в таблице значения меньше 1000, то значение 700 будет отмечено функцией как истинное, а значение 3500 — как ложное.
Можно задавать несколько условий одновременно. Например, найти значения меньше 300, но больше 200. В этом случае функция определит значение 100 как ложное, а 250 — как истинное. Так можно проверять не только числовые значения, но и текст.
Синтаксис функции ЕСЛИ: =ЕСЛИ(лог_выражение;значение_если_истина;значение_если_ложь), где:
- лог_выражение — запрос пользователя, который функция будет проверять;
- значение_если_истина — результат, который функция принесёт в ячейку, если значение совпадёт с запросом пользователя;
- значение_если_ложь — результат, который функция принесёт в ячейку, если значение не совпадёт с запросом пользователя.
Пример работы функции ЕСЛИ. Предположим, из столбца с ценами нам нужно выбрать значения менее 2 млн рублей.
Создадим отдельный столбец для результатов работы функции и выберем первую ячейку.
Скриншот: Excel / Skillbox Media
В строке формул введём: =ЕСЛИ(A2<2000000;»Подходит»;»Не подходит»)
Скриншот: Excel / Skillbox Media
Дальше нажимаем Enter и растягиваем результат из первой ячейки вниз до конца таблицы.
Скриншот: Excel / Skillbox Media
Функция показала, какие значения соответствуют условию «меньше 2000000», и отметила их как «Подходит». Значения, которые не соответствуют этому условию, отмечены как «Не подходит».
В Skillbox Media есть статья, где подробно объясняли, как использовать функцию ЕСЛИ в Excel — в частности, как запустить функцию ЕСЛИ с несколькими условиями.
Эту функцию используют, чтобы определить, есть ли ошибки в значениях таблицы или в формулах.
Синтаксис функции ЕСЛИОШИБКА: =ЕСЛИОШИБКА(значение;значение_если_ошибка), где:
- значение — выражение, которое нужно проверить;
- значение_если_ошибка — текст, число или формула, которые будут выводиться или выполняться в случае, если в результате проверки аргумента «значение» получен результат ЛОЖЬ.
Если ошибка есть, возвращается значение второго аргумента. Если ошибки нет — первого.
Пример работы функции ЕСЛИОШИБКА. Предположим, нам нужно разделить значения ячеек столбца A на значения ячеек столбца B. Проверим, будут ли ошибки в этих выражениях.
Выделим первую ячейку столбца C и введём: =ЕСЛИОШИБКА(A1/B1;»Ошибка в расчёте»)
Скриншот: Excel / Skillbox Media
Дальше нажмём Enter и растянем результат из первой ячейки вниз до конца таблицы.
Скриншот: Excel / Skillbox Media
В первой строке функция не нашла ошибок в выражении (360/60), поэтому провела расчёт и показала результат (6).
Во второй строке функция тоже не нашла ошибок (деление 0 на 76) — и показала результат расчёта (0).
В третьей строке функция нашла ошибку — делить на 0 нельзя. Поэтому вместо результата расчёта показала второй аргумент функции: «Ошибка в расчёте».
Эта функция проверяет, не содержат ли заданные ячейки ошибочных значений:
- #Н/Д
- #ЗНАЧ
- #ЧИСЛО!
- #ДЕЛ/0!
- #ССЫЛКА!
- #ИМЯ?
- #ПУСТО!
Синтаксис функции ЕОШИБКА: =ЕОШИБКА(значение), где значение — ячейка или диапазон ячеек, которые нужно проверить.
Если функция находит ошибочные значения, она возвращает значение ИСТИНА. Если не находит — возвращает значение ЛОЖЬ.
Пример работы функции ЕОШИБКА. Обычно функцию ЕОШИБКА применяют в работе с большими диапазонами, где искать ошибочные значения самостоятельно долго и энергозатратно. Но для примера покажем, как она работает на небольшом диапазоне.
Выберем любую ячейку, в которой функция должна будет вывести результат. В строке формул введём: =ЕОШИБКА(A1:A6), где A1:A6 — диапазон, который нужно проверить.
Скриншот: Excel / Skillbox Media
Нажимаем Enter — функция возвращает значение ИСТИНА. Это значит, что она нашла ошибку в выделенном диапазоне.
Скриншот: Excel / Skillbox Media
Дальше эту функцию используют для выполнения других действий.
Например, при возникновении ошибки можно использовать функцию ЕОШИБКА в сочетании с функцией ЕСЛИ: =ЕСЛИ(ЕОШИБКА(B1);»Произошла ошибка»;B1*6).
Эта формула проверит наличие ошибки в ячейке B1. При возникновении ошибки функция ЕСЛИ возвращает сообщение «Произошла ошибка». Если ошибки отсутствуют, функция ЕСЛИ вычисляет произведение B1*6.
Функция ЕПУСТО проверяет, есть ли в выбранной ячейке какие-либо значения — например, число, текст, формула, пробел — или эти ячейки пустые. Если ячейка пустая, функция возвращает значение ИСТИНА, если в ячейке есть данные — ЛОЖЬ.
Синтаксис функции ЕПУСТО: =ЕПУСТО(значение), где значение — ячейка, которую нужно проверить.
Пример работы функции ЕПУСТО. Проверим, есть ли скрытые символы в ячейках А5 и А6. Визуально эти ячейки пустые.
Выберем любую ячейку и в строке формул введём: =ЕПУСТО(A5), где A5 — ячейка, которую нужно проверить.
Скриншот: Excel / Skillbox Media
Нажимаем Enter — функция возвращает значение ЛОЖЬ. Это значит, что ячейка А5 на самом деле не пустая, в ней есть значение, которое не видно, — например, пробел.
Скриншот: Excel / Skillbox Media
Проверим вторую ячейку. Выберем любую ячейку и в строке формул введём: =ЕПУСТО(A6) и нажмём Enter. Функция возвращает значение ИСТИНА. Это значит, что в ячейке А6 нет никаких значений.
Скриншот: Excel / Skillbox Media
Как и в случае с функцией ЕОШИБКА, эту функцию можно использовать для выполнения других действий. Например, в сочетании с функцией ЕСЛИ.
- В Excel много функций, которые упрощают и ускоряют работу с таблицами. В этой подборке перечислили 15 статей и видео об инструментах Excel, необходимых в повседневной работе.
- В Skillbox есть курс «Excel + Google Таблицы с нуля до PRO». Он подойдёт как новичкам, которые хотят научиться работать в Excel с нуля, так и уверенным пользователям, которые хотят улучшить свои навыки. На курсе учат быстро делать сложные расчёты, визуализировать данные, строить прогнозы, работать с внешними источниками данных, создавать макросы и скрипты.
- Кроме того, Skillbox даёт бесплатный доступ к записи онлайн-интенсива «Экспресс-курс по Excel: осваиваем таблицы с нуля за 3 дня». Он подходит для начинающих пользователей. На нём можно научиться создавать и оформлять листы, вводить данные, использовать формулы и функции для базовых вычислений, настраивать пользовательские форматы и создавать формулы с абсолютными и относительными ссылками.
Другие материалы Skillbox Media по Excel
Научитесь: Excel + Google Таблицы с нуля до PRO
Узнать больше
Содержание
- Функция ИСТИНА
- Функция ЛОЖЬ
- Функция ЕСЛИОШИБКА
- Формула ЕСЛИ в Excel – примеры нескольких условий
- Основные операции
- Ведение простейших подсчётов
- Логический набор
- ИСКИЛИ
- ЕСЛИМН (УСЛОВИЯ) и ПЕРЕКЛЮЧ
- Оформление и примеры использования
- Работа с ПЕРЕКЛЮЧ
- Использование ЕСЛИОШИБКА
- И/ИЛИ
- Основные операторы
- Функции ЕОШИБКА и ЕПУСТО
- Пример применения функций
- Практический пример использования логических функций
- Логическая функция ИСКЛИЛИ в Excel
- Заключение
Функция ИСТИНА
Не принимает никаких аргументов и просто возвращает логическое значение «ИСТИНА».
Синтаксис: =ИСТИНА()
Функция ЛОЖЬ
Аналогична функции ИСТИНА, за исключением то, что возвращает противоположный результат ЛОЖЬ.
Синтаксис: =ЛОЖЬ()
Функция ЕСЛИОШИБКА
Предназначена для проверки возврата выражением ошибки. Если ошибка обнаружена, то она возвращает значение второго аргумента, иначе первого.
Функция принимает 2 аргумента, все они являются обязательными.
Синтаксис: =ЕСЛИОШИБКА(значение;значение_если_ошибка)
Пример использования функции:
В приведенном примере видно, что выражение в первом аргументе возвращает ошибку деления на ноль, но так как оно вложено в нашу функцию, то ошибка перехватывается и подменяется вторым аргументов, а именно строкой «Делить на ноль нельзя», которую мы ввели самостоятельно. Вместо данной строки могли бы быть другие функции, все зависит от поставленной перед Вами задачи.
Довольно часто количество возможных условий не 2 (проверяемое и альтернативное), а 3, 4 и более. В этом случае также можно использовать функцию ЕСЛИ, но теперь ее придется вкладывать друг в друга, указывая все условия по очереди. Рассмотрим следующий пример.
Нескольким менеджерам по продажам нужно начислить премию в зависимости от выполнения плана продаж. Система мотивации следующая. Если план выполнен менее, чем на 90%, то премия не полагается, если от 90% до 95% — премия 10%, от 95% до 100% — премия 20% и если план перевыполнен, то 30%. Как видно здесь 4 варианта. Чтобы их указать в одной формуле потребуется следующая логическая структура. Если выполняется первое условие, то наступает первый вариант, в противном случае, если выполняется второе условие, то наступает второй вариант, в противном случае если… и т.д. Количество условий может быть довольно большим. В конце формулы указывается последний альтернативный вариант, для которого не выполняется ни одно из перечисленных ранее условий (как третье поле в обычной формуле ЕСЛИ). В итоге формула имеет следующий вид.

Комбинация функций ЕСЛИ работает так, что при выполнении какого-либо указанно условия следующие уже не проверяются. Поэтому важно их указать в правильной последовательности. Если бы мы начали проверку с B2<1, то условия B2<0,9 и B2<0,95 Excel бы просто «не заметил», т.к. они входят в интервал B2<1 который проверился бы первым (если значение менее 0,9, само собой, оно также меньше и 1). И тогда у нас получилось бы только два возможных варианта: менее 1 и альтернативное, т.е. 1 и более.
При написании формулы легко запутаться, поэтому рекомендуется смотреть на всплывающую подсказку.

В конце нужно обязательно закрыть все скобки, иначе эксель выдаст ошибку

Основные операции
Создание формулы в Excel не сопровождается особыми сложностями, если пользователь полноценно освоит некоторые азы работы с табличным редактором. Начинать изучение этого офисного приложения лучше всего с тех вычислительных примеров, которые являются самыми простыми и максимально распространёнными. Это позволит понять суть и важные правила работы с табличным редактором.
Освоив простейшие азы, можно приступать к созданию логических формул.
Ведение простейших подсчётов
Для начала работы следует запустить само офисное приложение. Далее важно определиться, что должно посчитаться автоматически. Чаще всего к работе приступают, когда уже имеется числовая информация, на основе которой приходится осуществлять множественные операции при помощи калькулятора. Теперь эту счётную машинку нужно отложить в сторону и полностью довериться электронной таблице.
Запись любого числового выражения совершается со знака «=». Не выставив его, Excel воспримет введённый запрос, как текстовую запись, отобразит её, но не осуществить подсчёт.
Часто необходимо не просто осуществлять подсчёты, используя данные в таблице, а проводить анализ, сопровождаемый несколькими условиями. Опять-таки всё это проделывать самостоятельно вручную неразумно, когда имеются такие уникальные возможности Excel, способной выполнять любые требования пользователя.
В категории «Логические» самой распространённой является функция ЕСЛИ. Эта функция рассматривает предложенные варианты, а далее определяет, выполняется это условие или нет. Результат функции ЕСЛИ зависит от того, что в итоге желает видеть пользователь. А для того чтобы результат правильно отображался, следует знать, как задать условие в Excel.
Функция ЕСЛИ состоит из трёх аргументов:
- Логического (основного) выражения (требование, которое пользователь желает проверить в таблице);
- значения, отображающегося, если условие будет полностью соблюдаться;
- значения, если заданное требование не выдерживается.
Итак, можно попробовать создать простейшую вычислительную таблицу, взяв за основу пример, где главной будет логическая функция ЕСЛИ.
В частности, в ячейку А1 ввести числовой показатель «5», а в ячейку А2 показатель «8». Если пользователю необходимо сравнить два показателя и выдать автоматический итог произведённых действий, составляется выражение, которое, безусловно, начинается со знака «равно»: =ЕСЛИ(А1>А2; «Больше»; «Меньше»). После введения этой записи в любую свободную ячейку, нажатия Enter, в ней сразу будет демонстрироваться ответ. Если пользователь заменит значения в А1 или А2, то ответ также автоматически перестроится.
В тех случаях, когда важно выявить несовпадение двух показателей, введённых в соседние столбцы, первоначально нужно вникнуть, как в Excel правильно записать условие неравно, после чего создать запрос, используя логические функции. Знак «неравно» в Excel обозначается двумя операторами — «<>». Соответственно, нужно записать так: =ЕСЛИ(А1<>А2; «Значения разные»; «Значения одинаковые»).
Логический набор
Количество логических функций меняется в зависимости от версии программы. В приложении 2007 года их было 7, впоследствие добавилось еще несколько. Список доступных логических операций можно посмотреть так:
- зайти во вкладку «Формулы» на главной панели;
- кликнуть по иконке fx с надписью «Вставить формулу
- в появившемся окне выбрать категорию «Логические
- внизу откроется список доступных операторов.
Большинство имеют аргументы, задающие условия применения. Формат записи следующий: «=оператор(аргумент1;аргумент2…)». Логическая запись включает в себя знаки сравнения.
ИСКИЛИ
Появилась в версии программы 2013. Реализует операцию «Исключающее ИЛИ». Написание аналогично «И»: =ИСКЛИЛИ(логический_вопрос1;логический_вопрос2;…) и может иметь до 255 аргументов.
Если присутствует только 2 варианта действия, то общий результат будет «ИСТИНА» при наличии одного аргумента с таким же ответом. В этом работа «ИСКИЛИ» совпадает с «ИЛИ». Если оба решения получат ответ ИСТИНА или ЛОЖЬ, то итог будет ЛОЖЬ. Для пояснения приведена следующая таблица:
| Исходные данные | Результат | Примечания |
|---|---|---|
| =ИСКЛИЛИ(3>0; 4<1) | ИСТИНА | В итоге ИСТИНА, потому что одно из значений ИСТИНА. |
| =ИСКЛИЛИ(3<0; 4<1) | ЛОЖЬ | ЛОЖЬ, так как имеется 2 ответа ЛОЖЬ . |
| =ИСКЛИЛИ(3>0; 4>1) | ЛОЖЬ | ЛОЖЬ, так как имеется 2 ответа ИСТИНА |
ЕСЛИМН (УСЛОВИЯ) и ПЕРЕКЛЮЧ
«ЕСЛИМН» и «ПЕРЕКЛЮЧ» появились в Excel 2016 и 2019 соответственно. Предназначены для облегчения составления формул, так как уменьшают количество вложений.
Способы вставки таблицы из Microsoft Excel в Word
«ЕСЛИМН» ранее называлась «УСЛОВИЯ». Введение ее связано с попыткой облегчить работу при вложении нескольких «ЕСЛИ». Не надо писать несколько раз «ЕСЛИ» и открывать многочисленные скобки. Синтаксис: «=ЕСЛИМН(условие1; значение1;условие2; значение2;условиe3; значение3…)». Можно создать до 127 условий.
«ПЕРЕКЛЮЧ» имеет следующую структуру: «=ПЕРЕКЛЮЧ(значение для переключения; значение, которое должно совпасть1…[2–126]; значение, возвращаемое при совпадении1…[2–126]; значение, возвращаемое при отсутствии совпадений)».
Первый аргумент указывает на местоположение проверяемого выражения, остальные присваивают ячейке первую совпавшую величину.
Оформление и примеры использования
Алгоритм написания логических формул в Эксель следующий:
- Нужно выделить пустую ячейку, в которую будет записываться формула и выводиться результат действия.
Вписывать можно и в строке формул, после выделения ячейки.
- Перед формулами в программе ставится знак «=». Поставить его.
- Напечатать название оператора.
- После этого вписываются аргументы, если они есть. Начинается запись со знака «открывающаяся круглая скобка “(“».
- Аргументы вводятся последовательно через знак ”;”. Также, если после ввода названия функции нажать клавиши Ctrl + A, то откроется меню аргументов и вписать их можно здесь.
- В конце ставится символ «закрывающаяся круглая скобка “)”». Контролировать написание можно в строке формул.
- После завершения нажать кнопку ENTER. Результат появится в ячейке.
Работа с ПЕРЕКЛЮЧ
Сравнивает указанную величину в ячейке или формулу со списком данных и вписывает в ячейку первое совпавшее значение. Если совпадений не будет, и не проставлена величина по умолчанию, оператор выдаст ошибку «#Н/Д». Функция схожа с ЕСЛИМН, но в отличие от нее условие ставится точно, без сравнительных знаков.
Работа оператора иллюстрируется на рисунке.
Здесь вместо чисел 1, 2, 7 — нужно проставить прописью дни недели им соответствующие. Если будут другие цифры, то возвратится значение по умолчанию «Нет совпадений (No match)».
Использование ЕСЛИОШИБКА
Оператор используется для нахождения ошибки в таблице. Найдя ее, функция не пишет в ячейке какую-либо из ошибок, а возвращает указанный ответ, который может быть текстом, пустой строкой: =ЕСЛИОШИБКА(Что_проверять;Что_выводить_вместо_ошибки).
Например, нужно поделить значения в столбце А на величины в столбце В. Если по ошибке в строках стоят 0, то получится деление на 0.
Применение оператора «=ЕСЛИОШИБКА(A2/B2;»»)» скрывает ошибки.
Здесь сравнивается выражение A2/B2. В случае обнаружения ошибки в ячейку ставится пустая строка, указанная пробелом в кавычках ““.
ЕСЛИОШИБКА появилась в Excel 2007. До этого использовалась функция ЕОШИБКА, которая самостоятельно не могла обработать ошибку, так как имела только один аргумент, проверяющий указанную ячейку. Для ввода ответа в случае обнаружения ошибки, нужно было использовать оператор ЕСЛИ: «ЕСЛИ(ЕОШИБКА(А2/В2);”“;А2/В2)».
И/ИЛИ
Простые операторы, редко применяются без связки с другими функциями.
На рисунке показан принцип действия функции И.
Пример использования: «=И(A1>B1; A2<>25)». Здесь созданы два условия:
- Значение в ячейке А1 должно быть больше числа в В1.
- Число в А2 должно быть не равно 25.
При исполнении обоих получается ИСТИНА.
Если одно из заданий нарушено, получается ЛОЖЬ. В данном случае число в А1 меньше чем в В1.
Ниже представлен алгоритм функционирования оператора ИЛИ.
Пусть даны 3 выражения: A1>B1; A2>B2; A3>B3. Требуется применить к ним действие ИЛИ: «=ИЛИ(A1>B1; A2>B2; A3>B3)». Возможные варианты показаны на рисунках:
Здесь конечный результат ИСТИНА, так как из трех выражений одно верно: A3>B3. На следующем изображении функция выдала ответ «ЛОЖЬ», так как на все вопросы получены аналогичные ответы.
Основные операторы
Существуют и менее распространенные логические функции.
У каждого из вышеуказанных операторов, кроме первых двух, имеются аргументы. Аргументами могут выступать, как конкретные числа или текст, так и ссылки, указывающие адрес ячеек с данными.
Функции ЕОШИБКА и ЕПУСТО
Функция ЕОШИБКА проверяет, не содержит ли определенная ячейка или диапазон ячеек ошибочные значения. Под ошибочными значениями понимаются следующие:
- #Н/Д;
- #ЗНАЧ;
- #ЧИСЛО!;
- #ДЕЛ/0!;
- #ССЫЛКА!;
- #ИМЯ?;
- #ПУСТО!
В зависимости от того ошибочный аргумент или нет, оператор сообщает значение ИСТИНА или ЛОЖЬ. Синтаксис данной функции следующий: = ЕОШИБКА(значение) . В роли аргумента выступает исключительно ссылка на ячейку или на массив ячеек.
Оператор ЕПУСТО делает проверку ячейки на то, пустая ли она или содержит значения. Если ячейка пустая, функция сообщает значение ИСТИНА, если ячейка содержит данные – ЛОЖЬ. Синтаксис этого оператора имеет такой вид: =ЕПУСТО(значение) . Так же, как и в предыдущем случае, аргументом выступает ссылка на ячейку или массив.
Пример применения функций
Теперь давайте рассмотрим применение некоторых из вышеперечисленных функций на конкретном примере.
Имеем список работников предприятия с положенными им заработными платами. Но, кроме того, всем работникам положена премия. Обычная премия составляет 700 рублей. Но пенсионерам и женщинам положена повышенная премия в размере 1000 рублей. Исключение составляют работники, по различным причинам проработавшие в данном месяце менее 18 дней. Им в любом случае положена только обычная премия в размере 700 рублей.
Попробуем составить формулу. Итак, у нас существует два условия, при исполнении которых положена премия в 1000 рублей – это достижение пенсионного возраста или принадлежность работника к женскому полу. При этом, к пенсионерам отнесем всех тех, кто родился ранее 1957 года. В нашем случае для первой строчки таблицы формула примет такой вид: =ЕСЛИ(ИЛИ(C4<1957;D4="жен.");"1000";"700") . Но, не забываем, что обязательным условием получения повышенной премии является отработка 18 дней и более. Чтобы внедрить данное условие в нашу формулу, применим функцию НЕ: =ЕСЛИ(ИЛИ(C4<1957;D4="жен.")*(НЕ(E4<18));"1000";"700") .
Для того, чтобы скопировать данную функцию в ячейки столбца таблицы, где указана величина премии, становимся курсором в нижний правый угол ячейки, в которой уже имеется формула. Появляется маркер заполнения. Просто перетягиваем его вниз до конца таблицы.
Таким образом, мы получили таблицу с информацией о величине премии для каждого работника предприятия в отдельности.
Как видим, логические функции являются очень удобным инструментом для проведения расчетов в программе Microsoft Excel. Используя сложные функции, можно задавать несколько условий одновременно и получать выводимый результат в зависимости от того, выполнены эти условия или нет. Применение подобных формул способно автоматизировать целый ряд действий, что способствует экономии времени пользователя.
Практический пример использования логических функций
В примере ниже попробуем частично использовать описанные выше функции для решения задачи, приближенной к реальной ситуации с расчетом премии, зависящей от определенных условий.
В качестве исходных данных – таблица со сведениями о работниках, в которой указан их пол и возраст.
Нам необходимо произвести расчет премии. Ключевые условия, от которых зависит размер премии:
- величина обычной премии, которую получат все сотрудники без исключения – 3 000 руб.;
- сотрудницам женского пола положена повышенная премия – 7 000 руб.;
- молодым сотрудникам (младше 1984 г. рождения) положена повышенная премия – 7 000 руб.;
Выполним необходимые расчеты, используя логические функции.
- Встаем в первую ячейку столбца, в которой хотим посчитать размеры премий и щелкаем кнопку “Вставить функцию” (слева от сроки формул).
- В открывшемся Мастере функций выбираем категорию “Логические”, затем в предложенном перечне операторов кликаем по строке “ЕСЛИ” и жмем OK.
- Теперь нам нужно задать аргументы функции. Так как у нас не одно, а два условия получения повышенной премии, причем нужно, чтобы выполнялось хотя бы одно из них, чтобы задать логическое выражение, воспользуемся функцией ИЛИ. Находясь в поле для ввода значения аргумента “Лог_выражение” кликаем в основной рабочей области книги на небольшую стрелку вниз, расположенную в левой верхней части окна программы, где обычно отображается адрес ячейки. В открывшемся списке функций выбираем оператор ИЛИ, если он представлен в перечне (или можно кликнуть на пункт “Другие функции” и выбрать его в новом окне Мастера функций, как мы изначально сделали для выбора оператора ЕСЛИ).
- Мы переключимся в окно аргументов функци ИЛИ. Здесь задаем наши условия получения премии в 7000 руб.:
- год рождения позже 1984 года;
- пол – женский;
- Теперь обращаем внимание на строку формул. Кликаем в ней на название первоначального оператора ЕСЛИ, чтобы переключиться в аргументы этой функции.
- Заполняем аргументы функции и щелкаем OK:
- в значении “Истина” пишем цифру 7000;
- в значении “Ложь” указываем цифру 3000;
- Результат работы логических операторов отобразится в первой ячейке столбца, которую мы выбрали. Как мы можем видеть, окончательный вид формулы выглядит следующим образом:
=ЕСЛИ(ИЛИ(C2>1984;D2="жен.");7000;3000).
Кстати, вместо использования Мастера функций можно было вручную составить и прописать данную формулу в требуемой ячейке. - Чтобы рассчитать премию для всех сотрудников, воспользуемся Маркером заполнения. Наведем курсор на правый нижний угол ячейки с формулой. После того, как курсор примет форму черного крестика (это и есть Маркер заполнения), зажимаем левую кнопку мыши и протягиваем выделение вниз, до последней ячейки столбца.
- Все готово. Благодаря логическим операторам мы получили заполненные данные для столбца с премиями.
Логическая функция ИСКЛИЛИ в Excel
В Excel 2013 Microsoft представила функцию ИСКЛИЛИ, которая является логической функцией исключающего ИЛИ. Для тех, кто не знаком с понятием «Исключающего ИЛИ», сначала может быть немного сложно понять суть логической функции, но, надеюсь, приведенное ниже объяснение иллюстрируемое примерами формул поможет прояснить суть.
Синтаксис логической функции ИСКЛИЛИ идентичен синтаксису ИЛИ:
=ИСКЛИЛИ(логическое_значение1; [логическое_значение2];…)
В простейшей версии формулы ИСКЛИЛИ, содержащей только 2 логических оператора, логическая функция Excel ИСКЛИЛИ вернет ИСТИНУ, если любой из аргументов имеет значение ИСТИНА. Если оба аргумента ИСТИНА, либо оба ЛОЖЬ, ИСКЛИЛИ возвращает ЛОЖЬ. Рассмотрим примеры формул:
|
Формула |
Результат |
Описание |
|
=ИСКЛИЛИ(1>0; 2<1) |
ИСТИНА |
Логическая функция возвращает ИСТИНА, потому что первый аргумент ИСТИНА, а второй аргумент ЛОЖЬ. |
|
=ИСКЛИЛИ(1<0; 2<1) |
ЛОЖЬ |
Логическая функция возвращает ЛОЖЬ, потому что оба аргумента ЛОЖЬ. |
|
=ИСКЛИЛИ(1>0; 2>1) |
ЛОЖЬ |
Логическая функция возвращает ЛОЖЬ, потому что оба аргумента ИСТИНА. |
Когда добавляется больше логических операторов, функция ИСКЛИЛИ в Excel работает следующим образом:
- ИСТИНА, если нечетное число аргументов оценивается как ИСТИНА;
- ЛОЖЬ, если общее число ИСТИННЫХ утверждений четно, или если все операторы ЛОЖЬ.
Представленное ниже изображение наглядно это иллюстрирует:
Заключение
Логические операторы используются практически во всех сложных формулах, в которых значение в ячейке зависит от соблюдения одного или нескольких условий и позволяют строить гибкие конструкции, объединяя простые функции и расчеты в одной ячейке. Это дает возможность значительно сократить время на обработку данных и повысить эффективность работы, так как снимает большое количество промежуточных шагов в расчетах и вычислениях.
Источники
- https://office-menu.ru/uroki-excel/13-uverennoe-ispolzovanie-excel/31-logicheskie-funktsii-excel
- https://statanaliz.info/excel/funktsii-i-formuly/neskolko-uslovij-funktsii-esli-eslimn-excel/
- https://nastroyvse.ru/programs/review/pravilno-zapisat-logicheskie-formuly-v-excel.html
- http://composs.ru/logicheskie-funkcii-v-microsoft-excel/
- https://lumpics.ru/logical-functions-in-excel/
- https://MicroExcel.ru/logicheskie-funkczii/
- https://naprimerax.org/posts/76/logicheskie-funktcii-v-excel
На чтение 2 мин Опубликовано 13.01.2015
В этом уроке мы познакомимся с понятием Сложная формула в Excel, а также разберем порядок выполнения действий при решении таких формул. Представленная информация является базовой и предназначена в первую очередь для начинающих пользователей Microsoft Excel.
Простая формула – это математическое выражение с одним оператором, такое как 7+9. Сложная формула содержит более одного оператора, к примеру, 5+2*8. Если формула содержит несколько математических операторов, Excel руководствуется порядком действий при выполнении вычислений. Используя Excel для вычисления сложных формул, необходимо знать порядок выполнения действий.
Содержание
- Порядок действий в формулах Excel
- Пример решения сложной формулы
- Операции, заключенные в скобки
- Возведение в степень
- Деление
- Умножение
- Сложение
- Вычитание
Порядок действий в формулах Excel
Excel выполняет действия, опираясь на следующий порядок:
- Выражения, помещенные в скобки.
- Возведение в степень (например, 3^2).
- Умножение и деление, что идет раньше.
- Сложение и вычитание, что идет раньше.
Пример решения сложной формулы
В качестве примера, попробуем вычислить значение формулы, представленной на следующем рисунке. На первый взгляд это выражение выглядит довольно сложным, но мы можем воспользоваться порядком выполнения операций поэтапно, чтобы найти правильный ответ.
Операции, заключенные в скобки
В первую очередь, мы начнем с выполнения действия в скобках. В данном случае нам необходимо вычислить: 6-3=3.
Возведение в степень
Можно заметить, что сложная формула теперь выглядит немного проще. Далее мы проверим наличие степеней в нашем выражении. Да, она встречается один раз: 2^2=4.
Деление
Далее мы выполним все операции умножения и деления, в порядке следования слева направо. Поскольку деление встречается раньше умножения, то деление выполняется первым: 3/4=0,75.
Умножение
Теперь мы выполним оставшуюся операцию умножения: 0,75*4=3.
Сложение
Далее мы выполним все операции сложения и вычитания, в порядке следования слева направо. Поскольку сложение встречается раньше вычитания, то сложение выполняется первым: 10+3=13.
Вычитание
В заключение остается последнее действие – вычитание: 13-1=12.
В итоге мы получили ответ: 12.
Точно такой же результат вы получите, если введете эту формулу в Excel.
Как видите, в этом нет ничего сложного!
Оцените качество статьи. Нам важно ваше мнение: