Содержание
- Процесс транспонирования
- Способ 1: оператор ТРАНСП
- Способ 2: транспонирование матрицы с помощью специальной вставки
- Вопросы и ответы
При работе с матрицами иногда нужно их транспонировать, то есть, говоря простыми словами, перевернуть. Конечно, можно перебить данные вручную, но Эксель предлагает несколько способов сделать это проще и быстрее. Давайте разберем их подробно.
Процесс транспонирования
Транспонирование матрицы – это процесс смены столбцов и строк местами. В программе Excel имеется две возможности проведения транспонирования: используя функцию ТРАНСП и при помощи инструмента специальной вставки. Рассмотрим каждый из этих вариантов более подробно.
Способ 1: оператор ТРАНСП
Функция ТРАНСП относится к категории операторов «Ссылки и массивы». Особенностью является то, что у неё, как и у других функций, работающих с массивами, результатом выдачи является не содержимое ячейки, а целый массив данных. Синтаксис функции довольно простой и выглядит следующим образом:
=ТРАНСП(массив)
То есть, единственным аргументом данного оператора является ссылка на массив, в нашем случае матрицу, который следует преобразовать.
Посмотрим, как эту функцию можно применить на примере с реальной матрицей.
- Выделяем незаполненную ячейку на листе, планируемую сделать крайней верхней левой ячейкой преобразованной матрицы. Далее жмем на значок «Вставить функцию», который расположен вблизи строки формул.
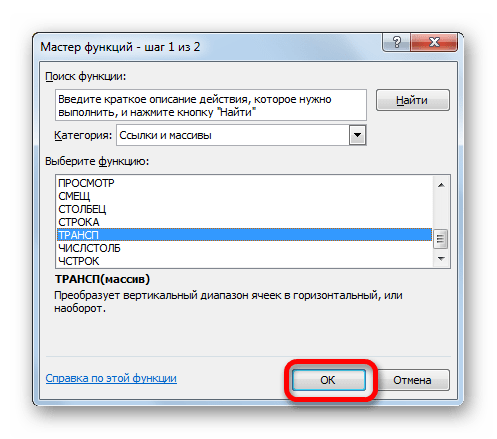
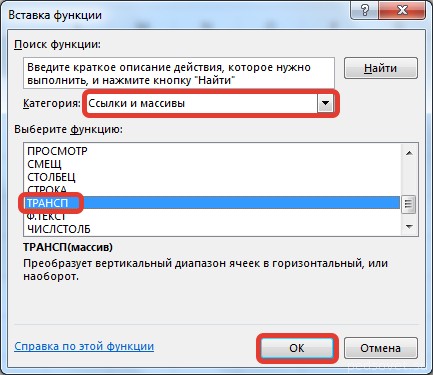
- Производится запуск Мастера функций. Открываем в нем категорию «Ссылки и массивы» или «Полный алфавитный перечень». После того, как отыскали наименование «ТРАНСП», производим его выделение и жмем на кнопку «OK».
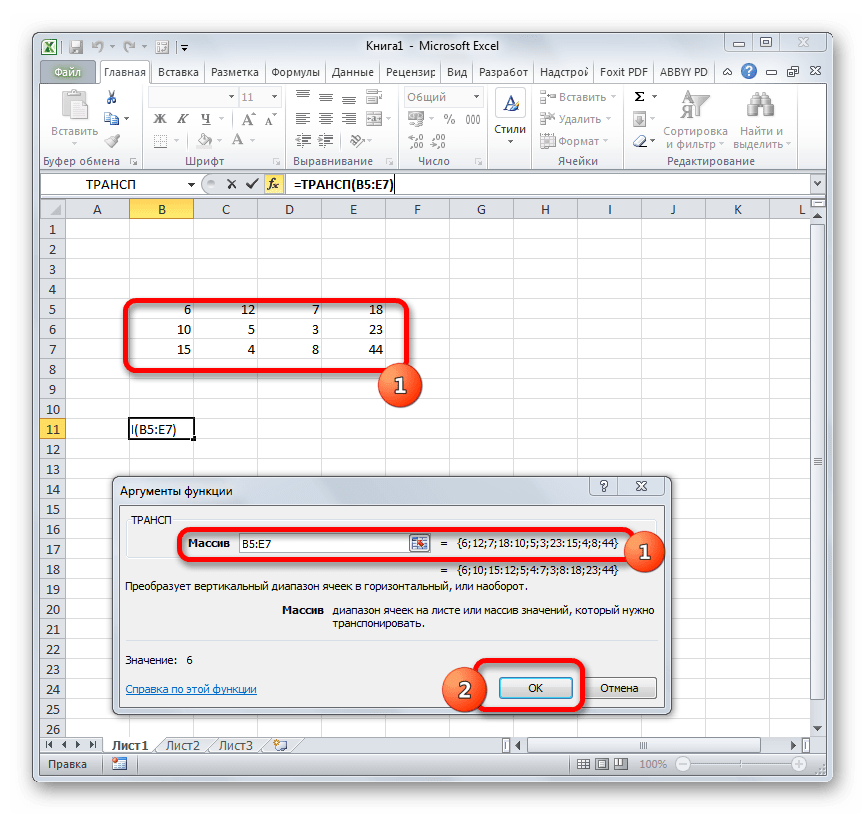
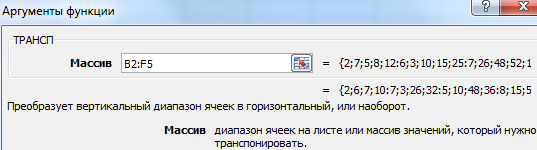
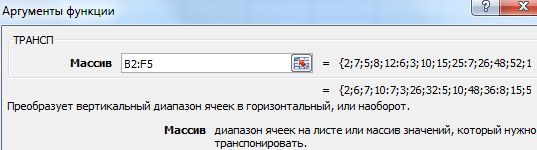
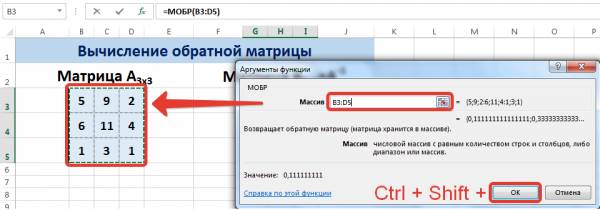
- Происходит запуск окна аргументов функции ТРАНСП. Единственному аргументу данного оператора соответствует поле «Массив». В него нужно внести координаты матрицы, которую следует перевернуть. Для этого устанавливаем курсор в поле и, зажав левую кнопку мыши, выделяем весь диапазон матрицы на листе. После того, как адрес области отобразился в окне аргументов, щелкаем по кнопке «OK».
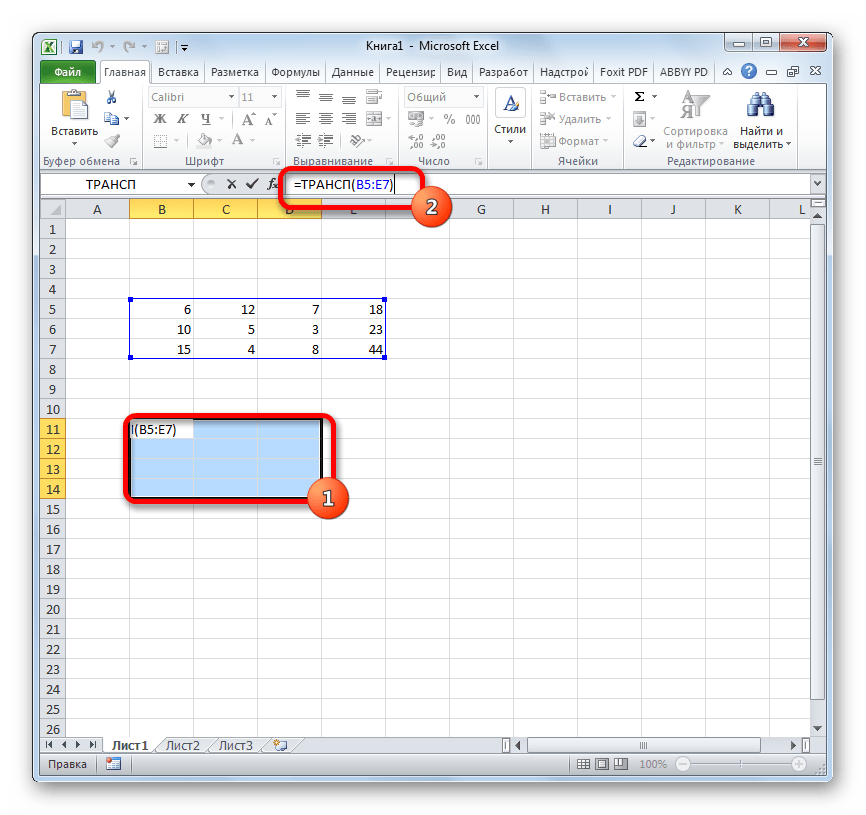
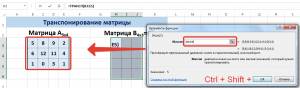
- Но, как видим, в ячейке, которая предназначена для вывода результата, отображается некорректное значение в виде ошибки «#ЗНАЧ!». Это связано с особенностями работы операторов массивов. Чтобы исправить эту ошибку, выделяем диапазон ячеек, в котором число строк должно быть равным количеству столбцов первоначальной матрицы, а число столбцов – количеству строк. Подобное соответствие очень важно для того, чтобы результат отобразился корректно. При этом, ячейка, в которой содержится выражение «#ЗНАЧ!» должна быть верхней левой ячейкой выделяемого массива и именно с неё следует начинать процедуру выделения, зажав левую кнопку мыши. После того, как вы провели выделение, установите курсор в строку формул сразу же после выражения оператора ТРАНСП, которое должно отобразиться в ней. После этого, чтобы произвести вычисление, нужно нажать не на кнопку Enter, как принято в обычных формулах, а набрать комбинацию Ctrl+Shift+Enter.
- После этих действий матрица отобразилась так, как нам надо, то есть, в транспонированном виде. Но существует ещё одна проблема. Дело в том, что теперь новая матрица представляет собой связанный формулой массив, который нельзя изменять. При попытке произвести любое изменение с содержимым матрицы будет выскакивать ошибка. Некоторых пользователей такое положение вещей вполне удовлетворяет, так как они не собираются производить изменения в массиве, а вот другим нужна матрица, с которой полноценно можно работать.
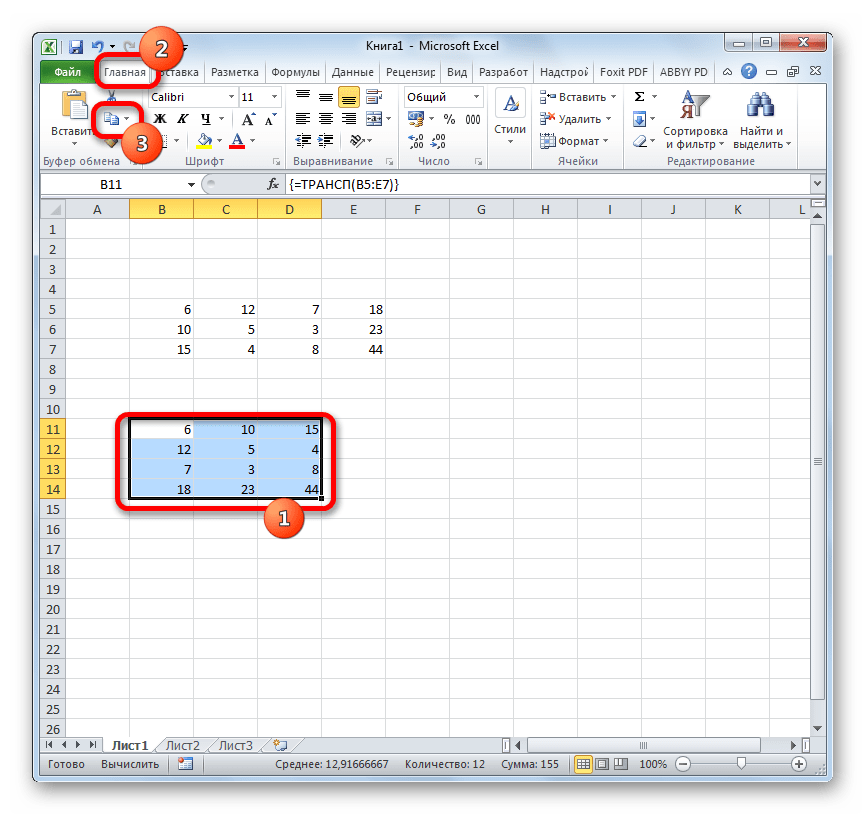
Чтобы решить данную проблему, выделяем весь транспонированный диапазон. Переместившись во вкладку «Главная» щелкаем по пиктограмме «Копировать», которая расположена на ленте в группе «Буфер обмена». Вместо указанного действия можно после выделения произвести набор стандартного сочетания клавиш для копирования Ctrl+C.
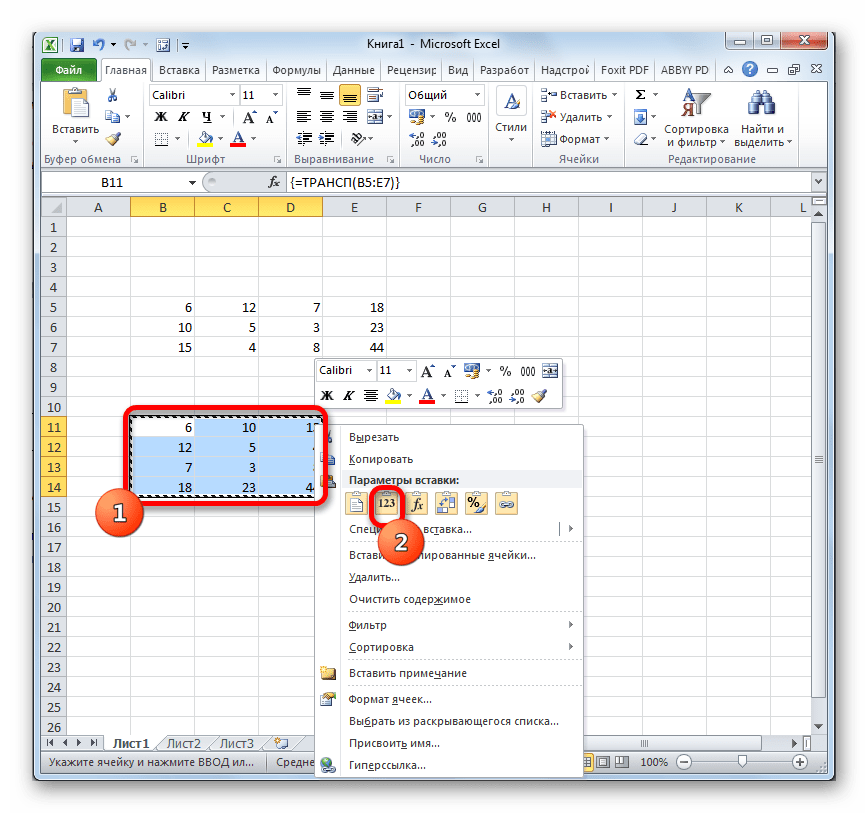
- Затем, не снимая выделения с транспонированного диапазона, производим клик по нему правой кнопкой мыши. В контекстном меню в группе «Параметры вставки» щелкаем по иконке «Значения», которая имеет вид пиктограммы с изображением чисел.
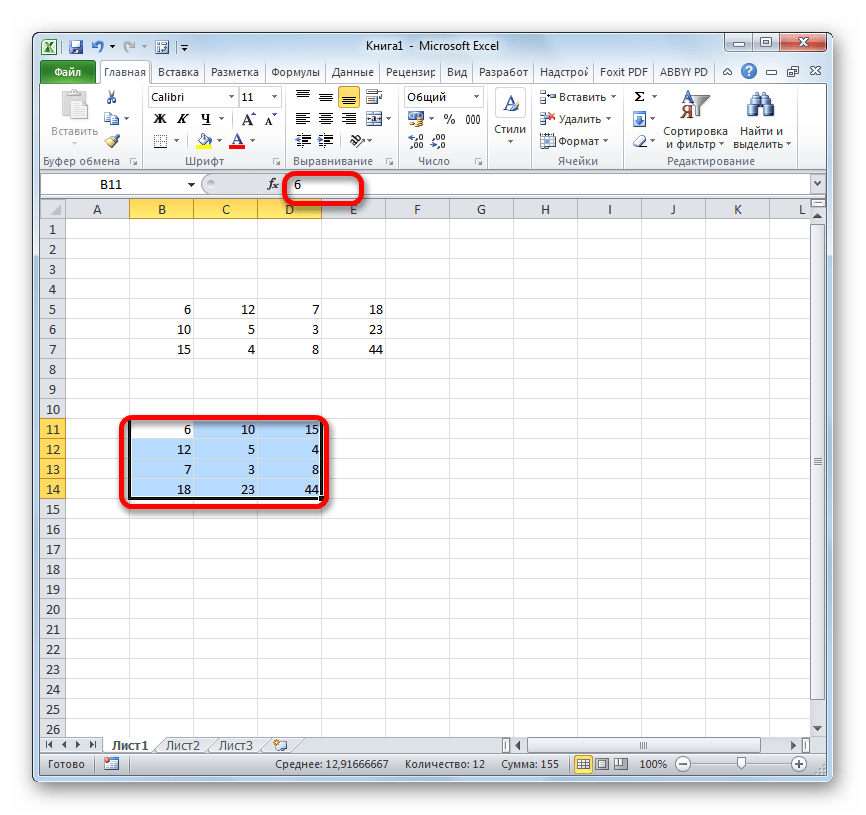
Вслед за этим формула массива ТРАНСП будет удалена, а в ячейках останутся только одни значения, с которыми можно работать так же, как и с исходной матрицей.
Урок: Мастер функций в Экселе
Способ 2: транспонирование матрицы с помощью специальной вставки
Кроме того, матрицу можно транспонировать с помощью одного элемента контекстного меню, который носит название «Специальная вставка».
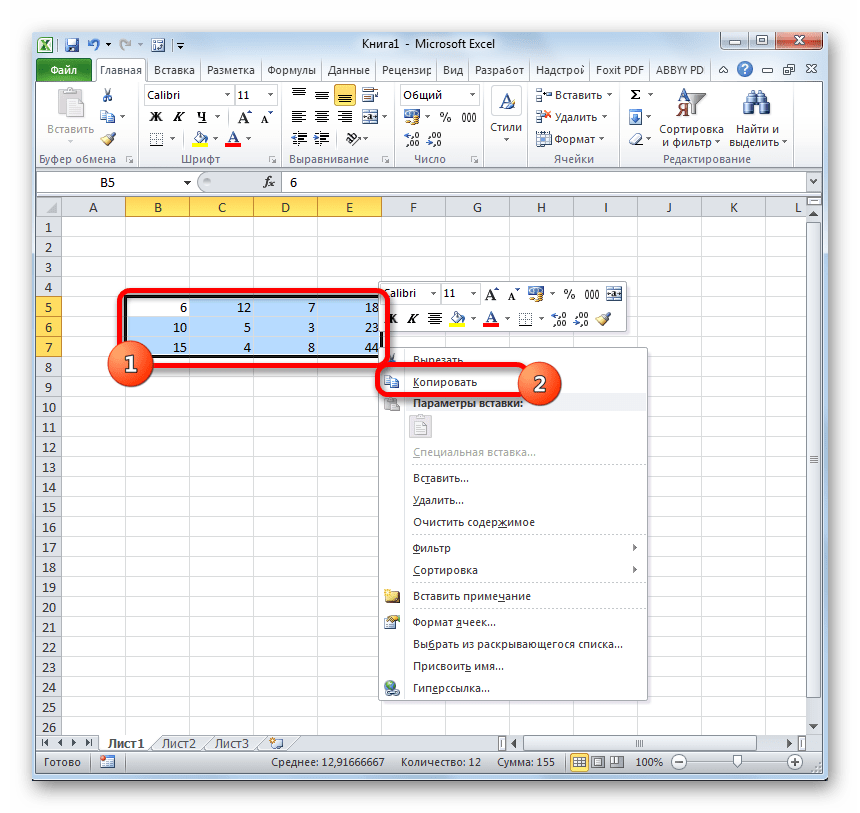
- Выделяем исходную матрицу курсором, зажав левую кнопку мыши. Далее, перейдя во вкладку «Главная», щелкаем по пиктограмме «Копировать», размещенной в блоке настроек «Буфер обмена».
Вместо этого можно сделать и по-другому. Выделив область, кликаем по ней правой кнопкой мыши. Активируется контекстное меню, в котором следует выбрать пункт «Копировать».
В виде альтернативы двум предыдущим вариантам копирования, можно после выделения произвести набор комбинации горячих клавиш Ctrl+C.
- Выбираем на листе незаполненную ячейку, которая должна стать крайним верхним левым элементом транспонированной матрицы. Производим щелчок по ней правой кнопкой мыши. Вслед за этим активируется контекстное меню. В нем выполняем перемещение по пункту «Специальная вставка». Появляется ещё одно небольшое меню. В нем также имеется пункт под названием «Специальная вставка…». Кликаем по нему. Также можно, совершив выделение, вместо вызова контекстного меню набрать на клавиатуре комбинацию Ctrl+Alt+V.
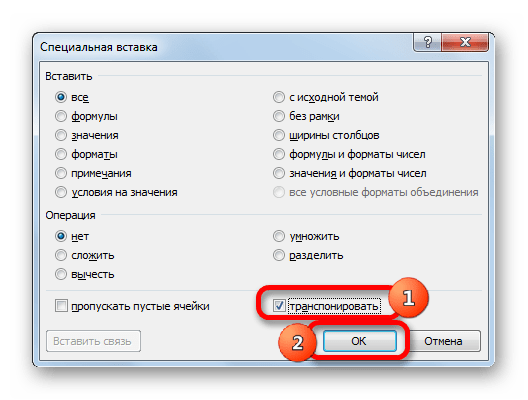
- Активируется окно специальной вставки. Тут представлено много вариантов выбора, как именно можно вставить ранее скопированные данные. В нашем случае нужно оставить практически все настройки по умолчанию. Только около параметра «Транспонировать» следует установить галочку. Затем требуется нажать на кнопку «OK», которая размещена в нижней части данного окошка.
- После этих действий транспонированная матрица отобразится в заранее выбранной части листа. В отличие от предыдущего способа, мы уже получили полноценную матрицу, которую можно изменять, как и исходник. Никакой дальнейшей доработки или преобразований не требуется.
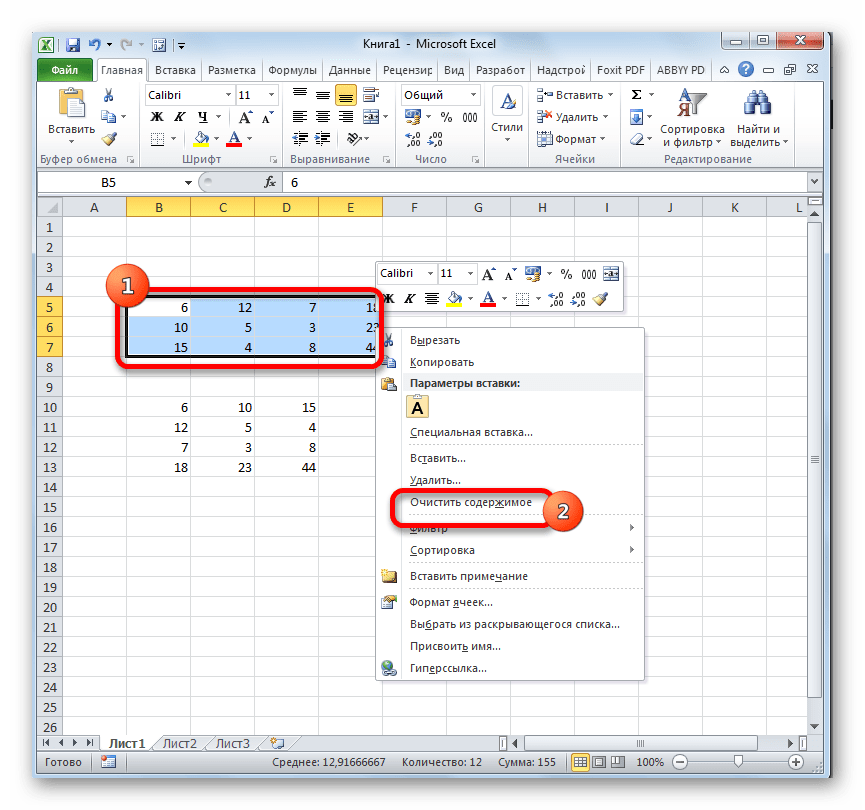
- Но при желании, если первоначальная матрица вам не нужна, её можно удалить. Для этого выделяем её курсором, зажав левую кнопку мыши. Затем выполняем щелчок по выделенному элементу правой кнопкой. В контекстном меню, которое откроется вслед за этим, выбираем пункт «Очистить содержимое».
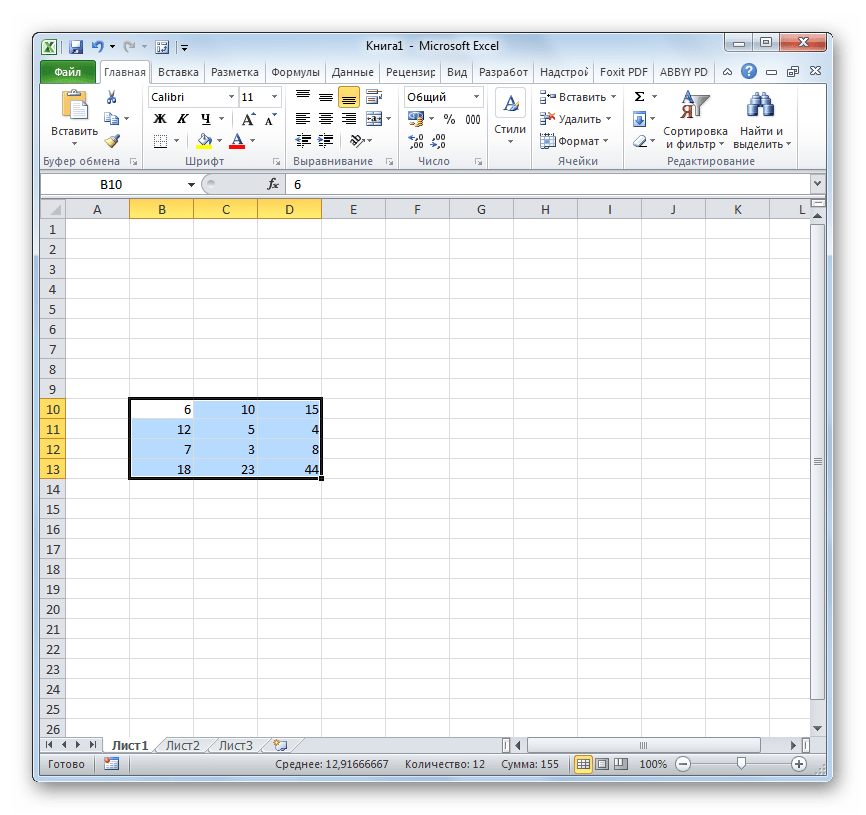
После указанных действий на листе останется только преобразованная матрица.
Этими же двумя способами, о которых шла речь выше, можно транспонировать в Excel не только матрицы, но и полноценные таблицы. Процедура при этом будет практически идентичной.
Урок: Как перевернуть таблицу в Экселе
Итак, мы выяснили, что в программе Excel матрицу можно транспонировать, то есть, перевернуть, поменяв столбцы и строчки местами, двумя способами. Первый вариант предполагает использование функции ТРАНСП, а второй – инструменты специальной вставки. По большому счету конечный результат, который получается при использовании обоих этих способов, ничем не отличается. Оба метода работают практически в любой ситуации. Так что при выборе варианта преобразования, на первый план выходят личные предпочтения конкретного пользователя. То есть, какой из данных способов для вас лично удобнее, тот и используйте.
Еще статьи по данной теме:
Помогла ли Вам статья?
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
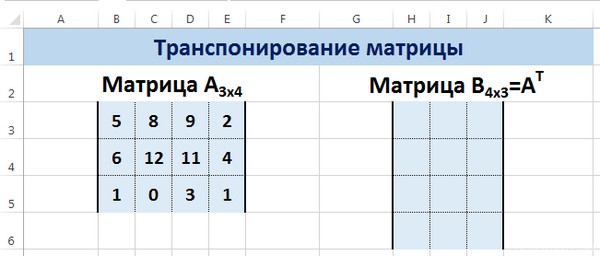
Транспонировать матрицу – поменять строки и столбцы местами.
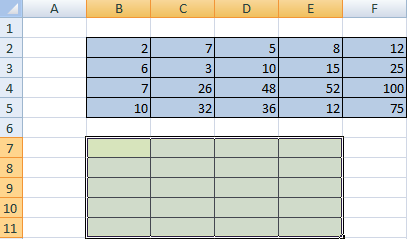
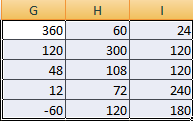
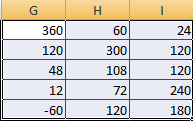
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
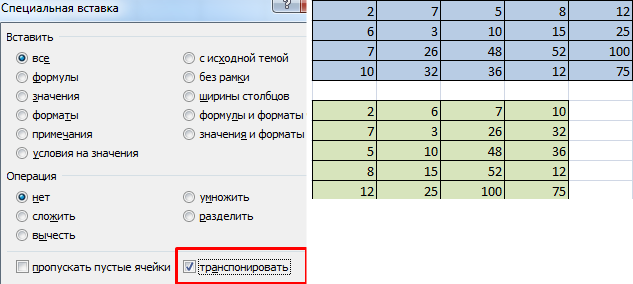
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
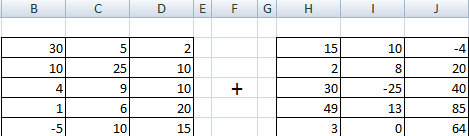
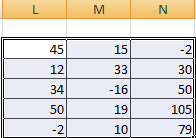
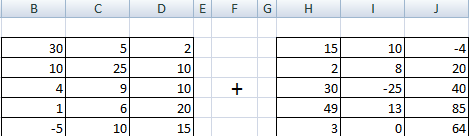
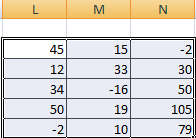
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
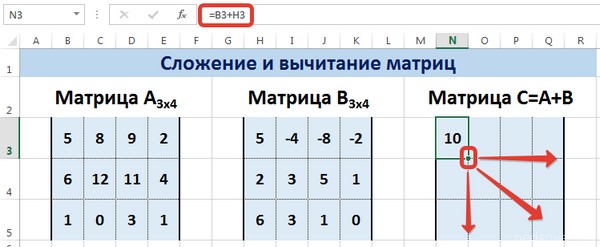
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Условие задачи:
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
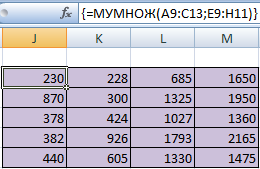
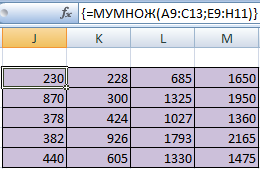
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
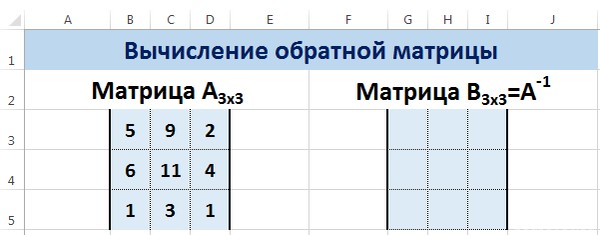
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
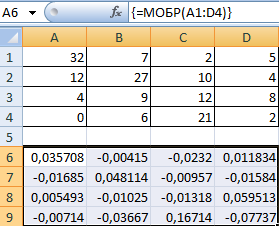
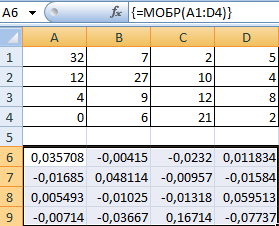
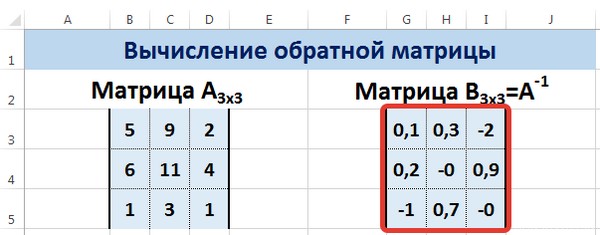
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
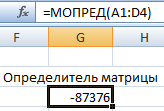
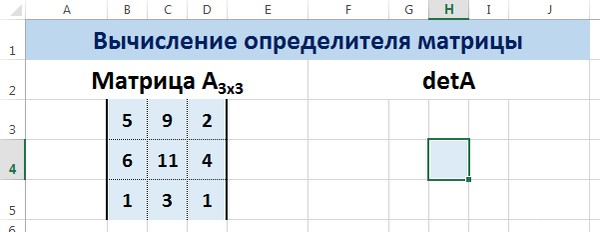
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
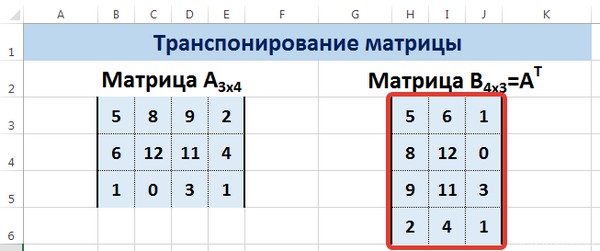
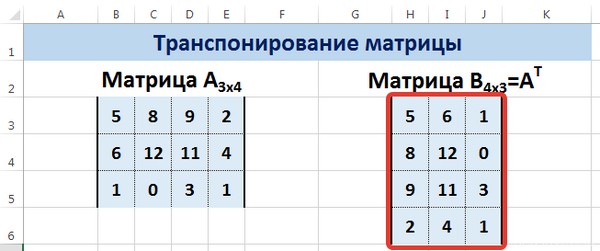
Транспонирование матрицы
— это операция над матрицей, при которой ее строки и столбцы меняются местами. Для этой операции в MS EXCEL существует специальная функция
ТРАНСП()
или англ.
TRANSPOSE.
Если матрица A имеет размер
n
×
m
, то транспонированная матрица A
t
имеет размер
m
×
n.
В MS EXCEL существует специальная функция
ТРАНСП()
для нахождения транспонированной матрицы.
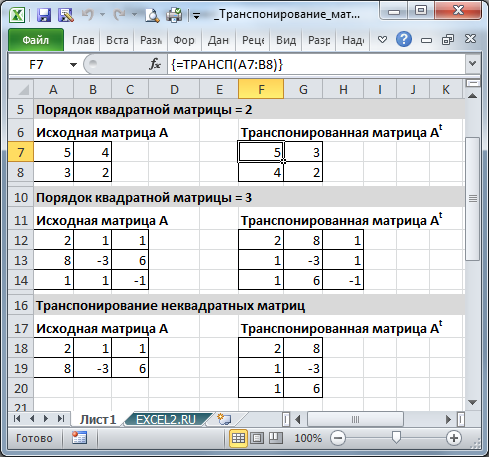
Если элементы исходной матрицы 2 х 2 расположены в диапазоне
А7:В8
, то для получения транспонированной матрицы нужно:
-
выделить диапазон 2 х 2, который не пересекается с исходным диапазоном
А7:В8
-
в
строке формул
ввести формулу
=ТРАНСП(A7:B8)
и нажать комбинацию клавиш
CTRL+SHIFT+ENTER
, т.е. нужно ввести ее какформулу массива
(формулу можно ввести прямо в ячейку, предварительно нажав клавишу
F2
)
Если исходная матрица не квадратная, например, 2 строки х 3 столбца, то для получения транспонированной матрицы нужно выделить диапазон из 3 строк и 2 столбцов. В принципе можно выделить и заведомо больший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
СОВЕТ
: В статьях раздела про транспонирование таблиц (см.
Транспонирование
) можно найти полезные приемы, которые могут быть использованы для транспонирования матриц другим способом (через специальную вставку или с использованием функций
ДВССЫЛ()
,
АДРЕС()
,
СТОЛБЕЦ()
).
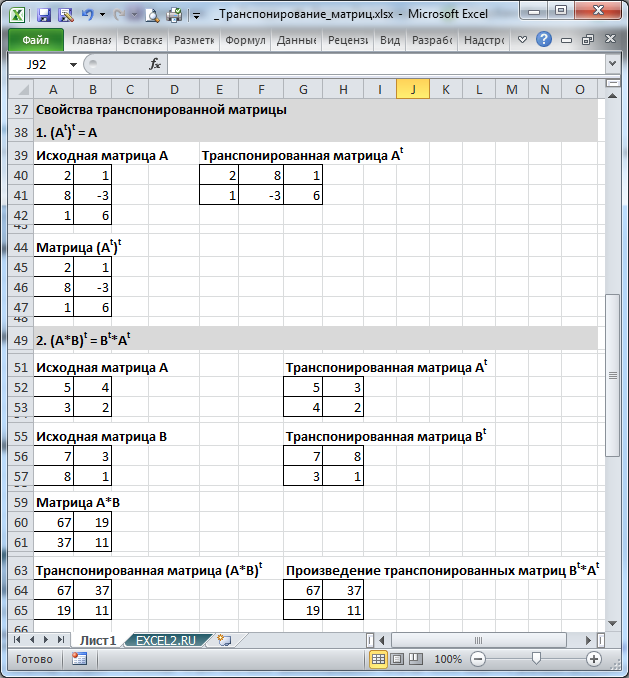
Напомним некоторые свойства транспонированных матриц (см.
файл примера
).
(A
t
)
t
= A(
k
· A)
t
=
k
· A
t
(про умножение матриц на число и сложение матриц см. статью
Сложение и вычитание матриц, умножение матриц на число в MS EXCEL
)(A + B)
t
= A
t
+ B
t
(A · B)
t
= B
t
· A
t
(про умножение матриц см. статью
Умножение матриц в MS EXCEL
)
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Иногда требуется изменить направление, в котором располагаются ячейки. Это можно сделать путем копирования и вставки и применения команды «Транспонировать». Но в этом случае образуются повторяющиеся данные. Чтобы такого не происходило, можно вместо этого ввести формулу с функцией ТРАНСП. Например, на следующем изображении показано, как расположить горизонтально ячейки с A1 по B4 с помощью формулы =ТРАНСП(A1:B4).
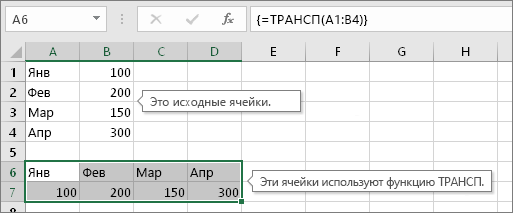
Примечание: Если у вас есть текущая версия Microsoft 365, вы можете ввести формулу в левую верхнюю ячейку диапазона вывода, а затем нажать ввод, чтобы подтвердить формулу как формулу динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Шаг 1. Выделите пустые ячейки
Сначала выделите пустые ячейки. Их число должно совпадать с числом исходных ячеек, но располагаться они должны в другом направлении. Например, имеется 8 ячеек, расположенных по вертикали:
Нам нужно выделить 8 ячеек по горизонтали:
Так будут располагаться новые ячейки после транспонирования.
Шаг 2. Введите =ТРАНСП(
Не снимая выделение с пустых ячеек, введите =ТРАНСП(
Лист Excel будет выглядеть так:
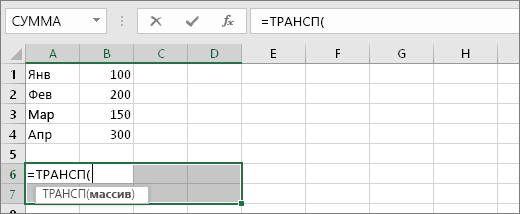
Обратите внимание на то, что восемь ячеек по-прежнему выделены даже несмотря на то, что мы начали вводить формулу.
Шаг 3. Введите исходный диапазон ячеек
Теперь введите диапазон ячеек, которые нужно транспоннять. В этом примере мы хотим транспоннять ячейки с A1 по B4. Поэтому формула для этого примера будет такой: =ТРАНСП(A1:B4) — но не нажимайте ввод! Просто остановите ввод и перейдите к следующему шагу.
Лист Excel будет выглядеть так:
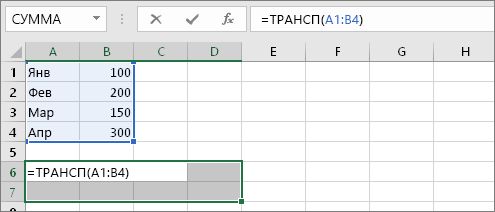
Шаг 4. Нажмите клавиши CTRL+SHIFT+ВВОД
Теперь нажмите клавиши CTRL+SHIFT+ВВОД. Зачем это нужно? Дело в том, что функция ТРАНСП используется только в формулах массивов, которые завершаются именно так. Если говорить кратко, формула массива — это формула, которая применяется сразу к нескольким ячейкам. Так как в шаге 1 вы выделили более одной ячейки, формула будет применена к нескольким ячейкам. Результат после нажатия клавиш CTRL+SHIFT+ВВОД будет выглядеть так:
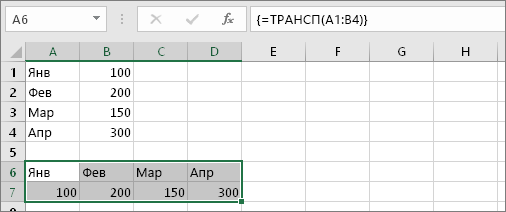
Советы
-
Вводить диапазон вручную не обязательно. Введя =ТРАНСП(, вы можете выделить диапазон с помощью мыши. Простой щелкните первую ячейку диапазона и перетащите указатель к последней. Но не забывайте: по завершении нужно нажать клавиши CTRL+SHIFT+ВВОД, а не просто клавишу ВВОД.
-
Нужно также перенести форматирование текста и ячеек? Вы можете копировать ячейки, вставить их и применить команду «Транспонировать». Но помните, что при этом образуются повторяющиеся данные. При изменении исходных ячеек их копии не обновляются.
-
Вы можете узнать больше о формулах массивов. Создайте формулу массива или ознакомьтесь с подробными рекомендациями и примерами.
Технические подробности
Функция ТРАНСП возвращает вертикальный диапазон ячеек в виде горизонтального и наоборот. Функцию ТРАНСП необходимо вводить как формула массива в диапазон, содержащий столько же строк и столбцов, что и аргумент диапазон. Функция ТРАНСП используется для изменения ориентации массива или диапазона на листе с вертикальной на горизонтальную и наоборот.
Синтаксис
ТРАНСП(массив)
Аргументы функции ТРАНСП описаны ниже.
-
Массив. Обязательный аргумент. Массив (диапазон ячеек) на листе, который нужно транспонировать. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая — вторым столбцом и т. д. Если вы не знаете, как ввести формулу массива, см. статью «Создание формулы массива».
См. также
Транспонирование (поворот) данных из строк в столбцы и наоборот
Создание формулы массива
Поворот и выравнивание данных в ячейке
Использование формул массива: рекомендации и примеры
Нужна дополнительная помощь?
Под матрицей подразумевается набор ячеек, расположенных непосредственно друг возле друга и которые образуют вместе прямоугольник. Не требуется особых навыков, чтобы выполнять различные действия с матрицей, достаточно тех же, какие используются во время работы с классическим диапазоном.
Каждая матрица имеет свой адрес, записывающийся аналогичным диапазону способом. Первая составная часть – первая ячейка диапазона (расположенная в верхнем левом углу), а второй – последняя ячейка, которая находится в нижнем правом углу.
Содержание
- Формулы массива
- Что можно делать с матрицами
- Транспонирование
- Сложение
- Умножение
- Обратная матрица
- Поиск определителя матрицы
- Несколько примеров
- Умножение и деление
- Метод 1
- Метод 2
- Сложение и вычитание
- Метод 1
- Метод 2
- Пример транспонирования матрицы
- Поиск обратной матрицы
- Выводы
Формулы массива
В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:
- Выделить набор ячеек, где будут выводиться значения.
- Непосредственно введение формулы.
- Нажатие последовательности клавиш Ctrl + Shift + Ввод.
После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.
Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.
Что можно делать с матрицами
В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.
Транспонирование
Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием.
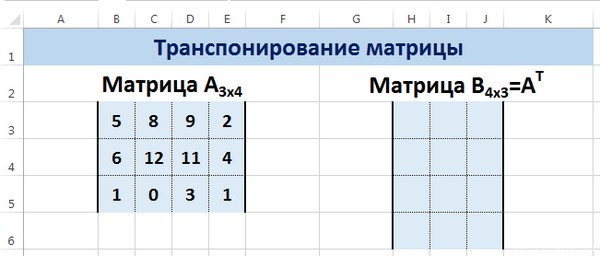
Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.
Далее есть несколько методов, как можно осуществить транспонирование.
Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».
Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.
Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП. Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.
После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:
- Выделить набор ячеек, отведенных под транспонированную матрицу.
- Нажать клавишу F2.
- Нажать на горячие клавиши Ctrl + Shift + Enter.
Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.
Сложение
Эта операция возможна лишь применительно к тем диапазонам, количество элементов которых такое же самое. Проще говоря, у каждой из матриц, с которыми пользователь собирается работать, должны быть одинаковые размеры. И приводим скриншот для наглядности.
В матрице, которая должна получиться, нужно выделить первую ячейку и ввести такую формулу.
=Первый элемент первой матрицы + Первый элемент второй матрицы
Далее подтверждаем ввод формулы с помощью клавиши Enter и используем автозаполнение (квадратик в правом нижнем углу), чтобы скопировать все значения на новую матрицу.
Умножение
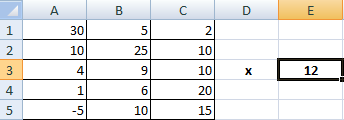
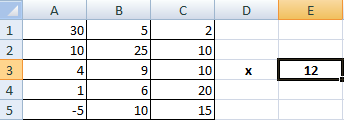
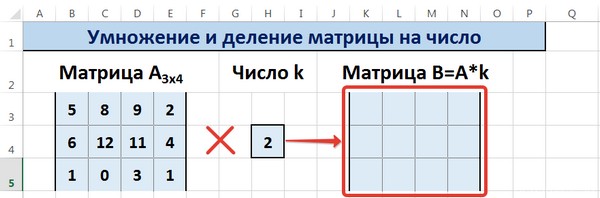
Предположим, у нас есть такая таблица, которую следует умножить на 12.
Догадливый читатель может легко понять, что метод очень похож на предыдущий. То есть, каждая из ячеек матрицы 1 должна умножаться на 12, чтобы в итоговой матрице каждая ячейка содержала значение, умноженное на этот коэффициент.
При этом важно указывать абсолютные ссылки на ячейки.
Итого, получится такая формула.
=A1*$E$3
Дальше методика аналогична предыдущей. Нужно это значение растянуть на необходимое количество ячеек.
Предположим, что необходимо перемножить матрицы между собой. Но есть лишь одно условие, при котором это возможно. Надо, чтобы количество столбцов и строк у двух диапазонов было зеркально одинаковое. То есть, сколько столбцов, столько и строк.
Чтобы было более удобно, нами выделен диапазон с результирующей матрицей. Надо переместить курсор на ячейку в верхнем левом углу и ввести такую формулу =МУМНОЖ(А9:С13;Е9:H11). Не стоит забыть нажать Ctrl + Shift + Enter.
Обратная матрица
Если наш диапазон имеет квадратную форму (то есть, количество ячеек по горизонтали и вертикали одинаковое), то тогда получится найти обратную матрицу, если в этом есть такая необходимость. Ее величина будет аналогичной исходной. Для этого используется функция МОБР.
Для начала следует выделить первую ячейку матрицы, в какую будет вставляться обратная. Туда вводится формула =МОБР(A1:A4). В аргументе указывается диапазон, для какого нам надо создать обратную матрицу. Осталось только нажать Ctrl + Shift + Enter, и готово.
Поиск определителя матрицы
Под определителем подразумевается число, находящееся матрицы квадратной формы. Чтобы осуществить поиск определителя матрицы, существует функция – МОПРЕД.
Для начала ставится курсор в какой-угодно ячейке. Далее мы вводим =МОПРЕД(A1:D4)
Несколько примеров
Давайте для наглядности рассмотрим некоторые примеры операций, которые можно осуществлять с матрицами в Excel.
Умножение и деление
Метод 1
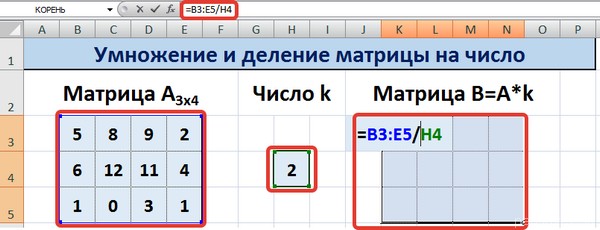
Предположим, у нас есть матрица A, имеющая три ячейки в высоту и четыре – в ширину. Также есть число k, которое записывается в другой ячейке. После выполнения операции умножения матрицы на число появится диапазон значений, имеющий аналогичные размеры, но каждая ее часть умножается на k.
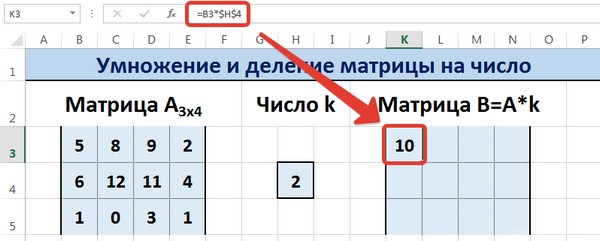
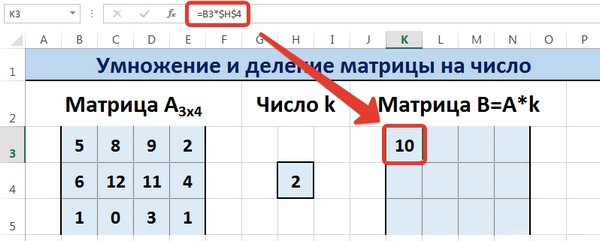
Диапазон B3:E5 – это исходная матрица, которая будет умножаться на число k, которое в свою очередь расположено в ячейке H4. Результирующая матрица будет находиться в диапазоне K3:N5. Исходная матрица будет называться A, а результирующая – B. Последняя образуется путем умножения матрицы А на число k.
Далее вводится =B3*$H$4 в ячейку K3, где В3 — элемент A11 матрицы А.
Не стоит забывать о том, ячейку H4, где указано число k необходимо вводить в формулу с помощью абсолютной ссылки. Иначе значение будет изменяться при копировании массива, и результирующая матрица потеряет работоспособность.
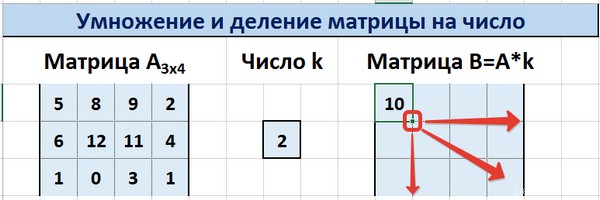
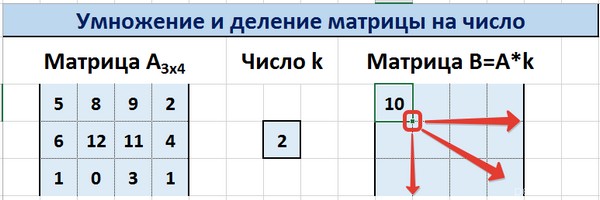
Далее маркер автозаполнения (тот самый квадратик в правом нижнем углу) используется для того, чтобы скопировать значение, полученное в ячейке K3, во все другие ячейки этого диапазона.
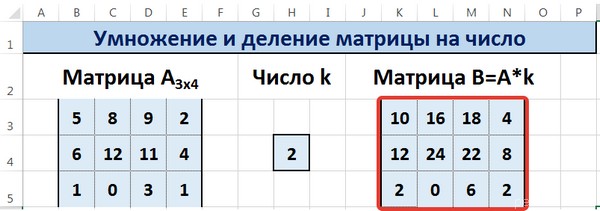
Вот у нас и получилось умножить матрицу A на определенное число и получить на выходе матрицу B.
Деление осуществляется аналогичным образом. Только вводить нужно формулу деления. В нашем случае это =B3/$H$4.
Метод 2
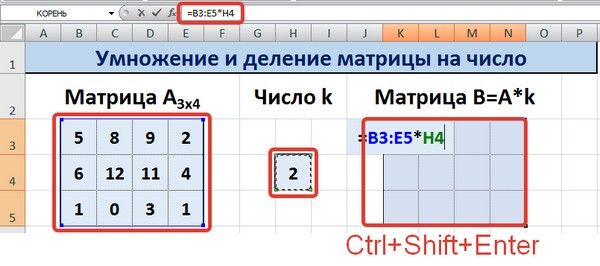
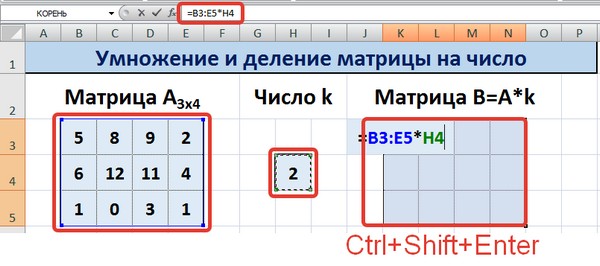
Итак, основное отличие этого метода в том, в качетве результата выдается массив данных, поэтому нужно применить формулу массива, чтобы заполнить весь набор ячеек.
Необходимо выделить результирующий диапазон, ввести знак равно (=), выделить набор ячеек, с соответствующими первой матрице размерами, нажать на звездочку. Далее выделяем ячейку с числом k. Ну и чтобы подтвердить свои действия, надо нажать на вышеуказанную комбинацию клавиш. Ура, весь диапазон заполняется.
Деление осуществляется аналогичным образом, только знак * нужно заменить на /.
Сложение и вычитание
Давайте опишем несколько практических примеров использования методов сложения и вычитания на практике.
Метод 1
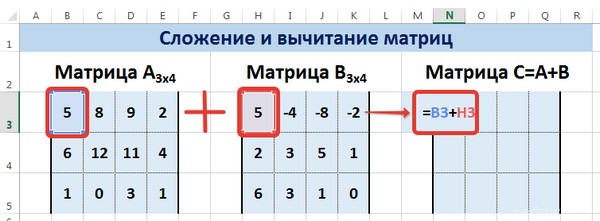
Не стоит забывать, что возможно сложение лишь тех матриц, размеры которых одинаковые. В результирующем диапазоне все ячейки заполняются значением, являющим собой сумму аналогичных ячеек исходных матриц.
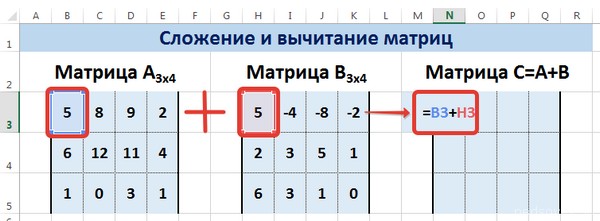
Предположим, у нас есть две матрицы, имеющие размеры 3х4. Чтобы вычислить сумму, следет в ячейку N3 вставить такую формулу:
=B3+H3
Тут каждый элемент являет собой первую ячейку матриц, которые мы собрались складывать. Важно, чтобы ссылки были относительными, поскольку если использовать абсолютные, не будут отображаться правильные данные.
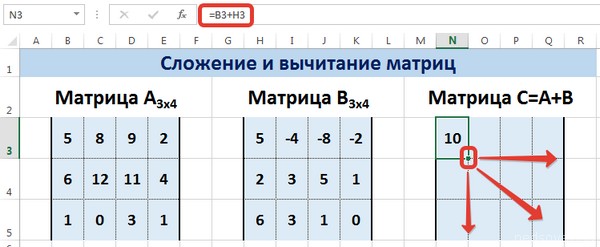
Далее, аналогично умножению, с помощью маркера автозаполнения распространяем формулу на все ячейки результирующей матрицы.
Вычитание осуществляется аналогично, за тем лишь исключением, что используется знак вычитания (-), а не сложения.
Метод 2
Аналогично методу сложения и вычитание двух матриц, этот способ подразумевает использование формулы массива. Следовательно, в качестве ее результата будет выдаваться сразу набор значений. Поэтому нельзя редактировать или удалять какие-то элементы.
Сперва надо выделить диапазон, отделенный под результирующую матрицу, а потом нажать на «=». Затем надо указать первый параметр формулы в виде диапазона матрицы А, нажать на знак + и записать второй параметр в виде диапазона, соответствующему матрице B. Подтверждаем свои действия нажатием комбинации Ctrl + Shift + Enter. Все, теперь вся результирующая матрица заполнена значениями.
Пример транспонирования матрицы
Допустим, нам надо создать матрицу АТ из матрицы А, которая у нас есть изначально методом транспонирования. Последняя имеет, уже по традиции, размеры 3х4. Для этого будем использовать функцию =ТРАНСП().
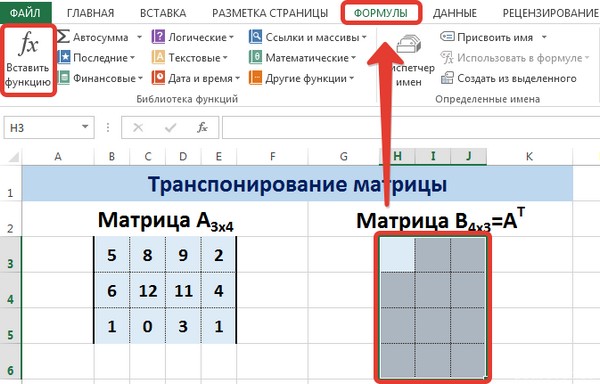
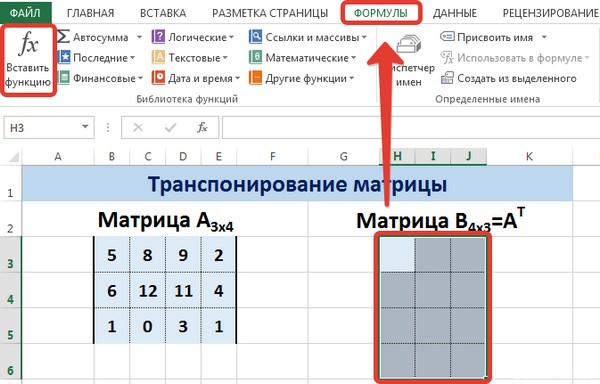
Выделяем диапазон для ячеек матрицы АТ.
Для этого надо перейти на вкладку «Формулы», где выбрать опцию «Вставить функцию», там найти категорию «Ссылки и массивы» и найти функцию ТРАНСП. После этого свои действия подтверждаются кнопкой ОК.
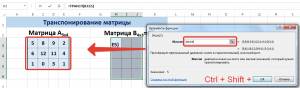
Далее переходим в окно «Аргументы функции», где вводится диапазон B3:E5, который повторяет матрицу А. Далее надо нажать Shift + Ctrl, после чего кликнуть «ОК».
Важно. Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.
В результате, у нас получается такая транспонированная таблица, которая изменяет свои значения вслед за исходной.
Поиск обратной матрицы
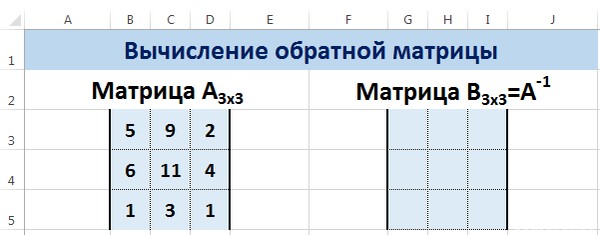
Предположим, у нас есть матрица А, которая имеет размеры 3х3 ячеек. Мы знаем, что для поиска обратной матрицы необходимо использовать функцию =МОБР().
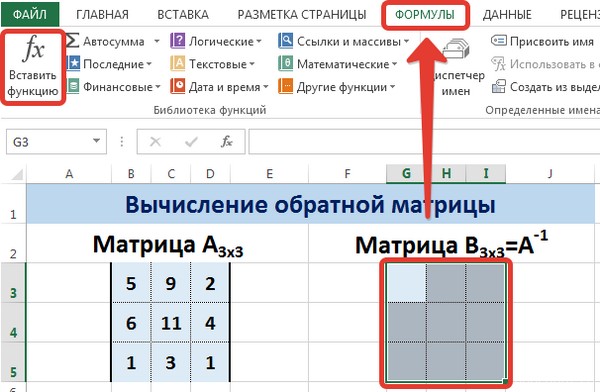
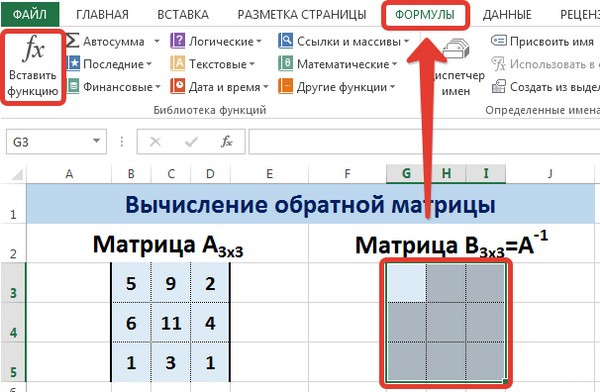
Теперь опишем, как это делать на практике. Сначала необходимо выделить диапазон G3:I5 (там будет располагаться обратная матрица). Необходимо найти на вкладке «Формулы» пункт «Вставить функцию».
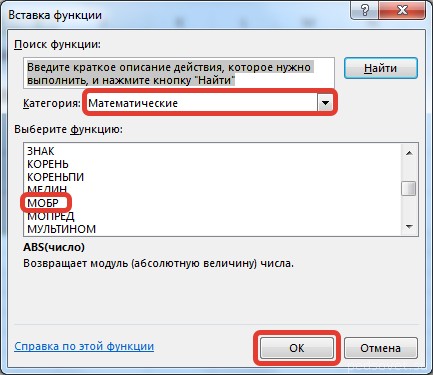
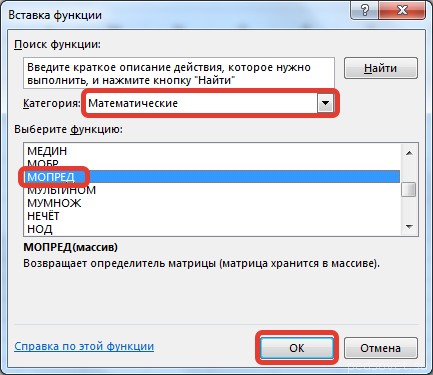
Откроется диалог «Вставка функции», где нужно выбрать категорию «Математические». И там в перечне будет функция МОБР. После того, как мы ее выберем, нужно нажать на клавишу ОК. Далее появляется диалоговое окно «Аргументы функции», в котором записываем диапазон B3:D5, который соответствует матрице А. Далее действия аналогичные транспонированию. Нужно нажать на комбинацию клавиш Shift + Ctrl и нажать ОК.
Выводы
Мы разобрали некоторые примеры, как можно работать с матрицами в Excel, а также описали теорию. Оказывается, что это не так страшно, как может показаться на первый взгляд, не так ли? Это только звучит непонятно, но на деле с матрицами среднестатистическому пользователю приходится иметь дело каждый день. Они могут использоваться почти для любой таблицы, где есть сравнительно небольшое количество данных. И теперь вы знаете, как можно себе упростить жизнь в работе с ними.
Оцените качество статьи. Нам важно ваше мнение:
Умножение и деление матрицы на число в Excel
Способ 1
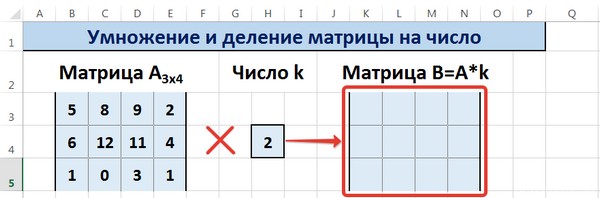
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
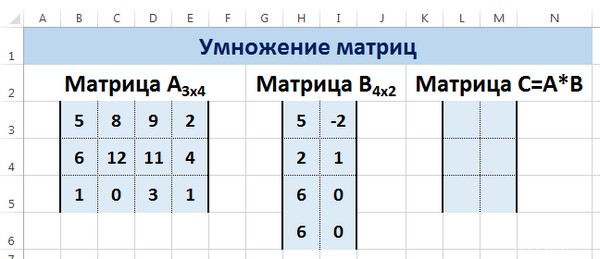
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
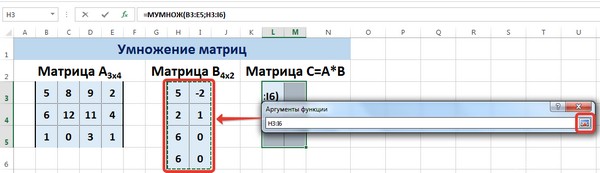
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
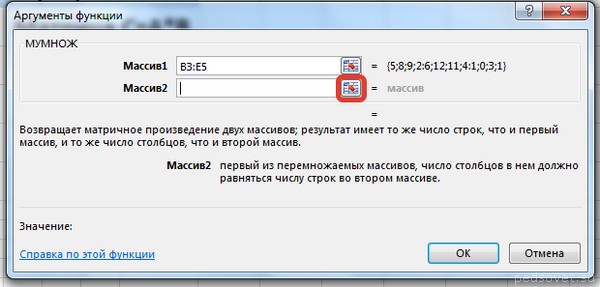
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
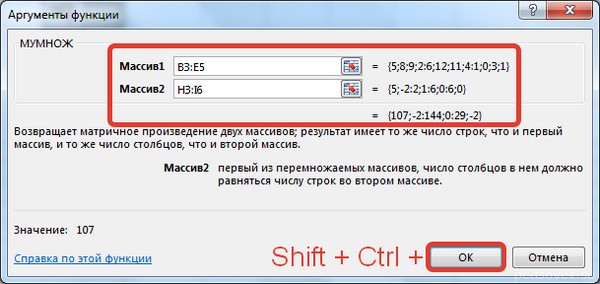
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
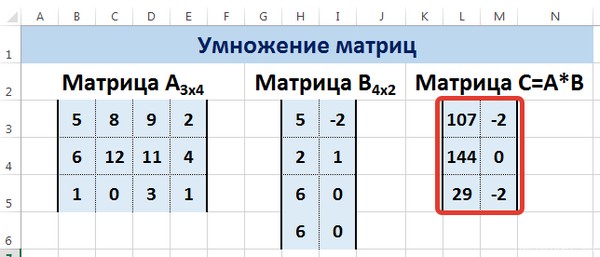
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу АТ.
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу АТ, причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы АТ.
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А-1 называется обратной для матрицы А, если АА-1=А-1А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А-1.
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
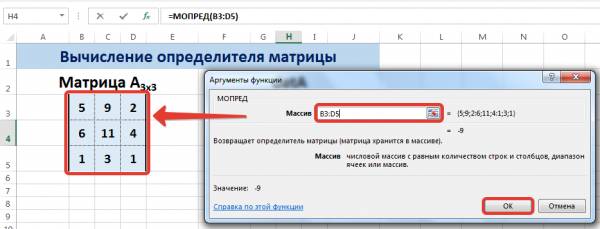
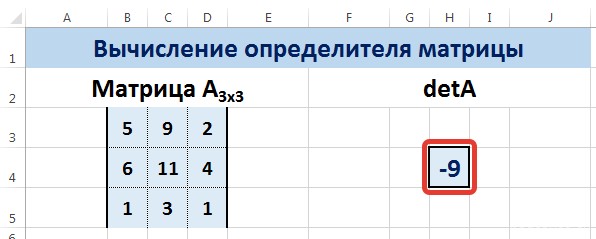
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
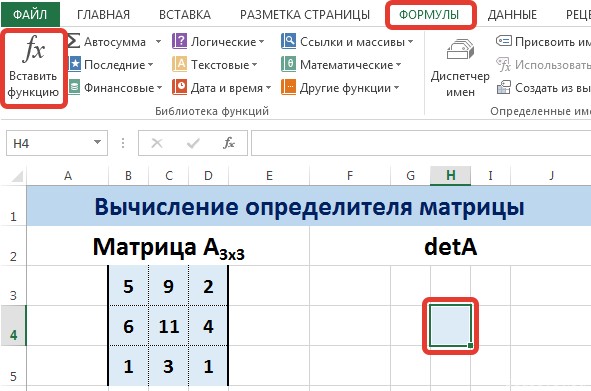
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
Нажмите для увеличения
Мы вычислили определитель матрицы А.
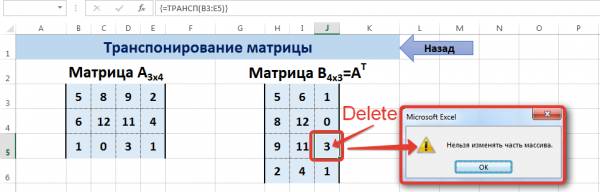
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Содержание
- Транспонирование матриц в EXCEL
- Транспонирование матрицы и таблицы в Excel
- Способ 1. Транспонирование с помощью специальной вставки
- Способ 2. Транспонирование с помощью функции ТРАНСП
- Транспонирование матрицы в программе Microsoft Excel
- Процесс транспонирования
- Способ 1: оператор ТРАНСП
- Способ 2: транспонирование матрицы с помощью специальной вставки
- Функции для работы с матрицами в Excel
- Формулы массива
- Решение матриц в Excel
- Транспонирование
- Сложение
- Умножение матриц в Excel
- Обратная матрица в Excel
- Нахождение определителя матрицы
Транспонирование матриц в EXCEL
history 6 декабря 2015 г.
Транспонирование матрицы — это операция над матрицей, при которой ее строки и столбцы меняются местами. Для этой операции в MS EXCEL существует специальная функция ТРАНСП() или англ. TRANSPOSE.
Если матрица A имеет размер n × m , то транспонированная матрица A t имеет размер m × n.
В MS EXCEL существует специальная функция ТРАНСП() для нахождения транспонированной матрицы.
Если элементы исходной матрицы 2 х 2 расположены в диапазоне А7:В8 , то для получения транспонированной матрицы нужно:
- выделить диапазон 2 х 2, который не пересекается с исходным диапазоном А7:В8
- в строке формул ввести формулу =ТРАНСП(A7:B8) и нажать комбинацию клавиш CTRL+SHIFT+ENTER , т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2 )
Если исходная матрица не квадратная, например, 2 строки х 3 столбца, то для получения транспонированной матрицы нужно выделить диапазон из 3 строк и 2 столбцов. В принципе можно выделить и заведомо больший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
СОВЕТ : В статьях раздела про транспонирование таблиц (см. Транспонирование ) можно найти полезные приемы, которые могут быть использованы для транспонирования матриц другим способом (через специальную вставку или с использованием функций ДВССЫЛ() , АДРЕС() , СТОЛБЕЦ() ).
Напомним некоторые свойства транспонированных матриц (см. файл примера ).
(A t ) t = A( k · A) t = k · A t (про умножение матриц на число и сложение матриц см. статью Сложение и вычитание матриц, умножение матриц на число в MS EXCEL )(A + B) t = A t + B t (A · B) t = B t · A t (про умножение матриц см. статью Умножение матриц в MS EXCEL )
Источник
Транспонирование матрицы и таблицы в Excel
Зачастую у нас в работе возникает необходимость перевернуть данные — из строк сделать столбцы и наоборот.
Рассмотрим различные способы транспонирования матрицы или таблицы в Excel.
Предположим, что у нас имеется следующая матрица, которую мы хотим транспонировать:
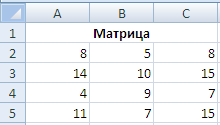
Разберем 2 способа транспонирования матрицы в Excel: с помощью специальной вставки и с помощью функции ТРАНСП.
Способ 1. Транспонирование с помощью специальной вставки
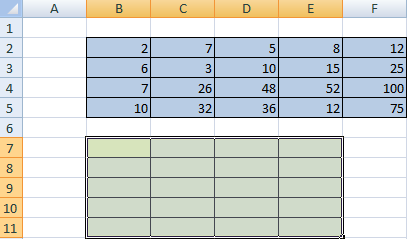
Чтобы транспонировать матрицу выделяем диапазон ячеек A2:C5, в котором находится матрица.
Нажимаем правой кнопкой мыши на выделенный диапазон и в всплывающем окне выбираем Копировать (или нажимаем комбинацию клавиш Ctrl + C).
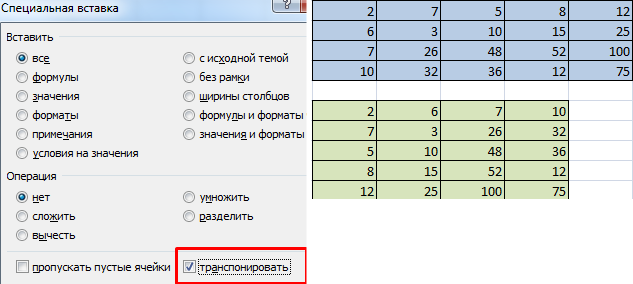
Переходим в ячейку, куда хотим вставить транспонированную матрицу, нажимаем правую кнопку мыши и выбираем Специальная вставка -> Транспонировать (или нажимаем комбинацию клавиш Ctrl + Alt + V и выбираем Транспонировать):

На выходе мы получаем транспонированную матрицу:
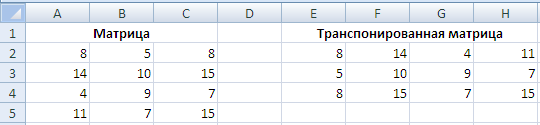
Элементы транспонированной матрицы представляют собой вставленные значения, другими словами полученная транспонированная матрица не является динамической и при изменении элементов исходной матрицы элементы транспонированной меняться не будут.
Чтобы этого избежать воспользуемся другим инструментом Excel — функцией ТРАНСП.
Способ 2. Транспонирование с помощью функции ТРАНСП
Синтаксис и описании функции транспонирования:
ТРАНСП(массив)
Преобразует вертикальный диапазон ячеек в горизонтальный, или наоборот.
- Массив(обязательный аргумент) — массив (диапазон ячеек), для которого применяется транспонирование.
Выделим диапазон пустых ячеек E2:H4, в которых будет находиться транспонированная матрица.
Не снимая выделения с пустых ячеек вводим формулу ТРАНСП и в качестве аргумента функции выбираем диапазон ячеек A2:C5, который нужно транспонировать:
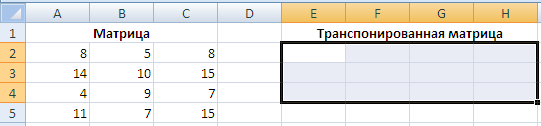
После ввода формулы =ТРАНСП(A2:C5) нажмите Ctrl + Shift + Ввод, чтобы применить формулу массива ко всем выделенным ячейкам.
В результате получаем транспонированную матрицу:
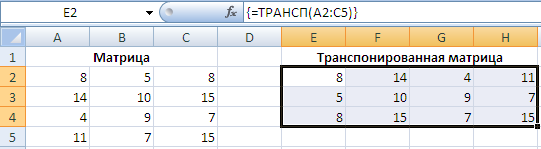
При этом при изменении элементов исходной матрицы также будет перестраиваться и транспонированная матрица, в отличие от способа с специальной вставкой.
Источник
Транспонирование матрицы в программе Microsoft Excel
При работе с матрицами иногда нужно их транспонировать, то есть, говоря простыми словами, перевернуть. Конечно, можно перебить данные вручную, но Эксель предлагает несколько способов сделать это проще и быстрее. Давайте разберем их подробно.
Процесс транспонирования
Транспонирование матрицы – это процесс смены столбцов и строк местами. В программе Excel имеется две возможности проведения транспонирования: используя функцию ТРАНСП и при помощи инструмента специальной вставки. Рассмотрим каждый из этих вариантов более подробно.
Способ 1: оператор ТРАНСП
Функция ТРАНСП относится к категории операторов «Ссылки и массивы». Особенностью является то, что у неё, как и у других функций, работающих с массивами, результатом выдачи является не содержимое ячейки, а целый массив данных. Синтаксис функции довольно простой и выглядит следующим образом:
То есть, единственным аргументом данного оператора является ссылка на массив, в нашем случае матрицу, который следует преобразовать.
Посмотрим, как эту функцию можно применить на примере с реальной матрицей.
- Выделяем незаполненную ячейку на листе, планируемую сделать крайней верхней левой ячейкой преобразованной матрицы. Далее жмем на значок «Вставить функцию», который расположен вблизи строки формул.
- Производится запуск Мастера функций. Открываем в нем категорию «Ссылки и массивы» или «Полный алфавитный перечень». После того, как отыскали наименование «ТРАНСП», производим его выделение и жмем на кнопку «OK».
- Происходит запуск окна аргументов функции ТРАНСП. Единственному аргументу данного оператора соответствует поле «Массив». В него нужно внести координаты матрицы, которую следует перевернуть. Для этого устанавливаем курсор в поле и, зажав левую кнопку мыши, выделяем весь диапазон матрицы на листе. После того, как адрес области отобразился в окне аргументов, щелкаем по кнопке «OK».
- Но, как видим, в ячейке, которая предназначена для вывода результата, отображается некорректное значение в виде ошибки «#ЗНАЧ!». Это связано с особенностями работы операторов массивов. Чтобы исправить эту ошибку, выделяем диапазон ячеек, в котором число строк должно быть равным количеству столбцов первоначальной матрицы, а число столбцов – количеству строк. Подобное соответствие очень важно для того, чтобы результат отобразился корректно. При этом, ячейка, в которой содержится выражение «#ЗНАЧ!» должна быть верхней левой ячейкой выделяемого массива и именно с неё следует начинать процедуру выделения, зажав левую кнопку мыши. После того, как вы провели выделение, установите курсор в строку формул сразу же после выражения оператора ТРАНСП, которое должно отобразиться в ней. После этого, чтобы произвести вычисление, нужно нажать не на кнопку Enter, как принято в обычных формулах, а набрать комбинацию Ctrl+Shift+Enter.
Чтобы решить данную проблему, выделяем весь транспонированный диапазон. Переместившись во вкладку «Главная» щелкаем по пиктограмме «Копировать», которая расположена на ленте в группе «Буфер обмена». Вместо указанного действия можно после выделения произвести набор стандартного сочетания клавиш для копирования Ctrl+C.
Затем, не снимая выделения с транспонированного диапазона, производим клик по нему правой кнопкой мыши. В контекстном меню в группе «Параметры вставки» щелкаем по иконке «Значения», которая имеет вид пиктограммы с изображением чисел.
Вслед за этим формула массива ТРАНСП будет удалена, а в ячейках останутся только одни значения, с которыми можно работать так же, как и с исходной матрицей.
Способ 2: транспонирование матрицы с помощью специальной вставки
Кроме того, матрицу можно транспонировать с помощью одного элемента контекстного меню, который носит название «Специальная вставка».
- Выделяем исходную матрицу курсором, зажав левую кнопку мыши. Далее, перейдя во вкладку «Главная», щелкаем по пиктограмме «Копировать», размещенной в блоке настроек «Буфер обмена».
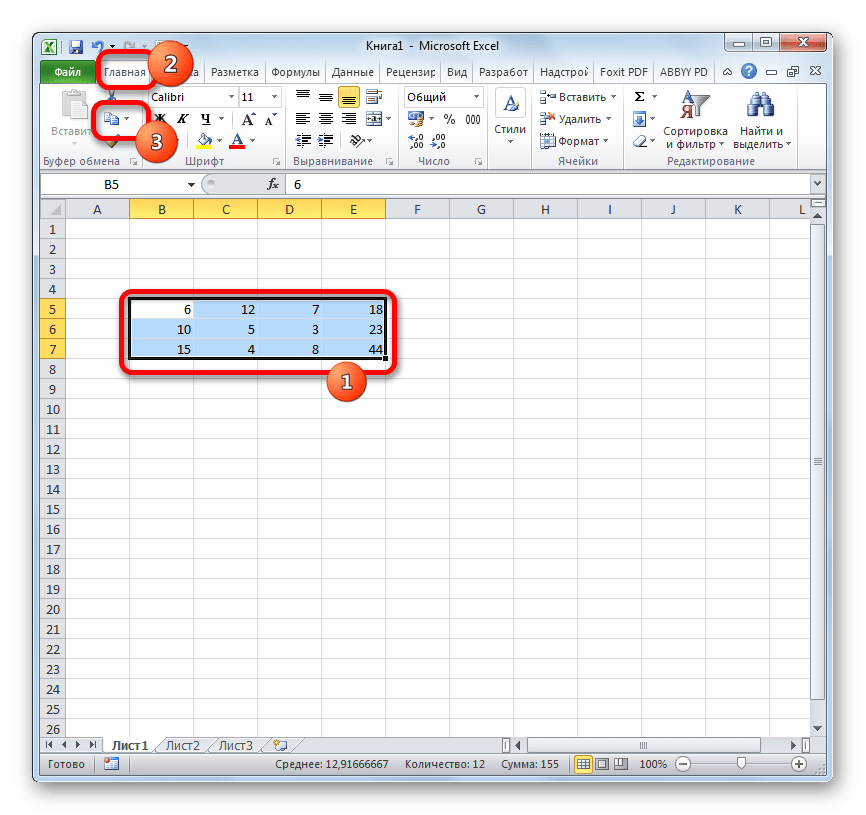
Вместо этого можно сделать и по-другому. Выделив область, кликаем по ней правой кнопкой мыши. Активируется контекстное меню, в котором следует выбрать пункт «Копировать».
В виде альтернативы двум предыдущим вариантам копирования, можно после выделения произвести набор комбинации горячих клавиш Ctrl+C.
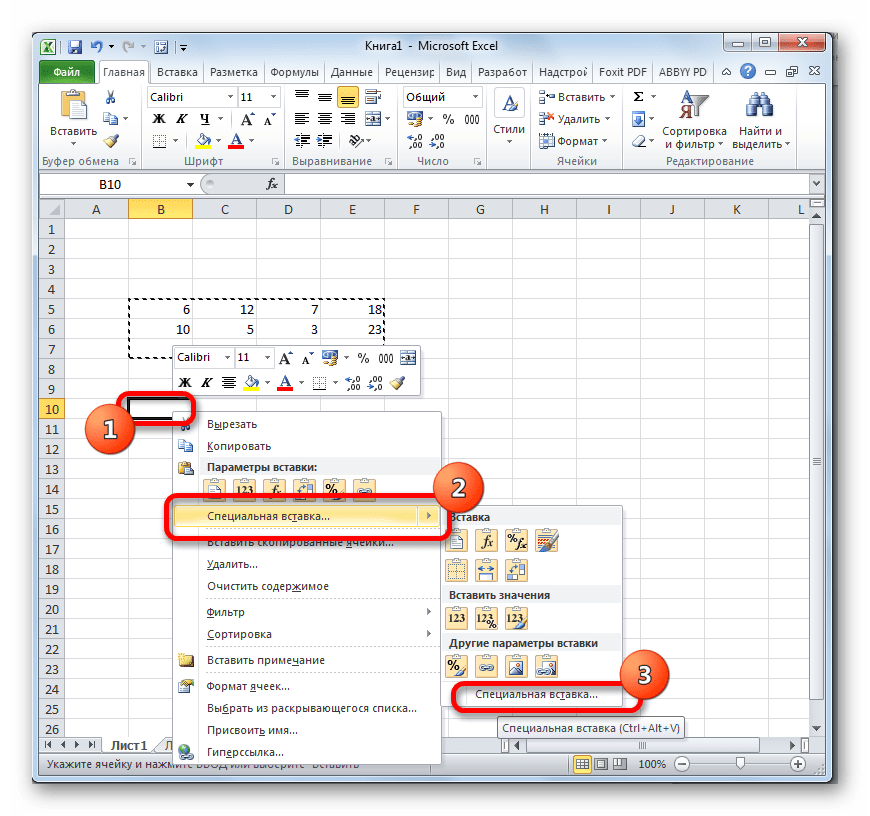
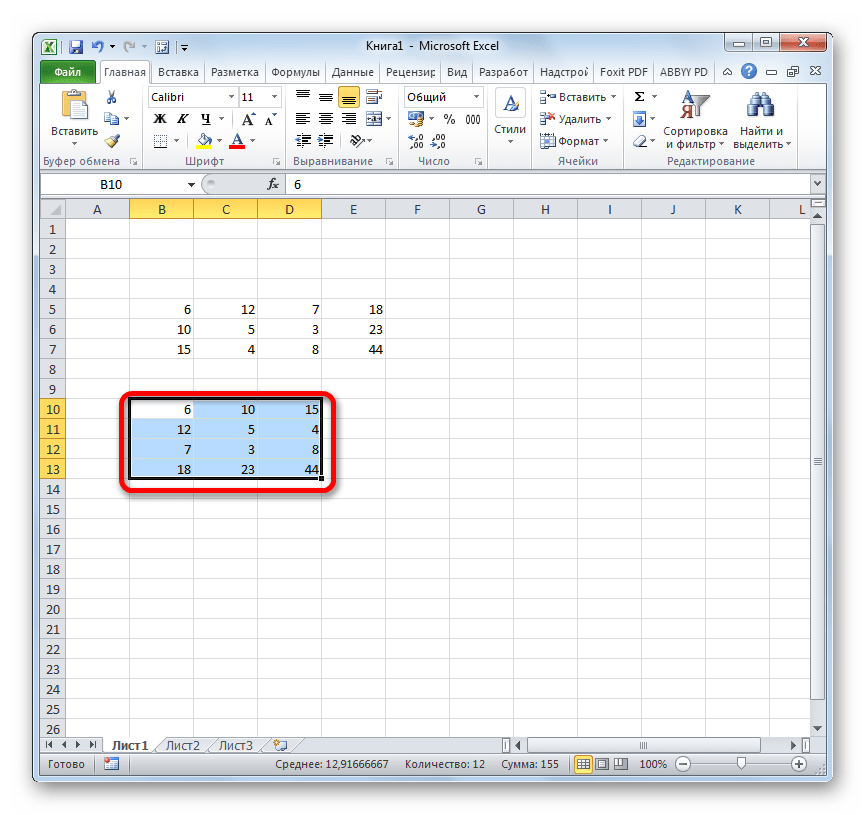
После указанных действий на листе останется только преобразованная матрица.
Этими же двумя способами, о которых шла речь выше, можно транспонировать в Excel не только матрицы, но и полноценные таблицы. Процедура при этом будет практически идентичной.
Итак, мы выяснили, что в программе Excel матрицу можно транспонировать, то есть, перевернуть, поменяв столбцы и строчки местами, двумя способами. Первый вариант предполагает использование функции ТРАНСП, а второй – инструменты специальной вставки. По большому счету конечный результат, который получается при использовании обоих этих способов, ничем не отличается. Оба метода работают практически в любой ситуации. Так что при выборе варианта преобразования, на первый план выходят личные предпочтения конкретного пользователя. То есть, какой из данных способов для вас лично удобнее, тот и используйте.
Источник
Функции для работы с матрицами в Excel
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Источник
Зачастую у нас в работе возникает необходимость перевернуть данные — из строк сделать столбцы и наоборот.
Рассмотрим различные способы транспонирования матрицы или таблицы в Excel.
Предположим, что у нас имеется следующая матрица, которую мы хотим транспонировать:
Разберем 2 способа транспонирования матрицы в Excel: с помощью специальной вставки и с помощью функции ТРАНСП.
Способ 1. Транспонирование с помощью специальной вставки
Чтобы транспонировать матрицу выделяем диапазон ячеек A2:C5, в котором находится матрица.
Нажимаем правой кнопкой мыши на выделенный диапазон и в всплывающем окне выбираем Копировать (или нажимаем комбинацию клавиш Ctrl + C).
Переходим в ячейку, куда хотим вставить транспонированную матрицу, нажимаем правую кнопку мыши и выбираем Специальная вставка -> Транспонировать (или нажимаем комбинацию клавиш Ctrl + Alt + V и выбираем Транспонировать):
На выходе мы получаем транспонированную матрицу:
Элементы транспонированной матрицы представляют собой вставленные значения, другими словами полученная транспонированная матрица не является динамической и при изменении элементов исходной матрицы элементы транспонированной меняться не будут.
Чтобы этого избежать воспользуемся другим инструментом Excel — функцией ТРАНСП.
Способ 2. Транспонирование с помощью функции ТРАНСП
Синтаксис и описании функции транспонирования:
ТРАНСП(массив)
Преобразует вертикальный диапазон ячеек в горизонтальный, или наоборот.
- Массив (обязательный аргумент) — массив (диапазон ячеек), для которого применяется транспонирование.
Выделим диапазон пустых ячеек E2:H4, в которых будет находиться транспонированная матрица.
Не снимая выделения с пустых ячеек вводим формулу ТРАНСП и в качестве аргумента функции выбираем диапазон ячеек A2:C5, который нужно транспонировать:
После ввода формулы =ТРАНСП(A2:C5) нажмите Ctrl + Shift + Ввод, чтобы применить формулу массива ко всем выделенным ячейкам.
В результате получаем транспонированную матрицу:
При этом при изменении элементов исходной матрицы также будет перестраиваться и транспонированная матрица, в отличие от способа с специальной вставкой.
Удачи вам и до скорой встречи на страницах блога Tutorexcel.ru!
Поделиться с друзьями:
Поиск по сайту:
Вы когда-нибудь пытались преобразовать матрицу ячеек в одну строку или столбец в Excel? Возможно, вы можете скопировать строку или столбец и вставить их одну за другой в один вектор, но это займет много времени, если есть несколько строк и столбцов. В этой статье я расскажу о некоторых интересных методах и надеюсь, что они помогут вам.
Преобразование матрицы ячеек в одну строку или столбец с помощью формул
Преобразование матрицы ячеек в одну строку или столбец с помощью Kutools for Excel
Преобразование нескольких столбцов или строк в один столбец или строку:
Программа Kutools for Excel Transform Range может помочь вам преобразовать диапазон ячеек только в один столбец или строку, напротив, он также может преобразовывать одну строку или столбец в диапазон ячеек.

Kutools for Excel : с более чем 200 удобными надстройками Excel, которые можно бесплатно попробовать без ограничений в течение 60 дней. Скачать и бесплатную пробную версию сейчас!
->
Содержание
- Преобразование матрицы ячейки в одну строку или столбец с формулами
- Преобразование матрицы ячеек в одну строку или столбец с помощью Kutools for Excel
- Демо: преобразование матрицы ячеек в одну строку или столбец с помощью Kutools for Excel
Преобразование матрицы ячейки в одну строку или столбец с формулами
Следующие формулы могут помочь вам быстро преобразовать матрицу в одну строку или столбец. Пожалуйста, сделайте следующее:
Преобразуйте матрицу ячеек в один столбец
1 . Прежде всего, вы должны определить имя диапазона для данных матрицы. Выберите диапазон ячеек и введите имя диапазона в поле Имя , которое находится рядом со строкой формул, а затем нажмите клавишу Enter . В этом случае я набираю «Матрица» в качестве определенного имени, см. Снимок экрана:

2 . Затем введите следующие формулы:
(1.) Преобразуйте матрицу в один столбец на основе строки, это означает, что значения берутся из каждой строки, перемещаясь затем вниз: = OFFSET (Matrix, TRUNC ((ROW () – ROW ($ G $ 1))/COLUMNS (матрица)), MOD (ROW () – ROW ($ G $ 1), COLUMNS (Matrix)), 1,1) ( Matrix – это имя диапазона, которое вы определили на шаге 1, а G1 – это ячейка, в которую вы вводите эту формулу). Затем перетащите маркер заполнения к ячейкам, пока не отобразится 0, см. Снимок экрана:

(2.) Преобразуйте матрицу в один столбец на основе столбца, это означает, что значения берутся из столбцов, перемещаясь вниз на один столбец, а затем в правый столбец: = OFFSET (Matrix, MOD (ROW () – ROW ($ G $ 1), ROWS (матрица)), TRUNC ((ROW () – ROW ($ G $ 1))/ROWS (матрица)), 1,1) ( Matrix – это имя диапазона, которое вы определили на шаге 1, а G1 – это ячейка, в которую вы вводите эту формулу). Затем перетащите маркер заполнения в ячейки, пока не отобразится 0, см. Снимок экрана:

Преобразование матрицы ячеек в одну строку
Чтобы преобразовать матрицу ячеек в одну строку, вы можете использовать следующие формулы:
(1.) Преобразуйте матрицу в одну строку на основе строки, это означает, что значения берутся из каждой строки слева направо в одной строке, а затем перемещаются вниз в следующую строку: = OFFSET (Matrix, TRUNC ((COLUMN () – COLUMN ($ A $ 7))/COLUMNS (Matrix)), MOD ((COLUMN () – COLUMN ($ A $ 7)) , COLUMNS (Matrix)), 1,1) ( Matrix – это имя диапазона, которое вы создали для своего диапазона данных, а A7 – это (введите эту формулу). Затем перетащите маркер заполнения вправо в ячейки, пока не отобразится 0, см. снимок экрана:

(2.) Преобразование матрицы в одну строку на основе столбца, это означает, что значения берутся из каждого столбца, перемещаясь на один столбец вниз, а затем в правый столбец: = OFFSET (Matrix, MOD ((COLUMN () – COLUMN ($ A $ 7)), ROWS (Matrix)), TRUNC ((COLUMN () – COLU MN ($ A $ 7))/(ROWS (Matrix))), 1,1) ( Matrix – это имя диапазона, которое вы создали для своего диапазона данных, а A7 – ячейка, в которой вы вводите эту формулу). Затем перетащите маркер заполнения вправо к ячейкам, пока не отобразится 0, см. Снимок экрана:

Преобразование матрицы ячеек в одну строку или столбец с помощью Kutools for Excel
Если приведенные выше формулы слишком длинные напомню, что здесь я могу порекомендовать простой и мощный инструмент – Kutools for Excel , с его утилитой Transform Range , вы можете быстро преобразовать несколько столбцов и строк в один столбец или строку по мере необходимости.
| Kutools for Excel : с более чем 300 удобными надстройками Excel, которые можно попробовать бесплатно без ограничений в течение 30 дней . |
|
Перейти к загрузке |
После установки Kutools for Excel выполните следующие действия:
1 . Выберите матрицу ячеек, которую вы хотите преобразовать.
2 . Затем нажмите Kutools > Range > Transform Range , см. Снимок экрана:

3 . В диалоговом окне Преобразовать диапазон выберите Диапазон в один столбец , если вы хотите преобразовать матрицу в один столбец, или выберите Диапазон в одна строка , если вы хотите преобразовать матрицу в одну строку, см. снимок экрана:

4 . Затем нажмите кнопку OK и в появившемся поле Transform Range выберите ячейку, в которую вы хотите поместить результат, см. Снимок экрана:

5 . Затем нажмите кнопку OK , выбранная матрица ячеек была преобразована в одну строку или столбец.
Чтобы узнать больше об этом диапазоне преобразования утилита.
Загрузите бесплатную пробную версию Kutools for Excel прямо сейчас!
Демо: преобразование матрицы ячеек в одну строку или столбец с помощью Kutools for Excel
Kutools for Excel : с более чем 300 удобными надстройками Excel, вы можете попробовать бесплатно без ограничений в течение 30 дней. Загрузить и бесплатная пробная версия сейчас!