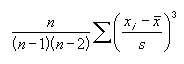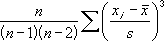Функция СКОС в Excel предназначена для определения коэффициента асимметрии для последовательности числовых данных и возвращает соответствующее числовое значение.
Расчет коэффициента асимметрии распределения чисел в Excel
Коэффициент асимметрии показывает степень несимметричности распределения числовых данных относительно среднего значения. Может принимать следующие значения:
- Из диапазона отрицательных чисел – отклонение в сторону отрицательных значений (отрицательные величины преобладают).
- Из диапазона положительных чисел – отклонение в сторону положительных значений (преобладание положительных величин).
- 0 – асимметрия отсутствует (например, для последовательности 1, 2, 3, -1, -2, -3 асимметрический коэффициент равен нулю – 0).
Для определения коэффициента асимметрии используется уравнение:
Пример 1. В таблице Excel содержатся два ряда числовых данных. Определить, какой из числовых рядов характеризуется наименьшим коэффициентом асимметрии.
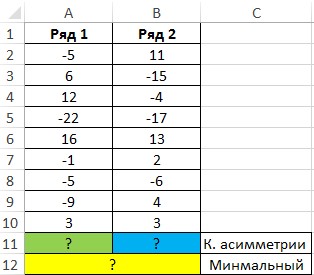
Вид таблицы данных:
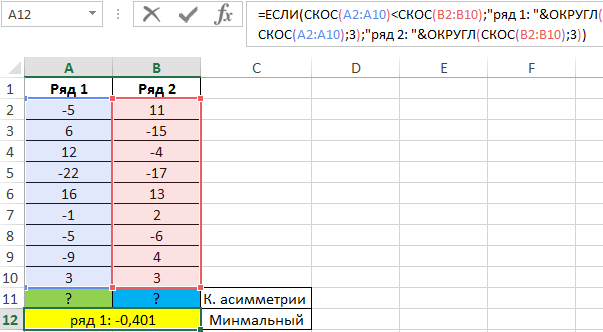
Для решения используем следующую формулу:
С помощью функции ЕСЛИ выполняем проверку коэффициента симметрии («имеет ли второй ряд большее значение скоса?») и возвращаем соответствующее значение с пояснением.
Результат вычислений:
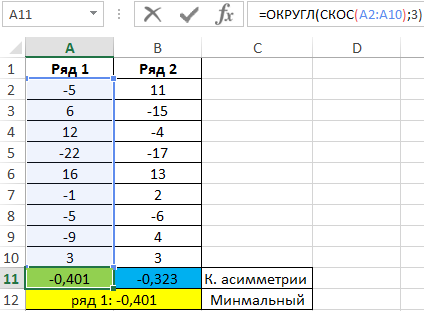
Проверим значения для каждого ряда по отдельности с помощью функций:
=ОКРУГЛ(СКОС(A2:A10);3)
=ОКРУГЛ(СКОС(B2:B10);3)
Полученные результаты:
Обе последовательности имеют отклонения в отрицательную сторону, но у ряда 1 это выражено в большей степени.
Коэффициент асимметрии и аппроксимация нормальным распределением в Excel
Пример 2. Имеем последовательность чисел. Необходимо проанализировать данную последовательность и сделать вывод о возможности аппроксимации нормальным распределением.
Вид таблицы данных:
Для проверки нормального распределения величины применяют довольно сложные статистические критерии. Однако, в простейшем случае можно определить две величины (коэффициент асимметрии и эксцесс), чтобы сделать определенные выводы. Если они близки к нулю, аппроксимация нормальным распределением допустима.
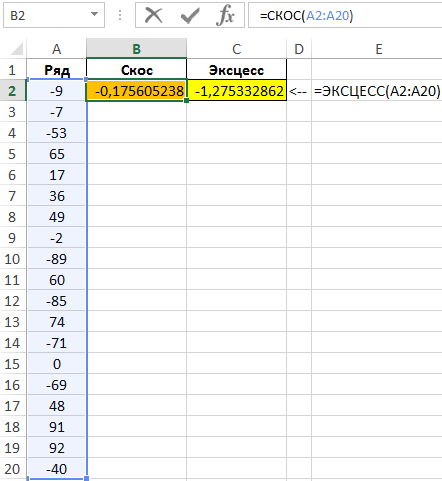
Определим значения асимметрии и эксцесса следующими функциями:
=СКОС(A2:A20)
=ЭКСЦЕСС(A2:A20)
Результаты:
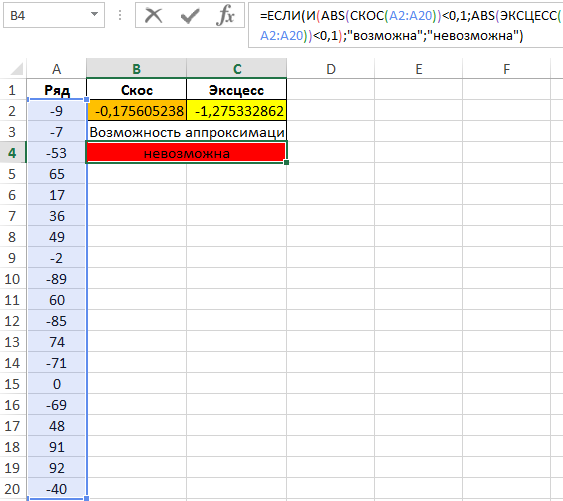
Отклонения от 0 значительны, поэтому аппроксимация невозможна. Чтобы автоматизировать подобные расчеты введем некоторые условия:
В данном случае принято допущение о том, что максимальное допустимое отклонение модулей асимметрии и эксцесса составляет 0,1
Результат:
Правила использования функции СКОС в Excel
Функция имеет следующую синтаксическую запись:
=СКОС(число1;[число2];…)
Описание аргументов:
- число1 – обязательный, принимает первое значение числовой последовательности или ссылку на диапазон ячеек с числовыми данными.
- [число2];… — второй и последующие необязательные аргументы, принимающие числовые значения второго и последующих чисел исследуемого ряда.
Примечания:
- Функция принимает в качестве аргументов числа или данные, которые могут быть преобразованы к числовым данным, а также ссылки на ячейки с числами или преобразуемыми к числам данными. Иначе СКОС будет возвращать код ошибки #ЗНАЧ!
- Не преобразуемые к числам значения, содержащиеся в ячейках, в расчете не учитываются. Логические ИСТИНА и ЛОЖЬ также игнорируются рассматриваемой функцией.
- Если исследуемый ряд значений содержит менее трех числовых значений, функция СКОС вернет код ошибки # ЧИСЛО!
17 авг. 2022 г.
читать 2 мин
Асимметрия — это мера асимметрии набора данных или распределения. Это значение может быть положительным или отрицательным. Это полезно знать, потому что это помогает нам понять форму распределения.
Отрицательная асимметрия указывает на то, что хвост находится в левой части распределения, которая простирается в сторону более отрицательных значений.
Положительная асимметрия указывает на то, что хвост находится на правой стороне распределения, которая простирается в сторону более положительных значений.
Нулевое значение указывает на то, что в распределении вообще нет асимметрии, что означает, что распределение совершенно симметрично. Это необычно и редко встречается на практике.
Как рассчитать асимметрию в Excel
Excel предлагает следующую встроенную функцию для вычисления асимметрии распределения:
=СКОС(массив значений)
Эта функция использует следующую формулу для вычисления асимметрии:
Асимметрия = [n/(n-1)(n-2)] * Σ[(x i – x )/s] 3
куда:
n = размер выборки
Σ = причудливый символ, означающий «сумма»
x i = значение i -го значения в наборе данных
х = среднее
с = стандартное отклонение
Формула немного сложна, но, к счастью, Excel выполняет этот расчет за вас, так что вам не нужно делать это вручную.
Пример: расчет асимметрии в Excel
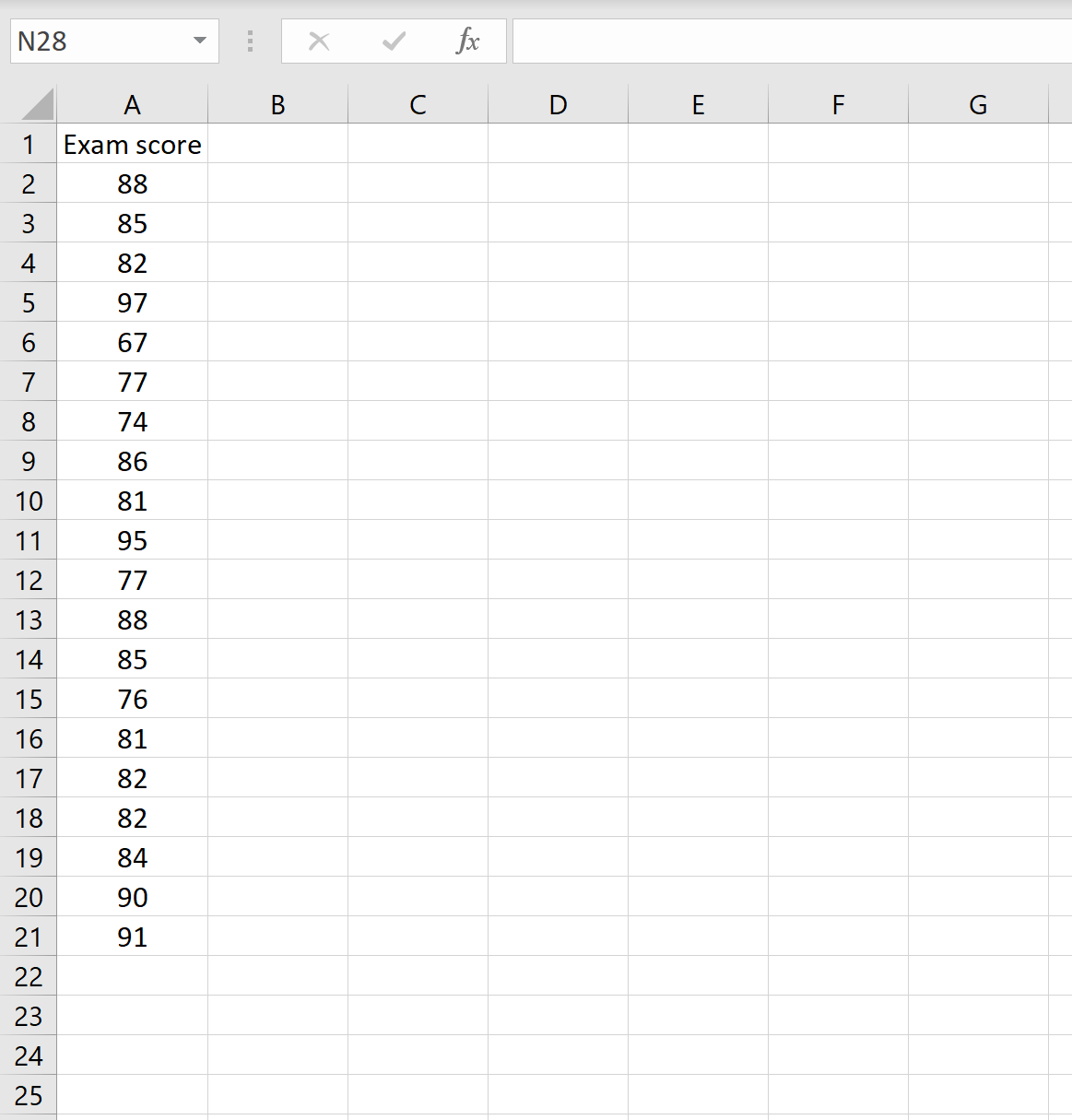
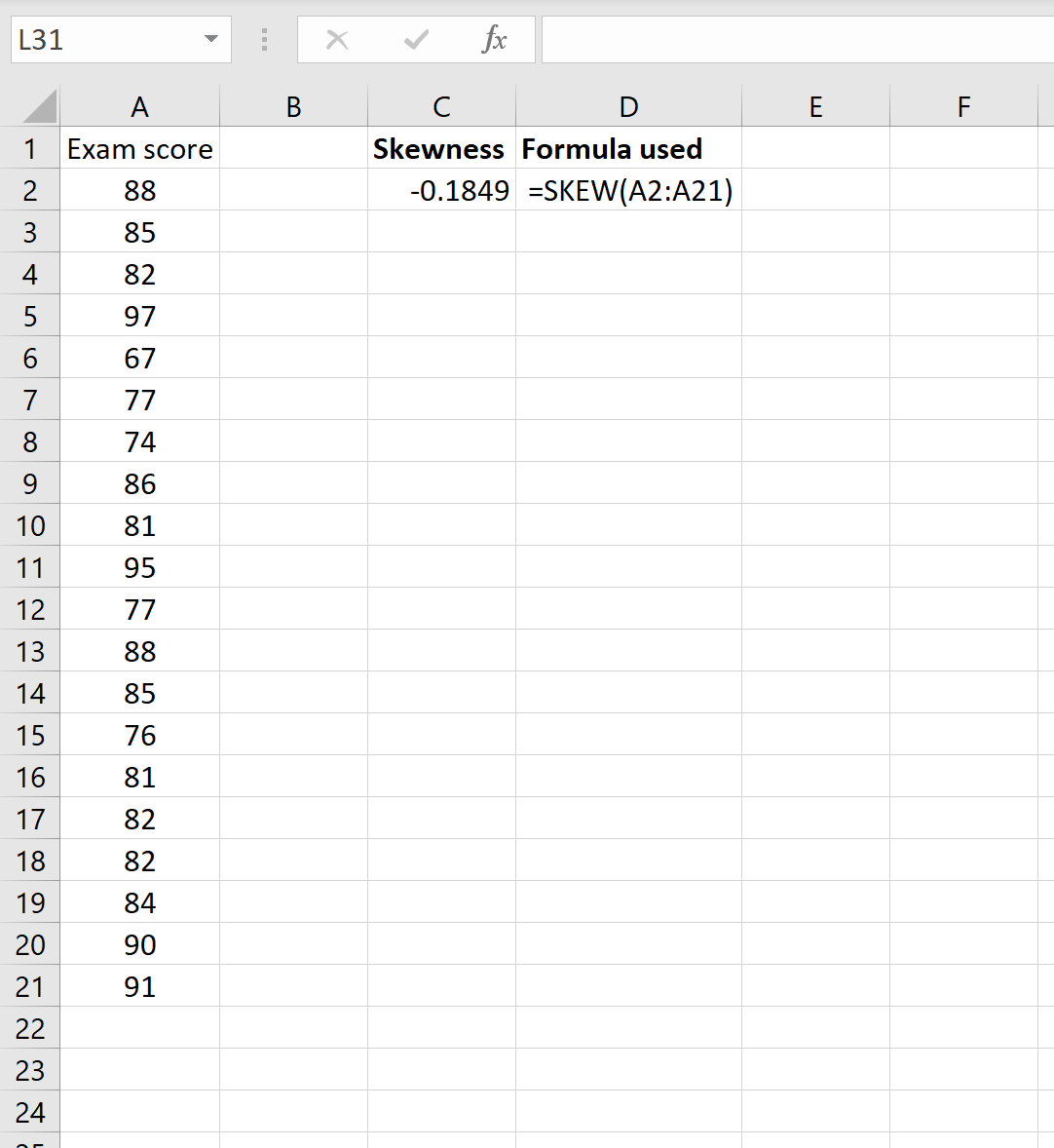
Предположим, у нас есть следующий набор данных, содержащий экзаменационные оценки 20 студентов:
Мы можем рассчитать асимметрию распределения, используя =SKEW(A2:A21)
Это говорит нам о том, что асимметрия этого набора данных составляет -0,1849.Поскольку это значение отрицательное, мы знаем, что хвост распределения простирается влево.
Техническое примечание:
Функция SKEW() вернет ошибку #DIV/0! в следующих двух сценариях:
- Если имеется менее трех точек данных
- Если стандартное отклонение выборки равно нулю
Дополнительный ресурс: Калькулятор асимметрии и эксцесса
Вы также можете рассчитать асимметрию для заданного набора данных с помощью статистического калькулятора асимметрии и эксцесса, который автоматически вычисляет как асимметрию, так и эксцесс для заданного набора данных. Вы просто вводите необработанные значения данных для своего набора данных в поле ввода, затем нажимаете «Рассчитать».
Например, вот как рассчитать асимметрию для набора данных из приведенного выше примера:
Обратите внимание, что значение асимметрии из калькулятора совпадает со значением асимметрии, которое мы нашли в Excel.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции СКОС в Microsoft Excel.
Описание
Возвращает асимметрию распределения. Асимметрия характеризует степень несимметричности распределения относительно его среднего. Положительная асимметрия указывает на отклонение распределения в сторону положительных значений. Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений.
Синтаксис
СКОС(число1;[число2];…)
Аргументы функции СКОС описаны ниже.
-
Число1; число2… Аргумент «число1» является обязательным, последующие числа необязательные. От 1 до 255 аргументов, для которых вычисляется асимметрия. Вместо аргументов, разделенных точкой с запятой, можно использовать один массив или ссылку на массив.
Замечания
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, приводят к возникновению ошибки.
-
Если имеется менее трех точек данных или стандартное отклонение выборки имеет нулевое значение, то СКОС возвращает значение #DIV/0! значение ошибки #ЗНАЧ!.
-
Уравнение для асимметрии имеет следующий вид:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
3 |
||
|
4 |
||
|
5 |
||
|
2 |
||
|
3 |
||
|
4 |
||
|
5 |
||
|
6 |
||
|
4 |
||
|
7 |
||
|
Формула |
Описание |
Результат |
|
=СКОС(A2:A11) |
Асимметрия распределения набора данных в диапазоне A2:A11. |
0,359543 |
Нужна дополнительная помощь?
Skewness is a measure of the asymmetry of a dataset or distribution. This value can be positive or negative. It’s useful to know because it helps us understand the shape of a distribution.
A negative skew indicates that the tail is on the left side of the distribution, which extends towards more negative values.
A positive skew indicates that the tail is on the right side of the distribution, which extends towards more positive values.
A value of zero indicates that there is no skewness in the distribution at all, meaning the distribution is perfectly symmetrical. This is unusual and rarely occurs in practice.
Excel offers the following built-in function to calculate the skewness of a distribution:
=SKEW(array of values)
This function uses the following formula to calculate skewness:
Skewness = [n/(n-1)(n-2)] * Σ[(xi–x)/s]3
where:
n = sample size
Σ = fancy symbol that means “sum”
xi = the value of the ith value in the dataset
x = mean
s = standard deviation
The formula is a bit complex, but luckily Excel performs this calculation for you so that you don’t have to do it manually.
Example: Calculating Skewness in Excel
Suppose we have the following dataset that contains the exam scores of 20 students:
We can calculate the skewness of the distribution using =SKEW(A2:A21)
This tells us that the skewness of this dataset is -0.1849. Since this value is negative, we know that the tail of the distribution extends towards the left.
Technical Note:
The SKEW() function will return the error #DIV/0! in the following two scenarios:
- If there are fewer than three data points
- If the sample standard deviation is zero
Additional Resource: Skewness & Kurtosis Calculator
You can also calculate the skewness for a given dataset using the Statology Skewness and Kurtosis Calculator, which automatically calculates both the skewness and kurtosis for a given dataset. You simply enter the raw data values for your dataset into the input box, then click “Calculate.”
For example, here is how to calculate the skewness for the dataset from the example above:
Note that the skewness value from the calculator matches the skewness value that we found in Excel.
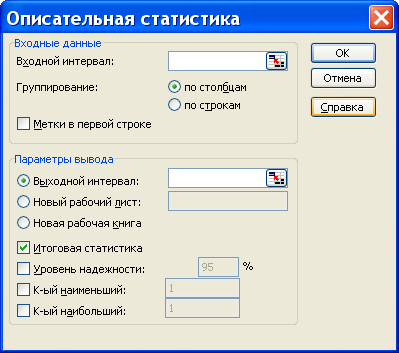
Процедура «Описательные статистики » пакета «Анализ данных.
В процедуре автоматически вычисляются следующие числовые характеристики выборки:
Для того чтобы выполнить вычисления, вводим в поле «Водной интервал» адреса ячеек, в которых записаны выборочные значения;
помечаем «Выходной интервал» и вводим в поле адрес первой ячейки, начиная с которой в листе Excel будет отображён резгультат; помечаем «Итоговая статистика»:
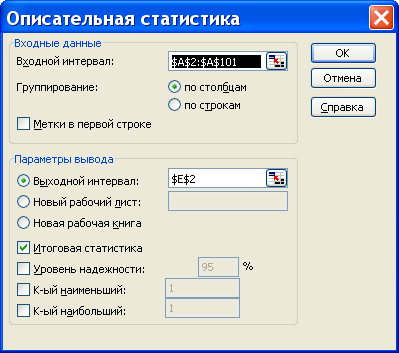
Результаты вычислений процедуры представлены в виде таблицы:
|
Столбец1 |
|
|
Среднее |
120.10 |
|
Стандартная ошибка |
0.22 |
|
Медиана |
120.12 |
|
Мода |
118.69 |
|
Стандартное отклонение |
2.15 |
|
Дисперсия выборки |
4.63 |
|
Эксцесс |
0.21 |
|
Асимметричность |
-0.16 |
|
Интервал |
11.21 |
|
Минимум |
114.46 |
|
Максимум |
125.67 |
|
Сумма |
12010.34 |
|
Счет |
100 |
Здесь: «Асимметричность» – коэффициент асимметрии, «Интервал» – размах варьирования, «Счёт» – объём выборки.
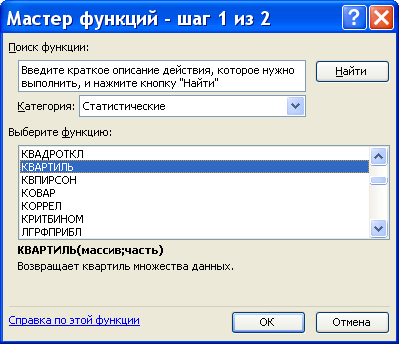
Функция «Квартиль» для вычисления квартилей и межквартильного размаха
КВАРТИЛЬ(массив;часть)
Функция вычисляет (в зависимости от значения параметра «Часть»), выборочные значения верхней квартили («Часть» = 3) или нижней квартили («Часть» = 13), медиану («Часть» = 2) , наибольшее («Часть» = 4) или наименьшее («Часть» = 03) значения для выборки, определённой как «массив»..