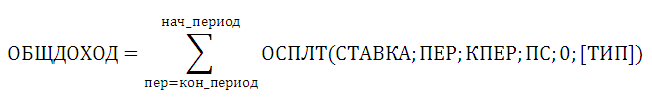Как вычислить долг в excel

Практический пример применения функции Excel «СУММЕСЛИ» при анализе дебиторской задолженности из списка клиентов.

Делаем выбор компаний-контрагентов, объем денежной задолженности, которых превышает сумму издержек, в случае судебного разбирательства.

В условиях рыночной экономики подавляющее число предприятий работают по принципу отсрочки платежа. Как следствие, около девяноста процентов всех фирм непременно сталкиваются с проблемами просроченной дебиторской задолженности. Нередко дело доходит до судебных разбирательств.

При этом общий объем просроченной дебиторской задолженности может быть как незначительным, так и вовсе мизерным. Другими словами, нет особого смысла доводить дело до суда, потому как уровень судебных издержек превышает объем просроченной оплаты.

Сегодня мы будем составлять каталог компаний-неплательщиков, а также определять те предприятия-должники, на которых можно будет подавать в судебные инстанции, рассчитывая на положительный исход дела (при учете выплаты всех набежавших процентов).

Для этого будет использоваться оператор «СУММЕСЛИ» в документе Excel.

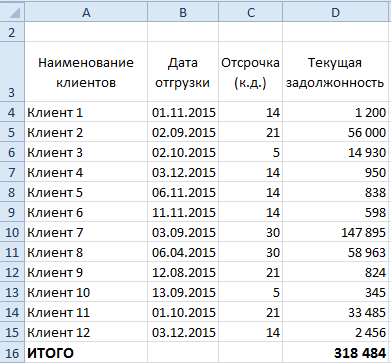
Начинать сортировку контрагентов-должников нужно с того, что в документе Excel создается каталог фирм следующего вида:

Применив пакет информации о времени отгрузки товара (либо поставки услуги) можно вычислить крайний временной срок оплаты по дебиторской задолженности, исходя из представленной отсрочки. Необходимо прибавить число дней предоставленной отсрочки ко дню, когда была произведена физическая поставка продукции.



Дабы можно было добавить количество дней ко времени отгрузки товара в файле Excel, следует выполнить следующий порядок действий.

Вычисление всех просроченных суток

Для начала активируется соответствующая ячейка, после чего в ней же прописывается соответствующая информация (без пробелов), а также производится активация необходимых полей следующим образом:

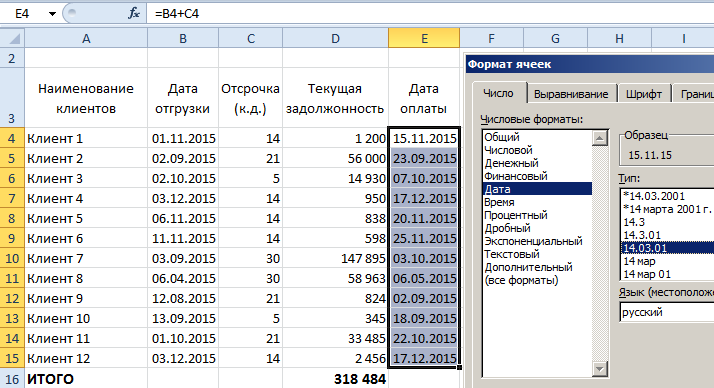
= ДАТА + ЧИСЛО и нажимаем ENTER.

В случае если дата не была отображена в таблице соответствующим образом, следует проверить формат поля, и увериться в том, что он установлен на значении «Дата»:

Если же все действия выполнены правильно, получаем следующее:

Теперь можно приступить к расчету всех просроченных суток. Для этого следует вычесть с текущей даты расчета день последнего срока оплаты дебиторской задолженности.

Быстро и эффективно вычесть в документе Excel из одной даты иную, следует сделать следующее:

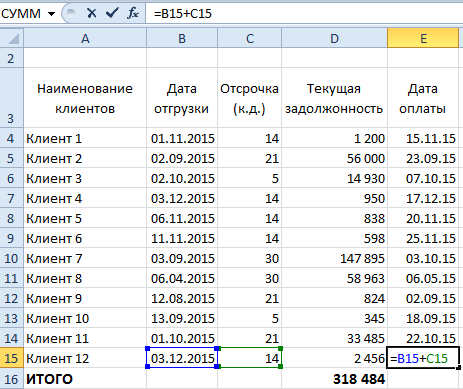
Проводится активация необходимой ячейки, после чего в ней же прописывается (БЕЗ ПРОБЕЛОВ) необходимое число. Также можно произвести активацию ячеек следующим образом:

= ДАТА(1) – ДАТА(2) ENTER.

Если в конечном результате дата отобразилась некорректно, стоит проверить, какой установлен на данной ячейке формат. Если же установлен какой-нибудь другой, отличающийся от «числового», его стоит заменить.

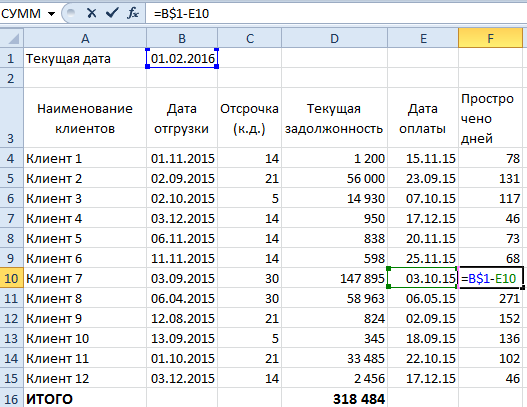
В текущем случае будем ссылаться только на одну и ту же дату, а потому можно воспользоваться абсолютной ссылкой.

Протянув нашу формулу до конца таблицы Excel, мы получим следующее:

Теперь можно приступать к расчету начисленного процентного штрафа за просрочку оплаты.

Расчет пени за все время просрочки

Рассмотрим два возможных варианта:

Ежедневно на сумму просроченной дебиторской задолженности начислялся 0,1 процент в сутки.

Исходим из объема рефинансирования на время расчета (возьмем десять процентов)

Расчет начисленной пени в документе Excel:

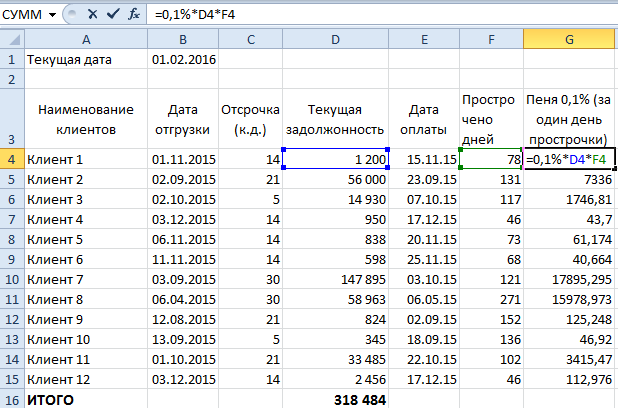
1. Ежедневно на сумму просроченной задолженности начислялось 0,1 процент

Проводим активацию необходимой ячейки в таблице, а также прописываем в ней соответствующие числовые значения (БЕЗ ПРОБЕЛОВ). Проводим активацию следующим образом:

= 0,1 процент х объем просроченной задолженности х число просроченных календарных суток ENTER.

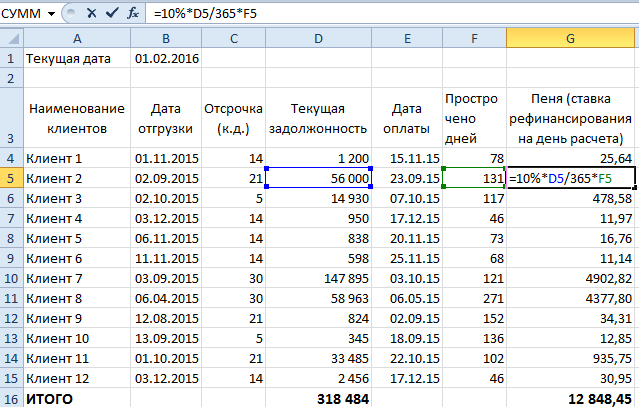
2. Процент рефинансирования на время расчета с контрагентом (десять процентов).

Производим активацию необходимой ячейки в Excel. Можем также активировать требуемые поля следующим способом:

= 10 процентов х Объем задолженности контрагента/365 х Число просроченных календарных дней ENTER.

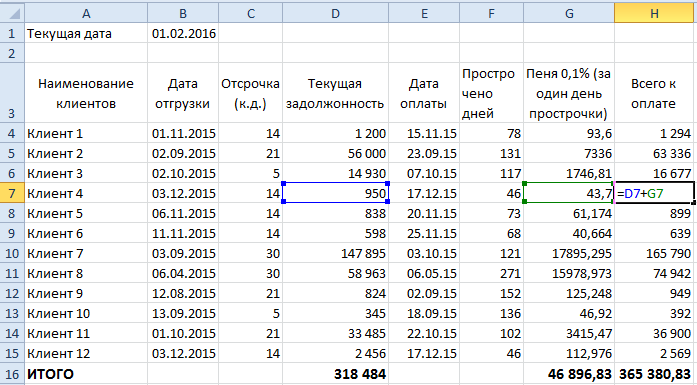
Просуммируем рассчитанный объем набежавшей пени и общую сумму просроченной дебиторской задолженности.

Теперь можно приступить к ранжировке тех предприятий-должников, на которых есть экономический смысл подавать в судебные инстанции.

Логический оператор «СУММЕСЛИ»

Допустим ситуацию, при которой стоимость судебных издержек достигает 950 российских рублей в расчете на одного клиента. Дабы узнать объем денежных средств, на которую можно рассчитывать после положительного завершения судебной тяжбы, используем логический оператор.

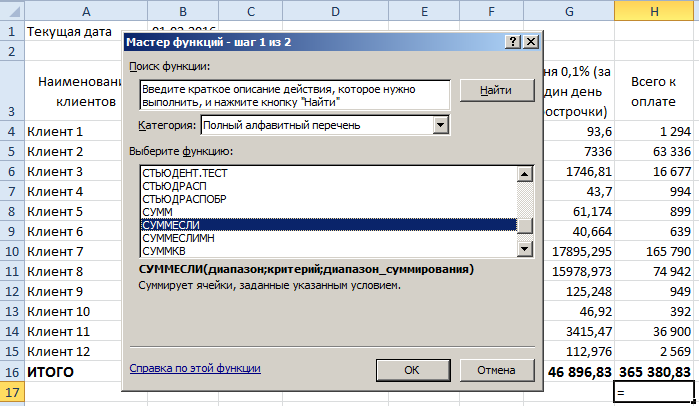
Сделаем активную ячейку, в которой должен быть получен расчет денежных средств. Находим в меню (выделено красным цветом) «Математические» и выбираем «СУММЕСЛИ».

Теперь посмотрим, что нужно указать:

Давайте разбираться по порядку.

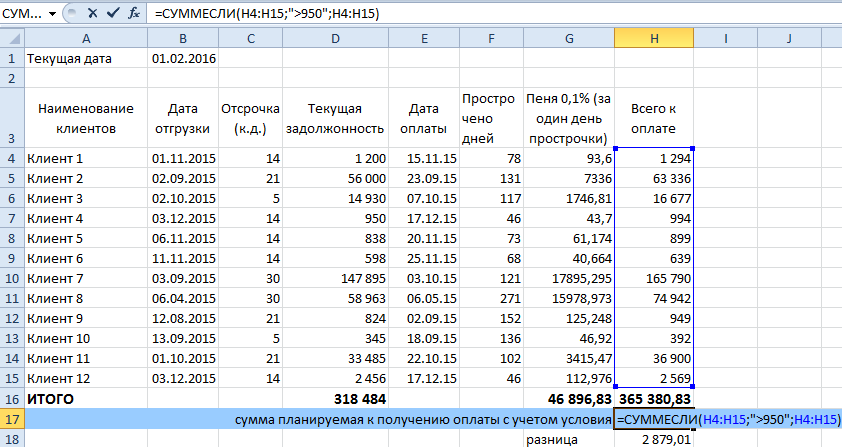
Окно под названием «Диапазон» необходимо с той целью, дабы можно было выбрать сферу значений, среди которых будет произведена необходимая нам выборка. В данном случае, это должна быть вся информация в последнем столбике, помимо итогового объема денежных средств.

Окно «Критерий» необходимо для того, чтобы можно было задать требуемые условия ранжировки. В текущем случае, этот диапазон будет достигать «>950».

«Диапазон суммирования» требуется для установления значений, объем которых нам необходимо рассчитать при учете условия. В частности, окно «Диапазон» будет совпадать с «Диапазон суммирования» по причине того, что нами устанавливается числовое значение, которое имеет прямое отношение исключительно к последнему столбцу.

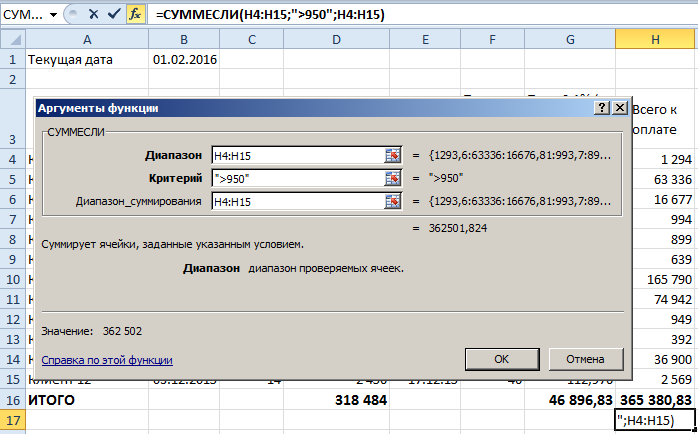
После того как заполнены все поля:

По результату произведенных расчетов, мы получаем общий объем денежных средств, планирующихся к получению при исключении всех компаний-должников, чей объем долга не превышает девятьсот пятьдесят российских рублей (стоимости судебного разбирательства).

Для практической демонстрации возможностей «СУММЕСЛИ» приведем еще одну выборку контрагентов.

В первом приведенном примере «Диапазон суммирования» и «Диапазон» полностью совпали. Теперь же рассмотрим случай, при котором в данных столбцах указываются совершенно иные значения.

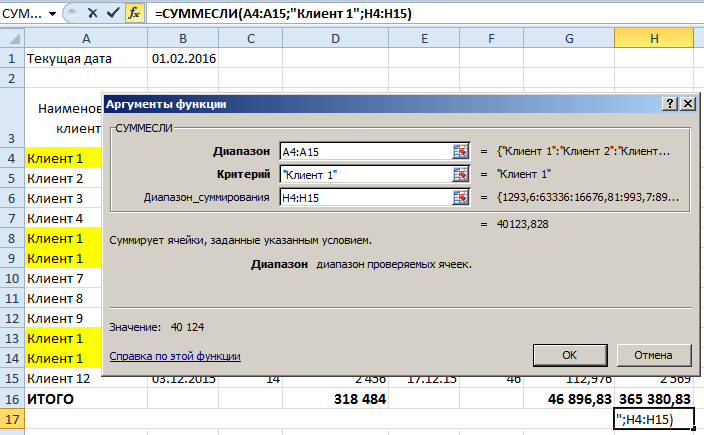
К примеру, наша задача заключается в расчете объема денежного долга только по «Контрагенту №1»

В данном случае, нам следует в окне «Диапазон» проставить значения первого столбца, а в окне «Критерий» вручную прописать «Контрагент №1». Также можно выбрать любую ячейку, которая содержала бы в себе подобные значения.

В окне «Диапазон суммирования» стоит выбрать последний столбец, потому как нам необходимо выбрать дебиторскую задолженность по Контрагенту №1 из общего объема.

Получаем следующий результат:

Как видно из представленного примера, функция Excel «СУММЕСЛИ» располагает широким спектром возможностей, а при правильном использовании может оказать незаменимую помощь для решения многих задач.

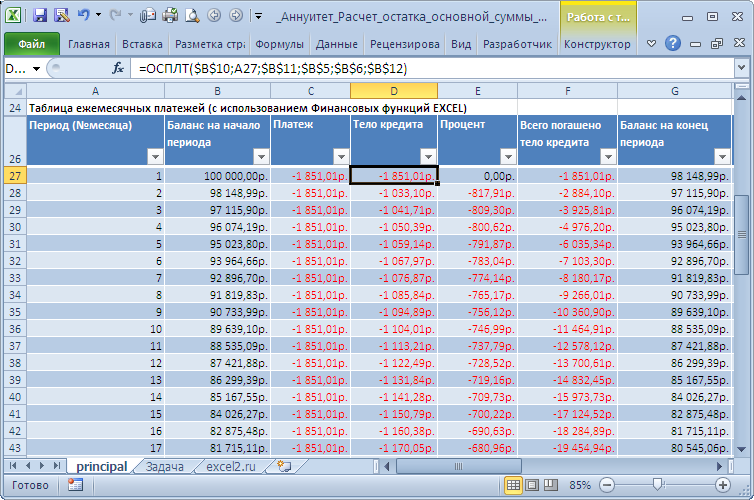
Рассчитаем в MS EXCEL остаток основной суммы долга, который требуется погасить после заданного количества периодов. Выплата кредита производится равными ежемесячными платежами (аннуитетная схема). Процентная ставка и величина платежа — известны, начисление процентов за пользование кредитом – также ежемесячное.

Аннуитетная схема

предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат. В статье

Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)

показано как рассчитать величину регулярной суммы для погашения кредита или ссуды. В данной статье научимся вычислять остаток основной суммы долга, который требуется погасить после заданного количества периодов (а также сумму основного долга, которая была выплачена в промежутке между двумя периодами).

Вычисление остатка суммы основного долга (при БС=0, тип=0)

Пусть был взят кредит в размере 100 000руб. на 10 лет под ставку 9%. Кредит должен гаситься ежемесячными равными платежами (в конце периода). Требуется вычислить сумму основного долга, которая будет выплачена в первом месяце третьего года выплат. Решение простое – используйте функцию ОСПЛТ():

=ОСПЛТ(9%/12;25;10*12;100000)

Ставка за период (ставка): 9%/12 Номер периода (первый месяц третьего года выплат): 25=2*12+1 Всего периодов (кпер): 10*12 Кредит: 100000 Ответ: Сумма основного долга, которая будет выплачена в первом месяце третьего года выплат: -618,26руб.

Теперь выполним те же вычисления, только осмысленно, т.е. понимая, суть расчета.

1. Вычислим ежемесячный платеж, используя формулу

   Приведенной стоимости

   . Обозначим сумму кредита как ПС, ежемесячный платеж как ПЛТ: ПС=ПМТ*(1-(1+ставка)^-кпер)/ставка. Отсюда, ПМТ=ПС* ставка /(1-(1+ставка)^-кпер)=1266,76 (правильность расчета можно проверить с помощью
   
   ПЛТ()
   
   – см.
   
   файл примера, лист Задача
   
   ).
   
   ПЛТ()
   
   вернет -1266,76. Знак минус указывает на различные направления денежных потоков + (из банка сумма кредита), — (в банк ежемесячные платежи). Формула приведенной стоимости является следствием того, что сумма долей ежемесячных платежей, идущих на погашение основной суммы долга, должна быть равна сумме кредита.

Выведем формулу:

1. Доля платежа, которая идет на погашение основной суммы долга в 1-й период =ПМТ-ПС*ставка, а с учетом знаков =-ПМТ-ПС*ставка (чтобы сумма долей была того же знака, что и ПС). Обозначим эту долю как ПС1. ПС*ставка – это сумма процентов, уплаченная за пользование кредитом в первый период.
2. Доля платежа, которая идет на погашение основной суммы долга в 2-й период =-ПМТ-(ПС-ПС1)*ставка=-ПМТ-(ПС +ПМТ+ПС*ставка) *ставка=(-ПМТ-ПС*ставка)*(1+ставка)=ПС1*(1+ставка). Обозначим эту долю как ПС2. ПС-ПС1 – это остаток суммы долга в конце второго периода.
3. Доля платежа, которая идет на погашение основной суммы долга в 3-й период =-ПМТ-(ПС-ПС1-ПС2)*ставка=-ПМТ-(ПС-ПС1)*ставка+ПС2*ставка =ПС2+ПС2*ставка= ПС2*(1+ставка) =ПС1*(1+ставка)^2
4. Очевидно, что доля платежа, которая идет на погашение основной суммы долга в последний период (кпер)= ПС1*(1+ставка)^ кпер =-(ПМТ+ПС*ставка) *(1+ставка)^ кпер
5. Чтобы погасить кредит полностью, необходимо, чтобы сумма долей, идущих на погашение кредита, была равна сумме кредита, т.е. =-(ПМТ+ПС*ставка)*(1-(1+ставка)^ кпер)/ставка=ПС. Эта формула получена как сумма членов геометрической прогрессии: первый член =-(ПМТ+ПС*ставка), знаменатель =(1+ставка).
6. Решая нехитрое уравнение, полученное на предыдущем шаге, получим, что ПС=ПМТ*(1-(1+ставка)^-кпер)/ставка. Это и есть формула приведенной стоимости (при БС=0 и платежах, осуществляемых в конце периода (тип=0)).
1. Вычислим сумму основного долга, которую нужно будет выплатить начиная с 25-го месяца (т.е. в начиная с 25 и заканчивая 120 периодом). Сделаем это используя формулу приведенной стоимости ПС=ПМТ*(1-(1+ставка)^-кпер)/ставка. Теперь ПМТ нам известно, ПС – это искомая сумма основного долга, которую нужно будет выплатить, начиная с 25-го месяца, т.е. за 96 периодов (120-24=кпер). ПС=86466,91 Правильность расчета можно проверить с помощью
   
   ОБЩДОХОД()
   
   .
2. Вычислим сумму процентов, которые будут выплачены в 25-й месяц: 86466,91*ставка=648,50 Правильность расчета можно проверить с помощью
   
   ПРПЛТ()
   
   .
3. Наконец, т.к. каждый платеж содержит сумму, идущую в оплату основной суммы долга и начисленные за период проценты, то Сумму основного долга, которая будет выплачена в первом месяце третьего года выплат получим как: ПМТ-648,50=618,26

Как видим, сумма совпадает результатом

ОСПЛТ()

, вычисленную ранее (с точностью до знака).

Вычисление суммы основного долга, которая была выплачена в промежутке между двумя периодами

Данные расчеты можно сделать несколькими разными способами (см.

файл примера

).

Способ 1. Функция ОБЩДОХОД()

Функция ОБЩДОХОД(ставка; кол_пер; нз; нач_период; кон_период; тип)

возвращает кумулятивную (нарастающим итогом) сумму, выплачиваемую в погашение основной суммы займа в промежутке между двумя периодами (

нач_период и кон_период

).

Примечание

.

Английская версия функции: CUMPRINC(rate, nper, pv, start_period, end_period, type) returns the CUMulative PRincipal paid for an investment period with a Constant interest rate.

Аргументы функции: Ставка — обязательный аргумент. Процентная ставка за период. Кол_пер — обязательный аргумент (кол_пер – это аргумент кпер в других функциях аннуитета, например в ПЛТ()). Общее количество периодов выплат. Нз — обязательный аргумент (нз – это аргумент пс в других функциях аннуитета, например в ПЛТ()). Начальное значение (чаще всего — сумма кредита). Нач_период — обязательный аргумент. Номер первого периода, включенного в вычисления. Нумерация периодов выплат начинается с 1. Кон_период — обязательный аргумент. Номер последнего периода, включенного в вычисления. Тип — обязательный аргумент, определяющий время платежа. Для аннуитета постнумерандо Тип=0, для пренумерандо Тип=1.

Примечание

. Убедитесь, что аргумент «Ставка» соответствуют ставке за период (период не обязательно = году). Например, при ежемесячных выплатах по 4-х летнему займу из расчета 12 процентов годовых используйте значение 12%/12 для аргумента «Ставка». Аргумент «Кол_пер» будет равен 4*12. При ежегодных платежах по тому же займу используйте значение 12% для аргумента «ставка» и 4 — для аргумента «Кол_пер». При ежеквартальных платежах по тому же займу используйте значение 12%/4 для аргумента «ставка» и 4*4 — для аргумента «Кол_пер».

Примечание

. Функция

ОБЩДОХОД()

возвращает значение ошибки #ЧИСЛО! если «Ставка» ≤ 0, «кол_пер» ≤ 0 или «нз» ≤ 0, «нач_период» < 1, «кон_период» < 1 «нач_период» > «кон_период» «тип» является любым числом, отличным от 0 и 1

Примечание

. Функция

ОБЩДОХОД()

возвращает значение ошибки #ЗНАЧ! если для «тип» использованы значения ЛОЖЬ или ИСТИНА.

Альтернативная формула

Из анализа альтернативной формулы ясно, что функция

ОБЩДОХОД()

может использоваться, только если БС=0, т.е. когда предполагается, что по прошествии количества периодов «Кол_пер» займ полностью погашается. Это ограничение можно обойти, записав выражение =ОБЩДОХОД(ставка; кол_пер; нз+БС; нач_период; кон_период; тип)+(нач_период=1)*тип*БС* ставка /(1+ ставка)

Способ 2. Функция ОСПЛТ()

Функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип])

используется для вычисления регулярных сумм идущих на погашение основной суммы долга практически с теми же аргументами, что и

ПЛТ()

.

Примечание

.

Английский вариант функции: PPMT(rate, per, nper, pv, [fv], [type]), т.е. Principal Payment – платеж основной части долга.

Чтобы вычислить сумму основного долга, которая была выплачена в промежутке между двумя периодами, нужно использовать не одну, а несколько функций

ОСПЛТ()

. Например, вычислим сумму долга, выплаченную в 3-м и 4-м периоде: =ОСПЛТ(ставка; 3; кпер; пс; [бс]; [тип])+ОСПЛТ(ставка; 4; кпер; пс; [бс]; [тип])

Чтобы вычислить сумму основного долга, которая была выплачена в промежутке между двумя произвольными периодами нач_период и кон_период используйте формулу: =СУММПРОИЗВ(ОСПЛТ(ставка;СТРОКА(ДВССЫЛ(нач_период&»:»&кон_период)); кпер; пс; [бс]; [тип]))

Выражение СТРОКА(ДВССЫЛ(нач_период&»:»&кон_период)) создает

массив последовательных чисел

, например 2:3:4:5 (если нач_период=2 и кон_период=5). Функция

СУММПРОИЗВ()

суммирует результаты

ОСПЛТ()

, т.е. вышеуказанная формула эквивалентна формуле: =ОСПЛТ(ставка; 2; кпер; пс; [бс]; [тип])+ОСПЛТ(ставка; 3; кпер; пс; [бс]; [тип]) + ОСПЛТ(ставка; 4; кпер; пс; [бс]; [тип])+ОСПЛТ(ставка; 5; кпер; пс; [бс]; [тип])

Способ 3. Вычисление суммы основного долга через Будущую стоимость

Функция БС(ставка; кпер; плт; [пс]; [тип])

возвращает будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки. Подробнее см. статью

Аннуитет. Определяем в MS EXCEL Будущую Стоимость

. Чтобы вычислить сумму основного долга, которая была выплачена в промежутке между двумя произвольными периодами нач_период и кон_период используйте формулу:

=- БС(ставка; кон_период; плт; [пс]; [тип]) /(1+тип *ставка) + БС(ставка; нач_период-1; плт; [пс]; [тип]) /ЕСЛИ(нач_период =1;1; 1+тип *ставка)

В

файле примера

также приведена эквивалентная формула без использования функции

БС()

.

Способ 4. Вычисление суммы основного долга через Приведенную стоимость

Функция ПС(ставка; кпер; плт; [бс]; [тип])

возвращает приведенную (к текущему моменту) стоимость инвестиций. Подробнее см. статью

Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость

. Чтобы вычислить сумму основного долга, которая была выплачена в промежутке между двумя произвольными периодами нач_период и кон_период используйте формулу:

=ПС(ставка; кпер-кон_период; плт; [бс]; [тип]) /(1+тип *ставка) — ПС(ставка; кпер-нач_период+1; плт; [пс]; [тип]) /ЕСЛИ(нач_период =1;1; 1+тип *ставка)

В

файле примера

также приведена эквивалентная формула без использования функции

ПС()

. Чтобы убедиться в идентичности вышеуказанных способов, в файле примера приведен график платежей, рассчитанный на основе функции

ОСПЛТ()

.

a:

В корпоративной оценке, как и в корпоративном учете, для оценки стоимости бизнеса и его способности получать прибыль при выполнении своих финансовых обязательств используются многочисленные показатели. Одним из простейших способов оценить финансовую пригодность компании является расчет ее чистого долга. Чистый долг рассчитывается путем суммирования всех краткосрочных и долгосрочных обязательств компании и вычета ее текущих активов. Эта цифра отражает способность компании выполнять все свои обязательства одновременно, используя только те активы, которые легко ликвидируются.

Краткосрочные обязательства — это те долги, которые должны быть выплачены в течение одного года. Как правило, они состоят из таких предметов, как кредиторская задолженность и счета за поставки и эксплуатационные расходы. Долгосрочные обязательства погашаются в течение более длительного периода, таких как ипотечные кредиты, займы и лизинг капитала. Текущие активы относятся к сумме денег, которую компания имеет в наличии для погашения долгов. Таким образом, текущие активы включают только денежные средства или их эквиваленты, такие как акции, товарные ценные бумаги, дебиторская задолженность и другие ликвидные активы. Вся информация, необходимая для расчета чистого долга, легко доступна на балансе компании.

Чтобы рассчитать чистый долг с помощью Microsoft Excel, проверьте баланс, чтобы найти следующую информацию: общие краткосрочные обязательства, общие долгосрочные обязательства и общие оборотные активы. Введите эти три элемента в ячейки от A1 до A3. В ячейке A4 введите формулу «= A1 + A2-A3», чтобы сделать чистый долг.

Например, предположим, что компания ABC имеет краткосрочные обязательства в размере 10 000 долларов США в операционных расходах и 30 000 долларов США в кредиторской задолженности. Его долгосрочные обязательства состоят из банковского кредита в размере 100 000 долларов США и аренды для оборудования стоимостью 25 000 долларов США. Его текущие активы состоят из 75 000 долларов США наличными и 150 000 долларов США в рыночных активах. В балансовом отчете перечислены промежуточные итоги по этим трем категориям как 40, 000, 125, 000 и 225 000 долларов США соответственно. Используя Excel, бизнес-бухгалтер определяет, что чистый долг составляет $ 40, 000 + $ 125, 000 — $ 225, 000 или — $ 60 000, что указывает на то, что у бизнеса более чем достаточно средств для погашения всех своих обязательств, если все они стали обязательными одновременно.