Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?
Как посчитать отклонение в процентах в Excel
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.
Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки.
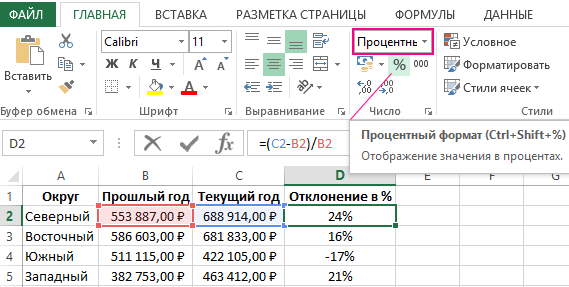
Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2
Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.
Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.
Альтернативная формула для вычисления процента отклонения в Excel
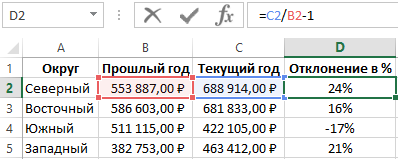
В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.
Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.
Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.
Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.
Как работает стандартное отклонение в Excel

В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику. А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается. В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.
В Excel используются несколько вариантов этой функции отклонения:
- Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
- Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
- Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
- Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.
Математическая теория
Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.
Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!
Для начала нам нужно определить «среднеквадратическое отклонение», что бы в дальнейшем произвести расчёт «стандартного отклонения», в этом нам поможет формула: 
Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так: 
Практическое воплощение в Excel
Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.
Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:
- Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.
Теперь создадим файл примера и на его основе рассмотрим работу этой функции. 
Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4). 


С возрастом желание заработать переходит в желание сэкономить.
Михаил Жванецкий
Как рассчитать процент отклонения факта от плана?
Как посчитать процент отклонения факта от плана?
Расчёт показателей, позволяющих определить, на сколько выполнен план, очень важен.
Если отклонение от плана слишком большое, то это может сильно повлиять на бюджет организации — возникнет необходимость принимать соответствующие меры.
Итак, как найти процент отклонения от плана?
Как известно, отклонение бывает двух видов — абсолютное и относительное.
Абсолютное отклонение представляет собой разницу между 2 показателями (плановым и фактическим, базовым и расчётным). Это числовая величина.
Относительное отклонение — это отношение между 2 показателями в процентах.
Так как речь идёт о проценте отклонения, то будем пользоваться формулой относительного отклонения.
Процент отклонения факта от плана рассчитывается для заданного отчётного периода — месяц, квартал, год.
1) Pi — плановые показатели по продукции / услуге / виду деятельности i.
2) Fi — фактические показатели.
В качестве базового показателя берём план, в качестве текущего показателя — факт.
Отклонение в процентах будет рассчитываться по формуле:
Oo = (Fi / Pi) * 100% — 100%
Другой вид формулы:
Oo = (Fi / Pi — 1) * 100%
Ещё можно воспользоваться такой формулой:
Oo = ((Fi — Pi) / Pi) * 100%
При этом возможны несколько ситуаций:
1) Oo > 0 — план перевыполнен.
2) Oo = 0 — плановые показатели были достигнуты.
Пример
Предприятие работает в целлюлозно-бумажной отрасли. Имеются плановые и фактические показатели по выпуску (в тоннах) различных видов бумаги за 1 квартал 2017 года.
Нужно найти процент отклонения факта от плана.
Для каждого вида продукции делим значения «факт» на значения «план», вычитаем единицу и переводим в проценты.
По 1 и 2 показателю план не выполнен. По 3 показателю план перевыполнен.
По сути, одно из основных направлений в работе экономиста — это планирование, сбор фактической информации и проведение сравнительного анализа для оптимизации расходов предприятия.
Отклонения принято рассчитывать, как абсолютные, так и относительные.
В формулировке вопроса имеется в виду расчёт относительных отклонений.
Относительное отклонение в результате даёт процент отклонения Факта от Плана.
Вообще, на своей практике встречался с двумя вариантами расчёта.
В первом варианте относительное отклонение рассчитывается, как
Результат расчёта можно наблюдать на рисунке ниже.
Полученное отклонение показывает на сколько процентов выполнен План, то есть 100% будет идеальным значением, когда фактические данные будут полностью соответствовать плановым. Если значение меньше 100%, то План недовыполнили, если больше — перевыполнили.
Второй способ расчёта практически отражает первый, только полученное значение вычитается из 100%, то есть формула расчёта относительного отклонения во втором случае будет следующей
100-(Факт/План)*100, либо (План-Факт)/План*100
Результат данного расчёта можно наблюдать также на рисунке ниже.
При данном варианте расчёта мы видим на сколько процентов произошло отклонение от Плана. Таким образом 0% показывает соответствие Факта Плану, отрицательное значение говорит о перевыполнении Плна, а положительное — недовыполнении.
При расчёте Абсолютного отклонения всё гораздо проще.
Таким образом, мы сможем увидеть абсолютное отклонение Факта от Плана. Если значение равно 0, то Факт равен Плану, если получаем положительное значение, то произошло перевыполнение Плана, отрицательное — недовыполнение.
Бывает отставание фактических показателей от плановых, а бывает перевыполнение плана. В обоих случаях требуется рассчитать процент отклонения факта от плана.
Проще всего работать с конкретными цифрами. Например, завод должен был произвести 150 автомобилей, а выпустил 175 шт. На сколько процентов перевыполнен план?
Можно построить пропорцию:
х = 175*100/150 = 116,67%
Процент отклонения факта от нормы 116,67% — 100% = 16,67%
Или сначала посчитаем, что завод выпустил «лишние» 25 авто (175-150),
а потом составляем пропорцию:
у = 25*100 / 150 = 16,67%.
Ещё проще воспользоваться возможностями таблицы excel:
Часто требуется рассчитать процент отклонения факта от плана в excel.
Составляем таблицу, состоящую из 4-х столбиков:
Наименование показателя, план, факт и процент отклонения.
Формула для расчета процента отклонения факта от плана приведена на рисунке выше.
Можно записать как =ОКРУГЛ(B3/A3*100;2) или =ОКРУГЛ(B3/A3*100-10 0;2)
В зависимости от того, какие вам показатели нужны, абсолютные или относительные.
Если у нас есть таблица, в которой занесены все данные, т.е. прописан определенный показатель, и даны исходные данный (в виде план и факт), тогда высчитать процент отклонения не составит труда.
Не стоит забывать, что отклонение есть абсолютное и относительное.
Мы высчитывает относительное отклонение, подставляя данные в формулу
Факт :(делим) на План х(умножаем) 100%
Чтобы было более понятно приведем пример. Для этого найдем таблицу:
Высчитываем первый показатель «Товарная продукция»
936,5 : 982,1 х 100% = 0,95 х 100% = 95%
Получается, что план был не выполнен в полном объеме, так как показатель менее 100%.
Если после высчитывания получится 100%, значит план полностью выполнен.
А если будет более 100%, значит перевыполнен.
Так как вопрос о проценте отклонения, то речь идет об относительном отклонении факта от плана, но мы посчитаем в нашем примере и абсолютное отклонение.
Допустим, мы запланировали выпустить в 2018 году 120 единиц продукции, а выпустили фактически — 130 единиц. Процент отклонения факта от плана считается так: факт поделить на план, умножить на 100, и вычесть из полученного результата 100.
Считаем: 130 / 120 = 1,083, умножаем на 100, получается 108,3, вычитаем 100 = 8,3 %
Отклонение равно 8,3 %. Так как мы получили положительный результат, то речь идет о перевыполнении плана на 8,3 процентов, если бы результат был отрицательным, то план был бы недовыполнен. Абсолютное же отклонение считается вообще очень просто — от факта отнимается план, в нашем случае это 130-120 = 10 единиц продукции, план перевыполнен на 10 единиц продукции.
С этим вопросом сталкиваются экономисты многих предприятий, особенно когда нужно предоставить начальству расчет. Лучше всего рассмотреть на примере:
Например, нам нужно выпустить 1000 единиц продукции, но по факту предприятие выпустило 900 единиц продукции. Чтобы узнать насколько выполнен план, необходимо будет фактическое значение на планируемое значение и умножить на 100 процентов.
Итак, получаем 900/1000*100 = 90%. Значит план был выполнен только на девяносто процентов.
В данном примере, который представлен в ответе выше, предприятие не смогло выполнить план на десять процентов.
Такие задачки лучше всего решать в Экселе.
Для того, чтобы понимать на сколько процентов отличается факт от плана нужно воспользоваться простой формулой рассчёта, которая представлена ниже:
(Ф ÷ П) • 100, где в формуле
Рассмотрим на примере для большей наглядности.
Фабрика по пошиву одежды должна была сшить по плану 300 рабочих комбинезонов, но за отведенный срок сшили всего 250 комбинезонов. Производим рассчёт.
250 ÷ 300 = 0,83 • 100 = 83,33 %
Получается, что план не был выполнен на 100 %, а лишь 83,33 %.
Поменяем значения в задаче: П = 250, Ф = 300.
300 ÷ 250 = 1,2 • 100 = 120 %.
Получается, что план был перевыполнен на 20 %.
Посчитать процент отклонения не так и сложно.
Чтобы было проще можно объяснить на примере.
Производство должно было выпустить за одни месяц 200 000 книг, а выпустили только 180000.
Факт делим на план и умножаем на 100%.
Теперь высчитываем 100%-90%=10% — наш план не выполнили на 10%, это и есть показатель недовыполнения.
Теперь посчитаем, если мы план перевыполнили.
План составляет 200000 книжек, мы выпустили 210000.
Таким образом перевыполнение плана равняется 5%.
Почему-то проценты у многих вызывают сложности. Много раз наблюдал, как на уроках даже те, у кого с остальными темами все в порядке, столкнувшись с процентами и долями начинают «буксовать». И почему-то у учителей не получалось понять, из-за чего тема процентов вызывает такие проблемы и как её объяснять. Впрочем, непонимание процентов выражается хотя бы в распространенных выражениях типа «это гарантировано на 120%» или «я выложился на 200%». Прежде всего очень важно осознать, что 100% — это основа, норма. 100% — это всё, что есть или должно быть. То есть нельзя гарантировать что-то больше, чем на 100%, и нельзя усилий приложить на 200%, так как все ваши возможные усилия и гарантии составляют эту основу, эти 100%.
В примере про план и факт за план берется 100%. Это — наша основа, норма, и нам надо понять, насколько этот план выполнен. В случае с планом может быть и 98%, и 134%, так как технически можно выпустить больше продукции, чем запланировано.
Чтобы узнать, насколько выполнен план, нам необходимо знать цифры плана и факта и сравнить их. Из этих цирф делаем два простых и понятных уравнения:
Со школы в наших головах должно было отпечататься, что такие системы составляются в одно уравнение крест-накрест, то есть мы берем диагонали: (план) и (Х) и (факт) и (100%):
Посчитать отклонение в Excel
Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Для его нахождения производятся довольно сложные расчеты. Инструменты Microsoft Excel позволяют значительно облегчить их для пользователя.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…) = СТАНДОТКЛОН.Г(Число1;Число2;…) = СТАНДОТКЛОН.В(Число1;Число2;…)
-
Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Урок: Формула среднего квадратичного отклонения в Excel
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция — СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
Урок: Как посчитать среднее значение в Excel
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
-
Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
-
Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Как посчитать проценты в Excel
Мы сталкиваемся с процентами не только на работе или учебе, но и в нашей повседневной жизни – скидки, чаевые, депозитные ставки, кредиты и прочее. Поэтому умение работать с процентами будет полезно в разных сферах жизни. В этой статье мы ближе познакомимся с процентами, и рассмотрим, как быстро посчитать проценты в Excel, а также на примерах разберем следующие вопросы:
- как посчитать проценты в Excel формула;
- как посчитать процент от числа в Excel;
- как посчитать проценты от суммы в Excel;
- посчитать разницу в процентах Excel;
Как посчитать проценты в Excel формула
Прежде чем перейти к вопросу подсчета процентов в Excel, давайте вспомним основные знания о процентах. Процент – это сотая часть единицы. Из школьной программы вы наверняка знаете, что для того чтобы посчитать проценты, необходимо разделить искомую часть на целое и умножить на 100. Таким образом формула расчёта процентов выглядит следующим образом:
Посчитать проценты в Excel намного проще, так как вычисление некоторых математических операций в Excel происходит автоматически. Поэтому формула расчета процентов в Excel преобразуется следующим образом:
Для того чтобы посчитать проценты в Excel нет необходимости умножать результат на 100, если для ячейки используется Процентный формат.
Рассмотрим наглядный пример, как посчитать процент выполнения плана в Excel. Пусть у нас есть таблица с данными о запланированном объеме реализации продукции и фактическом объеме.
Как посчитать проценты в Excel – Исходные данные для расчета процентов
Для того чтобы посчитать процент выполнения плана необходимо:
- В ячейке D2 ввести формулу =C2/B2 и скопировать ее в остальные ячейки с помощью маркера заполнения.
- На вкладке « Главная » в группе « Число » выбрать «Процентный формат» для отображения результатов в формате процентов.
В результате мы получаем значения, округленные до целых чисел, которые показывают процент выполнения плана:
Как посчитать проценты в Excel – Процент выполнения плана
Следует отметить, что универсальной формулы, как посчитать проценты нет. Все зависит от того, что вы хотите получить в результате. Поэтому в этой статье мы рассмотрим примеры формул вычисления процента от числа, от общей суммы, прироста в процентах и многое другое.
Как посчитать процент от числа в Excel
Для того, чтобы посчитать процент от числа, необходимо использовать следующую формулу:
Рассмотрим пример расчета процента от числа. У нас есть таблица со стоимостью товаров без НДС и ставкой НДС для каждого товара.
Как посчитать проценты в Excel – Исходные данные для расчета процента от числа
Примечание : если вы вручную вводите в ячейке числовое значение и после него ставите знак %, то Excel применяет к данной ячейке процентный формат и воспринимает это число как его сотую часть. Например, если в ячейку ввести 18%, то для расчётов Excel будет использовать значение 0,18.
Пусть нам необходимо рассчитать НДС и стоимость продуктов с налогом на добавленную стоимость.
- Для того чтобы посчитать НДС в денежном эквиваленте, т.е. посчитать процент от числа в ячейке D2 вводим формулу =B2*C2 и заполняем остальные ячейки.
- В ячейке E2 суммируем ячейки B2 и D2 , для того чтобы получить стоимость с НДС.
В результате получаем следующие данные расчета процента от числа:
Как посчитать проценты в Excel – Процент от числа в Excel
Как посчитать проценты от суммы в Excel
Рассмотрим пример, когда нам необходимо посчитать проценты от суммы по каждой позиции. Пусть у нас есть таблица продаж некоторых видов продуктов с итоговой суммой. Нам необходимо посчитать проценты от суммы по каждому виду товара, то есть посчитать в процентном соотношении сколько выручки приносит каждый товар от общей суммы.
Как посчитать проценты в Excel – Исходные данные для расчета процентов от суммы
Для этого проделываем следующее:
- В ячейке C2 вводим следующую формулу: =B2/$B$9 . Для ячейки B9 мы используем абсолютную ссылку (со знаками $), чтобы она была неизменной, а для ячейки B2 – относительную, чтобы она изменялась при копировании формулы в другие ячейки.
- Используя маркер заполнения копируем эту формулу расчета процентов от суммы для всех значений.
- Для отображения результатов в формате процентов, на вкладке « Главная » в группе « Число », задаем «Процентный формат» с двумя знаками после запятой.
В результате мы получаем следующие значения процентов от суммы:
Как посчитать проценты в Excel – Проценты от суммы в Excel
Посчитать разницу в процентах Excel
Для того чтобы посчитать разницу в процентах, необходимо использовать следующую формулу:
где А – старое значение, а B – новое.
Рассмотрим пример, как посчитать разницу в процентах. Пусть у нас есть данные о продажах за два года. Нам необходимо определить процентное изменение продаж в отчетном году, по сравнению с предыдущим.
Как посчитать проценты в Excel – Исходные данные для расчета разницы в процентах
Итак приступим к расчетам процентов:
- В ячейке D2 вводим формулу =(C2-B2)/B2 .
- Копируем формулу в остальные ячейки, используя маркер заполнения.
- Применяем процентный формат для результирующих ячеек.
В результате у нас получается следующая таблица:
Как посчитать проценты в Excel – Вычисление разницы в процентах
В нашем примере положительные данные показывают прирост в процентах, а отрицательные значения – уменьшение в процентах.
Теперь вы знаете, как посчитать проценты в Excel, например, как посчитать процент от числа, проценты от общей суммы и прирост в процентах.
Как посчитать процент отклонения в Excel по двум формулам
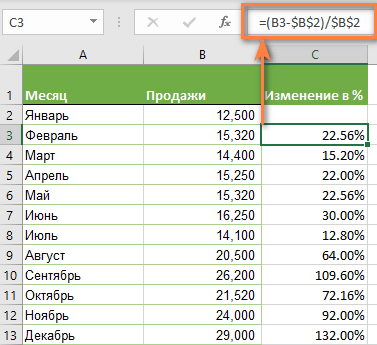
Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?
Как посчитать отклонение в процентах в Excel
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.
Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки.
Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2
Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.
Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.
Альтернативная формула для вычисления процента отклонения в Excel
В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.
Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.
Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.
Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.
Skip to content
В этом руководстве вы познакомитесь с быстрым способом расчета процентов в Excel, найдете базовую формулу процента и еще несколько формул для расчета процентного изменения, процента от общей суммы и т.д.
Расчет процента нужен во многих ситуациях, будь то комиссия продавца, ваш подоходный налог или процентная ставка по кредиту. Допустим, вам посчастливилось получить скидку 25% на новый телевизор. Это хорошая сделка? И сколько в итоге придется заплатить?
Сейчас мы рассмотрим несколько методов, которые помогут вам эффективно вычислять процент в Excel, а также освоим основные формулы процента, которые избавят вас от догадок при расчетах.
- Базовая формула подсчета процента от числа.
- Как посчитать процент между числами по колонкам.
- Как рассчитать процент по строкам.
- Доля в процентах.
- Считаем процент скидки
- Отклонение в процентах для отрицательных чисел
- Вычитание процентов
- Как избежать ошибки деления на ноль
Что такое процент?
Как вы, наверное, помните из школьного урока математики, процент — это доля от 100, которая вычисляется путем деления двух чисел и умножения результата на 100.
Основная процентная формула выглядит следующим образом:
(Часть / Целое) * 100% = Процент
Например, если у вас было 20 яблок и вы подарили 5 своим друзьям, сколько вы дали в процентном отношении? Проведя несложный подсчет =5/20*100% , вы получите ответ — 25%.
Так обычно рассчитывают проценты в школе и в повседневной жизни. Вычислить процентное соотношение в Microsoft Excel еще проще, поскольку он выполняет некоторые операции за вас автоматически.
К сожалению, универсальной формулы расчета процентов в Excel, которая охватывала бы все возможные случаи, не существует. Если вы спросите кого-нибудь: «Какую формулу процентов вы используете, чтобы получить желаемый результат?», Скорее всего, вы получите ответ типа: «Это зависит от того, какой именно результат вы хотите получить».
Итак, позвольте мне показать вам несколько простых формул для расчета процентов в Excel.
Расчет процентов в Excel.
Основная формула для расчета процента от числа в Excel такая же, как и во всех сферах жизни:
Часть / Целое = Процент
Если вы сравните ее с основной математической формулой для процента, которую мы указали чуть выше, то заметите, что в формуле процента в Excel отсутствует часть * 100. При вычислении процента в Excel вам совершенно не обязательно умножать полученную дробь на 100, поскольку программа делает это автоматически, когда процентный формат применяется к ячейке.
И если в Экселе вы будете вводить формулу с процентами, то можно не переводить в уме проценты в десятичные дроби и не делить величину процента на 100. Просто укажите число со знаком %.
То есть, чтобы, к примеру, посчитать 10% в Экселе, то вместо =A1*0,1 или =A1*10/100, просто запишите формулу процентов =A1*10%.
Хотя с точки зрения математики все 3 варианта возможны и все они дадут верный результат.
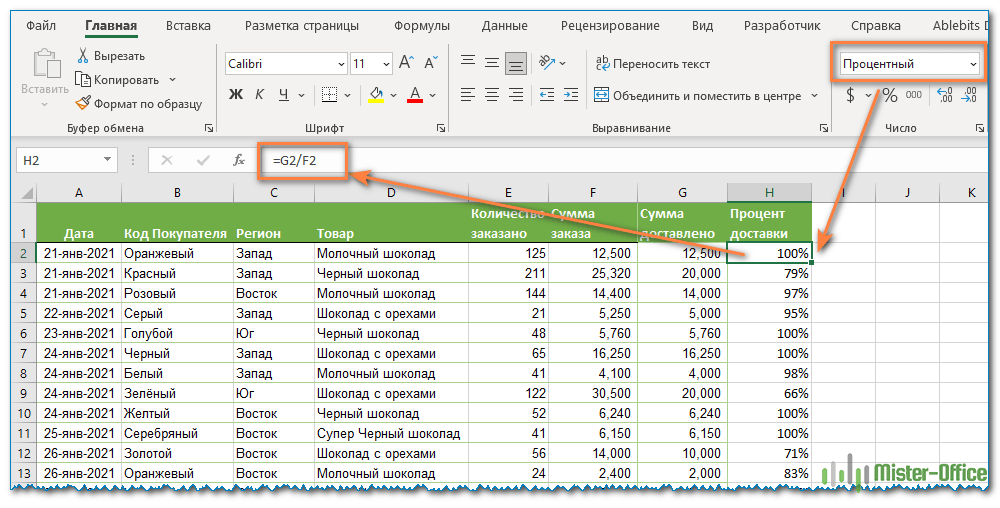
А теперь давайте посмотрим, как можно использовать формулу процента в Excel для реальных данных. Предположим, в вашей таблице Эксель записана сумма заказанных товаров в столбце F и оставленных товаров в столбце G. Чтобы высчитать процент доставленных товаров, выполните следующие действия:
- Введите формулу =G2/F2 в ячейку H2 и скопируйте ее на столько строк вниз, сколько вам нужно.
- Нажмите кнопку «Процентный стиль» ( меню «Главная» > группа «Число»), чтобы отобразить полученные десятичные дроби в виде процентов.
- Не забудьте при необходимости увеличить количество десятичных знаков в полученном результате.
- Готово!
Такая же последовательность шагов должна быть выполнена при использовании любой другой формулы процентов в Excel.
На скриншоте ниже вы видите округленный процент доставленных товаров без десятичных знаков.
Чтобы определить процент доставки, мы сумму доставленных товаров делим на сумму заказов. И используем в ячейке процентный формат, при необходимости показываем десятичные знаки.
Запишите формулу в самую верхнюю ячейку столбца с расчетами, а затем протащите маркер автозаполнения вниз по столбцу. Таким образом, мы посчитали процент во всём столбце.
Как найти процент между числами из двух колонок?
Предположим, у нас имеются данные о продажах шоколада за 2 месяца. Необходимо определить, какие произошли изменения в реализации. Проще и нагляднее всего отклонения в продажах выразить в процентах.
Чтобы вычислить разницу в процентах между значениями A и B, используйте следующую формулу:
Процентное изменение = (B — A) / A
При применении этой формулы к реальным данным важно правильно определить, какое значение равно A, а какое — B. Например, вчера у вас было 80 яблок, а сейчас — 100. Это означает, что теперь у вас на 20 яблок больше, чем раньше, что произошло увеличение на 25%. Если у вас было 100 яблок, а теперь – 90, то количество яблок у вас уменьшилось на 10, то есть на 10%.
Учитывая вышеизложенное, наша формула Excel для процентного изменения принимает следующую форму:
=(новое_значение – старое_значение)/старое_значение
А теперь давайте посмотрим, как вы можете использовать эту формулу процентного изменения в своих таблицах.
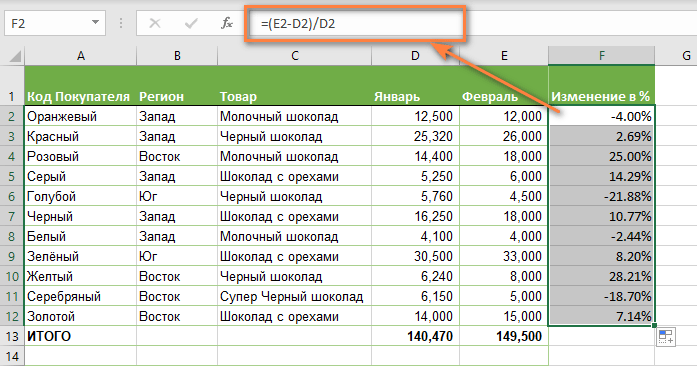
В нашем случае —
=(E2-D2)/D2
Эта формула процентного изменения вычисляет процентное увеличение (либо уменьшение) в феврале (столбец E) по сравнению с январём (столбец В).
И затем при помощи маркера заполнения копируем ее вниз по столбцу. Не забудьте применить процентный формат.
Отрицательные проценты, естественно, означают снижение продаж, а положительные — их рост.
Аналогичным образом можно подсчитать и процент изменения цен за какой-то период времени.
Как найти процент между числами из двух строк?
Такой расчет применяется? Если у нас есть много данных об изменении какого-то показателя. И мы хотим проследить, как с течением времени изменялась его величина. Поясним на примере.
Предположим, у нас есть данные о продажах шоколада за 12 месяцев. Нужно проследить, как изменялась реализация от месяца к месяцу. Цифры в столбце С показывают, на сколько процентов в большую или меньшую сторону изменялись продажи в текущем месяце по сравнению с предшествующим.
Обратите внимание, что первую ячейку С2 оставляем пустой, поскольку январь просто не с чем сравнивать.
В С3 записываем формулу:
=(B3-B2)/B2
Можно также использовать и другой вариант:
=B3/B2 — 1
Копируем содержимое этой ячейки вниз по столбцу до конца таблицы.
Если нам нужно сравнивать продажи каждого месяца не с предшествующим, а с каким-то базисным периодом (например, с январём текущего года), то немного изменим нашу формулу, использовав абсолютную ссылку на цифру продаж января:
Абсолютная ссылка на $B$2 останется неизменной при копировании формулы в C4 и ниже:
=(B3-$B$2)/$B$2
А ссылка на B3 будет изменяться на B4, B5 и т.д.
Напомню, что по умолчанию результаты отображаются в виде десятичных чисел. Чтобы отобразить проценты , примените к столбцу процентный формат. Для этого нажмите соответствующую кнопку на ленте меню или используйте комбинацию клавиш Ctrl + Shift + %.
Десятичное число автоматически отображается в процентах, поэтому вам не нужно умножать его на 100.
Расчет доли в процентах (удельного веса).
Давайте рассмотрим несколько примеров, которые помогут вам быстро вычислить долю в процентах от общей суммы в Excel для различных наборов данных.
Пример 1. Сумма находится в конце таблицы в определенной ячейке.
Очень распространенный сценарий — это когда у вас есть итог в одной ячейке в конце таблицы. В этом случае формула будет аналогична той, которую мы только что обсудили. С той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (со знаком $). Знак доллара фиксирует ссылку на итоговую ячейку, чтобы она не менялась при копировании формулы по столбцу.
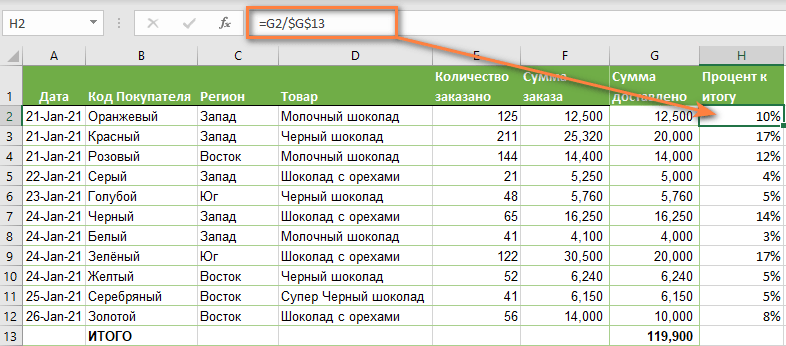
Возьмем данные о продажах шоколада и рассчитаем долю (процент) каждого покупателя в общем итоге продаж. Мы можем использовать следующую формулу для вычисления процентов от общей суммы:
=G2/$G$13
Вы используете относительную ссылку на ячейку для ячейки G2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца G. Но вы вводите $G$13 как абсолютную ссылку, потому что вы хотите оставить знаменатель фиксированным на G13, когда будете копировать формулу до строки 12.
Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.
На скриншоте ниже показаны результаты, возвращаемые формулой. Столбец «Процент к итогу» отформатирован с применением процентного формата.
Пример 2. Часть итоговой суммы находится в нескольких строках.
В приведенном выше примере предположим, что у вас в таблице есть несколько записей для одного и того же товара, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного товара.
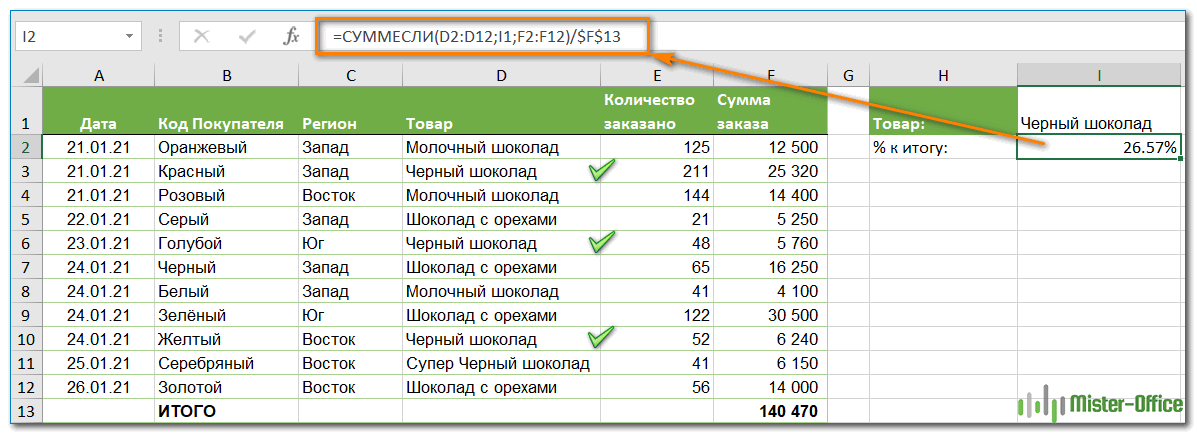
В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному товару, а затем разделить это число на общую сумму заказов:
=СУММЕСЛИ( диапазон; критерий; диапазон_суммирования ) / Итог
Учитывая, что столбец D содержит все наименования товаров, столбец F перечисляет соответствующие суммы, ячейка I1 содержит наименование, которое нас интересует, а общая сумма находится в ячейке F13, ваш расчет может выглядеть примерно так:
=СУММЕСЛИ(D2:D12;I1;F2:F12)/$F$13
Естественно, вы можете указать название товара прямо в формуле, например:
=СУММЕСЛИ(D2:D12;”Черный шоколад”;F2:F12)/$F$13
Но это не совсем правильно, поскольку эту формулу придется часто корректировать. А это затратно по времени и чревато ошибками.
Если вы хотите узнать, какую часть общей суммы составляют несколько различных товаров, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на итоговую сумму. Например, по следующей формуле рассчитывается доля черного и супер черного шоколада:
=(СУММЕСЛИ(D2:D12;”Черный шоколад”;F2:F12)/$F$13 + =СУММЕСЛИ(D2:D12;”Супер черный шоколад”;F2:F12)) / $F$13
Естественно, текстовые наименования товаров лучше заменить ссылками на соответствующие ячейки.
Для получения дополнительной информации о функции суммирования по условию ознакомьтесь со следующими руководствами:
- Как использовать функцию СУММЕСЛИ в Excel
- СУММЕСЛИМН и СУММЕСЛИ в Excel с несколькими критериями
Процент скидки
Формулы процентов пригодятся для расчета уровня скидки. Итак, отправляясь за покупками, помните следующее:
Скидка в % = (цена со скидкой – обычная цена) / обычная цена
Скидка в % = цена со скидкой / обычная цена — 1
В результатах вычисления процент скидки отображается как отрицательное значение, поскольку новая цена со скидкой меньше старой обычной цены. Чтобы вывести результат в виде положительного числа , оберните формулы в функцию ABS. Например:
=ABS((C2-B2)/B2)
или
=ABS((C2/B2 — 1)
Так будет гораздо привычнее.
Как рассчитать отклонение в процентах для отрицательных чисел
Если некоторые из исходных значений представлены отрицательными числами, приведенные выше формулы не будут работать.
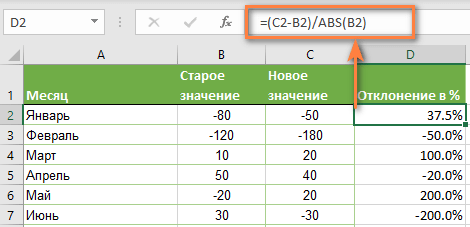
Обычный обходной путь — сделать знаменатель в формуле положительным числом. Для этого воспользуйтесь функцией ABS:
( Новое_значение – старое_значение ) / ABS( старое_значение )
Со старым значением в B2 и новым значением в C2 формула выглядит следующим образом:
=(C2-B2)/ABS(B2)
Как видите, достаточно корректно работает с самыми разными комбинациями положительных и отрицательных чисел.
Положительный процент означает рост, отрицательный — снижение величины показателя.
Вычитание процентов.
Часто случается, что вам известен процент скидки на товар. И вам нужно высчитать, какой процент от первоначальной стоимости придётся заплатить. Как мы уже говорили, процент в Экселе — это обычное число. Поэтому и правила вычисления здесь – как с обычными числами.
Формула расчета в Excel будет выглядеть так:
=1 – процент_скидки
Как обычно, не забываем про процентный формат ячеек.
Предотвратить ошибки деления на ноль #ДЕЛ/0
Если вы хотите посчитать процент от числа в таблице, и ваш набор данных содержит несколько нулевых значений, заключите формулы в функцию ЕСЛИОШИБКА, чтобы предотвратить появление ошибок деления на ноль (#ДЕЛ/0! или #DIV/0!).
=IFERROR(=ЕСЛИОШИБКА((C2-B2)/B2;0)
=IFERROR(=ЕСЛИОШИБКА(C2/B2-1;0)
Вот как можно вычислить процент от числа в Excel. И даже если работа с процентами никогда не была вашим любимым видом математики, с помощью этих основных процентных формул вы можете заставить Excel делать работу за вас.
На сегодня все, спасибо, что прочитали!
Содержание материала
- Как посчитать относительно отклонение?
- Как вычислить стандартное отклонение в Excel?
- Среднеквадратическое отклонение
- Как рассчитать отклонение показателей?
- Абсолютное отклонение
- Отклонение в процентах при отрицательных величинах
- Как посчитать отклонение от среднего?
- Селективное отклонение
- Как рассчитать процент выполнения плана?
Как посчитать относительно отклонение?
А относительное отклонение — соотношение тех же показателей друг к другу, только выраженное в процентах. Показатели текущего периода надо разделить на показатели базового периода и умножить на 100. Так мы получаем в процентах относительное отклонение.
Метод 3 Вычисление стандартного отклонения
- Поставьте курсор в ячейку ниже последнего введенного значения. Вы также можете вычислить стандартное отклонение в любой другой пустой ячейке электронной таблицы Excel. …
- Введите знак равенства. …
- Наберите «СТАНДОТКЛОН». …
- Укажите диапазон данных. …
- Нажмите кнопку «Enter «.
19 окт. 2018 г.
Среднеквадратическое отклонение
Для превращения дисперсии в логично понятные баллы, килограммы или доллары используется среднеквадратическое отклонение, которое представляет собой квадратный корень из дисперсии. Давайте вычислим его для нашего примера:
S = sqrt(D) = sqrt(2,78) = 1,667
Мы получили баллы и теперь можем использовать их для связки с математически ожиданием. Наиболее вероятный результат выстрела в этом случае будет выражен как 7,75 плюс-минус 1,667. Этого достаточно для ответа, но так же мы можем сказать, что практически наверняка стрелок попадет в область мишени между 6,08 и 9,41.
Стандартное отклонение или сигма — информативный показатель, иллюстрирующий разброс величины относительно ее центра. Чем больше сигма, тем больший разброс демонстрирует выборка. Это хорошо изученный коэффициент и для нормального распределения известно занимательное правило трех сигм. Установлено, что 99,7 % значений нормально распределенной величины лежат в области плюс-минус трех сигм от среднего арифметического.
Как рассчитать отклонение показателей?
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%.
Абсолютное отклонение
Как рассчитать абсолютное отклонение? Абсолютным отклонением можно назвать разницу, получаемую при вычитании одной величины из другой, этот способ является выражением сложившихся положений вещей между плановым и фактическим параметрами.
Известно, что определенную проблему обычно вызывает такой показатель, как знак абсолютного отклонения. Обычно считается, что отклонение, которое позитивно сказывается на прибыли предприятия, считается положительным, и в вычислениях его ставят со знаком «+». Что же касается банальной математики, такой подход считается не совсем корректным, а это, в свою очередь, вызывает конфликты и разногласия среди специалистов. Исходя из этого, на практике вычисления абсолютного отклонения зачастую пользуются не базовой экономической, а математической моделью. Математическая модель заключается в том, что повышение фактического оборота в сравнении с запланированным обозначается знаком «+», а уменьшение фактических издержек в сравнении с плановыми обозначается знаком «-«.
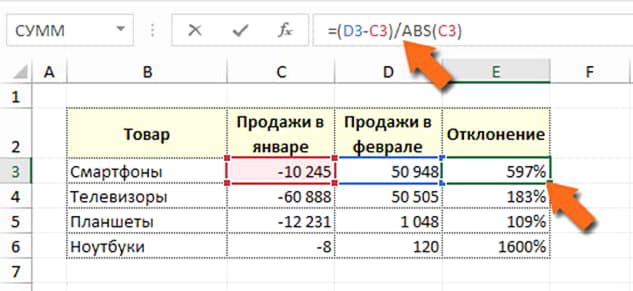
Отклонение в процентах при отрицательных величинах
Что будет с изменением прибыли, если какие-то товары имеют отрицательное старое значение? Пусть в нашем примере в январе мы продавали в убыток и прибыль была негативной. А ведь это не такой уж и редкий случай!
Фактически, прибыль выросла, а по расчётам – нет. Исправим формулу, нужно знаменатель взять по модулю (отбросить знак минус). Это распространенный подход, многие его используют. Применим функцию ABS, которая возвращает модуль числа:
Проблема исправлена, этими результатами можно пользоваться. Однако, хочу вас предостеречь. Результаты могут быть недостаточно корректными. Взгляните на картинку еще раз. Прибыль от смартфонов выросла на 60 тысяч, и это 597%. А прибыль от телевизоров – на 110 тысяч, и это лишь 183%. Я использую такие результаты лишь для поверхностной оценки. Или можно не выводить отклонение для таких случаев.
Как посчитать отклонение от среднего?
Вычисление стандартного отклонения
- вычисляем среднее арифметическое выборки данных
- отнимаем это среднее от каждого элемента выборки
- все полученные разницы возводим в квадрат
- суммируем все полученные квадраты
- делим полученную сумму на количество элементов в выборке (или на n-1, если n>30)
12 авг. 2020 г.
Селективное отклонение
Как рассчитать отклонение такого рода? Этот способ расчета отклонения подразумевает сравнение контролируемых величин на определенном промежутке времени, это может быть такой показатель времени, как квартал или месяц, иногда даже это бывает день. Сравнивание интересующих нас величин за определенный промежуток времени (к примеру, месяц, давайте возьмем май) текущего года с тем же маем предыдущего года может дать нам более информативное сравнение с предыдущим месяцем, который рассматривается в плановом периоде.
Селективное отклонение актуальны для фирм, которые занимаются поставкой сезонных услуг. Далее будут описаны еще несколько видов отклонений, знание которых может существенно облегчить вашу жизнь.
Как рассчитать процент выполнения плана?
Для того, чтобы рассчитать процент выполнения плана, нужно воспользоваться формулой: %плана = (факт / план) * 100%. Эти показатели могут быть выражены как в количественных, так и в стоимостных единицах, а также складываться из нескольких компонентов.
Теги
Содержание
- Как высчитать стандартный показатель? Как посчитать отклонение в процентах в Excel
- Среднеквадратическое отклонение Excel. Расчет среднего квадратичного отклонения в Microsoft Excel
- Определение среднего квадратичного отклонения
- Расчет в Excel
- Способ 1: мастер функций
- Способ 2: вкладка «Формулы»
- Способ 3: ручной ввод формулы
- Стандартное отклонение онлайн. CFA — Дисперсия и стандартное отклонение.
- Дисперсия генеральной совокупности.
- Формула дисперсии генеральной совокупности.
- Стандартное отклонение генеральной совокупности.
- Формула стандартного отклонения генеральной совокупности.
- Пример расчета стандартного отклонения для генеральной совокупности.
- Чем отличается Дисперсия от стандартного отклонения. Что такое Дисперсия и стандартное отклонение? — 2020
- Строительство Дисперсии
- Дисперсия и стандартное отклонение
- Коэффициент вариации
- Состав работников промышленного предприятия n
Как высчитать стандартный показатель? Как посчитать отклонение в процентах в Excel
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.
Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки .
Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2
Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.
Среднеквадратическое отклонение Excel. Расчет среднего квадратичного отклонения в Microsoft Excel
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Расчет в Excel
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию» , расположенную слева от строки функций.
- В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г . В списке имеется также функция СТАНДОТКЛОН , но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK» .
- Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK» .
- Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы» .
- Выделяем ячейку для вывода результата и переходим во вкладку «Формулы» .
- В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции» . Из появившегося списка выбираем пункт «Статистические» . В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
- После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
- Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)или=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).Всего можно записать при необходимости до 255 аргументов.
- После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Мы рады, что смогли помочь Вам в решении проблемы.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Стандартное отклонение онлайн. CFA — Дисперсия и стандартное отклонение.
Рассмотрим дисперсию и стандартное отклонение, — две наиболее широко используемые меры дисперсии для анализа финансовых данных, — в рамках изучения количественных методов по программе CFA.
(см. начало)
Среднее абсолютное отклонение позволяет решить проблему, заключающуюся в том, что сумма отклонений от среднего равна нулю. Для этого при расчете среднего используется абсолютное значение отклонений .
Второй подход к расчету отклонений состоит в их возведении в квадрат.
Дисперсия и стандартное отклонение, основанные на квадрате отклонений, являются двумя наиболее широко используемыми мерами дисперсии:
- Дисперсия определяется как среднее квадратов отклонений от среднего значения.
- Стандартное отклонение — это положительный квадратный корень дисперсии.
Далее обсуждается расчет и использования дисперсии и стандартного отклонения.
Дисперсия генеральной совокупности.
Если нам известен каждый элемент генеральной совокупности, мы можем вычислить дисперсию генеральной совокупности или просто дисперсию (англ. ‘population variance’) .
Она обозначается символом σ2и представляет собой среднее арифметическое квадратов отклонений от среднего значения.
Формула дисперсии генеральной совокупности.
(mathbf{ sigma^2 = { sum_{i=1}^{N} ( X_i — mu )^2 over N } }) (формула 11) ,
где μ — это среднее генеральной совокупности, а N — размер генеральной совокупности.
Зная среднее значение μ, мы можем использовать Формулу 11 для вычисления суммы квадратов отклонений от среднего с учетом всех N элементов в генеральной совокупности, а затем для определения среднего квадратов отклонений путем деления этой суммы на N.
Независимо от того, является ли отклонение от среднего положительным или отрицательным, возведение в квадрат этой разности дает положительное число.
Таким образом, дисперсия решает проблему отрицательных отклонений от среднего значения, устраняя их посредством операции возведения в квадрат этих отклонений.
Рассмотрим пример.
Прибыль в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год составляла 0.9%, 1.6% и 3.5% соответственно. Мы рассчитали среднюю прибыль в процентах от выручки как 2.0%.
Следовательно, дисперсия прибыли в процентах от выручки составляет:
Стандартное отклонение генеральной совокупности.
Поскольку дисперсия измеряется в квадратах, нам нужен способ вернуться к исходным единицам. Мы можем решить эту проблему, используя стандартное отклонение, т.е. квадратный корень из дисперсии.
Стандартное отклонение легче интерпретировать, чем дисперсию, поскольку стандартное отклонение выражается в той же единице измерения, что и наблюдения.
Формула стандартного отклонения генеральной совокупности.
Стандартное отклонение генеральной совокупности (или просто стандартное отклонение, а также среднеквадратическое отклонение, от англ. ‘population standard deviation’) , определяемое как положительный квадратный корень из дисперсии генеральной совокупности, составляет:
(mathbf{ sigma = sqrt{sum_{i=1}^{N} ( X_i — mu )^2 over N} }) (формула 12),
где μ — это среднее генеральной совокупности, а N — размер генеральной совокупности.
Используя пример прибыли в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год, в соответствии с Формулой 12, мы вычислим дисперсию 1.21, а затем возьмем квадратный корень: ( sqrt{1.21} ) = 1.10.
Как дисперсия, так и стандартное отклонение являются примерами параметров распределения . В последующих чтениях мы введем понятие дисперсии и стандартного отклонения как меры риска.
Занимаясь инвестициями, мы часто не знаем среднего значения интересующей совокупности, обычно потому, что мы не можем практически идентифицировать или провести измерения для каждого элемента генеральной совокупности.
Поэтому мы рассчитываем среднее значение по генеральной совокупности и среднее выборки, взятой из совокупности, и вычисляем выборочную дисперсию или стандартное отклонение выборки, используя формулы, немного отличающиеся от Формул 11 и 12 .
Мы обсудим эти вычисления далее.
Однако в инвестициях у нас иногда есть определенная группа, которую мы можем считать генеральной совокупностью. Для четко определенных групп наблюдений мы используем Формулы 11 и 12 , как в следующем примере.
Пример расчета стандартного отклонения для генеральной совокупности.
В Таблице 20 представлен годовой оборот портфеля из 12 фондов акций США, которые вошли в список Forbes Magazine Honor Roll 2013 года.
Журнал Forbes ежегодно выбирает американские взаимные фонды, отвечающие определенным критериям для своего почетного списка Honor Roll.
Критериями являются:
- сохранение капитала (эффективность на медвежьем рынке),
- непрерывность управления (у фонда должен управлять менеджер непрерывно, в течение не менее 6 лет), диверсификация портфелей,
Оборачиваемость или оборот портфеля , показатель торговой активности, является меньшим значением из стоимости продаж или покупок за год, деленным на среднюю чистую стоимость активов за год. Количество и состав списка Forbes Honor Roll меняются из года в год.
Чем отличается Дисперсия от стандартного отклонения. Что такое Дисперсия и стандартное отклонение? — 2020
Table of Contents:
Когда мы измеряем изменчивость набора данных, есть две тесно связанные статистики, связанные с этим: дисперсия и стандартное отклонение, которые оба указывают, насколько разбросаны значения данных, и включают в себя аналогичные этапы при их расчете. Однако основное различие между этими двумя статистическими анализами заключается в том, что стандартное отклонение является квадратным корнем из дисперсии.
Чтобы понять различия между этими двумя наблюдениями статистического разброса, необходимо сначала понять, что представляет каждое из них: Разница представляет все точки данных в наборе и рассчитывается путем усреднения квадрата отклонения каждого среднего значения, тогда как стандартное отклонение является мерой разброса вокруг среднего, когда центральная тенденция рассчитывается через среднее.
В результате дисперсия может быть выражена как среднеквадратичное отклонение значений от среднего значения или квадратное отклонение среднего значения, деленное на число наблюдений, а стандартное отклонение может быть выражено как квадратный корень из дисперсии.
Строительство Дисперсии
Чтобы полностью понять разницу между этими статистическими данными, нам нужно понять расчет дисперсии. Шаги для расчета выборочной дисперсии следующие:
- Рассчитать среднее значение выборки данных.
- Найдите разницу между средним и каждым из значений данных.
- Урегулируйте эти различия.
- Добавьте квадратичные различия вместе.
- Разделите эту сумму на единицу меньше, чем общее количество значений данных.
Причины каждого из этих шагов следующие:
- Среднее значение обеспечивает центральную точку или среднее значение данных.
- Отличия от среднего значения помогают определить отклонения от этого среднего. Значения данных, которые далеки от среднего, будут давать большее отклонение, чем значения, близкие к среднему.
- Различия возводятся в квадрат, потому что, если различия добавляются без возведения в квадрат, эта сумма будет равна нулю.
- Сложение этих квадратов отклонений обеспечивает измерение общего отклонения.
- Деление на единицу меньше размера выборки дает своего рода среднее отклонение. Это сводит на нет эффект наличия множества точек данных, каждая из которых вносит вклад в измерение разброса.
Как указывалось ранее, стандартное отклонение просто рассчитывается путем нахождения квадратного корня этого результата, который обеспечивает абсолютный стандарт отклонения независимо от общего числа значений данных.
Дисперсия и стандартное отклонение
Когда мы рассматриваем дисперсию, мы понимаем, что есть один существенный недостаток ее использования. Когда мы следуем шагам вычисления дисперсии, это показывает, что дисперсия измеряется в единицах квадрата, потому что мы добавили квадратные различия в нашем расчете. Например, если наши выборочные данные измеряются в метрах, то единицы для дисперсии будут даны в квадратных метрах.
Чтобы стандартизировать нашу меру разброса, нам нужно взять квадратный корень из дисперсии. Это устранит проблему квадратов и даст нам меру разброса, которая будет иметь те же единицы, что и наша исходная выборка.
Есть много формул в математической статистике, которые имеют более привлекательные формы, когда мы формулируем их в терминах дисперсии вместо стандартного отклонения.
Коэффициент вариации
Недостатков,
свойственных дисперсии и среднеквадратическому
отклонению, лишен ( ).
Этот коэффициент представляет процентное
отношение среднеквадратического
отклонения к среднему арифметическому =.
Арифметически отношение и нивелирует влияние абсолютной величины
этих характеристик, а процентное
соотношение делает коэффициент вариации
величиной не именованной. Кроме того,
этот коэффициент позволяет оценивать
вариабельность (разброс) признака в
нормированных границах. Если его значение
не превышает 10% , то можно говорить о
слабом разбросе. Если коэффициент
вариации находится в пределах 10-20% ,
разброс средний, если превышает 20%, то
разброс вариант считают большим. Отличие
коэффициента вариации от других критериев
разброса наглядно демонстрирует :
Состав работников промышленного предприятия n
На
основании приведенных в примере
статистических характеристик можно
сделать вывод об относительной
однородности возрастного состава и
образовательного уровня работников
предприятия, при низкой профессиональной
устойчивости обследованного контингента.
Нетрудно заметить, что попытка судить
об этих социальных тенденциях по
среднеквадратическому отклонению,
привела бы к ошибочному заключению, а
попытка сравнения учетных признаков
«стаж работы» и «возраст» с учетным
признаком образование вообще была бы
некорректной из-за разнородности этих
признаков.
В
некоторых видах распределений
среднеквадратическое отклонение и
дисперсия ( )
отсутствуют или не могут служить
характеристиками рассеяния вариант по
другим причинам. В частности, указанное
обстоятельство может быть связано с
тем, что и вычисляются по отклонениям от среднего
арифметического, которое не вычисляется
в открытых вариационных рядах и в рядах
распределений качественных признаков.
Поэтому для сжатого описания такого
рода распределений используется другой
параметр разброса – (синонимы
«перцентиль», «персентиль»), пригодный
для статистического описания качественных
и количественных признаков при любой
форме их распределения. Этот параметр
может использоваться и для перевода
количественных признаков в качественные.
В этом случае качественные оценки
присваиваются в зависимости от того,
какому по порядку квантилю соответствует
та или иная конкретная варианта. Особым
свойством квантилей является их полная
независимость от конкретных значений
каждой, отдельно взятой единицы
наблюдения. Значение имеет только
порядковый номер, место расположение
этой единицы в ряду распределения.