Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ПРОЦПЛАТ в Microsoft Excel.
Описание
Вычисляет проценты, уплаченные (или полученные) за указанный период займа (или инвестиции) с даже основными выплатами.
Синтаксис
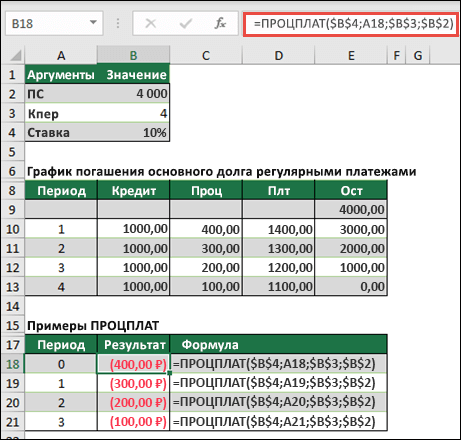
ПРОЦПЛАТ(ставка;период;кпер;пс)
Аргументы функции ПРОЦПЛАТ описаны ниже.
|
Аргумент |
Описание |
|---|---|
|
Ставка |
Обязательный. Процентная ставка для инвестиции. |
|
Период |
— обязательный аргумент. Период, для которого вы хотите найти проценты и должен находиться в промежутке от 1 до «Кпер». |
|
Кпер |
Обязательный. Общее число периодов выплат для данной инвестиции. |
|
Пс |
Обязательный. Стоимость инвестиции на текущий момент. Для займа Пс — это сумма займа. |
Замечания
-
Убедитесь, что единицы, которые используются для указания rate и Nper, согласованы. При ежемесячных выплатах по четырехлетнему займу под 12 процентов годовых используйте 12/12 для платы «Ставка» и 4*12 — для «Кпер». При ежегодных выплатах по одному и том же займу используйте 12% для платы «Ставка» и 4 для «Кпер».
-
Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются в виде отрицательных чисел, а получаемые (например, дивиденды) — в виде положительных.
-
IsPMT подсчитывают каждый период, начиная с нуля, а не с одного.
-
В большинстве из них используется календарный план с даже периодическими выплатами. Функция IPMT возвращает выплату процентов за данный период для этого типа займа.
-
В некоторых из них используется календарный план с даже основными платежами. Функция ISPMT возвращает выплату процентов за данный период для этого типа займа.
-
Для иллюстрации в приведенной ниже таблице амортизации используется порядок нулевую оплату. Сумма процентов за каждый период равна ставке, равной времени неоплаченного остатка за предыдущий период. Выплата за каждый период равна 1-й основной сумме и проценту за период.
Пример
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
ПРПЛТ
Функция ПС
Нужна дополнительная помощь?
SharePoint Server 2019 SharePoint Server 2016 SharePoint Server 2013 SharePoint Server 2013 Enterprise SharePoint в Microsoft 365 SharePoint Foundation 2010 SharePoint Server 2010 SharePoint Server 2007 SharePoint в Microsoft 365 для малого бизнеса Windows SharePoint Services 3.0 Еще…Меньше
Примечание:
Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим
ссылку на оригинал (на английском языке)
.
Вычисляет проценты, выплачиваемые за определенный инвестиционный период.
Синтаксис
ПРОЦПЛАТ(ставка;период;кпер;пс)
Ставка — процентная ставка для инвестиции.
Период — период, для которого требуется найти прибыль; число в интервале от 1 до «кпер».
Кпер — общее число периодов выплат для данной инвестиции.
Пс — стоимость инвестиции на текущий момент. Для займа пс — это сумма займа.
Замечания
-
Убедитесь, что единицы измерения, выбранные для аргументов «ставка» и «кпер», соответствуют друг другу. При ежемесячных выплатах по четырехгодичному займу из расчета 12 процентов годовых используйте значение 12%/12 для аргумента «ставка» и 4*12 — для аргумента «кпер». При ежегодных платежах по тому же займу используйте значение 12% для аргумента «ставка» и 4 — для аргумента «кпер».
-
Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются в виде отрицательных чисел, а получаемые (например, дивиденды) — в виде положительных.
-
Дополнительные сведения о финансовых функциях см. в описании функции ПС.
Примеры
Чтобы получить месячную процентную ставку в первом примере, разделите годовую ставку на 12. Чтобы узнать количество выплат, умножьте количество лет кредита на 12.
|
R |
Период |
Кпер |
ПС |
Формула |
Описание (результат) |
|
10% |
1 |
15 |
8000000 |
=ПРОЦПЛАТ([Ставка]/12;[Период];[Кол_пер]*12;[ПС]) |
Сумма первого из ежемесячных платежей за кредит на приведенных условиях (-64814,8) |
|
10% |
1 |
15 |
8000000 |
=ПРОЦПЛАТ(([Ставка],1,[Кол_пер],[ПС]) |
Сумма процентов, выплаченных в первом году за кредит на приведенных выше условиях (-533333) |
Нужна дополнительная помощь?

Вам приходилось брать кредит в банке? Тогда эта статья для Вас. При оценке и анализе вариантов займов необходимо получить конечные значения (а сколько же придется заплатить?) для разных наборов исходных данных (в данном случае процентных ставок). Одним из преимуществ табличного процессора MS Excel является возможность быстрого решения подобных задач и автоматического перерасчета результатов при изменении исходных данных. Допустим вы планируете какой-либо проект и для этого берете кредит в банке. В какой срок лучше отдать кредит, какие процентные ставки выбрать? Для решения подобных задач в MS Excel применяется Таблица подстановки. Использование этого средства MS Excel происходит таким образом.
Возможные значения одного или двух аргументов функций необходимо представить в виде списка или таблицы. Для одного аргумента список исходных значений задается в виде строки или столбца таблицы. MS Excel представляет эти значения в формулу (функцию), заданную пользователем, а потом подставляет результаты в соответствующую строку или столбец.
При использовании таблицы с двумя переменными значения одной из них располагаются в колонке, другой – в столбце, а результат расчета по одной или нескольким формулам, и таблицу для двух переменных, содержащую расчеты для одной формулы.
В этой статье рассмотрим таблицу подстановки для одной переменной. Таблицу с двумя переменными значениями смотрите в следующей статье.
Допустим, Вы берете кредит в 100 тысяч рублей, сроком на 5 лет и определяете ежемесячные выплаты при различных процентных ставках.
Для решения этой задачи используется Таблица подстановки MS Excel. Сначала записываем исходные данные – сумму займа, срок, процентная ставка согласно рисунка.
В ячейку D7 вводим формулу периодических постоянных выплат по займу при условии, что сумму необходимо погасить в течении срока займа: = ПЛТ (C4/12;C3*12;C2)
Процентную ставку делим на 12 в случае ежемесячных платежей и формат ячейки выбираем процентный – процентная ставка в этом случае записывается т.о.: 12% – 0,0125 – формат ячейки – процентный.
Кпер – число периодов выплат. Если период в годах, то для вычисления ежемесячных выплат умножаем на 12.
Пс – указываем сумму, которую берем взаймы (в нашем случае – это 100000).
Бс и Тип – необязательные параметры. Бс – будущая стоимость или баланс наличности, который нужно достичь после последней выплаты; принимается равной 0, если значение не указано. Тип – логическое значение (0 или 1), обозначающее, должна ли производится выплата в конце периода или в начале периода.

Выполните команду Данные – Анализ “что если” – Таблица данных. На экране появится диалоговое окно Таблица данных. (см.рис). Это окно используется для задания рабочей ячейки, на которую ссылается формула расчета. В нашем примере это ячейка С4, которую необходимо указать в поле Подставлять значения по строкам в:.
Если исходные данные расположены в столбце, то ссылку на рабочую ячейку необходимо ввести в поле Подставлять значения по столбцам в:. После нажатия кнопкиОК программа заполнит колонку результатами. Полученные числа имеют знак “-”.
Допустим, что вам захотелось определить, какая часть платежа идет на погашение процента по кредиту, а какая – проценты по кредиту. Для этого в следующий столбец, в ячейку Е7 необходимо ввести формулу: = ПРОЦПЛАТ (C4/12;1;C3*12;C2) (см.рис).
Затем опять выполните команду Данные – Анализ “что если” – Таблица данных, предварительно выделив необходимый диапазон ячеек. После нажатия кнопки ОКпоявляется таблица Плата по процентам за 1 мес. (см.рис). Если вас не испугают эти цифры, то можете смело отправляться в банк за ссудой.

Функция ПРОЦПЛАТ вычисляет проценты, выплачиваемые за определенный инвестиционный период. Эта функция обеспечивает совместимость с Lotus 1-2-3.
Описание функции ПРОЦПЛАТ
Вычисляет проценты, выплачиваемые за определенный инвестиционный период. Эта функция обеспечивает совместимость с Lotus 1-2-3.
Синтаксис
=ПРОЦПЛАТ(ставка; период; кпер; пс)Аргументы
ставкапериодкперпс
Обязательный. Процентная ставка для инвестиции.
Обязательный. Период, для которого требуется найти проценты; число в интервале от 1 до «кпер».
Обязательный. Общее число периодов выплат для данной инвестиции.
Обязательный. Стоимость инвестиции на текущий момент. Для займа «пс» представляет собой сумму займа.
Замечания
- Убедитесь, что единицы измерения, выбранные для аргументов «ставка» и «кпер», соответствуют друг другу. При ежемесячных выплатах по четырехгодичному займу из расчета 12 процентов годовых используйте значение 12%/12 для аргумента «ставка» и 4*12 — для аргумента «кпер». При ежегодных платежах по тому же займу используйте значение 12% для аргумента «ставка» и 4 — для аргумента «кпер».
- Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются в виде отрицательных чисел, а получаемые (например, дивиденды) — в виде положительных.
- Дополнительные сведения о финансовых функциях см. в описании функции ПС.
Пример
В этом учебном материале вы узнаете, как использовать Excel функцию ПРОЦПЛАТ с синтаксисом и примерами.
Описание
Microsoft Excel функция ПРОЦПЛАТ возвращает процентные платежи по инвестициям на основе процентной ставки и постоянного графика платежей. Эта функция была создана для обратной совместимости с Lotus 1-2-3.
Функция ПРОЦПЛАТ — это встроенная в Excel функция, которая относится к категории финансовых функций.
Её можно использовать как функцию рабочего листа (WS) в Excel.
Как функцию рабочего листа, функцию ПРОЦПЛАТ можно ввести как часть формулы в ячейку рабочего листа.
Синтаксис
Синтаксис функции ПРОЦПЛАТ в Microsoft Excel:
ПРОЦПЛАТ(ставка;период;кпер;пс)
Аргументы или параметры
- ставка
- Процентная ставка для инвестиций.
- период
- Период для расчета процентная ставка. Это должно быть значение от 1 до
кпер. - кпер
- Количество выплат аннуитета.
- пс
- Сумма кредита или приведенная стоимость платежей.
Возвращаемое значение
Функция ПРОЦПЛАТ возвращает числовое значение.
Применение
- Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000
Тип функции
- Функция рабочего листа (WS)
Пример (как функция рабочего листа)
Рассмотрим несколько примеров функции ПРОЦПЛАТ, чтобы понять, как использовать Excel функцию ПРОЦПЛАТ как функцию рабочего листа в Microsoft Excel:
Первый пример возвращает процентную выплату по инвестициям в размере $5000, которые приносят 7,5 % годовых на 2 года. Выплата процентов рассчитана за 8-й месяц.
|
=ПРОЦПЛАТ(7.5%/12; 8; 2*12; 5000) Результат: —20.83333333 |
В следующем примере возвращается процентная ставка для инвестиций в размере $8000, приносящих 6% годовых в течение 4 лет. Выплата процентов рассчитывается за 30-ю неделю.
|
=ПРОЦПЛАТ(6%/52; 30; 4*52; 8000) Результат: —7.899408284 |
В следующем примере возвращается выплата процентов по инвестициям в размере $6500, которые приносят 5,25% годовых в течение 10 лет. Выплата процентов рассчитана на 4-й год.
|
=ПРОЦПЛАТ(5.25%/1; 4; 10*1; 6500) Результат: —204.75 |
Расчет процентной ставки
Функция СТАВКА используется для
расчета процентной ставки, которая в
зависимости от ситуации может быть либо
нормой прибыли, либо процентом кредита.
Функция СТАВКА вычисляется методом
последовательных приближений и может
не иметь решения или иметь несколько
решений. Если после 20 итераций погрешность
определения ставки превышает 10-6,
то функция НОРМА возвращает значение
ошибки “#ЧИСЛО!”.
Вызов функции СТАВКА имеет следующий
общий синтаксис:
СТАВКА (Кпер;Плт;Пс;Бс;Тип;Предположение),
где Предположение — предполагаемая
величина процентной ставки (необязательный
аргумент). Если этот аргумент опущен,
то величина процентной ставки полагается
равной 10%. Если функцияСТАВКА не
сходится, следует попытаться использовать
различные значенияПредположение
(обычно между 0 и 1).
Задача №13. Фирме потребуется 1
млн р. через 2 года. Руководство фирмы
готово вложить 50 тыс. р. сразу и по 25 тыс.
р. каждый последующий месяц, чтобы
получить необходимую сумму в конце
второго года. Какой должна быть минимальная
годовая процентная ставка, чтобы фирма
достигла своей цели?
Решение. Для решения задачи необходимо
использовать формулу следующего вида:
=12*СТАВКА(2*12;-25000;-50000;1000000)
В результате будет получено значение
годовой процентной ставки приблизительно
равное 39,36%.
Рис. 11 Расчет значения процентной ставки
с помощью функции СТАВКА
Задача №14. Предположим, что
фирма отказалась от ежемесячных выплат
(см. задачу №13) и готова сегодня положить
на депозит 400 тыс. р. Определить, как в
этом случае изменится минимальная
годовая процентная ставка.
Решение. Для решения задачи необходимо
использовать формулу следующего вида:
=12*СТАВКА(2*12;;-400000;1000000)
В результате будет получено значение
годовой процентной ставки равное 46,7%.
Расчет периодических платежей
Ниже рассмотрены три функции Excel,
обеспечивающие расчеты величин, связанных
с периодическими выплатами:
ПЛТ — вычисление фиксированной
величины периодических платежей,
осуществляемых на основе постоянной
процентной ставки;
ПРОЦПЛАТ — вычисление величины
платежа по процентам за конкретный
период;
ОСПЛТ — вычисление величины основного
платежа за конкретный период. Величина
основного платежа получается как
разность между фиксированным периодическим
платежом и платежом по процентам за
конкретный период.
Вызов функции ПЛТ имеет следующий
общий синтаксис:
ПЛТ(Ставка;Кпер;Пс;Бс;Тип)
Задача №15. Необходимо накопить
4000 р. за три года, откладывая постоянную
сумму в конце каждого месяца. Какой
должна быть эта сумма, если процентная
ставка по вкладу составляет 12% годовых?
Решение. Для решения задачи необходимо
использовать вызов функцииПЛТследующего вида:
ПЛТ (Ставка;Кпер; ;Бс)
Для конкретных значений, заданных в
условии задачи, соответствующая формула
имеет вид
=ПЛТ(12%/12;3*12;;4000)
В результате будет получена величина
периодического платежа равная -92,82 р.
(знак “минус” показывает направление
потока платежей, т.е. вложение денег в
банк).
Рис. 12 Расчет величины постоянного
платежа с помощью функции ПЛТ
Задача №16. Определить текущую
стоимость обязательных ежемесячных
платежей, чтобы погасить ссуду в 100 тыс.
рублей в течение 5 лет, если процентная
ставка составляет 12% годовых.
Вызов функции ПРОЦПЛАТ имеет
следующий общий синтаксис:
ПРОЦПЛАТ(Ставка;Период;Кпер;Пс)
Задача №17. В начале года банк выдал
клиенту ссуду 80 тыс. р. на срок 3 года под
10% годовых с обязательством ежемесячного
погашения части долга.
Определить величины платежей по процентам
за первый и за предпоследний месяцы
срока погашения ссуды.
Решение. В данном случае используется
функцияПРОЦПЛАТ следующего вида:
ПРОЦПЛАТ(Норма;Период;Кпер;Пс)
Для конкретных значений, заданных в
условии задачи, соответствующая формула
имеет вид:
= ПРОЦПЛАТ(10%/12;1;12*3;80000)
= ПРОЦПЛАТ(10%/12;35;12*3;80000)
Окончательное решение задачи представлено
на рис. 13.
Рис. 13 Расчет величины платежей по
процентам за первый и предпоследний
месяцы срока погашения ссуды
Задача №18. В начале года банк
выдал клиенту кредит в сумме 150 000
руб. на срок 5 лет под 19% годовых с
обязательством ежеквартального погашения
части долга.
Определить величину платежей по процентам
за первый и за предпоследний кварталы
срока погашения кредита.
Вызов функции ОСПЛТ имеет следующий
общий синтаксис:
ОСПЛТ(Ставка;Период;Кпер;Пс;Бс;Тип)
Задача №19. Сделан займ 70 тыс. р.
на срок 3 года под 17% годовых. Рассчитать
размер основных выплат по займу за
каждый год.
Решение. Для значений, заданных в
условии задачи, соответствующие формулы
имеют вид
=ОСПЛТ(17%;1;3;70000)
= ОСПЛТ(17%;2;3;70000)
= ОСПЛТ(17%;3;3;70000)
Окончательное решение задачи представлено
на рис. 14.
Рис. 14 Расчет величины основного платежа
по займу
Задача №20. Использовать условия
задачи №19, однако выплаты по займу
производятся каждое полугодие.
Рассчитать размер основных выплат по
займу за каждое полугодие.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
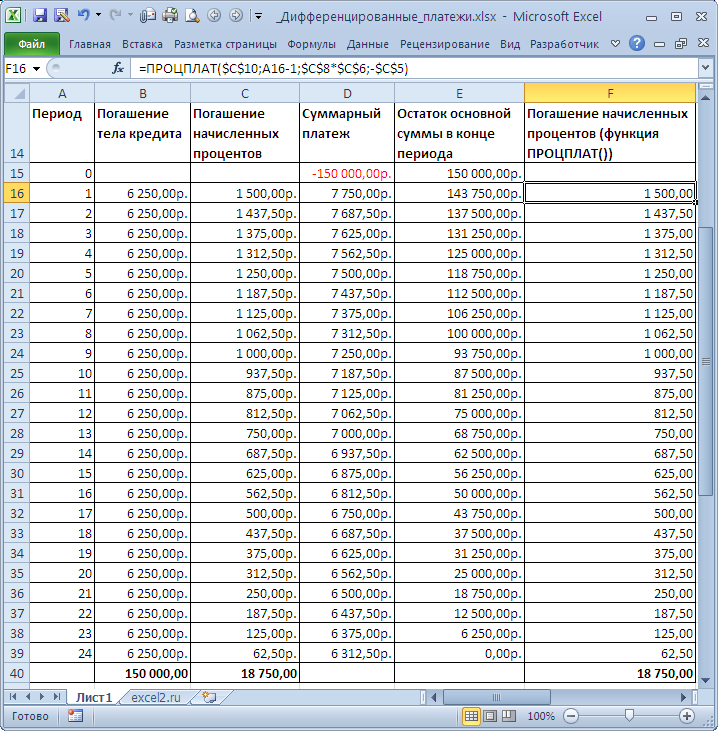
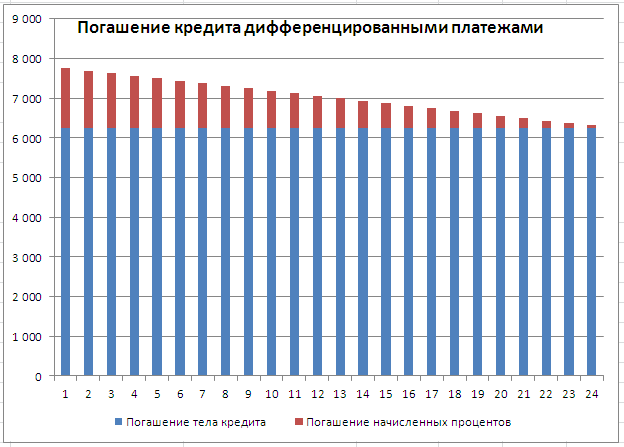
Составим в MS EXCEL график погашения кредита дифференцированными платежами.
При расчете графика погашения кредита дифференцированными платежами сумма основного долга делится на равные части пропорционально сроку кредитования. Регулярно, в течение всего срока погашения кредита, заемщик выплачивает банку эти части основного долга плюс начисленные на его остаток проценты. Если кредитным договором период погашения установлен равным месяцу, то из месяца в месяц сумма основного долга пропорционально уменьшается. Поэтому при дифференцированных платежах основные расходы заемщик несет в начале кредитования, размеры ежемесячных платежей в этот период самые большие. Но постепенно, с уменьшением остатка ссудной задолженности, уменьшается и сумма начисленных процентов по кредиту. Выплаты по кредиту значительно сокращаются и становятся не такими обременительными для заемщика.
Примечание
. При расчете кредита дифференцированными платежами сумма переплаты по процентам будет ниже, чем при
аннуитетных платежах
. Не удивительно, что сегодня практически все российские банки применяют в расчетах аннуитетную схему погашения кредита. Сравнение двух графиков погашения кредита приведено в статье
Сравнение графиков погашения кредита дифференцированными аннуитетными платежами в MS EXCEL
.
График погашения кредита дифференцированными платежами
Задача
. Сумма кредита =150т.р. Срок кредита =2 года, Ставка по кредиту = 12%. Погашение кредита ежемесячное, в конце каждого периода (месяца).
Решение. Сначала вычислим часть (долю) основной суммы кредита, которую заемщик выплачивает за период: =150т.р./2/12, т.е. 6250р. (сумму кредита мы разделили на общее количество периодов выплат =2года*12 (мес. в году)). Каждый период заемщик выплачивает банку эту часть основного долга плюс начисленные на его остаток проценты. Расчет начисленных процентов на остаток долга приведен в таблице ниже – это и есть график платежей.
Для расчета начисленных процентов может быть использована функция ПРОЦПЛАТ(ставка;период;кпер;пс), где Ставка — процентная ставка
за период
;
Период
– номер периода, для которого требуется найти величину начисленных процентов;
Кпер
— общее число периодов начислений;
ПС
–
приведенная стоимость
на текущий момент (для кредита ПС — это сумма кредита, для вклада ПС – начальная сумма вклада).
Примечание
. Не смотря на то, что названия аргументов совпадают с названиями аргументов
функций аннуитета
–
ПРОЦПЛАТ()
не входит в группу этих функций (не может быть использована для расчета параметров аннуитета).
Примечание
. Английский вариант функции — ISPMT(rate, per, nper, pv)
Функция
ПРОЦПЛАТ()
предполагает начисление процентов
в начале каждого периода
(хотя в справке MS EXCEL это не сказано). Но, функцию можно использовать для расчета процентов, начисляемых и в конце периода для это нужно записать ее в виде ПРОЦПЛАТ(ставка;период-1;кпер;пс), т.е. «сдвинуть» вычисления на 1 период раньше (см.
файл примера
). Функция
ПРОЦПЛАТ()
начисленные проценты за пользование кредитом указывает с противоположным знаком, чтобы отличить денежные потоки (если выдача кредита – положительный денежный поток («в карман» заемщика), то регулярные выплаты – отрицательный поток «из кармана»).
Расчет суммарных процентов, уплаченных с даты выдачи кредита
Выведем формулу для нахождения суммы процентов, начисленных за определенное количество периодов с даты начала действия кредитного договора. Запишем суммы процентов начисленных в первых периодов (начисление и выплата в конце периода): ПС*ставка (ПС-ПС/кпер)*ставка (ПС-2*ПС/кпер)*ставка (ПС-3*ПС/кпер)*ставка … Просуммируем полученные выражения и, используя формулу суммы арифметической прогрессии, получим результат. =ПС*Ставка* период*(1 — (период-1)/2/кпер) Где, Ставка – это процентная ставка за период (=годовая ставка / число выплат в году), период – период, до которого требуется найти сумму процентов. Например, сумма процентов, выплаченных за первые полгода пользования кредитом (см. условия задачи выше) = 150000*(12%/12)*6*(1-(6-1)/2/(2*12))=8062,50р. За весь срок будет выплачено =ПС*Ставка*(кпер+1)/2=18750р. Через функцию
ПРОЦПЛАТ()
формула будет сложнее: =СУММПРОИЗВ(ПРОЦПЛАТ(ставка;СТРОКА(ДВССЫЛ(«1:»&кпер))-1;кпер;-ПС))
Функция ПРОЦПЛАТ вычисляет проценты, выплаченные за определенный инвестиционный период.
Синтаксис
ПРОЦПЛАТ(ставка; период; число_платежей; текущий_размер_выплат)
| Аргумент | Описание | Примечания |
ставка |
Процентная ставка. | |
период |
Период выплаты процентов. | Число от 1 до значения «число_платежей». |
число_платежей |
Количество запланированных платежей. | |
текущий_размер_выплат |
Текущий размер ежегодных выплат. |
Пример использования
ПРОЦПЛАТ(15%; 2; 5; 1000)
Примечания
Убедитесь, что значения для ставки, периода и числа платежей указаны верно. Например, если платежи по кредиту на 36 месяцев производятся ежемесячно, годовую ставку нужно разделить на 12. Общее количество платежей будет равно 36. С другой стороны, если выплаты производятся раз в три месяца, годовая процентная ставка должна быть поделена на 4, а количество платежей составит 12.
Пример
| A | B | |
| 1 | Формула | Результат |
| 2 | =ПРОЦПЛАТ(B1; B2; B3; B4) | −2400 |
Похожие функции
- ОСПЛТ: Возвращает размер платежа для погашения основной суммы инвестиции, исходя из величины фиксированного платежа и фиксированной процентной ставки.
- ПЛТ: Возвращает сумму периодического платежа для годовых инвестиций на основании размера фиксированного платежа и фиксированной процентной ставки.
- КПЕР: Вычисляет количество платежных периодов для инвестиций с фиксированным размером выплат и фиксированной процентной ставкой.
- ПРПЛТ: Вычисляет сумму процентных выплат по кредиту с фиксированной процентной ставкой и фиксированными периодическими платежами.
- БЗРАСПИС: Вычисляет будущую стоимость инвестиций на основании переменной процентной ставки.
- БС: Вычисляет будущий размер годовых инвестиций на основе периодических фиксированных платежей и фиксированной процентной ставки.
Эта информация оказалась полезной?
Как можно улучшить эту статью?