Работа с финансовыми функциями в excel анализ что если

Работа с финансовыми функциями. Анализ «что-если»

Цель
работы:
научиться работать с финансовыми
функциями MS
Excel
и выполнять анализ «что-если»

Содержание
работы:

1. Финансовые
   функции при экономических расчётах

2. Прогнозирование
   с помощью анализа «что-если».

1 Финансовые функции при экономических расчётах

В
MS
Excel
имеется 50 финансовых функций, которые
позволяют выполнять наиболее характерные
финансовые операции.

1 Функция плт. Расчёт величины ежемесячной выплаты кредита

Пример
1
Определить ежемесячный платёж, если
банк предоставляет кредит в 140000р. с
рассрочкой в 5 лет под 8,5% годовых с
ежемесячной выплатой. Последний платёж
должен составить 10000р.

Заполним
таблицу MS
Excel
данными:

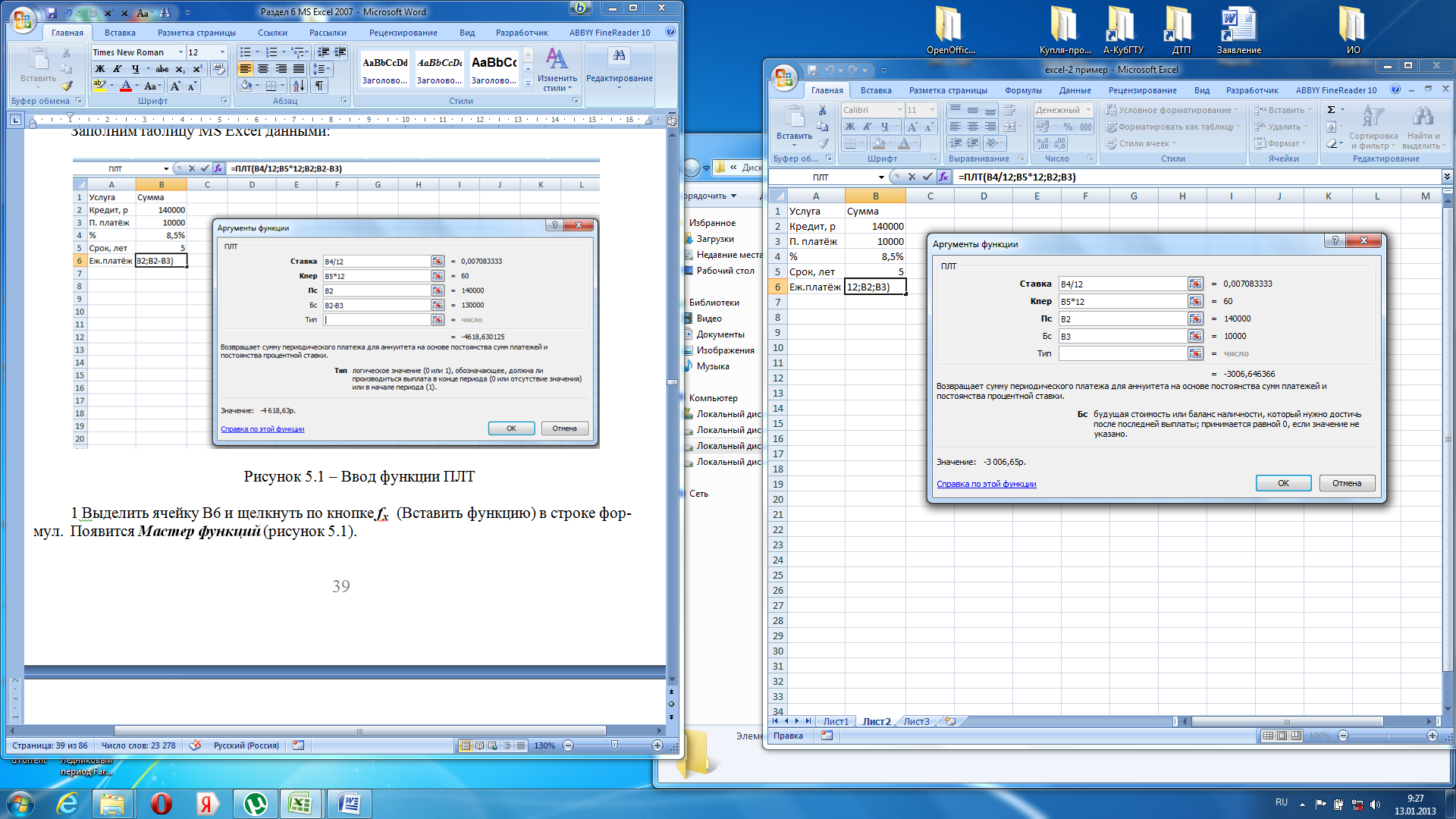
Рисунок
5.1 – Ввод функции ПЛТ

1
Выделить ячейку В6 и щелкнуть по кнопке
f_x
(Вставить функцию) в строке формул.
Появится Мастер
функций (рисунок
5.1).

Поле
Ставка
– это процент в месяц, вводим В4/12, т.к.
функции ПЛТ требуется не годовая, а
помесячная ставка.

• Кпер
  – количество периодов выплат, т.е.
  5лет*12мес, вводим В5*12

• Пс
  – приведённая (нынешняя) стоимость —
  сумма всех платежей с текущего момента,
  вводим В2,

• Бс
  – будущая стоимость, баланс наличности
  перед последней выплатой, т.е. 10000,
  поэтому вводим В4,

  • Тип
    – выплата в конце месяца, поэтому
    вводим 0 или ничего.

3.Нажать
ОК.

Результат:
–
3 006, 65 р.
ежемесячно нужно выплачивать, чтобы
погасить 130000 р. за 5 лет (в конце срока
последним платежом ещё 10000р.). Знак «-»
означает, что платим мы, а не банк.

2 Прогнозирование с помощью анализа «что-если».

Анализ «что-если»
позволяет прогнозировать значение
какой-либо функции (математической,
финансовой, статистической и др.) при
изменении её аргументов. Существует
четыре способа прогнозирования значений:
с помощью таблиц подстановки данных, с
помощью сценариев и с помощью подбора
параметров и поиска решения.

1
способ. Таблица подстановки данных –
это диапазон ячеек, показывающий, как
изменение значений подстановки влияет
на возвращаемый формулой результат.
Если в какой-либо ячейке записана
формула, содержащая элементы из других
ячеек, то при изменении значения в
какой-нибудь или нескольких ячейках
изменится результат в ячейке, содержащей
формулу.

Пример
2 Для
примера 1 определить:

—
ежемесячные выплаты при процентных
ставках 7%, 8% и 9% годовых,

—
ежемесячные выплаты при процентной
ставке 5%, 6% и 7% и сумме заема 100 000, 110 000,
120 000 и 130 000р .

1. Для
   определения выплат при ставках 7%, 8% и
   9% годовых введём таблицу данных в виде
   (рисунок 5.2):

Рисунок
5.2 – Таблица данных

для
изменения процентов

1. В
   ячейке А9
   сделаем
   ссылку на ячейку с формулой ПЛТ, т.е.
   введём знак «=» и щёлкнем на ячейке
   В6. В строке формул запишется =В6,
   а в ячейке А9
   появится
   результат –3 006,65р.

2. Выделим
   блок ячеек А9:В12
   и запустим инструмент Таблица
   данных на
   вкладке Данные,
   группа Работа
   с данными,
   кнопка Анализ
   «что-если»,
   пункт меню Таблица
   данных.

Рисунок
5.3 Окно Таблица данных

1. В
   появившемся окне (рисунок 5.3) введём в
   строке для столбцов адрес ячейки В2
   (щелкнем по
   ячейке В2),
   а в строке для столбцов щелкнем по
   В4 и нажмём
   ОК.
   Таблица данных заполнится числами –
   рисунок 5.4.

Рисунок
5.4 – Заполненная Таблица данных

5
Заготовим другую таблицу подстановок
– введём столбцы для изменения суммы
кредита (рисунок 5.5). В ячейке А14 также
сделаем ссылку на ячейку с формулой,
т.е. введём =В6,
затем выделим таблицу (блок А15:Е18) и
запустим инструмент Таблица
данных на
вкладке Данные,
группа Работа
с данными,
кнопка Анализ
«что-если»,
пункт меню Таблица
данных.
Введя В2
для столбцов
и
В4
для
строк, получим:

Рисунок
5.5 – Таблица данных для варьирования
ставки и кредита

Таблица
подстановок должна обязательно в одной
из ячеек содержать
формулу.

2
способ. Сценарий –
это набор значений подстановки,
используемый для прогнозирования
поведения модели. Если в Примере 1
изменить процентную ставку с 8,5% на 9%,
то формула ПЛТ в ячейке В6 автоматически
пересчитается и покажет результат
-3038,75р. При этом прежний результат
-3006,65р. для 8,5% пропадает. Чтобы его
сохранить, применяется сценарий, в
котором приводятся расчёты ПЛТ с новыми
значениями и сохраняется исходный
(текущий) вариант. На одном листе Excel
можно создать и сохранить несколько
различных сценариев и переключаться
на любой из них для просмотра результатов
и выбора наилучшего.

Пример
3
Оформим в виде сценария вариант
подстановки данных из примера 1.

Для
создания сценария необходимо выполнить
следующие действия:

1
Из вкладки Данные
выберете команду Анализ
«что-если»,
выбрать
Диспетчер
сценариев.

2
В открывшемся окне Диспетчер
сценариев
нажмите кнопку Добавить.

3
Введите имя сценария., например «Кредит
200 000, 10%».

4
В поле Изменяемые
ячейки
задайте те ячейки (если они не смежные,
то через Ctrl),
которые Вы собираетесь изменить, в
данном случае – ячейки В2
и
В4.

5
Введите новые значения этих ячеек
(рисунок 5.6). Нажмите кнопку ОК.

Рисунок
5.6 Новые значения кредита и ставки

6
Нажмите кнопку Отчёт,
выберите переключатель Структура,
задайте ячейки для вывода результата
В2:В6
(те, которые используются в формуле ПЛТ)
и нажмите ОК.

В
результате на отдельном листе MS
Excel
Структура
сценария
появится сценарий с текущими и новыми
значениями функции ПЛТ – рисунок 5.7.

Для
просмотра сценария необходимо
воспользоваться кнопкой Вывести
в окне Диспетчер
сценариев.
Знаки «+»(«-«) слева и сверху позволяют
разворачивать (сворачивать) отдельные
разделы отчёта. Серым выделены изменяемые
поля.

Рисунок
5.7 – Сценарий Кредит
20 000, 10%

Аналогично
через клавишу Добавить
можно создать несколько сценариев для
варьирования разных параметров.

3
способ. Подбор параметра.
Подбор параметра – это обратная задача
решения уравнений. Если в прямой задаче
для функции y
= f(x)
по известному аргументу х
вычисляется значение функции у,
то в обратной задаче значение функции
у
задаётся
числом, а величина х
подбирается
под заданное значение у.

При
подборе параметра значение влияющей
ячейки (параметра) изменяется до тех
пор, пока формула, зависящая от этой
ячейки не возвратит заданное значение.

Пример
4
Условие примера 1. Компания может
ежемесячно выплачивать не более 2500р.
Определить, каким должен для этого быть
последний платёж.

1.Выделим
ячейку В6:

2.
На вкладке Данные,
группа Работа
с данными,
кнопка Анализ
«что-если» щелкнуть
по пункту меню Подбор
параметра
– рисунок
5.8. Появится окно Подбор
параметра:

Рисунок
5.8 – Окно Подбор
параметра

В
окне Подбор
параметра:

-в
поле Установить
в ячейке
– введено В6,

-в
поле Значение
—
ввести -2500

-в
поле Изменяя
значение ячейки
– ввести В3
(ячейка последнего платежа),

-нажать
ОК.

В
итоге появится окно Результат
подбора параметра
– рисунок 5.9:

Рисунок
5.9 – Окно Результат
подбора параметра

Таким
образом, если выплачивать по 2500 р. В
месяц, то последний платёж составит
-27716 р.

При
подборе параметра одна из ячеек
обязательно должна содержать формулу.

4
способ.
Команда Поиск
решения
из вкладки Данные
Работа с данными Анализ «что-если»
используется для подбора одновременно
нескольких параметров с целью максимизации
или минимизации содержимого целевой
ячейки и подробно рассматривается в
лабораторной работе №7 (excel-7).

Контрольные
вопросы

1
Как вывести на экран список функций MS
Excel
и запустить Мастер
функций?

2
Какую операцию выполняет функция ПЛТ,
что вводится в её поля Ставка,
Кпер, ПС, Бс, Тип?

3
Назначение и способы анализа «что-если»?

4
Что такое «Таблица
данных»,
как её создать для одно- и двухмерного
массива?

5
Что такое сценарий, как его создать,
просмотреть, получить итоговый отчет
на отдельном листе?

6
Сущность операции Подбор
параметра,
как она выполняется?

Задания

1.
Выполнить задание примера 1, изменив
сумму кредита на 140000·n,
где n—
номер студента в журнале преподавателя.
Выполнить то же для новой суммы кредита,
изменив годовой процент с 8,5% на 5%, а срок
кредита с 5 на 10 лет.

2. Создать две
таблицы данных как в примере 2, изменив
сумму заёма на 80000·n,
где n-
номер студента в журнале преподавателя.

3. Оформить в виде
сценариев все операции из п.1 (два сценария
+ Текущие
значения)
задания.

4. Выполнить задание
примера 4, изменив сумму ежемесячной
выплаты на n·100.

Содержание
отчёта

1
Название,
цель, содержание работы

2
Задание своего варианта

3
Письменные ответы на контрольные вопросы

4
Выводы по работе

На
своём носителе должны быть сохранены
результаты работы

Практическое
занятие №6 (excel-6)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Использование финансовых функций при экономических расчётах

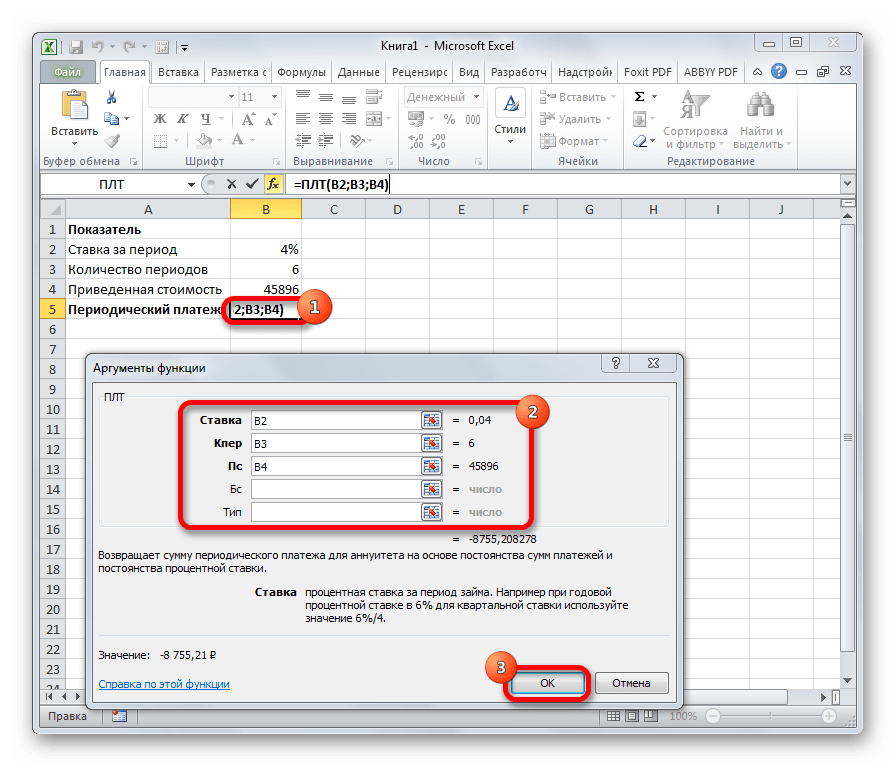
Функция ПЛТ

Функция ПЛТ (PMT) – возвращает сумму периодического платежа на основе постоянства сумм платежей и постоянства процентной ставки.

Синтаксис:

ПЛТ(СТАВКА;КПЕР;ПС;[БС];ТИП)

• СТАВКА – Удельная ставка за период займа.
• КПЕР– общее число периодов выплат.
• ПС– текущая стоимость: общая сумма всех будущих платежей с настоящего момента.
• БС – будущая стоимость или баланс наличности, которую нужно достичь после последней выплаты.Если аргумент БС опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение БС равно 0.
• ТИП– логическое значение (0 или 1), обозначающее, должна ли производиться выплата в конце периода (0) или в начале периода (1).

Функция ПЛТ может быть использована для анализа всевозможных ссуд. Необходимым условием является непротиворечивость аргументов функции.

Пример 1. Предположим, что нужно воспользоваться 9-процентной 15-летней ссудой. Объем ссуды составляет 150 000 000 рублей. C помощью Мастера функций можно определить величины ежемесячных выплат. Предварительно следует привести все другие значения к месячной норме.

Ввести таблицу (рис. 9.1
рис.
9.1 ), начиная с ячейки А1:

В ячейки В 3 и В 4 ввести соответствующие формулы.

Процентная ставка (СТАВКА) – годовая, поэтому для получения месячной ставки (Удельная ставка) соответствующее значение делится на 12 (0,09/12).

Срок действия ссуды – 15 лет, поэтому с учетом 12 платежей год общее количество месячных выплат (КПЕР) составит 12х15.

Для ячейки В6 пошаговыми действиями Мастера функций выполните настройку функции ПЛТ. Для вызова Мастера функций необходимо выбрать команду Вставить функцию (значок f_x) в меню Формулы.

После этого в поле Значение диалогового окна Мастера функций вы увидите сумму ежемесячного взноса. А после нажатия на кнопку Готово результат отобразится в ячейке.

Примечание. Необходимо исходные данные заносить в ячейки на рабочий лист Excel, давая им в левом столбце соответствующие названия параметров, а для рассчитываемых параметров использовать формулы. Тогда при изменении исходных данных будет автоматически выполнен перерасчет по формулам.

Функция БС

Функция БС(FV) предназначена для расчета будущей стоимости периодических постоянных платежей и единой суммы вклада или займа на основе постоянной процентной ставки.

БС – будущее значение, возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки.

Синтаксис:

БС (СТАВКА; КПЕР; ПЛТ; ПС; ТИП).

• СТАВКА – это процентная ставка за период.
• КПЕР– это общее число периодов платежей.
• ПЛТ– это выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно ПЛТ состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов.
• ПС – это текущая стоимость, или общая сумма всех будущих платежей с настоящего момента. Если аргумент ПС опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента ПЛТ.
• ТИП– это число 0 или 1, обозначающее, когда должна производиться выплата: 0 – в конце периода, 1 – в начале периода. Если аргумент опущен, то он полагается равным 0.

Для аргументов СТАВКА и КПЕР используются согласованные единицы измерения. Если производятся ежемесячные платежи по четырехгодичному займу из расчета 12% годовых, то СТАВКА должна быть 12%/12, а КПЕР должно быть 4*12. Если производятся ежегодные платежи по тому же займу, то СТАВКА должна быть 12%, а КПЕР должно быть 4.

Все аргументы, означающие деньги, которые вы платите (например, депозитные вклады), представляются отрицательными числами; деньги, которые вы получаете (например, дивиденды), представляются положительными числами.

Например, вы собираетесь вложить под 12% годовых (что составит в месяц 12%/12 или 1%). Вы собираетесь вкладывать по 1000 руб. в конце каждого следующего месяца в течении следующих 12 месяцев. Сколько денег будет на счету в конце12 месяцев?

Результат 12682,50 руб.

Для выполнения расчета вызывается Мастер функций, в поле Категории выбираются финансовые функции и в поле Функция выбирается функция БС. В появившемся окне заполняются соответствующие поля путем подстановки значений аргументов, а если данная функция вычисляется в расчете, то вместо этого указываются адреса исходных данных из таблицы расчета.

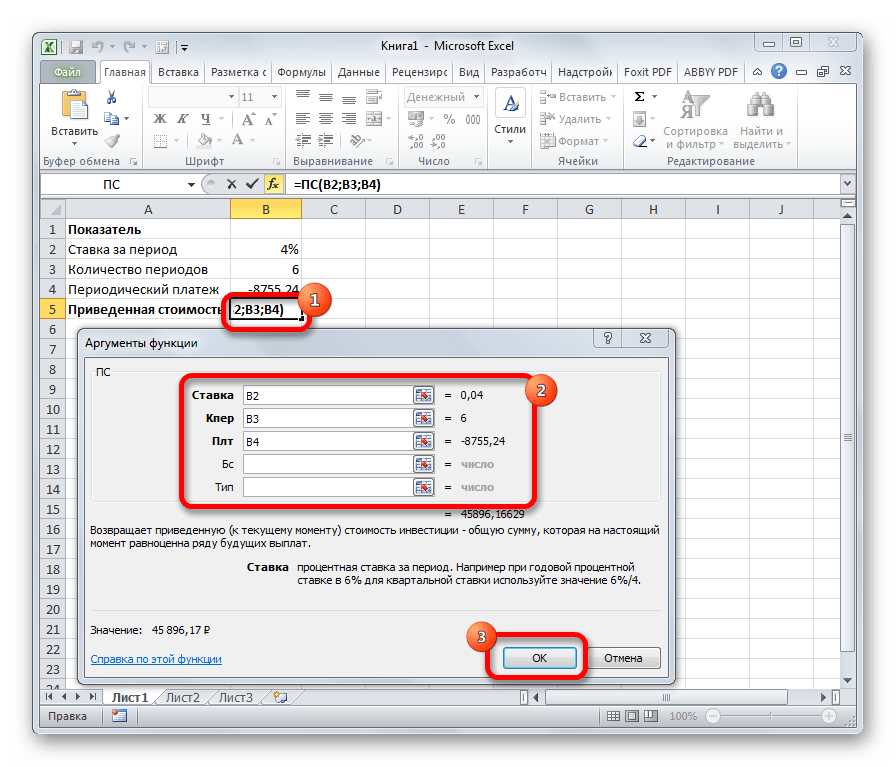
Функция ПС

Функция ПС (PV) предназначена для расчета текущей стоимости как единой суммы вклада (займа), так и будущих фиксированных периодических платежей. Этот расчет является обратным по отношению к будущей стоимости (БС).

ПС (PV )– возвращает текущий объем вклада. Текущий объем -это общая сумма, которую составят будущие платежи. Например, когда вы берете взаймы деньги, заимствованная сумма и есть текущий объем для заимодавца.

Синтаксис:

ПС (СТАВКА; КПЕР; ПЛТ; БС; ТИП).

Например, определите необходимую сумму текущего вклада в банк, чтобы через пять лет он достиг 5000 руб. при 20% годовых и ежегодном начислении процентов в конце года. Синтаксис: ПС (20%, 5, 5000). Результат 2009,39.

Функция КПЕР

Для определения срока платежа и процентной ставки используются функции КПЕР (NPER) и СТАВКА (RATE).

Функция КПЕР вычисляет общее число периодов выплат как для единой суммы вклада (займа), так и для периодических постоянных выплат на основе постоянной процентной ставки. Если платежи производятся несколько раз в год, то для того, чтобы найти число лет выплат, общее число периодов надо разделить на число периодов в году.

Синтаксис:

КПЕР (СТАВКА; ПЛТ; ПС; БС; ТИП).

• СТАВКА– это процентная ставка за период.
• ПЛТ– это выплата, производимая в каждый период; он не может меняться в течение всего периода выплат. Обычно платеж состоит из основного платежа и платежа по процентам, никакие другие сборы или налоги не учитываются.
• ПС– это текущая стоимость, или общая сумма всех будущих платежей с настоящего момента.
• БС– это будущая стоимость, или баланс наличности, который должен быть достигнут после последней выплаты. Если аргумент БС опущен, то предполагается, что он равен 0 (будущая стоимость займа, например, равна 0).
• ТИП– это число 0 или 1, обозначающее, когда должна производиться выплата.

Например, рассчитаем срок погашения ссуды размером 5000 руб., выданной под 20% годовых при погашении ежемесячными платежами по 200 руб.

КПЕР (20%/12; -200; 5000).

Результат 32,6 месяца или 2,7 года.

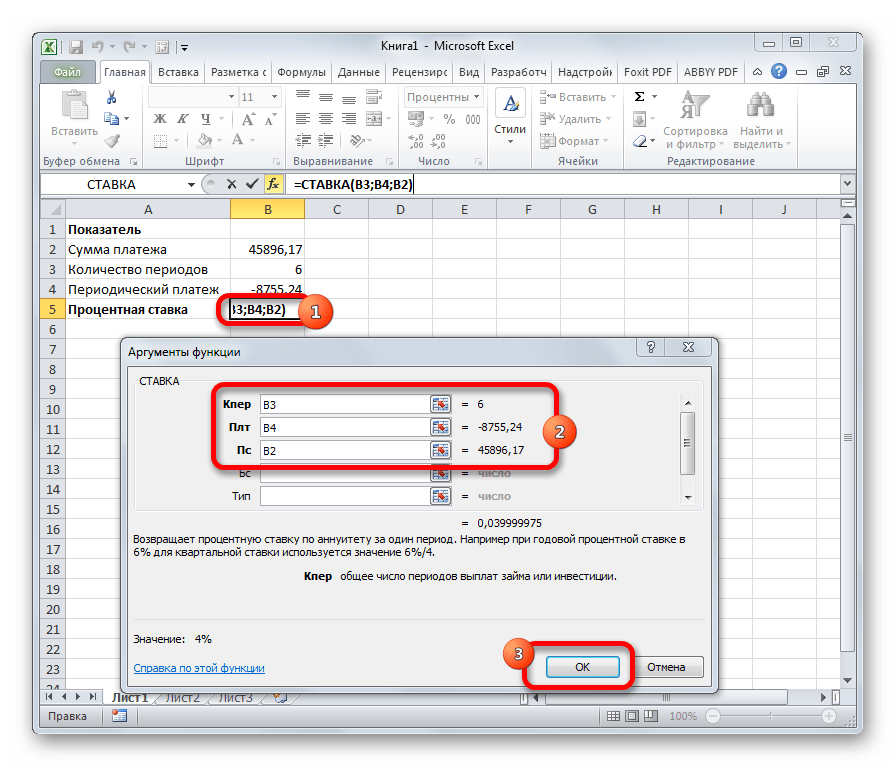
Функция СТАВКА

Функция СТАВКА (RATE) определяет значение процентной ставки за один расчетный период. Для нахождения годовой процентной ставки полученное значение необходимо умножить на число расчетных периодов в году.

СТАВКА вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО!.

Синтаксис:

СТАВКА (кпер; плт; пс; бс; тип; предположение).

• Кпер– общее число периодов платежей по аннуитету.
• Плт– регулярный платеж (один раз в период), величина которого остается постоянной в течение всего срока аннуитета. Обычно плт состоит из платежа основной суммы и платежа процентов, но не включает других сборов или налогов. Если аргумент опущен, должно быть указано значение аргумента БС.
• Пс– приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.
• Бс– требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (например, бс для займа равно 0).
• Тип– число 0 или 1, обозначающее, когда должна производиться выплата.
• Предположение – предполагаемая величина ставки. Если значение предположения опущено, то оно полагается равным 10 процентам.

Если функция СТАВКА не сходится, попробуйте подставить различные значения для предположения. СТАВКА обычно сходится, если величина предположения находится между числами 0 и 1.

Например, надо определить процентную ставку для четырёхлетнего займа в 8000 руб. с ежемесячной выплатой в 200 руб.

Результат 0,008, или 0,8 в месяц или 9,6% годовых.

Функции по расчету амортизации: AПЛ, АСЧ и ДДОБ

Под амортизацией подразумевается уменьшение стоимости имущества в процессе эксплуатации. Обычно оценивают величину этого уменьшения на единицу времени.

Функция АПЛ (SLN) возвращает величину амортизации имущества за один период времени, используя метод равномерной амортизации.

Синтаксис:

АПЛ (нач_стоимость;ост_стоимость;время_эксплуатации).

• нач_стоимость – начальная стоимость имущества;
• ост_стоимость –остаточная стоимость в конце периода амортизации;
• время_эксплуатации – количество периодов, за которые собственность амортизируется (иногда называется временем полной амортизации).

Предположим, вы купили за 6000 руб. компьютер, который имеет срок эксплуатации 5 лет, после чего оценивается в 1000 руб. Снижение стоимости для каждого года эксплуатации вычисляется формулой

которая возвращает значение 1000 р.

Функция АСЧ(SYD) возвращает годовую амортизацию имущества для указанного периода.

АСЧ (нач_стоимость; ост_стоимость; время_эксплуатации; период)

• нач_стоимость – начальная стоимость имущества;
• ост_стоимость – остаточная стоимость в конце периода амортизации;
• время_эксплуатации – количество периодов, за которые собственность амортизируется (иногда называется временем полной амортизации);
• период – номер периода для вычисления амортизации (должен быть измерен в тех же единицах, что и время полной амортизации).

При расчете предыдущего примера получим:

• за первый год эксплуатации компьютера амортизация вычисляется формулой

которая возвращает значение 1666.67р.

• за последний – формулой

которая возвращает 333. 33 р.

Функция ДДОБ (DDB) возвращает величину амортизации имущества для указанного периода, используя метод двукратного (или k-кратного) учета амортизации.

Синтаксис:

ДДОБ (стоимость; остаточная_стоимость; время_эксплуатации; период; k-коэффициент).

• стоимость–начальная стоимость имущества;
• остаточная_стоимость– остаточная стоимость в конце периода;
• время_эксллуатадии– количество периодов, за которые собственность амортизируется (иногда называется временем полной амортизации);
• период – номер периода для вычисления амортизации (должен быть измерен в тех же единицах, что и время полной амортизации);
• коэффициент– норма снижения балансовой стоимости (амортизации). Если коэффициент опущен, то предполагается, что он равен 2 (методдвукратного учета амортизации).

Метод двукратного учета амортизации предполагает ускоренную амортизацию имущества. При этом амортизация максимальна в первый период и снижается в последующие периоды.

В примере с компьютером по методу двукратной амортизации она составит:

• =ДДОБ (6000; 1000; 5; 1) возвращает 2400.00р.
• =ДДОБ (6000; 1000; 5; 2) возвращает 1440.00р.
• =ДДОБ (6000; 1000; 5; 3) возвращает 864.00р.
• =ДДОБ (6000; 1000; 5; 4) возвращает 296.00р.
• =ДДОБ (6000; 1000; 5; 5) возвращает 0.00р.

Примечание

В заключение попытаемся разобраться, как работают функции АПЛ, АСЧ, ДОБ и ДДОБ.

Проще всего дело обстоит с функцией АПЛ. Она возвращает одну и ту же амортизацию за каждый период.

Значения функции АСЧ изменяются по линейному закону. Разность любых двух ее значений за последовательные периоды постоянна. Таким образом значения за последовательные периоды образуют убывающую арифметическую прогрессию, подобранную таким образом, чтобы суммарная амортизация равнялась разности между начальной и остаточной стоимостью.

Значения функции ДДОБ изменяются также по экспоненциальному закону. Но коэффициент этой геометрической прогрессии не вычисляется, а является параметром.

Анализ «Что-если»

Анализ «Что-если» позволяет прогнозировать значение какой-либо функции (математической, финансовой, статистической и др.) при изменении её аргументов.

Существует четыре способа прогнозирования значений с помощью:

• таблиц подстановки данных,
• сценариев
• подбора параметров
• поиска решения.

1 способ. Таблица подстановки данных

Таблица подстановки данных представляет собой блок ячеек, в котором выводятся результаты подстановки различных значений переменных в одну или несколько формул.

Анализ может проводиться для функций с одной переменной или для функций с двумя переменными. Причем в случае одной переменной можно табулировать сразу несколько функций, зависящих от этой переменной.

Анализ формулы начинается с подготовки таблицы подстановки:

1. Левую верхнюю ячейку блока, отведенного под таблицу, оставить пустой.
2. В левый столбец блока, начиная со второй ячейки, последовательно ввести значения варьируемой переменной.
3. В верхнюю строку блока, начиная со второй ячейки, ввести ссылки на ячейки с анализируемыми формулами.

Допускается и другая ориентация таблицы, когда значения варьируемой переменной вводятся в первую строку, а анализируемые форму-лы – в первый столбец блока.

1. Выделить таблицу подстановки (в ячейки, расположенные рядом с таблицей, можно ввести пояснительные надписи, но эти ячейки не входят в таблицу подстановки данных и, следовательно, не выделяются).
2. В меню Данные выбрать Анализ «Что-если» и выбрать команду Таблица данных.
3. Если значения варьируемой переменной расположены в столбце, то надо щелкнуть по полю Подставлять значения по строкам и ввести в это поле адрес изменяемой ячейки (т.е. ячейки, которая играет роль варьируемой переменной в формуле). Если значения варьируемой переменной расположены в строке, то адрес изменяемой ячейки вводится в поле Подставлять значения по столбцам.
4. Щелкнуть по кнопке ОК. Таблица будет заполнена значениями.

В случае анализа зависимости формулы от двух переменных таблица подстановки подготавливается по-другому:

1. В левую верхнюю ячейку блока, отведенного под таблицу, ввести ссылку на ячейку с анализируемой формулой.
2. В левый столбец блока, начиная со второй ячейки, последовательно ввести значения одной из варьируемых переменных.
3. В верхнюю строку блока, начиная со второй ячейки, ввести значения другой варьируемой переменной.
4. Выделить таблицу подстановки.
5. В меню Данные выбрать Анализ «Что-если» и выбрать команду Таблица данных.
6. В поле Подставлять значения по строкам в ввести ссылку на ячейку с переменной, значения для которой расположены в левом столбце таблицы подстановки.
7. В поле Подставлять значения по столбцам ввести ссылку на ячейку с переменной, значения для которой расположены в первой строке таблицы подстановки.
8. Щелкнуть по кнопке ОК. Таблица будет заполнена значениями.

Если в какой-либо ячейке записана формула, содержащая элементы из других ячеек, то при изменении значения в какой-нибудь или нескольких ячейках изменится результат в ячейке, содержащей формулу.

Пример 2.

Определить какими будут выплаты по ссуде при меняющейся процентной ставке (для примера 1)

В ячейки А9:В13 введите следующие значения, оставив пустой строку перед числовыми значениями (рис. 9.2
рис.
9.2 ):

В ячейку В10 скопировать ссылку на ячейку с формулой для расчета ежемесячных выплат.

Для расчета выплат по каждой из ставок воспользуйтесь возможностью автоматической подстановки значений в нужную ячейку (в нашем случае в В1).

Для этого нужно:

1. Выделить диапазон А10:В13, включив в него значения процентных ставок и расчетную формулу (формула должна находиться в ячейке, расположенной правее и выше заданных значений).
2. В меню Данные выбрать Анализ «Что-если» и выбрать команду Таблица данных.
3. В поле «Подставлять значения по строкам в:» указать ячейку В1 (рис.9.3 ).

Рядом с каждой процентной ставкой появится соответствующий результат.

Измените значения процентных ставок или расширьте предлагаемый диапазон и вновь воспользуйтесь таблицей подстановки значений.

2 способ. Диспетчер сценариев

Средства Microsoft Excel позволяют создавать и сохранять в виде сценариев наборы входных значений, приводящих к различным результатам.

Сценарий – это множество входных значений, называемых изменяемыми ячейками, которое можно сохранить под указанным именем, а затем применить к модели рабочего листа, чтобы проследить, как значения изменяемых ячеек влияют на другие значения модели. Для каждого сценария можно определить до 32 изменяемых ячеек.

Чтобы создать сценарий, следует:

1. В меню Данные выбрать команду Анализ «Что-если», указав Диспетчер сценариев (рис. 9.4
рис.
9.4 ).

Появится окно «Диспетчер сценариев» (рис. 9.5
рис.
9.5)

2. Щелкнуть по кнопке Добавить. Откроется окно Добавление сценария (рис. 9.6
рис.
9.6).

3. В поле Название сценария ввести имя сценария.

4. В поле Изменяемые ячейки ввести ссылки на изменяемые ячейки. Несколько ссылок отделяются друг от друга точками с запятыми. Ссылки можно ввести с клавиатуры или выделить их на рабочем листе. Несмежные ячейки добавляются при нажатой клавише <Ctrl>.

5. Щелкнуть по кнопке ОК.

6. В открывшемся диалоговом окне Значения ячеек сценария ввести значения каждой изменяемой ячейки (рис. 9.7
рис.
9.7).

7. Для создания других сценариев щелкнуть по кнопке Добавить (откроется диалоговое окно Добавление сценария) и повторить пункты 3 – 6.

Для завершения работы с Диспетчером сценариев щелкнуть по кнопке ОК, а затем – по кнопке Закрыть.

Рекомендуется сохранить в качестве сценария первоначальные значения изменяемых ячеек, чтобы потом можно было быстро восстановить эти значения.

Для просмотра сценария нужно:

1. В меню Данные выбрать команду Анализ данных и указать Диспетчер сценариев.
2. В поле Сценарии выделить имя сценария, который необходимо просмотреть.
3. Щелкнуть по кнопке Вывести.

Вместо пунктов 2 и 3 можно дважды щелкнуть по имени нужного сценария.

Чтобы отредактировать сценарий, надо:

1. В меню Данные выбрать команду Анализ данных и указать Диспетчер сценариев.
2. В поле Сценарии выделить имя сценария, который необходимо отредактировать.
3. Щелкнуть по кнопке Изменить.
4. Внести необходимые изменения: можно изменить имя сценария, изменяемые ячейки, значения изменяемых ячеек.
5. Для завершения работы с Диспетчером сценариев щелкнуть по кнопке ОК, а затем – по кнопке Закрыть.

Для создания итогового отчета по сценариям следует:

1. В меню Данные выбрать команду Анализ данных и указать Диспетчер сценариев.
2. Щелкнуть по кнопке Отчет.
3. Выбрать тип отчета: Структура или Сводная таблица.

В отчете типа Структура перечислены все сценарии с определенными для них значениями ячеек. Этот тип отчета полезен тогда, когда каждый пользователь определяет сценарий со своими данными.

Отчет типа Сводная таблица предоставляет возможность эмпирического анализа сценариев. Этот тип отчета полезен тогда, когда сценарий имеет несколько наборов значений изменяющихся ячеек, заданных различными пользователями; с помощью сводных таблиц можно выполнить анализ для разных комбинаций сценариев.

1. В поле Ячейки результата ввести ссылки на ячейки, значения которых надо представить в отчете. В качестве разделителя ссылок используется запятая. Ссылки можно ввести с клавиатуры или выделить их на рабочем листе. Несмежные ячейки добавляются при нажатой клавише <Ctrl>. Итоговые отчеты создаются на отдельных листах.

3 способ. Подбор параметра

Пусть имеется формула, которая прямо или косвенно зависит от некоторого параметра. Задача состоит в определении такого значения этого параметра, которое позволяет получить нужный результат формулы. При подборе параметра значение влияющей ячейки (параметра) изменяется до тех пор, пока формула, зависящая от этой ячейки не возвратит заданное значение.

Математическая суть задачи состоит в решении уравнения X = a, где функция х описывается заданной формулой, х – искомый параметр, а – требуемый результат формулы.

Для решения этой задачи необходимо выполнить следующие действия:

1. Выделить ячейку, содержащую формулу, для которой нужно найти определенное решение.
2. В меню Данные > Анализ «что-если» выбрать команду Подбор параметра. В поле Установить в ячейке ввести ссылку на ячейку, содержащую формулу (по умолчанию в это поле вводится адрес текущей ячейки).
3. В поле Значение ввести значение, которое нужно получить по заданной формуле.
4. В поле Изменяя ячейку ввести ссылку на ячейку, содержащую значение изменяемого параметра (эта ячейка называется изменяемой).
5. Щелкнуть по кнопке ОК.

Пример 3.

Дано уравнение: ,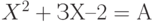

где: А – требуемый результат формулы; Х – искомый параметр.

Определить такое значение параметра X, при котором А будет равно 20.

1. Занести в ячейку A1 любое значение, например, 1.
2. Ввести в ячейку А2 указанную формулу, которая примет следующий вид: =A1^2+3*A1-2. В формуле указана ссылка на ячейку А1, в которой условно находится параметр X.
3. Задать команду Данные > Анализ «что-если» > Подбор параметра (рис. 9.8
   рис.
   9.8 ).
4. В поле Установить в ячейке указать А2 (по умолчанию в это поле вводится адрес текущей ячейки).
5. В поле Значение ввести – 20.
6. В поле Изменяя значение ячейки указать адрес ячейки, в которой должен находиться параметр X, т.е. А1.

После выполнения команды в изменяемой ячейке появится значение параметра X, при котором результат формулы равняется заданной величине. При этом будет пересчитана вся таблица, т.е. изменятся значения, прямо или косвенно зависящие от изменяемого параметра.

Подбор параметра можно выполнять графически, перетаскивая точки данных на диаграмме.

При подборе параметра одна из ячеек обязательно должна содержать формулу.

ЗАДАНИЯ

1. Используя соответствующие финансовые функции, решите следующие задачи, (номер варианта задания – номер компьютера в учебной аудитории).
2. Для созданной задачи изменить величины ее параметров так, чтобы (не меняя формулы) результат вычислений тоже изменился.
3. Выполнить анализ данных «Что – если», используя таблицу подстановок.
4. Изменить результат вычислений задачи с помощью Сценария. Вывести итоговый отчет типа структура.
5. Изменить результат вычисления при помощи Подбора параметров.

Вариант 1.

1. Определить величину ежемесячной амортизации имущества (АПЛ (SLN)) при условии, что начальная стоимость его 10000р., а остаточная (в конце периода амортизации) 2000р.; амортизация имущества занимает период 10 месяцев.
2. Затем вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 1500р..
3. Определить величину ежемесячной амортизации имущества (АПЛ), используя таблицу подстановок:
4. при различных периодах: 5, 7, 8, 9, 10, 12 месяцев;
5. при различных периодах: 5, 7, 8, 9, 10, 12 месяцев, а также при остаточных стоимостях 5000, 4500, 4000, 3000, 2000, 1000 соответственно.
6. Составить сценарий, если начальная стоимость имущества изменится на 15000р.
7. Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 1500р.

Вариант 2.

1. Вычислить, на сколько снизится стоимость основных фондов, рассчитанная по методу двойной амортизации (ДДОБ), если начальная стоимость имущества 30000р., а в конце периода эксплуатации 4000р. Время эксплуатации считать равным 3 года, период, для которого вычисляется амортизация, равным 2,5 года.
2. Вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 5000р..
3. Определить величину ДДОБ используя таблицу подстановок:
4. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года;
5. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года; и начальной стоимости 70000, 60000, 50000, 40000, 30000 руб. соответственно.
6. Составить сценарий, если величина начальной стоимости изменится на 35000р.
7. Подобрать параметр срока эксплуатации, если стоимость основных фондов снизится на 1000р.

Вариант 3.

1. Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 50000р. со ставкой 5% годовых сроком на 4 года и будущей стоимостью 5000р.
2. Вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 7%.
3. Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сроком на 5, 7, 8, 9, 10 лет соответственно.
6. Составить сценарий, если величина кредита изменится на 60000р, а срок на 5 лет.
7. Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 7000р.

Вариант 4.

1. Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 45000р., сроком на год, с ежемесячной выплатой 3000р. и годовой ставкой процента, равной 5%.
2. Затем, вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 3%.
3. Определить величину всех выплат (БС) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 50000, 60000, 70000, 80000, 90000, 100000 руб. соответственно.
6. Составить сценарий, если величина кредита изменится на 50000р.
7. Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 85000р.

Вариант 5.

1. Вычислить общее количество периодов выплаты (КПЕР) фирмой, взявшей кредит в размере 73000р. Ставка процента постоянна и равна 6%. Ежемесячные выплаты фирмой также постоянны и равны 5500р.
2. Вычислить эту величину (не меняя формулу) при условии, что величина кредита изменится на 60000р.
3. Определить величину КПЕР используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 50000, 60000, 70000, 80000, 90000, 100000 руб. соответственно.
6. Затем составить сценарий, если величина процентной ставки изменится на 12%.
7. Подобрать параметр величины кредита, если выплата будет производиться 19 месяцев.

Вариант 6.

1. Определить величину ежемесячной амортизации имущества (АПЛ) при условии, что начальная стоимость его 40000р., а остаточная (в конце периода амортизации) 9000р.; амортизация имущества занимает период 2 года.
2. Вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 7000р.
3. Определить величину АПЛ используя таблицу подстановок:
4. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и том же периоде;
5. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и периоде 0,5; 1, 1,5; 2, 3 года соответственно.
6. Составить сценарий, если начальная стоимость имущества изменится на 55000р.
7. Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 3500р.

Вариант 7.

1. Вычислить, на сколько снизится стоимость основных фондов, рассчитанная по методу двойной амортизации (ДДОБ), если начальная стоимость имущества 80000р., а в конце периода эксплуатации 10000р. Время эксплуатации считать равным 17 месяцев, период, для которого вычисляется амортизация, равным10 месяцев.
2. Вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 7000р.
3. Определить величину ДДОБ спользуя таблицу подстановок:
4. при варьировании начальной стоимости: 50000, 60000, 70000, 90000, 110000 и том же периоде амортизации;
5. при варьировании начальной стоимости: 50000, 60000, 70000, 90000, 110000 и периоде 5; 6, 7, 8, 9 месяцев соответственно.
6. Составить сценарий, если величина начальной стоимости изменится на 75000р.
7. Подобрать параметр срока эксплуатации, если стоимость основных фондов снизится на 2500р.

Вариант 8.

1. Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 90000р. со ставкой 7% на период, равный 1 году и будущей стоимостью 9000р.
2. После, вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 10%.
3. Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 70000, 80000, 90000, 100000, 120000 руб. соответственно.
6. Составить сценарий, если величина кредита изменится на 80000р., а срок на 2 года.
7. Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 5000р.

Вариант 9.

1. Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 67000р., сроком на 3 года, с ежемесячной выплатой 7000р. и годовой ставкой процента, равной 4,5%.
2. Вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 6%.
3. Определить величину БС используя таблицу подстановок:
4. при процентных ставках 5%, 6%, 7% , 8% и 9% годовых;
5. при процентной ставке 5%, 6%, 7% , 8% и 9% годовых, и суммах кредита 70000, 80000, 90000, 100000, 120000 руб. соответственно.
6. После, составить сценарий, если величина кредита изменится на 59000р.
7. Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 103000р.

Вариант 10.

1. Вычислить общее количество периодов выплаты (КПЕР) фирмой, взявшей кредит в размере 93000р. Ставка процента постоянна и равна 6,5%. Ежемесячные выплаты фирмой также постоянны и равны 6500р.
2. Вычислить эту величину (не меняя формулу) при условии, что величина кредита изменится на 80000р.
3. Определить величину КПЕР используя таблицу подстановок:
4. при процентных ставках 5%, 6%,7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 100000,90000, 80000, 70000, 60000, 50000 руб. соответственно.
6. Затем составить сценарий (условие п.1), если величина процентной ставки изменится на 9%, а ежемесячная выплата 4500р.
7. Подобрать параметр величины кредита, если выплата будет производиться 2 года.

Вариант 11.

1. Определить величину ежемесячной амортизации имущества (АПЛ) при условии, что начальная стоимость его 100000р., а остаточная (в конце периода амортизации) 10000р.; амортизация имущества занимает период 4 года.
2. Затем вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 12000р.
3. Определить величину АПЛ используя таблицу подстановок:
4. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и том же периоде;
5. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 10000 и периоде 1, 2, 3, 3,5 и 4 года соответственно.
6. После, составить сценарий, если начальная стоимость имущества изменится на 97000р.
7. Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 7500р.

Вариант 12.

1. Вычислить, на сколько снизится стоимость основных фондов, рассчитанная по методу двойной амортизации (ДДОБ), если начальная стоимость имущества 123000р., а в конце периода эксплуатации 9000р. Время эксплуатации считать равным 13 месяцев, период, для которого вычисляется амортизация, равным8 месяцев.
2. После, вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 9500р.
3. Определить величину ДДОБ используя таблицу подстановок:
4. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года;
5. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года; и начальной стоимости 70000, 60000, 50000, 40000, 30000 руб. соответственно.
6. Затем составить сценарий, если величина начальной стоимости изменится на 115000р.
7. Подобрать параметр срока эксплуатации, если стоимость основных фондов снизится на 5500р.

Вариант 13.

1. Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 74000р. со ставкой 8% годовых на период, равный 5 лет и будущей стоимостью 5000р.
2. После, вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 14%.
3. Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% ,10%, 12% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10%, 12% годовых, и сроке кредита 3, 4, 5, 6, 7, 8 лет соответственно.
6. Затем составить сценарий, если величина кредита изменится на 87000р.
7. Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 7500р.

Вариант 14.

1. Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 77000р., сроком на 2 года, с ежемесячной выплатой 9000р. и годовой ставкой процента, равной 7,5%.
2. Затем, вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 9%.
3. Определить, используя таблицу подстановок:
4. величину всех выплат (БС) при процентных ставках 7%, 8% , 9% и 10% годовых;
5. величину всех выплат (БС) при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, а сроке займа 5, 7, 8, 9, 10 лет соответственно.
6. Составить сценарий, если величина кредита изменится на 86000р.
7. Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 120000р.

Вариант 15.

1. Вычислить общее количество периодов выплаты (КПЕР) фирмой, взявшей кредит в размере 113000р. Ставка процента постоянна и равна 10%. Ежемесячные выплаты фирмой также постоянны и равны 8500р.
2. Вычислить эту величину (не меняя формулу) при условии, что величина кредита изменится на 100000р.
3. Определить общее количество периодов выплаты (КПЕР), используя таблицу подстановок:
4. при процентных ставках 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сумме кредита 50000, 70000, 80000, 90000, и 100000 руб. соответственно.
6. Составить сценарий, если величина процентной ставки изменится на 8,5%, а сумма кредита на 85000 руб. Сохранить отчет типа структура.
7. Подобрать параметр величины кредита, если выплата будет производиться 4 года.

Вариант 16.

1. Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 80000р. со ставкой 8% годовых сроком на 6 лет и будущей стоимостью 8000р.
2. Вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 12%.
3. Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сроком на 5, 7, 8, 9, 10 лет соответственно.
6. Составить сценарий, если величина кредита изменится на 120000р, а срок на 10 лет.
7. Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 7000р.

Вариант 17.

1. Вычислить величину всех выплат (БС) фирмой, взявшей кредит в размере 65000р., сроком на 3 года, с ежемесячной выплатой 4000р. и годовой ставкой процента, равной 6,5%.
2. Затем, вычислить эту величину (не меняя формулу) при условии, что величина процентной ставки изменится на 5%.
3. Определить величину всех выплат (БС) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и суммах кредита 50000, 60000, 70000, 80000, 90000, 100000 руб. соответственно.
6. Составить сценарий, если величина кредита изменится на 70000р., а срок на 5 лет.
7. Подобрать параметр ежемесячной выплаты, если величина всех выплат составит 95000р.

Вариант 18.

1. Определить величину ежемесячной амортизации имущества (АПЛ) при условии, что начальная стоимость его 90000р., а остаточная (в конце периода амортизации) 9000р.; амортизация имущества занимает период 5 лет.
2. Затем вычислить эту величину (не меняя формулу) при условии, что остаточная амортизация равна 10000р.
3. Определить величину АПЛ используя таблицу подстановок:
4. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 9000 и том же периоде;
5. при варьировании остаточной амортизации: 5000, 6000, 7000, 8000, 10000 и периоде 1, 2, 3, 3,5 и 4 года соответственно.
6. После, составить сценарий, если начальная стоимость имущества изменится на 127000р., а период на 7 лет
7. Подобрать параметр срока полной амортизации при условии, что ежемесячные отчисления составят 7500р.

Вариант 19.

1. Вычислить величину ежемесячной выплаты (ПЛТ) фирмой, взявшей кредит в размере 60000р. со ставкой 6% годовых сроком на 4 года и будущей стоимостью 6000р.
2. Вычислить эту величину (не меняя формулу) при условии, что ставка процента изменится на 7%.
3. Определить величину ежемесячной выплаты (ПЛТ) используя таблицу подстановок:
4. при процентных ставках 5%, 7%, 8% , 9% и 10% годовых;
5. при процентной ставке 5%, 7%, 8%, 9%, 10% годовых, и сроком на 5, 7, 8, 9, 10 лет соответственно.
6. Составить сценарий, если величина кредита изменится на 80000р, а срок на 5 лет.
7. Подобрать параметр срока, на который был взят кредит, если ежемесячные выплаты составят 2000р.

Вариант 20.

1. Определить, на сколько снизится стоимость имущества (ДДОБ) на заданный период, используя метод двойной амортизации,если начальная стоимость имущества 120000р., а в конце периода эксплуатации 12000р. Время эксплуатации считать равным 26 месяцев, период, для которого вычисляется амортизация, равным 12 месяцев.
2. Вычислить эту величину (не меняя формулу) при условии, что остаточная стоимость имущества равна 9000р.
3. Определить величину ДДОБ используя таблицу подстановок:
4. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года;
5. при изменении времени эксплуатации: 7, 6, 5, 4, 3 года и варьировании начальной стоимости: 70000, 80000, 90000, 100000, 110000 соответственно.
6. Составить сценарий, если величина начальной стоимости изменится на 95000р.
7. Подобрать параметр срока эксплуатации, если стоимость имущества снизится до 7000р.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Для чего предназначены функции: ПЛТ; БС; ПС; КПЕР и СТАВКА? Поясните синтаксис перечисленных функций.
2. Назначение и способы анализа «Что если»?
3. Для чего предназначена «Таблица подстановок», опишите технологию ее применение для функций с одной переменной и для функций с двумя переменными?
4. Что такое сценарий, как его создать, просмотреть, изменить, получить итоговый отчет на отдельном листе?
5. Сущность операции Подбор параметра, как она выполняется?

Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.

Выполнение расчетов с помощью финансовых функций

В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.

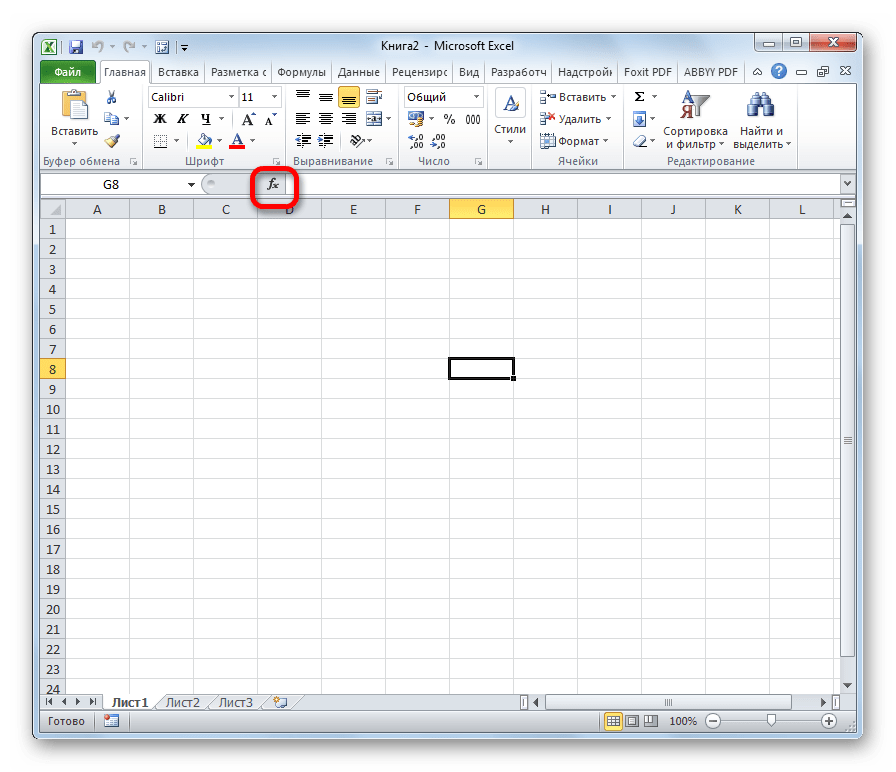
Переход к данному набору инструментов легче всего совершить через Мастер функций.

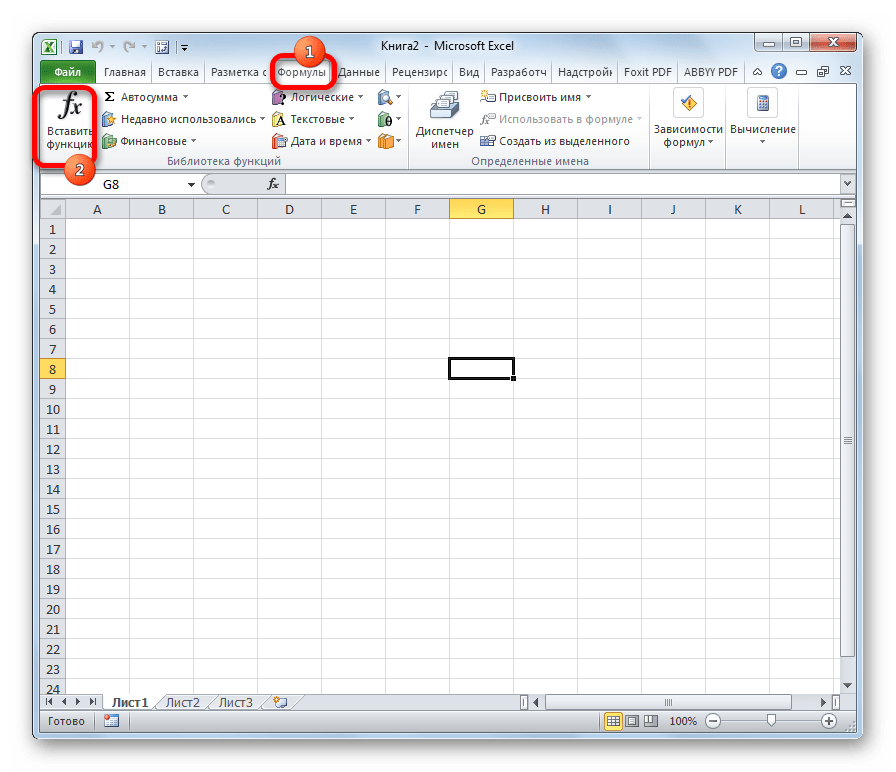
1. Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.



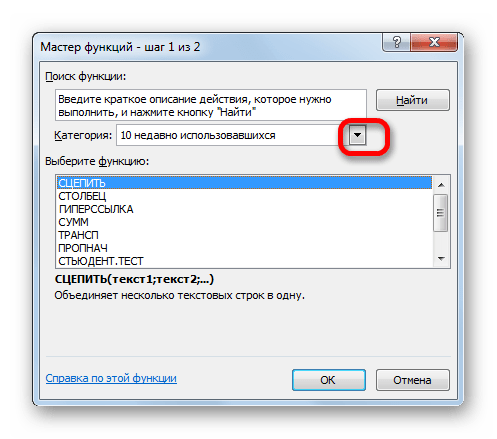
2. Запускается Мастер функций. Выполняем клик по полю «Категории».



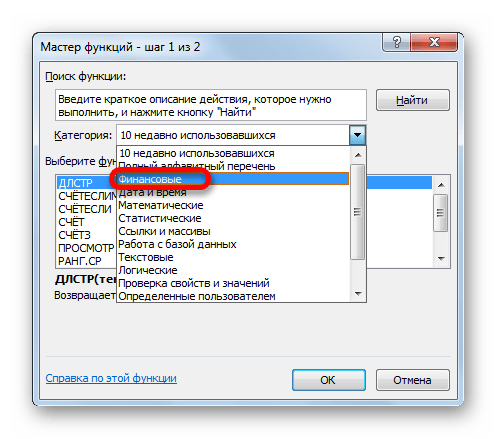
3. Открывается список доступных групп операторов. Выбираем из него наименование «Финансовые».



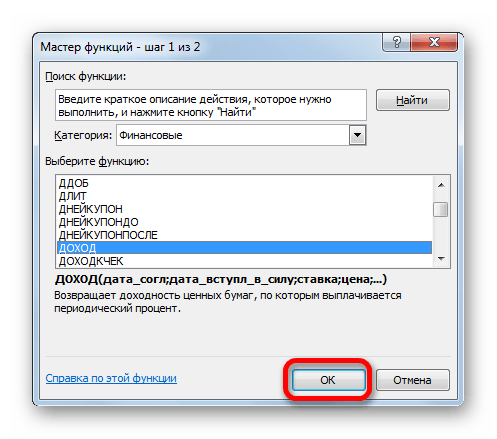
4. Запускается перечень нужных нам инструментов. Выбираем конкретную функцию для выполнения поставленной задачи и жмем на кнопку «OK». После чего открывается окно аргументов выбранного оператора.

В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.

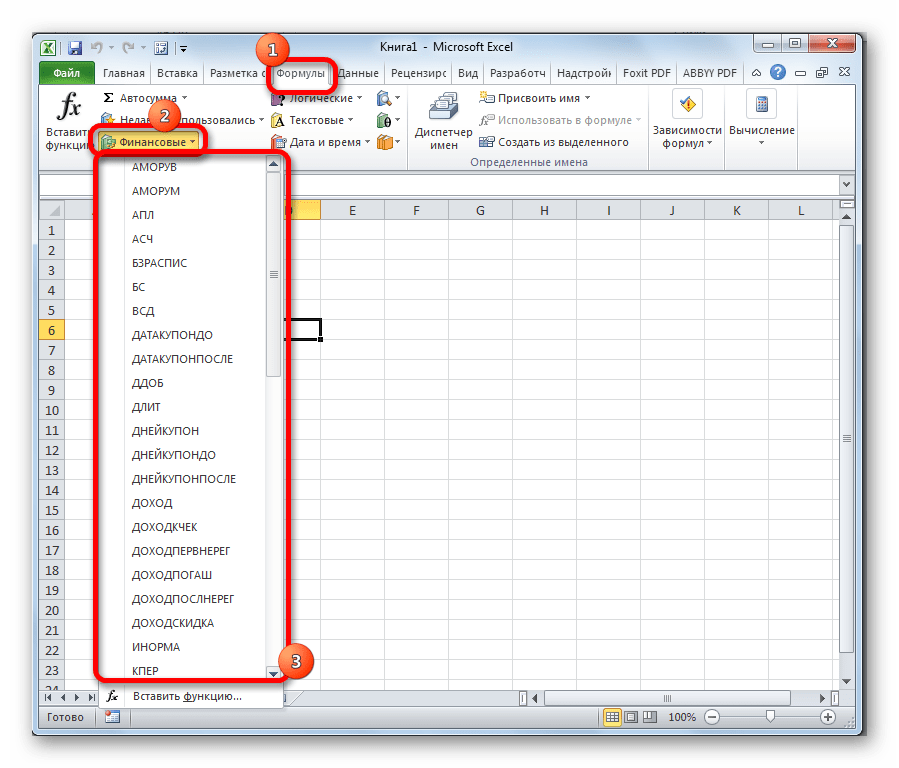
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.

Урок: Мастер функций в Excel

ДОХОД

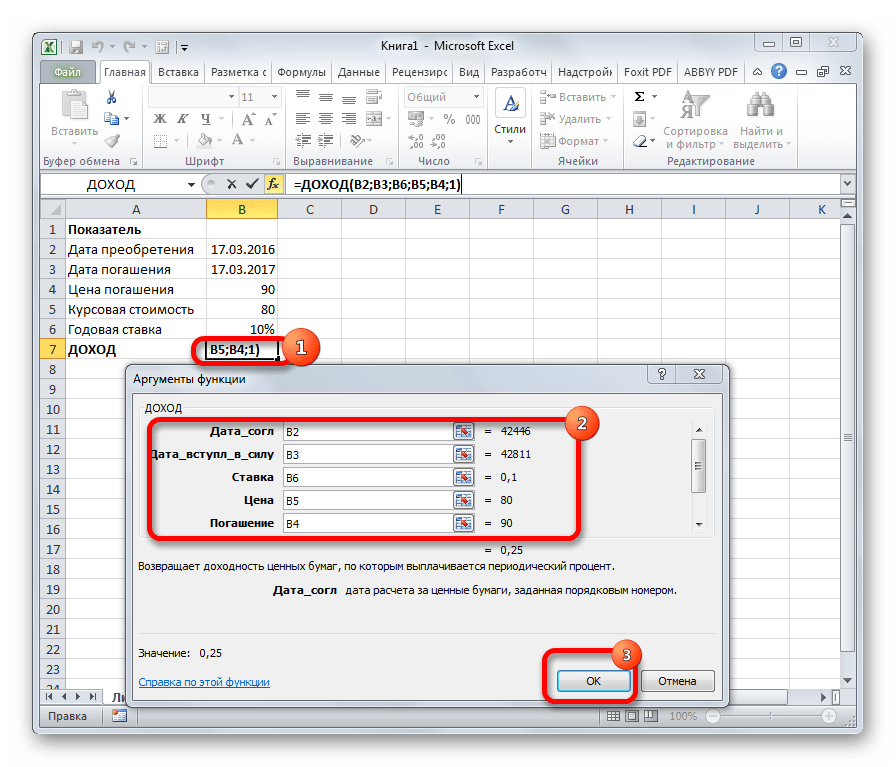
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:

=ДОХОД(Дата_сог;Дата_вступ_в_силу;Ставка;Цена;Погашение»Частота;[Базис])

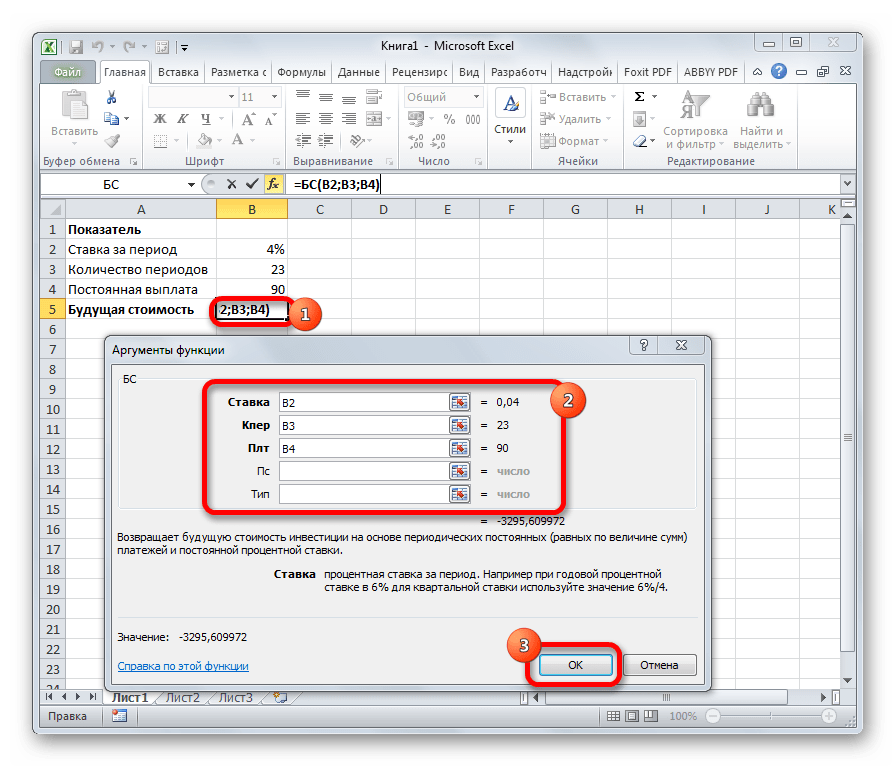
БС

Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:

=БС(Ставка;Кол_пер;Плт;[Пс];[Тип])

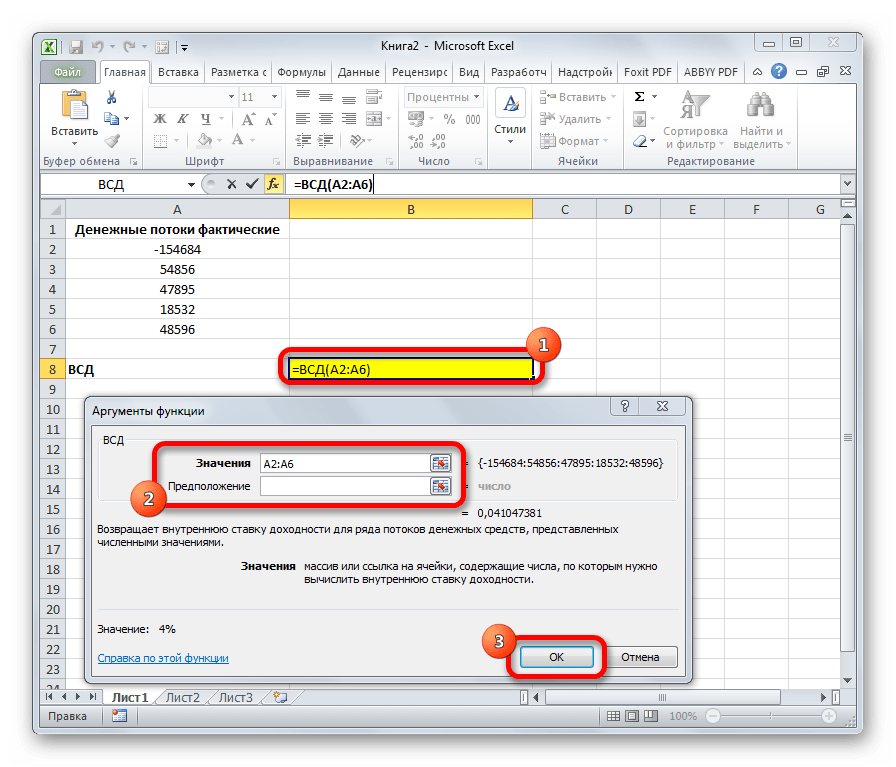
ВСД

Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:

=ВСД(Значения;[Предположения])

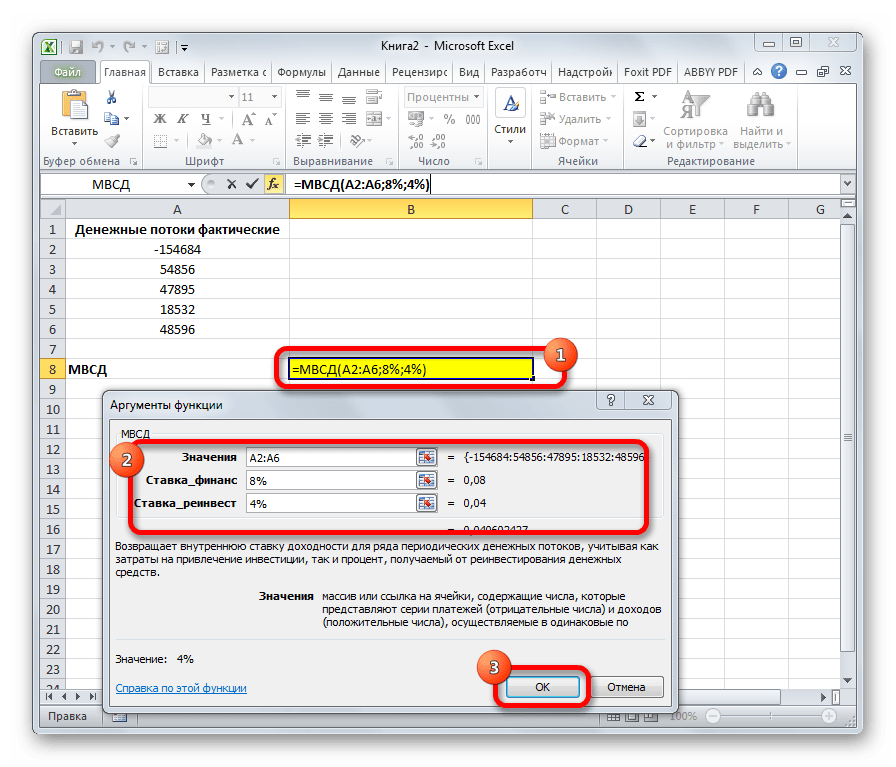
МВСД

Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:

=МВСД(Значения;Ставка_финансир;Ставка_реинвестир)

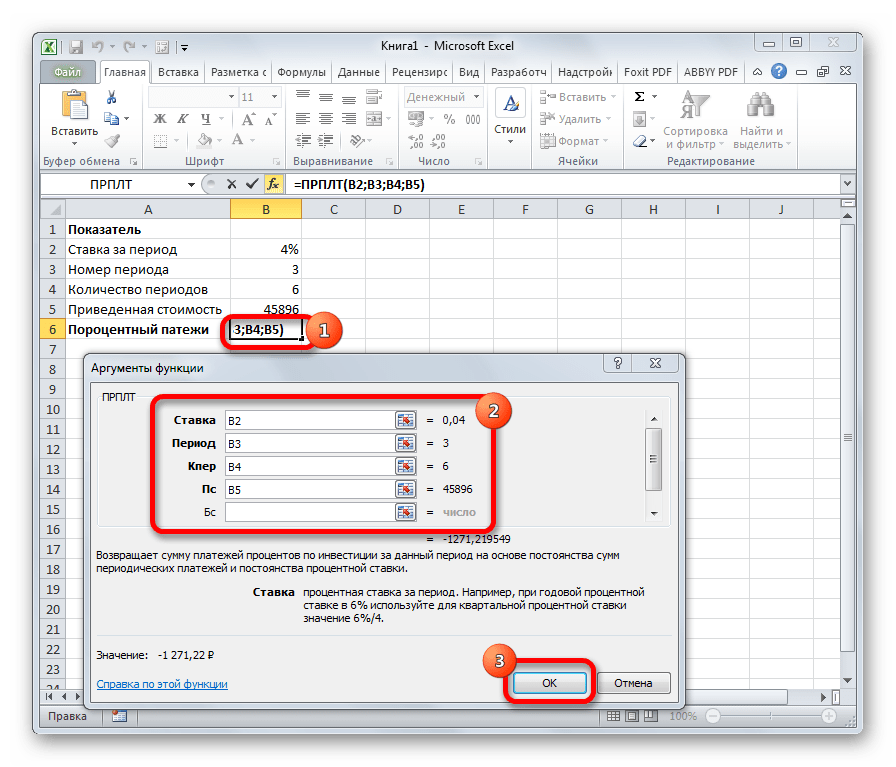
ПРПЛТ

Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:

=ПРПЛТ(Ставка;Период;Кол_пер;Пс;[Бс])

ПЛТ

Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:

=ПЛТ(Ставка;Кол_пер;Пс;[Бс];[Тип])

ПС

Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:

=ПС(Ставка;Кол_пер;Плт;[Бс];[Тип])

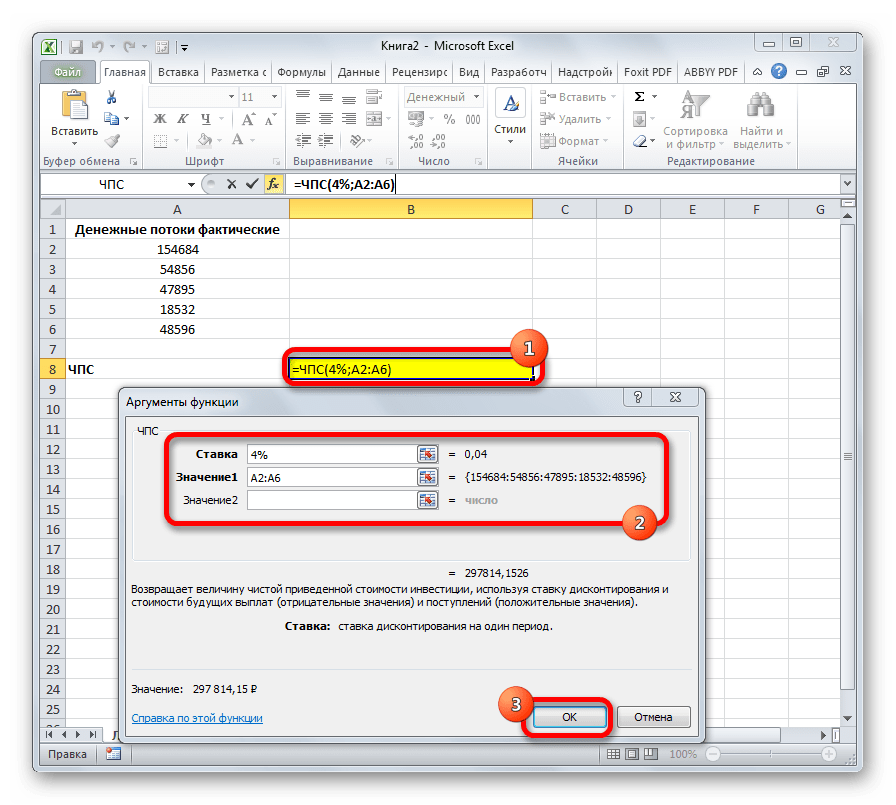
ЧПС

Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:

=ЧПС(Ставка;Значение1;Значение2;…)

СТАВКА

Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:

=СТАВКА(Кол_пер;Плт;Пс[Бс];[Тип])

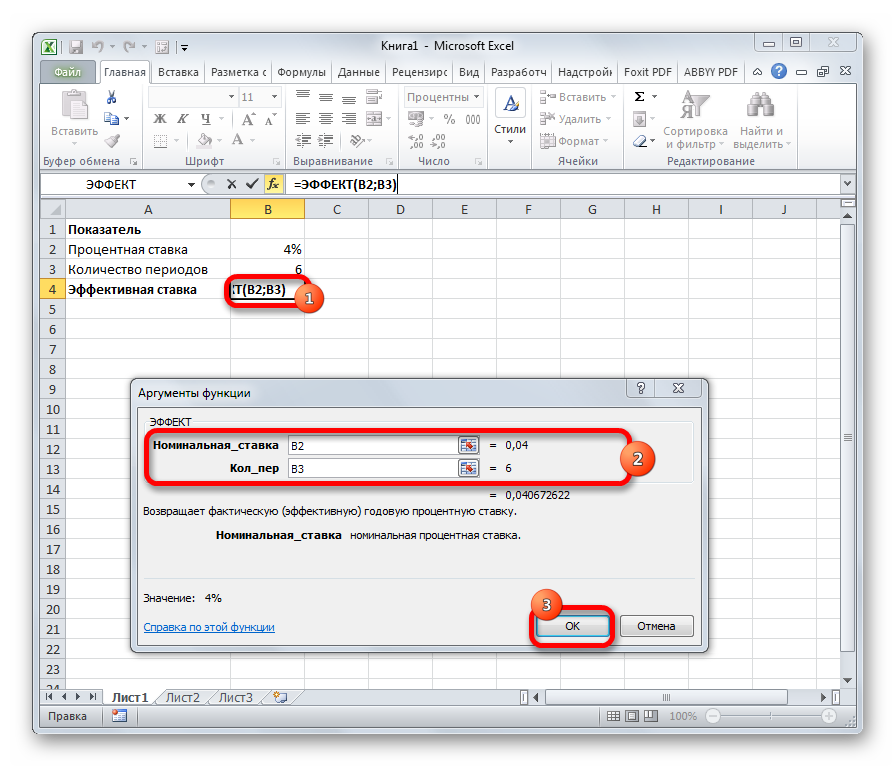
ЭФФЕКТ

Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:

=ЭФФЕКТ(Ном_ставка;Кол_пер)

Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.

Анализ данных «ЧТО-ЕСЛИ» в Excel

С помощью средств анализа «что если» в Microsoft Excel можно экспериментировать с различными наборами значений в одной или нескольких формулах для изучения всех возможных результатов. 

Формулы и функции в Excel автоматически пересчитывают результат при изменении содержимого ячеек, на которые имеются ссылки в данной формуле или функции. Другими словами, можно отвечать на вопросы типа «что-если». Например, при анализе финансовой функции ПЛТ ответить на вопрос, что будет, если первый взнос при получении ипотечной ссуды будет составлять не 20% от цены, а 15%. 

Итак, проиллюстрируем проведение анализа данных «что-если» на примере работы функции ПЛТ, которая вычисляет величину выплаты по ссуде на основе постоянных выплат и постоянной процентной ставки. 

Вызов функции имеет вид: ПЛТ (ставка;кпер;пс;бс;тип) 

Ставка —  процентная ставка по ссуде. 

Кпер — общее число выплат по ссуде. 

Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой. 

Бс — значение будущей стоимости, т. е. желаемого остатка средств после последней выплаты. Если этот аргумент опущен, предполагается, что он равен 0 (например, значение «бс» для займа равно 0). 

Тип — число 0 (ноль) или 1, обозначающее, когда должна производиться выплата. 

Рассмотрим пример использования функции ПЛТ в Exceel.

Итак, требуется определить ежемесячные выплаты по займу в 20 000 руб., взятому на 16 месяцев под 11% годовых. 

Для решения задачи выделяем ячейку на рабочем листе Excel (в нашел случаи ячейка А1) и в строку формул вводим следующее выражение: =ПЛТ(11%/12; 16; 20000) (Рис.1.1)

Рис. 1.1 —  Ввод формулы Excel. 

Нажав на клавишу  Enter   , мы получаем величину ежемесячных выплат по ссуде, которая составит -1350 руб. Рис.1.2

Рис. 1.2 – Величина ежемесячной выплаты по ссуде.

При ином значении банковской учетной ставки, следует сделать исправления в ранее введенной функции в Excel.  

Другой подход к вычислению функции ПЛТ методом «что если» в Excel проиллюстрирован на Рис. 1.3. Функция ПЛТ определена в ячейке D7, а значения аргументов записаны в ячейках D2, D3 и D4. Для получения значения функции при новых значениях аргумента достаточно внести соответствующие изменения в исходные данные. В этом случаи в строке формул на рис.1.3 мы вводим не конкретное значение аргумента, а ссылку ни соответствующую ячейку.  

Рис. 1.3 — Пример расчета Excel, в котором исходные данные в отдельные ячейки 

При изменении любых значений на рис.3 результаты расчета автоматически обновляются в разделе Результат расчета.  

Вывод: Рассмотренный выше примеры показывают, что размещение исходных данных в отдельные ячейки упрощает анализ зависимости выходного результата от изменения исходных данных с использованием анализа данных «Что если» в Exceel. 

Подбор параметра в Excel

При вычислении различных функций возникает вопрос: «Каким должно быть значение определенного аргумента функции, чтобы функция возвратила заданный результат?».  

Для решения такой задач в состав Excel включен специальный инструмент — Подбор параметра. С помощью этого инструмента определяется значение в одной ячейке исходных данных, которое требуется для получения требуемого значения в ячейке результата. 

Из расчетной части рис.1.3  видно, что при заданных исходных данных требуется ежемесячно выплачивать по 1350 руб. для погашения займа. Предположим, что по каким-то причинам кредитор имеется возможность выплачивать не более 1200 руб. в месяц. Спрашивается, какую максимальную величину ссуды может он запросить, если все прочие условия сохраняются? 

Для решения этой задачи выберем команду Данные > Анализ «что если» > Подбор параметра (рис. 2.1). В верхнем поле этого окна указывается ссылка на ячейку D7, в которой устанавливается желаемый результат (в нашем случае – это -1200 руб). В нижнее поле диалогового окна вставляется ссылка на ячейку, в которой хранится значение искомого параметра, т.е. D4.

Рис. 2.1 — Диалоговое окно Подбор параметра в Excel

Министерство науки и высшего образования Российской Федерации

Университетский колледж

федерального государственного бюджетного образовательного учреждения высшего образования

«Оренбургский государственный университет»

Н.А. Кривошеева

ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ

В ПРОФЕССИОНАЛЬНОЙ ДЕЯТЕЛЬНОСТИ

Финансовые функции Excel

Методические указания

Рекомендовано к изданию редакционно-издательским советом федерального государственного бюджетного образовательного учреждения высшего образования «Оренбургский государственный университет» для обучающихся по программе среднего профессионального образования по специальности 38.02.07 Банковское дело

Оренбург

2019

УДК 004(075.32)

ББК 32.97я723

К19

Рецензент – доцент кафедры программного обеспечения вычислительной техники и автоматизированных систем И.А. Щудро

Кривошеева, Н.А.

К82 Информационные технологии в профессиональной деятельности: финансовые функции Excel: методические указания / Н.А. Кривошеева; Оренбургский гос. ун-т. – Оренбург: ОГУ, 2019. – 55 с.

Методические указания предназначены для выполнения лабораторных работ по дисциплине «Информационные технологии в профессиональной деятельности» в Университетском колледже ОГУ для обучающихся третьего курса специальности 38.02.07 Банковское дело.

Методические указания составлены с учетом Федерального государственного образовательного стандарта среднего профессионального образования.

УДК 004(075.32)

ББК 32.97я723

©Кривошеева Н.А.,2019

©ОГУ, 2019

Содержание

Введение

Изначально данные методические указания планировались для обучающихся Университетского колледжа ОГУ по специальности 38.02.07 Банковское дело, которым по роду своей деятельности предстоит работать с финансами и банковскими расчетами. При написании методических указаний были внесены корректировки по теоретической части и внесены дополнения по практической части, методические указания были дополнены индивидуальными заданиям для обучающихся, заданиями для самостоятельного решения и контрольным вопросам для самопроверки усвоенного материала.

Прежде, чем приступить к освоению финансовых функций, необходимо изучить материал, который облегчит работу с оформлением формул и поможет усвоить материал по применению функций в короткие сроки. Особенность данных методических указаний заключается в том, что за несколько практических занятий, сопровождающихся теоретическим материалом, изложенным в доступной форме, обучающийся сможет выполнить не только элементарные операции, но и научится пользоваться функциями Excel. Все примеры дополнены наглядными рисунками. Материал методических указаний рассчитан для самостоятельно изучения и дает возможность использовать его не только на аудиторных (практических) занятиях, но и в домашних условиях, а в дальнейшем и в профессиональной деятельности.

Методические указания изложены в краткой и понятной форме, учтен необходимый минимум теоретического материала по изучению отдельного раздела Microsoft Excel (финансовые функции). Пользователем данных методических указаний могут быть не только обучающиеся колледжей, но и учащиеся школ, а также любой человек, которому интересно данное направление. Первый раздел знакомит пользователя с интерфейсом Excel, после чего пользователь может спокойно переходить к изучению функций.

1 Знакомство с интерфейсом

При первом запуске Microsoft Excel открывается новый файл, который принято называть книгой (рисунок 1). Книга изначально содержит три чистых листа (в левом нижнем углу есть ярлычки Лист1, Лист2, Лист3). Листы помогают распределить информацию в одной книге по целевому назначению. Количество листов в книге не ограничено. Можно добавить новый лист с помощью кнопки добавления листа; удалить ненужный лист, переименовать лист и выделить его цветом (нажав правую кнопку мыши на листе). Если листов в книге больше, чем может поместиться в области отображения ярлычков, то передвигаться между листами можно с помощью кнопок прокрутки листов.

Рисунок 1 – Интерфейс Excel 2010

Рабочую зону условно можно разделить на несколько областей, каждая из которых имеет свое значение и выполняет определенную функцию. Пользователю очень важно познакомиться с ними на начальном этапе изучения Excel. Рассмотрим их поподробнее.

В версии Office 2010 есть отличия от более ранней версии 2007, на которые мы будем обращать внимание. Кнопка Office заменена на вкладку Файл (рисунок 2). Здесь находятся команды создания, сохранения, открытия документов, а также печать.

Рисунок 2 – Вкладка «Файл»

Панель быстрого доступа расположена в левом верхнем углу (рисунок 3) и позволяет разместить часто встречающиеся команды для пользователя, обозначенные соответствующими кнопками. Эти кнопки называются инструментами.

Рисунок 3 – Панель быстрого доступа

Изначально на панели расположены три кнопки, но в зависимости от потребностей конкретного пользователя она может быть дополнена или изменена, так как панель быстрого доступа является настраиваемой.

Для того, чтобы настроить панель быстрого доступа нужно нажать на стрелочку вниз справа на панели и выбрать часто встречающиеся команды (рисунок 4).

Рисунок 4 – Настройка панели быстрого доступа через стандартные команды

Если в предложенном списке не обнаружено нужной команды, необходимо выбрать «Другие команды…», найти необходимую команду и с помощью кнопки «Добавить» настроить Панель быстрого доступа. Выбранные кнопки появятся на Рабочем столе Панели (рисунки5, 6).

Рисунок 5 – Добавление других команд на Панель быстрого доступа

В поле «Выбрать команды из:» выбрать нужный раздел или воспользоваться предлагаемым вариантом — «Часто используемые команды». В предлагаемом списке выбрать нужную команду, нажав на нее левой кнопкой мыши и с помощью кнопки «Добавить», в центре окна, перенести нужную команду из левой части экрана в правую, которая отвечает за наличие данной кнопки на Панели быстрого доступа. Удалить ненужную команду можно аналогичным образом, но в другой последовательности выбора ненужной команды из окна Панель быстрого доступа и выбрать кнопку «Удалить» в центре экрана.

Рисунок 6 – Настройка панели быстрого доступа через настройку параметров

Далее рассмотрим уже известные нам по MicrosoftOffice 2007 кнопки, вспомним их предназначение.

В верхнем правом углу расположены кнопки управления основным окном программы (развернуть, свернуть и закрыть основное окно программы).

Лента инструментов располагается в верхней части экрана исостоит из вкладок, которые, в свою очередь, позволяют получить быстрый доступ к определенной категории команд и кнопок, собранных по функциональному признаку в отдельные группы (рисунок 7).

Рисунок 7 – Лента с расположенными на ней вкладками и группами

При наведении курсора мыши на любой из инструментов отображается подсказка, которая обозначаетназвание используемого инструмента.

Рабочая область экрана состоит из строк и столбцов. Строки нумеруются цифрами, столбцы обозначаются буквами латинского алфавита (рисунок 8).

Рисунок 8 – Рабочая область Excel

На пересечении строк и столбцов образуется ячейка, каждая из которых имеет свое имя – по умолчанию имя ячейки включает букву столбца и номер строки. По имени ячейки можно к ней «обращаться», чтобы сделать ссылку в формуле.Имя текущей ячейки отображается в поле«Имя ячейки», например А1, В2, С12 и т.д. (рисунок 9).

Рисунок 9 – Обозначение имени текущей ячейки

Справа от «Имени ячейки» расположена «Строка формул», которая дублирует информацию, зафиксированную в текущей ячейке. Если в ячейке использовался текст или число, то в строке формул информация дублируется. Если в ячейке применялась формула, то на экране будет отображаться результат выполнения формулы, а в строке формул сама формула (рисунок 10).

Рисунок 10 – Отображение формулы в Строке формул

Получив элементарные навыки работы в Excel, можно переходить к следующему разделу.

Познакомившись с интерфейсом Excel2010 и рассмотрев небольшую часть возможностей настроек табличного процессора можно сделать вывод, что каждый пользователь может легко настроить внешний вид программы «под себя», изменив ряд параметров, сделав его удобным и привлекательным для себя.

2 Полезные «мелочи»

В этом разделе мы рассмотрим несколько полезных кнопок и команд, которые помогут вам эргономично расположить элементы окна в зоне видимости и наиболее рационально использовать время для поиска нужной информации на экране.

2.1 Стиль ссылок

Привычным стилем оформления ссылок на ячейки служит ссылка на строку и столбец, которые определяются соответственно буквой и цифрой, например F5 или А8. Бывают случаи, когда вы открываете присланный вам файл, а ссылки на ячейки выглядят как на рисунке 11.

Рисунок 11 – Стиль цифровой нумерации столбцов

Стиль цифровой нумерации выставлен в Excel 2010 по умолчанию, но не для всех пользователей он удобен. Особенно это заметно, когда необходимо использовать ссылки, тогда не опытному пользователю прочитать ссылку становится трудно. Вернуть привычное буквенное обозначение столбцов не составит труда, выполнив несколько несложных операций.

Для этого на вкладке «Файл» необходимо выбрать команду «Параметры» (рисунок 12). В открывшемся диалоговом окне выбрать вкладку «Формулы» и отключить «галочку» со строки «Стиль ссылок R1C1» (рисунки 12, 13).

Рисунок 12 – Настройка параметров нумерации столбцов

Рисунок 13 – Вкладка формулы для изменения стиля ссылок

2.2 Инструменты вкладки Вид

С помощью вкладки Вид (рисунок 14) можно настроить расположение окон при одновременном открытии нескольких документов, разделить область рабочего листа или закрепить видимую область экрана.

Рисунок 14– Вкладка Вид – группа Окно

Команда «Разделить» выводит в рабочую область текущего листа разделительные линии (рисунок 15), которые можно перемещать влево, вправо, вверх, вниз, причем области разделения листа становятся независимыми друг от друга по навигации. Вы можете заметить, что появилось несколько линеек прокрутки (и вертикальных, и горизонтальных).

Рисунок 15 – Разделение рабочей области листа

На рисунке 15 приведен пример разделение окна при работе с одним листом. Можно заметить, что нумерация строк и обозначение столбцов прерываются во всех зонах, но мы все равно находимся на одном листе. Такое разделение листа позволяет работать с удаленными друг от друга данными одного текущего листа.

Другая команда «Закрепить области», в отличие от ранее рассмотренной команды «Разделить», не добавляет дополнительные полосы прокрутки и делает разделительные линии на листе практически не заметными. Такая команда незаменима в тех случаях, когда нужно, чтобы «шапка таблицы» (верхняя строка или первый столбец) была всегда видимой. На рисунке 16 можно заметить, что после первой строки сразу идет двадцатая. Данные остальных строк никуда не исчезли, они, как будто «прокручены» вверх. Если переместить линейку прокрутки вверх, то нижние строчки сместятся вниз, а верхние появятся на экране.Перемещение по листу можно производить с помощью колесика мыши, верхняя строка всегда будет оставаться видимой.

Рисунок 16 – Закрепление области верхней строки

2.3 Маркер автозаполнения

При необходимости ввода повторяющихся данных в несколько смежных ячеек можно скопировать данные одной ячейки и вставить в другую, но можно воспользоваться более простым способом – использовать Маркер автозаполнения.

Обратите внимание на нижний правый угол текущей ячейки и вы увидите небольшой черный квадратик, который называется Маркером автозаполения и несет в себе несколько важных функций. Если выделено несколько смежных ячеек, то маркер находится также в правом нижнем углу выделенного диапазона. Далее мы рассмотрим несколько примеров применения данного маркера.

При заполнении ячейки произвольными данными Маркер автозаполнения (далее Маркер)позволяет скопировать данные этой ячейки в соседние (рисунок 17). Маркер можно протягивать вниз, вверх, вправо, влево – данные будут копироваться.

Рисунок 17 – Использование Маркера автозаполнения

Если в текущую ячейку, например, А1 записать название месяца, дня недели или даты, то Маркер позволит заполнить соседние ячейки последовательными месяцами, днями недели или датами соответственно (рисунки 18, 19, 20). Причем, протягивая Маркер вправо или вниз происходит наращивание приведенных показателей на одну условную единицу, а при протягивании влево или вверх происходит уменьшение на одну условную единицу.

Рисунок 18 – Применение Маркера при вводе месяцев

Рисунок 19 – Применение Маркера при вводе дней недели

Рисунок 20 – Применение Маркера при заполнении дат

При создании в ячейке формулы, нет необходимости перенабирать эту формулу в остальные ячейки столбца или строки. Маркер автозаполнения позволяет копировать формулу относительно перемещения курсора (ссылка называется относительной). Ссылки на ячейки, используемые в копируемой формуле сместятся ровно на столько ячеек, насколько переместился курсор (рисунок 21).

Рисунок 21 – Применение Маркера при копировании формул

Теперь вы познакомились с некоторыми особенностями работы в Excel, которые помогут вам в дальнейшей работе. Применяя эти несложные правила, вы сможете быстро вводить данные и находить нужную информацию в созданном документе.

3Вычисления в Excel 2010

3.1 Общие сведения о создании формул

При наборе формулы важно помнить о том, что формула обязательно начинается со знака равенства (=). Основными операторами для создания формулы или функции являются:

— оператор сложения (+);

— оператор вычитания (-);

— оператор умножения (*);

— оператор деления (/);

— оператор возведения в степень (^);

— оператор процента (%).

На рисунке 22 приведены примеры использования основных операторов.

Рисунок 22 – Использование основных операторов

3.2 Относительные и абсолютные ссылки

При работе с формулами возникает необходимость ссылаться на ячейки с данными расположенными не только на текущем рабочем листе, но и на другом листе или даже в другой книге. Причем эти данные могут быть как числовые, так и текстовые. При создании формулы ссылка идет на ячейку, а вычисления производятся с данными, расположенными в указанной ячейке.

В подразделе 2.2 на рисунке 21 был приведен пример использования относительной ссылки. При копировании относительной ссылки вниз или вверх по столбцу ссылки на ячейки в формуле тоже будут меняться. Если ячейку, содержащую относительную ссылку переместить, например перетаскиванием, копированием или вырезанием, то ссылка станет абсолютной.

Абсолютная ссылка всегда указывает на одну и ту же фиксированную ячейку, которая не меняется ни при каких обстоятельствах ее перемещения (при перетаскивании, копировании, вырезании).Отличие в использовании формулы с относительной и абсолютной ссылкой приведено на рисунке 23.

Чтобы создать абсолютную ссылку самостоятельно, нужно добавить знак доллара ($) перед каждым элементом имени ячейки в формуле, например $A$1. Знак доллара можно использовать при создании смешанной ссылки:

— если нужно, чтобы строка менялась, а столбец не менялся, то знак доллара добавляется только перед обозначением столбца, например А$1;

— если нужно, чтобы столбец менялся, а строка не менялась, то знак доллара добавляется только перед обозначением строки, например $А1.

Переключение между относительными и абсолютными ссылками производится клавишей F4.

Рисунок 23 – Применение относительных и абсолютных ссылок

3.3 Как читать сообщение об ошибке

При работе с формулами и финансовыми вычислениями в Excel есть вероятность допустить неточность в оформлении ссылок или ошибку в написании функции. Опытному пользователю не составит труда выявить и устранить этот недочет, но как разобраться с формулировками об ошибке тому, кто только начинает осваивать Excel? Рассмотрим на примере часто встречающиеся записи об ошибках и дадим рекомендации как их устранить.

3.3.1 Ошибка #### самая распространенная и легко устранимая. Такая ошибка означает, что ширина столбца не достаточна велика для отображения значения в ячейке (рисунок 24).

Рисунок 24 – Ошибка#### недостаточная ширина столбца

Чтобы исправить ошибку, нужно увеличить ширину столбца с помощью мыши. Можно отрегулировать ширину столбца по самому длинному значению в столбце нажав, для этого два раза левой кнопкой мыши на разделительной полосе между названиями соседних столбцов.

Такая же ошибка может появиться в том случае, если после производимых вычислений с датами или временем появляется отрицательное число, так как дата и время должны быть положительными (рисунок 25).

Рисунок 25 – Ошибка#### дата или время

Чтобы исправить появившуюся ошибку нужно или исправить ссылки в используемой формуле, чтобы вычисляемое число часов (дней) было положительными или изменить формат выводимых данных.

3.3.2 Ошибка #ИМЯ? означает, что используемой в данной формуле ячейке изначально не было определено Имя или оно в процессе редактирования было удалено (рисунок 26).

Рисунок 26– Ошибка #ИМЯ? в Имени ячейки

Для того, чтобы устранить данную ошибку нужно сначала определить Имя ячейки, на которую будет ссылаться формула, только после этого применять ссылку на Имя. Внимательно работать с Диспетчером имен при удалении Имен.

Аналогичная ошибка может появиться в том случае, если в написании функции допущена ошибка (рисунок 27).

Рисунок 27 — Ошибка #ИМЯ? в функции

Для решения этой проблемы нужно проверить написание функции. В данном примере при написание функции должно быть ПОИСКПОЗ. Диапазон здесь указан правильно. Можно привести другой пример, когда ошибка возникает из-за неправильно указанного диапазона (рисунок 28).

Рисунок 28 – Ошибка #ИМЯ? в диапазоне ячеек

В данном примере между А1 и А3 пропущено двоеточие. Правильно будет указать диапазон следующим образом: А1:А3.

Если в формуле используется текстовое значение, то оно должно быть заключено в кавычки, иначе в ячейке появится такая же ошибка (рисунок 29).

Рисунок 29- Ошибка #ИМЯ? в текстовом значении

Ошибка будет устранена при заключении текста в двойные кавычки: =»Итого»&А4.

3.3.3 Ошибка #ЧИСЛО означает, что в формуле используется некорректное число (рисунок 30).

Рисунок 30 – Ошибка #ЧИСЛО при некорректном использовании чисел

При анализе данной функции можно сделать вывод, что корень извлекается из положительного числа, а в ячейке А1 введено отрицательное. Достаточно будет убрать минус в числе 64 и ошибка будет исправлена.

3.3.4 Ошибка #ЗНАЧ! Означает, что в формуле используется аргумент, значение которого не допустимо для данной формулы.

Например в формуле складываются ячейки, но в одной или нескольких из них вместо числа стоит пробел, символ или текст, которые, как очевидно, не могут складываться с числом (рисунок 31).

Рисунок 31 – Ошибка #ЗНАЧ! при текстовом значении

Исправить такую ошибку не составит труда, поставив в нужную ячейку число.

Такая же ошибка появится в том случае, если при использовании функции вы введете диапазон ячеек в том месте, где предполагается ввод одного значения (рисунок 32).

Рисунок 32 — Ошибка #ЗНАЧ! при задании аргументов функции

Устранить ошибку можно в строке формул, указав правильную ссылку или пересмотреть используемую функцию через Мастер функций.

3.3.5 Ошибка #ССЫЛКА появляется в том случае, когда формула содержит ссылку на несуществующую или удаленную ячейку (рисунок 33).

Рисунок 33 — Ошибка #ССЫЛКА при несуществующей ячейке

В данном случае рекомендуется изменить формулу и внести корректные ссылки на существующие ячейки.

3.3.6 Ошибка #ДЕЛ/0!

При появлении данной ошибки у пользователя появляется неправильное восприятие, читаемое как ДЕЛО, на самом деле, все довольно просто. Такая ошибка появляется при делении на ноль, так как делить на ноль нельзя! (рисунок 34).

Рисунок 34 — Ошибка #ДЕЛ/0! при делении на ноль

3.3.7 Ошибка #Н/Д означает, что в данной формуле использовалось недоступное значение (рисунок 35).

Рисунок 35 — Ошибка #Н/Д недопустимое значение

Такая ошибка может возникнуть в функциях ВПР (вертикальный просмотр), ГПР (горизонтальный просмотр), ПРОСМОТР, ПОИСКПОЗ (поиск позиции) и означает, что задан неверный аргумент для поиска (искомое_значение). По формуле видно, что ищется значение 255, в используемом списке такого значения нет. Такая же ошибка появится в том случае, если в функции будет пропущен один или несколько обязательных аргументов.

3.3.8 Ошибка #ПУСТО! означает, что в формуле были использованы непересекающиеся значения (рисунок 36).

Рисунок 36 – Ошибка #ПУСТО! непересекающиеся значения

Для исправления формулы рекомендуется проверить правильность написания формулы и выставить правильный диапазон.

4 Финансовые функции

Большой популярностью у экономистов пользуется Excel благодаря которому выполнение различных финансовых расчетов можно автоматизировать у упростить с помощью финансовых функций. Многие из них могут пригодиться не только специалистам экономического профиля, но и работникам банковской сферы и других смежных отраслей. Обычному пользователю подобные расчеты пригодятся в их бытовых нуждах. Рассмотрим особенности создания финансовых функций с помощью возможностей Excel, обратив внимание на самые популярные операторы группы финансовых функций.

Для того, чтобы создать финансовую функцию можно воспользоваться Мастером создания функций. Для этого нажать кнопку «Вставить функцию», которая расположена на вкладке «Формулы».

Поместить курсор в ячейку, в которой будет производиться расчет и выводится результат. На вкладке «Формулы» нажать кнопку «Вставить функцию». На первом шаге Мастера функций изначально будут выведены 10 недавно использовавшихся функций (рисунок 37).

Рисунок 37 – Первый шаг Мастера функций

В поле Категория выбираем финансовые функции (рисунок 38).

Рисунок 38 – Выбор категории Финансовые функции

Выбрав одну из предложенных функций, вы перейдете в окно заполнения аргументов данной функции (в нашем примере функция БС). Переменные можно вводить несколькими способами:

1) с клавиатуры ввести числовые данные (рисунок 39);

2) мышкой поочередно выделить ячейки в которой хранятся данные той или иной переменной (рисунок 40), на экране ячейка будет выделена рамкой;

3) ввести имя ячейки (например А1, В2 и т.д.) с клавиатуры в английской раскладке. В этом случае процесс заполнения визуально будет похож на второй способ. Если ссылки на ячейки ошибочно введены на русской раскладке клавиатуры, то вычислений не произойдет, будет отображена ошибка введение имен ячеек (рисунок 41).

Рисунок 39 – Заполнение аргументов функции БС с клавиатуры

Рисунок 40 – Заполнение аргументов функции БС с помощью ссылок на соответствующие ячейки

Рисунок 41 – Заполнение аргументов функции БС с записью имен ячеек с клавиатуры (ошибочный ввод)

Обратите внимание как выглядят формулы на рисунках 39-41. Результат вычислений получается во всех случаях одинаковый.

Во вкладке «Формулы» в группе «Библиотека функций» также можно воспользоваться вставкой функции, для этого нужно выбрать категорию функций «Финансовые» (рисунок 42).

Рисунок 42 – Выбор финансовых функций в группе «Библиотека функций» текущей вкладки «Формулы»

Из появившегося списка выбрать необходимую функцию (рисунок 43) и далее в появившемся диалоговом окне выбрать аргументы функции.

Рисунок 43 – Выбор финансовой функции через список функций

В зависимости от применяемой функции количество переменных и их очередность в формуле может меняться.

Рассмотрим основные переменные, используемые при создании финансовых функций:

1) кпер – число периодов платежей по кредиту (указывается количество лет, если выплаты производятся ежемесячно, тогда указанное количество лет умножается на 12, а процентная ставка в этом случае будет делиться на 12);

2) ставка – процентная ставка (годовая — указывается в процентах, если выплаты производятся ежемесячно, то необходимо ставку поделить на 12, то есть 17%/12);

3) плт – платеж, производимый в каждый период (состоит из основного платежа и платежа по процентам);

4) пс – сумма на текущий момент;

5) бс – будущая стоимость;

6) тип – по умолчанию принимаетсяноль — означает, что оплата производится в конце периода, если оплата производится в начале периода, то в формуле вместо нуля ставится единица.

При создании финансовых функций нужно запомнить, что переменные могут быть как отрицательными числами, так и положительными, в зависимости от того получаем мы деньги или отдаем (поступления задаются положительными числами, а выплаты – отрицательными).

Рассмотрим наиболее востребованные финансовые функции в деятельности банковского работника на конкретных примерах. Усвоив принцип работы по созданию основных финансовых функций, вы сможете перейти к решению более сложных задач, связанных с вашей профессиональной деятельностью.

4.1 Функция БС определяетбудущую стоимость инвестиций

Функция БС() — рассчитывает будущую стоимость периодических постоянных платежей и будущее значение вклада (или займа) на основе постоянной процентной ставки.

Синтаксис функции БС: =БС(ставка;кпер;плт;[пс];[тип]). Аргументы [пс] и [тип] относятся к необязательным, поэтому помещены в квадратные скобки.

Пример 1. Определить наращенную сумму для вклада в размере 10000 рублей, размещенного под 15% годовых на один год

Результат =БС(B2;B3;;B4) = 11500 рублей.

Рисунок 44 – Результат выполнения примера 1

Пример 2.На банковский счет под 11,5% годовых внесли 37000 рублей. Определить размер вклада по истечение 3 лет, если проценты начисляются каждые полгода.

Результат =БС(B10;B11;;B13) = 51746,86 рублей.

Рисунок 45 – Результат выполнения примера 2

Пример 3. Определить, сколько денег окажется на банковском счете, если ежегодно в течение 5 лет под 17% годовых вносятся 20000 рублей. Взносы осуществляются в начале каждого года.

Результат =БС(B20;B21;B22;;B24) = 164136,96 рублей.

Рисунок 46 – Результат выполнения примера 3

Пример 4. Если нам необходимо сделать вклад под 15 % годовых с ежемесячным начислением процентов на сумму 100000 рублей на три года. Какую сумму мы получим в конце периода?

В этом примере переменная ПС равна минус 100000 рублей, так как мы отдаем деньги, тогда результат у нас будет положительными числом, так как получаем доход.

Результат: =БС(B1;B2;;B4) = 156394,38 рублей.

Рисунок 47 – Результат выполнения примера 4

4.2 Функция ПС определяет сумму денег в настоящий момент

Функция ПС() — предназначена для расчета текущей стоимости, как единой суммы вклада (займа), так и будущих фиксированных периодических платежей. Текущий объем — это общая сумма, которую составят будущие платежи. Например, когда деньги берутся взаймы, заимствованная сумма и есть текущий объем для заимодавца. Этот расчет является обратным к определению будущей стоимости при помощи функции ПС.

Синтаксис: =ПС(ставка;кпер;плт;[бс];[тип]). Аргументы [бс] и [тип] относятся к необязательным, поэтому помещены в квадратные скобки.

Пример 5. Фирме потребуется 5000000 рублей через 10 лет. В настоящее время располагает деньгами и готова положить их на депозит единым вкладом с тем, чтобы через 10 лет получить необходимую сумму. Определить необходимую сумму текущего вклада если ставка процента по нему составляет 12% в год.

Результат =ПС(B2;B3;;B5) = -1609866,18 рублей. Результат отрица-тельный, так как эти деньги фирме нужно отдать в настоящий момент.

Рисунок 48 – Результат выполнения примера 5

Пример 6. Клиент заключает с банком договор о выплате ему в течение 5 лет ежегодной ренты в размере 5000 рублей в конце каждого года. Какую сумму необходимо внести клиенту в начале первого года, чтобы обеспечить эту ренту, исходя из годовой процентной ставки 20%?

Результат =ПС(B10;B11;B12) = — 14953,06 рублей. Результат о трица-тельный, так как клиент должен ее отдать.

Рисунок 49 – Результат выполнения примера 6

Пример 7. Предположим, что мы хотим получать доход, равный 1000 рублей в год, на протяжении 4-х лет. Какая сумма обеспечит получение такого дохода, если ставка по срочным депозитам равна 10% годовых, выплаты производятся вначале года.

Результат =ПС(B18;B19;B20;;1) = — 3486,85 рублей.

Рисунок 50– Результат выполнения примера 7

Пример 8. На какую сумму можно взять кредит, если ставка 17 % годовых и выплачивать мы можем по 10000 рублей в месяц на протяжении двух лет?

Результат: =ПС(B1;B2;B3) = 202256,11 рублей.

Рисунок 51 – Результат выполнения примера 8

Пример 9. Какую сумму кредита можно взять под 17 % годовых с ежемесячным начислением процентов, если выплачивать мы можем ежемесячно на протяжении двух лет и в итоге готовы выплатить 300000 рублей?

В этом примере нет переменной ПЛТ, но есть переменная БС, которую пишем с минусом, так как отдаем эту сумму.

Результат: =ПС(B1;B2;;B4) = 214041,15 рублей.

Рисунок 52 – Результат выполнения примера 9

4.3 Функция ПЛТ определяет сумму ежемесячных платежей

Функция ПЛТ() — позволяет рассчитать сумму постоянных периодических платежей, необходимых для равномерного погашения займа при известных сумме займа, ставки процентов и срока на который выдан заем.

Синтаксис: =ПЛТ(ставка;кпер;нз;[бс];[тип]). Аргументы [бс] и [тип] относятся к необязательным, поэтому помещены в квадратные скобки.

Пример 10. Необходимо накопить 4000 рублей за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой должна быть эта сумма, если норма процента по вкладу составляет 12% годовых.

Результат =ПЛТ(B2;B3;;B5) = — 92,86 рублей.

Рисунок 53 – Результат выполнения примера 10

Пример 11. Клиент банка осуществляет заем в размере 5000 рублей под 6 % годовых на 6 месяцев. Определить ежемесячные платежи клиента, если платежи осуществляются в конце месяца.

Результат =ПЛТ(B10;B11;B12) = — 922,99 рублей.

Рисунок 54 – Результат выполнения примера 11

Пример 12. Допустим, банк выдал ссуду 200000 рублей, на 4 года под 18 % годовых. Ссуда выдана в начале года, а погашение начинается в конце года одинаковыми платежами. Определите размер ежегодного погашения ссуды

Результат =ПЛТ(B20;B21;B22) = -74347,73 рубля.

Рисунок 55 – Результат выполнения примера 12

4.4 Функция КПЕР определяет количество периодов платежей

Функция КПЕР() — вычисляет количество периодов начисления процентов.

Синтаксис: КПЕР(ставка;плт;пс;[бс];[тип]). Аргументы [бс] и [тип] относятся к необязательным, поэтому помещены в квадратные скобки.

Пример 13. По вкладу в 10000 рублей, помещенному в банк под 5% годовых, начисляемых ежегодно была выплачена сумма 12762,82 рубля. Определить срок проведения операции (количество периодов начисления)

Результат=КПЕР(B2;;B4;B5) = 5 периодов (5 лет).

Рисунок 56 – Результат выполнения примера 13

Пример 14. Через сколько лет вклад размером 500 рублей достигнет величины 1000 рублей при ставке процентов 10% с ежемесячным начислением процентов.

Результат:

а)=КПЕР(B10;;B12;B13) = 7,27 лет;

б)=КПЕР(D10;;D12;D13) = 83,52 месяцев.

Рисунок 57 – Результат выполнения примера 14

Пример 15. Пусть ставка кредита 17 % годовых, сумма кредита 100000 рублей и мы можем выплачивать по 5000 рублей ежемесячно. Определить за сколько периодов мы погасим кредит?

Пишем минус 5000, так как мы отдаем деньги. Получаем приблизительно 23,68 периодов, то есть месяцев, что соответствует почти двум годам.

Результат: =КПЕР(B1;B2;B3) = 23,68 (месяцев), примерно 2 года.

Рисунок 58 – Результат выполнения примера 15

4.5 Функция СТАВКА определяет процентную ставку за период

Функция СТАВКА() — вычисляет процентную ставку, которая в зависимости от условий операции может выступать либо в качестве цены, либо в качестве нормы ее рентабельности.

Синтаксис: СТАВКА(кпер;плт;пс;[бс];[тип]). Аргументы [бс] и [тип] относятся к необязательным, поэтому помещены в квадратные скобки.

Пример 16. Фирме через 2 года потребуется 100000 рублей. Для достижения этой цели фирма готова положить на депозит 25000 рублей (ежемесячно). Каким должен быть процент на инвестированные средства с тем, чтобы к концу второго года была получена необходимая сумма

Результат =СТАВКА(B2;;B4;B5) = 6 %.

Рисунок 59 – Результат выполнения примера 16

Пример 17. На полтора года в долг дана сумма 20000 рублей с условием возврата 30000 рублей. Вычислить годовую процентную ставку.

Результат =СТАВКА(B10;;B12;B13) = 31 %.

Рисунок 60 – Результат выполнения примера 17

Пример 18. Допустим мы хотим взять кредит в 100000 рублей на два года, выплачивать мы можем по 5000 рублей ежемесячно. Какая ставка нам подходит?

Результат: =СТАВКА(B1;B2;B3) = 1,51 % на месяц = 18,157 % годовых.

Рисунок 61 – Результат выполнения примера 18

При заполнении поля КПЕР было указано 24 месяца, следовательно в результате получили ставку за месяц, умножим ее на 12 месяцев, получим годовую ставку равную 18,157 %.

Мы рассмотрели часто встречающиеся функции и на конкретных примерах увидели процесс решения той или иной задачи. Если вы разобрались с принципом создания основных финансовых функций, то вам не составит труда рассмотреть и другие функции данного раздела. Для закрепления полученных знаний обучающимся предлагается выполнить практическую работу с аналогичными заданиями. Для закрепления пройденного материала обучающимся предлагаются задания для самостоятельного решения с применением и других функций данного раздела.

5 Практическая часть работы

Цель работы: обобщить полученные знания по теме «Финансовые функции», уметь находить верное решение, научиться пользоваться функциями.

Ход работы:

1) внимательно прочитайте заданиясвоего варианта (вариант определяется по номеру рабочего места);

2) определите с помощью какой финансовой функции нужно произвести расчет для данных задач;

3) откройте Ecxel, создайте новую книгу, создайте в ней пять листов;

4) каждое заданиевыполняйте на новом листе, переименовав листы под название функции для расчета;

5) на каждом листе задайте параметры для вычислений и решите задачу;

5) покажите работу преподавателю, обоснуйте свое решение.

Вариант 1

1) Рассчитать какая сумма окажется на счете, если 27 тыс. руб. положены на 4 года под 13,5% годовых. Проценты начисляются каждые полгода.

2) Компании X потребуется 100000 тыс. руб. через 2 года:

а) компания готова вложить 5000 тыс. руб. сразу и по 2500 тыс. руб. каждый последующий месяц. Каким должен быть процент на инвестированные средства, чтобы получить необходимую сумму в конце второго года.

б) компания отказалась от ежемесячных платежей и готова единовременно вложить 40000 тыс. руб. Определите, как изменится в этом случае процентная ставка.

3) Банк выдал ссуду 150 тыс. руб. на 3 года под 17% годовых. Ссуда выдана в начале года, а погашение начинается в конце года одинаковыми платежами. Определите размер ежегодного погашения ссуды.

4). Предположим, что мы хотим получать доход, равный $1000 в год, на протяжении 4-х лет. Какая сумма обеспечит получение такого дохода, если ставка по срочным депозитам равна 10% годовых?

Вариант 2

1) У Вас есть возможность ежегодно в течение 4 лет инвестировать 300 тыс. руб. в два проекта: под 26% в начале каждого года или 38% в конце года. Определите, какой из вариантов вложения средств предпочтительнее.

2) По вкладу в 10000 помещенному в банк под 5% годовых, начисляемых ежегодно, была выплачена сумма 12762,82. Определить срок проведения операции (количество периодов начисления).

3) Фирме через 2 года потребуется 100000 руб. Для достижения этой цели фирма готова положить на депозит 25000 руб. Каким должен быть процент на инвестированные средства с тем, чтобы к концу второго года была получена необходимая сумма?

4) Необходимо накопить 4000 руб. за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой должна быть эта сумма, если норма процента по вкладу составляет 12% годовых

5) Рассматриваются два варианта покупки недвижимости: заплатить сразу 70 000 руб. или платить ежемесячно по 800 руб.в течение 12 лет при ставке 9% годовых. Какой вариант более выгоден?

Вариант 3

1) Вы решили приобрести автомобиль стоимостью 200000 руб. Какую сумму Вы должны вложить в банк под 12% годовых для того, чтобы иметь возможность его приобретения:

а) начисление процентов производится один раз в начале года;

б) начисления производятся 2 раза в год в начале периода.

2) Для обеспечения будущих расходов создается фонд. Средства в фонд поступают в виде постоянной годовой ренты. Размер разового платежа составляет 16 млн. руб. На поступившие взносы начисляется 11,18% годовых. Определить, когда величина фонда будет равна 100 млн. руб.

3) Вычислить 10 годичную ипотечную ссуду покупки квартиры за 800000 руб. с годовой ставкой 13% и начальным взносом 25%. Сделать расчет для ежемесячных и ежегодных выплат.

4) Пусть в долг на полтора года дана сумма 20000 руб. с условием возврата 30000 руб. Вычислить годовую процентную ставку.

5) На счет в банке в течение пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30%. Определить сумму, которую банк выплатит владельцу счета.

Вариант 4

1) Предположим, что выкупается страховка, по которой выплачивается по 500 руб. в конце каждого месяца в течение 20 последующих лет. Стоимость ренты составляет 60 000 руб. и выплачиваемые деньги принесут 8 % годовых. Необходимо определить, будет ли это хорошим способом инвестировать капитал.

2)Какую сумму необходимо ежемесячно вносить на счет, чтобы через три года получить 10 тыс. руб., если годовая процентная ставка 13,5%.

3) Рассчитайте процентную ставку для четырехлетнего займа в 7000 тыс. руб. с ежемесячным погашением по 250 тыс. руб. при условии, что заем полностью погашается.

4)Предположим, что каждый год ежемесячно в банк помещается сумма в 1000 руб. Ставка равна 12% годовых, начисляемых в конце каждого месяца. Какова будет величина вклада к концу 4-го года?

5) Рассчитайте, через сколько месяцев вклад размером 15000 руб. достигнет величины 24500 руб. при ежемесячном начислении процентов и ставке процента 22% годовых.

Вариант 5

1) Вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Предположим, Вы собираетесь вложить 1000 рублей под 6% годовых (что составит в месяц 6%/12 или 0,5%). Вы собираетесь вкладывать по 100 рублей в начале каждого следующего месяца в течение следующих 12 месяцев. Сколько денег будет на счету в конце 12 месяцев?

2) За какой срок в годах сумма, равная 75 000 руб., достигнет 200 000 руб. при начислении процентов по сложной ставке 15%раз в году и поквартально.

3) Выдан кредит 200 000 долл. на два с половиной года. Проценты начисляются раз в полгода. Определить величину процентной ставки за период, если известно, что возврат составит 260 000 долл.

4)Банк выдал ссуду 200 тыс. руб. на 4 года под 18% годовых. Ссуда выдана в начале года, а погашение начинается в конце года одинаковыми платежами. Определите размер ежегодного погашения ссуды

5). Предположим, что мы хотим получать доход, равный $1000 в год, на протяжении 4-х лет. Какая сумма обеспечит получение такого дохода, если ставка по срочным депозитам равна 10% годовых?

Вариант 6

1) Рассматриваются два варианта покупки недвижимости: заплатить сразу 70 000 руб. или платить ежемесячно по 800 руб.в течение 12 лет при ставке 9% годовых. Какой вариант более выгоден?

2) Ожидается, что ежегодные доходы от реализации проекта составят 33 млн. руб. Рассчитайте срок окупаемости проекта, если инвестиции к началу поступления доходов составят 100 млн.руб., а норма дисконтирования – 12,11%.

3) Заем в 144 тыс. руб. погашается равномерными периодическими платежами по 14 тыс. руб. каждые полгода в течение восьми лет. Определите годовую ставку процента.

4) Рассматриваются две схемы вложения денег на 3 года: в начале каждого года под 24% годовых или в конце каждого года под 36%. Ежегодно вносится по 4000. Какая схема выгоднее?

5) Необходимо накопить 4000 руб. за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой должна быть эта сумма, если норма процента по вкладу составляет 12% годовых

Вариант 7

1) Фирма создает фонд для погашения долгосрочных обязательств, срок которых истекает через пять лет, путем ежегодного пополнения депозита, с начальной суммой 10000 тыс. руб. Размер ежегодного взноса 1000 тыс. руб. Ставка по депозиту – 5% годовых, начисляемых в конце каждого периода. Определите величину фонда к концу пятого года.

2) Рассчитайте, через сколько месяцев вклад размером 15000 руб. достигнет величины 24500 руб. при ежемесячном начислении процентов и ставке процента 22% годовых.

3) В долг на 2 года дана сумма 150 000 руб. с условием возврата 190 000 руб. Вычислить годовую процентную ставку.

4) Фирме потребуется 5000 тыс. руб. через 10 лет. В настоящее время располагает деньгами и готова положить их на депозит единым вкладом с тем, чтобы через 10 лет получить необходимую сумму.

Определитьнеобходимую сумму текущего вклада если ставка процента по нему составляет 12% в год

5) Определите ежемесячные выплаты по займу в 220 тыс. руб., взятому на семь месяцев под 11% годовых.

Вариант 8

1) Ссуда в 20 000 руб. дана на полтора года под ставку 28% годовых с ежеквартальным начислением. Определить сумму конечного платежа.

2) Ссуда 87000 руб., выданная под 30% годовых, погашается ежеквартальными платежами по 9500 руб. Рассчитайте срок погашения ссуды.

3) Какой должна быть годовая процентная ставка по вкладу размером 10000 руб., если ее величина к концу года составила 11723 руб., а проценты начислялись ежемесячно.

4) Предположим, что мы хотим получать доход, равный $1000 в год, на протяжении 4-х лет. Какая сумма обеспечит получение такого дохода, если ставка по срочным депозитам равна 10% годовых?

5) Банк выдал ссуду 150 тыс. руб. на 3 года под 17% годовых. Ссуда выдана в начале года, а погашение начинается в конце года одинаковыми платежами. Определите размер ежегодного погашения ссуды.

Вариант 9

1) Вексель на 3 000 000 руб. с годовой учетной ставкой 10% с дисконтированием два раза в год выдан на два года. Найти исходную сумму, выданную под этот вексель. В данном случае задача осложняется тем, что задана ставка дисконта, а аргумент норма подразумевает процентную ставку. Поэтому предварительно нужно пересчитать дисконтную ставку в процентную (9%/2/(1-9%/2)).

2) Ссуда размером 61000 руб. погашается ежемесячными платежами по 2144 руб. Рассчитайте, через сколько лет произойдет погашение, если годовая славка процента 16%.

3) Рассчитайте годовую ставку процента по вкладу размером 230 тыс.руб., если за 11 лет эта сумма возросла до 3 млн. руб. при ежеквартальном начислении процентов.

4) Определить, какая сумма окажется на банковском счете, если 52000 руб. положены на 20 лет под 11% годовых. Проценты начисляются ежемесячно.

5) Какую сумму необходимо ежемесячно вносить на счет, чтобы через три года получить 10 тыс. руб., если годовая процентная ставка 13,5%.

Вариант 10

1) Рассматриваются две схемы вложения денег на 3 года: в начале каждого года под 24% годовых или в конце каждого года под 36%. Ежегодно вносится по 4000. Какая схема выгоднее?

2) Физическому лицу выдан кредит 97 000 руб. на три года. Проценты начисляются ежегодно. Определить величину процентной ставки за период, если известно, что возврат составит 140 000 руб.

3) Ссуда 63200 руб., выданная под 32% годовых, погашается ежеквартальными платежами по 8400 руб. Рассчитайте срок погашения ссуды.

4) Определите ежемесячные выплаты по займу в 220 тыс. руб., взятому на семь месяцев под 11% годовых.

5) Фирме потребуется 5000 тыс. руб. через 10 лет. В настоящее время располагает деньгами и готова положить их на депозит единым вкладом с тем, чтобы через 10 лет получить необходимую сумму.

Определитьнеобходимую сумму текущего вклада если ставка процента по нему составляет 12% в год

6 Задачи для самостоятельного решения

Ознакомьтесь с другими функциями раздела «Финансовые функции» самостоятельно. Перечень финансовых функций приведен в приложении А. Найдите решение для приведенных ниже задач, используя изученный материал.

1) На банковский счет под 11,5 % годовых внесли 37000 рублей. Определить размер вклада по истечение трех лет, если проценты начисляются каждые полгода.

2) Определить сколько денег окажется на банковском счете, если ежегодно в течение пяти лет под 17 % годовых вносится 20000 рублей. Взносы осуществляются в начале каждого года.

3) Достаточно ли положить на счет 85000 рублей для приобретения через пять лет легкового автомобиля стоимостью 160000 рублей? Банк начисляет проценты ежеквартально, годовая ставка 12 %. Определить необходимую сумму (с помощью «подбора параметра»).

4) По облигации номиналом 50000 рублей, выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов:

а) в первый год – 10 %;

б) в следующие два года – 20 %;

в) в оставшиеся три года – 25 %.

Определить будущую стоимость облигации с учетом переменной процентной ставки.

5) По облигации, выпущенной на шесть лет, предусмотрен порядок начисления процентов, приведенный в задаче 4. Рассчитать номинал облигации, если известно, что ее будущая стоимость составила 216562,50 рублей.

6) Фирме требуется 500000 рублей через три года. Определить, какую сумму необходимо внести фирме сейчас, чтобы к концу третьего года вклад увеличился до 500000 рублей, если процентная ставка составляет 12 % годовых.

7) Клиент заключает с банком договор о выплате ему в течение пяти лет ежегодной ренты в размере 5000 рублей в конце каждого года. Какую сумму необходимо внести клиенту в начале первого года, чтобы обеспечить эту ренту, исходя из годовой процентной ставки 20 %?

Пусть инвестиции в проект к концу первого года его реализации составят 20000 рублей. В последующие четыре года ожидаются годовые доходы по проекту: 6000 рублей, 8200 рублей, 12600 рублей и 18800 рублей. Рассчитать чистую текущую стоимость проекта к началу первого года, если процентная ставка составляет 10 % годовых.

9) Инвестор с целью инвестирования рассматривает два проекта, рассчитанные на пять лет. Проекты характеризуются следующими данными:

а) по первому проекту – начальные инвестиции составляют 550000 рублей, ожидаемые доходы за пять лет соответственно 100000, 190000, 270000, 300000 и 35000 рублей;

б) по второму проекту – начальные инвестиции составляют 650000 рублей, ожидаемые доходы за пять лет соответственно 150000, 230000, 470000, 180000 и 320000 рублей.

Определить, какой проект является наиболее привлекательным для инвестора при ставке банковского процента – 15 % годовых.

10)Определите чистую текущую стоимость по проекту на 05.04.2018 при ставке дисконтирования 8 %, если затраты по нему на 05.08.2018 составят 90 млн.рублей, а ожидаемые доходы в течение следующих месяцев будут:

а) 10 млн.руб. на 10.01.2019;

б) 20 млн.руб. на 01.03.2019;

в) 30 млн.руб. на 15.04.2019;

г) 40 млн.руб. на 25.07.2019.

11) Рассчитать через сколько лет вклад размером 100000 рублей достигнет 1000000 рублей, если годовая процентная ставка по вкладу 13,5 % и начисление процентов производится ежеквартально.

12) Для покрытия будущих расходов фирма создает фонд. Средства в фонд поступают в виде годовой ренты в конце года. Сумма разового платежа 16000 рублей. На поступившие взносы начисляются 11,2 % годовых. Необходимо определить, когда величина фонда будет равна 100000 рублей.

13) Предположим, что для получения через два года суммы в 1000000 рублей предприятие готово вложить 250000 рублей сразу и затем каждый месяц по 25000 рублей. Определить годовую процентную ставку.

14) Выдан кредит 50000 рублей на 2,5 года. Проценты начисляются раз в полгода.Определить величину процентной ставки за период, если известно, что возврат составит 700000 рублей.

15) Клиент банка осуществляет заем в размере 5000 рублей под 6 % годовых на 6 месяцев. Определите ежемесячные платежи клиента. Платежи осуществляются в конце месяца.

16) Клиенту банка необходимо накопить 200000 рублей за два года. Клиент обязуется вносить в начале каждого месяца постоянную сумму под 9 % годовых. Какой должна быть сумма?

17) Определите платежи по процентам за первый месяц от трехгодичного займа в 100000 рублей из расчета 10 % годовых.

18) Клиент ежегодно в течение пяти лет вносил деньги на свой счет в банке и накопил 40000 рублей. Определите, какой доход получил клиент банка за последний год, если годовая ставка составила 13,5 %.

19) Определите значение основного платежа для первого месяца двухгодичного займа в 60000 рублей под 12 % годовых.

20) Организация взяла ссуду в банке в размере 500000 рублей на 10 лет под 10,5 % годовых, проценты начисляются ежемесячно. Определите сумму выплат по процентам за первый месяц и за третий год периода.

21) Ссуда размером 1000000 рублей выдана под 13 % годовых сроком на три года. Проценты начисляются ежеквартально.Определите величину общих выплат по займу за второй год.

22) Рассчитать сумму процентов, начисленных на вклад в 750000 рублей за два года, если банк начисляет проценты ежеквартально из расчета 28 % годовых. Какова должна быть годовая депозитная ставка, если за два года необходимо удвоить первоначальный вклад?

23) Потребитель получает заем на покупку автомобиля 20000$ под 8 % годовых сроком на три года при ежемесячных выплатах. Какова будет сумма по процентам и основной платеж за первый и последний месяцы выплат?

24) Потребитель занимает сумму 250000$, подлежащую выплате в течение 10 лет при 12 % годовых на ежемесячной основе. Какова сумма процента и основного капитала на первом году займа?

25) Кредит в сумме 5000000 рублей предоставлен под 20 % годовых сроком на 10 лет. Рассчитайте величину остатка основной суммы без учета выплаченных процентов на начало третьего года.

7 Контрольные вопросы

Интерфейс Excel 2010

Вкладка «Файл»

Настройка Панели быстрого доступа

Рабочая область Excel

Строка формул

Абсолютные и относительные ссылки

Стили ссылок

Инструменты вкладки Вид

Разделение рабочей области листа

Закрепление областей

Применение Маркера автозаполнения

Общие правила при создании формул

Сообщения об ошибках

Способы устранения ошибок

Мастер создания функций

Расчет будущей стоимости инвестиций

Расчет суммы денег в настоящий момент

Расчет суммы ежемесячных платежей

Расчет количества периодов платежей

Расчет процентной ставки на период

Список использованных источников

1 Зимин, В.П. Информатика. Лабораторный практикум. В 2ч. Ч.1 : учеб. пособие для спо / В.П. Зимин.- М.: Юрайт, 2018.- 110 с.- (Профессиональное образование).- ISBN 978-5-534-03446-0.

2 Каджаева, М.Р. Ведение расчетных операций : учебник для спо / М.Р. Каджаева.- 3-е изд., стер.- М.: Академия, 2017. – 272с. — (Профессиональное образование).- ISBN 978-5-4468-4267-2.

3 Коршунов, М.К. Экономика и управление: применение информационных технологий : учеб. пособие для спо / М.К. Коршунов; под ред. Э.П. Макарова.- М.: Юрайт; Екатеринбург : Изд-во Урал. ун-та, 2018. – 111 с.- (Профессиональное образование).- ISBN 978-5-534-007725-4.

4 Информационные технологии [Электронный ресурс]: лабораторный практикум / авт.-сост. С.В. Говорова, М.А. Лапина; Министерство образования и науки Российской Федерации, Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Северо-Кавказский федеральный университет». — Ставрополь : СКФУ, 2016. — 168 с. –ЭБС Университетская библиотека Online. – Режим доступа: http://biblioclub.ru/index.php?page=book&id=459048.

На сегодняшний день разработано большое количество специализированных программных продуктов для проведения экономических расчетов, однако сотрудники финансово-экономических служб чаще всего пользуются табличным редактором Excel. Причина популярности данного инструмента — обширный функционал Excel и постоянное его развитие практически в каждой новой версии табличного редактора.

В рамках одной статьи невозможно рассмотреть все достоинства Excel, которые экономисты могут применить в своей работе, поэтому остановимся на анализе лучших функций редактора, используемых для решения экономических задач.

Для удобства восприятия материала сгруппируем эти функции в три блока:

1. Функционал расчетных формул в Excel.

2. Функционал Excel для обработки табличных данных.

3. Инструменты Excel для моделирования и анализа экономических данных.

ФУНКЦИОНАЛ РАСЧЕТНЫХ ФОРМУЛ В EXCEL

Расчетные формулы являются изначальным и основополагающим функционалом табличного редактора Excel, поэтому рассмотрим их в первую очередь.

Пакет встроенных расчетных формул включает в себя десятки наименований, но самыми востребованными в работе экономистов являются следующие формулы: ЕСЛИ, СУММЕСЛИ и СУММЕСЛИМН, ВПР и ГПР, СУММПРОИЗВ, СЧЕТЕСЛИ.

Решение экономической задачи с помощью формулы ЕСЛИ

Формула ЕСЛИ — расчетная функция Excel, которую наиболее часто используют для решения несложных экономических расчетов. Она относится к группе логических формул и позволяет рассчитать необходимые данные по условиям, заданным пользователями.

С помощью формулы ЕСЛИ можно сравнить числовые или текстовые значения по прописанным в формуле условиям.

Запись расчетной формулы в заданной ячейке в общем виде выглядит так:

=ЕСЛИ(логическое_выражение;[значение_если_истина];[значение_если_ложь]),

где логическое выражение — данные, которые нужно проверить/сравнить (числовые или текстовые значения в ячейках);

значение_если_истина — результат, который появится в расчетной ячейке, если значение будет верным;

значение_если_ложь — результат, который появится в расчетной ячейке при неверном значении.

Задача № 1. Предприятие реализует три номенклатурные группы продукции: лимонад, минеральная вода и пиво. С 01.09.2020 запланировано установить скидку в размере 15 % на пиво.

Чтобы сформировать новый прайс на продукцию, сохраняем ее перечень в виде таблицы Excel. В первом столбце таблицы отражена номенклатура всей продукции в алфавитном порядке, во втором — признак группы продукции.

Для решения задачи создаем в таблице третий столбец и прописываем в первой ячейке номенклатуры формулу: =ЕСЛИ(C4=»пиво»;15%;0).

Эту формулу продлеваем до конца перечня номенклатуры продукции. В итоге получаем сведения о продукции, на которую с сентября снизится цена (табл. 1).

В данном примере показано использование формулы ЕСЛИ для обработки текстовых значений в исходных данных.

Решение экономической задачи с помощью формулы СУММЕСЛИ

Формулы СУММЕСЛИ и СУММЕСЛИМН также используют для экономических расчетов, но они обладают более широкими возможностями для выборки и обработки данных. Можно задать не одно, а несколько условий отборов и диапазонов.

Задача № 2. На основе ведомости начисления заработной платы сотрудникам магазина нужно определить общую сумму зарплаты продавцов.

Чтобы решить эту задачу, сохраняем ведомость из учетной базы данных в виде таблицы Excel. В данном случае нам нужно не просто произвести выборку значений, но и суммировать их результат. Поэтому будем использовать более сложную разновидность формулы ЕСЛИ — СУММЕСЛИ.

Для решения задачи добавим внизу таблицы еще одну строку «Всего продавцы». В ее ячейке под суммой зарплаты, начисленной сотрудникам магазина, пропишем следующую формулу:=СУММЕСЛИ(C4:C13;»продавец»;D4:D13).

Таким образом мы задали условие, при котором табличный редактор обращается к столбцу с наименованием должностей (столбец С), выбирает в нем значение «Продавец» и суммирует данные ячеек с начисленной заработной платой из столбца D в привязке к этой должности.

Результат решения задачи — в табл. 2.

Решение экономической задачи с помощью формул ВПР и ГПР

Формулы ВПР и ГПР используют для решения более сложных экономических задач. Они популярны среди экономистов, так как существенно облегчают поиск необходимых значений в больших массивах данных. Разница между формулами:

• ВПР предназначена для поиска значений в вертикальных списках (по строкам) исходных данных;
• ГПР используют для поиска значений в горизонтальных списках (по столбцам) исходных данных.

Формулы прописывают в общем виде следующим образом:

=ВПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер столбца, из которого будут подставлены данные; [интервал просмотра данных]);

=ГПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер строки, из которой будут подставлены данные; [интервал просмотра данных]).

Указанные формулы имеют ценность при решении задач, связанных с консолидацией данных, которые разбросаны на разных листах одной книги Excel, находятся в различных рабочих книгах Excel, и размещении их в одном месте для создания экономических отчетов и подсчета итогов.

Задача № 3. У экономиста есть данные в виде таблицы Excel о реализации продукции за сентябрь в натуральном измерении (декалитрах) и данные о реализации продукции в сумме (рублях) в другой таблице Excel. Экономисту нужно предоставить руководству отчет о реализации продукции с тремя параметрами:

• продажи в натуральном измерении;
• продажи в суммовом измерении;
• средняя цена реализации единицы продукции в рублях.

Для решения этой задачи с помощью формулы ВПР нужно последовательно выполнить следующие действия.

Шаг 1. Добавляем к таблице с данными о продажах в натуральном измерении два новых столбца. Первый — для показателя продаж в рублях, второй — для показателя цены реализации единицы продукции.

Шаг 2. В первой ячейке столбца с данными о продажах в рублях прописываем расчетную формулу: =ВПР(B4:B13;Табл.4!B4:D13;3;ЛОЖЬ).

Пояснения к формуле:

В4:В13 — диапазон поиска значений по номенклатуре продукции в создаваемом отчете;

Табл.4!B4:D13 — диапазон ячеек, где будет производиться поиск, с наименованием таблицы, в которой будет организован поиск;

3 — номер столбца, по которому нужно выбрать данные;

ЛОЖЬ — значение критерия поиска, которое означает необходимость строгого соответствия отбора наименований номенклатуры таблицы с суммовыми данными наименованиям номенклатуры в таблице с натуральными показателями.

Шаг 3. Продлеваем формулу первой ячейки до конца списка номенклатуры в создаваемом нами отчете.

Шаг 4. В первой ячейке столбца с данными о цене реализации единицы продукции прописываем простую формулу деления значения ячейки столбца с суммой продаж на значение ячейки столбца с объемом продаж (=E4/D4).

Шаг 5. Продлим формулу с расчетом цены реализации до конца списка номенклатуры в создаваемом нами отчете.

В результате выполненных действий появился искомый отчет о продажах (табл. 3).

На небольшом количестве условных данных эффективность формулы ВПР выглядит не столь внушительно. Однако представьте, что такой отчет нужно сделать не из заранее сгруппированных данных по номенклатуре продукции, а на основе реестра ежедневных продаж с общим количеством записей в несколько тысяч.

Тогда эта формула обеспечит такую скорость и точность выборки нужных данных, которой трудно добиться другими функциями Excel.

Решение экономической задачи с помощью формулы СУММПРОИЗВ

Формула СУММПРОИЗВ позволяет экономистам справиться практически с любой экономической задачей, для решения которой нужно работать с несколькими массивами данных. Она обладает всеми возможностями рассмотренных выше формул, умеет суммировать произведения данных из списка до 255 источников (массивов).

Задача № 4. Есть реестр продаж различной номенклатуры продукции за сентябрь 2020 г. Нужно рассчитать из общего реестра данные о суммах реализации по основным номенклатурным группам продукции.

Чтобы выполнить задачу, добавим внизу реестра три новые строки с указанием групп продукции и пропишем в ячейке с будущими данными о продажах первой группы (пиво) следующую формулу: =СУММПРОИЗВ(((C4:C13=C16)*D4:D13)). Здесь указано, что в ячейке должно быть выполнено суммирование произведений значений диапазона ячеек столбца с наименованием групп продукции (C4:C13) с условием отбора наименования группы «Пиво» (С16) на значения ячеек столбца с суммами продаж (D4:D13).

Далее копируем эту формулу на оставшиеся две ячейки, заменив в них условия отбора на группу «Лимонад» (С17) и группу «Минеральная вода» (С18).

Выполнив указанные действия, получим искомое решение задачи в табл. 4.

Решение экономической задачи с помощью формулы СЧЕТЕСЛИ

Формула СЧЕТЕСЛИ используется не так широко, как предыдущие, но она выручает экономистов, если нужно минимизировать ошибки при работе с таблицами Excel. Эта формула удобна для проверки корректности вводимых данных и установке различного рода запретов, что особенно важно, если с данными работает несколько пользователей.

Задача № 5. Экономисту поручили провести корректировку справочника номенклатуры ТМЦ в учетной базе данных компании. Справочник долгое время не проверяли, данные в него вносили порядка 10 человек, поэтому появилось много некорректных и дублирующих наименований.

Чтобы повысить качество работы, приняли решение создать обновленный справочник в книге Excel, а затем сопоставить его с данными в учетной базе и исправить их. Проблема заключалась в том, что перечень номенклатуры составляет порядка 3000 наименований. Вносить его в книгу будут шесть человек, а это создает риск дублирования позиций.

Экономист может решить эту проблему с помощью формулы СЧЕТЕСЛИ. Нужно выполнить следующие действия:

• выбираем диапазон ячеек, куда будут вноситься наименования номенклатуры (В5:В3005);
• в меню редактора выбираем путь: Данные → Проверка данных;
• в появившемся диалоговом окне выбираем вкладку Параметры и указываем в выпадающем списке Тип данных вариант Другой;
• в строке Формула указываем: =СЧЕТЕСЛИ($В$5:$В$3005;В5)<=1;
• в диалоговом окне на вкладке Сообщение об ошибке вводим текст сообщения и нажимаем кнопку «ОК».

Если кто-либо из сотрудников будет пытаться ввести в указанный диапазон ячеек наименование ТМЦ, которое уже есть в диапазоне, у него это не получится. Excel выдаст сообщение в таком виде (рис. 1).

ФУНКЦИОНАЛ EXCEL ДЛЯ ОБРАБОТКИ ТАБЛИЧНЫХ ДАННЫХ

Помимо расчетных формул в табличном редакторе Excel присутствует набор инструментов, значительно облегчающих жизнь экономистам, которые работают с большими объемами данных. К наиболее популярным из них можно отнести функцию сортировки данных, функцию фильтрации данных, функцию консолидации данных и функцию создания сводных таблиц.

Решение экономической задачи с применением функции сортировки данных

Функционал сортировки данных позволяет изменить расположение данных в таблице и выстроить их в новой последовательности. Это удобно, когда экономист консолидирует данные нескольких таблиц и ему нужно, чтобы во всех исходных таблицах данные располагались в одинаковой последовательности.

Другой пример целесообразности сортировки данных — подготовка отчетности руководству компании. С помощью функционала сортировки из одной таблицы с данными можно быстро сделать несколько аналитических отчетов.

Сортировку данных выполнить просто:

• выделяем курсором столбцы таблицы;
• заходим в меню редактора: Данные → Сортировка;
• выбираем нужные параметры сортировки и получаем новый вид табличных данных.

Задача № 6. Экономист должен подготовить отчет о заработной плате, начисленной сотрудникам магазина, с последовательностью от самой высокой до самой низкой зарплаты.

Для решения этой задачи берем табл. 2 в качестве исходных данных. Выделяем в ней диапазон ячеек с показателями начисления зарплат (B4:D13).

Далее в меню редактора вызываем сортировку данных и в появившемся окне указываем, что сортировка нужна по значениям столбца D (суммы начисленной зарплаты) в порядке убывания значений.

Нажимаем кнопку «ОК», и табл. 2 преобразуется в новую табл. 5, где в первой строке идут данные о зарплате директора в 50 000 руб., в последней — данные о зарплате грузчика в 18 000 руб.

Решение экономической задачи с использованием функционала Автофильтр

Функционал фильтрации данных выручает при решении задач по анализу данных, особенно если возникает необходимость проанализировать часть исходной таблицы, данные которой отвечают определенным условиям.

В табличном редакторе Excel есть два вида фильтров:

• автофильтр — используют для фильтрации данных по простым критериям;
• расширенный фильтр — применяют при фильтрации данных по нескольким заданным параметрам.

Автофильтр работает следующим образом:

• выделяем курсором диапазон таблицы, данные которого собираемся отфильтровать;
• заходим в меню редактора: Данные → Фильтр → Автофильтр;
• выбираем в таблице появившиеся значения автофильтра и получаем отфильтрованные данные.

Задача № 7. Из общих данных о реализации продукции за сентябрь 2020 г. (см. табл. 4) нужно выделить суммы продаж только по группе лимонадов.

Для решения этой задачи выделяем в таблице ячейки с данными по реализации продукции. Устанавливаем автофильтр из меню: Данные → Фильтр → Автофильтр. В появившемся меню столбца с группой продукции выбираем значение «Лимонад». В итоге в табл. 6 автоматически остаются значения продаж лимонадов, а данные по группам «Пиво» и «Минеральная вода» скрываются.

Для применения расширенного фильтра нужно предварительно подготовить «Диапазон условий» и «Диапазон, в который будут помещены результаты».

Чтобы организовать «Диапазон условий», следует выполнить следующие действия:

• в свободную строку вне таблицы копируем заголовки столбцов, на данные которых будут наложены ограничения (заголовки несмежных столбцов могут оказаться рядом);
• под каждым из заголовков задаем условие отбора данных.

Строка копий заголовков вместе с условиями отбора образуют «Диапазон условий».

Порядок работы с функционалом консолидации данных

Функционал консолидации данных помогает экономистам в решении задач по объединению данных из нескольких источников в одну общую таблицу. Например, экономисты холдинговых компаний часто создают однотипные таблицы с данными по разным компаниям холдинга и им требуется предоставить руководству сводные данные о работе всей группы компаний. Для упрощения формирования сводных показателей как раз и подходит функционал консолидации данных.

Консолидация работает только с идентичными таблицами Excel, поэтому для успеха все объединяемые таблицы должны отвечать следующим требованиям:

• макеты всех консолидируемых таблиц одинаковые;
• названия столбцов во всех консолидируемых таблицах идентичные;
• в консолидируемых таблицах нет пустых столбцов и строк.

Работа с функционалом консолидации включает ряд последовательных действий:

1) открываем файлы со всеми таблицами, из которых собираемся консолидировать данные;

2) в отдельном файле, где будет находиться консолидированный отчет, ставим курсор на первую ячейку диапазона консолидированной таблицы;

3) в меню Excel открываем вкладки: Данные → Работа с данными → Консолидация;

4) в открывшемся диалоговом окне выбираем функцию консолидации (как правило, это «сумма», потому что нам требуется суммировать значения нескольких таблиц);

5) в диалоговом окне консолидации указываем ссылки на диапазоны объединяемых таблиц (диапазоны должны быть одинаковые);

6) если требуется автоматическое обновление данных консолидированной таблицы при изменении данных исходных таблиц, ставим галочку напротив «Создавать связи с исходными данными»;

7) завершаем консолидацию нажатием кнопки «ОК». В итоге получаем сводную структурированную таблицу, объединяющую данные всех исходных таблиц.

Решение экономической задачи с использованием функционала сводной таблицы для создания нового отчета

Функционал сводных таблиц позволяет сформировать различного рода отчеты из одного или нескольких массивов данных с возможностью обновления отчетных данных в случае изменения информации в исходных массивах. Используя сводные таблицы, можно быстро перенастроить параметры отчета.

Для создания сводной таблицы нужно зайти в меню Excel и вызвать Мастера сводных таблиц. В моей версии редактора это выполняется через Вставка → Сводная таблица, в некоторых версиях нужно выбрать Данные → Сводная таблица.

В появившемся диалоговом окне формируем параметры будущей таблицы:

• указываем исходную таблицу или диапазон ячеек Excel, откуда будут взяты данные для сводной таблицы. В последних версиях Excel также можно выбрать вариант обработки данных из внешних источников;
• указываем место, куда размещать создаваемый отчет сводной таблицы (новый лист, ячейки открытого листа);
• в открывшемся конструкторе отчета указываем, какие исходные данные будут выведены в строки и столбцы отчета, при необходимости настраиваем фильтры для показателей сводной таблицы и создаем новый отчет.

Задача № 8. Экономисту нужно создать отчет на основе реестра данных о реализации продукции за сентябрь 2020 г. В отчете должно быть два уровня группировки данных. На первом уровне нужно вывести итоги по группам продукции, на втором уровне — по ее номенклатурным позициям. Чтобы решить эту задачу, вызываем Мастера сводных таблиц. Указываем, что данные берем из ячеек табл. 4, а отчет будем размещать на новом листе книги Excel. В конструкторе отчета указываем, что в первой колонке отчета будут показатели групп и номенклатурных единиц продукции, во второй — данные о суммах реализации. После этого даем команду создать сводную таблицу. Результат — в табл. 7.

ИНСТРУМЕНТЫ EXCEL ДЛЯ МОДЕЛИРОВАНИЯ И АНАЛИЗА ЭКОНОМИЧЕСКИХ ДАННЫХ

Постоянное развитие функционала табличного редактора Excel привело к тому, что появилось много новых инструментов, которые могут помочь экономистам в решении выполняемых ими задач. К числу наиболее значимых можно отнести функцию «Поиск решения», пакет расширенного анализа данных и специализированные надстройки.

Решение экономической задачи с помощью надстройки «Поиск решения»

Функция «Поиск решения» позволяет найти наиболее рациональный способ решения экономической задачи математическими методами. Она может автоматически выполнить расчеты для задач с несколькими вводными данными при условии накладывания определенных ограничений на искомое решение.

Такими экономическими задачами могут быть:

• расчет оптимального объема выпуска продукции при ограниченности сырья;
• минимизация транспортных расходов на доставку продукции покупателям;
• решение по оптимизации фонда оплаты труда.

Функция поиска решения является дополнительной надстройкой, поэтому в стандартном меню Excel мы ее не найдем. Чтобы использовать в своей работе функцию «Поиск решения», экономисту нужно сделать следующее:

• в меню Excel выбрать путь: Файл → Параметры → Надстройки;
• в появившемся списке надстроек выбрать «Поиск решения» и активировать эту надстройку;
• вернуться в меню Excel и выбрать: Данные → Поиск решения.

Задача № 9. Туристической компании необходимо организовать доставку 45 туристов в четыре гостиницы города с трех пунктов прибытия при минимально возможной сумме затрат. Для решения задачи составляем таблицу с исходными данными:

1. Количество прибывающих с каждого пункта — железнодорожный вокзал, аэропорт и автовокзал (ячейки Н6:Н8).

2. Количество забронированных для туристов мест в каждой из четырех гостиниц (ячейки D9:G9).

3. Стоимость доставки одного туриста с каждого пункта прибытия до каждой гостиницы размещения (диапазон ячеек D6:G8).

Исходные данные, размещенные таким образом, показаны в табл. 8.1.

Далее приступаем к подготовке поиска решения.

1. Создаем внизу исходной таблицы такую же таблицу для расчета оптимального количества доставки туристов при условии минимизации затрат на доставку с диапазоном ячеек D15:G17.

2. Выбираем на листе ячейку для расчета искомой функции минимизации затрат (J4) и прописываем в ячейке расчетную формулу: =СУММПРОИЗВ(D6:G8;D15:G17).

3. Заходим в меню Excel, вызываем диалоговое окно надстройки «Поиск решения» и указываем там требуемые параметры и ограничения (рис. 2):

• оптимизировать целевую функцию — ячейка J4;
• цель оптимизации — до минимума;
• изменения ячейки переменных — диапазон ячеек второй таблицы D15:G17;
• ограничения поиска решения:

– в диапазоне ячеек второй таблицы D15:G17 должны быть только целые значения (D15:G17=целое);

– значения диапазона ячеек второй таблицы D15:G17 должны быть только положительными (D15:G17>=0);

– количество мест для туристов в каждой гостинице таблицы для поиска решения должно быть равно количеству мест в исходной таблице (D18:G18 = D9:G9);

– количество туристов, прибывающих с каждого пункта, в таблице для поиска решения должно быть равно количеству туристов в исходной таблице (Н15:Н17 = Н6:Н8).

Далее даем команду найти решение, и надстройка рассчитывает нам результат оптимальной доставки туристов (табл. 8.2).

При такой схеме доставки целевое значение общей суммы расходов действительно минимальное и составляет 1750 руб.

Пакет расширенного анализа данных

Пакет расширенного анализа данных применяют, если нужно исследовать различного рода статистические анализы, ряды данных, спрогнозировать тренды и т. д.

Пакет является надстройкой к Excel, устанавливается в основное меню аналогично функции поиска решений (Файл → Параметры → Надстройки → Пакет анализа). Вызвать его можно командой Данные → Анализ данных через диалоговое окно, в котором отражены все заложенные в надстройке виды анализа (рис. 3).

Специализированные надстройки для финансово-экономической работы

В последние годы значительно расширился перечень специализированных надстроек к табличному редактору Excel, которые могут использовать в своей работе экономисты. Практически все они бесплатные, легко устанавливаются самим пользователем.

Не будем останавливаться на таких надстройках, как Power Query, Power Pivot, Power Quick, так как они в большей степени используются в целях бизнес-аналитики, чем для решения экономических задач.

Есть и другие надстройки к Excel, которые могут облегчить работу специалистов финансово-экономических служб. Интерес представляют две бесплатные надстройки — «Финансист» и PowerFin.

Надстройку «Финансист» можно установить на свою версию Excel как в автоматическом, так и ручном режиме. В надстройке собрано много полезных для экономистов функций. Достаточно перечислить основные блоки данной надстройки:

• финансовые функции (ликвидность, платежеспособность, финансовая устойчивость, рентабельность, оборачиваемость, безубыточность продаж, отсрочка платежа, налоги и т. д.);
• работа с формулами;
• работа с текстом;
• работа с книгами и листами Excel;
• работа с ячейками Excel;
• поиск дубликатов и сравнение диапазонов данных;
• вставка дат и примечаний к диапазонам данных;
• загрузка курсов валют;
• создание выпадающих списков.

Надстройка PowerFin будет полезна прежде всего экономистам, которые работают с кредитами и инвестициями. Она без проблем устанавливается в меню надстроек Excel и имеет следующие функции:

• кредитный калькулятор (с функцией выведения калькулятора на лист, в том числе с возможностью автоматического формирования графика платежей);
• депозитный калькулятор для вычисления основных параметров инвестиций (с функцией выведения калькулятора на лист);
• вычисление требуемой процентной ставки исходя из первоначальной и будущей стоимости инвестиций;
• набор основных формул для расчета эффективности проекта: дисконтированного денежного потока, чистого денежного дохода, внутренней нормы доходности, срока окупаемости.