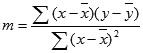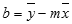Содержание
- Как рассчитать коэффициенты в Excel (с примером)
- Пример: расчет коэффициентов в Excel
- Дополнительные ресурсы
- Расчет KPI в Excel примеры и формулы
- KPI ключевые показатели эффективности: примеры в Excel
- Матрица KPI и пример в Excel
- Использование коэффициентов
- Корреляционно-регрессионный анализ в Excel: инструкция выполнения
- Регрессионный анализ в Excel
- Корреляционный анализ в Excel
- Корреляционно-регрессионный анализ
Как рассчитать коэффициенты в Excel (с примером)
Соотношение используется для сравнения двух чисел. Соотношения полезны для понимания того, насколько велико одно значение по сравнению с другим.
Например, предположим, что A = 40 и B = 10.
Чтобы рассчитать отношение A к B, мы можем использовать следующий двухэтапный процесс:
Шаг 1 : Найдите наибольший общий делитель (наибольшее целое число, на которое будет делиться каждое значение)
- Наибольшее значение, которое будет делиться как на 40, так и на 10, равно 10 .
Шаг 2 : Разделите каждое значение на наибольший общий делитель и запишите результат в виде A:B.
- Отношение 40 к 10 будет записано как 4:1 .
Чтобы вычислить соотношение между любыми двумя числами в Excel, мы можем использовать следующую формулу:
Эта конкретная формула вычисляет отношение между значением в ячейке A2 и значением в ячейке B2 , используя функцию НОД в Excel для автоматического поиска наибольшего общего делителя между двумя значениями.
В следующем примере показано, как использовать эту функцию на практике.
Пример: расчет коэффициентов в Excel
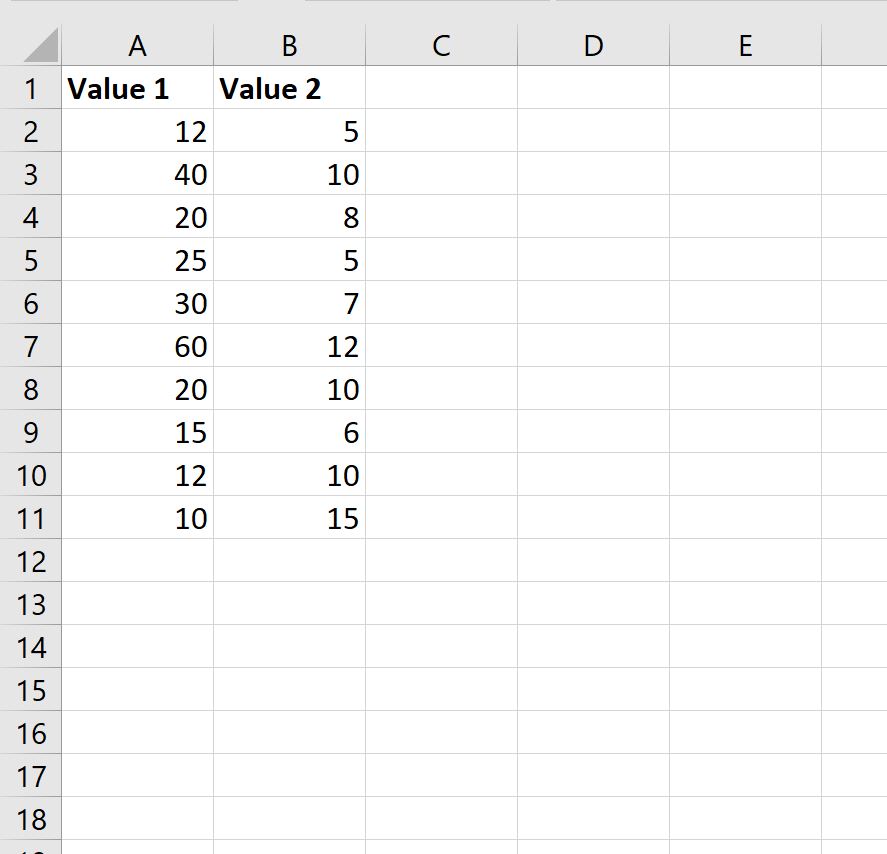
Предположим, у нас есть следующие два списка значений в Excel:
Предположим, мы хотели бы рассчитать отношение значения 1 к значению 2 в каждой строке.
Мы можем ввести следующую формулу в ячейку C2 :
На следующем снимке экрана показано, как использовать эту формулу на практике:
Оказывается, наибольший общий делитель 12 и 5 равен 1. Таким образом, когда мы делим каждое значение на 1, у нас просто остается отношение 12:5 .
Мы можем скопировать и вставить эту формулу в ячейку C2 до каждой оставшейся ячейки в столбце C, чтобы вычислить соотношение для двух значений в каждой строке:
Вот как интерпретировать результаты:
- Соотношение между 12 и 5 составляет 12:5 .
- Соотношение между 40 и 10 составляет 4:1 .
- Соотношение между 20 и 8 составляет 5:2 .
Примечание.Полную документацию по функции НОД в Excel можно найти здесь .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Источник
Расчет KPI в Excel примеры и формулы
KPI – показатель эффективности, позволяющий объективно оценить результативность выполняемых действий. Данная система применяется для оценки различных показателей (деятельности всей компании, отдельных структур, конкретных специалистов). Она выполняет не только функции контроля, но и стимулирует трудовую активность. Часто на основе KPI строится система оплаты труда. Это методика формирования переменной части зарплаты.
KPI ключевые показатели эффективности: примеры в Excel
Стимулирующий фактор в системе мотивации KPI – денежное вознаграждение. Получить его может тот работник, который выполнил поставленную перед ним задачу. Сумма премии / бонуса зависит от результата конкретного сотрудника в отчетном периоде. Объем вознаграждения может быть фиксированным или выражаться в процентах к окладу.
Каждое предприятие определяет ключевые показатели эффективности и вес каждого индивидуально. Данные зависят от задач компании. Например:
- Цель – обеспечить план продаж продукта в размере 500 000 рублей ежемесячно. Ключевой показатель – план продаж. Система измерения: фактическая сумма продаж / плановая сумма продаж.
- Цель – повысить сумму отгрузки в периоде на 20%. Ключевой показатель – средняя сумма отгрузки. Система измерения: фактическая средняя величина отгрузки / плановая средняя величина отгрузки.
- Задача – увеличить число клиентов на 15% в определенном регионе. Ключевой показатель – число клиентов в базе данных предприятия. Система измерения: фактическое число клиентов / плановое число клиентов.
Разброс коэффициента (весы) предприятие также определяет самостоятельно. Например:
- Выполнение плана менее 80% — недопустимо.
- Выполнение плана 100% — коэффициент 0,45.
- Выполнение плана 100-115% — коэффициент 0,005 за каждые 5%.
- Отсутствие ошибок – коэффициент 0,15.
- В отчетном периоде не было замечаний – коэффициент 0,15.
Это лишь возможный вариант определения мотивационных коэффициентов.
Ключевой момент в измерении KPI – отношение фактического показателя к плановому. Практически всегда заработная плата сотрудника складывается из оклада (постоянной части) и премии (переменной / изменяемой части). Мотивационный коэффициент влияет на формирование переменной.
Предположим, что соотношение постоянной и изменяемой частей в зарплате – 50 × 50. Ключевые показатели эффективности и вес каждого из них:
Примем следующие значения коэффициентов (одинаковые для показателя 1 и показателя 2):
Таблица KPI в Excel:
- Оклад – постоянная часть заработной платы зависит от количества отработанных часов. Для удобства расчетов мы предположили, что фиксированная и переменная часть зарплаты равны.
- Процент выполнения плана продаж и плана работ рассчитывается как отношение фактических показателей к плановым.
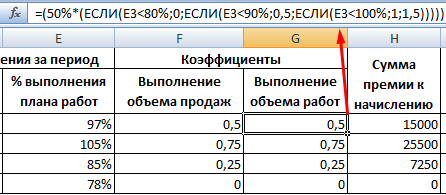
- Для расчета премии используются коэффициенты. Формулы в Excel расчета KPI по каждому сотруднику: Мы приняли, что влияние показателя 1 и показателя 2 на сумму премиальных одинаковое. Значения коэффициентов тоже равны. Поэтому для расчета показателя 1 и показателя 2 используются одинаковые формулы (меняются только ссылки на ячейки).
- Формула для расчета суммы премии к начислению – =C3*(F3+G3). Плановую премию умножаем на сумму показателя 1 и показателя 2 по каждому сотруднику.
- Заработная плата – оклад + премия.
Это примерная таблица KPI в Excel. Каждое предприятие составляет собственную (с учетом особенностей работы и системы премирования).
Матрица KPI и пример в Excel
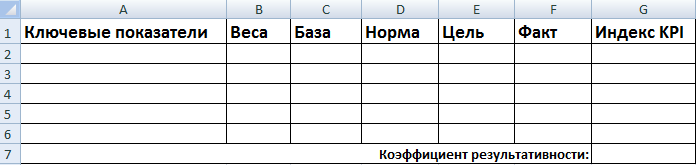
Для оценки работников по ключевым показателям эффективности составляется матрица, или соглашение о целях. Общая форма выглядит так:
- Ключевые показатели – критерии, по которым оценивается работа персонала. Для каждой должности они свои.
- Веса – числа в интервале от 0 до 1, общая сумма которых равняется 1. Отражают приоритеты каждого ключевого показателя с учетом задач компании.
- База – допустимое минимальное значение показателя. Ниже базового уровня – отсутствие результата.
- Норма – плановый уровень. То, что сотрудник должен выполнять обязательно. Ниже – работник не справился со своими обязанностями.
- Цель – значение, к которому нужно стремиться. Сверхнормативный показатель, позволяющий улучшить результаты.
- Факт – фактические результаты работы.
- Индекс KPI показывает уровень результата по отношению к норме.
Формула расчета kpi:
Индекс KPI = ((Факт – База) / (Норма – База)) * 100%.
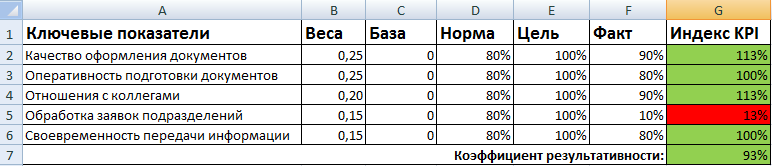
Пример заполнения матрицы для офис-менеджера:
Коэффициент результативности – сумма произведений индексов и весов. Оценка эффективности сотрудника наглядно показана с помощью условного форматирования.
Источник
Использование коэффициентов
Еще один метод расчета новых окладов заключается в том, что размер оклада каждого сотрудника с помощью определенного коэффициента «привязывается» к зарплате ведущего специалиста (например, директора или начальника отдела). Допустим, оклад начальника отдела реализации составляет 1400 руб. Новая зарплата начальников других отделов определяется умножением их прежних окладов на некоторый заранее установленный коэффициент. А заработная плата сотрудников этих отделов вычисляется путем умножения оклада их начальника на заданный коэффициент. Такой алгоритм расчета окладов показан на рис. 5.7.
Для применения данной методики в наш рабочий лист нужно внести некоторые изменения. В ячейку G3 введите сумму прежнего оклада начальника отдела реализации (1400), а в ячейку G4 — коэффициент, на который увеличиваются все оклады. Будущий оклад начальника отдела реализации (то есть оклад после повышения) будет вычисляться в ячейке G5 по формуле
Как вы понимаете, здесь прежний оклад умножается на индекс повышения и округляется до рублей.
В столбец Н занесите все коэффициенты, используемые при перерасчете окладов, а в диапазон Е2:Е11 — формулы, по которым рассчитывается размер будущего оклада (на основании алгоритма, представленного на рис. 5.7). Как теперь должна выглядеть таблица с формулами, показано на рис. 5.8.
Если в ячейку G4 ввести значение коэффициента, равное нулю, то в диапазоне Е2:Е11 отобразятся прежние оклады.
Если на предприятии еще раз будет принято решение о повышении окладов сотрудников, то достаточно внести в ячейку G4 новое значение коэффициента увеличения — и новые ставки в диапазоне Е2:Е11 будут рассчитаны автоматически.
Допустим, что руководство за существенный вклад в развитие предприятия решило увеличить на 10% оклад сотрудникам отдела снабжения. В этом случае при повышении коэффициента, который используется для вычисления оклада начальника данного отдела, с 0,65 до 0,75 автоматически возрастет на 10% зарплата у работников отдела. Взяв данную систему за основу, можно разработать ряд промежуточных или поправочных коэффициентов, посредством которых нетрудно будет регулировать размер заработной платы.
Обратите внимание на формулы, расположенные в столбце Е (рис. 5.8). Именно они отражают тот факт, что размер оклада сотрудника зависит либо от оклада начальника отдела реализации (если речь идет о начальнике), либо от оклада его начальника (рядовые сотрудники). В ячейке Е4 содержится формула
В ней увеличенный размер оклада умножается на коэффициент, привязанный к окладу начальника отдела реализации (в данном случае на 1, поскольку речь идет о самом начальнике отдела реализации).
Ячейка Е4 является управляющей для ячеек Е2 и Е9, где производится расчет сумм окладов начальников других отделов, а также для ячеек области Е5:Е8, в которых рассчитываются оклады рядовых сотрудников отдела реализации. Ячейки Е2 и Е9, в свою очередь, являются управляющими для ячеек, в которых производится расчет окладов для рядовых сотрудников отделов контроля и снабжения. В частности, ячейка Е9 управляет расчетами в ячейках ЕЮ и Е11.
В ячейке Е2 находится формула
с помощью которой вычисляется произведение значения, находящегося в ячейке Е4, и коэффициента из ячейки Н2, а результат округляется до рублей.
Обратите внимание, что формула содержит абсолютную ссылку на ячейку Е4.
Это оправданно по следующим причинам:
- При копировании формулы в другие ячейки (в нашем случае — в ячейку Е9), где производится расчет окладов начальников отделов, ссылка на ячейку Е4 не поменяется. А вот ссылка на ячейку с коэффициентом изменится в зависимости от того, в какую ячейку столбца Е будет скопирована формула (если это будет ячейка Е9, то вместо ссылки на ячейку Н2 появится ссылка на ячейку Н9).
- Если не ввести абсолютную ссылку на ячейку, то в случае изменения местоположения этой ячейки после сортировки списка, мы получим неправильный результат. Если после сортировки адрес ячейки Е4 изменится, то изменятся и ссылки не нес в формулах с абсолютной ссылкой. (О сортировке мы поговорим ниже.)
В ячейке ЕЗ располагается формула для расчета оклада сотрудника из отдела контроля:
Формула содержит ссылку на ячейку, где производится расчет оклада начальника отдела контроля. Оклады сотрудников других отделов определяются аналогичным образом.
Источник
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2 );
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
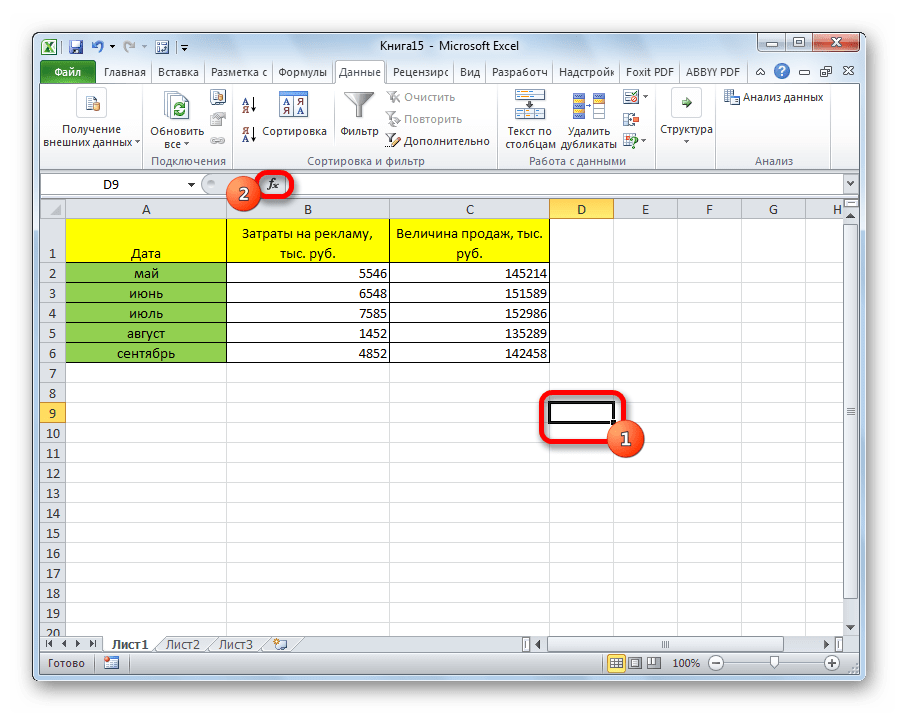
Ставим курсор в любую ячейку и нажимаем кнопку fx.
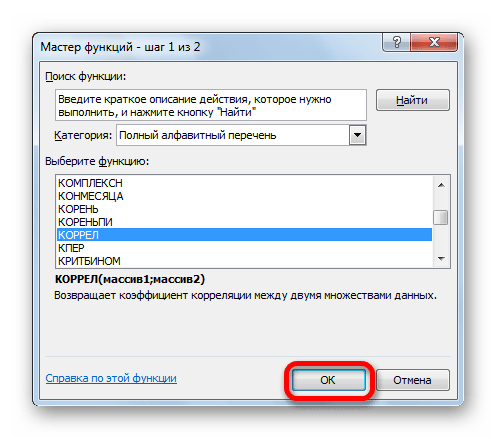
- В категории «Статистические» выбираем функцию КОРРЕЛ.
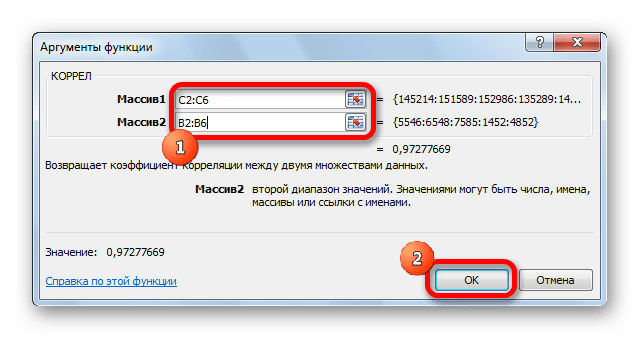
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Источник
KPI – показатель эффективности, позволяющий объективно оценить результативность выполняемых действий. Данная система применяется для оценки различных показателей (деятельности всей компании, отдельных структур, конкретных специалистов). Она выполняет не только функции контроля, но и стимулирует трудовую активность. Часто на основе KPI строится система оплаты труда. Это методика формирования переменной части зарплаты.
KPI ключевые показатели эффективности: примеры в Excel
Стимулирующий фактор в системе мотивации KPI – денежное вознаграждение. Получить его может тот работник, который выполнил поставленную перед ним задачу. Сумма премии / бонуса зависит от результата конкретного сотрудника в отчетном периоде. Объем вознаграждения может быть фиксированным или выражаться в процентах к окладу.
Каждое предприятие определяет ключевые показатели эффективности и вес каждого индивидуально. Данные зависят от задач компании. Например:
- Цель – обеспечить план продаж продукта в размере 500 000 рублей ежемесячно. Ключевой показатель – план продаж. Система измерения: фактическая сумма продаж / плановая сумма продаж.
- Цель – повысить сумму отгрузки в периоде на 20%. Ключевой показатель – средняя сумма отгрузки. Система измерения: фактическая средняя величина отгрузки / плановая средняя величина отгрузки.
- Задача – увеличить число клиентов на 15% в определенном регионе. Ключевой показатель – число клиентов в базе данных предприятия. Система измерения: фактическое число клиентов / плановое число клиентов.
Разброс коэффициента (весы) предприятие также определяет самостоятельно. Например:
- Выполнение плана менее 80% — недопустимо.
- Выполнение плана 100% — коэффициент 0,45.
- Выполнение плана 100-115% — коэффициент 0,005 за каждые 5%.
- Отсутствие ошибок – коэффициент 0,15.
- В отчетном периоде не было замечаний – коэффициент 0,15.
Это лишь возможный вариант определения мотивационных коэффициентов.
Ключевой момент в измерении KPI – отношение фактического показателя к плановому. Практически всегда заработная плата сотрудника складывается из оклада (постоянной части) и премии (переменной / изменяемой части). Мотивационный коэффициент влияет на формирование переменной.
Предположим, что соотношение постоянной и изменяемой частей в зарплате – 50 × 50. Ключевые показатели эффективности и вес каждого из них:
Примем следующие значения коэффициентов (одинаковые для показателя 1 и показателя 2):
Таблица KPI в Excel:
Пояснения:
- Оклад – постоянная часть заработной платы зависит от количества отработанных часов. Для удобства расчетов мы предположили, что фиксированная и переменная часть зарплаты равны.
- Процент выполнения плана продаж и плана работ рассчитывается как отношение фактических показателей к плановым.
- Для расчета премии используются коэффициенты. Формулы в Excel расчета KPI по каждому сотруднику: Мы приняли, что влияние показателя 1 и показателя 2 на сумму премиальных одинаковое. Значения коэффициентов тоже равны. Поэтому для расчета показателя 1 и показателя 2 используются одинаковые формулы (меняются только ссылки на ячейки).
- Формула для расчета суммы премии к начислению – =C3*(F3+G3). Плановую премию умножаем на сумму показателя 1 и показателя 2 по каждому сотруднику.
- Заработная плата – оклад + премия.
Это примерная таблица KPI в Excel. Каждое предприятие составляет собственную (с учетом особенностей работы и системы премирования).
Матрица KPI и пример в Excel
Для оценки работников по ключевым показателям эффективности составляется матрица, или соглашение о целях. Общая форма выглядит так:
- Ключевые показатели – критерии, по которым оценивается работа персонала. Для каждой должности они свои.
- Веса – числа в интервале от 0 до 1, общая сумма которых равняется 1. Отражают приоритеты каждого ключевого показателя с учетом задач компании.
- База – допустимое минимальное значение показателя. Ниже базового уровня – отсутствие результата.
- Норма – плановый уровень. То, что сотрудник должен выполнять обязательно. Ниже – работник не справился со своими обязанностями.
- Цель – значение, к которому нужно стремиться. Сверхнормативный показатель, позволяющий улучшить результаты.
- Факт – фактические результаты работы.
- Индекс KPI показывает уровень результата по отношению к норме.
Формула расчета kpi:
Индекс KPI = ((Факт – База) / (Норма – База)) * 100%.
Пример заполнения матрицы для офис-менеджера:
Коэффициент результативности – сумма произведений индексов и весов. Оценка эффективности сотрудника наглядно показана с помощью условного форматирования.
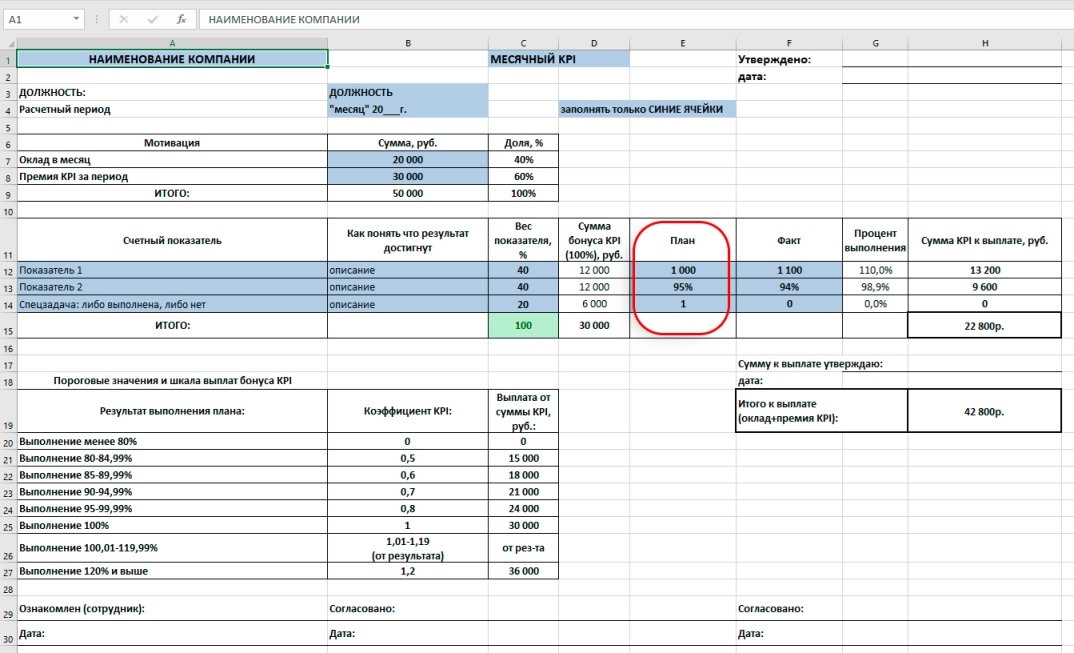
KPI в Excel. Пошаговая технология разработки и расчета KPI в excel. Готовый шаблон — таблица расчета с порядком заполнения. Формулы для расчета показателей KPI и подведения итогов. С возможностью скачать шаблон, excel-таблицу расчета KPI.
Рассматриваемая таблица расчета KPI сотрудников достаточна универсальна. Она применима практически для всех должностей в любом бизнесе. Таблица на практике доказала свою эффективность в сотнях бизнесов России и СНГ
Конечно, нюансов и подводных камней при разработке системы KPI (или КПЭ — ключевых показателей эффективности) более чем достаточно, поэтому руководствуйтесь логикой и главным критерием эффективности KPI — они должны существенно влиять на движение компании к стратегическим целям. KPI (кипиай) — это инструмент реализации стратегии. Сначала нужно определить долгосрочные цели бизнеса, затем разработать стратегию их достижения и только после этого, придать скорость при помощи KPI.
Начнем. Для оформления в excel шаблоне расчета KPI, мы должны располагать разработанной на базе стратегии и целей системой KPI, выбранными показателями для премирования и планами по ним. Имея их, нам нужно оформить расчетный лист KPI, заполнить таблицу, прописать формулы и получить расчет премии KPI сотрудника.
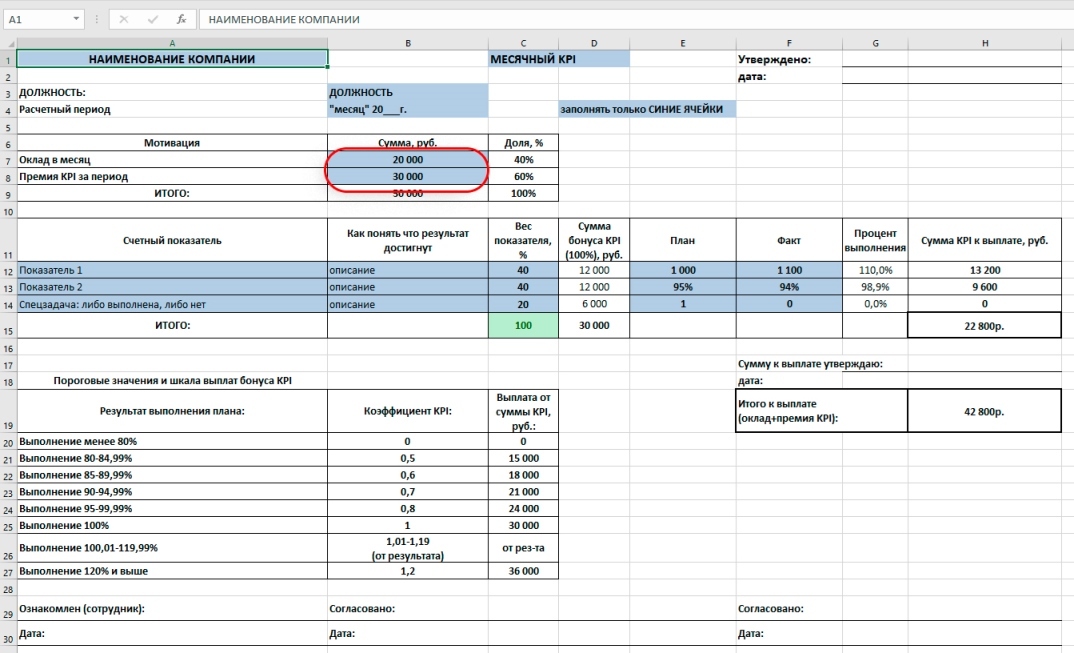
Шаг 1. Фиксируем расчетный период KPI, заполняем шапку
Расчетный период KPI – период на который устанавливаются целевые показатели и выплачивается премия. Мы рассматриваем период в один месяц. Фиксируем это в таблице, а также вносим наименование своей организации, должность, месяц и год расчетного периода.
Шаг 2. Определяем сумму и долю KPI
Определяем структуру заработной платы. В нашем примере устанавливаем оклад в сумме 20 тыс. руб. И премию KPI в сумме 30 тыс. руб. Вносим суммы в таблицу расчета KPI. Доля оклада и премии KPI рассчитываются автоматически. В нашем примере это 40% и 60% соответственно.
Оклад выплачивается за процесс, являясь фиксированной суммой. Премия KPI выплачивается за процесс и является переменной величиной.
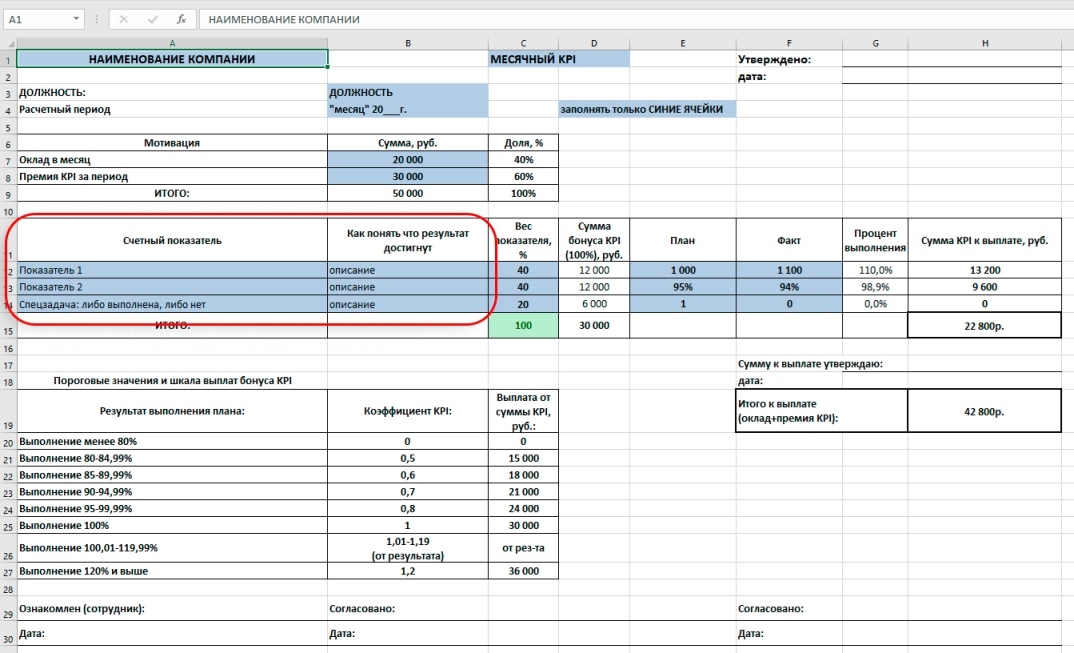
Шаг 3. Вносим ключевые показатели для премирования
Выбор показателей для премирования по KPI, один из наиболее сложных этапов при премировании по KPI. Скопированные показатели не работают, зачастую приводя к негативным последствиям. Поэтому, показатели KPI всегда разрабатывайте самостоятельно, конкретно для своего бизнеса и должности. Максимум три показателя. В нашем случае мы установили два расчетных показателя и один в виде спецзадачи. Расчетные показатели рассчитываются в соответствии со шкалой премирования, а спецзадача по принципу: либо выполнена, либо нет.
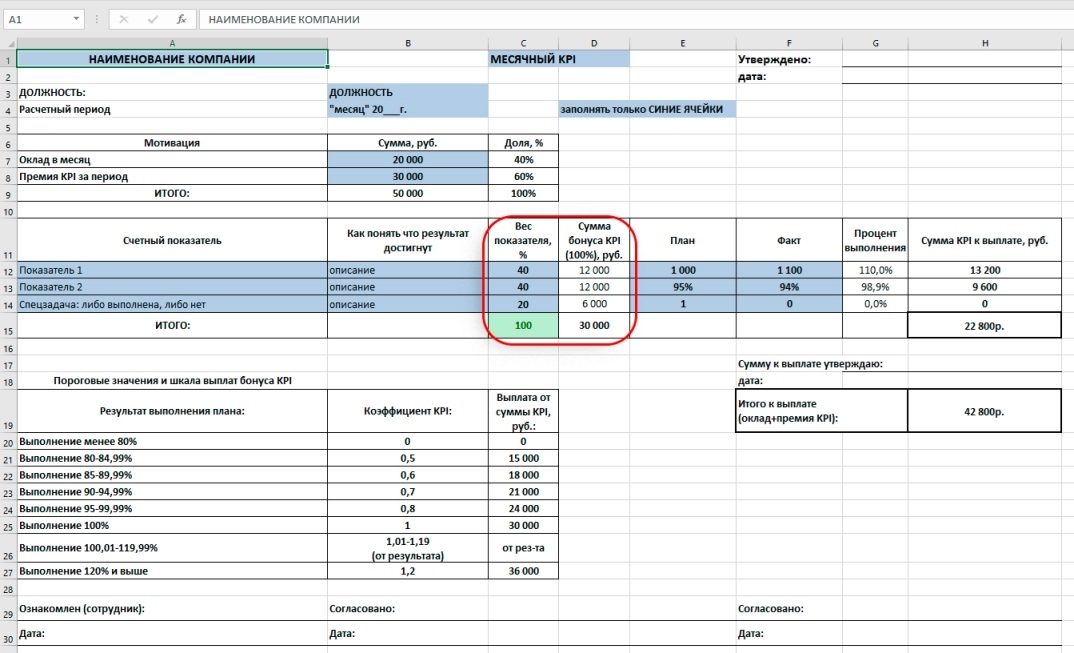
Шаг 4. Устанавливаем веса для показателей KPI
Вес показателя KPI — это доля данного показателя в общей премии KPI. Он устанавливается в зависимости от значимости, помогая расставить приоритеты, если показателей больше одного. Мы в примере устанавливаем: для первых двух показателей по 40% и для спецзадачи 20% от суммы премии KPI. Вносим в таблицу. Сумма премии в рублях для каждого показателя рассчитывается автоматически. Получаем в рублях: по 12 тыс. рублей для первого и второго показателя и 6 тыс. руб. для третьего показателя.
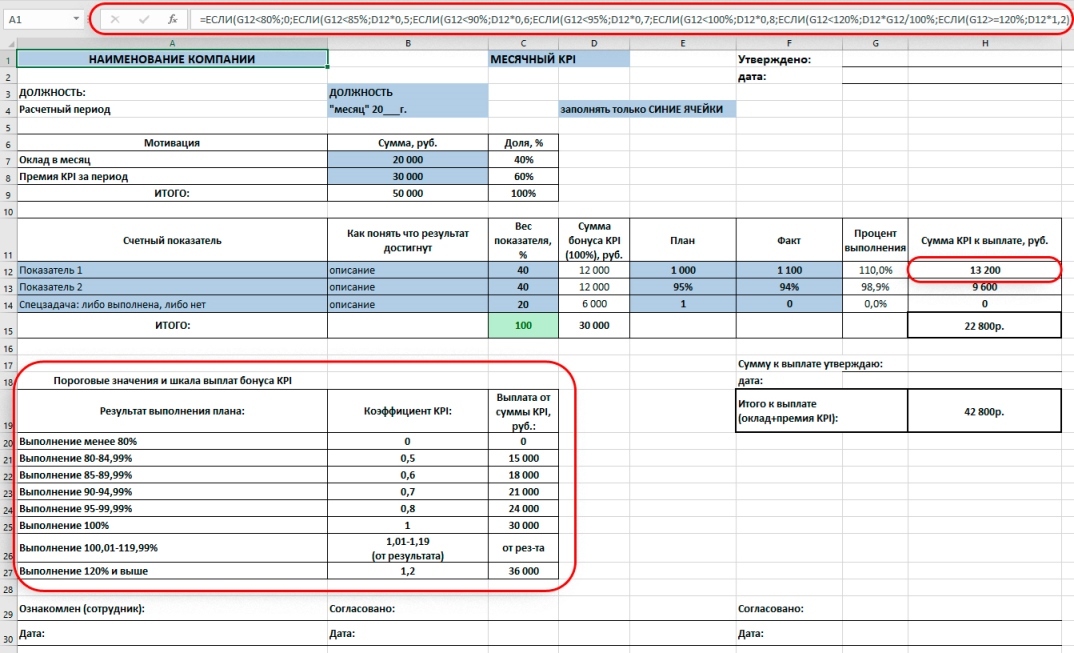
Шаг 5 Устанавливаем пороговые значения и шкалу выплат
- Для первых двух задач устанавливаем расчетный вариант выплаты премии в зависимости от процента выполнения плана.
Нижний уровень премирования – выполнение плана на 80%. Если выполнение ниже 80% – премия не выплачивается. Далее, выплата производится с понижающим коэффициентом. Каждые 5% выполнения плана коэффициент растет. 100% премии KPI выплачивается за 100% выполнение плана. При перевыполнении, премия выплачивается с повышающим коэффициентом в соответствии с процентом перевыполнения. За 101% выполнения плана коэффициент составляет 1,01; за 102% коэффициент 1,02 и так далее. Верхний уровень премирования устанавливаем с коэффициентом 1,2 при выполнении плана 120% и выше. Фиксируем справочно шкалу премирования в нижней части таблицы. Для расчета премии KPI по первому показателю в ячейке «H12» прописываем формулу «ЕСЛИ»:
=ЕСЛИ(G12<80%;0;ЕСЛИ(G12<85%;D12*0,5;ЕСЛИ(G12<90%;D12*0,6;ЕСЛИ(G12<95%;D12*0,7;ЕСЛИ(G12<100%;D12*0,8;ЕСЛИ(G12<120%;D12*G12/100%;ЕСЛИ(G12>=120%;D12*1,2)))))))
Для второго показателя прописываем аналогичную формулу в ячейке «H13».
- Для третьего показателя — спецзадачи устанавливаем вариант выплаты по принципу: либо выполнил, либо нет.
Выполнил – получил 100% премии. Не выполнил — не получил ничего. Прописываем для ячейки «H14» следующую формулу:
=ЕСЛИ(G14<100%;0;$D$14)
Шаг 6. Вносим в таблицу планы по KPI
В нашем примере мы установили следующие планы: Показатель 1 = 1000 ед; Показатель 2 = 95%; Спецзадача: либо выполнена, либо нет, в план выставляем «1» (при выполнении в Факт внесем «1», а при невыполнении «0»).
Шаг 7. Подводим итоги, рассчитываем премию KPI
По завершении расчетного периода, вносим по каждому показателю KPI полученные результаты в графу «Факт».
В нашем примере это: Показатель 1 = 1100 ед. (выполнение 110%); Показатель 2 = 94% (выполнение плана 98,9%); Спецзадача: не выполнена, вбиваем «0».
По прописанным формулам, получаем расчет премии KPI: Показатель 1 = 13,2 тыс. руб; Показатель 2 = 9,6 тыс. руб; Спецзадача: 0 руб.
Суммируем начисленные премии по показателям и получаем общую премию KPI сотрудника за период в 22,8 тыс. руб. Формула в ячейке «H15»: =СУММ(H12:H14)
Общая сумма зарплаты, оклад плюс премия KPI, составила 42,8 тыс. руб. и зафиксирована в ячейке «H19».
Заключение
Готово! Мы прошли все этапы расчета KPI при помощи Excel таблицы. Прописали формулы, внесли данные и получили расчет премии KPI сотрудника.
ГЛАВНОЕ! Таблица — лишь инструмент оформления и расчета премии KPI за период. Эффект от внедрения лежит в области разработки системы KPI, выбора правильных показателей, выставления корректных планов и соблюдения базовых принципов системы. Скопированные напрямую показатели KPI из примеров в интернете, с похожих бизнесов, из книг и любых других источников — не работают!!! Всегда разрабатывайте систему KPI и показатели в том числе, индивидуально. А excel-таблица, в том числе рассмотренный образец, поможет оформить расчет премии.
Полезности. В полезных ссылках можно бесплатно скачать excel таблицу расчета KPI из рассмотренного примера.
А также пройти авторский онлайн-курс практикум Александра Шведова «Пошаговая разработка KPI» для самостоятельного внедрения KPI в своей организации (первая ступень курса бесплатно). Курс разработан на базе 18 лет работы с KPI, поможет быстро и правильно внедрить KPI, избежать ошибок. В итоге с помощью KPI увеличить прибыль, повысить эффективность и ответственность сотрудников!
Полезные ссылки:
СКАЧАТЬ БЕСПЛАТНО EXCEL ТАБЛИЦУ РАСЧЕТА KPI
ОНЛАЙН-КУРС ПРАКТИКУМ «РАЗРАБОТКА KPI»
Содержание
- Суть корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью пакета анализа
- Вопросы и ответы
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Расчет коэффициента корреляции
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
- В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
- Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
Жмем на кнопку «OK».
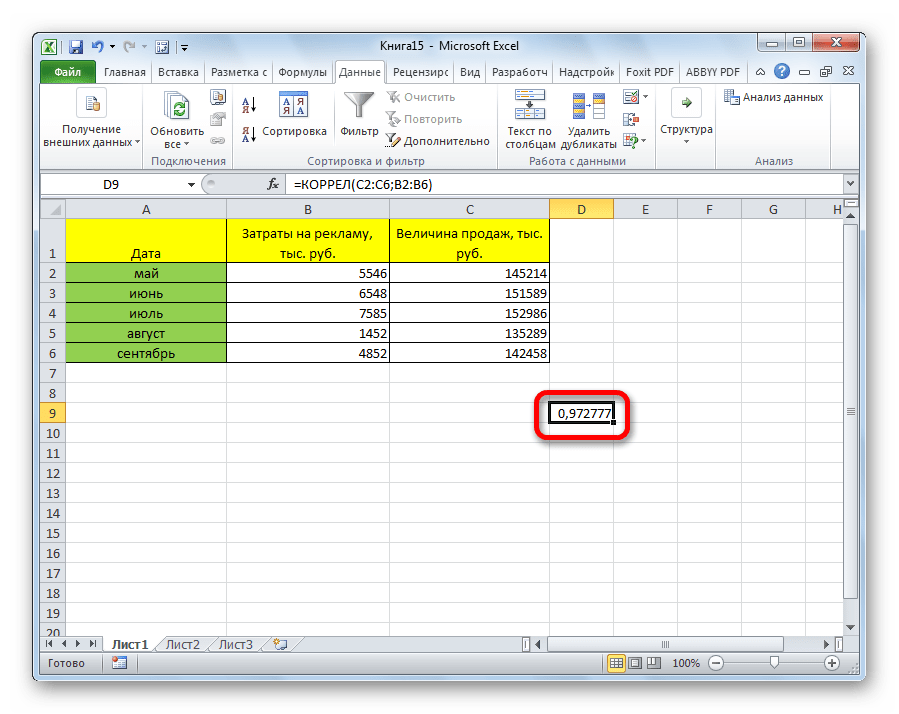
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
- В открывшемся окне перемещаемся в раздел «Параметры».
- Далее переходим в пункт «Надстройки».
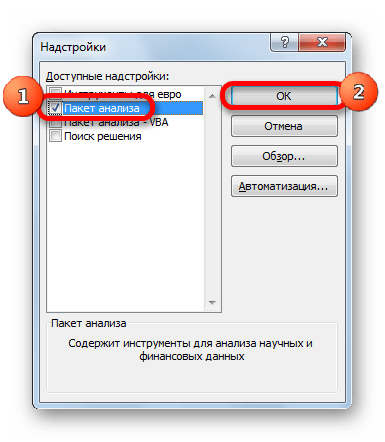
- В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
- В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
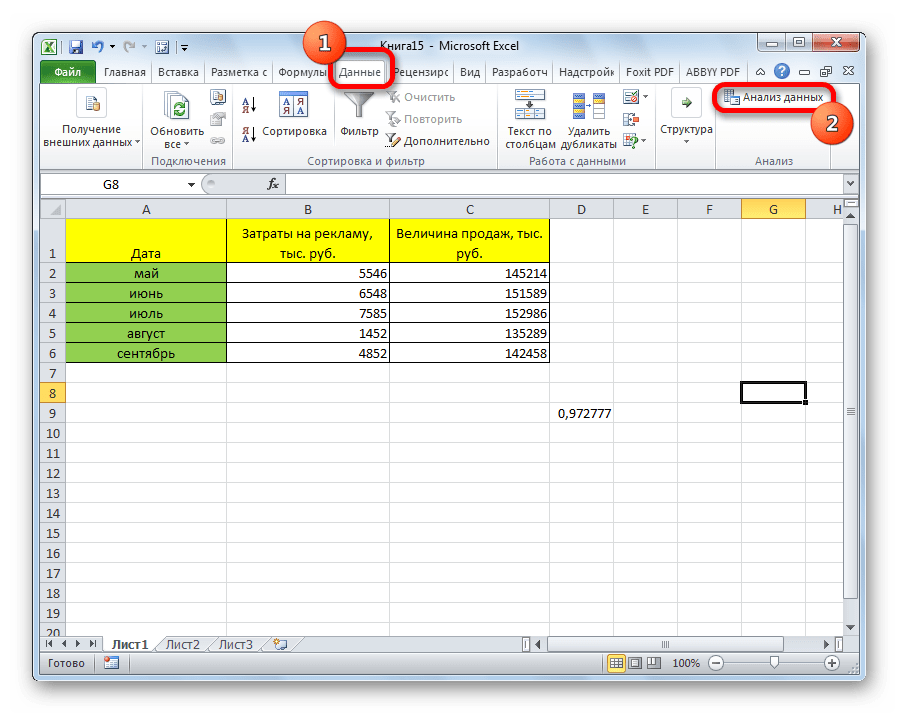
- После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
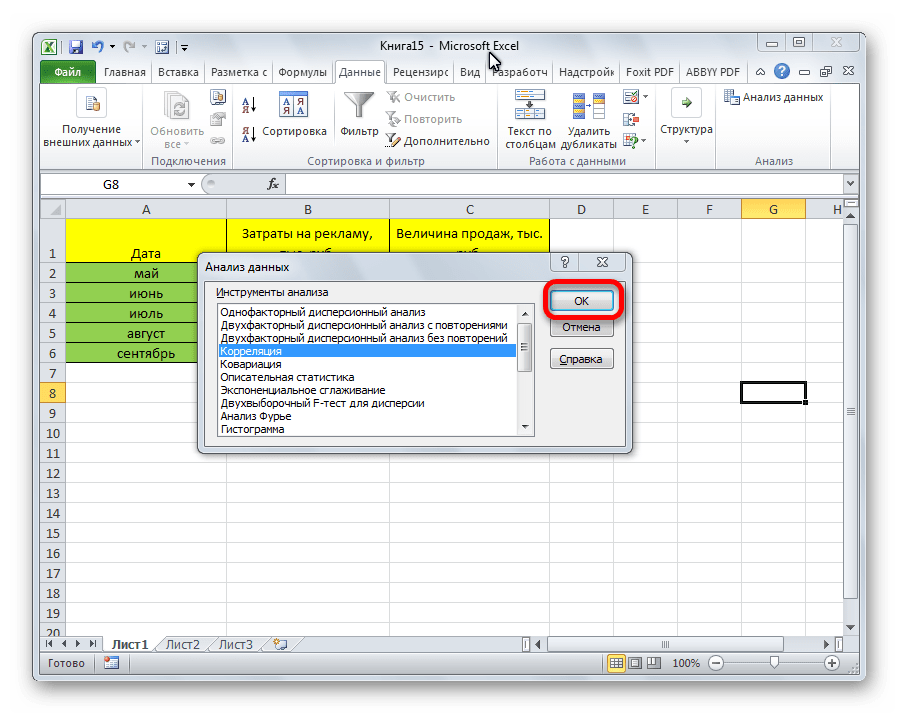
- Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
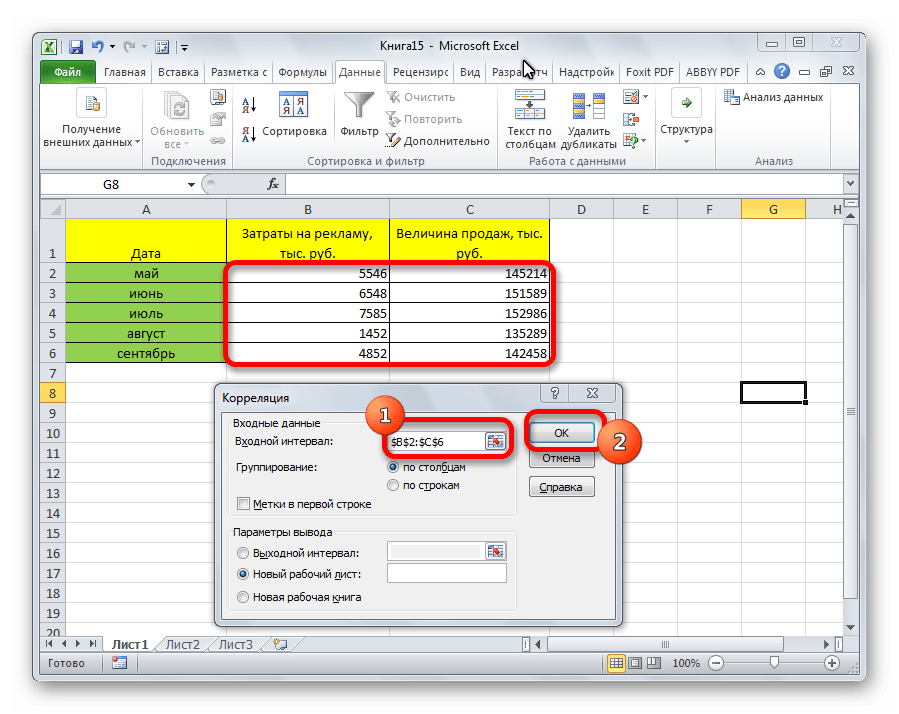
- Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
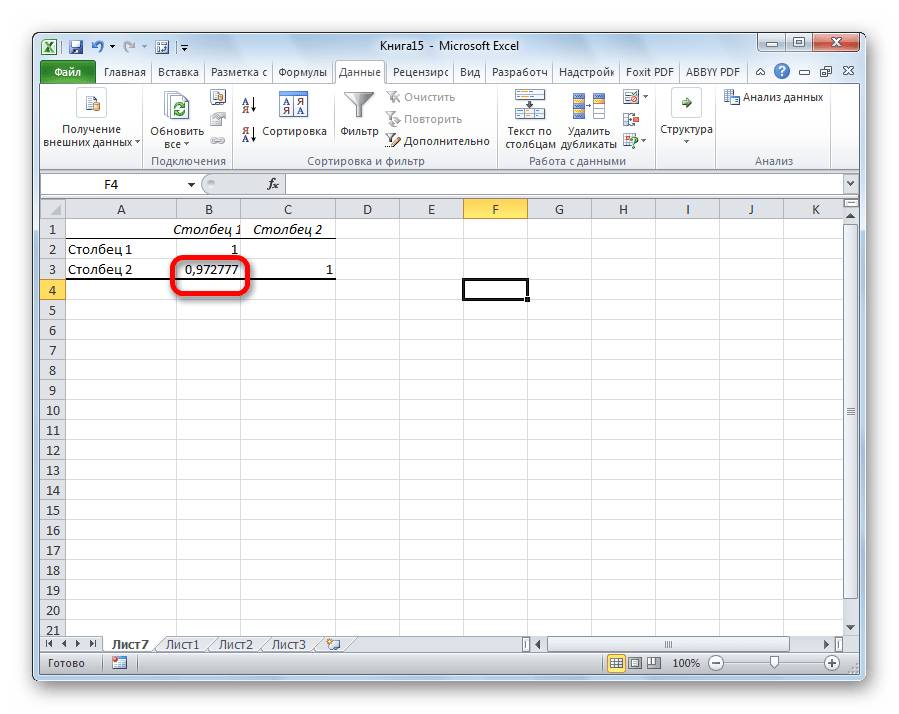
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Еще статьи по данной теме:
Помогла ли Вам статья?
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Функция ЛИНЕЙН
В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.
Описание
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.
Уравнение для прямой линии имеет следующий вид:
y = m1x1 + m2x2 +. + b
если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив . Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Синтаксис
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Аргументы функции ЛИНЕЙН описаны ниже.
Синтаксис
Известные_значения_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
Известные_значения_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
Если массив известные_значения_x опущен, то предполагается, что это массив <1;2;3;. >, имеющий такой же размер, что и массив известные_значения_y.
Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.
Если статистика имеет true, то LINEST возвращает дополнительную регрессию; в результате возвращается массив .
Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика.
Стандартные значения ошибок для коэффициентов m1,m2. mn.
Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ).
Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, как вычисляется 2, см. в разделе «Замечания» далее в этой теме.
Стандартная ошибка для оценки y.
F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными.
Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе «Замечания». Далее в примере 4 показано использование величин F и df.
Регрессионная сумма квадратов.
Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела.
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.
Замечания
Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m):
Чтобы найти наклон линии, обычно записанной как m, возьмите две точки на строке (x1;y1) и (x2;y2); наклон равен (y2 — y1)/(x2 — x1).
Y-перехват (b):
Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.
Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон:
=ИНДЕКС( LINEST(known_y,known_x’s);1)
Y-перехват:
=ИНДЕКС( LINEST(known_y,known_x),2)
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:
где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ( известные_значения_y ).
Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y( known_x) для прямой линии или РОСТ( known_y, known_x в ) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r 2 — индикатор того, насколько хорошо уравнение, выданное в результате регрессионного анализа, объясняет связь между переменными. Значение r 2 равно ssreg/sstotal.
В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется «коллинеарность», так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце «самец» из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.
Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
Наклон и ОТОКП возвращают #DIV/0! ошибка «#ЗНАЧ!». Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.
Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y = m1*x + m2*x^2 + m3*x^3 + b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.
Примеры
Пример 1. Наклон и Y-пересечение
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2 );
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
источники:
http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD-84d7d0d9-6e50-4101-977a-fa7abf772b6d
http://exceltable.com/otchety/korrelyacionno-regressionnyy-analiz