|
Расчет премии по факту выполнения плана |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
1. Откройте файл marks.xls, который содержит таблицу с отметками учеников по четырём предметам.
2. Найдите коэффициенты корреляции (взаимосвязь) между оценками по разным предметам, а также между средним баллом и оценками по каждому из предметов. Оформите данные в виде таблицы:
Оставьте у всех значений только три знака в дробной части.
3. Откройте файл salary.xls, который содержит таблицу расчёта зарплаты работников фирмы «Рога и Копыта». Требуется добавить нужные формулы в столбцах Премия и Сумма.
Работник получает премию пропорционально перевыполнению плана. Например, если план выполнен на 120% (перевыполнение на 20%), размер премии составит 20% от его зарплаты. Работник, сделавший меньше нормы, не получает премии.
4. Решение и вопросы можете отправить на почту на infmatem208@gmail.com (в письме укажите фамилию и класс).

Здравствуйте всем.
Необходимо помощь в составлении формулы. Суть такая, необходимо в ячейке рассчитывать премиальную часть менеджера по продажам в зависимости от % выполнения плана продаж, есть соответствующий коэффициент.
Премиальная часть фиксир. 25 000р. рассчитываться по разным группам товара из след условий:
1. Если процент менее 90%, то премия не выплачивается.
2. Если процент выполнения от 90% до 99%, то коэффициент понижающий 0,6.
3. Если план выполнен от 100% до 119%, то с коэффициентом 1.
4. Если план свыше 120%, то с повышающим коэффициентом 1,3.
То есть, если менеджер выполнил план на 129%, то его премия считается — 25000*1,3=32500р.
Нужно чтоб при проставлении фактического оборота, автоматом подтягивался нужный коэффициент на основании % выполнения плана.
Я так понимаю, что необходимо использовать формулу «Если», но никак не получается сообразить как всё это разместить в одной ячейке, как не пытаюсь но в расчет берет только 2 значения.
Буду благодарна всем, кто поможет!!!
Спасибо!
во вложении шаблон
Посчитать премию от оклада: варианты начисления
На первый взгляд, размер премии, начисляемой от оклада, определяется крайне просто: умножением оклада на величину процента, установленного для такого расчета. Однако определения только одного этого показателя для исчисления подобной премии оказывается недостаточно. В числе правил расчета должны быть также прописаны:
- целевое назначение премии;
- периодичность ее начисления;
- наличие зависимости (или независимости) величины премиальных от времени фактической работы сотрудника в периоде, за который делается ее начисление;
- условия лишения премии полностью (например, за дисциплинарный проступок) или частично (например, исчисление может не производиться за не полностью отработанный месяц);
- правила расчета премиальных за период, в котором произошло изменение величины оклада.
Отражают такие правила в особых документах, создание которых преследует 2 цели:
- включение премий в систему оплаты за труд;
- установление применяемого порядка премирования.
Как правильно оформить премии сотрудникам и отразить их в учете, узнайте в «КонсультантПлюс». Получите пробный доступ к системе и бесплатно переходите в Типовую ситуацию.
О том, какие бывают премии и вознаграждения, читайте в специальном материале.
Как правило, документом, содержащим информацию о процедуре начисления премий, становится либо положение об оплате труда, либо положение о премировании. С 2017 года эти документы, представляющие собой внутренние нормативные акты, в ТК РФ (ст. 309.2) указаны как необязательные для создания в микропредприятиях. Однако отсутствие такого документа требует прописывать правила премирования, действующие у работодателя, в трудовом соглашении с каждым сотрудником. По существу, такой же порядок, допускающий варианты отражения условий премирования в разных внутренних документах (в т. ч. и в трудовом договоре), действовал и до нововведений 2017 года. Причем разработка отдельного документа о правилах премирования, касающихся всех сотрудников одновременно, всегда считалась более предпочтительной, поскольку позволяла сократить объемы информации, вносимые в трудовые соглашения.
О том, какие моменты должны найти отражение в нормативном акте о премировании в отношении премий за квартал, читайте в статье «Расчет квартальной премии за фактически отработанное время».
Какие коэффициенты применяются при расчете премии
Правила начисления премии могут не ставить процедуру ее расчета в зависимость от каких-либо иных условий, кроме величины оклада и размера доли, установленной для исчисления премиальных. В этом случае премия фактически становится фиксированной. Размер ее не будет зависеть от времени фактической работы или правил лишения премии.
Измениться величина премиальных в такой ситуации может только при изменении базы начисления, т. е. оклада. В зависимости от алгоритма, внесенного в основной документ о премировании, изменение оклада, произошедшее в периоде начисления премии, может быть учтено по-разному:
- с начала периода, за который считают премиальные;
- с периода, следующего за повышением оклада;
- с учетом соотношения числа дней (календарных или рабочих) в периоде изменения оклада, соответствующих каждому из окладов.
Последний вариант потребует расчета коэффициентов, учитывающих соответствующие соотношения количества дней.
Эксперты «КонсультантПлюс» рассказали о переходе с окладной системы оплаты труда на окладно-премиальную. Получите пробный доступ к материалу на данную тему бесплатно.
Если условия начисления премии предусматривают зависимость ее величины от времени фактической работы в периоде премирования или исключают какие-либо периоды из расчета, то сумма премиальных будет считаться с применением коэффициента, учитывающего эти обстоятельства. В первом случае полная величина премии за период будет умножаться на показатель, учитывающий долю времени фактической работы в общей продолжительности рабочего времени в периоде премирования. При исключении каких-либо периодов из расчета (чаще всего таким периодом становится месяц) соответствующий коэффициент, снижающий размер премии, учтет соотношение полностью отработанных в периоде премирования месяцев и общей протяженности периода премирования.
Если в регионе, где работает работодатель, действует районный коэффициент к зарплате, то сумма премии, рассчитанная от оклада, должна быть умножена на этот коэффициент.
О налогообложении начисленных премиальных читайте в материале «Какими налогами и взносами облагается премия сотрудникам?».
Пример расчета премии в файле Excel (он же — калькулятор)
Рассмотрим пример расчета премии сотрудникам на цифрах. Предположим, что в ООО «Импульс» установлена начисляемая поквартально премия, если ООО за соответствующий квартал достигнуты определенные финансовые результаты по итогам работы. Размер премии составляет 30% от оклада.
В положении о премировании, утвержденном в ООО, зафиксировано, что начисление не производится за не полностью отработанные работником месяцы. Для квартальной премии это означает, что сумма, рассчитанная как 30%-ная доля оклада, должна быть умножена на коэффициент, учитывающий количество полностью отработанных в квартале месяцев. Соответственно, этот коэффициент может составлять величину 2/3 либо 1/3.
За совершение дисциплинарного проступка в периоде премирования предусмотрено лишение сотрудника премии за этот период полностью.
При изменении оклада в любом из месяцев периода премирования расчет премии за квартал делается от новой величины оклада.
В регионе работы ООО действует районный коэффициент к зарплате, равный 1,4.
Расчет премии приводится нами в файле Excel, который может быть использован и как калькулятор для расчета премиальных, и как образец для создания собственной таблицы расчетов, учитывающей иные условия начисления премии.
Скачать пример расчета
Учет премии при расчете среднего заработка
Премии, предусмотренные системой оплаты труда и имеющие установленные правила их начисления, учитывают в расчете среднего заработка (ст. 139 ТК РФ). Однако они по-разному входят в этот расчет в зависимости от ряда обстоятельств (положение об особенностях порядка исчисления среднего заработка, утвержденное постановлением Правительства РФ от 24.12.2007 № 922):
- периодичности начисления премий и наличия выплат дублирующего характера;
- полноты отработки периода исчисления среднего заработка;
- полноты вхождения периода, за который начислена премия, в период исчисления среднего заработка;
- привязки к периоду расчета в силу начисления в нем, фактического вхождения в него или потому, что премия должна быть учтена в этом периоде;
- учета или неучета времени фактической работы в момент начисления премии.
Различные сочетания этих обстоятельств приводят к тому, что премию оказывается возможным взять в расчет:
- полностью — невзирая на то, что она может оказаться начисленной:
- не за период расчета;
- вне периода расчета;
- без учета времени фактической работы;
- с пересчетом в пропорции ко времени, отработанному в периоде расчета среднего заработка, или к числу месяцев, соответствующих той части периода начисления премии, которая может быть взята в расчет.
Читайте подробнее о расчете среднего заработка в тематической публикации, подготовленной экспертами «КонсультантПлюс». Получите пробный доступ к документу бесплатно.
Для премий, определяемых от оклада, возможны практически все варианты принятия в расчет, поскольку они могут начисляться:
- за разные периоды (месяц, квартал, год и иные промежутки времени, а также разово);
- не в том периоде, за который начислены;
- как с учетом, так и без учета времени фактической работы в периоде начисления.
Обо всех возникающих вариантах учета премий в расчете среднего заработка читайте в материале «Учитывается ли премия при расчете отпускных?».
Итоги
Премия, начисляемая от оклада, устанавливается как выраженная в процентах доля этого оклада. Однако помимо определения величины доли оклада требуется разработать еще ряд правил, необходимых для установления порядка начисления премиальных, закрепив их во внутреннем документе работодателя. В зависимости от этих правил расчет величины премий может осуществляться по разным алгоритмам, а начисленные суммы по-разному будут учитываться при исчислении среднего заработка.
Практическая работа «Решение квадратного уравнения при помощи табличного процессора»
Данная практическая работа научит учащихся пользоваться табличным процессором и закрепить полученые знание во время учебного процесса.
Просмотр содержимого документа
«Практическая работа «Решение квадратного уравнения при помощи табличного процессора»»
«Решение квадратного уравнения
при помощи табличного процессора EXCEL»
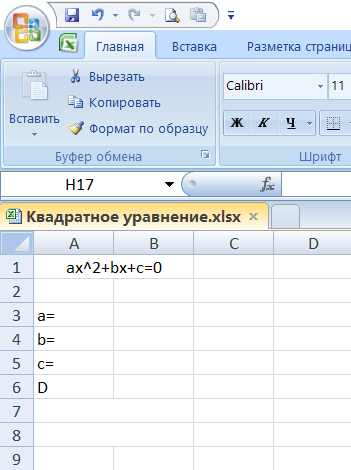
Подготовьте таблицу по образцу
Внесите коэффициенты квадратного уравнения в ячейки столбца В.
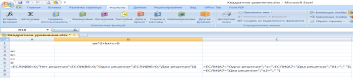
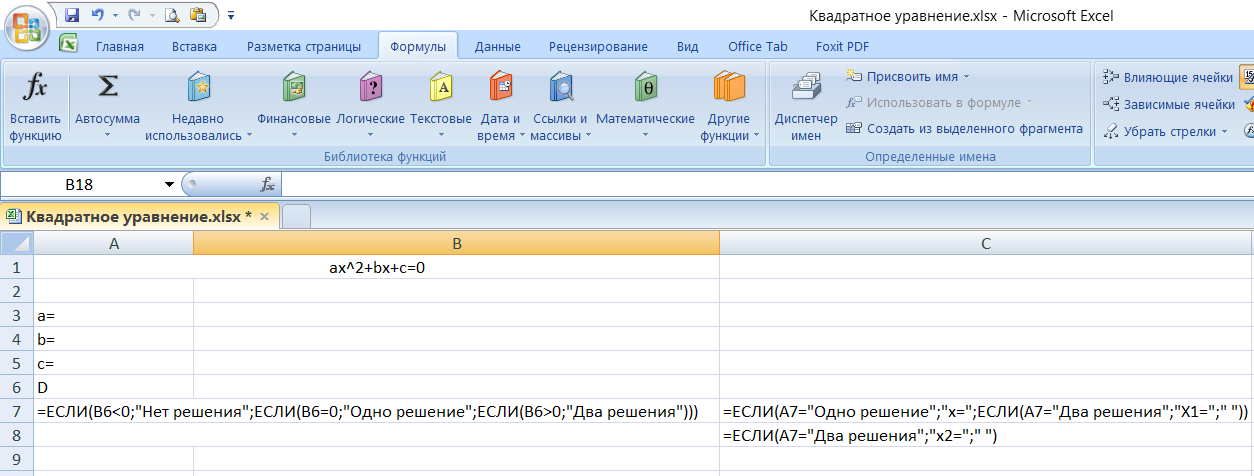
В соответствующие ячейки внесите формулы при помощи мастера функций
=ЕСЛИ(A7=»Одно решение»;»x=»;ЕСЛИ(A7=»Два решения»;»X1=»;» «))
В ячейку D7 и D8 внесите формулы нахождения корней квадратного уравнения.
В ячейке D2 проверьте правильность найденных корней, подставив их в квадратное уравнение
«Решение квадратного уравнения
при помощи табличного процессора EXCEL»
Подготовьте таблицу по образцу
Внесите коэффициенты квадратного уравнения в ячейки столбца В.
В соответствующие ячейки внесите формулы при помощи мастера функций
=ЕСЛИ(A7=»Одно решение»;»x=»;ЕСЛИ(A7=»Два решения»;»X1=»;» «))
В ячейку D7 и D8 внесите формулы нахождения корней квадратного уравнения.
В ячейке D2 проверьте правильность найденных корней, подставив их в квадратное уравнение
Практические работы «Решение систем уравнений в среде Microsoft Excel» и «Стандартные функции Microsoft Excel»
Практическая работа по теме “Решение систем уравнений в среде Microsoft Excel”
Цель работы:
- освоить основные приемы работы с Мастером диаграмм в MS Excel;
- научиться решать системы уравнений с помощью электронных таблиц.
Используемые программные средства: табличный процессор MS Excel.
Содержание работы:
Задача 1. Решить графически систему уравнений
Основное задание. Найти решение системы уравнений
1. Заполните таблицу, как показано на рисунке 1:
2. Выделите блок В2:В17. Постройте диаграмму – график, как показано на рис.2.
3. ПКМ вызовите вкладку Исходные данные. Выполните Ряд, Добавить, Значения. ЛКМ выделите блок С2 : С17.
4. В окне Подписи оси Х занесите значения x, выделив блок А2 : А17. Завершите построение диаграммы и найдите решение системы. Решение запишите в тетрадь. (Рис. 3)
Дополнительное задание. Оформите решение.
1. Выбрав вкладку Параметры диаграммы ПКМ, добавить основные линии сетки по осям OX и OY.
2. В “Исходных данных” во вкладке Ряд добавить имена рядов: 

3. Щелкнув ПКМ по оси OX, выбрать меню Формат оси, Шкала; установить соответствующие значения. (Рис.4)
4. Щелкнув ПКМ по оси OY, установить цену основных делений 1 и во вкладке Шрифт уменьшить размер шрифта.
5. Щелкнув ПКМ, выбрать Формат области построения, во вкладке Вид поставить флажок Заливка прозрачная.
6. Сравните полученный результат с образцом, представленным на рисунке 5.
Задача 2. Решить графически систему уравнений
Практическая работа по теме “Стандартные функции Microsoft Excel”
Цель работы:
- освоить основные приемы работы со стандартными функциями в MS Excel;
- научиться решать задачи табулирования функции с помощью электронных таблиц.
Используемые программные средства: табличный процессор MS Excel.
Содержание работы:
Функции
Для записи формул в электронных таблицах можно использовать стандартные функции. Всё множество встроенных функций табличного процессора делится на несколько групп: математические, статистические, функции даты и времени и т.д. В различных табличных процессорах наборы стандартных функций различаются.
Таблица некоторых стандартных функций Excel
| SIN() | синус |
| COS() | косинус |
| TAN() | тангенс |
| КОРЕНЬ()(SQRT) | корень |
| ABS() | модуль |
| СУММА() | сумма |
| СРЗНАЧ()(AVERAGE) | среднее значение |
| МАКС()(MAX) | максимум |
| МИН(MIN) | минимум |
Задача 1. На отрезке [0;1] вычислить значения функции 
1. Заполните таблицу, как показано ниже на рисунках 1 и 2.
2. Скопируйте формулу из ячейки А4 в ячейки А5 : А8, а формулу из ячейки В3 в ячейки В4 : В8.
При копировании абсолютный адрес $B$1, содержащий значение шага табуляции, не будет изменяться.
3. Загрузите режим отображения формул: Сервис/параметры/вид/формулы.
В режиме отображения формул таблица будет выглядеть так, как показано на рисунке 3:
4. Отмените режим отображения формул. В режиме отображения значений таблица будет выглядеть так, как показано на рисунке 4:
Задачи для самостоятельной работы:
Задача 2. На отрезке [1,2; 2] вычислить значения функции 
Задача 3. На отрезке [2;4] вычислить значения функции 
Решение вычислительных задач на компьютере
Глава 10. Решение вычислительных задач на компьютере
Практические работы
Практическая работа № 61.
Решение уравнений методом перебора
Напишите программу, которая находит все решения заданного вам уравнения на интервале [-5;5]. Программа должна выполнить следующие действия:
1. Определяет и выводит на экран интервалы, на которых расположены корни уравнения.
2. На каждом интервале, используя метод перебора, ищет решение с точностью 0,001 и выводит полученные решения на экран.
Вычисление функции, стоящей в левой части уравнения, оформите в виде подпрограммы.
Уровень A. Интервалы, на которых расположены корни, можно найти с помощью электронных таблиц. Программа запрашивает левую границу очередного интервала и выводит найденный корень уравнения.
Введите левую границу интервала:
Уровень B. Составить две программы, одна из которых выделяет все интервалы, на которых находятся корни, а вторая запрашивает левую границу очередного интервала и выводит найденный корень уравнения.
Уровень C. Составить одну программу, которая работает полностью автоматически: достаточно ввести в программу функцию и запустить. Программа находит все интервалы, на которых расположены корни и уточняет решения. После того, как очередной интервал найден, программа выводит его на экран и, применяя метод перебора с нужным шагом, уточняет решение.
Варианты заданий по теме «Решение уравнений»
Практическая работа № 62.
Решение уравнений методом деления отрезка пополам
Напишите программу, которая находит все решения заданного вам уравнения на интервале [-5;5]. Программа должна выполнить следующие действия:
1. Определяет и выводит на экран интервалы, на которых расположены корни уравнения.
2. Используя метод деления отрезка пополам, на каждом интервале ищет решение с точностью 0,001 и выводит полученные решения на экран.
Вычисление функции, стоящей в левой части уравнения, оформите в виде подпрограммы.
Уровень A. Интервалы, на которых расположены корни, можно найти с помощью электронных таблиц. Программа запрашивает границы очередного интервала и выводит найденный корень уравнения.
Введите границы интервала:
Уровень B. Составить две программы, одна из которых выделяет все интервалы, на которых находятся корни, а вторая запрашивает границы очередного интервала и выводит найденный корень уравнения, а также число шагов, которые потребовались для достижения заданной точности.
Введите границы интервала:
Уровень C. Составить одну программу, которая работает полностью автоматически: достаточно ввести в программу функцию и запустить. Программа находит все интервалы, на которых расположены корни и уточняет решения. После того, как очередной интервал найден, программа выводит его на экран и, применяя метод деления отрезка пополам, уточняет решение и определяет необходимое для этого количество шагов.
Практическая работа № 63.
Решение уравнений в табличных процессорах
Уровень A. С помощью табличного процессора найдите все решения уравнения из примера «Полёт мяча», разобранного в учебнике.
Уровень B. Выполните задание уровня А. Затем выделите отдельную ячейку, в которой вычисляется максимальное значение функции 
1) минимальную начальную скорость, при которой еще можно попасть в мишень;
2) максимальное расстояние, при котором можно попасть в мишень при начальной скорости 15 м/с.
Уровень C. Выполните задание уровня B. Затем, используя замену 
Практическая работа № 64.
Вычисление длины кривой
Уровень A. Найдите длину параболы 

Уровень B. Для примера «Полет мяча» вычислите длину траектории движения шарика для углов вылета 35,5° и 65,8°. Сравните полученные результаты.
Уровень C. Постройте с помощью табличного процессора эллипс, который описывается уравнением 



Экспериментально определите наибольший интервал дискретизации, при котором ошибка численного метода (в сравнении с результатом, полученным по формуле Рамануджана) составляет не более 1%.
Практическая работа № 65.
Вычисление площади фигуры
Уровень A. Найдите площадь фигуры, ограниченной параболой 

Уровень B. Найдите площадь фигуры, ограниченной графиками функций 

Уровень C. Найдите площадь фигуры, ограниченной эллипсом



Сравните ваш результат с точным значением 
Практическая работа № 66.
Оптимизация. Метод дихотомии
Уровень A. Напишите программу, которая находит все минимумы и максимумы функции (см. варианты на следующей странице) на интервале [-5;5] с точностью 0,001, используя метод «золотого сечения». Границы интервала для поиска каждого минимума и максимума задаются вручную.
Уровень B. Напишите программу, которая находит все минимумы и максимумы функции (см. варианты на следующей странице) на интервале [-5;5] с точностью 0,001, используя метод «золотого сечения». Границы интервала для поиска каждого минимума и максимума определяются автоматически.
Уровень C. Напишите программу, которая находит все минимумы и максимумы функции (см. варианты на следующей странице) на интервале [-5;5] с точностью 0,001, используя метод «золотого сечения», причём на каждом шаге цикла вычисляется только одно новое значение функции. Границы интервала для поиска каждого минимума и максимума определяются автоматически.
Варианты заданий по теме «Оптимизация. Метод дихотомии»
max:(-1.612,14.703) min:( 1.612,-12.703)
max:(-0.565,12.715) min:( 2.348,-10.426)
max:( 0.368,11.753) min:( 2.760,-4.867)
max:(-2.210,19.058) min:( 0.857,-16.862)
max:(-2.520,12.001) min:( 0.250,-11.374)
max:(-0.527,17.584) min:( 2.115,-3.568)
max:(-2.754,21.186) min:( 0.604,-5.861)
max:(-2.601,30.604) min:( 0.691,-15.677)
max:(-2.986,27.177) min:( 0.187,-11.281)
max:(-2.987,21.011) min:( 1.072,-9.490)
max:(-3.417,15.758) min:( 0.072,-28.036)
max:(-3.314,27.161) min:( 0.361,-10.723)
max:(-2.208, 5.835) min:( 0.916,-6.647)
max:(-0.430,11.088) min:( 2.003,-6.333)
max:( 0.246,15.493) min:( 2.400,-2.049)
Практическая работа № 67.
Оптимизация с помощью табличных процессоров
Уровень A. В углах квадратного листа железа, сторона которого равна 1 м, вырезают четыре квадрата со стороной x. Затем складывают получившуюся развертку (по штриховым линиям на рисунке), сваривают швы и таким образом получается бак:
Определите размер выреза x, при котором получится бак наибольшего объема.
Уровень B. Выполните задание уровня А. Затем решите следующую задачу.
Фирма «Рога и копыта» хочет провести рекламную кампанию в газетах. Данные о цене рекламного объявления и тиражах газет внесены в таблицу:
В каждую газету нужно дать не менее одного и не более 6 объявлений. С помощью надстройки «Поиск решения» табличного процессора определите, сколько объявлений нужно дать в каждую газету, чтобы обеспечить общий охват не менее 200000 человек и при этом израсходовать как можно меньше денег.
Уровень C. Выполните задание уровня B. Затем решите следующую задачу[1].
Банка имеет форму цилиндра, размеры которого задаются радиусом 

1) найдите размеры банки, которая имеет максимальный объем при площади полной поверхности 100 см2;
2) найдите размеры банки, которая имеет минимальную площадь полной поверхности при объеме 500 см3.
Практическая работа № 68.
Статистические расчеты
В файле marks. xls вы найдете таблицу с оценками учеников по четырем предметам. Часть ее показана на рисунке:
1. С помощью табличного процессора определите:
· сколько пятерок, четверок и троек получено по каждому предмету;
· среднюю оценку по каждому предмету;
· средний балл каждого ученика
· стандартное отклонение оценок по каждому предмету от среднего значения.
2. Отсортируйте список учеников по убыванию среднего балла.
3. Найдите коэффициенты корреляции (взаимосвязь) между оценками по разным предметам, а также между средним баллом и оценками по каждому из предметов. Оформите данные в виде таблицы:
Оставьте у всех значений только три знака в дробной части.
Практическая работа № 69.
Условные вычисления
Уровень A. В файле salary. xls вы найдете таблицу расчета зарплаты работников фирмы «Рога и Копыта». Требуется добавить нужные формулы в столбцах Премия и Сумма.
Работник получает премию пропорционально перевыполнению плана. Например, если план выполнен на 120% (перевыполнение на 20%), размер премии составит 20% от его зарплаты. Работник, сделавший меньше нормы, не получает премии.
Уровень B. В файле olimp. xls вы найдете таблицу результатов районной олимпиады по математике. На городской тур проходят те учащиеся, которые набрали на районном туре не менее 10 баллов или решили полностью одну из самых сложных задач 6 или 7. За полное решение задач 1-4 дается 2 балла, задач 5-6 – 3 балла, задачи 7 – 4 балла.
1) Добавьте необходимые формулы в столбцы Сумма и Прошел. Нужно сделать так, чтобы проходной балл можно было легко менять в отдельной ячейке.
2) Определите, сколько участников прошли на городскую олимпиаду.
3) Постройте график, который показывает, как изменяется количество прошедших на городскую олимпиаду при изменении проходного балла.
Уровень C. Выполните работу уровня B. После этого выполните дополнительное задание:
4) *Было принято решение предоставить льготы девушкам: сделать для них проходной балл на 1 меньше, чем для юношей. Внесите размер этой льготы в отдельную ячейку и определите число прошедших на городскую олимпиаду с учетом льготы.
Практическая работа № 70.
Метод наименьших квадратов
Уровень A. 
В текстовом файле mnk. txt результаты измерений записаны в два столбца: в первом столбце напряжение на проводнике, а во втором – соответствующая ему сила тока. Всего в файле 10 строчек с данными.
1) Напишите программу, которая читает данные из файла и вычисляет сопротивление резистора R, используя метод наименьших квадратов для закона Ома: 
2) Решите ту же задачу с помощью табличного процессора. Сравните результаты.
Уровень B. Выполните задание уровня А при условии, что точное количество измерений (количество строк с данными в файле) неизвестно, но не больше 100.
После этого решите задачу, решив задачу оптимизации в табличном процессоре. Для вычисления величины ошибки используйте функцию SUMXMY2 (СУММКВРАЗН). Сравните полученные результаты.
Уровень C. Выполните задание уровня B. Затем с помощью табличного процессора решите задачу двумя другими методами:
Метод 2. Используйте в качестве критерия оптимизации не сумму квадратов отклонений, а сумму абсолютных величин (модулей) этих отклонений. Для вычисления модуля примените стандартную функцию ABS.
Метод 3. Закон Ома можно записать в виде 



Сравните результаты, полученные тремя методами. Какой из них вы рекомендуете использовать и почему?
Практическая работа № 71.
Линии тренда
Уровень A. Доходы начинающей фирмы (в тысячах рублей) за первые 5 лет работы приведены в таблице:
источники:
http://urok.1sept.ru/articles/312409
http://pandia.ru/text/80/282/23508.php