Рассмотрим равномерное непрерывное распределение. Вычислим математическое ожидание и дисперсию. Сгенерируем случайные значения с помощью функции MS EXCEL
СЛЧИС()
и надстройки Пакет Анализа, произведем оценку среднего значения и стандартного отклонения.
Равномерно распределенная
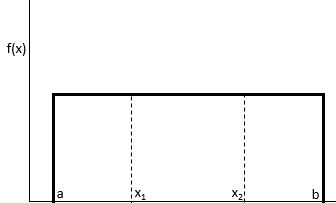
на отрезке [a; b] случайная величина имеет
плотность распределения (вероятности)
:
Функция распределения
определяется следующим образом:
Равномерное непрерывное распределение
(англ.
Continuous
uniform d
istribution
или
Rectangular
distribution
) часто встречается на практике.
Пример1.
Например, известно, что гейзер извергается каждые 50 минут. Найти вероятность, того что турист увидит извержение, если будет ждать у гейзера 20 минут. В соответствии с вышеуказанными формулами вероятность увидеть извержение в течение времени наблюдения равна 20/50=0,4, т.е. 40%.
Пример2.
Симметричный волчок после раскручивания падает набок. Вертикальная ось волчка после падения указывает на определенный угол от 0 до 360 градусов. Найти вероятность, того что ось волчка укажет на сектор от 90 до 180 градусов. Вероятность равна (180-90)/(360-0)=0,25.
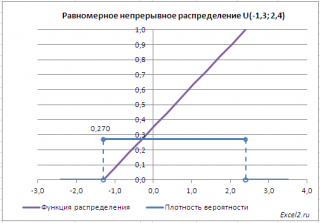
В
файле примера
приведены графики
плотности распределения вероятности
и
интегральной функции распределения
.
Математическое ожидание и дисперсия
Математическое ожидание
для
равномерного непрерывного распределения
вычисляется по формуле =(a+b)/2.
Дисперсия (квадрат стандартного отклонения)
вычисляется по формуле =((b-a)^2)/12.
Генерация случайных чисел
Случайные числа, имеющие
равномерное непрерывное распределение
на отрезке [0; 1), можно сгенерировать с помощью функции MS EXCEL
СЛЧИС()
. В функции нельзя задать нижнюю и верхнюю границу интервала, но записав формулу
=СЛЧИС()*(b-a)+a
можно сгенерировать равномерно распределенные числа на любом интервале [a; b).
Примечание
: Чтобы сгенерировать случайные числа, имеющие
равномерное дискретное распределение
, воспользуйтесь функцией
СЛУЧМЕЖДУ()
.
Сгенерировать случайные числа, извлеченные из
непрерывного равномерного
распределения,
можно также с помощью надстройки
Пакет анализа
.
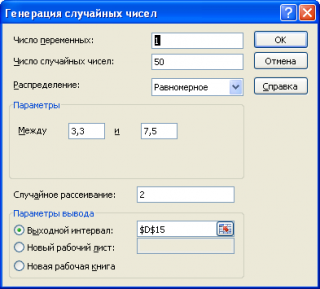
Сгенерируем массив из 50 чисел из диапазона [3,3; 7,5). Для этого в окне
Генерация случайных чисел
установим следующие параметры (см.
файл примера лист Генерация
):
Как видно из рисунка выше, в поле
Случайное рассеивание
установлен необязательный параметр равный 2. Параметр
Случайное рассеивание
может принимать значение от 1 до 32767. Если установить этот параметр, то MS EXCEL будет каждый раз генерировать один и тот же массив чисел, соответствующий этот значению. Этот подход удобен для генерации одинаковых массивов, например, на различных компьютерах.
Оценка среднего и стандартного отклонения
Нижнюю и верхнюю границу интервала возьмем [3,3; 7,5) и разместим их в ячейках
B4:B5
. Сгенерируем 50 чисел (
выборку
) и поместим их в диапазоне
С14:С63
.
Математическое ожидание
этого распределения
=(B4+B5)/2
и равно 5,4.
Стандартное отклонение
распределения равно
=КОРЕНЬ(((B5-B4)^2)/12)=1,21
Чтобы оценить
математическое ожидание
воспользуемся значениями
выборки
=СУММ(C14:C63)/СЧЁТ(C14:C63)
.
Оценить
стандартное отклонение
можно с помощью формулы
=СТАНДОТКЛОН.В(C14:C63)
в MS EXCEL 2010 или
=СТАНДОТКЛОН(C14:C63)
для более ранних версий.
Чтобы оценить
дисперсию
используйте формулу
=ДИСП.В(C14:C63)
в MS EXCEL 2010 или
=ДИСП(C14:C63)
для более ранних версий. Также можно использовать формулу
=СТАНДОТКЛОН.В(C14:C63)^2
.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
An example of a probability distribution where all possibilities are equally likely is called a uniform distribution. Since all four suits—heart, club, diamond, and spade—have an equal chance of appearing, a deck of cards has uniform distributions throughout. The chance of receiving either heads or tails in a coin toss is the same, hence a coin also has a uniform distribution. The easiest probability distribution to build in Excel is the uniform distribution. A uniform distribution is a probability distribution in which there is an equal chance of selecting any value between a and b.
The following formula can be used to calculate the probability that a value between x1 and x2 will fall within the range from a to b:
P = (x2 – x1) / (b – a)
Where P is the calculated value between x1 and x2
For calculating probability, we need:
- a: minimum value in the distribution
- b: maximum value in the distribution
- x1: the minimum value you’re interested in
- x2: the maximum value you’re interested in
Then just by using the formula mentioned above, you can easily calculate the chances or probability of anything.
The characteristics of the uniform distribution are as follows:
The distribution’s average is equal to (a + b) / 2 = μ
The distribution’s variance is σ2 = (b – a)2 / 12
The distribution’s standard deviation is σ = √σ2
How to calculate probability will be clear with the following Example
Example 1: A certain kind of bird has a weight range of 37.25 to 584.32 grams that are equally distributed throughout. What is the chance that a bird will weigh between 100.89 and 477.63 grams if a bird is randomly chosen?
Step 1: First you need to write all these given values in an excel sheet.
a (minimum value in distribution) = 37.25
b (maximum value in distribution) = 584.32
x1 (minimum value you’re interested in) = 100.89
x2 (maximum value you’re interested in) = 477.63
Entering a value in excel
Step 2: For calculating the probability you need to use the formula (x2-x1)/(b-a). Here we enter this enter =(B4-B3)/(B2-B1) because the value of x2 stores in cell B4, the value of x1 stores in cell B3, the value of b stores in cell B2, and the value of a is stored in the cell B1.
Entering the formula for calculating the chance
Step 3: Press enter then we will get the probability value which is our answer.
calculated value
Hence, the chance that a bird will weigh between 100.89 and 477.63 grams if a bird is randomly chosen is 0.68865.
Example 2: Every 10 minutes, a bus gets up to a bus stop. What is the chance that the bus will arrive in 5 minutes or less if you arrive at the bus stop?
Step 1: First you need to write all these given values in an excel sheet.
a (minimum value in distribution) = 0
b (maximum value in distribution) = 10
x1 (minimum value you’re interested in) = 0
x2 (maximum value you’re interested in) = 5
Step 2: For calculating the probability you need to use the formula (x2-x1)/(b-a). Here we enter =(B4-B3)/(B2-B1) because the value of x2 stores in cell B4, the value of x1 stores in cell B3, the value of b stores in cell B2, and the value of a is stored in cell B1.
Step 3: Press enter then we will get the probability value which is our answer.
Hence, the chance that the bus will arrive in 5 minutes or less if you arrive at the bus stop is 0.5
17 авг. 2022 г.
читать 2 мин
Равномерное распределение — это такое распределение вероятностей, при котором каждое значение в интервале от a до b будет выбрано с равной вероятностью.
Вероятность того, что мы получим значение между x 1 и x 2 на интервале от a до b , можно найти по формуле:
P(получить значение между x 1 и x 2 ) = (x 2 – x 1 ) / (b – a)
Равномерное распределение обладает следующими свойствами:
- Среднее значение распределения равно μ = (a + b)/2.
- Дисперсия распределения σ 2 = (b – a) 2 / 12
- Стандартное отклонение распределения равно σ = √σ 2
В следующих примерах показано, как рассчитать вероятности для равномерного распределения в Excel.
Примечание. Вы можете перепроверить решение каждого приведенного ниже примера с помощьюКалькулятора равномерного распределения .
Примеры: Равномерное распределение в Excel
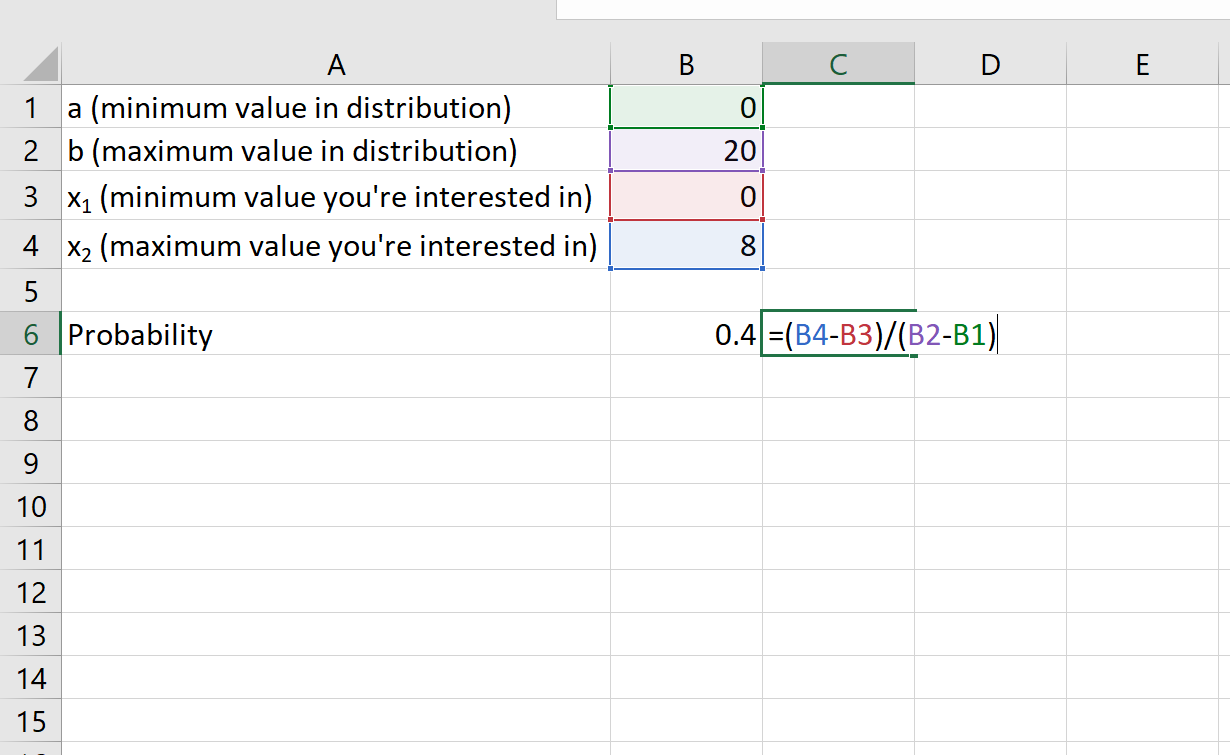
Пример 1: Автобус появляется на автобусной остановке каждые 20 минут. Если вы прибываете на автобусную остановку, какова вероятность того, что автобус приедет через 8 минут или меньше?
Решение:
- а: 0 минут
- б: 20 минут
- х 1 : 0 минут
- х 2 : 8 минут
Вероятность того, что автобус приедет через 8 минут или меньше, равна 0,4 .
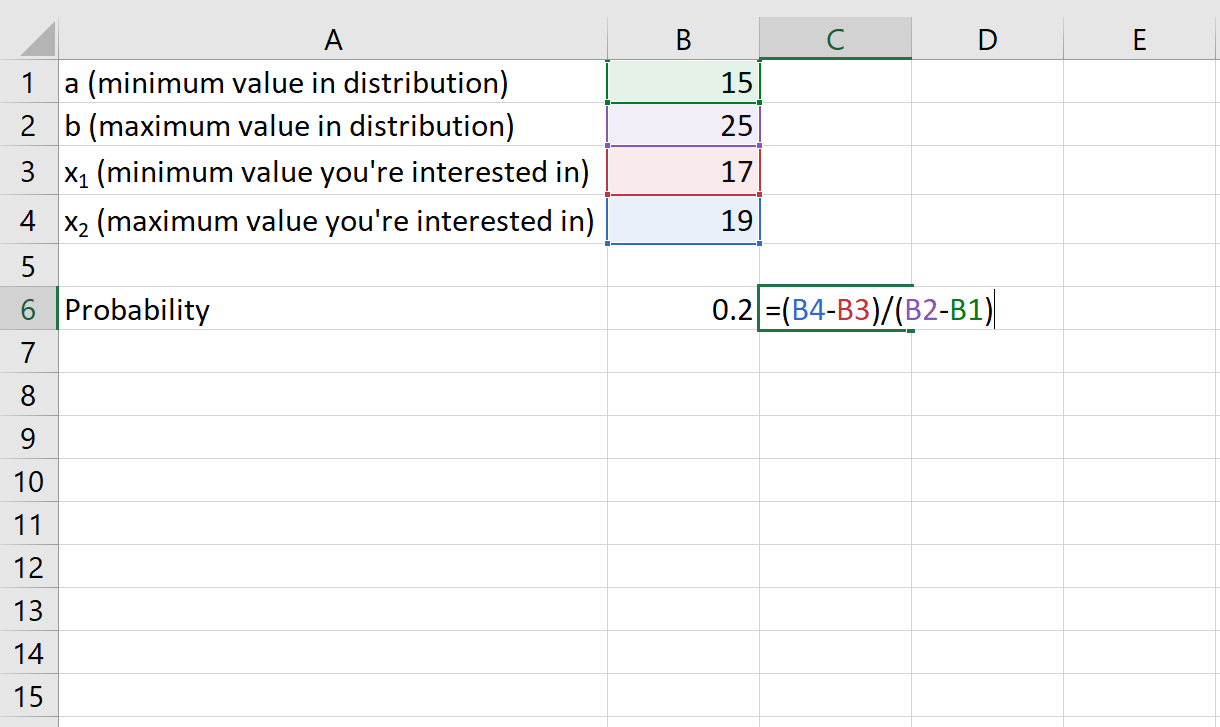
Пример 2: Вес определенного вида лягушек равномерно распределен между 15 и 25 граммами. Если вы случайно выберете лягушку, какова вероятность того, что она весит от 17 до 19 граммов?
Решение:
- а: 15 грамм
- б: 25 грамм
- х 1 : 17 грамм
- х 2 : 19 грамм
Вероятность того, что лягушка весит от 17 до 19 граммов, равна 0,2 .
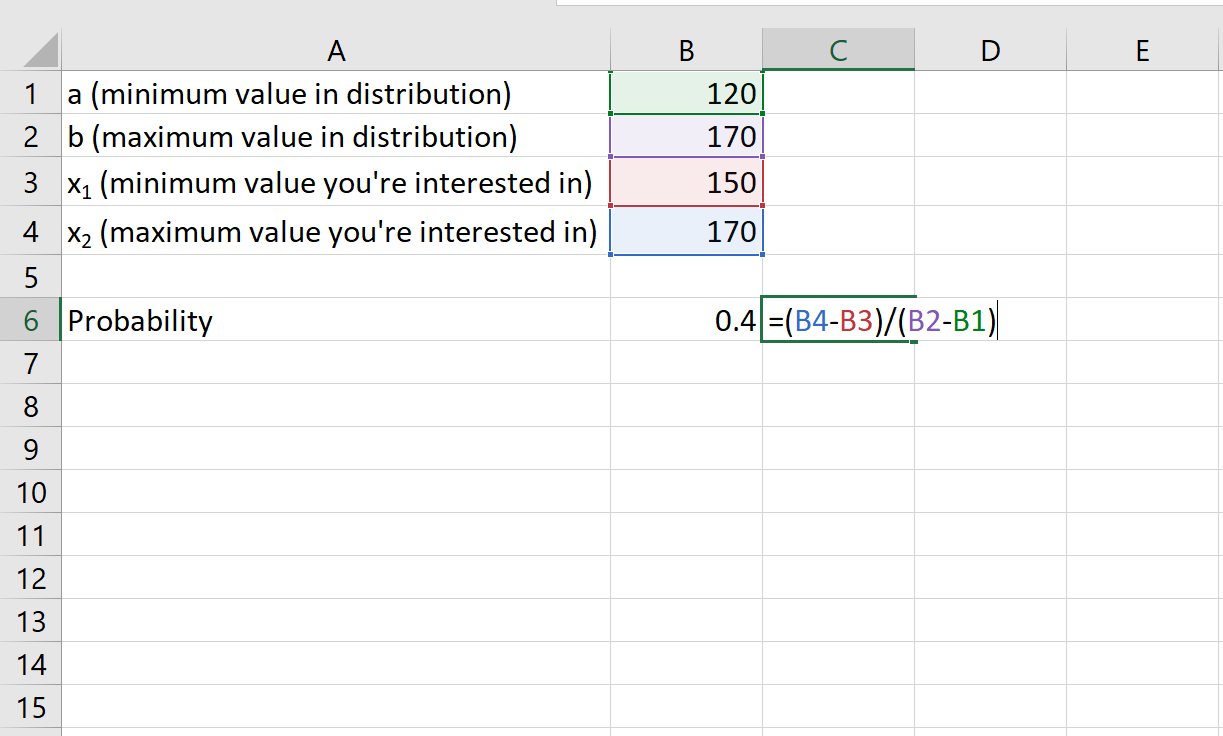
Пример 3. Продолжительность игры НБА равномерно распределена между 120 и 170 минутами. Какова вероятность того, что случайно выбранная игра НБА продлится более 150 минут?
Решение:
- а: 120 минут
- б: 170 минут
- х 1 : 150 минут
- х 2 : 170 минут
Вероятность того, что случайно выбранная игра НБА продлится более 150 минут, равна 0,4 .
Найдите больше руководств по Excel на этой странице .
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Распределение вероятностей – одно из центральных понятий теории
вероятности и математической статистики. Определение распределения вероятности
равносильно заданию вероятностей всех СВ, описывающих некоторое случайное
событие. Распределение вероятностей некоторой СВ, возможные значения которой x1, x2, … xn образуют
выборку, задается указанием этих значений и соответствующих им вероятностей p1, p2,… pn. (pn должны быть
положительны и в сумме давать единицу).
В данной лабораторной работе будут рассмотрены и построены с помощью MS Excel наиболее
распространенные распределения вероятности: биномиальное и нормальное.
1 Биномиальное распределение
Представляет собой распределение вероятностей числа наступлений
некоторого события («удачи») в n повторных
независимых испытаниях, если при каждом испытании вероятность наступления этого
события равна p. При этом
распределении разброс вариант (есть или нет события) является следствием
влияния ряда независимых и случайных факторов.
Примером практического использования биномиального распределения
может являться контроль качества партии фармакологического препарата. Здесь
требуется подсчитать число изделий (упаковок), не соответствующих требованиям.
Все причины, влияющие на качество препарата, принимаются одинаково вероятными и
не зависящими друг от друга. Сплошная проверка качества в этой ситуации не
возможна, поскольку изделие, прошедшее испытание, не подлежит дальнейшему
использованию. Поэтому для контроля из партии наудачу выбирают определенное
количество образцов изделий (n). Эти образцы всестороннее
проверяют и регистрируют число бракованных изделий (k). Теоретически число
бракованных изделий может быть любым, от 0 до n.
В Excel функция БИНОМРАСП
применяется для вычисления вероятности в задачах с фиксированным числом тестов
или испытаний, когда результатом любого испытания может быть только успех или
неудача.
Функция использует следующие
параметры:
БИНОМРАСП (число_успехов;
число_испытаний; вероятностъ_успеха; интегральная), где
число_успехов — это количество успешных
испытаний;
число_испытаний — это число независимых
испытаний (число успехов и число испытаний должны быть целыми числами);
вероятность_ успеха — это вероятность успеха
каждого испытания;
интегральный — это логическое значение,
определяющее форму функции.
Если данный параметр имеет
значение ИСТИНА (=1), то считается интегральная функция распределения
(вероятность того, что число успешных испытаний не менее значения число_
успехов);
если этот параметр имеет
значение ЛОЖЬ (=0), то вычисляется значение функции плотности
распределения (вероятность того, что число успешных испытаний в точности равно
значению аргумента число_ успехов).
Пример 1. Какова вероятность того,
что трое из четырех новорожденных будут мальчиками?
Решение:
1. Устанавливаем табличный курсор в свободную
ячейку, например в А1. Здесь должно оказаться значение искомой
вероятности.
2. Для получения значения вероятности
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка
функции (fx).
3. В появившемся диалоговом окне Мастер
функций — шаг 1 из 2 слева в поле Категория указаны виды функций.
Выбираем Статистическая. Справа в поле Функция выбираем функцию БИНОМРАСП
и нажимаем на кнопку ОК.
Появляется диалоговое окно
функции. В поле Число_s вводим с клавиатуры
количество успешных испытаний (3). В поле Испытания вводим с клавиатуры
общее количество испытаний (4). В рабочее поле Вероятность_s
вводим с клавиатуры вероятность успеха в отдельном испытании (0,5). В поле Интегральный
вводим с клавиатуры вид функции распределения — интегральная или весовая (0).
Нажимаем на кнопку ОК.
В ячейке А1 появляется
искомое значение вероятности р = 0,25. Ровно 3 мальчика из 4
новорожденных могут появиться с вероятностью 0,25.
Если изменить формулировку
условия задачи и выяснить вероятность того, что появится не более трех
мальчиков, то в этом случае в рабочее поле Интегральный вводим 1 (вид
функции распределения интегральный). Вероятность этого события будет равна
0,9375.
Задания для самостоятельной работы
1. Какова вероятность того, что восемь из десяти студентов,
сдающих зачет, получат «незачет». (0,04)
2.
Нормальное распределение
Нормальное распределение — это совокупность объектов, в которой крайние значения
некоторого признака — наименьшее и наибольшее — появляются редко; чем ближе значение признака к математическому ожиданию,
тем чаще оно встречается. Например, распределение студентов по их весу приближается
к нормальному распределению. Это распределение имеет очень широкий круг приложений в
статистике, включая проверку гипотез.
Диаграмма нормального
распределения симметрична относительно точки а (математического
ожидания). Медиана нормального распределения равна тоже а. При этом в
точке а функция f(x) достигает своего максимума, который равен
.
В Excel для вычисления значений
нормального распределения используются функция НОРМРАСП, которая
вычисляет значения вероятности нормальной функции распределения для указанного
среднего и стандартного отклонения.
Функция имеет параметры:
НОРМРАСП (х; среднее;
стандартное_откл; интегральная), где:
х — значения выборки, для
которых строится распределение;
среднее — среднее арифметическое
выборки;
стандартное_откл — стандартное отклонение
распределения;
интегральный — логическое значение,
определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то
функция НОРМРАСП возвращает интегральную функцию распределения; если это
аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности
распределения.
Если среднее = 0 и
стандартное_откл = 1, то функция НОРМРАСП возвращает стандартное
нормальное распределение.
Пример 2. Построить график
нормальной функции распределения f(x) при x, меняющемся от 19,8 до 28,8
с шагом 0,5, a=24,3 и
=1,5.
Решение
1. В ячейку А1 вводим символ
случайной величины х, а в ячейку B1 — символ функции
плотности вероятности — f(x).
2. Вводим в диапазон А2:А21
значения х от 19,8 до 28,8 с шагом 0,5. Для этого воспользуемся
маркером автозаполнения: в ячейку А2 вводим левую границу диапазона (19,8), в
ячейку A3 левую границу плюс шаг (20,3). Выделяем блок А2:А3. Затем за правый
нижний угол протягиваем мышью до ячейки А21 (при нажатой левой кнопке мыши).
3. Устанавливаем табличный курсор в ячейку В2 и
для получения значения вероятности воспользуемся специальной функцией —
нажимаем на панели инструментов кнопку Вставка функции (fx). В появившемся диалоговом
окне Мастер функций — шаг 1 из 2 слева в поле Категория указаны виды
функций. Выбираем Статистическая. Справа в поле Функция выбираем
функцию НОРМРАСП. Нажимаем на кнопку ОК.
4. Появляется диалоговое
окно НОРМРАСП. В рабочее поле X вводим адрес ячейки А2
щелчком мыши на этой ячейке. В рабочее поле Среднее вводим с клавиатуры
значение математического ожидания (24,3). В рабочее поле Стандартное_откл
вводим с клавиатуры значение среднеквадратического отклонения (1,5). В рабочее
поле Интегральная вводим с клавиатуры вид функции распределения (0).
Нажимаем на кнопку ОК.
5. В ячейке В2 появляется
вероятность р = 0,002955. Указателем мыши за правый нижний угол табличного
курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В21
копируем функцию НОРМРАСП в диапазон В3:В21.
6. По полученным данным строим искомую диаграмму
нормальной функции распределения. Щелчком указателя мыши на кнопке на панели
инструментов вызываем Мастер диаграмм. В появившемся диалоговом окне
выбираем тип диаграммы График, вид — левый верхний. После нажатия кнопки
Далее указываем диапазон данных — В1:В21 (с помощью мыши). Проверяем,
положение переключателя Ряды в: столбцах. Выбираем закладку Ряд и с
помощью мыши вводим диапазон подписей оси X: А2:А21. Нажав на кнопку Далее,
вводим названия осей Х и У и нажимаем на кнопку Готово.
Рис. 1 График нормальной функции распределения
Получен приближенный график
нормальной функции плотности распределения (см. рис.1).
Задания для самостоятельной работы
1. Построить график нормальной
функции плотности распределения f(x) при x, меняющемся от 20 до 40 с
шагом 1 при
= 3.
3. Генерация случайных величин
Еще одним аспектом
использования законов распределения вероятностей является генерация случайных величин. Бывают ситуации, когда необходимо
получить последовательность случайных чисел. Это, в частности, требуется для
моделирования объектов, имеющих случайную природу, по известному распределению
вероятностей.
Процедура генерации
случайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными из
одного или нескольких распределений.
В MS Excel для генерации СВ используются функции из категории Математические:
СЛЧИС () – выводит на экран равномерно
распределенные случайные числа больше или равные 0 и меньшие 1;
СЛУЧМЕЖДУ (ниж_граница; верх_граница) – выводит на экран
случайное число, лежащее между произвольными заданными
значениями.
В случае использования
процедуры Генерация случайных чисел из пакета Анализа необходимо
заполнить следующие поля:
— число переменных
вводится число столбцов значений, которые необходимо разместить в выходном диапазоне. Если это число не введено, то все
столбцы в выходном диапазоне будут заполнены;
— число случайных чисел
вводится число случайных значений, которое необходимо вывести для
каждой переменной, если число случайных чисел не будет введено, то все строки выходного диапазона будут заполнены;
— в поле распределение необходимо выбрать тип распределения,
которое следует использовать для генерации случайных переменных:
1. равномерное — характеризуется
верxней и нижней границами. Переменные извлекаются с одной и
той же вероятностью для всех значений интервала.
2. нормальное
— характеризуется средним значением и стандартным отклонением. Обычно для
этого распределения используют среднее значение
0 и стандартное отклонение 1.
3. биномиальное
— характеризуется вероятностью успеха (величина р) для некоторого числа попыток. Например, можно сгенерировать случайные двухальтернативные переменные по числу попыток, сумма которых будет биномиальной случайной
переменной;
4. дискретное
— характеризуется значением СВ и соответствующим ему интервалом вероятности, диапазон должен состоять из двух столбцов: левого,
содержащего значения, и правого, содержащего
вероятности, связанные со значением в данной строке. Сумма вероятностей должна быть
равна 1;
5. распределения Бернулли, Пуассона
и Модельное.
— в поле случайное рассеивание
вводится произвольное значение, для которого необходимо
генерировать случайные числа. Впоследствии можно снова использовать это
значение для получения тех же самых случайных чисел.
— выходной диапазон
вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и
на экран будет выведено сообщение в случае
возможного наложения выходного диапазона на исходные
данные.
Рассмотрим пример.
Пример 3. Повар столовой может готовить 4 различных первых блюда (уха, щи, борщ, грибной суп). Необходимо составить меню на месяц, так чтобы
первые блюда чередовались в случайном порядке.
Решение
1.
Пронумеруем первые
блюда по порядку: 1 — уха, 2 — щи, 3 — борщ, 4 — грибной суп. Введем числа 1-4 в диапазон А2:А5 рабочей таблицы.
2.
Укажем желаемую вероятность появления
каждого первого блюда. Пусть все блюда будут
равновероятны (р=1/4). Вводим число 0,25 в диапазон В2:В5.
3.
В меню Сервис
выбираем пункт Анализ данных и далее указываем строку Генерация
случайных чисел. В появившемся диалоговом окне указываем Число
переменных — 1, Число случайных чисел — 30 (количество
дней в месяце). В поле Распределение указываем Дискретное (только натуральные числа). В поле Входной
интервал значений и вероятностей
вводим (мышью) диапазон, содержащий номера супов и их
вероятности. – А2:В5.
4.
Указываем выходной
диапазон и нажимаем ОК. В столбце С появляются случайные числа: 1, 2, 3,
4.
Задание для
самостоятельной работы
1. Сформировать
выборку из 10 случайных чисел, лежащих в диапазоне от 0 до 1.
2. Сформировать
выборку из 20 случайных чисел, лежащих в диапазоне от 5 до 20.
3. Пусть
спортсмену необходимо составить график тренировок на 10 дней, так чтобы
дистанция, пробегаемая каждый день, случайным образом менялась от 5 до 10 км.
4. Составить
расписание внеклассных мероприятий на неделю для случайного проведения:
семинаров, интеллектуальных игр, КВН и спец. курса.
5. Составить
расписание на месяц для случайной демонстрации на телевидении одного из четырех
рекламных роликов турфирмы. Причем вероятность появления рекламного ролика №1
должна быть в два раза выше, чем остальных рекламных роликов.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Поделиться ссылкой:
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
=ЕСЛИ(A12;B11+$B$6; «»)
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.
Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.
График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.
Имеются следующие данные о количестве выпавших осадков:
Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):
Выбираем «Гистограмма»:
Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:
После нажатия ОК получаем такой график с таблицей:
В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.
Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.
Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.
Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:
Вычислим относительные частоты (как в предыдущем способе).
Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».
Частота распределения заданных значений:
Круговые диаграммы для иллюстрации распределения
С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.
С помощью любой круговой диаграммы можно показать распределение в том случае, если
- имеется только один ряд данных;
- все значения положительные;
- практически все значения выше нуля;
- не более семи категорий;
- каждая категория соответствует сегменту круга.
На основании имеющихся данных о количестве осадков построим круговую диаграмму.
Доля «каждого месяца» в общем количестве осадков за год:
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:
Получили количество выпавших осадков в процентном выражении по сезонам.
В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.
Уровень сложности: продвинутый.
На следующем рисунке показано, как выглядит готовая динамическая гистограмма:
Что такое гистограмма или график распределения частот?
Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.
В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.
На какие вопросы отвечает гистограмма распределения?
Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.
В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.
«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»
Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:
Динамическая гистограмма
После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.
Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!
Как это работает?
Краткий ответ: Формулы, динамические именованные диапазоны, элемент управления «Полоса прокрутки» в сочетании с гистограммой.
Формулы
Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.
Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.
Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.
=ЧАСТОТА(tblData;C13:C22)=FREQUENCY(tblData,C13:C22)
Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.
Динамический именованный диапазон
В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.
Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных — rngGroups (столбец Frequency) и второй для подписей горизонтальной оси — rngCount (столбец Bin Name).
Элемент управления «Полоса прокрутки»
Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).
На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.
Гистограмма
График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.
Есть вопросы?
Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.
Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать. Определённо, такой интерактивной диаграммой можно украсить любой отчёт.
Более простой вариант гистограммы можно создать, используя сводные таблицы.
Пишите в комментариях любые вопросы и предложения. Спасибо!
Урок подготовлен для Вас командой сайта office-guru.ru
Источник: /> Перевел: Антон Андронов
Правила перепечаткиЕще больше уроков по Microsoft Excel
Оцените качество статьи. Нам важно ваше мнение:


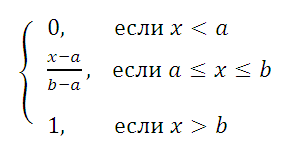
.png)

.png)
.png)

.png)
.png)