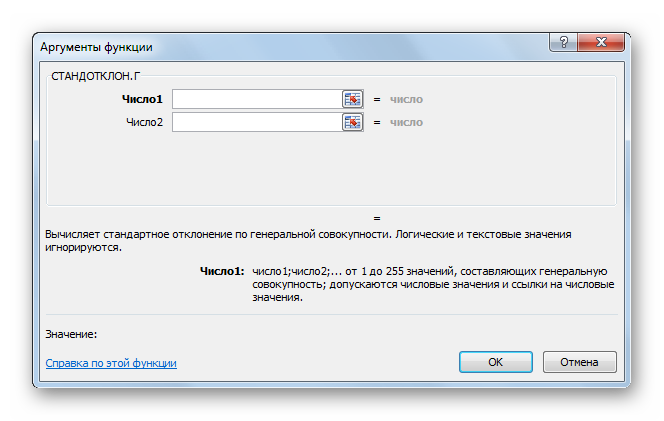
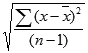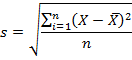Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции Функция СТАНДОТКЛОН.В.
Синтаксис
СТАНДОТКЛОН(число1;[число2];…)
Аргументы функции СТАНДОТКЛОН описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
-
Число2… Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
-
Функция СТАНДОТКЛОН предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП.
-
Стандартное отклонение вычисляется с использованием «n-1» метода.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОНА.
-
Функция СТАНДОТКЛОН вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание (результат) |
Результат |
|
=СТАНДОТКЛОН(A3:A12) |
Стандартное отклонение предела прочности (27,46392) |
27,46392 |
Нужна дополнительная помощь?
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции СТАНДОТКЛОНА в Microsoft Excel.
Описание
Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Синтаксис
СТАНДОТКЛОНА(значение1;[значение2];…)
Аргументы функции СТАНДОТКЛОНА описаны ниже.
-
Значение1,значение2,… Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 255 значений, соответствующих выборке из генеральной совокупности. Вместо аргументов, разделяемых точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
-
Функция СТАНДОТКЛОНА предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНПА.
-
Стандартное отклонение вычисляется с использованием «n-1» метода.
-
Допускаются следующие аргументы: числа; имена, массивы или ссылки, содержащие числа; текстовые представления чисел; логические значения, такие как ИСТИНА и ЛОЖЬ, в ссылке.
-
Аргументы, содержащие значение ИСТИНА, интерпретируются как 1; аргументы, содержащие текст или значение ЛОЖЬ, интерпретируются как 0 (ноль).
-
Если аргументом является массив или ссылка, учитываются только значения массива или ссылки. Пустые ячейки и текст в массиве или ссылке игнорируются.
-
Аргументы, представляющие собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы не включать логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОН.
-
Функция СТАНДОТКЛОНА вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(значение1,значение2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание (результат) |
Результат |
|
=СТАНДОТКЛОНА(A3:A12) |
Стандартное отклонение предела прочности для всех инструментов (27,46391572) |
27,46391572 |
Нужна дополнительная помощь?
Функция СТАНДОТКЛОН.В возвращает значение стандартного отклонения, рассчитанного для определенного диапазона числовых значений.
Функция СТАНДОТКЛ.Г используется для определения стандартного отклонения генеральной совокупности числовых значений и возвращает величину стандартного отклонения с учетом, что переданные значения являются всей генеральной совокупностью, а не выборкой.
Функция СТАНДОТКЛОНА возвращает значение стандартного отклонения для некоторого диапазона чисел, которые являются выборкой, а не всей генеральной совокупностью.
Функция СТАНДОТЛОНПА возвращает значение стандартного отклонения для всей генеральной совокупности, переданной в качестве ее аргументов.
Примеры использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА
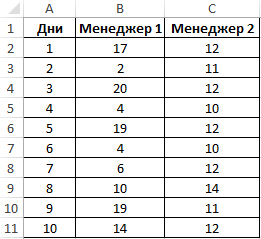
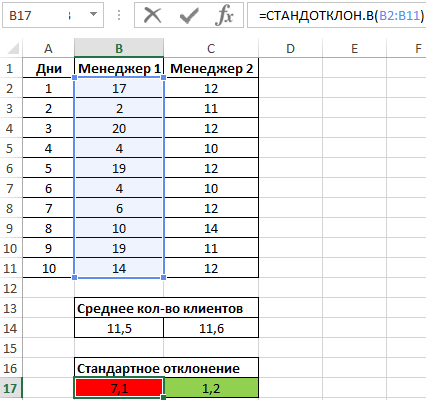
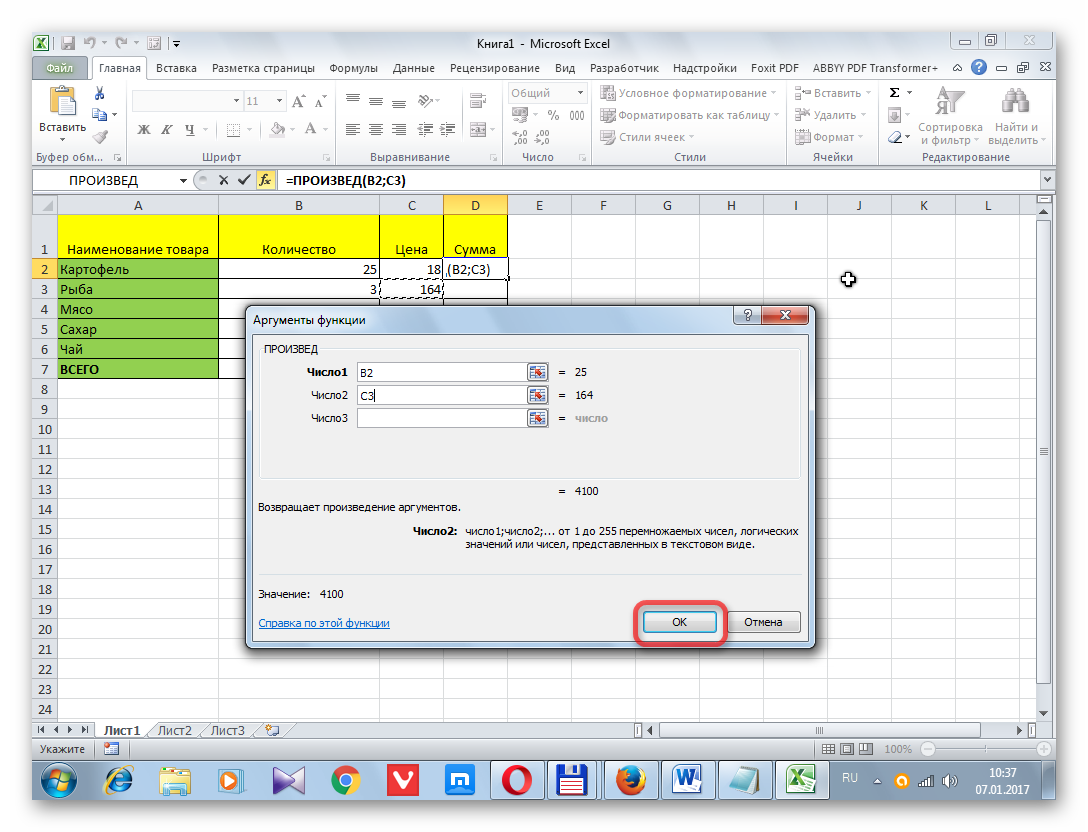
Пример 1. На предприятии работают два менеджера по привлечению клиентов. Данные о количестве обслуженных клиентов в день каждым менеджером фиксируются в таблице Excel. Определить, какой из двух сотрудников работает эффективнее.
Таблица исходных данных:
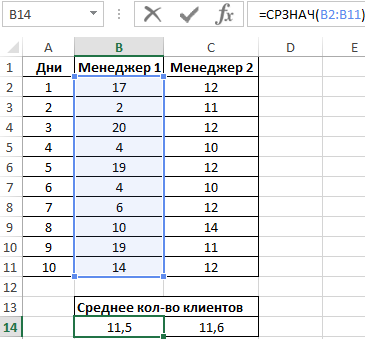
Вначале рассчитаем среднее количество клиентов, с которыми работали менеджеры ежедневно:
=СРЗНАЧ(B2:B11)
Данная функция выполняет расчет среднего арифметического значения для диапазона B2:B11, содержащего данные о количестве клиентов, принимаемых ежедневно первым менеджером. Аналогично рассчитаем среднее количество клиентов за день у второго менеджера. Получим:
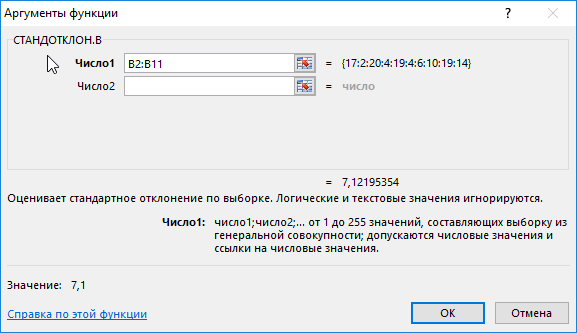
На основе полученных значений создается впечатление, что оба менеджера работают примерно одинаково эффективно. Однако визуально виден сильный разброс значений числа клиентов у первого менеджера. Произведем расчет стандартного отклонения по формуле:
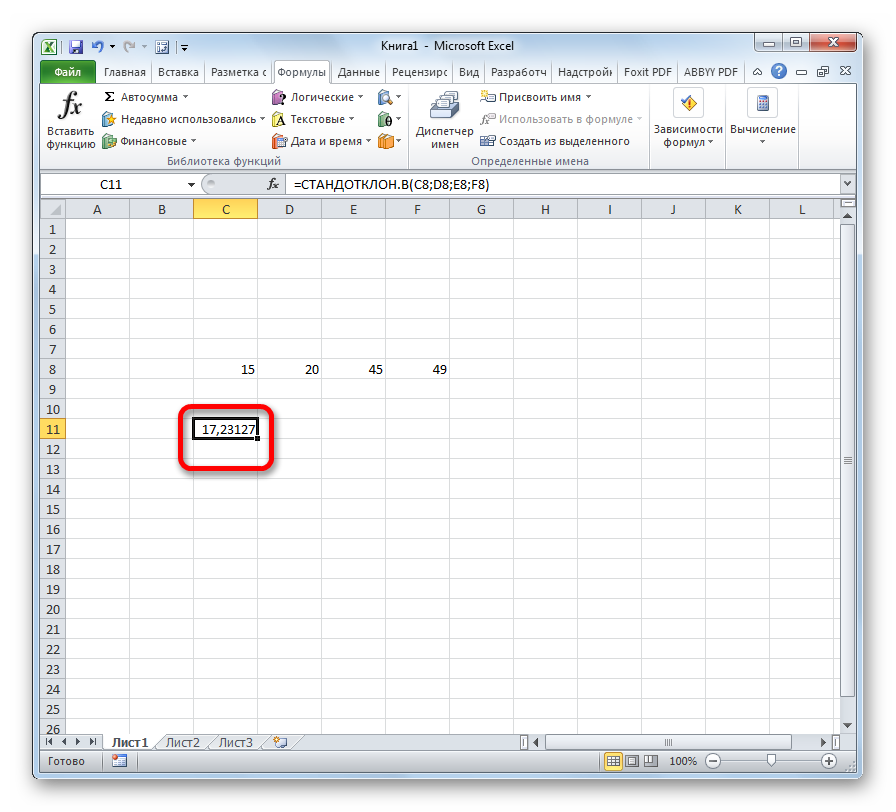
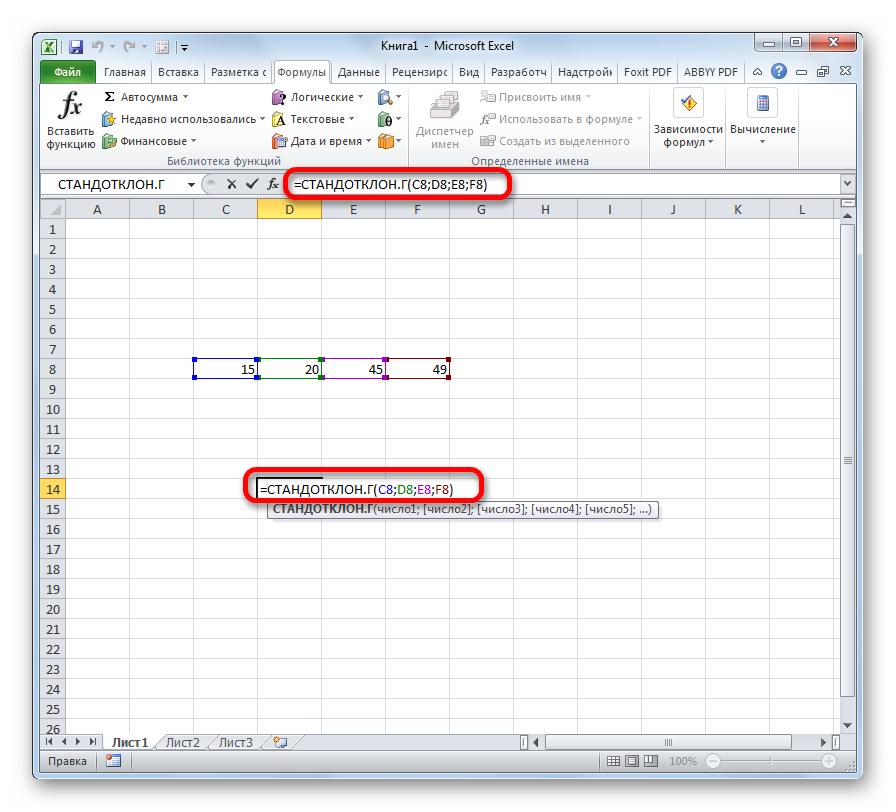
=СТАНДОТКЛОН.В(B2:B11)
B2:B11 – диапазон исследуемых значений. Аналогично определим стандартное отклонение для второго менеджера и получим следующие результаты:
Как видно, показатели работы первого менеджера отличаются высокой вариабельностью (разбросом) значений, в связи с чем среднее арифметическое значение абсолютно не отражает реальную картину эффективности работы. Отклонение 1,2 свидетельствует о более стабильной, а, значит, и эффективной работе второго менеджера.
Пример использования функции СТАНДОТКЛОНА в Excel
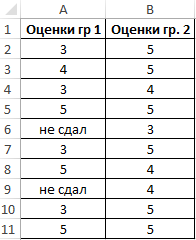
Пример 2. В двух различных группах студентов колледжа проводился экзамен по одной и той же дисциплине. Оценить успеваемость студентов.
Таблица исходных данных:
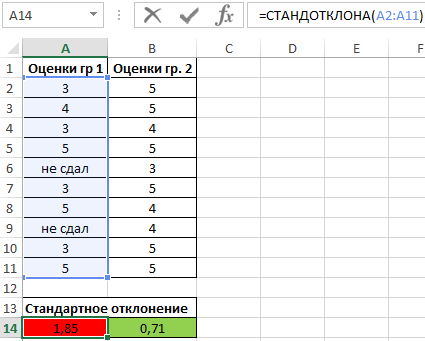
Определим стандартное отклонение значений для первой группы по формуле:
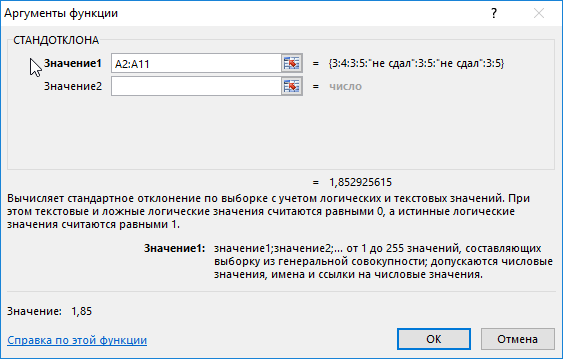
=СТАНДОТКЛОНА(A2:A11)
Аналогичный расчет произведем для второй группы. В результате получим:
Полученные значения свидетельствуют о том, что студенты второй группы намного лучше подготовились к экзамену, поскольку разброс значений оценок относительно небольшой. Обратите внимание на то, что функция СТАНДОТКЛОНА преобразует текстовое значение «не сдал» в числовое значение 0 (нуль) и учитывает его в расчетах.
Пример функции СТАНДОТКЛОН.Г в Excel
Пример 3. Определить эффективность подготовки студентов к экзамену для всех групп университета.
Примечание: в отличие от предыдущего примера, будет анализироваться не выборка (несколько групп), а все число студентов – генеральная совокупность. Студенты, не сдавшие экзамен, не учтены.
Заполним таблицу данных:
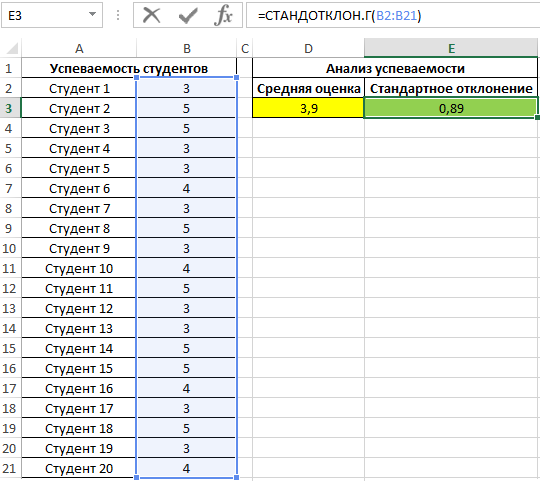
Для оценки эффективности будем оперировать двумя показателями: средняя оценка и разброс значений. Для определения среднего арифметического используем функцию:
=СРЗНАЧ(B2:B21)
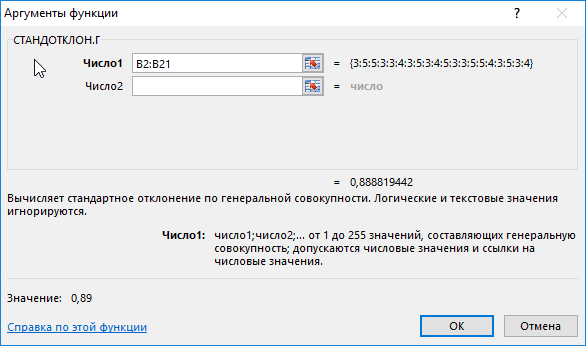
Для определения отклонения введем формулу:
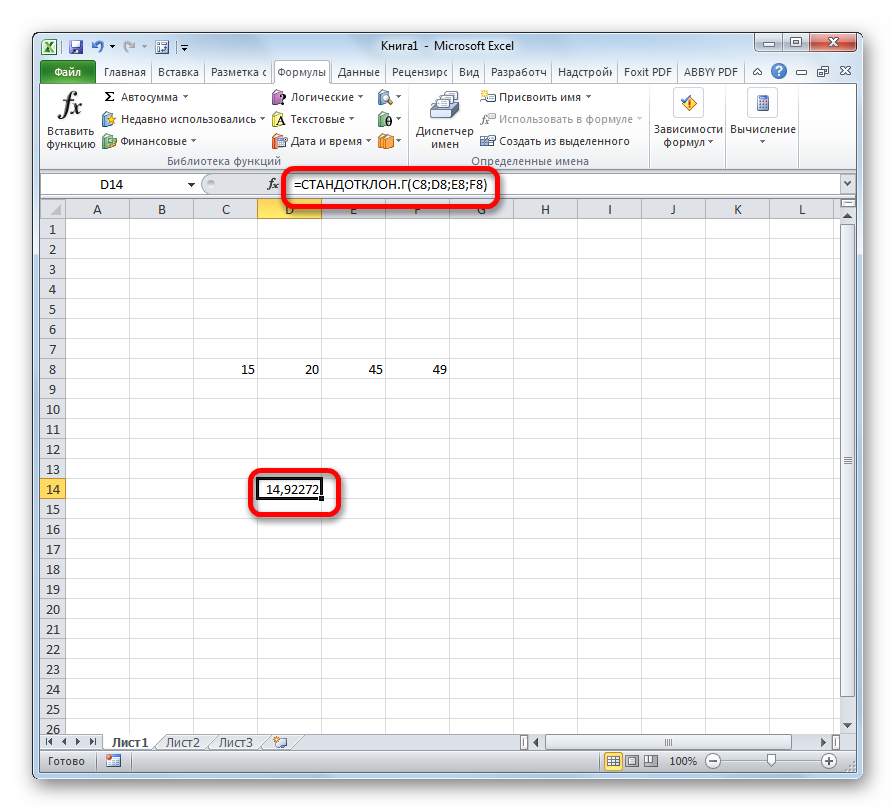
=СТАНДОТКЛОН.Г(B2:B21)
В результате получим:
Полученные данные свидетельствует об успеваемости немного ниже среднего (<4), величина разброса характеризует довольно большое количество студентов, получивших 5 и 3 соответственно (учитывая, что анализировались только данные из диапазона от 3 до 5).
Пример функции СТАНДОТКЛОНПА в Excel
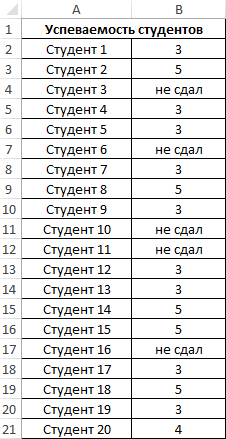
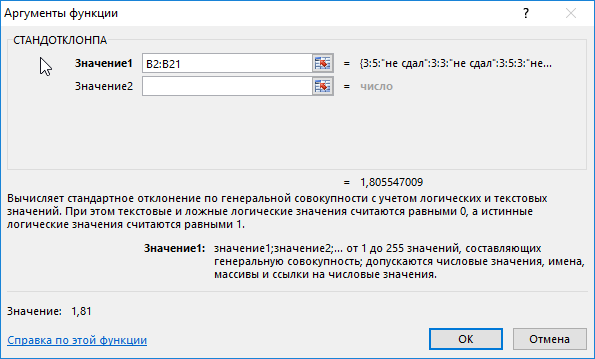
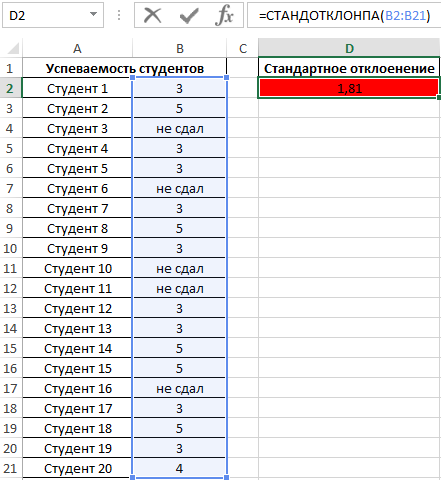
Пример 4. Проанализировать успеваемость студентов по результатам сдачи экзамена с учетом тех студентов, которым не удалось сдать этот экзамен.
Таблица данных:
В данном примере также анализируем генеральную совокупность, однако некоторые поля данных содержат текстовые значения. Для определения стандартного отклонения используем функцию:
=СТАНДОТКЛОНПА(B2:B21)
В результате получим:
Высокий разброс значений в последовательности свидетельствует о большом числе не сдавших экзамен студентов.
Особенности использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА
Функции СТАНДОТКЛОНА И СТАНДОТКЛОНПА имеют идентичную синтаксическую запись типа:
=ФУНКЦИЯ (значение1; [значение2];…)
Описание:
- ФУНКЦИЯ – одна из двух рассмотренных выше функций;
- значение1 – обязательный аргумент, характеризующий одно из значений выборки (либо генеральной совокупности);
- [значени2] – необязательный аргумент, характеризующий второе значение исследуемого диапазона.
Примечания:
- В качестве аргументов функций могут быть переданы имена, числовые значения, массивы, ссылки на диапазоны числовых данных, логические значения и ссылки на них.
- Обе функции игнорируют пустые значения и текстовые данные, содержащиеся в диапазоне переданных данных.
- Функции возвращают код ошибки #ЗНАЧ!, если в качестве аргументов были переданы значения ошибок или текстовые данные, которые не могут быть преобразованы в числовые значения.
Функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г имеют следующую синтаксическую запись:
=ФУНКЦИЯ(число1;[число2];…)
Описание:
- ФУНКЦИЯ – любая из функций СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г;
- число1 – обязательный аргумент, характеризующий числовое значение, взятое из выборки или всей генеральной совокупности;
- число2 – необязательный аргумент, характеризующий второе числовое значение исследуемого диапазона.
Примечание: обе функции не включают в процесс вычисления числа, представленные в виде текстовых данных, а также логические значения ИСТИНА и ЛОЖЬ.
Примечания:
- Стандартное отклонение широко используется в статистических расчетах, когда нахождение среднего значения диапазона величин не дает верное представление о распределении данных. Оно демонстрирует принцип распределения величин относительно среднего значения в конкретной выборке или всей последовательности целиком. В Примере 1 будет наглядно рассмотрено практическое применение данного статистического параметра.
- Функции СТАНДОТКЛОНА и СТАНДОТКЛОН.В следует использовать для анализа только части генеральной совокупности и производят расчет по первой формуле, а СТАНДОТКЛОН.Г и СТАНДОТКЛОНПА должны принимать на вход данные о всей генеральной совокупности и производят расчет по второй формуле.
- В Excel содержатся встроенные функции СТАНДОТКЛОН и СТАНДОТКЛОНП, оставленные для совместимости с более старыми версиями Microsoft Office. Они могут быть не включены в более поздние версии программы, поэтому их использование не рекомендуется.
- Для нахождения стандартного отклонения используются две распространенные формулы: S=√((∑_(i=1)^n▒(x_i-x_ср )^2 )/(n-1)) и S=√((∑_(i=1)^n▒(x_i-x_ср )^2 )/n), где:
- S – искомое значение стандартного отклонения;
- n – рассматриваемый диапазон значений (выборка);
- x_i – отдельно взятое значение из выборки;
- x_ср – среднее арифметическое значение для рассматриваемого диапазона.
На чтение 3 мин. Просмотров 19 Опубликовано 31.05.2021
Стандартное отклонение – это описательная статистика, которая сообщает нам о разбросе – или разбросе – набора данных. Как и многие другие формулы в статистике, вычисление стандартного отклонения – довольно утомительный процесс, выполняемый вручную. К счастью, статистическое программное обеспечение значительно ускоряет этот расчет.
Содержание
- Статистическое программное обеспечение
- Популяции и образцы
- Стандартное отклонение в Excel
- Предостережения
Статистическое программное обеспечение
Существует множество программных пакетов, которые выполняют статистические вычисления, но одна из наиболее доступных программ – Microsoft Excel. Хотя мы могли бы использовать пошаговый процесс с использованием формулы для стандартного отклонения для нашего расчета, можно выполнить этот расчет с помощью одной функции Excel.
Популяции и образцы
Прежде чем переходить к конкретным командам, используемым для вычисления стандартного отклонения, важно различать генеральную совокупность и выборку. Популяция – это совокупность каждого изучаемого человека. Выборка – это подмножество населения. Разница между этими двумя концепциями означает различие в том, как рассчитывается стандартное отклонение.
Стандартное отклонение в Excel
Для использования Excel, чтобы определить стандартное отклонение выборки набора количественных данных, введите эти числа в группу соседних ячеек в электронной таблице. В пустой ячейке введите кавычки “ = STDEV.S (” После этого типа укажите расположение ячеек, в которых находятся данные, а затем закройте круглые скобки. с “) “. В качестве альтернативы это можно сделать с помощью следующей процедуры. Если наши данные находятся в ячейках с A2 по A10, тогда (без кавычек) « = STDEV.S (A2 : A10 ) “получит образец стандартного отклонения записей в ячейках от A2 до A10.
Вместо того, чтобы вводить расположение ячеек, в которых находятся наши данные находится, мы можем использовать другой метод. Для этого нужно ввести первую половину формулы « = STDEV.S (» и щелкнуть первую ячейку, в которой находятся данные. Вокруг выбранной ячейки появится цветное поле. . Затем мы перетаскиваем мышь, пока не выберем все ячейки, содержащие наши данные. Завершаем это закрытием круглых скобок.
Предостережения
При использовании Excel для этого расчета необходимо сделать несколько предостережений. Мы должны убедиться, что не перепутали функции. Формула Excel STDEV.S внимательно похож на STDEV.P . Формула первого типа обычно является необходимой для наших расчетов, поскольку она используется, когда наши данные являются выборкой из генеральной совокупности. В случае, если наши данные составляют всю генеральную совокупность, изучено, то мы хотели бы использовать
Еще одна вещь, с которой мы должны быть осторожны, касается числа значений данных. Excel ограничен количеством значений, которые можно ввести в функцию стандартного отклонения. Все ячейки, которые мы используем для наших вычислений, должны быть числовыми. Мы должны быть уверены, что ячейки с ошибками и ячейки с текстом в них не вводятся в формулу стандартного отклонения.
Шаги
-
1
Запустите Microsoft Excel. Дважды щелкните по значку в виде белой буквы «X» на зеленом фоне. Как правило, он находится на рабочем столе или на панели задач. Откроется начальная страница Excel.
- Если у вас есть готовая таблица Excel с нужными данными, дважды щелкните по файлу, чтобы открыть его в Excel, а затем перейдите к шагу «Щелкните по пустой ячейке».
-
2
Нажмите Новая книга. Эта опция находится в верхней левой части начальной страницы Excel.
-
3
Введите данные. Выберите столбец, а затем введите нужные данные в ячейки этого столбца.
- Например, если вы выбрали столбец «A», введите числа в ячейки «A1», «A2», «A3» и так далее.
-
4
Щелкните по пустой ячейке. Это ячейка, в которой отобразится значение стандартного отклонения. Так вы выберете ячейку.
-
5
Введите формулу для вычисления стандартного отклонения. В пустой ячейке введите =СТАНДОТКЛОН.Г(), где «Г» — генеральная совокупность. Стандартное отклонение по генеральной совокупности учитывает все данные (N).[1]
- Чтобы найти стандартное отклонение по выборке, введите =СТАНДОТКЛОН.В(). В этом случае учитывается (N-1) данных.
-
6
Введите диапазон значений. Внутри круглых скобок введите букву и номер ячейки с первым числом, потом введите двоеточие (:), а затем введите букву и номер ячейки с посленим числом.
- Например, если вы ввели числа в столбце «A» в строках с 1 по 10, формула должна выглядеть так: =СТАНДОТКЛОН.Г(A1:A10).
- Чтобы посчитать стандартное отклонение нескольких чисел, которые, например, находятся в ячейках A1, B3 и C5, введите адреса ячеек через запятые (например, =СТАНДОТКЛОН.В(A1,B3,C5)).
-
7
Нажмите ↵ Enter. Формула будет выполнена, а в ячейке с формулой отобразится стандартное отклонение выбранных данных.
Реклама
Советы
- В большинстве случаев вычисляется стандартное отклонение по генеральной совокупности, чтобы учесть все данные.
Реклама
Предупреждения
- Старая формула =СТАНДОТКЛОН() не работает в версиях Excel старше 2007 года.
Реклама
Об этой статье
Эту страницу просматривали 115 468 раз.
Была ли эта статья полезной?
Функция СТАНДОТКЛОН.В оценивает стандартное отклонение по выборке.
Описание функции СТАНДОТКЛОН.В
Оценивает стандартное отклонение по выборке. Логические значения и текст игнорируются. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Синтаксис
=СТАНДОТКЛОН.В(число1; [число2];…)Аргументы
число1число2
Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно использовать массив или ссылку на массив.
Необязательный. Числовые аргументы 2—254, соответствующие выборке из генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
- Функция СТАНДОТКЛОН.В предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОН.Г.
- Стандартное отклонение вычисляется с использованием «n-1» метода.
- Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
- Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
- Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
- Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
- Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОНА.
- Функция СТАНДОТКЛОН.В вычисляется по следующей формуле:
где x (с чертой) — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Я уже несколько раз сталкивался с тем, что существуют две статистики, обе называемые стандартное отклонение, для описания меры рассеивания случайной величины. Недавно это произошло при чтении книги Дональд Уилер, Дэвид Чамберс. Статистическое управление процессами. Чтобы эти статистики различать, в книге они названы по-разному. Корень из среднего квадрата отклонения sn, определен для ряда, состоящего из n элементов формулой:
Стандартное отклонение рассчитывается по формуле:
Скачать заметку в формате Word или pdf, примеры в формате Excel
При этом авторы вскользь упоминают: «Несмотря на то что некоторые учебники говорят о применении s для генеральных совокупностей, а sn — для выборок, и то, и то — статистики, они обе — просто арифметические функции данных». На мой взгляд, то ли авторы, то ли переводчики напутали, потому что, как раз наоборот. «Некоторые учебники» трактуют sn, как меру рассеивания генеральной совокупности, а s, как меру рассеивания выборки.
Не добавляют понимания и определения в Википедии, где говорится, что sn – среднеквадратичное отклонение, а s – стандартное отклонение, или оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии. В статье Несмещенная дисперсия можно прочитать, что sn – выборочная дисперсия, а s – исправленная выборочная дисперсия. Причем sn является смещённой, а s – несмещённой оценками параметра σ2.
Excel не отстает от теории и содержит две функции для определения стандартного отклонения: СТАНДОТКЛОН.В – оценивает стандартное отклонение по выборке, и использует в формуле знаменатель (n – 1); СТАНДОТКЛОН.Г – вычисляет стандартное отклонение по генеральной совокупности, и в знаменателе – n.
Ситуация с двумя формулами прояснилась для меня при чтении книги Фишер. Статистический вывод. Фишер рассматривал генеральные совокупности, которые описываются параметрами, традиционно обозначаемыми греческими буквами. Параметры нам не известны. Мы пытаемся оценить их, извлекая отдельные выборки, и измеряя их статистики (статистика – число, характеризующее выборку; статистики традиционно обозначаются латинскими буквами). Фишер сформулировал несколько критериев хорошей оценки. И среди них – смещение. Оценка статистики Т считается правильной и несмещенной для параметра Θ, если среднее значение Т (по множеству выборок) стремится к истинному значению Θ. Иначе оценка считается смещенной.
Для иллюстрации я создал модель в Excel, и случайным образом задал 10 000 чисел в диапазоне от 0 до 100. А затем создал 100 выборок по 100 последовательных значений: от 1 до 100, от 101 до 200 и т.д. Далее построил три графика: для среднего значения, СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В. На каждый график в виде пунктирной линии нанес среднее значение, СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В для всех 10 000 случайных чисел, а также в виде точек – скользящее среднее этих статистик для последовательности выборок. Например, первая точка – значение статистики для первой выборки: 1…100, вторая точка – среднее статистик двух выборок: 1…100 и 101…200 и т.д. Видно, что среднее выборок стремится к своему истинному значению – среднему по всей совокупности, так же ведет себя и СТАНДОТКЛОН.В. А вот скользящее среднее СТАНДОТКЛОН.Г стремится к числу меньшему, чем значение СТАНДОТКЛОН.Г для всех 10 000 чисел. Это и означает, что статистика СТАНДОТКЛОН.В дает несмещенную оценку параметра дисперсии σ2, а СТАНДОТКЛОН.Г – смещенную.
Рис. 1. Три статистики – среднее значение, СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В – дают оценку параметров генеральной совокупности; среднее значение и СТАНДОТКЛОН.В – несмещенную оценку, а СТАНДОТКЛОН.Г – смещенную; откройте Excel-файл и нажмите F9; случайные числа пересчитаются, и графики изменятся; неизменным будет только стремление среднего значения и СТАНДОТКЛОН.В по выборкам к своим истинным значениям (по всей совокупности), и постоянно заниженная оценка статистики СТАНДОТКЛОН.Г; Excel-файл тяжелый, поэтому пересчет происходит медленно
Если тема вас заинтересовала, но не полностью отложилась в голове, рекомендую также заметку Выборочная несмещенная дисперсия.
Дополнение от 15.12.2022. Еще один подход к описанию различий формул (1) и (2) я встретил в книге Александра Орлова «Математика случая». Рекомендую))
На чтение 5 мин Опубликовано 15.01.2021
Для вычисления среднеквадратического отклонения в Microsoft Office Excel используется специальная формула, которой можно пользоваться несколькими способами. О них пойдет речь в данной статье.
Содержание
- Как вычислить среднее квадратическое отклонение в Excel
- Способ 1. С помощью Мастера функций
- Способ 2. Расчет стандартного отклонения в разделе «Формулы»
- Способ 3. Ручной ввод формулы среднеквадратичного отклонения в Эксель
- Способ 4. Ручной подсчет
- Заключение
Как вычислить среднее квадратическое отклонение в Excel
Это один из показателей вариации. В теории вероятностей этот показатель рассчитывается по формуле:
В Эксель пользователю не нужно будет вручную рассчитывать среднеквадратичное отклонение. Существует ряд способов, позволяющих найти эту величину в кратчайшие сроки с помощью встроенных в Excel инструментов. Далее будут рассмотрены самые распространенные из них.
Способ 1. С помощью Мастера функций
Данный метод расчета стандартного отклонения в Excel занимает минимальное количество времени. Вычисление производится следующим образом:
- Левой клавишей манипулятора на рабочем листе программы выделить ячейку, в которой будет отображаться результат вычисления.
- Кликнуть по кнопке «Вставка функции», расположенной с левой стороны от строки ввода.
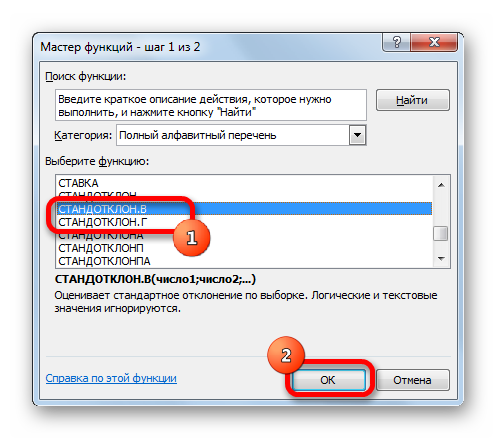
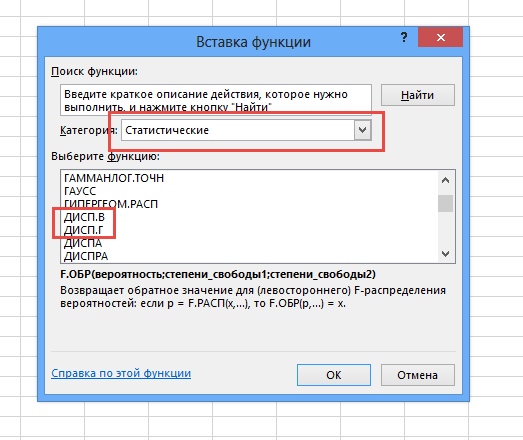
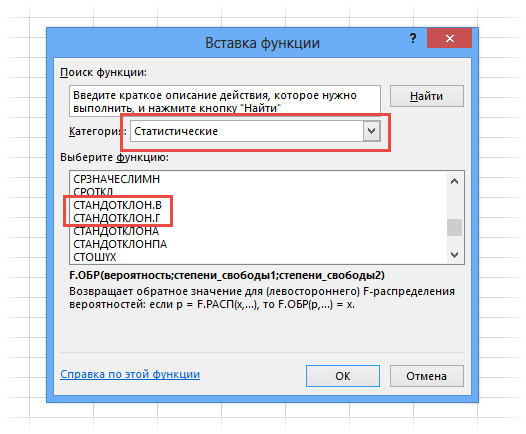
- После выполнения предыдущего действия откроется окошко Мастера функций. Здесь пользователю потребуется найти строку «СТАНДОТКЛОН.В», выделить ее ЛКМ и нажать на «ОК» внизу меню. В списке функций также есть записи «СТАНДОТКЛОН.Г» и просто «СТАНДОТКЛОН». На них нажимать не нужно!
- В следующем окне аргументов функции необходимо прописать числа совокупности в каждом поле. Если эти значения уже написаны на рабочем листе Excel, то можно указать координаты соответствующих ячеек.
- Нажать на «ОК» внизу меню «Аргументы функции», когда все строчки будут заполнены.
- Проверить результат. В выделенной на первом этапе ячейке будет прописано число. Это и есть среднее квадратичное отклонение.
Обратите внимание! Если после выполнения вышеуказанных манипуляций в ячейке будут отображаться знаки «###», то значит результатом является большое число, и ячейку нужно растянуть.
Способ 2. Расчет стандартного отклонения в разделе «Формулы»
Через вкладку «Формулы» в программе Excel также возможно рассчитать стандартное отклонение. Алгоритм вычисления состоит из следующих шагов:
- По аналогичной схеме выделить любую свободную ячейку на рабочем листе. В этот элемент в дальнейшем будет выводиться результат.
- В графе инструментов сверху главного меню программы найти слово «Формулы» и щелкнуть по нему ЛКМ.
- В открывшейся области найти подраздел «Библиотека функций, а затем развернуть вкладку «Другие функции».
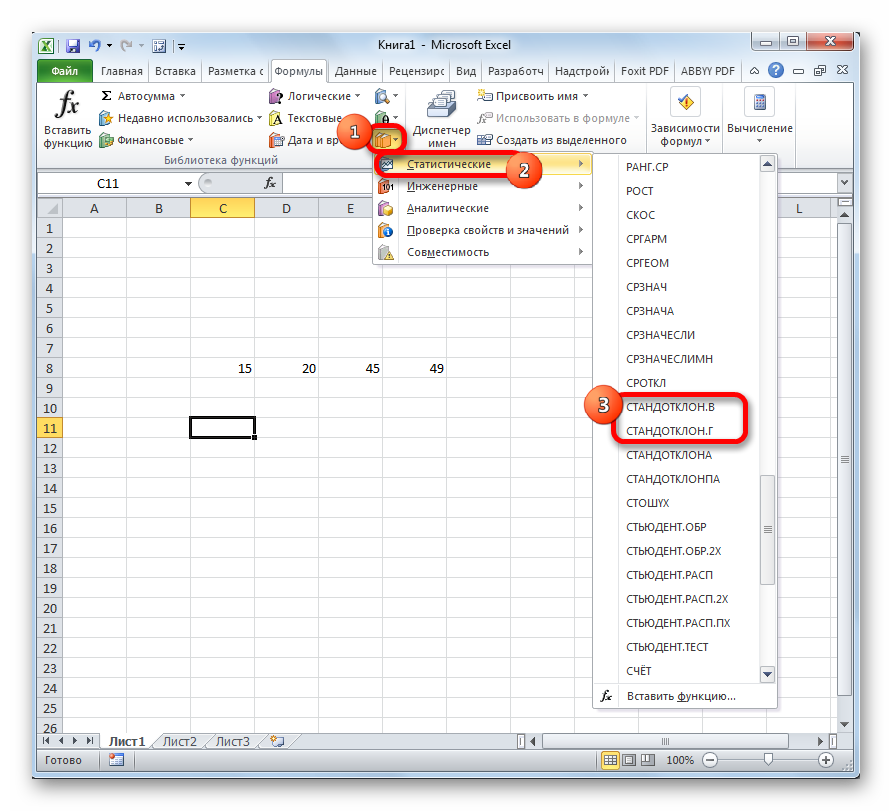
- В контекстном меню выбрать тип «Статистические» и поставить курсор мышки на это слово.
- Развернется дополнительное контекстное окно, в котором пользователю необходимо щелкнуть по строчке «СТАНДОТКЛОН.В».
- В запустившемся окне «Аргументы функции» надо заполнить два поля, указав координаты соответствующих ячеек на рабочем листе или в табличном массиве. Нужные значения также можно прописать вручную.
- После выполнения этих манипуляций нажать на «ОК».
- Удостовериться, что в указанной ранее ячейке отобразился результат работы формулы – число, характеризующее среднеквадратичное отклонение.
Важно! Если необходимо посчитать стандартное отклонение у нескольких параметров, то исходную формулу можно растянуть на оставшиеся ячейки табличного массива.
Способ 3. Ручной ввод формулы среднеквадратичного отклонения в Эксель
Чтобы рассчитать стандартное отклонение в Microsoft Office Excel, можно ввести специальную формулу с клавиатуры, результат будет одинаковым. Такой метод вычисления заключается в выполнении следующих этапов:
- Поставить курсор мыши в ячейку, куда будет выводиться результат.
- В выделенный элемент ввести с клавиатуры формулу «=СТАНДОТКЛОН.В(а,b,c,d)». Вместо букв в скобках нужно указать соответствующие аргументы. Это числа из табличного массива данных.
- Нажать на «Enter» для завершения процедуры.
- Проверить результат. В итоге в ячейке должно отобразиться конкретное значение среднеквадратичного отклонения.
Дополнительная информация! Также для расчета можно использовать формулу «СТАНОТКЛОН.Г()». Получится идентичный результат. Данный метод будет работать независимо от версии программного обеспечения.
Способ 4. Ручной подсчет
Такую операцию в Microsoft Office Excel нецелесообразно выполнять. Данный метод основан на применении обычного калькулятора, который также присутствует в Эксель. Для ручного счета необходимо проделать следующие действия по алгоритму:
- Левой клавишей манипулятора выделить ячейку табличного массива, в которую будет выводиться результат.
- Поставить знак «=» и с клавиатуры компьютера прописать числовые значения для расчета среднеквадратичного отклонения, указывая координаты соответствующих ячеек из таблички. Здесь надо подставлять параметры в формулу из первого рисунка.
- После написания формулы нажать на «Enter» и убедиться, что в ячейке отобразился результат стандартного отклонения.
Обратите внимание! Формулу для вычисления среднеквадратичного отклонения, написанную вручную в Excel, также можно растянуть на оставшиеся ячейки для их автоматического заполнения.
Заключение
Таким образом, стандартное отклонение в Microsoft Office Excel рассчитывается с помощью формулы или выбора соответствующей функции. Основные методы вычисления данного параметра были рассмотрены выше.
Оцените качество статьи. Нам важно ваше мнение:
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
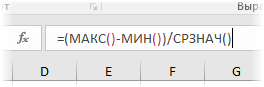
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях: