Статистические методы прогнозирования с помощью excel

Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.

Процедура прогнозирования

Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.

Способ 1: линия тренда

Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.

Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.

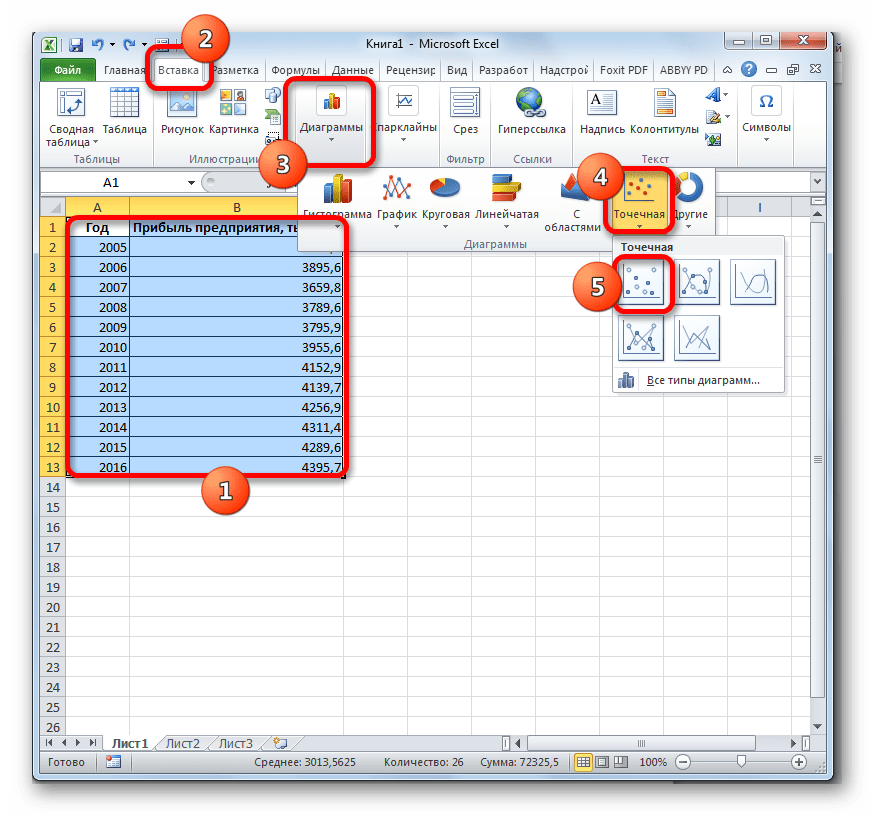
1. Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.



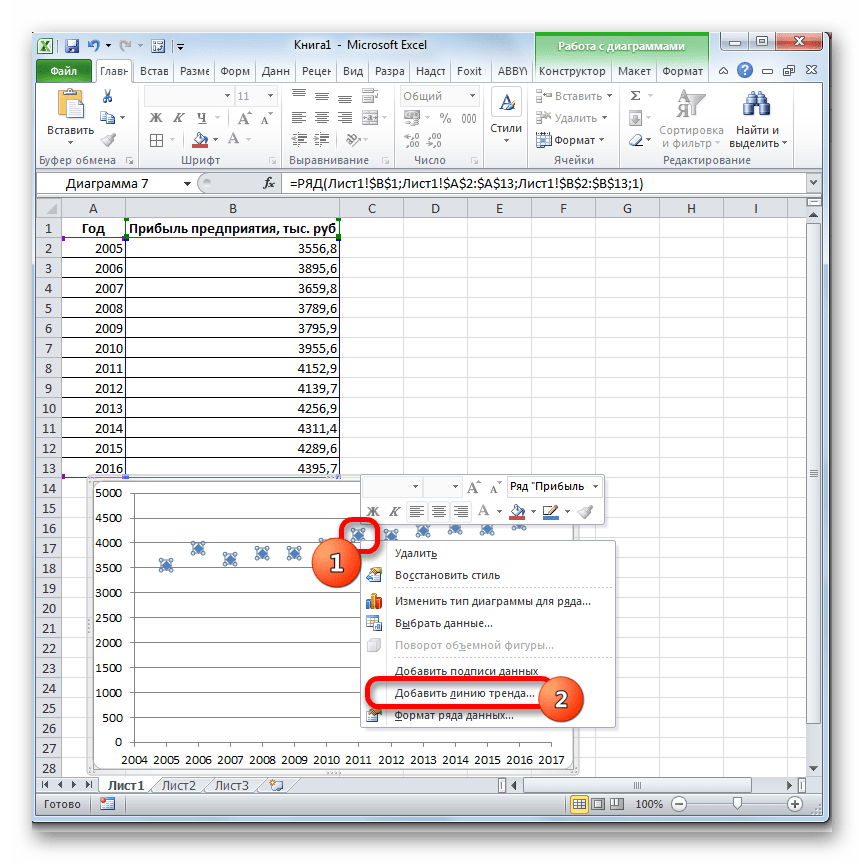
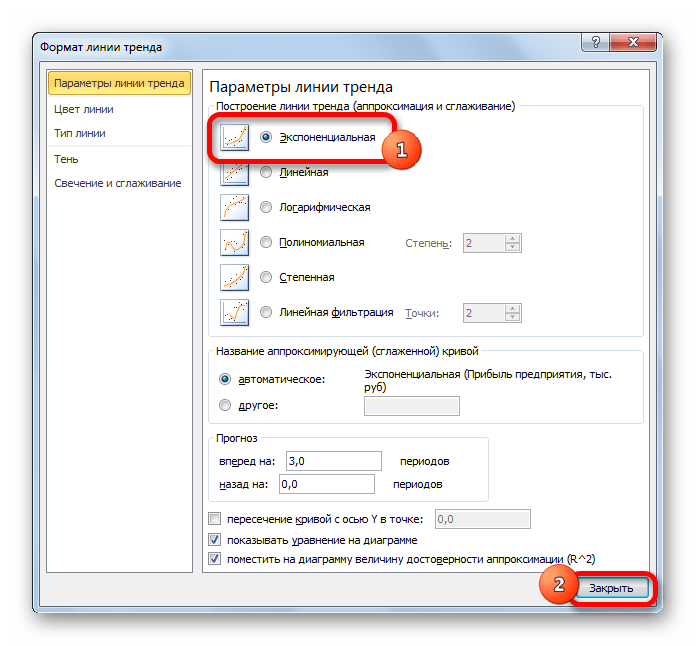
2. Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».



3. Открывается окно форматирования линии тренда. В нем можно выбрать один из шести видов аппроксимации:
   • Линейная;
   • Логарифмическая;
   • Экспоненциальная;
   • Степенная;
   • Полиномиальная;
   • Линейная фильтрация.

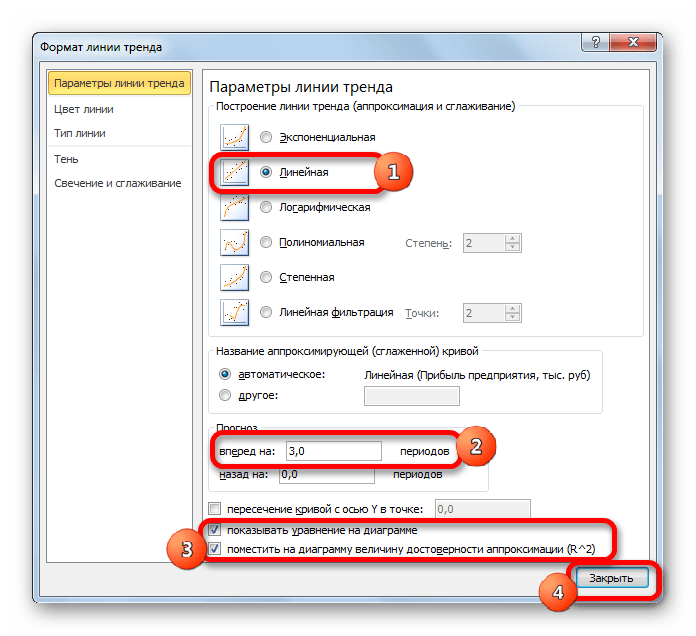
   Давайте для начала выберем линейную аппроксимацию.

   В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».



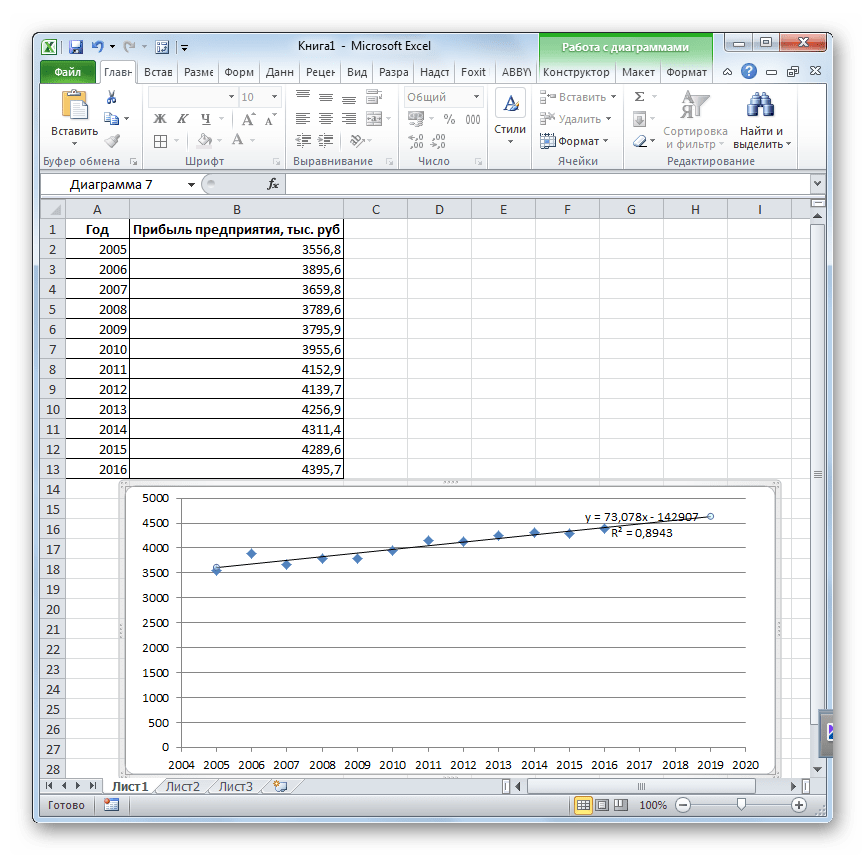
4. Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.



5. Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
   

   Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.

Урок: Как построить линию тренда в Excel

Способ 2: оператор ПРЕДСКАЗ

Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:

=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x)

«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.

«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.

«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.

Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.

При вычислении данным способом используется метод линейной регрессии.

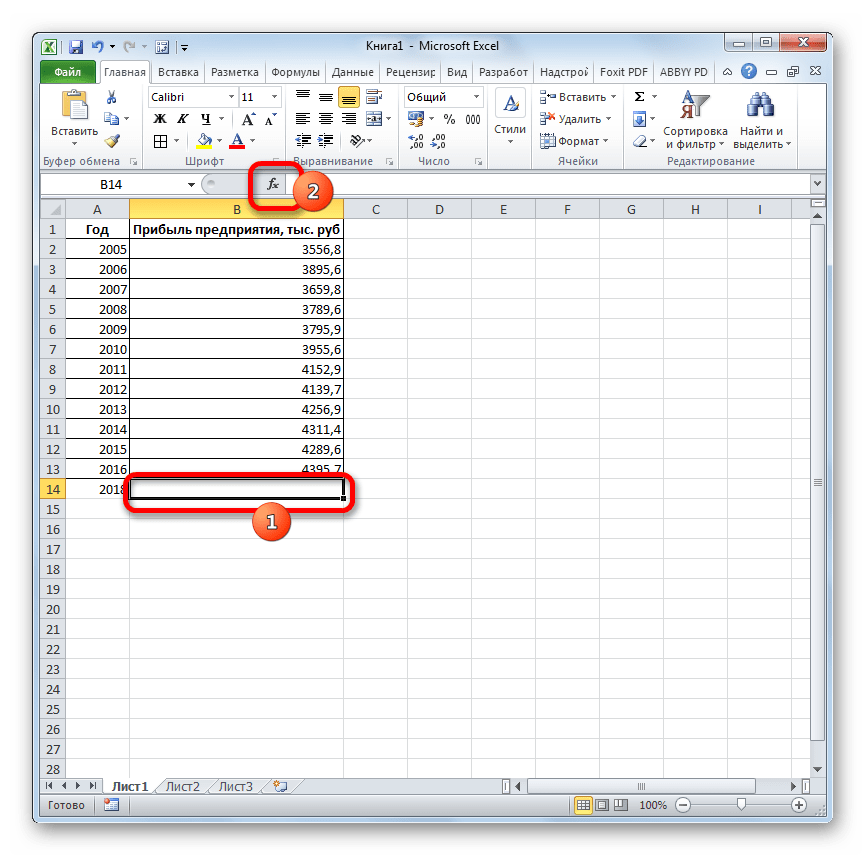
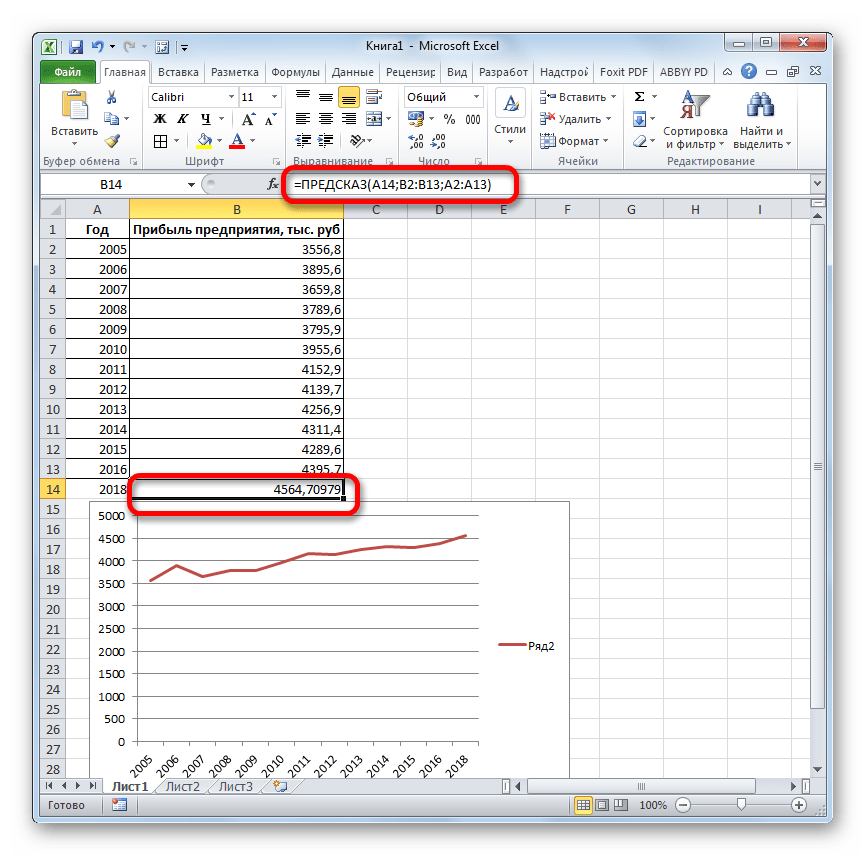
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.

1. Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».



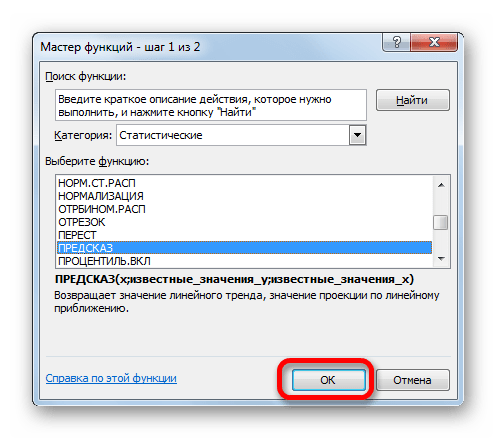
2. Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».



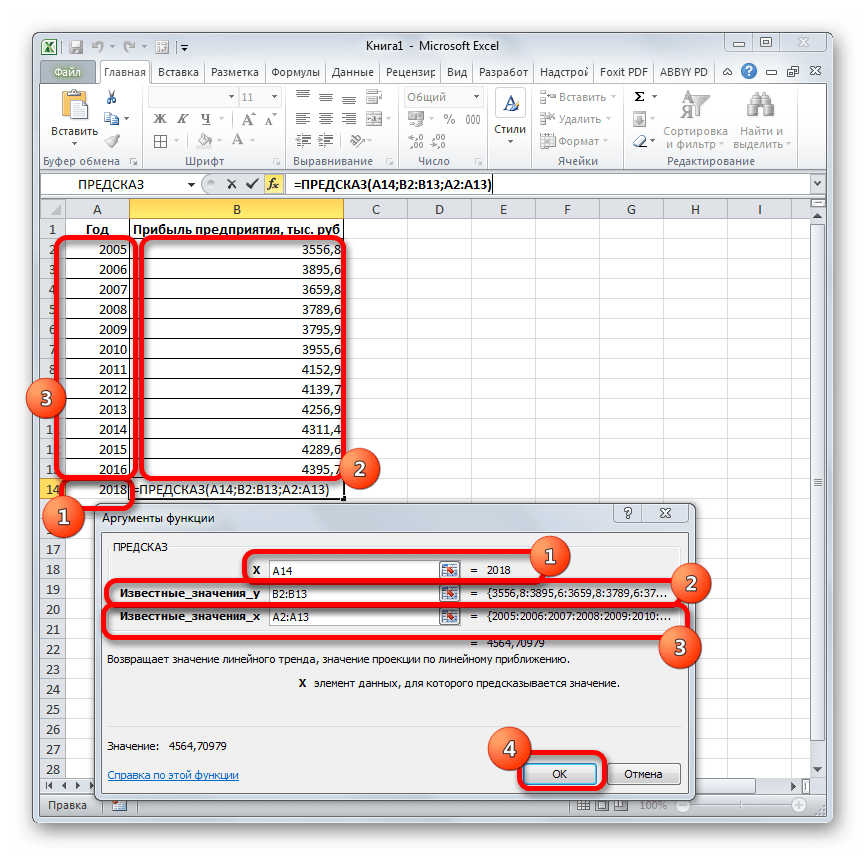
3. Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.

   В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.

   Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.

   После того, как вся информация внесена, жмем на кнопку «OK».



4. Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.



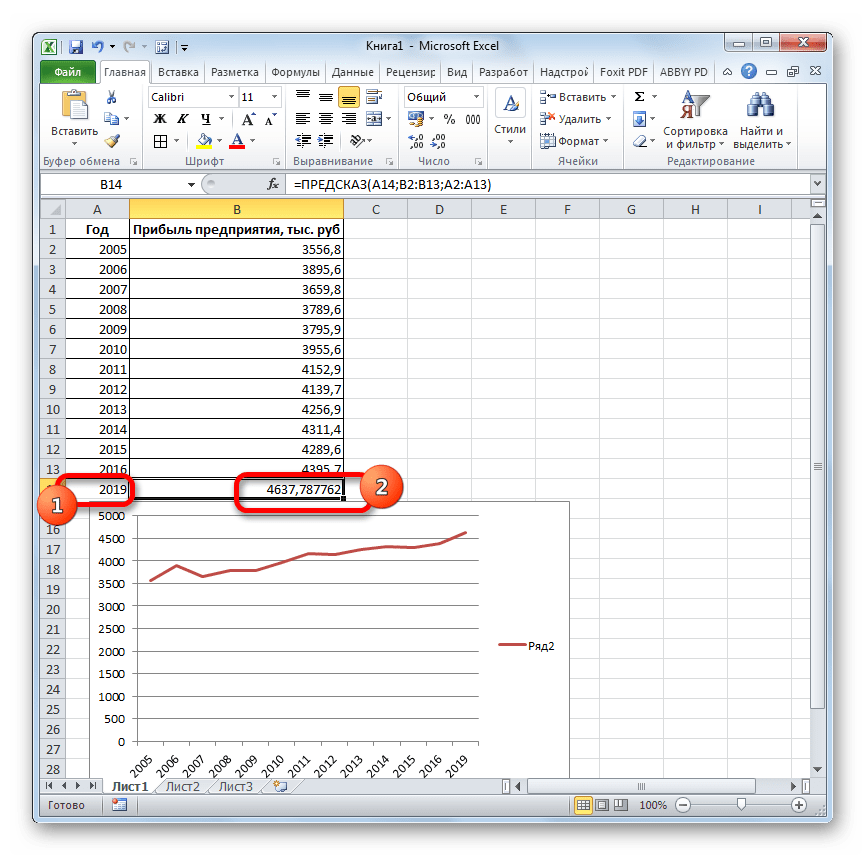
5. Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.

Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.

Урок: Экстраполяция в Excel

Способ 3: оператор ТЕНДЕНЦИЯ

Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:

=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.

Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.

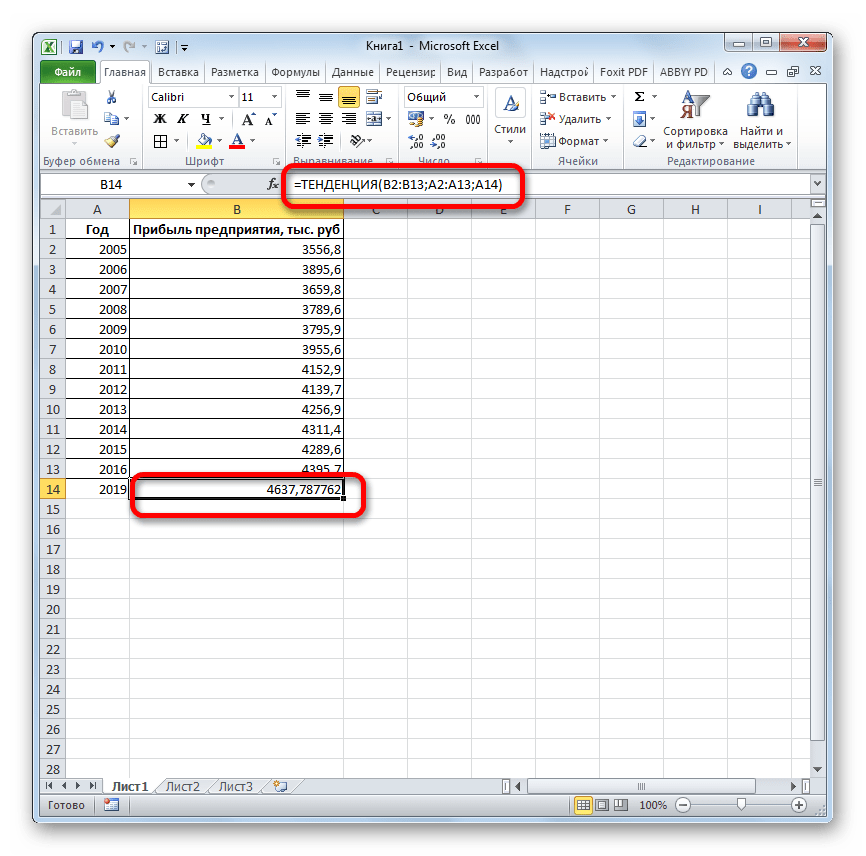
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.

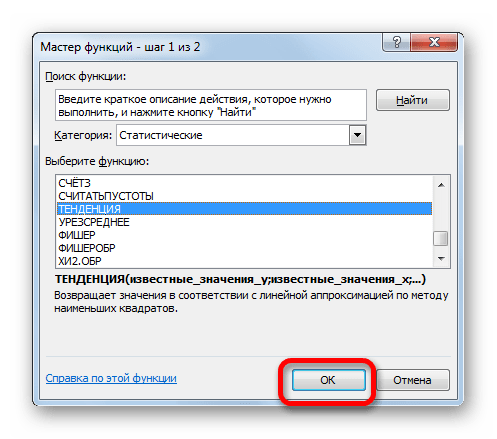
1. Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».



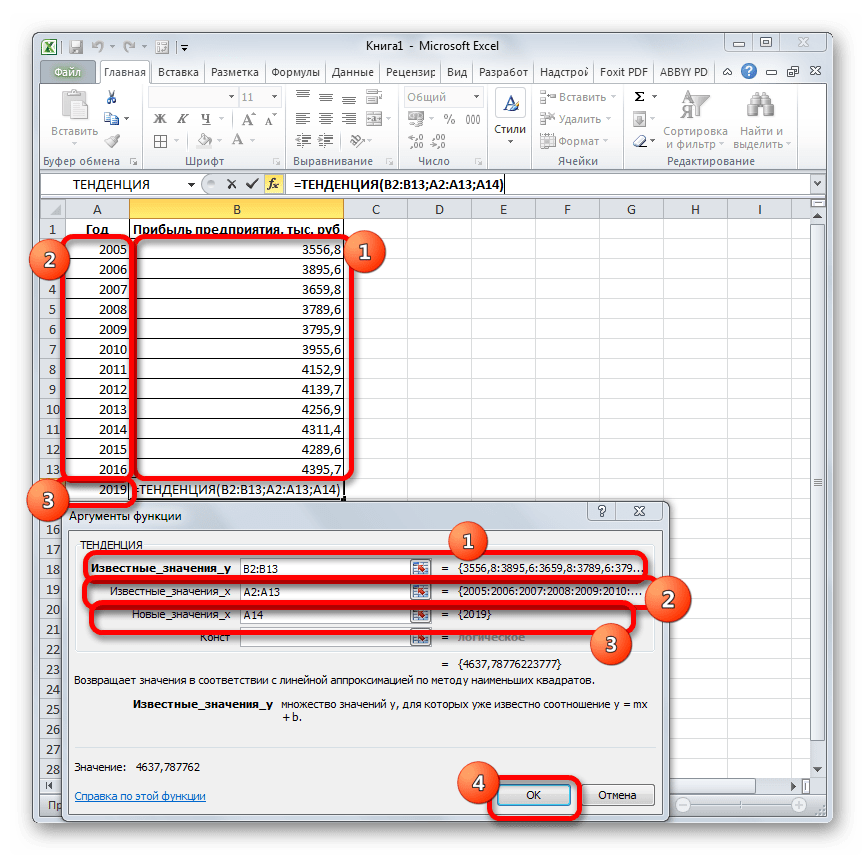
2. Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».



3. Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.

Способ 4: оператор РОСТ

Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:

=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.

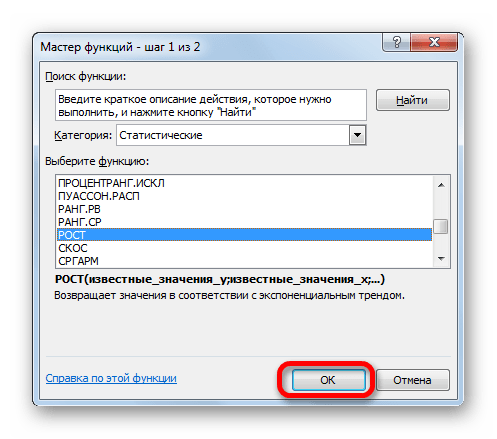
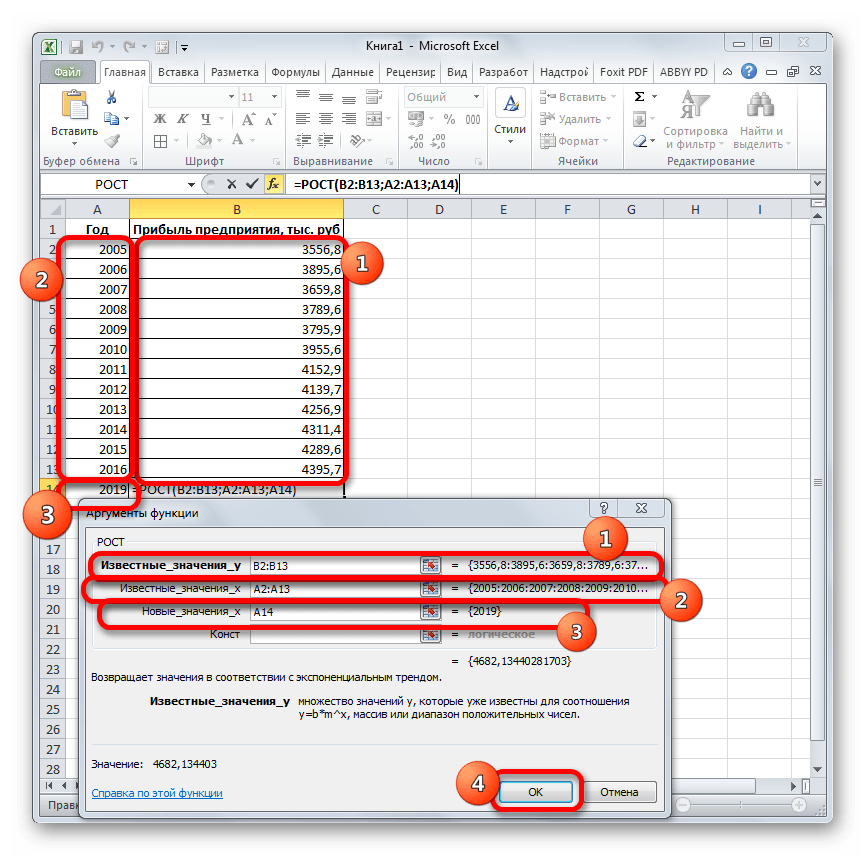
1. Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».



2. Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».



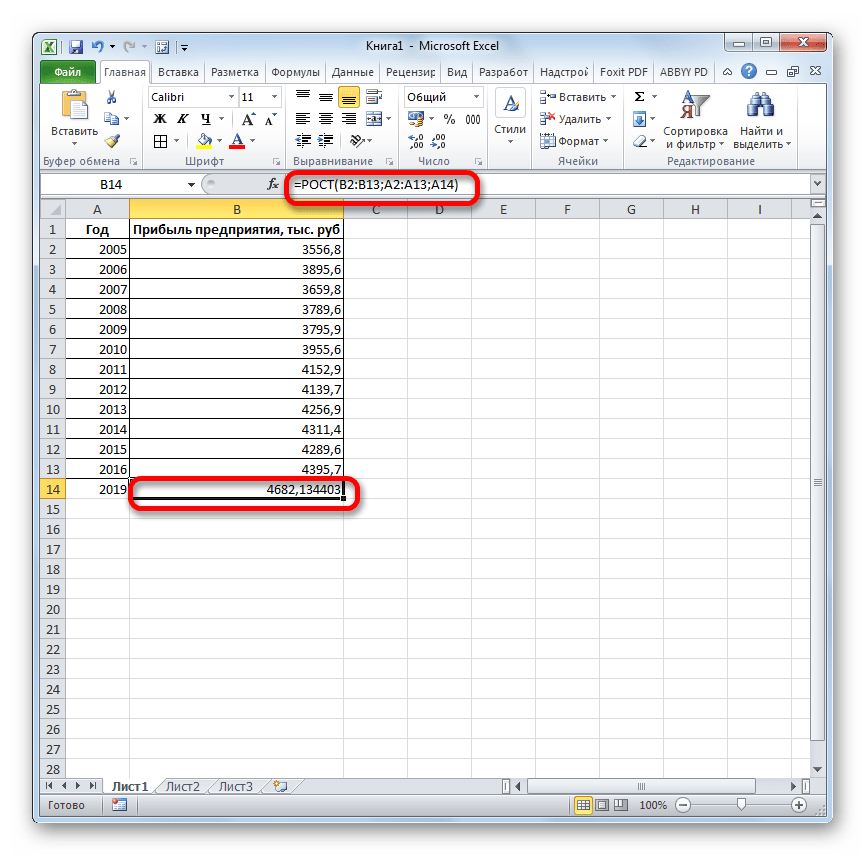
3. Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.

Способ 5: оператор ЛИНЕЙН

Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:

=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])

Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.

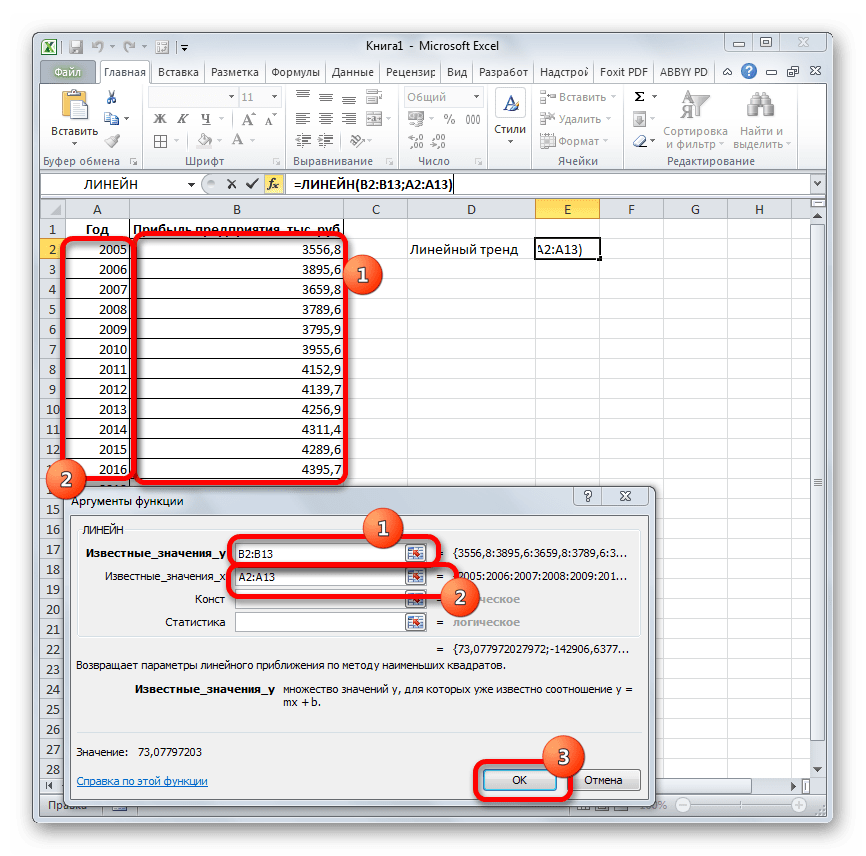
1. Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».



2. В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».



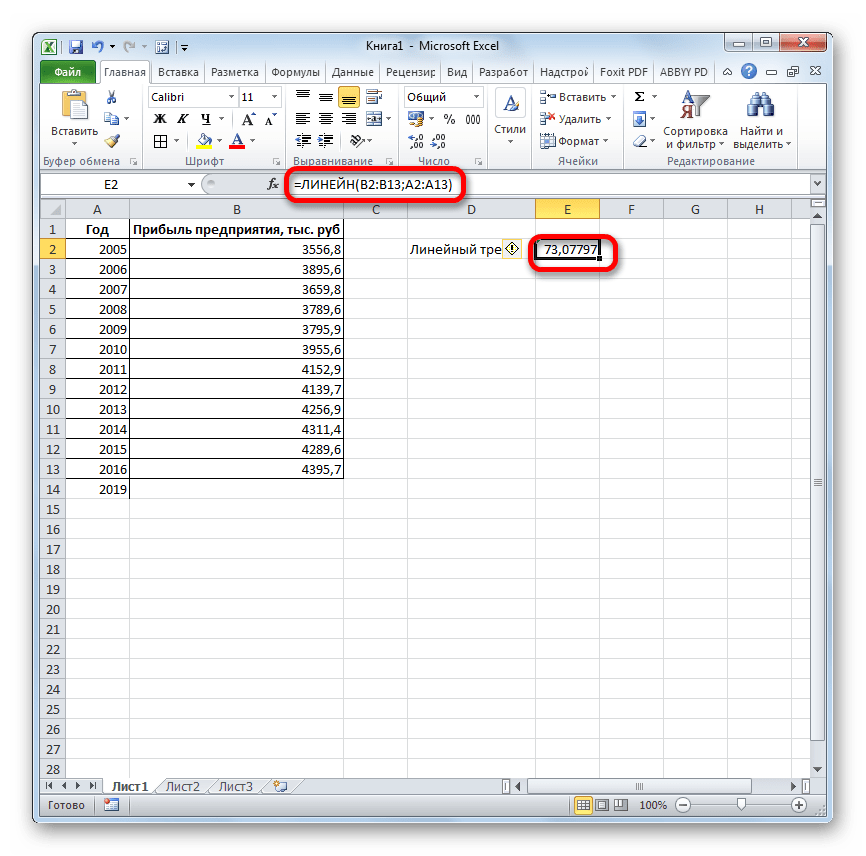
3. Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.



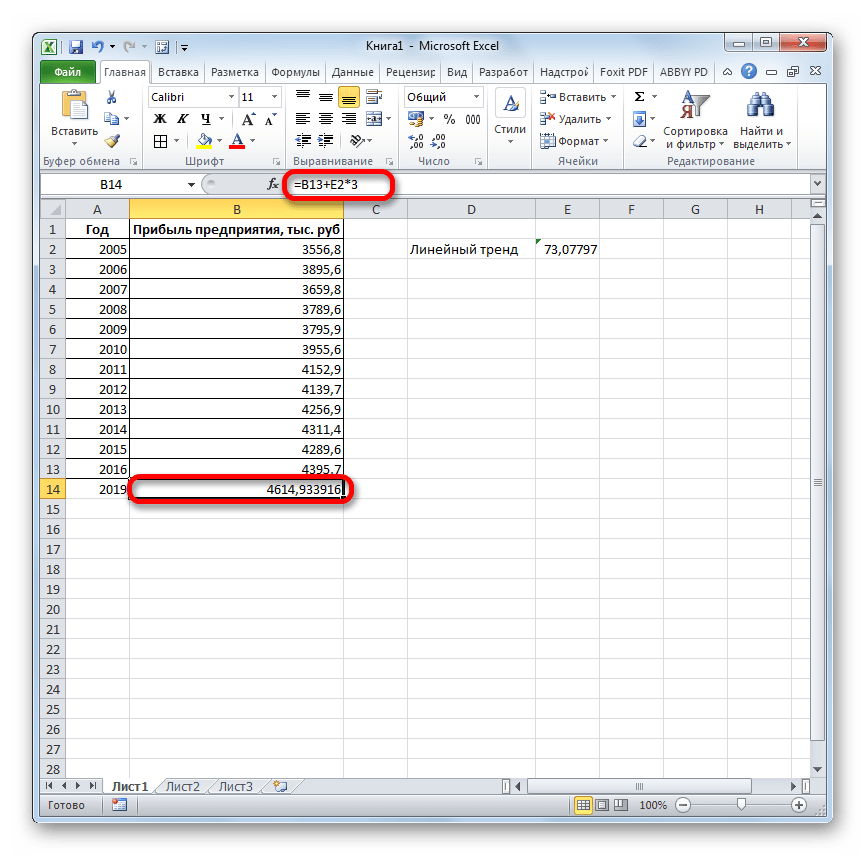
4. Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.

Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.

Способ 6: оператор ЛГРФПРИБЛ

Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:

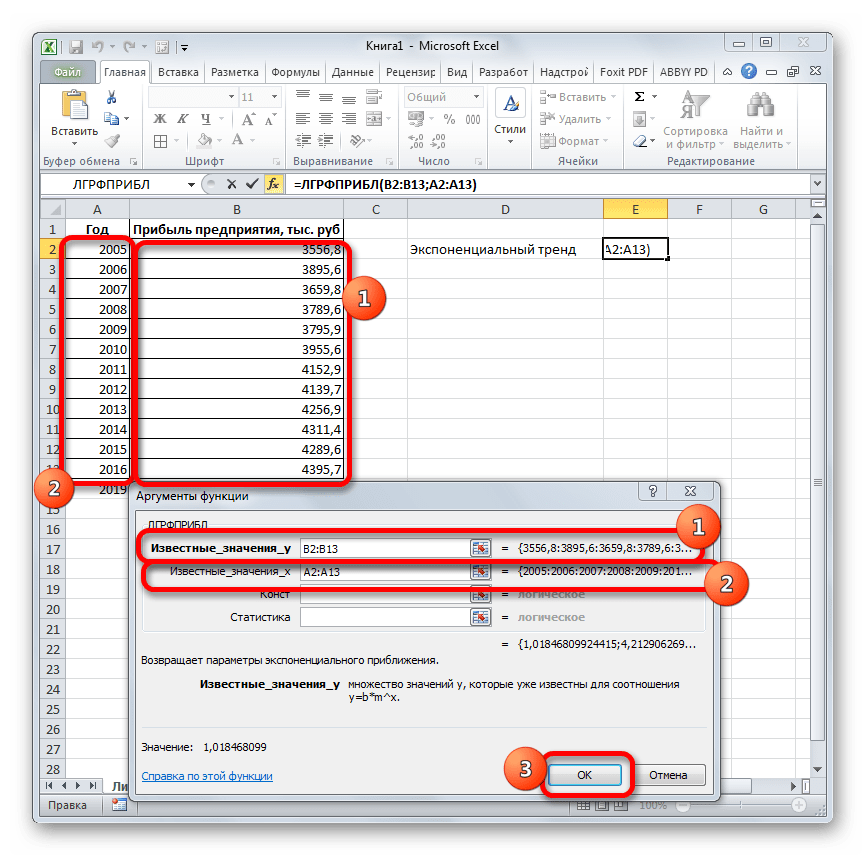
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])

Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.

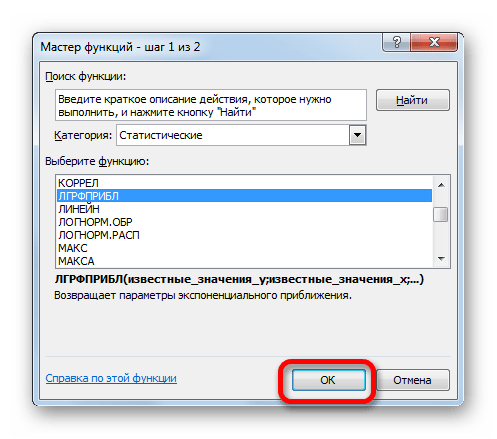
1. В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».



2. Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».



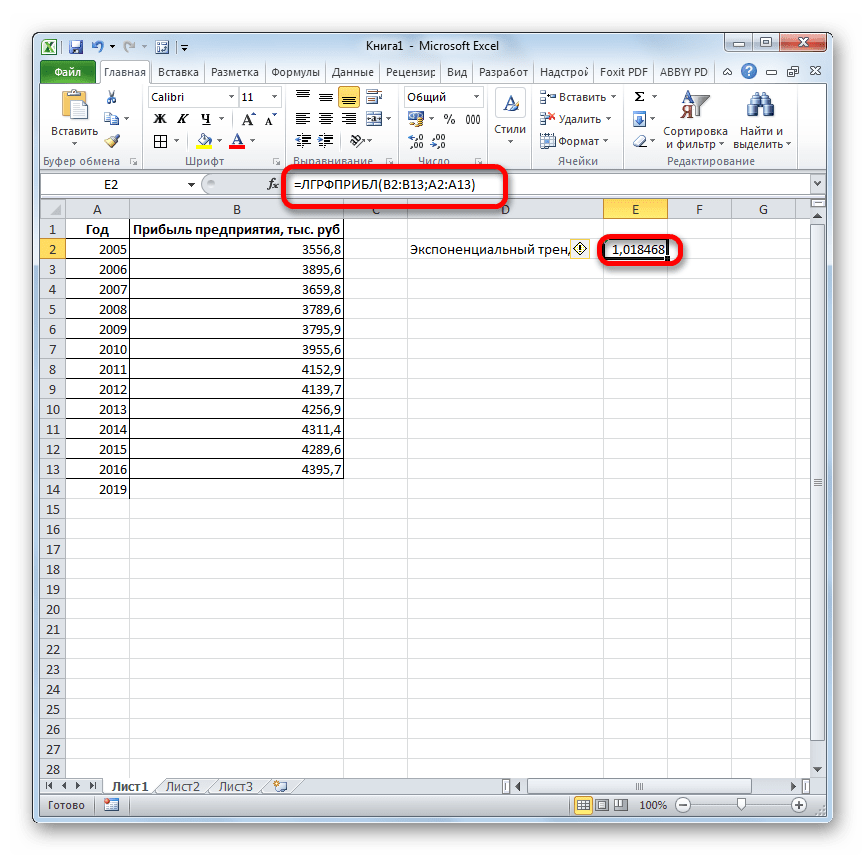
3. Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.



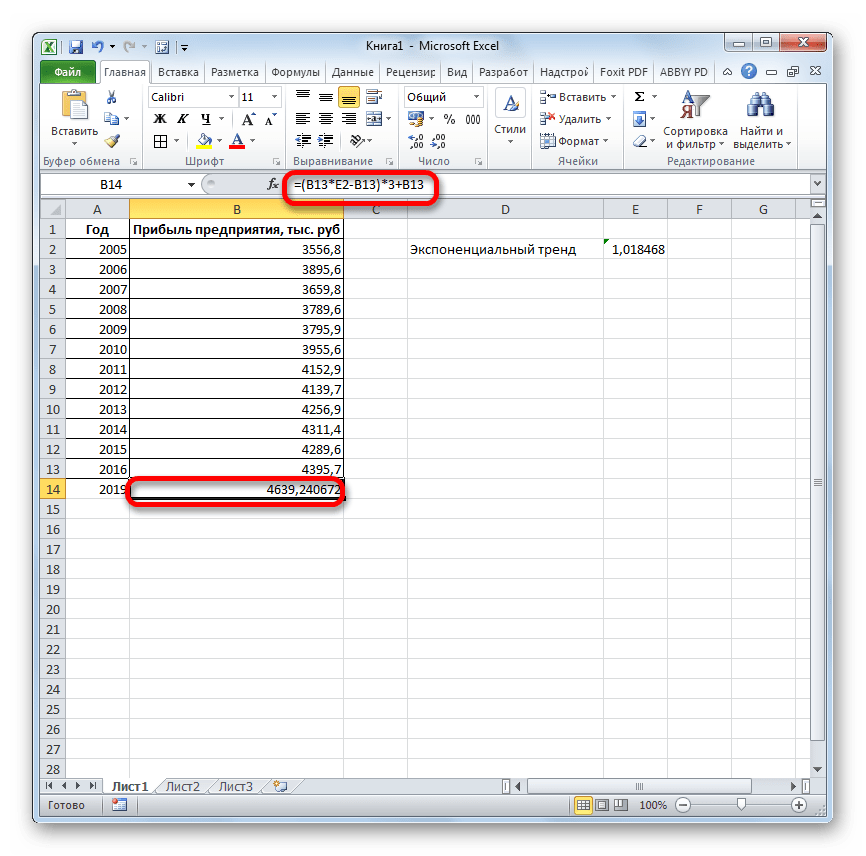
4. Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.

Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.

Урок: Другие статистические функции в Excel

Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.

Если у вас есть статистические данные с зависимостью от времени, вы можете создать прогноз на их основе. При этом в Excel создается новый лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены. С помощью прогноза вы можете предсказывать такие показатели, как будущий объем продаж, потребность в складских запасах или потребительские тенденции.

Сведения о том, как вычисляется прогноз и какие параметры можно изменить, приведены ниже в этой статье.

Создание прогноза

1. На листе введите два ряда данных, которые соответствуют друг другу:

   • ряд значений даты или времени для временной шкалы;

   • ряд соответствующих значений показателя.

     Эти значения будут предсказаны для дат в будущем.

   Примечание: Для временной шкалы требуются одинаковые интервалы между точками данных. Например, это могут быть месячные интервалы со значениями на первое число каждого месяца, годичные или числовые интервалы. Если на временной шкале не хватает до 30 % точек данных или есть несколько чисел с одной и той же меткой времени, это нормально. Прогноз все равно будет точным. Но для повышения точности прогноза желательно перед его созданием обобщить данные.

2. Выделите оба ряда данных.

   Совет: Если выделить ячейку в одном из рядов, Excel автоматически выделит остальные данные.

3. На вкладке Данные в группе Прогноз нажмите кнопку Лист прогноза.

   

4. В окне Создание прогноза выберите график или гограмму для визуального представления прогноза.

   

5. В поле Завершение прогноза выберите дату окончания, а затем нажмите кнопку Создать.

   В Excel будет создан новый лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены.

   Этот лист будет находиться слева от листа, на котором вы ввели ряды данных (то есть перед ним).

Настройка прогноза

Если вы хотите изменить дополнительные параметры прогноза, нажмите кнопку Параметры.

Сведения о каждом из вариантов можно найти в таблице ниже.

Параметры прогноза	Описание
Начало прогноза	Выберите дату, с которой должен начинаться прогноз. При выборе даты начала, которая наступает раньше, чем заканчиваются статистические данные, для построения прогноза используются только данные, предшествующие ей (это называется «ретроспективным прогнозированием»). Советы:  Если вы начинаете прогноз перед последней точкой, вы сможете получить оценку точности прогноза, так как сможете сравнить прогнозируемый ряд с фактическими данными. Но если начать прогнозирование со слишком ранней даты, построенный прогноз может отличаться от созданного на основе всех статистических данных. При использовании всех статистических данных прогноз будет более точным. Если в ваших данных прослеживаются сезонные тенденции, то рекомендуется начинать прогнозирование с даты, предшествующей последней точке статистических данных.
Доверительный интервал	Установите или снимите флажок Доверительный интервал, чтобы показать или скрыть его. Доверительный интервал — это диапазон вокруг каждого предсказанного значения, в который в соответствии с прогнозом (при нормальном распределении) предположительно должны попасть 95 % точек, относящихся к будущему. Доверительный интервал помогает определить точность прогноза. Чем он меньше, тем выше достоверность прогноза для данной точки. Доверительный интервал по умолчанию определяется для 95 % точек, но это значение можно изменить с помощью стрелок вверх или вниз.
Сезонность	Сезонность — это число для длины (количества точек) сезонного шаблона и автоматически обнаруживается. Например, в ежегодном цикле продаж, каждый из которых представляет месяц, сезонность составляет 12. Автоматическое обнаружение можно переопрепредидить, выбрав установить вручную и выбрав число. Примечание: Если вы хотите задать сезонность вручную, не используйте значения, которые меньше двух циклов статистических данных. При таких значениях этого параметра приложению Excel не удастся определить сезонные компоненты. Если же сезонные колебания недостаточно велики и алгоритму не удается их выявить, прогноз примет вид линейного тренда.
Диапазон временной шкалы	Здесь можно изменить диапазон, используемый для временной шкалы. Этот диапазон должен соответствовать параметру Диапазон значений.
Диапазон значений	Здесь можно изменить диапазон, используемый для рядов значений. Этот диапазон должен совпадать со значением параметра Диапазон временной шкалы.
Заполнить отсутствующие точки с помощью	Для обработки отсутствующих точек в Excel используется интерполяция, то есть отсутствующие точки будут заполнены в качестве взвешенного среднего значения соседних точек, если отсутствует менее 30 % точек. Чтобы нули в списке не были пропущены, выберите в списке пункт Нули.
Использование агрегатных дубликатов	Если данные содержат несколько значений с одной меткой времени, Excel находит их среднее. Чтобы использовать другой метод вычисления, например Медиана илиКоличество,выберите нужный способ вычисления из списка.
Включить статистические данные прогноза	Установите этот флажок, если хотите поместить на новом листе дополнительную статистическую информацию о прогнозе. При этом добавляется таблица статистики, созданная с помощью прогноза. Ets. Функция СТАТ и показатели, такие как коэффициенты сглаживания («Альфа», «Бета», «Гамма») и метрики ошибок (MASE, SMAPE, MAE, RMSE).

Формулы, используемые при прогнозировании

При использовании формулы для создания прогноза возвращаются таблица со статистическими и предсказанными данными и диаграмма. Прогноз предсказывает будущие значения на основе имеющихся данных, зависящих от времени, и алгоритма экспоненциального сглаживания (ETS) версии AAA.

Таблицы могут содержать следующие столбцы, три из которых являются вычисляемыми:

• столбец статистических значений времени (ваш ряд данных, содержащий значения времени);

• столбец статистических значений (ряд данных, содержащий соответствующие значения);

• столбец прогнозируемых значений (вычисленных с помощью функции ПРЕДСКАЗ.ЕTS);

• два столбца, представляющие доверительный интервал (вычисленные с помощью функции ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ). Эти столбцы отображаются только при проверке доверительный интервал в разделе Параметры.

Скачивание образца книги

Щелкните эту ссылку, чтобы скачать книгу с Excel FORECAST. Примеры функции ETS

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Статьи по теме

Функции прогнозирования

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Любому бизнесу интересно заглянуть в будущее и правильно ответить на вопрос: «А сколько денег мы заработаем за следующий период?» Ответить на такого рода вопросы позволяют различные методики прогнозирования. В данной статье мы с вами рассмотрим несколько таких методик и произведем все необходимые расчеты в Excel. Еще больше про анализ данных в Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».

Постановка задачи

Исходные данные

Для начала, давайте определимся, какие у нас есть исходные данные и что нам нужно получить на выходе. Фактически, все что у нас есть, это некоторые исторические данные. Если мы говорим о прогнозировании продаж, то историческими данными будут продажи за предыдущие периоды.

Примечание. Собранные в разные моменты времени значения одной и той же величины образуют временной ряд. Каждое значение такого временного ряда называется измерением. Например: данные о продажах за последние 5 лет по месяцам — временной ряд; продажи за январь прошлого года — измерение.

Составляющие прогноза

Следующий шаг: давайте определимся, что нам нужно учесть при построении прогноза. Когда мы исследуем наши данные, нам необходимо учесть следующие факторы:

• Изменение нашей пронозируемой величины (например, продаж) подчиняется некоторому закону. Другими словами, в временном ряде можно проследить некую тенденцию. В математике такая тенденция называется трендом.
• Изменение значений в временном ряде может зависить от промежутка времени. Другими словами, при построении модели необходимо будет учесть коэффициент сезонности. Например, продажи арбузов в январе и августе не могут быть одинаковыми, т.к. это сезонный продукт и летом продажи значительно выше.
• Изменение значений в временном ряде периодически повторяется, т.е. наблюдается некоторая цикличность.

Эти три пункта в совокупность образуют регулярную составляющую временного ряда.

Примечание. Не обязательно все три элемента регулярной составляющей должны присутствовать в временном ряде.

Однако, помимо регулярной составляющей, в временном ряде присутствует еще некоторое случайное отклонение. Интуитивно это понятно – продажи могут зависеть от многих факторов, некоторые из которых могут быть случайными.

Вывод. Чтобы комплексно описать временной ряд, необходимо учесть 2 главных компонента: регулярную составляющую (тренд + сезонность + цикличность) и случайную составляющую.

Виды моделей

Следующий вопрос, на который нужно ответить при построении прогноза: “А какие модели временного ряда бывают?”

Обычно выделяют два основных вида:

• Аддитивная модель: Уровень временного ряда = Тренд + Сезонность + Случайные отклонения
• Мультипликативная модель: Уровень временного ряда = Тренд X Сезонность X Случайные отклонения

Иногда также выделают смешанную модель в отдельную группу:

• Смешанная модель: Уровень временного ряда = Тренд X Сезонность + Случайные отклонения

С моделями мы определились, но теперь возникает еще один вопрос: «А когда какую модель лучше использовать?»

Классический вариант такой:
— Аддитивная модель используется, если амплитуда колебаний более-менее постоянная;
— Мультипликативная – если амплитуда колебаний зависит от значения сезонной компоненты.

Пример:

Решение задачи с помощью Excel

Итак, необходимые теоретические знания мы с вами получили, пришло время применить их на практике. Мы будем с вами использовать классическую аддитивную модель для построения прогноза. Однако, мы построим с вами два прогноза:

1. с использованием линейного тренда
2. с использованием полиномиального тренда

Во всех руководствах, как правило, разбирается только линейный тренд, поэтому полиномиальная модель будет крайне полезна для вас и вашей работы!

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Модель с линейным трендом

Пусть у нас есть исходная информация по продажам за 2 года:

Учитывая, что мы используем линейный тренд, то нам необходимо найти коэффициенты уравнения

y = ax + b

где:

• y – значения продаж
• x – номер периода
• a – коэффициент наклона прямой тренда
• b – свободный член тренда

Рассчитать коэффициенты данного уравнения можно с помощью формулы массива и функции ЛИНЕЙН. Нам необходимо будет сделать следующую последовательность действий:

1. Выделяем две ячейки рядом
2. Ставим курсор в поле формул и вводим формулу =ЛИНЕЙН(C4:C27;B4:B27)
3. Нажимаем Ctrl+Shift+Enter, чтобы активировать формулу массива

На выходе мы получили 2 числа: первое — коэффициент a, второе – свободный член b.

Теперь нам нужно рассчитать для каждого периода значение линейного тренда. Сделать это крайне просто — достаточно в полученное уравнение подставить известные номера периодов. Например, в нашем случае, мы прописываем формулу =B4*$F$4+$G$4 в ячейке I4 и протягиваем ее вниз по всем периодам.

Нам осталось рассчитать коэффициент сезонности для каждого периода. Учитывая, что у нас есть исторические данные за два года, разумно будет учесть это при расчете. Можем сделать следующим образом: в ячейке J4 прописываем формулу =(C4+C16)/СРЗНАЧ($C$4:$C$27)/2 и протягиваем вниз на 12 месяцев (т.е. до J15).

Что нам это дало? Мы посчитали, сколько суммарно продавалось каждый январь/каждый февраль и так далее, а потом разделили это на среднее значение продаж за все два периода.

То есть мы выяснили, как продажи двух январей отклонялись от средних продаж за два года, как продажи двух февралей отклонялись и так далее. Это и дает нам коэффициент сезонности. В конце формулы делим на 2, т.к. в расчете фигурировало 2 периода.

Примечание. Рассчитали только 12 коэффициентов, т.к. один коэффициент учитывает продажи сразу за 2 аналогичных периода.

Итак, теперь мы на финишной прямой. Нам осталось рассчитать тренд для будущих периодов и учесть коэффициент сезонности для них. Давайте амбициозно построим прогноз на год вперед.

Сначала создаем столбец, в котором прописываем номера будущих периодов. В нашем случае нумерация начинается с 25 периода.

Далее, для расчета значения тренда просто прописываем уже известную нам формулу =L4*$F$4+$G$4 и протягиваем вниз на все 12 прогнозируемых периодов.

И последний штрих — умножаем полученное значение на коэффициент сезонности. Вуаля, это и есть итоговый ответ в данной модели!

Модель с полиномиальным трендом

Конструкция, которую мы только что с вами построили, достаточно проста. Но у нее есть один большой минус — далеко не всегда она дает достоверные результаты.

Посмотрите сами, какая модель более точно аппроксимирует наши точки — линейный тренд (прямая зеленая линия) или полиномиальный тренд (красная кривая)? Ответ очевиден. Поэтому сейчас мы с вами и разберем, как построить полиномиальную модель в Excel.

Пусть все исходные данные у нас будут такими же. Для простоты модели будем учитывать только тренд, без сезонной составляющей.

Для начала давайте определимся, чем полиномиальный тренд отличается от обычного линейного. Правильно — формой уравнения. У линейного тренда мы разбирали обычный график прямой:

У полиномиального тренда же уравнение выглядит иначе:

где конечная степень определяется степенью полинома.

Т.е. для полинома 4 степени необходимо найти коэффициенты уравнения:

Согласитесь, выглядит немного страшно. Однако, ничего страшного нет, и мы с легкостью можем решить эту задачку с помощью уже известных нам методов.

1. Ставим в ячейку F4 курсор и вводим формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;1). Функция ЛИНЕЙН позволяет произвести расчет коэффициентов, а с помощью функции ИНДЕКС мы вытаскиваем нужный нам коэффициент. В данном случае за выбор коэффициента отвечает самый последний аргумент. У нас стоит 1 — это коэффициент при самой высокой степени (т.е. при 4 степени, коэффициент). Кстати, узнать о самых полезных математических формулах Excel можно в нашем бесплатном гайде «Математические функции Excel».
2. Аналогично прописываем формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;2) в ячейке ниже.
3. Делаем такие же действия, пока не найдем все коэффициенты.

Кстати говоря, мы можем легко сами себя проверить. Давайте построим график наших продаж и добавим к нему полиномиальный тренд.

1. Выделяем столбец с продажами
2. Выбираем «Вставка» → «График» → «Точечный» → «Точечная диаграмма»
3. Нажимаем на любую точку графика правой кнопкой мыши и выбираем «Добавить линию тренда»
4. В открывшемся справа меню выбираем «Полиномиальная модель», меняем степень на 4 и ставим галочку на «Показывать уравнение на диаграмме»

Теперь вы наглядно можете видеть, как рассчитанный тренд аппроксимирует исходные данные и как выглядит само уравнение. Можно сравнить уравнение на графике с вашими коэффициентами. Сходится? Значит сделали все верно!

Помимо всего прочего, вы можете сразу оценить точность аппроксимации (не полностью, но хотя бы первично). Это делается с помощью коэффициента R^2. Тут у вас снова есть два пути:

1. Вы можете вывести коэффициент на график, поставив галочку «Поместить на диаграмму величину достоверности аппроксимации»
2. Вы можете рассчитать коэффициент R^2 самостоятельно по формуле =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4};;1);3;1)

Заключение

Мы с вами подробно разобрали вопрос прогнозирования — изучили необходимые термины и виды моделей, построили аддитивную модель в Excel с использованием линейного и полиномиального тренда, а также научились отображать результаты своих вычислений на графиках. Все это позволит вам эффективно внедрять полученные знания на работе, усложнять существующие модели и уточнять прогнозы. Чем большим количеством методов и инструментов вы будете владеть, тем выше будет ваш профессиональный уровень и статус на рынке труда.

Если вас интересуют еще какие-то модели прогнозирования — напишите нам об этом, и мы постараемся осветить эти темы в дальнейших своих статьях! Или запишитесь на курс «Excel Academy» от SF Education, где мы рассказываем про возможности Excel, необходимые для анализа.

Автор: Алексанян Андрон, эксперт SF Education

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.

Блог SF Education

Data Science

5 примеров экономии времени в Excel

Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на наш взгляд,…

Прогнозирование — хоть и неблагодарное, но необходимое дело и для решения таких задач в Microsoft Excel есть весьма приличный инструментарий — от простейших функций линейного тренда до навороченных статистических инструментов из надстройки Пакет Анализа (Analysis Toolpak). Одними из самых простых в реализации и при этом весьма эффективных являются функции прогнозирования по методу экспоненциального сглаживания.

Суть этого метода (если не вдаваться в математические подробности) можно объяснить относительно легко. Если бы мы, например, делали прогноз совсем примитивным способом по среднему арифметическому, то все исторические данные брались бы с одинаковым весом (в статистике этот метод «средней температуры по больнице» имеет, кстати, даже официальное название — «наивный прогноз»). При прогнозировании же по методу экспоненциального сглаживания принимается идея, что старые данные должны иметь вес меньше, чем новые. Изменение этого веса в зависимости от новизны или старости наших данных происходит по лавинообразной экспоненциальной кривой — отсюда и название методики.

В Microsoft Excel для её реализации есть две основные функции, появившиеся начиная с 2016-й версии Excel:

• ПРЕДСКАЗ.ETS (FORECAST.ETS) — вычисляет будущие спрогнозированные значения на основе исторических данных.
• ПРЕДСКАЗ.ETS.ДОВИНТЕРВАЛ (FORECAST.ETS.CONFINT) — вычисляет размах доверительного интервала — коридора погрешности, в пределах которого с заданной вероятностью наш прогноз должен сбыться.

Особенно приятно, что вводить вручную эти функции и их многочисленные аргументы совершенно не требуется — в Microsoft Excel для этого есть гораздо более удобный инструмент, получивший название Лист прогноза (Forecast Sheet). Давайте рассмотрим работу с ним на следующем примере.

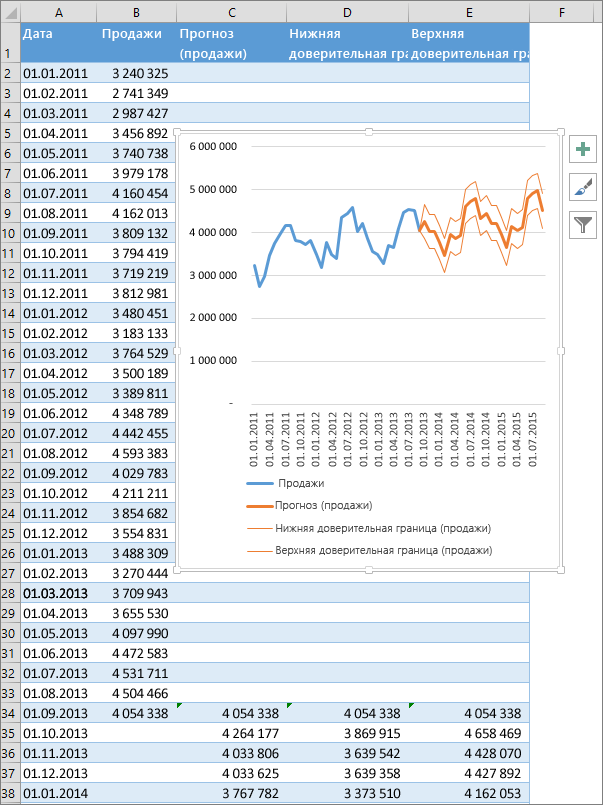
В качестве исходных исторических данных возьмем с сайта AutoVercity реальную статистику по продажам автомобилей в России за 2019-2020 годы (все марки суммарно):

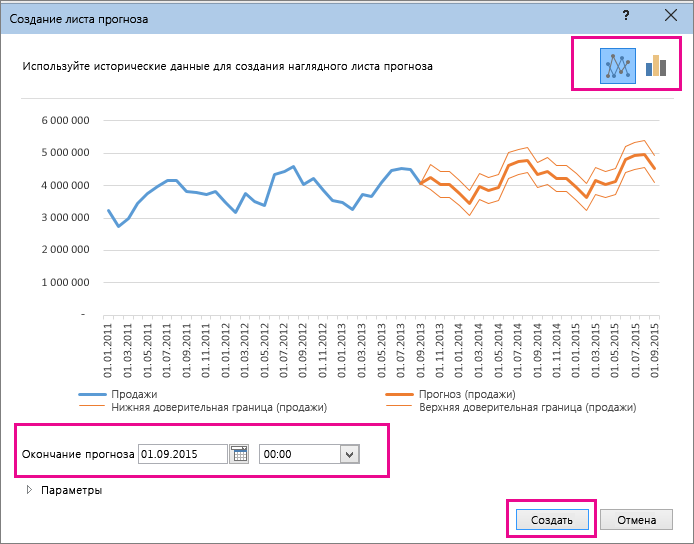
Представим на минуту, что сейчас конец 2020 года и мы хотим, используя эти данные, сделать помесячный прогноз продаж автомобилей на следующие полтора года. Выделим всю нашу таблицу и на вкладке Данные воспользуемся кнопкой Лист прогноза (Data — Forecast Sheet).

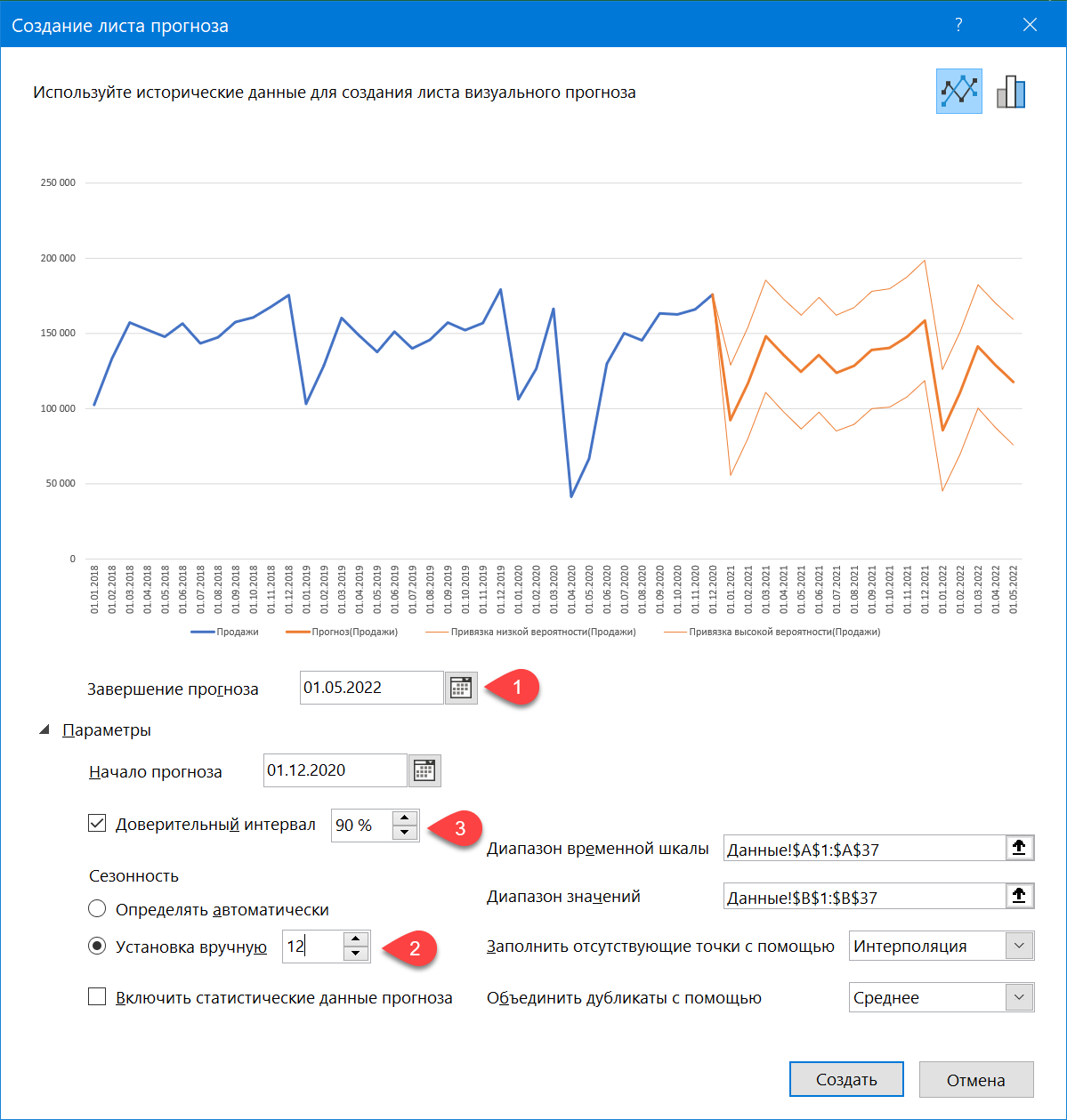
В открывшемся окне зададим следующие настройки:

1. Дату завершения прогноза
2. Сезонность — почти никогда корректно не определяется автоматически, к сожалению, так что лучше задать её вручную. В большинстве бизнесов она годовая (т.е. «узор» колебаний похожим образом повторяется из года в год), так что установим её равной 12 месяцам.
3. Вероятность, с которой мы требуем попадания будущих фактических значений в коридор доверительного интервала. Чем больше эта вероятность, тем шире интервал (т.е. более размыт прогноз). Обычно используют значения 90-95%.
4. В правом нижнем углу окна можно дополнительно выбрать реакцию на пустые ячейки (их можно заполнить нулями или средним соседних значений — интерполяцией) и на дубликаты (обычно их усредняют). Однако же, по возможности, лучше заранее подготовить исходные исторические данные, чтобы таких пробелов или дублей в них не было.

После нажатия на кнопку Создать будет сформирован новый лист с прогнозной таблицей и диаграммой, которая по ней построена:

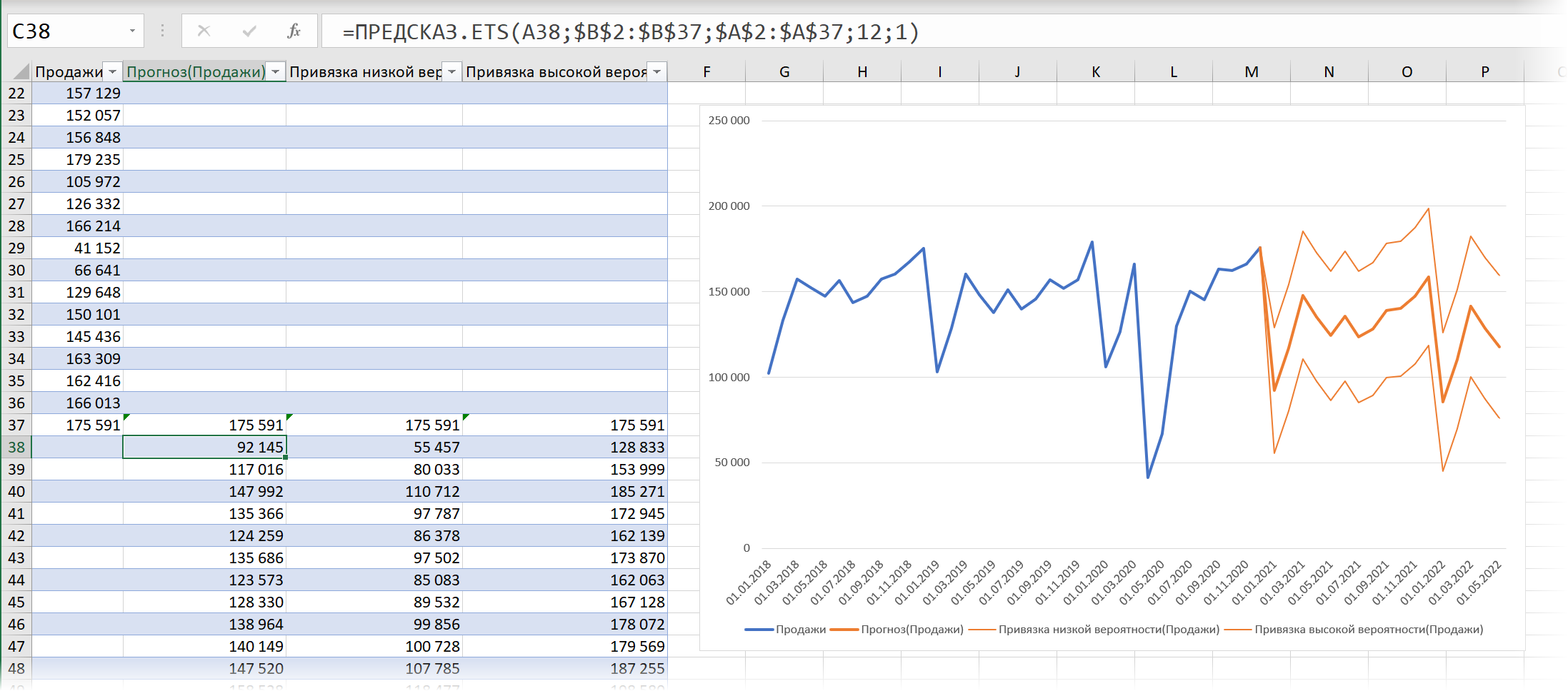
В верхней части таблицы будут идти строки с историческими данными (синяя линия), а в момент их окончания произойдет переключение на три новых столбца с прогнозом функцией ПРЕДСКАЗ.ETS и верхней и нижней границами доверительного интервала, вычисленного с помощью функции ПРЕДСКАЗ.ETS.ДОВИНТЕРВАЛ.

Ссылки по теме

• Моделирование и оценка вероятности выигрыша в лотерею
• Оптимизация доставки в Excel с помощью Поиска решения (Solver)
• Быстрое добавление новых данных в диаграмму

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ

В настоящее время статистические методы прогнозирования заняли вид­ное место в экономической практике. Широкому внедрению методов анализа и прогнозирования данных способствовало появление персональных компьюте­ров. Распространение статистических программных пакетов позволило сделать доступными и наглядными многие методы обработки данных.

Теперь уже не требуется проводить вручную трудоемкие расчеты, строить таблицы и графики – всю эту черновую работу выполняет компьютер. Человеку же остается исследовательская, творческая работа: постановка задачи, выбор методов прогнозирования, оценка качества полученных моделей, интерпретация результатов. Для этого необходимо иметь определенную подготовку в области статистических методов обработки данных и прогнозирования.

Поэтому мы решили изучить основные статистические методы анализа од­номерных временных рядов и прогнозирования и возможность их реализации в электронной таблице Excel.

Цель исследования: освоение основных понятий, математических моде­лей и методов для решения задач прогнозирования различных процессов и явле­ний, их практическая реализация в электронной таблице Excel.

Задачи исследования: изучить основные понятия теории временных ря­дов, статистические методы прогнозирования, научиться применять полученные знания для построения прогнозов.

Актуальность выбранной темы очевидна. Необходимость предвидеть бу­дущее осознавалась во все времена. Но особенно сильно роль прогнозирования возросла в наши дни, при стремительных темпах развития общества, науки и тех­ники, производства и производственных отношений. Сегодня прогнозов, осно­ванных на интуиции, уже явно недостаточно. Теперь необходимо прогнозирова­ние, основанное на объективных закономерностях, на использовании математи­ческого аппарата, проводимое на основе научных методов и моделей, на обра­ботке первичных данных с помощью информационных технологий.

ОСНОВНАЯ ЧАСТЬ

В современных условиях управленческие решения должны приниматься лишь на основе тщательного анализа имеющейся информации. Для решения задач, связанных с анализом данных при наличии случайных воздействий, предназначен мощный аппарат прикладной статистики, составной частью которого являются статистические методы прогнозирования. Эти методы позволяют выявлять закономерности на фоне случайностей, делать обоснованные прогнозы и оценивать вероятность их выполнения.

Статистические методы прогнозирования

1.1. Экономические прогнозы

Под прогнозом понимается научно обоснованное описание возможных состояний объектов в будущем, а также альтернативных путей и сроков достижения этого состояния. Процесс разработки прогнозов называется прогнозированием (от греч. prognosis – предвидение, предсказание).

Важной характеристикой является время (период) упреждения прогноза – отрезок времени от момента, для которого имеются последние статистические данные об изучаемом объекте, до момента, к которому относится прогноз.

По времени упреждения экономические прогнозы делятся на:

оперативные (с периодом упреждения до одного месяца);

краткосрочные (период упреждения – от одного, нескольких месяцев до года);

среднесрочные (период упреждения более 1 года, но не превышает 5 лет);

долгосрочные (с периодом упреждения более 5 лет).

Прогнозирование экономических явлений и процессов включает в себя следующие этапы:

1. постановка задачи и сбор необходимой информации;

2. первичная обработка исходных данных;

3. определение круга возможных моделей прогнозирования;

4. оценка параметров моделей;

5. исследование качества выбранных моделей, адекватности их реальному процессу и выбор лучшей из моделей;

6. построение прогноза;

7. содержательный анализ полученного прогноза.

1.2. Виды временных рядов. Требования, предъявляемые к исходной информации

Статистическое описание развития экономических процессов во времени осуществляется с помощью временных рядов.

Временным (динамическим) рядом называется последовательность значений показателя (признака), упорядоченная в хронологическом порядке, т.е. в порядке возрастания временного параметра. Отдельные наблюдения временного ряда называются уровнями этого ряда.

Каждый временной ряд содержит два элемента: значения времени; соответствующие им значения уровней ряда.

В качестве показателя времени в рядах динамики могут указываться либо определенные моменты времени (даты), либо отдельные периоды (сутки, месяцы, кварталы, полугодия, годы и т.д.). В зависимости от характера временного параметра ряды делятся на моментные и интервальные.

В моментных рядах динамики уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные интервалы (периоды) времени.

Важной особенностью интервальных рядов динамики абсолютных величин является возможность суммирования их уровней. Суммирование уровней моментного ряда динамики не практикуется, т.к. полученные накопленные итоги лишены всякого смысла. Моментные ряды динамики, в отличие от интервальных не обладают свойством аддитивности (термин происходит от английского глагола to add – добавлять).

При исследовании моментного ряда динамики определенный смысл имеет расчет разностей уровней, характеризующих изменение показателя за некоторый отрезок времени.

Успешность статистического анализа развития процессов во времени во многом зависит от правильного построения временных рядов.

Большое значение для дальнейшего исследования процесса имеет выбор интервалов между соседними уровнями ряда. Удобнее всего иметь дело с равноотстоящими друг от друга уровнями ряда.

Одним из важнейших условий, необходимых для правильного отражения временным рядом реального процесса развития, является сопоставимость уровней ряда. Для несопоставимых величин неправомерно проводить исследование динамики.

Чаще всего несопоставимость встречается в стоимостных показателях, что вызвано изменением цен в разные периоды времени, поэтому на практике осуществляют пересчет уровней в сопоставимые цены (цены одного периода).

Уровни рядов динамики могут содержать аномальные значения или «выбросы». Часто появление таких значений может быть вызвано ошибками при сборе, записи и передаче информации. Выявление, исключение таких значений, замена их истинными или расчетными является необходимым этапом первичной обработки данных, т.к. применение математических методов к «засоренной» информации приводит к искажению результатов анализа.

Соответствие исходной информации всем указанным требованиям проверяется на этапе предварительного анализа временных рядов. Лишь после этого переходят к расчету и анализу основных показателей динамики развития, построению моделей прогнозирования, получению прогнозных оценок.

1.3. Компоненты временных рядов

В практике исследования динамики явлений и прогнозирования принято считать, что значения уровней временных рядов экономических показателей могут содержать следующие компоненты (составные части или структурно-образующие элементы):

тренд;

сезонную компоненту;

циклическую компоненту;

случайную составляющую.

Под трендом понимают изменение, определяющее общее направление развития, основную тенденцию временного ряда. Это систематическая составляющая долговременного действия.

Наряду с долговременными тенденциями во временных рядах экономических процессов часто имеют место более или менее регулярные колебания – периодические составляющие рядов динамики.

Если период колебаний не превышает одного года, то их называют сезонными. Чаще всего причиной их возникновения считаются природно-климатические условия.

При большем периоде колебания считают, что во временных рядах имеет место циклическая составляющая. Примерами могут служить демографические, инвестиционные и другие циклы.

Если из временного ряда удалить тренд и периодические составляющие, то останется нерегулярная компонента.

Экономисты разделяют факторы, под действием которых формируется нерегулярная компонента, на 2 вида:

факторы резкого, внезапного действия;

текущие факторы.

Факторы первого вида (например, стихийные бедствия, эпидемии и др.), как правило, вызывают более значительные отклонения. Иногда такие отклонения называют катастрофическими колебаниями.

Факторы второго вида вызывают случайные колебания, являющиеся результатом действия большого числа побочных причин. Влияние каждого из текущих факторов незначительно, но ощущается их суммарное воздействие.

Если временной ряд представляется в виде суммы соответствующих компонент, то полученная модель носит название аддитивной (1.1), если в виде произведения – мультипликативной (1.2) или смешанного типа (1.3):

; (1)

; (2)

, (3)

где: – уровни временного ряда;

– трендовая составляющая;

– сезонная компонента;

– циклическая компонента;

– случайная компонента.

Решение любой задачи по анализу и прогнозированию временных рядов начинается с построения графика исследуемого показателя. Иногда на стадии графического анализа можно определить характер сезонных колебаний: аддитивный или мультипликативный. Отличительной особенностью аддитивной модели является то, что амплитуда сезонных колебаний, отражающая отклонения от тренда или среднего, остается примерно постоянной, неизменной во времени.

1.4. Сглаживание временных рядов с помощью простых скользящих средних

Распространенным приемом при выявлении и анализе тенденции развития является сглаживание временного ряда. Суть различных приемов сглаживания сводится к замене фактических уровней временного ряда расчетными уровнями, которые в меньшей степени подвержены колебаниям. Это способствует более четкому проявлению тенденции развития.

Мы рассмотрим методы сглаживания временных рядов с помощью скользящих средних. Скользящие средние позволяют сгладить как случайные, так и периодические колебания, выявить имеющуюся тенденцию в развитии процесса, и поэтому служат важным инструментом при фильтрации компонент временного ряда.

Алгоритм сглаживания по простой скользящей средней может быть представлен в виде следующей последовательности шагов:

1. Определяют длину интервала сглаживания , включающего в себя последовательных уровней ряда ( ). При этом надо иметь в виду, что чем шире интервал сглаживания, тем в большей степени взаимопогашаются колебания, и тенденция развития носит более плавный, сглаженный характер. Чем сильнее колебания, тем шире должен быть интервал сглаживания.

2. Разбивают весь период наблюдения на участки, при этом интервал сглаживания как бы скользит по ряду с шагом, равным 1.

3. Рассчитывают средние арифметические из уровней ряда, образующих каждый участок.

4. Заменяют фактические значения ряда, стоящие в центре каждого участка, на соответствующие средние значения.

При этом удобно брать длину интервала сглаживания в виде нечетного числа: , т.к. в этом случае полученные значения скользящей средней приходятся на средний член интервала.

Процедура сглаживания приводит к устранению периодических колебаний во временном ряду, если длина интервала сглаживания берется равной или кратной периоду колебаний.

Для устранения сезонных колебаний часто требуется использовать четырех- и двенадцатичленные скользящие средние, но при этом не будет выполняться условие нечетности длины интервала сглаживания.

При четной базе в сглаживаемой серии отсутствует член, соответствующий среднему промежутку времени. Нет промежутка, которому можно корректно приписать результат.

В таких ситуациях используют двухэтапное сглаживание. На первом этапе проводят сглаживание при четной длине интервала сглаживания (скажем, при ). Среднего промежутка времени здесь нет, и результат приписывают не точно середине, а со сдвигом на полпериода вперед или назад (например, назад). После этого проводят повторное сглаживание уже сглаженного ряда при длине интервала, который во всех случаях равен 2. База опять четная, и на этот раз результат опять сдвигают на полпериода, но в противоположную сторону (в нашем примере вперед). В итоге такой двухэтапной процедуры окончательный результат оказывается центрированным корректно.

При использовании скользящей средней с длиной активного участка первые и последние уровней ряда сгладить нельзя, их значения теряются.

1.5. Прогнозирование развития по линии тренда

Под тенденцией развития понимают общее направление развития, долговременную эволюцию. На практике для описания тенденции развития явления широко используются модели кривых роста, представляющие собой различные функции времени . При таком подходе изменение исследуемого показателя связывают лишь с течением времени; считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени.

Прогнозирование на основе модели кривой роста базируется на экстраполяции, т.е. на продлении в будущее тенденции, наблюдавшейся в прошлом. При этом предполагается, что во временном ряду присутствует тренд, характер развития показателя обладает свойством инерционности, сложившаяся тенденция не должна претерпевать существенных изменений в течение периода упреждения.

Прогнозирование на основе кривых роста предполагает выбор формы кривой, оценивание ее параметров, проверку адекватности, а также точечный и интервальный прогноз с помощью этой функции.

Наиболее распространенным вариантом кривой роста является полином:

, (4)

где

– параметры многочлена,

– независимая переменная (время), .

Коэффициенты полиномов невысоких степеней могут иметь конкретную интерпретацию в зависимости от содержания динамического ряда. Например, их можно трактовать как скорость роста ( ), ускорение роста ( ), изменение ускорения ( ), начальный уровень ряда при ( ).

Обычно в экономических исследованиях применяются полиномы не выше третьего порядка.

Оценки параметров в модели (4) определяются методом наименьших квадратов. Суть его состоит в нахождении таких параметров, при которых сумма квадратов отклонений расчетных значений уровней от фактических значений, была бы минимальной. Таким образом, эти оценки находятся в результате минимизации выражения:

где

– фактическое значение уровня временного ряда;

– расчетное значение;

– длина временного ряда.

В качестве другого варианта кривой роста можно рассмотреть простую показательную кривую, которая имеет вид:

. (6)

Если b, то кривая растет вместе с ростом , и падает, если . Параметр характеризует начальные условия развития, а параметр b – постоянный темп роста.

Существует несколько практических подходов, облегчающих процесс выбора формы кривой роста. Наиболее простой путь – визуальный анализ, опирающийся на изучение графического изображения временного ряда. Подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса.

На практике чаще всего к выбору формы кривой подходят исходя из значений критерия, в качестве которого принимают сумму квадратов отклонений фактических значений уровней от расчетных, получаемых выравниванием. Из рассматриваемых кривых предпочтение будет отдано той, которой соответствует минимальное значение критерия, т.к. чем меньше значение критерия, тем ближе к кривой ложатся данные наблюдений.

Также в качестве критерия выбора кривой роста используется средняя квадратическая ошибка:

(7)

где

– фактическое значение уровня ряда;

– расчетное значение уровня ряда, полученное по модели;

– длина ряда.

Средняя квадратическая ошибка всегда имеет положительное значение, которое уменьшается по мере приближения ошибки к нулю. Большее значение показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

Заключительным этапом применения кривых роста является экстраполяция тенденции на базе выбранного уравнения. Прогнозные значения исследуемого показателя вычисляют путем подстановки в уравнение кривой значений времени , соответствующих периоду упреждения. Полученный таким образом прогноз называют точечным, так как для каждого момента времени определяется только одно значение прогнозируемого показателя.

На практике в дополнении к точечному прогнозу желательно определить границы возможного изменения прогнозируемого показателя, задать «вилку» возможных значений прогнозируемого показателя, т.е. вычислить прогноз интервальный.

Несовпадение фактических данных с точечным прогнозом, полученным путем экстраполяции тенденции по кривым роста, может быть вызвано:

1. субъективной ошибочностью выбора вида кривой;

2. погрешностью оценивания параметров кривых;

3. погрешностью, связанной с отклонением отдельных наблюдений от тренда, характеризующего некоторый средний уровень ряда на каждый момент времени.

Погрешность, связанная со вторым и третьим источником, может быть отражена в виде доверительного интервала прогноза. Границы доверительного интервала, учитывающего неопределенность, связанную с положением тренда, и возможность отклонения от этого тренда, упрощенно определяется в виде:

, (8)

где

– расчетное значение уровня ряда, полученное по модели,

– средняя квадратическая ошибка,

– одно из чисел: 1, 2 или 3. При границы доверительного интервала обеспечивают приблизительно 68% надежность прогноза, при обеспечивается 95% надежность, при обеспечивается 99% надежность.

Построение модели сезонности с использование электронной таблицы Excel

В настоящее время существует большое количество программного обеспечения, специализирующегося именно на прогнозировании. Но и обычная электронная таблица Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. В данном разделе нашей работы мы выясним, что это за инструменты и постоим модель сезонности на практике.

В качестве исходных данных возьмем данные по объему перевозки пассажиров за 2019-2021 года.

Таблица 1.

Объем перевозки пассажиров за 2019-2021 года

Год	Квартал	Данные
2019	1 кв.	464,39
2 кв.	369,45
3 кв.	350,3
4 кв.	199,62
2020	1 кв.	809,63
2 кв.	440,88
3 кв.	501,51
4 кв.	327,26
2021	1 кв.	842,55
2 кв.	715,45
3 кв.	813,8
4 кв.	545,1

Задача прогнозирования заключается в том, чтобы вычислить прогнозные значения квартальных объемов перевозок за 2022 года при условии, что сохранятся существующие тенденции.

Как мы знаем решение любой задачи по анализу и прогнозированию временных рядов начинается с построения графика исследуемого показателя. Для этого перенесем исходные данные в Excel и построим график.

Рис. 1. Диаграмма «Данные по перевозкам»

Данный график наглядно демонстрируют устойчивые сезонные колебания при повышающемся тренде.

При изучении сезонности имеют дело с периодическим воздействием, связанным с календарным циклом. Эти воздействия рассматриваются как внешние по отношению к основным причинам, характеризующим поведение системы. Поэтому при изучении ряда сезонные колебания отделяют от тренда.

Построение прогноза предполагает:

Выявление обобщенных характеристик циклических колебаний.

Расчет трендового прогноза, выражающего общую тенденцию ряда.

Совмещение трендового прогноза с характеристиками циклических колебаний.

Такое построение может быть основано на аддитивной модели или на мультипликативной модели.

В обеих моделях (1), (3) предполагается, что исходный ряд данных представляет собой комбинацию трех составляющих:

– трендовая составляющая, характеризующая основную долговременную тенденцию ряда;

– циклическая (обычно сезонная) составляющая, характеризующая регулярно повторяющиеся изменения исходного ряда;

– остаточная составляющая, отражающая случайные воздействия (ее называют также ошибкой модели).

2.1. Построение аддитивной модели

Аддитивная модель предполагает, что к тренду ряда прибавляется циклическая составляющая в виде периодически изменяющегося дополнительного слагаемого, принимающего положительные и отрицательные значения. Значения, лежащие на линии тренда, в связи с этим увеличиваются в одни периоды времени (циклическая составляющая для таких периодов положительна) и уменьшаются в другие периоды времени (циклическая составляющая отрицательна). Средняя величина всех таких слагаемых, входящих в циклическую составляющую, за время одного цикла равна 0.

Пошаговая процедура построения аддитивной модели:

1. Устранение циклических колебаний из исходного ряда (сглаживание ряда методом скользящей средней по базе, равной длине цикла; в случае четной базы проведение двухэтапного сглаживания).

2. Выявление колебаний ряда (построение разности между исходным и сглаженным рядом).

3. Определение средних значений циклических характеристик (вычисление средних значений по однородным периодам).

4. Нормирование средних значений циклических характеристик (определение их среднего значения с последующим смещением всех характеристик на эту величину так, чтобы среднее значение смещенных характеристик было равно 0). Результат рассматривается как циклическая составляющая ряда .

5. Устранение циклической составляющей из исходного временного ряда (построение разности между исходным и циклическим рядом). Результатом является трендовая составляющая.

6. Выбор вида тренда и расчет его параметров (определение формулы тренда).

7. Расчет прогнозных значений по формуле тренда.

8. Наложение нормированных циклических характеристик на трендовый прогноз (их суммирование с трендовым прогнозом).

9. Построение графика исходного ряда, продолженного прогнозными значениями.

10. Построение доверительного интервала.

Полученные результаты при условии прогнозирования на 1 год вперед приведены ниже. Описание построения модели приведено в Приложении 1.

Рис. 2. Прогноз по аддитивной модели на основе экспоненциального тренда

Рис. 3. Прогноз по аддитивной модели на основе экспоненциального тренда с доверительным интервалом

2.2. Построение мультипликативной модели

В мультипликативной модели предполагается, что тренд ряда умножается на циклическую составляющую , имеющую вид периодически изменяющегося коэффициента, принимающего значения большие и меньшие единицы. Этот коэффициент увеличивает значения, лежащие на линии тренда, в те периоды времени, когда циклическая составляющая больше 1, и уменьшаются, в те периоды, когда циклическая составляющая меньше 1. Средняя величина всех таких слагаемых за время одного цикла равна 1.

Пошаговая процедура построения мультипликативной модели:

1. Устранение циклических колебаний из исходного ряда (сглаживание ряда методом скользящей средней по базе, равной длине цикла; в случае четной базы проведение двухэтапного сглаживания).

2. Выявление колебаний ряда (деление исходного ряда на сглаженный).

3. Определение средних значений циклических характеристик (вычисление средних значений по однородным периодам).

4. Нормирование средних значений циклических характеристик (определение их среднего значения с последующим смещением всех характеристик на эту величину так, чтобы среднее значение смещенных характеристик было равно 1). Результат рассматривается как циклическая составляющая ряда .

5. Устранение циклической составляющей из исходного временного ряда (деление исходного ряда на циклический).

6. Выбор вида тренда и расчет его параметров (определение формулы тренда).

7. Расчет прогнозных значений по формуле тренда.

8. Наложение нормированных циклических характеристик на трендовый прогноз (их перемножение с трендовым прогнозом).

9. Построение графика исходного ряда, продолженного прогнозными значениями.

10. Построение доверительного интервала.

Полученные результаты приведены ниже. Описание построения модели приведено в Приложении 2.

Рис. 4. Прогноз по мультипликативной модели на основе линейного и экспоненциального трендов

Рис. 5. Прогноз по мультипликативной модели на основе экспоненциального тренда с доверительным интервалом

ЗАКЛЮЧЕНИЕ

Статистические методы все шире проникают в экономическую практику. С развитием компьютеров, распространением пакетов прикладных программ эти методы вышли за стены учебных и научно-исследовательских институтов. Они стали важным инструментом в деятельности аналитических, плановых, маркетинговых отделов различных фирм и предприятий.

При прогнозировании часто исходят из того, что уровни временных рядов экономических показателей могут содержать следующие компоненты: тренд, сезонную, циклическую и случайную составляющие. В зависимости от способа сочетания этих компонент модели временных рядов делятся на аддитивные, мультипликативные или модели смешанного типа.

По результатам проведенного исследования были сделаны следующие выводы:

Статистические методы прогнозирования имеют важное практическое значение в современном мире.

Электронная таблица Excel имеет достаточно средств для быстрого построения разнообразных функций для выделения трендовой составляющей модели данных и для построения на этой основе прогноза.

Как мы увидели построение качественного прогноза – процесс весьма трудоемкий. Качественный прогноз может дать только качественная модель данных. Прогнозирование действительно помогает заглянуть за горизонт завтрашнего дня и тем приносит несомненную пользу в процессах принятия решений.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

Дуброва Т.А. Статистические методы прогнозирования в экономике: Учебное пособие, практикум, тесты, программа курса. – М.: Московский государственный университет экономики, статистики и информатики, 2004. – 136 с.

Литвинчук С.Ю. Информационные технологии в экономике. Анализ и прогнозирование временных рядов с помощью Excel: учебное пособие. – Нижний Новгород: Нижегородский государственный архитектурно-строительный университет, 2010. – 78 с. .

Кувайская Ю.Г. Статистические методы прогнозирования: учебное пособие.– Ульяновск: УлГТУ, 2019. – 197 с.

Приложение 1.

Построение аддитивной модели в электронной таблице Excel на основе линейного тренда

В исходные данные добавим столбец с порядковым номера квартала (). Учитываем, что мы хотим построить прогноз на 2022 год (4 шага вперед):

Подготовим шаблон модели в соответствии с шагами, описанными в разделе 2.1 работы.

ШАГ 1. Устранение циклических колебаний из исходного ряда .

Как мы увидели из графического анализа исходных данных, имеют место устойчивые циклические колебания. Потому необходимо провести сглаживание ряда методом скользящей средней (в наш случае длина интервала сглаживания равна 4). Так как длина интервала представляет собой четное число, то мы будем проводить двухэтапное сглаживание.

На первом этапе проведем сглаживание при определенной нами длине интервала ( ), результат укажем в ячейке Е5 со сдвигом на полпериода вперед. Для вычисления среднего значения воспользуемся встроенной функцией СРЗНАЧ, которая возвращает среднее арифметическое своих аргументов. В ячейку Е5 вводим функцию СРЗНАЧ со следующими аргументами:

и протягиваем ее до ячейки Е13. В результате получим сглаженные годовые данные.

Теперь проведем повторное сглаживание уже сглаженного ряда при длине интервала, равному 2. База опять четная, и на этот раз результат мы сдвинем на полпериода назад. В ячейку F6 вводим функцию СРЗНАЧ со следующими аргументами:

и протягиваем ее до ячейки F13. В результате получим сглаженные, центрированные корректно, годовые данные

ШАГ 2. Выявление колебаний ряда.

Для того, чтобы выделить сезонные колебания, необходимо из исходного ряда данных вычесть полученный на шаге 1 ряд сглаженных данных.

В ячейку G6 вводим формулу: «=D6-F6» и протягиваем ее до ячейки G13. В итоге мы получим сезонные колебания нашего исходного ряда.

ШАГ 3. Определение средних значений циклических характеристик.

Для каждого однородного периода найдем среднее значение сезонных колебаний. Для 1 квартала найдем среднее значение колебаний, относящихся к первому кварталу, для 2 кварталу – ко второму и т.д. В ячейку H16 вводим формулу «=СРЗНАЧ(G8;G12)», в ячейку H17 вводим формулу «=СРЗНАЧ(G9;G13)», в H18 – «=СРЗНАЧ(G6;G10)», в H19 – «=СРЗНАЧ(G7;G11)». Получим поквартальные средние значения циклических колебаний.

ШАГ 4. Нормирование средних значений циклических характеристик.

Определим среднее значение поквартальных средних значений циклических колебаний. В ячейку H2 вводим формулу: «=СРЗНАЧ(H16:H19)».

Получаем среднее значение, равное -5. Смещаем все характеристики поквартальных средних значений циклические колебаний на эту величину так, чтобы среднее значение смещенных характеристик было равно 0.

В ячейку I16 вводим формулу: «=H16-$H$2», закрепляя ячейку H2 и протягиваем ее до ячейки I19. В итоге мы получим нормированные средние значения сезонных колебаний.

Проверим, что среднее значение нормированных поквартальных средних значений циклических колебаний равняется 0. В ячейку I2 вводим формулу: =СРЗНАЧ(I16:I19)». Результатом вычисления является 0.

В итоге мы получили – циклическую составляющую исходного ряда . Внесем полученные данные в соответствующий столбец.

ШАГ 5. Устранение циклической составляющей из исходного временного ряда .

Для устранения цикличности и построения обессезоненного ряда данных необходимо построить разность между исходным рядом и циклическим рядом . В ячейку К4 вводим формулу «=D4-J4» и протягиваем ее до ячейки К15. В результате получим обессезоненную составляющую исходного ряда.

Отобразим на диаграмме полученные на Шагах 1-5 данные: исходные данные , сезонную составляющую и обессезоненные данные.

ШАГ 6. Выбор вида тренда и расчет его параметров (определение формулы тренда).

Средство построения диаграмм и графиков Excel автоматически строит линии тренда и автоматически рассчитывает его параметры. Обратим внимание, что линию тренда нельзя добавить в объемную, лепестковую, круговую и кольцевую диаграммы, а также в диаграмму с накоплением.

Для построения линии тренда необходимо сначала построить график обессезоненных данных. Для этого выделим в таблице столбец обессезоненных данных вместе с заголовком, затем во вкладке «Вставка» в блоке «Диаграммы» выберем пункт «Вставить график» и тип «График с маркерами».

С помощью кнопки блока «Диаграммы» перенесем диаграмму на отдельный лист.

Чтобы по этому ряду данных построить линию тренда, выполним следующие действия.

Щелкнем по графику правой клавишей мыши, чтобы вызвать контекстное меню .

Выбираем раздел «Добавить линию тренда», чтобы открыть диалоговое окно «Формат линия тренда»:

В диалоговом окне «Формат линии тренда» выберем тип линии тренда. Для выбора предоставляются следующие типы линии тренда:

Экспоненциальная,

Линейная,

Логарифмическая,

Полиномиальная,

Степенная,

Линейная фильтрация.

Если ряд данных содержит нулевые или отрицательные значения, то линии тренда Экспоненциальная и Степенная будут недоступны.

В диалоговом окне «Формат линии тренда» также предлагается:

определить название линии тренда, которое будут включено в легенду,

задать количество периодов, на которые будут прогнозироваться данные (вперед и назад).

Три дополнительные опции позволяют отобразить на диаграмме:

пересечение линии тренда с осью Y (опция Пересечение кривой с осью Y в точке);

уравнение линии тренда (опция Показывать уравнение на диаграмме);

значение коэффициента детерминации , определяющее достоверность аппроксимации (опция Поместить на диаграмму величину достоверности аппроксимации (R^2)).

Построим линейную, степенную и экспоненциальную линии тренда с отображением уравнения и коэффициента детерминации на 4 месяца вперед.

Коэффициент детерминации характеризует степень близости линии тренда к исходным данным. Он может принимать значения от 0 до 1. Чем больше его значение, тем лучше линия тренда аппроксимирует исходные данные.

Как мы видим ближе всего к 1 значение коэффициента детерминации у степенной линии тренда.

На основе полученных уравнений можно рассчитать точечный прогноз путем подстановки в уравнение кривой значений времени , соответствующие периоду упреждения.

ШАГ 7. Расчет прогнозных значений по формуле тренда.

Прогнозирование с помощью встроенных функций Excel предоставляет большие возможности, чем графические средства.

Для быстрого вычисления прогнозных значений переменной без явного построения функции тренда используют статистические функции РОСТ и ТЕНДЕНЦИЯ.

Функция ТЕНДЕНЦИЯ возвращает значения в соответствии с линейным трендом.

Функция РОСТ рассчитывает прогнозируемый экспоненциальный рост на основе имеющихся данных.

Функции ТЕНДЕНЦИЯ и РОСТимеют одинаковый синтаксис:

=ТЕНДЕНЦИЯ(Известные_значения_Y; [Известные_значения_Х]; [Новые_значения_х]; [Конст])

=РОСТ(Известные_значения_Y; [Известные_значения_Х]; [Новые_значения_х]; [Конст]),

где

Известные_значения_Y – обязательный аргумент. Множество значений переменной Y, которые уже известны;

Известные_значения_Х – обязательный аргумент. Множество значений факторов;

Новые_значения_х – обязательный аргумент. Значения факторов, для которых вычисляется прогнозное значение;

Константа – необязательный аргумент.

Если в функциях ТЕНДЕНЦИЯ и РОСТ аргумент Известные_значения_Х опущен, то предполагается, что это массив натуральных чисел {1; 2; 3; …} такого же размера, как и массив аргумента Известные_значения_Y. Если опущен аргумент Новые_значения_х, то по умолчанию предполагается, что он совпадает с аргументом Известные_значения_Х.

Рассчитаем прогнозные значения с помощью функции ТЕНДЕНЦИЯ (сделаем прогноз на основе линейного тренда). Для этого в ячейку L4 введем функцию ТЕНДЕНЦИЯ со следующими аргументами, предварительно закрепив нужные диапазоны данных, где

Известные_значения_Y – множество обессезоненных данных (диапазон данных $K$4:$K$15);

Известные_значения_Х – множество значений периодов (диапазон данных $A$4:$A$15);

Новые_значения_х – значения времени , соответствующие периоду построения прогноза (значение ячейки A4).

Протягиваем формулу до ячейки L19. Таким образом, мы получим – трендовую составляющую исходного ряда , рассчитанную на основе линейного тренда.

ШАГ 8. Наложение нормированных циклических характеристик на трендовый прогноз.

Построим окончательный прогноз на основе линейного тренда, для этого сложим сезонную и трендовые составляющие. В ячейку М4 введем формулу: «=L4+J4» и протянем ее до ячейки M19. В итоге получим прогнозные значения.

ШАГ 9. Построение графика исходного ряда, продолженного прогнозными значениями.

Построим графики исходного ряда и полученных прогнозных значений. Для этого выделим два столбца соответствующих данных вместе с заголовками, затем во вкладке «Вставка» в блоке «Диаграммы» выберем пункт «Вставить график» и тип «График с маркерами».

ШАГ 10. Построение доверительного интервала.

На данном шаге мы определим границы возможного изменения прогнозируемого показателя, зададим «вилку» возможных значений прогнозируемых показателей, т.е. вычислим прогноз интервальный.

Границы доверительного интервала, учитывающего неопределенность, связанную с положением тренда, и возможность отклонения от этого тренда, упрощенно определяется в виде:

где

– расчетное значение уровня ряда, полученное по модели,

– средняя квадратическая ошибка,

– одно из чисел: 1, 2 или 3. При границы доверительного интервала обеспечивают приблизительно 68% надежность прогноза, при обеспечивается 95% надежность, при обеспечивается 99% надежность.

В работе мы рассмотрели формулу средней квадратической ошибки:

где

– фактическое значение уровня ряда;

– расчетное значение уровня ряда, полученное по модели;

– длина ряда.

Для расчета средней квадратической ошибки воспользуемся встроенной в Excel функцией СУММКВРАЗН, которая возвращает сумму квадратов разностей соответствующих значений в двух массивах и встроенной функцией СЧЕТ, которая подсчитывает количество ячеек, содержащих числа.

Функция СУММКВРАЗН имеет следующий синтаксис:

СУММКВРАЗН(массив_x; массив_y)

где

Массив_x – обязательный аргумент. Первый массив или диапазон значений;

Массив_y – обязательный аргумент. Второй массив или диапазон значений.

Введем в ячейку N2 формулу: «=(СУММКВРАЗН(D4:D15;M4:M15)/(СЧЁТ($D:$D)-2))^0,5». Таким образом, мы рассчитаем среднюю квадратическую ошибку.

Ограничим ввод данных в ячейке О2. Мы хотим, чтобы в нее можно было вводить только числа 1, 2 или 3. Для этого выделяем эту ячейку, затем во вкладке «Данные» в блоке «Работа с данными» выберем пункт «Проверка данных» и подпункт «Проверка данных».

В диалоговом окне «Проверка вводимых значений» во вкладке «Параметры» задаем следующие ограничения:

Во вкладках «Сообщение для ввода» и «Сообщение об ошибке» следующие данные:

Теперь в ячейку О2 мы сможем внести только значения 1, 2 или 3.

Осталось только отобразить в ячейке Р2 надежность нашего доверительного интервала. Сделаем это при помощи функции ЕСЛИ, которая возвращает одно значение, если указанное условие дает в результате значение ИСТИНА, и другое значение, если условие дает в результате значение ЛОЖЬ.

Функция ЕСЛИ имеет следующий синтаксис:

ЕСЛИ(лог_выражение; [значение_если_истина]; [значение_если_ложь])

Лог_выражение – обязательный аргумент. Любое значение или выражение, дающее в результате значение ИСТИНА или ЛОЖЬ. В этом аргументе может использоваться любой оператор сравнения.

Значение_если_истина – необязательный аргумент. Значение, которое возвращается, если аргумент лог_выражение соответствует значению ИСТИНА. Если аргумент лог_выражение соответствует значению ИСТИНА, а аргумент значение_если_истина опущен (т.е. после аргумента лог_выражение есть только запятая), возвращается значение 0.

Значение_если_ложь – необязательный аргумент. Значение, которое возвращается, если аргумент лог_выражение соответствует значению ЛОЖЬ. Если аргумент лог_выражение соответствует значению ЛОЖЬ, а аргумент значение_если_ложь опущен (т.е. после аргумента значение_если_истина нет запятой), функция ЕСЛИ возвращает логическое значение ЛОЖЬ. Если аргумент лог_выражение соответствует значению ЛОЖЬ, а значение аргумента значение_если_ложь пусто (т. е. после аргумента значение_если_истина стоит только запятая), функция ЕСЛИ возвращает значение 0 (ноль).

Введем в ячейку Р2 функцию если со следующими параметрами:

Теперь при значении , в ячейке Р2 отобразится 68%, при значении – 95%, при – значение 99%.

Построим доверительный интервал при надежности 95%.

Для построения нижней границы доверительного интервала введем в ячейку N4 формулу: «=$M4-$N$2*$O$2», закрепив при этом необходимые ячейки, и протянем ее до ячейки N19. Таким образом мы найдем значения нижней границы доверительного интервала.

Для построения верхней границы доверительного интервала введем в ячейку О4 формулу: «=$M4+$N$2*$O$2», закрепив при этом необходимые ячейки, и протянем ее до ячейки О19. Таким образом мы найдем значения верхней границы доверительного интервала.

Наша аддитивная модель сезонности на основе линейного тренда построена. Осталось только изобразить ее графически. Добавим на диаграмму, полученную на шаге 9, верхнюю и нижнюю границы доверительного интервала. Для этого выделим соответствующие столбцы данных вместе с заголовками, скопируем их, перейдем на лист с диаграммой и нажнем кнопку «Вставить». Соответствующие графики отобразятся на исходной диаграмме.

Построение аддитивной модели в электронной таблице Excel на основе экспоненциального тренда

Подготовим шаблон модели в соответствии с шагами, описанными в разделе 2.1 работы.

Повторим Шаги с 1 по 6, описанные первом разделе данного приложения.

ШАГ 7. Расчет прогнозных значений по формуле тренда.

Прогнозирование с помощью встроенных функций Excel предоставляет большие возможности, чем графические средства.

Для быстрого вычисления прогнозных значений переменной без явного построения функции тренда используют статистические функции РОСТ и ТЕНДЕНЦИЯ.

Функция ТЕНДЕНЦИЯ возвращает значения в соответствии с линейным трендом.

Функция РОСТ рассчитывает прогнозируемый экспоненциальный рост на основе имеющихся данных.

Функции ТЕНДЕНЦИЯ и РОСТимеют одинаковый синтаксис:

=ТЕНДЕНЦИЯ(Известные_значения_Y; [Известные_значения_Х]; [Новые_значения_х]; [Конст])

=РОСТ(Известные_значения_Y; [Известные_значения_Х]; [Новые_значения_х]; [Конст]),

где

Известные_значения_Y – обязательный аргумент. Множество значений переменной Y, которые уже известны;

Известные_значения_Х – обязательный аргумент. Множество значений факторов;

Новые_значения_х – обязательный аргумент. Значения факторов, для которых вычисляется прогнозное значение;

Константа – необязательный аргумент.

Если в функциях ТЕНДЕНЦИЯ и РОСТ аргумент Известные_значения_Х опущен, то предполагается, что это массив натуральных чисел {1; 2; 3; …} такого же размера, как и массив аргумента Известные_значения_Y. Если опущен аргумент Новые_значения_х, то по умолчанию предполагается, что он совпадает с аргументом Известные_значения_Х.

Рассчитаем прогнозные значения с помощью функции РОСТ (сделаем прогноз на основе экспоненциального тренда). Для этого в ячейку L4 введем функцию РОСТ со следующими аргументами, предварительно закрепив нужные диапазоны данных, где

Известные_значения_Y – множество обессезоненных данных (диапазон данных $K$4:$K$15);

Известные_значения_Х – множество значений периодов (диапазон данных $A$4:$A$15);

Новые_значения_х – значения времени , соответствующие периоду построения прогноза (значение ячейки A4).

Протягиваем формулу до ячейки L19. Таким образом, мы получим – трендовую составляющую исходного ряда , рассчитанную на основе экспоненциального тренда.

ШАГ 8. Наложение нормированных циклических характеристик на трендовый прогноз.

Построим окончательный прогноз на основе экспоненциального тренда, для этого сложим сезонную и трендовые составляющие. В ячейку М4 введем формулу: «=L4+J4» и протянем ее до ячейки M19. В итоге получим прогнозные значения.

ШАГ 9. Построение графика исходного ряда, продолженного прогнозными значениями.

Построим графики исходного ряда и полученных прогнозных значений. Для этого выделим два столбца соответствующих данных вместе с заголовками, затем во вкладке «Вставка» в блоке «Диаграммы» выберем пункт «Вставить график» и тип «График с маркерами».

ШАГ 10. Построение доверительного интервала.

На данном шаге мы определим границы возможного изменения прогнозируемого показателя, зададим «вилку» возможных значений прогнозируемых показателей, т.е. вычислим прогноз интервальный.

Границы доверительного интервала, учитывающего неопределенность, связанную с положением тренда, и возможность отклонения от этого тренда, упрощенно определяется в виде:

,

где

– расчетное значение уровня ряда, полученное по модели,

– средняя квадратическая ошибка,

– одно из чисел: 1, 2 или 3. При границы доверительного интервала обеспечивают приблизительно 68% надежность прогноза, при обеспечивается 95% надежность, при обеспечивается 99% надежность.

В работе мы рассмотрели формулу средней квадратической ошибки:

где

– фактическое значение уровня ряда;

– расчетное значение уровня ряда, полученное по модели;

– длина ряда.

Для расчета средней квадратической ошибки воспользуемся встроенной в Excel функцией СУММКВРАЗН, которая возвращает сумму квадратов разностей соответствующих значений в двух массивах и встроенной функцией СЧЕТ, которая подсчитывает количество ячеек, содержащих числа.

Функция СУММКВРАЗН имеет следующий синтаксис:

СУММКВРАЗН(массив_x; массив_y)

где

Массив_x – обязательный аргумент. Первый массив или диапазон значений;

Массив_y – обязательный аргумент. Второй массив или диапазон значений.

Введем в ячейку N2 формулу: «=(СУММКВРАЗН(D4:D15;M4:M15)/(СЧЁТ($D:$D)-2))^0,5». Таким образом, мы рассчитаем среднюю квадратическую ошибку.

Ограничим ввод данных в ячейке О2. Мы хотим, чтобы в нее можно было вводить только числа 1, 2 или 3. Для этого выделяем эту ячейку, затем во вкладке «Данные» в блоке «Работа с данными» выберем пункт «Проверка данных» и подпункт «Проверка данных».

В диалоговом окне «Проверка вводимых значений» во вкладке «Параметры» задаем следующие ограничения:

Теперь в ячейку О2 мы сможем внести только значения 1, 2 или 3.

Осталось только отобразить в ячейке Р2 надежность нашего доверительного интервала. Сделаем это при помощи функции ЕСЛИ, которая возвращает одно значение, если указанное условие дает в результате значение ИСТИНА, и другое значение, если условие дает в результате значение ЛОЖЬ.

Функция ЕСЛИ имеет следующий синтаксис:

ЕСЛИ(лог_выражение; [значение_если_истина]; [значение_если_ложь])

Лог_выражение – обязательный аргумент. Любое значение или выражение, дающее в результате значение ИСТИНА или ЛОЖЬ. В этом аргументе может использоваться любой оператор сравнения.

Значение_если_истина – необязательный аргумент. Значение, которое возвращается, если аргумент лог_выражение соответствует значению ИСТИНА. Если аргумент лог_выражение соответствует значению ИСТИНА, а аргумент значение_если_истина опущен (т.е. после аргумента лог_выражение есть только запятая), возвращается значение 0.

Значение_если_ложь – необязательный аргумент. Значение, которое возвращается, если аргумент лог_выражение соответствует значению ЛОЖЬ. Если аргумент лог_выражение соответствует значению ЛОЖЬ, а аргумент значение_если_ложь опущен (т.е. после аргумента значение_если_истина нет запятой), функция ЕСЛИ возвращает логическое значение ЛОЖЬ. Если аргумент лог_выражение соответствует значению ЛОЖЬ, а значение аргумента значение_если_ложь пусто (т. е. после аргумента значение_если_истина стоит только запятая), функция ЕСЛИ возвращает значение 0 (ноль).

Введем в ячейку Р2 функцию если со следующими параметрами:

Теперь при значении , в ячейке Р2 отобразится 68%, при значении – 95%, при – значение 99%.

Построим доверительный интервал при надежности 95%.

Для построения нижней границы доверительного интервала введем в ячейку N4 формулу: «=$M4-$N$2*$O$2», закрепив при этом необходимые ячейки, и протянем ее до ячейки N19. Таким образом мы найдем значения нижней границы доверительного интервала.

Для построения верхней границы доверительного интервала введем в ячейку О4 формулу: «=$M4+$N$2*$O$2», закрепив при этом необходимые ячейки, и протянем ее до ячейки О19. Таким образом мы найдем значения верхней границы доверительного интервала.

Наша аддитивная модель сезонности на основе экспоненциального тренда построена. Осталось только изобразить ее графически. Добавим на диаграмму, полученную на шаге 9, верхнюю и нижнюю границы доверительного интервала. Для этого выделим соответствующие столбцы данных вместе с заголовками, скопируем их, перейдем на лист с диаграммой и нажнем кнопку «Вставить». Соответствующие графики отобразятся на исходной диаграмме.

Приложение 2.

Построение мультипликативной модели в электронной таблице Excel на основе линейного и экспоненциального трендов

В исходные данные добавим столбец с порядковым номера квартала (). Учитываем, что мы хотим построить прогноз на 2022 год (4 шага вперед):

Подготовим шаблон модели в соответствии с шагами, описанными в разделе 2.2 работы.

ШАГ 1. Устранение циклических колебаний из исходного ряда .

Как мы увидели из графического анализа исходных данных, имеют место устойчивые циклические колебания. Потому необходимо провести сглаживание ряда методом скользящей средней (в наш случае длина интервала сглаживания равна 4). Так как длина интервала представляет собой четное число, то мы будем проводить двухэтапное сглаживание.

На первом этапе проведем сглаживание при определенной нами длине интервала ( ), результат укажем в ячейке Е5 со сдвигом на полпериода вперед. Для вычисления среднего значения воспользуемся встроенной функцией СРЗНАЧ, которая возвращает среднее арифметическое своих аргументов. В ячейку Е5 вводим функцию СРЗНАЧ со следующими аргументами:

Теперь проведем повторное сглаживание уже сглаженного ряда при длине интервала, равному 2. База опять четная, и на этот раз результат мы сдвинем на полпериода назад. В ячейку F6 вводим функцию СРЗНАЧ со следующими аргументами:

и протягиваем ее до ячейки F13. В результате получим сглаженные, центрированные корректно, годовые данные

Ш

АГ 2. Выявление колебаний ряда.

Для того, чтобы выделить сезонные колебания, необходимо разделить исходный ряд данных на полученный на шаге 1 ряд сглаженных данных.

ШАГ 3. Определение средних значений циклических характеристик.

Для каждого однородного периода найдем среднее значение сезонных колебаний. Для 1 квартала найдем среднее значение колебаний, относящихся к первому кварталу, для 2 кварталу – ко второму и т.д. В ячейку H16 вводим формулу «=СРЗНАЧ(G8;G12)», в ячейку H17 вводим формулу «=СРЗНАЧ(G9;G13)», в H18 – «=СРЗНАЧ(G6;G10)», в H19 – «=СРЗНАЧ(G7;G11)». Получим поквартальные средние значения циклических колебаний.

ШАГ 4. Нормирование средних значений циклических характеристик.

Определим среднее значение поквартальных средних значений циклических колебаний. В ячейку H2 вводим формулу: «=СРЗНАЧ(H16:H19)».

Получаем среднее значение, равное 0,9797. Смещаем все характеристики поквартальных средних значений циклические колебаний на эту величину так, чтобы среднее значение смещенных характеристик было равно 1.

В ячейку I16 вводим формулу: «=H16/$H$2», закрепляя ячейку H2 и протягиваем ее до ячейки I19. В итоге мы получим нормированные средние значения сезонных колебаний.

Проверим, что среднее значение нормированных поквартальных средних значений циклических колебаний равняется 1. В ячейку I2 вводим формулу: =СРЗНАЧ(I16:I19)». Результатом вычисления является 1.

В итоге мы получили – циклическую составляющую исходного ряда . Внесем полученные данные в соответствующий столбец.

ШАГ 5. Устранение циклической составляющей из исходного временного ряда .

Отобразим на диаграмме полученные на Шагах 1-5 данные: исходные данные , сезонную составляющую и обессезоненные данные.

Так как значения ряда сезонности изменяется в диапазоне от 0 до 2, то диаграмма в таком виде неинформативна. Добавим для данного ряда значений дополнительную ось. Для этого выделим диаграмму, затем в пункте меню «Работа с диаграммами» во вкладке «Конструктор» в блоке «Тип» нажимаем кнопку «Изменить тип диаграммы». Во всплывающем диалоговом окне «Изменение типа диаграммы» переходим на вкладку «Вид диаграммы». Выбираем вид – комбинированная и напротив ряда данных «Сезонность» указываем необходимость наличия дополнительной оси.

Получим более информативный график, на котором видно цикличность изменения ряда данных сезонности.

ШАГ 6. Выбор вида тренда и расчет его параметров (определение формулы тренда).

Средство построения диаграмм и графиков Excel автоматически строит линии тренда и автоматически рассчитывает его параметры. Обратим внимание, что линию тренда нельзя добавить в объемную, лепестковую, круговую и кольцевую диаграммы, а также в диаграмму с накоплением.

Для построения линии тренда необходимо сначала построить график обессезоненных данных. Для этого выделим в таблице столбец обессезоненных данных вместе с заголовком, затем во вкладке «Вставка» в блоке «Диаграммы» выберем пункт «Вставить график» и тип «График с маркерами».

С помощью кнопки блока «Диаграммы» перенесем диаграмму на отдельный лист.

Чтобы по этому ряду данных построить линию тренда, выполним следующие действия.

Щелкнем по графику правой клавишей мыши, чтобы вызвать контекстное меню .

Выбираем раздел «Добавить линию тренда», чтобы открыть диалоговое окно «Формат линия тренда»:

.

В диалоговом окне «Формат линии тренда» выберем тип линии тренда. Для выбора предоставляются следующие типы линии тренда:

Экспоненциальная,

Линейная,

Логарифмическая,

Полиномиальная,

Степенная,

Линейная фильтрация.

Если ряд данных содержит нулевые или отрицательные значения, то линии тренда Экспоненциальная и Степенная будут недоступны.

В диалоговом окне «Формат линии тренда» также предлагается:

определить название линии тренда, которое будут включено в легенду,

задать количество периодов, на которые будут прогнозироваться данные (вперед и назад).

Три дополнительные опции позволяют отобразить на диаграмме:

пересечение линии тренда с осью Y (опция Пересечение кривой с осью Y в точке);

уравнение линии тренда (опция Показывать уравнение на диаграмме);

значение коэффициента детерминации , определяющее достоверность аппроксимации (опция Поместить на диаграмму величину достоверности аппроксимации (R^2)).

Построим линейную, степенную и экспоненциальную линии тренда с отображением уравнения и коэффициента детерминации на 4 месяца вперед.

Коэффициент детерминации характеризует степень близости линии тренда к исходным данным. Он может принимать значения от 0 до 1. Чем больше его значение, тем лучше линия тренда аппроксимирует исходные данные.

Как мы видим ближе всего к 1 значение коэффициента детерминации у экспоненциальной линии тренда.

На основе полученных уравнений можно рассчитать точечный прогноз путем подстановки в уравнение кривой значений времени , соответствующие периоду упреждения.

2.1 Построение мультипликативной модели в электронной таблице Excel на основе линейного тренда

ШАГ 7. Расчет прогнозных значений по формуле тренда.

Прогнозирование с помощью встроенных функций Excel предоставляет большие возможности, чем графические средства.

Для быстрого вычисления прогнозных значений переменной без явного построения функции тренда используют статистические функции РОСТ и ТЕНДЕНЦИЯ.

Функция ТЕНДЕНЦИЯ возвращает значения в соответствии с линейным трендом.

Функция РОСТ рассчитывает прогнозируемый экспоненциальный рост на основе имеющихся данных.

Функции ТЕНДЕНЦИЯ и РОСТимеют одинаковый синтаксис:

=ТЕНДЕНЦИЯ(Известные_значения_Y; [Известные_значения_Х]; [Новые_значения_х]; [Конст])

=РОСТ(Известные_значения_Y; [Известные_значения_Х]; [Новые_значения_х]; [Конст]),

где

Известные_значения_Y – обязательный аргумент. Множество значений переменной Y, которые уже известны;

Известные_значения_Х – обязательный аргумент. Множество значений факторов;

Новые_значения_х – обязательный аргумент. Значения факторов, для которых вычисляется прогнозное значение;

Константа – необязательный аргумент.

Если в функциях ТЕНДЕНЦИЯ и РОСТ аргумент Известные_значения_Х опущен, то предполагается, что это массив натуральных чисел {1; 2; 3; …} такого же размера, как и массив аргумента Известные_значения_Y. Если опущен аргумент Новые_значения_х, то по умолчанию предполагается, что он совпадает с аргументом Известные_значения_Х.

Рассчитаем прогнозные значения с помощью функции ТЕНДЕНЦИЯ (сделаем прогноз на основе линейного тренда). Для этого в ячейку L4 введем функцию ТЕНДЕНЦИЯ со следующими аргументами, предварительно закрепив нужные диапазоны данных, где

Известные_значения_Y – множество обессезоненных данных (диапазон данных $K$4:$K$15);

Известные_значения_Х – множество значений периодов (диапазон данных $A$4:$A$15);

Новые_значения_х – значения времени , соответствующие периоду построения прогноза (значение ячейки A4).

Протягиваем формулу до ячейки L19. Таким образом, мы получим – трендовую составляющую исходного ряда , рассчитанную на основе линейного тренда.

ШАГ 8. Наложение нормированных циклических характеристик на трендовый прогноз.

П
остроим окончательный прогноз на основе линейного тренда, для этого перемножим сезонную и трендовые составляющие. В ячейку М4 введем формулу: «=L4*J4» и протянем ее до ячейки M19. В итоге получим прогнозные значения.

ШАГ 9. Построение графика исходного ряда, продолженного прогнозными значениями.

Построим графики исходного ряда и полученных прогнозных значений. Для этого выделим два столбца соответствующих данных вместе с заголовками, затем во вкладке «Вставка» в блоке «Диаграммы» выберем пункт «Вставить график» и тип «График с маркерами».

ШАГ 10. Построение доверительного интервала.

На данном шаге мы определим границы возможного изменения прогнозируемого показателя, зададим «вилку» возможных значений прогнозируемых показателей, т.е. вычислим прогноз интервальный.

Границы доверительного интервала, учитывающего неопределенность, связанную с положением тренда, и возможность отклонения от этого тренда, упрощенно определяется в виде:

,

где

– расчетное значение уровня ряда, полученное по модели,

– средняя квадратическая ошибка,

– одно из чисел: 1, 2 или 3. При границы доверительного интервала обеспечивают приблизительно 68% надежность прогноза, при обеспечивается 95% надежность, при обеспечивается 99% надежность.

В работе мы рассмотрели формулу средней квадратической ошибки:

где

– фактическое значение уровня ряда;

– расчетное значение уровня ряда, полученное по модели;

– длина ряда.

Для расчета средней квадратической ошибки воспользуемся встроенной в Excel функцией СУММКВРАЗН, которая возвращает сумму квадратов разностей соответствующих значений в двух массивах и встроенной функцией СЧЕТ, которая подсчитывает количество ячеек, содержащих числа.

Функция СУММКВРАЗН имеет следующий синтаксис:

СУММКВРАЗН(массив_x; массив_y)

где

Массив_x – обязательный аргумент. Первый массив или диапазон значений;

Массив_y – обязательный аргумент. Второй массив или диапазон значений.

Введем в ячейку N2 формулу: «=(СУММКВРАЗН($D$4:$D$15;M4:M15)/(СЧЁТ($D:$D)-2))^0,5». Таким образом, мы рассчитаем среднюю квадратическую ошибку.

Ограничим ввод данных в ячейке О2. Мы хотим, чтобы в нее можно было вводить только числа 1, 2 или 3. Для этого выделяем эту ячейку, затем во вкладке «Данные» в блоке «Работа с данными» выберем пункт «Проверка данных» и подпункт «Проверка данных».

В диалоговом окне «Проверка вводимых значений» во вкладке «Параметры» задаем следующие ограничения:

Теперь в ячейку О2 мы сможем внести только значения 1, 2 или 3.

Осталось только отобразить в ячейке T2 надежность нашего доверительного интервала. Сделаем это при помощи функции ЕСЛИ, которая возвращает одно значение, если указанное условие дает в результате значение ИСТИНА, и другое значение, если условие дает в результате значение ЛОЖЬ.

Функция ЕСЛИ имеет следующий синтаксис:

ЕСЛИ(лог_выражение; [значение_если_истина]; [значение_если_ложь])

Лог_выражение – обязательный аргумент. Любое значение или выражение, дающее в результате значение ИСТИНА или ЛОЖЬ. В этом аргументе может использоваться любой оператор сравнения.

Значение_если_истина – необязательный аргумент. Значение, которое возвращается, если аргумент лог_выражение соответствует значению ИСТИНА. Если аргумент лог_выражение соответствует значению ИСТИНА, а аргумент значение_если_истина опущен (т.е. после аргумента лог_выражение есть только запятая), возвращается значение 0.

Значение_если_ложь – необязательный аргумент. Значение, которое возвращается, если аргумент лог_выражение соответствует значению ЛОЖЬ. Если аргумент лог_выражение соответствует значению ЛОЖЬ, а аргумент значение_если_ложь опущен (т.е. после аргумента значение_если_истина нет запятой), функция ЕСЛИ возвращает логическое значение ЛОЖЬ. Если аргумент лог_выражение соответствует значению ЛОЖЬ, а значение аргумента значение_если_ложь пусто (т. е. после аргумента значение_если_истина стоит только запятая), функция ЕСЛИ возвращает значение 0 (ноль).

Введем в ячейку T2 функцию если со следующими параметрами:

Теперь при значении , в ячейке T2 отобразится 68%, при значении – 95%, при – значение 99%.

Построим доверительный интервал при надежности 95%.

Для построения нижней границы доверительного интервала введем в ячейку N4 формулу: «=$M4-$N$2*$O$2», закрепив при этом необходимые ячейки, и протянем ее до ячейки N19. Таким образом мы найдем значения нижней границы доверительного интервала.

Для построения верхней границы доверительного интервала введем в ячейку О4 формулу: «=$M4+$N$2*$O$2», закрепив при этом необходимые ячейки, и протянем ее до ячейки О19. Таким образом мы найдем значения верхней границы доверительного интервала.

Наша мультипликативная модель сезонности на основе линейного тренда построена. Осталось только изобразить ее графически. Добавим на диаграмму, полученную на шаге 9, верхнюю и нижнюю границы доверительного интервала. Для этого выделим соответствующие столбцы данных вместе с заголовками, скопируем их, перейдем на лист с диаграммой и нажнем кнопку «Вставить». Соответствующие графики отобразятся на исходной диаграмме.

Построение мультипликативной модели в электронной таблице Excel на основе экспоненциального тренда

ШАГ 7. Расчет прогнозных значений по формуле тренда.

Прогнозирование с помощью встроенных функций Excel предоставляет большие возможности, чем графические средства.

Для быстрого вычисления прогнозных значений переменной без явного построения функции тренда используют статистические функции РОСТ и ТЕНДЕНЦИЯ.

Функция ТЕНДЕНЦИЯ возвращает значения в соответствии с линейным трендом.

Функция РОСТ рассчитывает прогнозируемый экспоненциальный рост на основе имеющихся данных.

Функции ТЕНДЕНЦИЯ и РОСТимеют одинаковый синтаксис:

=ТЕНДЕНЦИЯ(Известные_значения_Y; [Известные_значения_Х]; [Новые_значения_х]; [Конст])

=РОСТ(Известные_значения_Y; [Известные_значения_Х]; [Новые_значения_х]; [Конст]),

где

Известные_значения_Y – обязательный аргумент. Множество значений переменной Y, которые уже известны;

Известные_значения_Х – обязательный аргумент. Множество значений факторов;

Новые_значения_х – обязательный аргумент. Значения факторов, для которых вычисляется прогнозное значение;

Константа – необязательный аргумент.

Если в функциях ТЕНДЕНЦИЯ и РОСТ аргумент Известные_значения_Х опущен, то предполагается, что это массив натуральных чисел {1; 2; 3; …} такого же размера, как и массив аргумента Известные_значения_Y. Если опущен аргумент Новые_значения_х, то по умолчанию предполагается, что он совпадает с аргументом Известные_значения_Х.

Рассчитаем прогнозные значения с помощью функции РОСТ (сделаем прогноз на основе экспоненциального тренда). Для этого в ячейку Р4 введем функцию РОСТ со следующими аргументами, предварительно закрепив нужные диапазоны данных, где

Известные_значения_Y – множество обессезоненных данных (диапазон данных $K$4:$K$15);

Известные_значения_Х – множество значений периодов (диапазон данных $A$4:$A$15);

Новые_значения_х – значения времени , соответствующие периоду построения прогноза (значение ячейки A4).

Протягиваем формулу до ячейки P19. Таким образом, мы получим – трендовую составляющую исходного ряда , рассчитанную на основе экспоненциального тренда.

ШАГ 8. Наложение нормированных циклических характеристик на трендовый прогноз.

Построим окончательный прогноз на основе экспоненциального тренда, для этого перемножим сезонную и трендовые составляющие. В ячейку Q4 введем формулу: «=P4*J4» и протянем ее до ячейки Q19. В итоге получим прогнозные значения.

ШАГ 9. Построение графика исходного ряда, продолженного прогнозными значениями.

Построим графики исходного ряда и полученных прогнозных значений. Для этого выделим два столбца соответствующих данных вместе с заголовками, затем во вкладке «Вставка» в блоке «Диаграммы» выберем пункт «Вставить график» и тип «График с маркерами».

ШАГ 10. Построение доверительного интервала.

На данном шаге мы определим границы возможного изменения прогнозируемого показателя, зададим «вилку» возможных значений прогнозируемых показателей, т.е. вычислим прогноз интервальный.

Границы доверительного интервала, учитывающего неопределенность, связанную с положением тренда, и возможность отклонения от этого тренда, упрощенно определяется в виде:

,

где

– расчетное значение уровня ряда, полученное по модели,

– средняя квадратическая ошибка,

– одно из чисел: 1, 2 или 3. При границы доверительного интервала обеспечивают приблизительно 68% надежность прогноза, при обеспечивается 95% надежность, при обеспечивается 99% надежность.

В работе мы рассмотрели формулу средней квадратической ошибки:

где

– фактическое значение уровня ряда;

– расчетное значение уровня ряда, полученное по модели;

– длина ряда.

Для расчета средней квадратической ошибки воспользуемся встроенной в Excel функцией СУММКВРАЗН, которая возвращает сумму квадратов разностей соответствующих значений в двух массивах и встроенной функцией СЧЕТ, которая подсчитывает количество ячеек, содержащих числа.

Функция СУММКВРАЗН имеет следующий синтаксис:

СУММКВРАЗН(массив_x; массив_y)

где

Массив_x – обязательный аргумент. Первый массив или диапазон значений;

Массив_y – обязательный аргумент. Второй массив или диапазон значений.

Введем в ячейку R2 формулу: «=(СУММКВРАЗН($D$4:$D$15;Q4:Q15)/(СЧЁТ($D:$D)-2))^0,5». Таким образом, мы рассчитаем среднюю квадратическую ошибку.

Ограничим ввод данных в ячейке S2. Мы хотим, чтобы в нее можно было вводить только числа 1, 2 или 3. Для этого выделяем эту ячейку, затем во вкладке «Данные» в блоке «Работа с данными» выберем пункт «Проверка данных» и подпункт «Проверка данных».

В диалоговом окне «Проверка вводимых значений» во вкладке «Параметры» задаем следующие ограничения:

Теперь в ячейку S2 мы сможем внести только значения 1, 2 или 3.

Осталось только отобразить в ячейке U2 надежность нашего доверительного интервала. Сделаем это при помощи функции ЕСЛИ, которая возвращает одно значение, если указанное условие дает в результате значение ИСТИНА, и другое значение, если условие дает в результате значение ЛОЖЬ.

Функция ЕСЛИ имеет следующий синтаксис:

ЕСЛИ(лог_выражение; [значение_если_истина]; [значение_если_ложь])

Лог_выражение – обязательный аргумент. Любое значение или выражение, дающее в результате значение ИСТИНА или ЛОЖЬ. В этом аргументе может использоваться любой оператор сравнения.

Значение_если_истина – необязательный аргумент. Значение, которое возвращается, если аргумент лог_выражение соответствует значению ИСТИНА. Если аргумент лог_выражение соответствует значению ИСТИНА, а аргумент значение_если_истина опущен (т.е. после аргумента лог_выражение есть только запятая), возвращается значение 0.

Значение_если_ложь – необязательный аргумент. Значение, которое возвращается, если аргумент лог_выражение соответствует значению ЛОЖЬ. Если аргумент лог_выражение соответствует значению ЛОЖЬ, а аргумент значение_если_ложь опущен (т.е. после аргумента значение_если_истина нет запятой), функция ЕСЛИ возвращает логическое значение ЛОЖЬ. Если аргумент лог_выражение соответствует значению ЛОЖЬ, а значение аргумента значение_если_ложь пусто (т. е. после аргумента значение_если_истина стоит только запятая), функция ЕСЛИ возвращает значение 0 (ноль).

Введем в ячейку U2 функцию если со следующими параметрами:

Теперь при значении , в ячейке U2 отобразится 68%, при значении – 95%, при – значение 99%.

Построим доверительный интервал при надежности 99%.

Для построения нижней границы доверительного интервала введем в ячейку R4 формулу: «=$Q4-$R$2*$S$2», закрепив при этом необходимые ячейки, и протянем ее до ячейки R19. Таким образом мы найдем значения нижней границы доверительного интервала.

Для построения верхней границы доверительного интервала введем в ячейку S4 формулу: «=$Q4+$R$2*$S$2», закрепив при этом необходимые ячейки, и протянем ее до ячейки S19. Таким образом мы найдем значения верхней границы доверительного интервала.

Наша мультипликативная модель сезонности на основе экспоненциального тренда построена. Осталось только изобразить ее графически. Добавим на диаграмму, полученную на шаге 9, верхнюю и нижнюю границы доверительного интервала. Для этого выделим соответствующие столбцы данных вместе с заголовками, скопируем их, перейдем на лист с диаграммой и нажнем кнопку «Вставить». Соответствующие графики отобразятся на исходной диаграмме.

Просмотров работы: 31