В excel функция вычисления коэффициента корреляции входит в группу логических функций

Урок учителя информатики ГБОУ «Гимназия №8 им. Н.Т.
Хрусталева»

Бартош Светланы Александровны

Тема: Корреляционное
моделирование.

Цель урока:

Научиться находить зависимость
между величинами, в которых она выражена неявно, и научить производить расчеты
коэффициента корреляции при помощи MS  Excel.

Задачи урока:

Образовательные: систематизация представлений
учащихся по информационному моделированию, демонстрация применения метода информационному
моделирования для решения прикладных задач, установление и констатация связи
наук математика-экономика-информатика;

Развивающие: развитие системно-аналитического
стиля мышления (на основе использования анализа, сравнения, обобщения,
формализации информации, выявление причинно-следственных связей), развитие
умения принимать обдуманные, рациональные решения;

Воспитательные: повышение уровня компьютерной и экономической
грамотности учащихся.

Тип урока: комбинированный урок

Техническое обеспечение урока: компьютеры с операционной системой Windows
XP, раздаточный материал (задания группам, листы для выполнения практической
работы), мультимедийный проектор, презентация.

Формы обучения: фронтальная, индивидуальная, групповая.

Приемы обучения: словесные, наглядные, практические, работа с
учебником, выполнение практических заданий, тестирование.

Содержание
урока

1.    
Организационный момент

2.    
Актуализация опорных
знаний

3.    
Изучение нового материала:
теоретическая часть

4.    
Практическая работа

5.    
Физминутка

6.    
Закрепление полученных
знаний.

7.    
Подведение итогов

8.    
Домашнее задание

9.    
Рефлексия

Ход урока

Организационный момент

Актуализация опорных знаний

Фронтальная беседа

Сегодня мы продолжим изучать раздел «Информационное
моделирование» и мне хотелось бы начать изучение новой темы с актуализации
опорных знаний, полученных вами на предыдущих уроках. Давайте вспомним:

Ø
Какие бывают виды
зависимостей между величинами? (Прямая пропорциональность, обратная
пропорциональность)

Ø
Перечислите способы
отображения зависимостей между величинами. (математическая модель, табличная
модель, графическая модель, динамическая модель)

Ø
Что такое статистика?
(Статистика – наука о сборе, измерении и анализе массовых количественных
данных)

Ø
В чём заключается
функциональная зависимости между величинами? (Можно подобрать функцию,
связывающую две величины.)

Рассмотрим несколько примеров связанных между собой
величин. (Рассматриваем таблицы, ищем зависимости, строим графики. Первая
таблица – по графику делаем вывод о прямой зависимости. Вторая зависимость –
говорим, что график не показывает зависимость, но мы предполагаем, что она
есть.)

Давайте сделаем вывод: существуют такие величины,
зависимость между которым не  видна явно на графике, но с такими величинами
тоже надо уметь работать.

Изучение нового материала

Давайте попробуем сформулировать цель сегодняшнего
урока. (Ученики формулируют цель: научиться находить зависимость между
величинами, которая выражена неявно)

Раздел моделирования, который занимается неявной
зависимостью между величинами, называется Корреляционное моделирование
– и это тема сегодняшнего урока.

Для реализации цели нам необходимо сформулировать задачи, которые мы
постарается достигнуть сегодня на уроке. (Ученики формулируют задачи урока: изучить
теоретический материал темы; рассмотреть технические приёмы, применяемые в
корреляционном моделировании; на практике научиться находить корреляционную
зависимость между  величинам).

Работа в группах

Задание №1: Просмотрите фрагмент видеоурока. Используя полученные
данные и материал учебника (§ 19 с. 121), дайте ответы на вопросы:

Группа А

1.      Что такое корреляционная зависимость? (Корреляционная
зависимость – это зависимость между величинами, каждая из которых подвергается
неконтролируемому полностью разбросу.)

2.      Какие задачи решает корреляционный анализ? (Определяет,
оказывает ли один фактор существенное влияние на другой фактор; позволяет
выбрать из нескольких факторов наиболее существенный.)

3.      Как обозначается и в каком диапазоне
определяется количественная мера корреляции? (Коэффициент корреляции: ρ[-1;1])

Группа Б

1.      Что такое корреляционный анализ? (Корреляционный
анализ – это раздел математической статистики, который исследует корреляционные
зависимости.)

2.      Какая величина является количественной мерой
корреляции? (Количественной мерой корреляционной зависимости является
коэффициент корреляции.)

3.      Что показывает количественная мера корреляции?
(Если | ρ |1 – корреляционная зависимость сильная, | ρ |0 – корреляционная
зависимость слабая; ρ>0 – прямая зависимость, ρ<0 – обратная зависимость.)

Группы поочередно докладывают результаты
работы

Давайте теперь попробуем вычислить коэффициент
корреляции на уже знакомом нам примере. (Подробно представляется вычисление
коэффициента корреляции)

Давайте попробуем сделать вывод о нашей зависимости,
проанализировав коэффициент корреляции. (Зависимость прямая и средняя. Делаем
вывод, что от оснащённости школы зависит желание учиться, а значит и средний
балл)

Практическая работа

Метод моделирования ситуации

Представьте, что вы не просто ученики 11 класса, а
финансовые аналитики двух крупных конкурирующих фирм. Доходы ваших фирм в
последние годы начали резко падать. Ваша задача:

Задание №2: Подсчитать коэффициент корреляции между расходами на
рекламу и полиграфию и прибылью предприятия за период с 2012 по 2016 года.
Сделать вывод о зависимости между величинами. Предложить стратегию для
повышения прибыли фирмы.

Индивидуальная работа за ПК

Я прошу вас индивидуально разместиться за компьютерами
и, пользуясь заданиями, которые находятся около них, провести корреляционный
анализ имеющихся в вашем распоряжении данных. После этого вернитесь в свои
группы, сформулируйте выводы и предложите выигрышную стратегию. (Слежу, чтобы
дети делали чёткие выводы.)

Работа в группах: анализ, сравнение и обобщение полученных
индивидуально данных.

Группы докладывают результаты работы

Учащиеся делают выводы о важности определения
корреляции

Физминутка

Психоэмоциональная разгрузка с элементами
гимнастики для глаз

Закрепление полученных знаний

Индивидуальная работа

Ученики пересаживаются за компьютеры и выполняют тест
в программе MyTestStudent.

Тест

Задание # 1

Вопрос:

Что характеризует коэффициент корреляции?

Выберите один из 3 вариантов ответа:

1) характеризует величину отражающую степень отдалённости
двух переменных между собой

2) характеризует величину отражающую степень
приближённости двух переменных между собой

3) характеризует величину отражающую степень
взаимосвязи двух переменных между собой

Задание # 2

Вопрос:

В Excel функция вычисления коэффициента
корреляции входит в группу … функций

Выберите один из 4 вариантов ответа:

1) логических

2) статистических

3) математических

4) финансовых

Задание # 3

Вопрос:

Какая зависимость называется корреляционной?

Выберите один из 3 вариантов ответа:

1) это зависимость между величинами, каждая из которых
линейно зависит от другой

2) это зависимость между величинами, каждая из которых
подвергается неконтролируемому разбросу

3) это зависимость между величинами, каждая из которых
функционально зависит от другой

Задание # 4

Вопрос:

Если в процессе решения задачи получили
коэффициент корреляции равный 0,28. О чём это говорит?

Выберите один из 3 вариантов ответа:

1) Что зависимость слабая

2) Зависимость отсутствует

3) Что зависимость сильная

Задание # 5

Вопрос:

Какой буквой обозначается и какие значения
может принимать коэффициент корреляции?

Выберите один из 3 вариантов ответа:

1) 

2) 

3) 

Ответы:

1) Верный ответ (1 б.): 3;

2) Верный ответ (1 б.): 2;

3) Верный ответ (1 б.): 2;

4) Верный ответ (1 б.): 1;

5) Верный ответ (1 б.): 3;

(Подвожу итоги, собираю данные теста в диаграмму)

Исходя из полученных вами итогов, можно сделать вывод,
что тема освоена классом на _______ уровне.

Подведение итогов

Фронтальная беседа

Учащиеся делают выводы по теме

Домашнее задание

1.    
§ 19 читать и учить,
выполнить № 3 с. 126

2.    
Подготовить сообщение на
тему:

a.    
«Профессии, связанные с
корреляционным анализом»

b.   
«Самые интересные
корреляционные зависимости»

Рефлексия

Подводя итоги сегодняшнего урока, мне бы хотелось,
чтобы каждый из вас провёл самоанализ и самостоятельно оценил свою работу на
уроке.

Урок №__________ 11 класс Дата_____________

Конспект урока по информатике

Тема: «Корреляционное моделирование. Корреляционная зависимость. Корреляционный анализ. Коэффициент корреляции»

Цель урока:

Научиться находить зависимость между величинами, в которых она выражена неявно, и научить производить расчеты коэффициента корреляции при помощи MS Excel.

Задачи урока:

Образовательные: систематизация представлений учащихся по информационному моделированию, демонстрация применения метода информационному моделирования для решения прикладных задач, установление и констатация связи наук математика-экономика-информатика;

Развивающие: развитие системно-аналитического стиля мышления (на основе использования анализа, сравнения, обобщения, формализации информации, выявление причинно-следственных связей), развитие умения принимать обдуманные, рациональные решения;

Воспитательные: повышение уровня компьютерной и экономической грамотности учащихся.

Тип урока: комбинированный урок

Техническое обеспечение урока: компьютеры, раздаточный материал (листы для выполнения практической работы), мультимедийный проектор, презентация, тетради, учебники.

Формы обучения: фронтальная, индивидуальная.

Приемы обучения: словесные, наглядные, практические, работа с учебником, выполнение практических заданий, тестирование.

Ход урока

1. Организационный момент

2. Актуализация опорных знаний, проверка домашнего задания

• Что называют статистикой? (Наука о сборе, измерении и анализе массовых количественных данных).

• Что называется регрессионной моделью? (Регрессионная модель, есть, прежде всего, гипотеза, которая должна быть подвергнута статистической проверке, после чего, она принимается, или отвергается. График функций, проходящий вблизи экспериментальных точек, где отклонения должны быть минимальными и равномерными).

• Что подразумевается под восстановлением значения по регрессионной модели? (Прогноз, производимый в пределах экспериментальных значений независимой переменной, называется восстановлением значения по регрессионной модели)

• Что такое экстраполяция? (Прогнозирование за пределами экспериментальных данных называется экстраполяция).

• Для чего используется регрессионная модель? (Для прогнозирования).

1. Изучение нового материала:

Регрессионные математические модели строятся в тех случаях, когда известно, что зависимость между двумя факторами существует и требуется получить ее математическое описание. Давайте рассмотрим задачи другого рода. Пусть важной характеристикой некоторой сложной системы является фактор A, на него могут оказывать влияние одновременно многие другие факторы: B, C, D и так далее.

Рассмотрим два типа задач:

1) Требуется, определить, оказывает ли фактор В какое-либо заметное регулярное влияние на фактор А?

2) Какие из факторов B, C, D и так далее оказывают наибольшее влияние на фактор А?

В качестве примера сложной системы рассмотрим школу. Пусть, для первого типа задач фактором А, является средняя успеваемость учащихся школы, фактором В финансовые расходы школы на хозяйственные нужды: ремонт здания, обновление мебели, эстетическое оформление помещения и т. п. Здесь влияние фактора В на фактор А не очевидно. Наверное, гораздо сильнее на успеваемость влияют другие, причины: уровень квалификации учителей, контингент учащихся, уровень технических средств обучения и другие.

Специалисты по статистике знают, что для того, чтобы выявить зависимость от какого-то определенного фактора, нужно максимально исключить влияние других факторов. Проще говоря, собирая, информацию из разных школ, нужно выбирать такие школы., в которых приблизительно одинаковый контингент учеников, квалификация учителей и пр., нехозяйственные расходы школ разные (у одних школ могут быть богатые спонсоры, у других— нет).

Статистической называют зависимость, при которой каждому значению одной случайной величины соответствует свое распределение другой. Частным случаем статистической зависимости является корреляционная (от лат. correlation — соотношение, взаимосвязь) зависимость, когда изменение одной из случайных величин влечет изменение среднего значения другой.

Корреляционный анализ — это проверка гипотез о связях между переменными с использованием коэффициентов корреляции.

Коэффициент корреляции — это мера прямой или обратной пропорциональности между двумя переменными. Он чувствителен к связи только в том случае, если эта связь является монотонной, то есть не меняет направления по мере увеличения значений одной из переменных.

Итак, пусть хозяйственные расходы школы выражаются количеством рублей, отнесенных к числу учеников в школе (руб./чел.), потраченных за определенный период времени (например, за последние 5 лет). Успеваемость же, пусть оценивается средним баллом учеников школы по результатам окончания последнего учебного года (Таблица 1).

Итоги сбора данных по 20 школам, введенные в электронную таблицу, представлены на рис. 1.

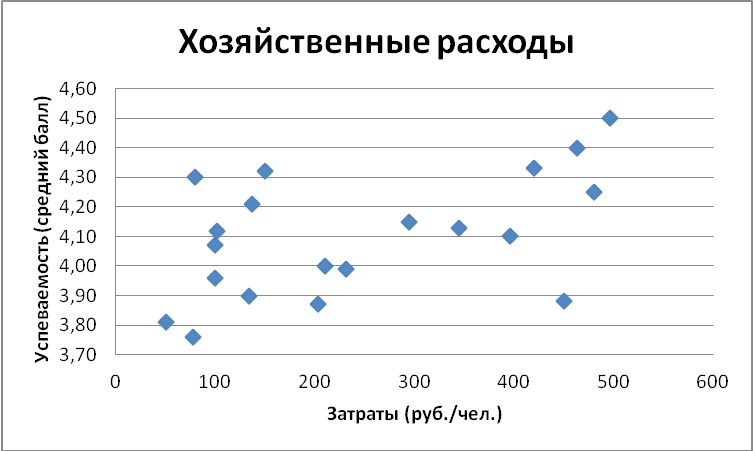
Рис. 1.

На рис. 1 приведена точечная диаграмма, построенная по этим данным, достаточно знать следующее: коэффициент корреляции (обычно обозначаемый греческой буквой р) есть число, заключенное в диапазоне, если это число по модулю близко к 1, то имеет место сильная корреляция, если к 0, то слабая: близость ρ к +1 означает, что возрастанию одного набора значений соответствует возрастание другого набора, близость к -1 означает обратное: значение р легко найти с помощью MS Excel без всяких, формул (разумеется, потому, что в MS Excel они встроены).

В Excel функция вычисления коэффициента корреляции называется КОРРЕЛ и входит в группу статистических функций. Как же ей воспользоваться? Установим курсор на любую свободную ячейку и запустим функцию КОРРЕЛ. Она запросит два диапазона значений. Укажем В2:В21 и С2:С21. После их ввода выведется ответ: р= 0,500273843. Эта величина говорит о среднем: уровне корреляции.

Наличие зависимости между хозяйственными затратами школы и успеваемостью нетрудно понять. Ученики с удовольствием: ходят в чистую, красивую, уютную школу, чувствуют там себя, как дома, и поэтому лучше учатся.

В следующем примере проводится исследование по определению зависимости успеваемости учащихся старших классов от двух факторов: обеспеченности школьной библиотеки учебниками и обеспеченности школы компьютерами. И та и другая характеристика количественно выражаются в процентах от нормы. Нормой обеспеченности учебниками является их полный комплект, то есть такое количество, когда каждому ученику выдаются из библиотеки все нужные ему для учебы: книги. Нормой обеспеченности компьютерами будем считать такое их количество, при котором на каждые четыре старшеклассника в школе приходится: один: компьютер. Предполагается, что компьютерами ученики пользуются не только на информатике, но и на других уроках, а также во внеурочное время.

В таблице 2, приведены результаты измерения обоих факторов в 10 разных школах. Напомним, что влияние каждого фактора исследуется независимо от других (то есть влияние других существенных факторов должно быть приблизительно одинаковым).

Значения обеих величин: финансовых затрат и успеваемости учеников имеют значительный разброс и, на первый взгляд, взаимосвязи между ними не видно. Однако она вполне может существовать.

Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционнными зависимостями.

Раздел математической статистики, который исследует такие зависимости, называется корреляиионным анализом. Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру такой зависимости.

Оценку корреляции величин начинают с высказывания гипотезы о возможном характере зависимости между их значениями. Чаще всего допускают наличие линейной зависимости. В таком случае мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции. Как и прежде, мы не будем писать формулы, по которым он вычисляется; их написать нетрудно, гораздо труднее понять, почему они именно такие.

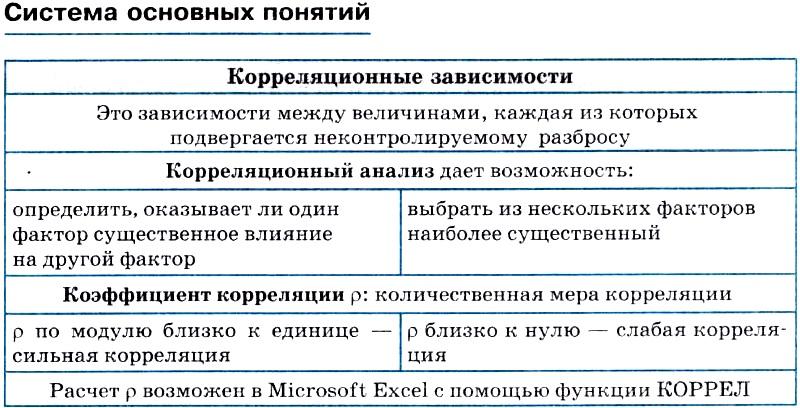
Таблица 4. Сравнение двух корреляционных зависимостей

Для обеих зависимостей получены коэффициенты линейной корреляции, как видно из таблицы, корреляция между обеспеченностью учебниками и успеваемостью сильнее, чем корреляция между компьютерным обеспечением, и. успеваемостью (хотя и тот и другой коэффициенты корреляции не очень большие). Отсюда можно сделать вывод, что пока, еще книга остается более значительным источником знаний, чем компьютер.

Физминутка

Практическая работа. ТБ.

Повторить технику безопасности при работе за компьютером.

Алгоритм действий по выполнению работы описан в практической работе. Расчет корреляционных зависимостей в MS Excel – с помощью функции КОРРЕЛ получить расчеты корреляционной зависимости величин, создать график. Все задания смотрите в практическом задании.

1. Оценки за практическую работу.

2. Закрепление полученного материала.

(Работа с учебником). Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными. С помощью корреляционного анализа можно решить следующие задачи:

• определить, оказывает ли один фактор существенное влияние на другой фактор;

• из нескольких факторов выбрать наиболее существенный фактор.

Количественной мерой корреляции двух величин является коэффициент корреляции.

Значение коэффициента корреляции лежит между -1 И +1. Чем его значение ближе по модулю к 1, тем корреляция (связь) сильнее.

В MS Excel для определения коэффициента корреляции используется функция КОРРЕЛ из группы статистических функций.

4.Рефлексация

5. Подведение итогов урока, выставление оценок

6. Домашнее задание:

Читать §__________с.____________, отвечать на вопросы, _____________________________________

Прежде чем приступить к изучению новой
темы, давайте повторим некоторые важные моменты из прошлых уроков.

Итак, в течение последних нескольких
уроков мы с вами изучаем «Информационное моделирование». Как вы помните, в информационной
модели отражаются знания человека об объекте моделирования. А информационная
модель – это описание в той или иной форме объекта моделирования.

Математические модели также относятся к
информационным моделям. Математической моделью называется совокупность
математических соотношений, уравнений, неравенств, описывающих основные
закономерности изучаемого объекта, процесса или явления.

Статистика
— это род практической деятельности людей цель, которой сбор, обработка и
анализ информации.

Также на прошлых уроках мы научились
строить математическую модель по статистическим данным, а затем делать прогноз
по полученной модели методом вычислений.

Есть два способа прогнозирования по
регрессионной модели.

Первый способ.
Если прогноз рассчитывается в пределах экспериментальных значений независимой
переменной. Такой прогноз называется восстановлением значения.

Второй способ.
Если прогноз рассчитывается за пределами экспериментальных данных. Такой
прогноз называется экстраполяцией.

То есть на прошлых уроках, при построении
регрессионной математической модели, мы с вами точно знали, что зависимость
между двумя факторами существует.

А что делать, если нужно рассмотреть и построить
модель по сложно системе? В которой на один важный фактор влияют многие другие
факторы?

Сегодня на уроке мы с вами будем
разбираться со следующими вопросами:

·       Что
такое корреляционная зависимость?

·       Какие
возможности даёт корреляционный анализ?

·       А
также разберёмся, какие задачи можно решать с помощью корреляционного анализа.

Важнейшей целью статистики является
изучение объективно существующих связей между явлениями. Например,
на прошлом уроке мы рассматривали связь между содержанием угарного газа в
воздухе и числом заболевших людей астмой.

В ходе статистического исследования связей
между явлениями, необходимо показать причинно-следственные зависимости между
показателями, т.е. насколько изменение одних показателей зависит от изменения
других показателей. В нашем примере как влияет увеличение содержания угарного
газа в воздухе на число больных астмой.

Существует два вида зависимостей. Вам уже
хорошо знакомая — функциональная (если определённому значению переменной «x»
соответствует строго определённое значение «y»).

Помните, мы рассматривали зависимость пути
от времени.

Однако далеко не всегда зависимость может
быть простой (или относительно простой). Часто случается так, что данному
значению одной величины соответствует целый ряд значений другой, причём при
изменении данной величины меняются и другие значения, а также и его среднее.

В таких случаях говорят о корреляционной
зависимости.

Корреляционная зависимость
– это зависимость между величинами, каждая из которых подвергается
неконтролируемому разбросу.

Образцовым примером такой зависимости
является связь между ростом отцов и детей. Конечно, у высокого отца может быть
низкорослый сын, а у низкорослого — высокий, но в большинстве случаев
прослеживается склонность увеличения роста детей с увеличением роста отцов.

Также примерами корреляционных
зависимостей являются: зависимость между количеством удобрений и урожайностью,
спросом на товары и ценой на рынке. Зависимость стажа работы на
производительность труда рабочего.

Естественно, стаж влияет на
производительность, но он не может определять её полностью, так как на
производительность также влияют квалификация и образование рабочего, возраст и
его состояние здоровья, да и другие факторы.

То есть можно сделать вывод, что стаж
далеко не единственный фактор производительности. И связь между этими
переменными – корреляционная.

Раздел математической статистики, который
исследует корреляционные зависимости, называется корреляционным анализом.

Пусть важным свойством какой-то сложной
системы является фактор А.

На А могут оказывать влияние многие другие
факторы, например, B, C
и D.

При изучении корреляционных зависимостей
мы рассмотрим два вида задач.

Первый вид
– Оказывает ли фактор В какое-либо заметное постоянное влияние на фактор А?

И второй – Какие из
факторов B, C
или D оказывают наибольшее
влияние на фактор А?

Рассмотрим пример сложной системы на
предприятии: здесь факторам А будет производительность труда
рабочих, то есть количество продукции, выпущенной работниками за единицу
времени.

Фактором B
рассмотрим так называемую «Энерговооружённость труда», то есть
количество всех видов энергии (электрической, тепловой и других), приходящееся
на какую-либо производственную единицу.

Специалисты по статистике знают, что для
того, чтобы выявить зависимость от какого-то определённого фактора, нужно
максимально исключить влияние других факторов. Иначе говоря, мы будем
рассматривать предприятия, которые занимаются выпуском подобной продукции, но с
разной энерговооружённостью. То есть предприятие может быть прибыльным или
убыточным. Иметь широкий рынок сбыта продукции, или узкий.

Будем рассматривать производительность
труда в тысячах рублей и энерговооружённость в киловаттах, в расчёте на одного
работающего, для 14 предприятий.

Напомним, статистические данные являются
относительными или усреднёнными.

Итак, перед нами таблица сбора данных по
14 предприятиям. Построим по этим данным точечную диаграмму. Для этого выделяем
диапазон ячеек А2 B 15. На вкладке Вставка в
разделе Диаграммы выбираем тип диаграммы – точечная, вид – точечная с
маркерами.

Обратите внимание, значения обеих величин:
производительность труда и энерговооружённость – имеют существенный разброс. И
кажется, что никакой взаимосвязи между ними нет, но она вполне может быть.

Мы получили графическое представление
корреляционной зависимости.

Корреляционный анализ
изучает вероятностную зависимость каждой из величин, при которой изменение
одной величины ведёт к изменению распределения другой, а также меру такой
зависимости.

Оценку корреляции величин начинают с
высказывания гипотезы о возможном характере зависимости между их значениями.

Чаще всего считают, что это линейная
зависимость. Тогда мера корреляционной зависимости – это величина, которая
называется коэффициентом корреляции.

Коэффициент корреляции (обычно обозначают
греческой буквой ƍ) характеризует величину отражающую степень взаимосвязи
двух переменных между собой.

Он может изменяться в пределах от -1 до
+1. (здесь и далее читать: единица)

Если ƍ равно нулю то, это говорит об
отсутствии корреляционных связей между величинами. Причём, если ƍ близко к
1 (или -1) то говориться о сильной корреляции, а если близко к 0, то о слабой.

Если ƍ близко к + 1, то это означает
что при увеличении (или уменьшении) значений одной переменной будет
закономерное увеличение (или уменьшение) другой переменной т.е. взаимосвязи
типа увеличение-увеличение (или уменьшение-уменьшение).

Если ƍ близко к — 1, то это означает,
что при увеличении (или уменьшении) значений одной переменной будет
закономерное уменьшение (или увеличение) другой переменной т.е. взаимосвязи
типа увеличение-уменьшение (уменьшение-увеличение).

Для построения корреляционных
зависимостей, а также для вычисления коэффициента корреляции ƍ удобно
пользоваться табличным процессором Excel.

В Excel функция вычисления коэффициента
корреляции называется CORREL
и входит в группу статистических функций.

Давайте вычислим коэффициент корреляции
для нашей зависимости.

Поместим курсор в любую свободную ячейку, например,
B 17. Теперь на вкладке Формулы в
разделе Библиотека функций нажимаем вставить функцию. В открывшемся окне
мастера функций введём в окошко Поиск функции название функции CORREL
и нажимаем поиск. Далее в окошке Выберите функцию нажимаем два раза мышкой по
необходимой нам функции. В открывшемся окне функции CORREL
в окошко Массив 1 укажем диапазон значений для фактора А, то есть А2 А15. В
окошко Массив 2 укажем диапазон значений для фактора B,
то есть B 2 B
15. И нажимаем Ок.

Теперь в ячейке Бэ 17 мы увидим ответ: ƍ
равно ноль целых восемьсот девяносто восемь тысяч триста девяносто четыре
миллионных (0, 898394)

Эта величина находится ближе к плюс
единице, следовательно, можно сделать вывод, что корреляция сильная.

Наличие зависимости между производительность
труда рабочих и энерговооружённостью нетрудно понять. Рабочие с удовольствием
будут работать на предприятии, где сделан ремонт, обновлено и исправно рабочее
оборудование, в помещениях хорошее освещение. На таких предприятиях люди работают
легко и с удовольствием и, естественно, производительность их труда будет выше.

А сейчас давайте повторим главные моменты
из сегодняшнего урока:

·       Корреляционная
зависимость – это зависимость между величинами,
каждая из которых подвергается неконтролируемому разбросу.

·       Раздел
математической статистики, который исследует корреляционные зависимости,
называется корреляционным анализом.

·       Коэффициент
корреляции ƍ, характеризует величину отражающую степень
взаимосвязи двух переменных между собой. Он может изменяться в пределах от -1
до +1.