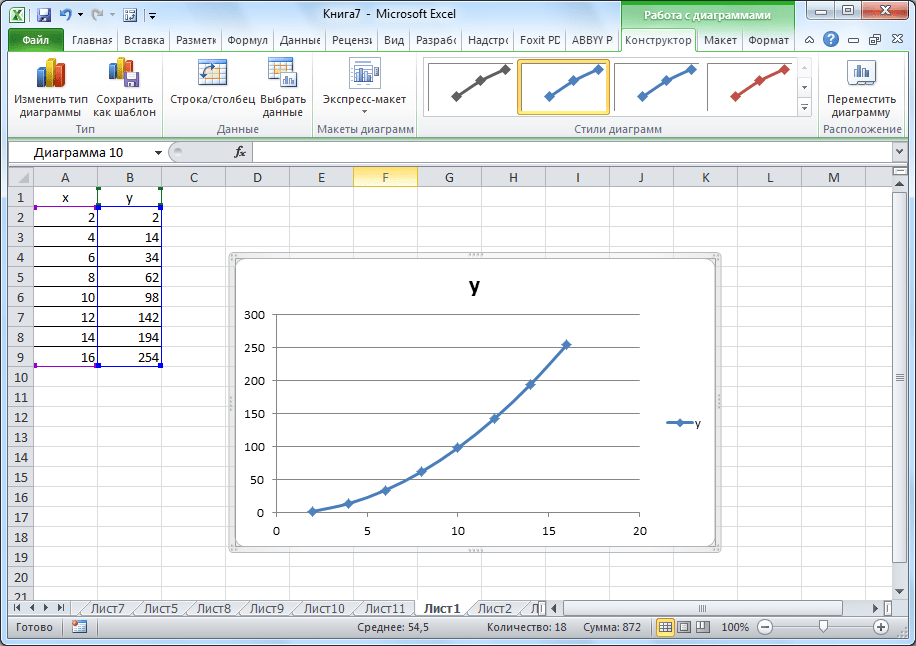
Табличные
данные часто удобнее и нагляднее
представить в виде графиков и диаграмм.
Для создания диаграммы выделяют
прямоугольный блок таблицы, в него
включаются числовые значения, по которым
должен быть построен график. Могут быть
также включены левый столбец с
наименованиями строк и верхняя строка
с наименованиями столбцов — программа
автоматически распознает их как
соответствующие надписи. Выделяемый
для построения графиков блок может
иметь разрывы, тогда используется
клавиша Ctrl.
4 способа создания
диаграмм
-
нажатием
клавиши F11
Excel
автоматически создает новый лист
рабочей книги левее листа с таблицей,
лист называется «Диаграмма», на нем —
автоматически построенная оптимальная
с точки зрения Excel
диаграмма -
с
помощью главного меню Вставка Диаграмма
На одном листе или На отдельном листе
и далее вызывается мастер диаграмм -
с
помощью панели инструментов Диаграмма
(Вид Панель инструментов Диаграмма) -
кнопкой
Мастер диаграмм на стандартной панели
инструментов
5
шагов мастера диаграмм
-
подтверждение
или изменение блока данных (диапазона)
для построения диаграммы -
выбор
типа диаграммы — двумерные (круговая,
кольцевая, график, смешанная, точечная
и т.п.) или трехмерные -
для
заданного типа выбирается вид диаграммы
(например, для круговой — с вырезанной
частью, с указанием процентов и т.п.) -
приводится
примерный вид диаграммы и некоторые
диалоги, например, подтвердить, что
первый столбец — названия секторов
круговой диаграммы и т.п. -
элементы
оформления диаграммы — вводится название
диаграммы, легенда — каким цветом какие
позиции обозначены, названия координатных
осей
Диаграмма
размещается в указанной области — на
том листе, где таблица, или на отдельном
листе.
При
использовании панели «Диаграмма» — она
имеет 1 поле для выбора типа диаграммы
и 4 кнопки- создание диаграммы выбранного
типа, мастер диаграмм (работает в два
шага — выбор диапазона данных и ввод
надписей), кнопка для построения
горизонтальной сетки, кнопка встраивания
легенды.
Диаграмма,
построенная по табличным данным, связана
с этими данными — при изменении числовых
значений диаграмма автоматически
изменяется вместе с ними.
Диаграмма может
быть перемещена буксировкой за рамку
(рамка появляется после щелчка мышью
по диаграмме). Для изменения размеров
диаграммы производится буксировка за
один из 8 квадратиков, расположенных на
рамке, в нужном направлении.
Для изменения
элементов диаграммы (редактирования
или правки) производится двойной щелчок
по ней — рамка становится штриховой,
серого цвета. После этого можно
редактировать любой из элементов
диаграммы — чертеж, ось 1, ось 2, текст оси
1, текст оси 2, названия, легенду. Для
этого производится двойной щелчок по
соответствующему элементу — при этом
вызывается диалоговое окно редактирования
соответствующего элемента.
Для редактирования
также может быть использовано главное
меню Вставка Название (легенды, оси
…) или Формат Тип диаграммы и др.
При создании
объемных диаграмм имеются дополнительные
возможности редактирования (Формат
Объемный вид): три основных операции
-
возвышение
— изменение угла, под которым видна
диаграмма -
поворот
относительно вертикальной оси -
вид
в перспективе — для его получения надо
отменить перпендикулярность осей
На
любой диаграмме могут использоваться
текстовые надписи трех типов
-
связанные
тексты — это наименования диаграммы,
названия осей — их можно форматировать,
перемещать, изменять текст -
свободные
тексты — для ввода свободного текста
на диаграмме не должно быть выделенных
элементов. Любой текст вводится в строке
формул, затем нажимается клавиша ввода
и текст появляется в средней части
диаграммы, где он может быть отредактирован
и перемещен в любое нужное место -
метки
данных числовые значения обычно
показываются у осей координат, однако
иногда полезно показать и числовое
значение у одного или нескольких
столбцов непосредственно на графике,
например, для максимального значения
Соответствующий столбец выделяется
двойным щелчком и с помощью главного
меню Вставка Метка указывается метка.
При
необходимости на диаграмме может быть
указана координатная сетка только по
одной или по обеим осям, сетка может
быть одно- и двухуровневой (то есть менее
или более густая), может быть выбрана
толщина линий сетки, ее цвет (меню Вставка
Сетка)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
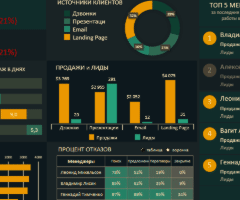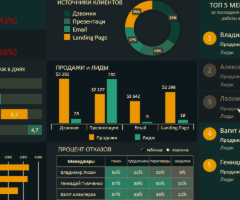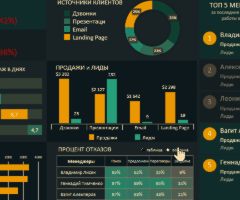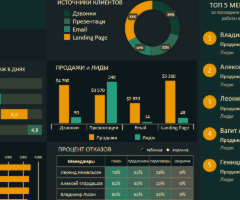
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
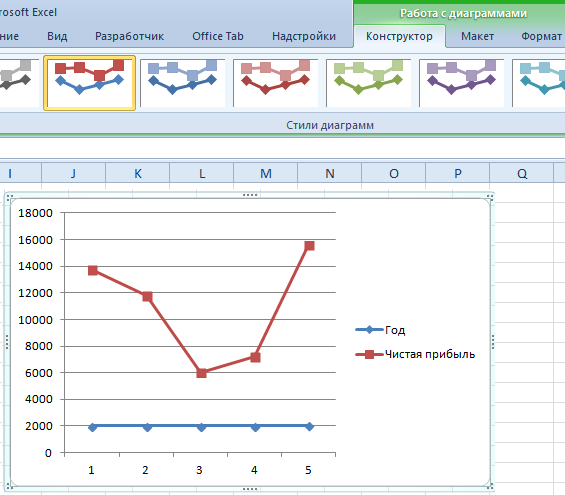
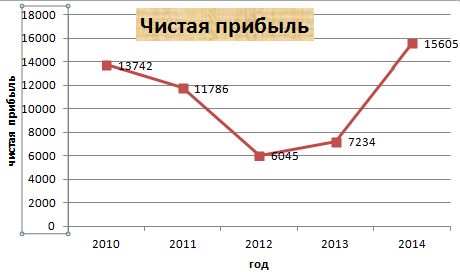
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
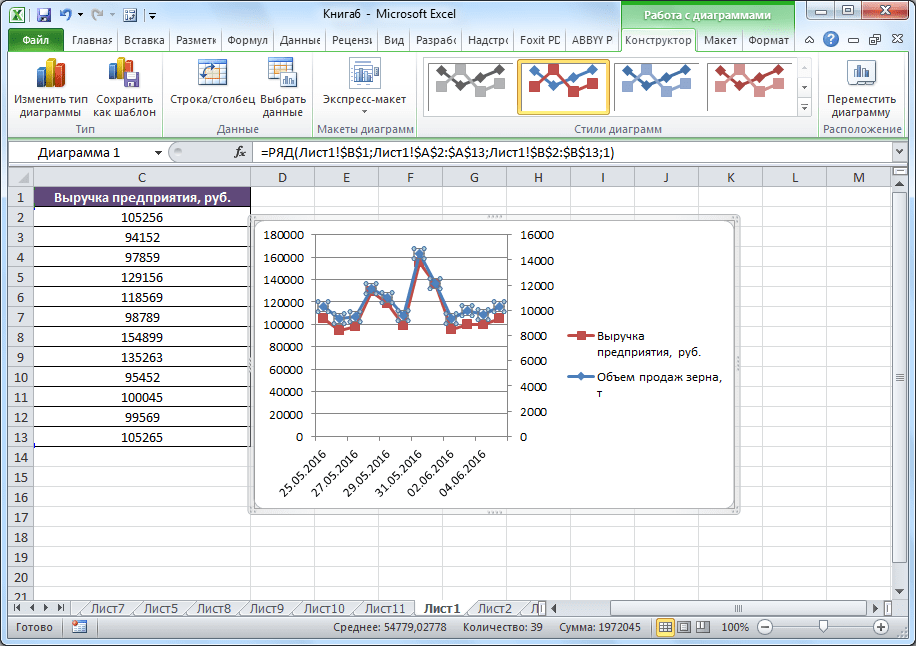
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
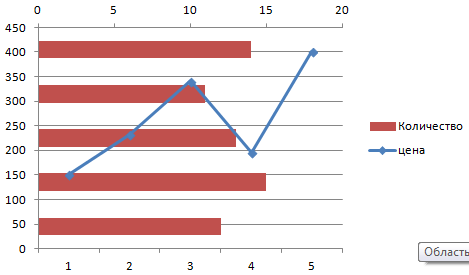
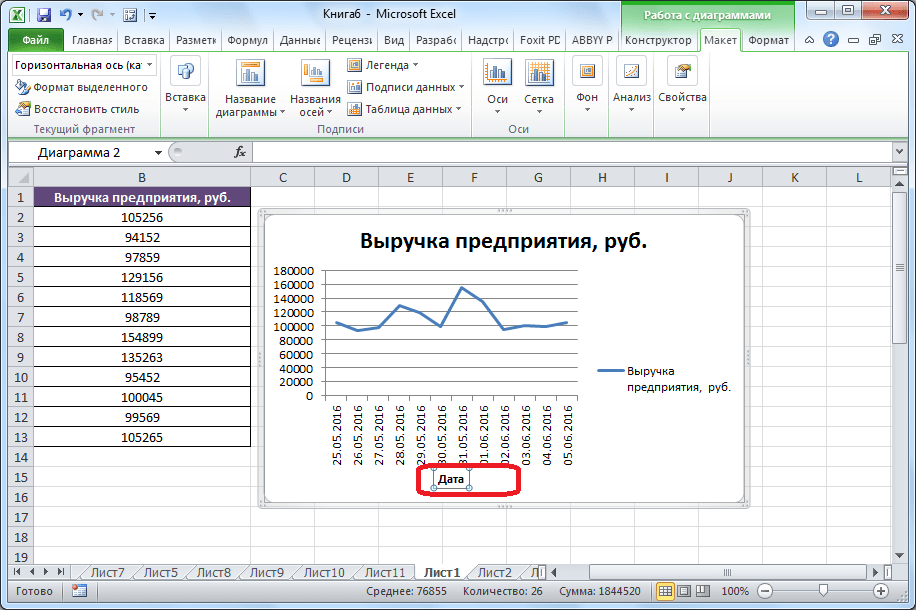
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
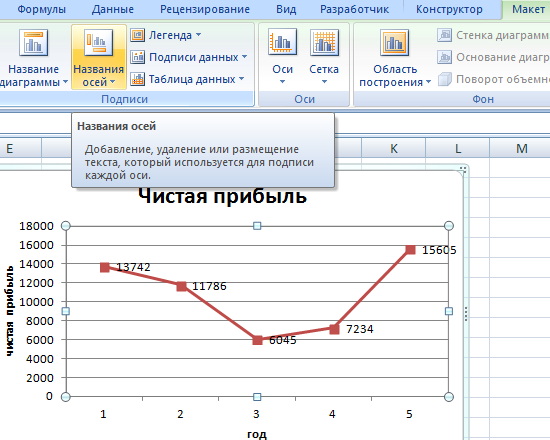
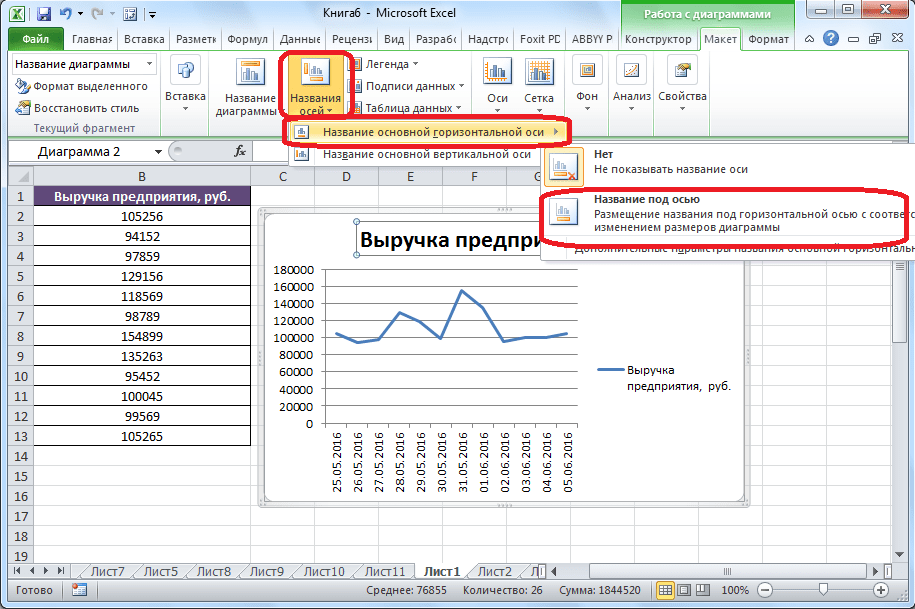
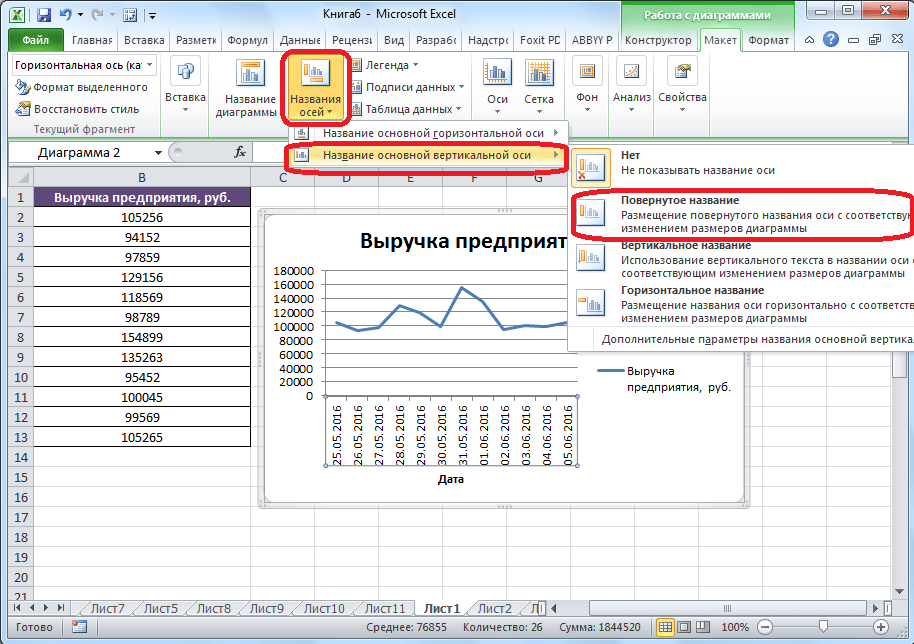
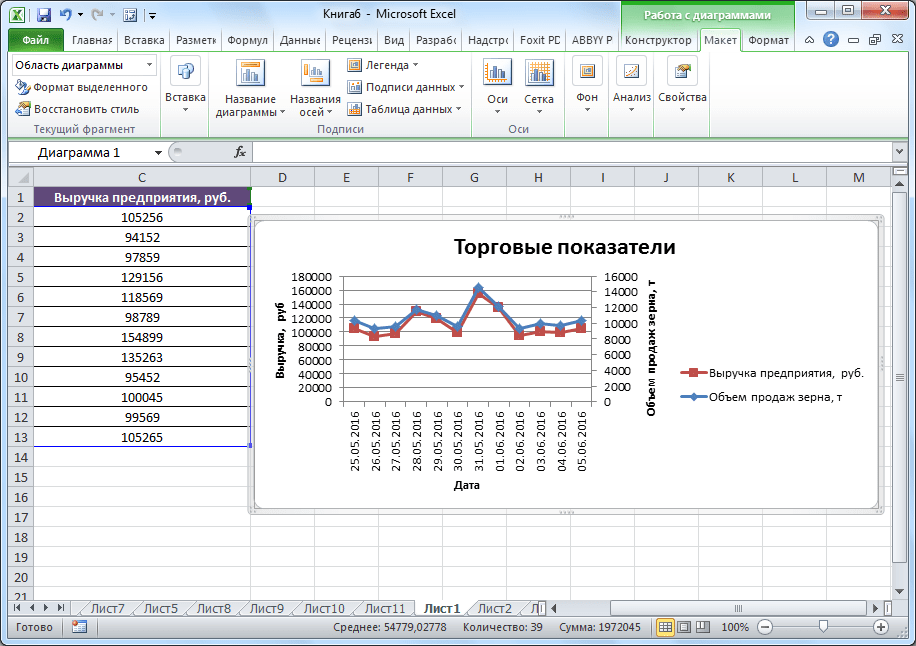
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
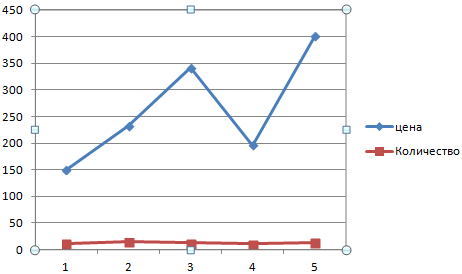
График с двумя и более кривыми
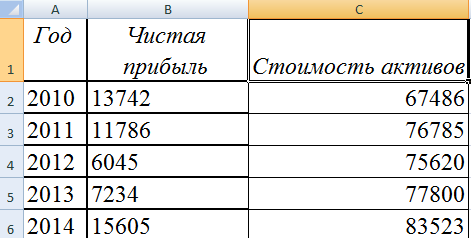
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
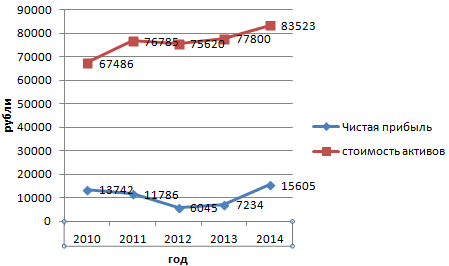
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
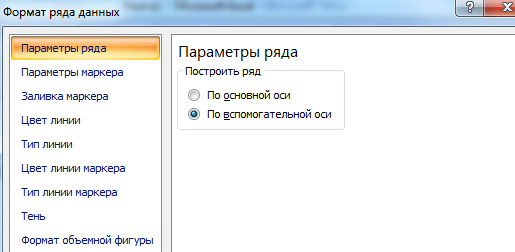
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
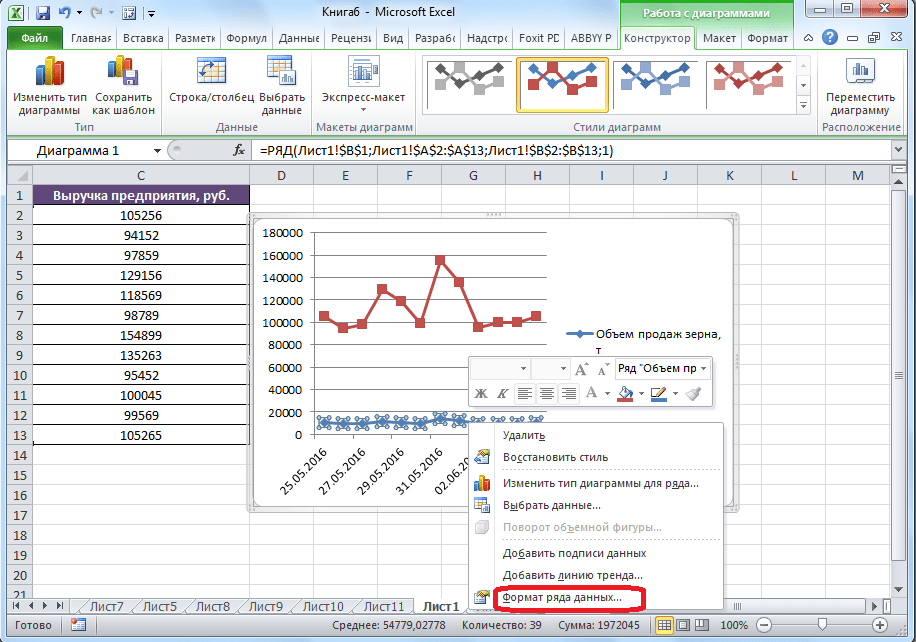
Сначала строим график так, будто у нас одинаковые единицы измерения.
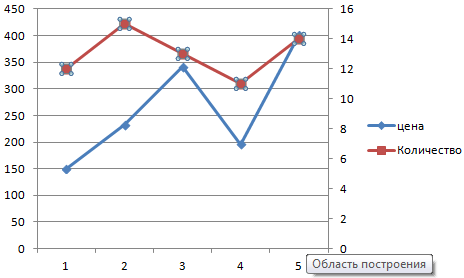
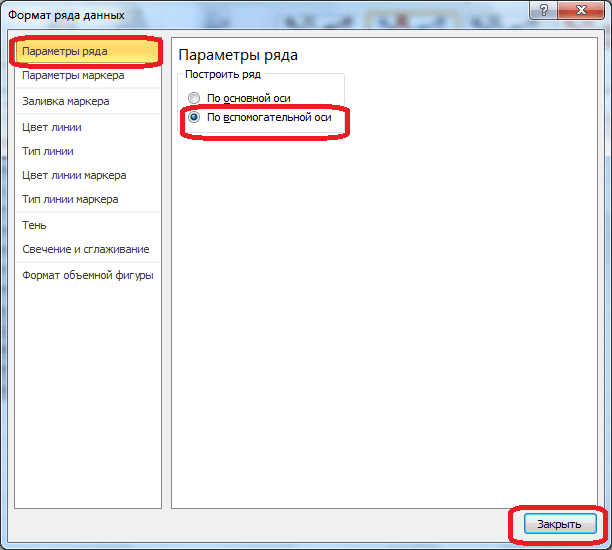
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
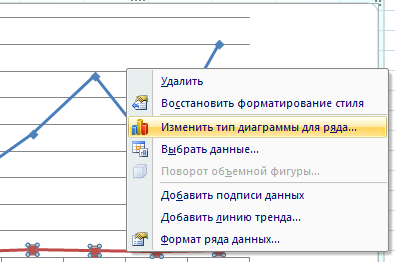
Это один из способов. Есть и другой – изменение типа диаграммы.
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
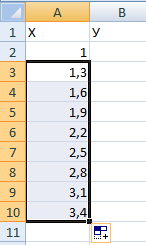
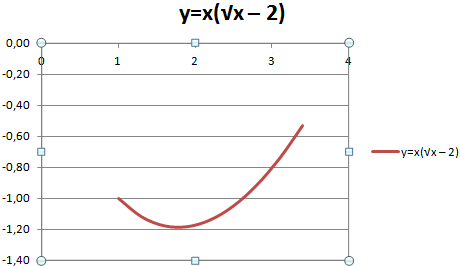
Пример: y=x(√x – 2). Шаг – 0,3.
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
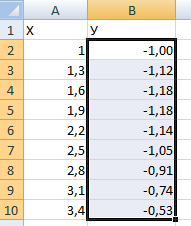
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
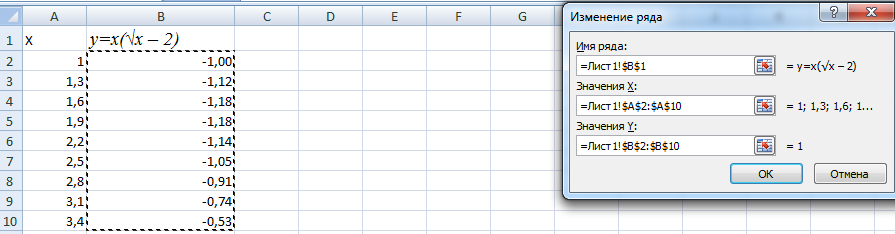
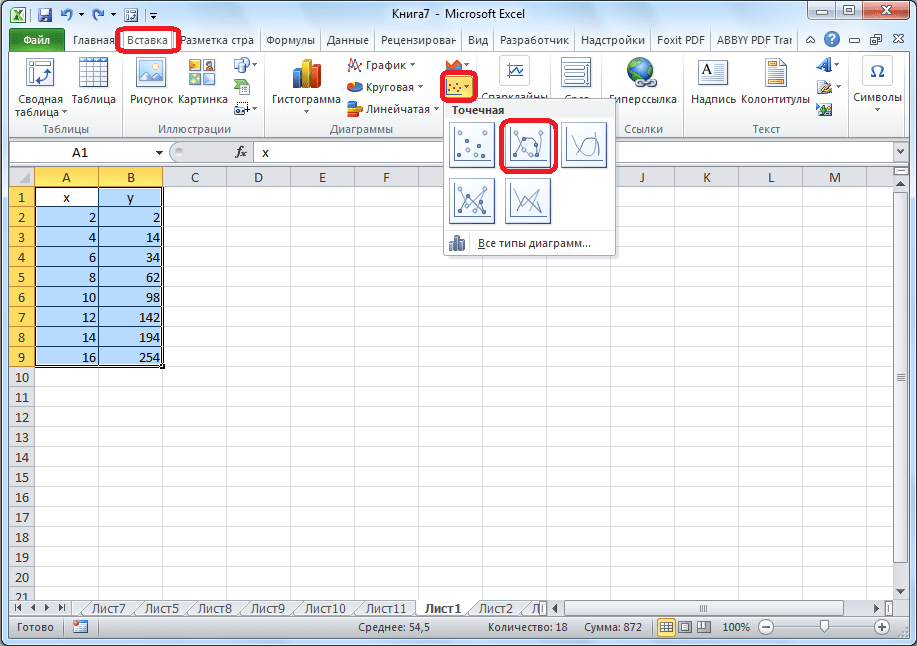
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
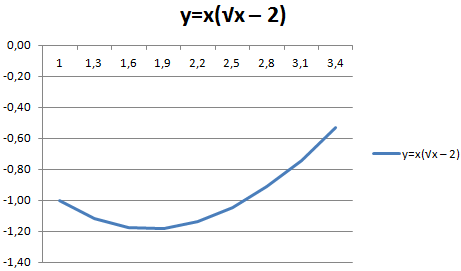
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
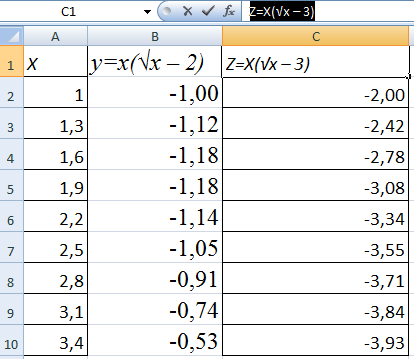
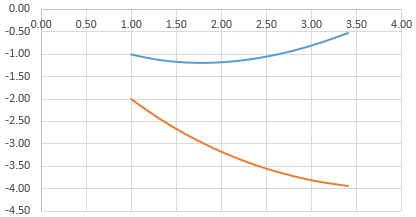
Наложение и комбинирование графиков
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
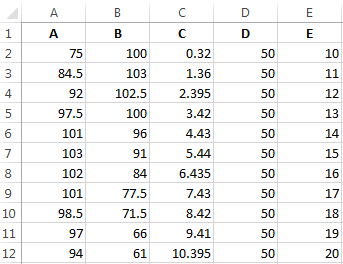
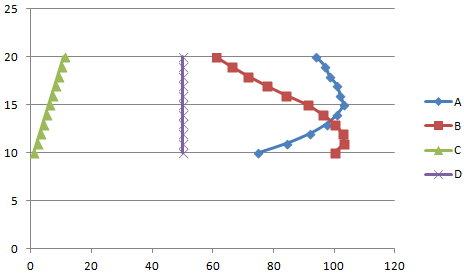
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Скачать все примеры графиков
Готовые примеры графиков и диаграмм в Excel скачать:
Как сделать шаблон, дашборд, диаграмму или график для создания красивого отчета удобного для визуального анализа в Excel? Выбирайте примеры диаграмм с графиками для интерактивной визуализации данных с умных таблиц Excel и используйте их для быстрого принятия правильных решений. Бесплатно скачивайте готовые шаблоны динамических диаграмм для использования их в дашбордах, отчетах или презентациях.
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Скачать материал

Скачать материал




- Сейчас обучается 266 человек из 64 регионов


- Сейчас обучается 395 человек из 62 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
ГРАФИЧЕСКИЕ СПОСОБЫ
ПРЕДСТАВЛЕНИЯ ДАННЫХ В EXCEL
Презентацию выполнила
учитель математики и
информатики
МБОУ СОШ №10 г.Елабуга РТ.
Саутина Анна Леонидовна
2010 год -
2 слайд
ВВЕДЕНИЕ 3
ЧТО ТАКОЕ ДИАГРАММА? 5
ТИПЫ ДИАГРАММ: ГИСТОГРАММЫ И ЛИНЕЙЧАТЫЕ 6
ТИПЫ ДИАГРАММ: ГРАФИКИ И КРУГОВЫЕ 7
ТИПЫ ДИАГРАММ: ТОЧЕЧНЫЕ И С ОБЛАСТЯМИ 8
ТИПЫ ДИАГРАММ: КОЛЬЦЕВЫЕ И ЛЕПЕСТКОВЫЕ 9
ТИПЫ ДИАГРАММ: ПОВЕРХНОСТИ И ПУЗЫРЬКОВЫЕ 10
ТИПЫ ДИАГРАММ: БИРЖЕВЫЕ, ЦИЛИНДРИЧЕСКИЕ,НЕСТАНДАРТНЫЕ ТИПЫ И
ПОЛЬЗОВАТЕЛЬСКИЕ ФОРМАТЫ ДИАГРАММ 11
РЕКОМЕНДАЦИИ ПО ПОСТРОЕНИЮ ДИАГРАММ, ГРАФИКОВ ФУНКЦИЙ И ПОВЕРХНОСТЕЙ 12
ОПЕРАЦИИ, КОТОРЫЕ МОЖНО ПРОИЗВОДИТЬ С ДИАГРАММАМИ I 13
ОПЕРАЦИИ, КОТОРЫЕ МОЖНО ПРОИЗВОДИТЬ С ДИАГРАММАМИ II 14
ЗАДАНИЕ №1: ПОСТРОИТЬ ДИАГРАММУ 15
ЗАДАНИЕ №2: ПОСТРОИТЬ ГРАФИК ФУНКЦИИ 16
ПОСТРОИТЬ ГРАФИК ФУНКЦИИ, ЗАДАННУЮ УРАВНЕНИЕМ В ПОЛЯРНЫХ
КООРДИНАТАХ 17
ЗАДАНИЕ №3: ПОСТРОИТЬ ПОВЕРХНОСТЬ 18
ЗАДАНИЕ №4: ПОСТРОИТЬ ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД 19
СЛОВАРЬ ТЕРМИНОВ 20
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 21оглавление
-
3 слайд
Microsoft Excel — ведущая программа обработки электронных таблиц. Первая версия MS Excel появилась в 1985 году и обеспечивала только простые арифметические операции в строку или в столбец. В 1993 году вышла пятая версия Excel, ставшая первым приложением Microsoft Office. Начиная с Office 97 фирма Microsoft включает VBA во все приложения пакета Microsoft Office .
В настоящее время Microsoft Excel представляет собой достаточно мощное средство разработки информационных систем, которое включает как электронные таблицы (со средствами финансового и статистического анализа, набором стандартных математических функций, доступных в компьютерных языках высокого уровня, рядом дополнительных функций, встречающихся только в библиотеках дорогостоящих инженерных подпрограмм), так и средства визуального программирования. Электронные таблицы позволяют производить обработку чисел и текста, задавать формулы и функции для автоматического выполнения, прогнозировать бюджет на основе сценария, представлять данные в виде диаграмм, публиковать рабочие листы и диаграммы в Интернете.
введение -
4 слайд
В предлагаемой книге на различных примерах продемонстрированы широкие возможности Microsoft Excel для решения математических задач. Изложение в первую очередь ориентировано на Microsoft Excel ХР, однако использовать материал книги можно, начиная с версии Microsoft Excel 97, практически без изменений.
Материал книги может быть полезен:
в качестве учебного пособия для студентов математических и экономических специальностей, изучающих Microsoft Excel в различных курсах информатики, информационных технологий и систем обработки данных;
преподавателям при подготовке лекций и проведении практических и лабораторных работ;
пользователям — для расширения профессиональных возможностей при использовании табличного процессора Microsoft Excel. -
5 слайд
Диаграмма- это графическое представление данных рабочего листа.
Данные, представленные в виде диаграммы нагляднее и поэтому проще для сравнения.
Для построения диаграмм следует предварительно подготовить диапазон необходимых данных,
а затем воспользоваться командой Вставка-Диаграмма или соответствующей кнопкой мастера
диаграмм на панели инструментов Стандартная.
В EXCEL можно строить два типа диаграмм: внедренные и диаграммы на отдельных листах. Внедренные диаграммы создаются на рабочем листе рядом с таблицами, данными и текстом и используются при создании отчетов. Диаграммы на отдельном листе удобны для подготовки слайдов или для вывода на печать. EXCEL предлагает различные типы диаграмм и предусматривает широкий спектр возможностей для их изменения (типа диаграммы, надписей, легенды и т. д.) и для форматирования всех объектов диаграммы. Последнее достигается использованием соответствующих команд панели инструментов Диаграммы или с Помощью контекстного меню соответствующего объекта диаграммы (достаточно щелкнуть правой кнопкой мыши на нужном объекте и из контекстного меню выбрать команду Формат). -
6 слайд
ГИСТОГРАММЫ
Используется для сравнения отдельных величин или их изменений в течение некоторого периода времени. Удобны для отображения дискретных данных.ЛИНЕЙЧАТЫЕ
Похожи на гистограммы(отличие- повернуты на 90º по часовой стрелке). Используется для сопоставления отдельных значений в определенный момент времени, не дают представления об изменении объектов во времени. Горизонтальное расположение полос позволяет подчеркнуть положительные или отрицательные отклонения от некоторой величины. Линейчатые диаграммы можно использовать для отображения отклонений по разным статьям бюджета в определенный момент времени. Можно перетаскивать точки в любое положение.ТИПЫ ДИАГРАММ
-
7 слайд
ГРАФИКИ
Отображают зависимость данных осьY) от величины, которая меняется с постоянным шагом (ось Х). Метки оси категорий должны располагаться по
возрастанию или убыванию. Графики чаще используют для коммерческих или финансовых данных, равномерно распределенных во времени (отображение непрерывных данных), или таких категорий, как продажи, цены и т. п.КРУГОВЫЕ
Отображают соотношение частей и целого и строятся только по одному ряду данных, первому в выделенном диапазоне. Эти диаграммы можно использовать, когда компоненты в сумме составляют 100%.ТИПЫ ДИАГРАММ
-
8 слайд
ТОЧЕЧНЫЕ
Хорошо демонстрируют тенденции изменения данных при неравных интервалах времени или других интервалах измерения, отложенных по оси категорий. Можно использовать для представления дискретных измерений по осям X и У. очечной диаграмме деления на оси категорий наносятся равномерно между самым низким и самым высоким значением X.
С ОБЛАСТЯМИ
Позволяют отслеживать непрерывное изменение суммы значений всех рядов данных и вклад каждого ряда в эту сумму. Этот тип применяется для отображения процесса производства или продажи изделий (с равно отстоящими интервалами).ТИПЫ ДИАГРАММ
-
9 слайд
КОЛЬЦЕВЫЕ
Сравнивают вклад частей в целое. Сравнивают вклад частей в целое. В отличие от круговой, на кольцевой диаграмме могут быть представлены два и более ряда данных.
ЛЕПЕСТКОВЫЕ
Используют обычно, чтобы показать соотношения отдельных рядов данных, а также — одного определенного ряда данных и всех остальных рядов. Каждая категория лепестковой диаграммы имеет собственную ось координат (луч). Точки данных располагаются вдоль луча. Линии, соединяющие точки данных одного ряда, охватывают площадь, характеризующую совокупность значений в этом ряду. На лепестковой диаграмме можно отобразить, например, динамику затрат времени на проект, включающий несколько задач. В этом случае каждой категории (лучу) соответствует определенная задача проекта, а точке на луче — затраты времени на нее к какому-то сроку.ТИПЫ ДИАГРАММ
-
10 слайд
ПОВЕРХНОСТИ
Показывает низкие и высокие точки поверхности. Эти диаграммы используются для набора данных, который зависит от двух переменных. Диаграмму можно поворачивать и рассматривать с разных точек зрения.ПУЗЫРЬКОВЫЕ
Позволяют отображать на плоскости наборы из трех значений. Первые два значения откладываются по осям X и У. Третье значение представляется размером пузырька.ТИПЫ ДИАГРАММ
-
11 слайд
БИРЖЕВЫЕ
Используется для отображения изменения информации о ценах на бирже. Отображает наборы данных из трех значений.
ЦИЛИНДРИЧЕСКИЕ
Являются объемными вариантами гистограмм и линейчатых диаграмм.
НЕСТАНДАРТНЫЕ ТИПЫ ДИАГРАММ
Нестандартные типы основаны на стандартных, но имеют некоторые улучшения в форматировании и отображении.
ПОЛЬЗОВАТЕЛЬСКИЕ ФОРМАТЫ ДИАГРАММ
Добавляются в список дополнительных типов диаграмм. Пользовательские форматы создаются на основе базовых с применением различных средств форматирования.ТИПЫ ДИАГРАММ
-
12 слайд
Работа по построению диаграмм предполагает использование следующей методики:
1. Подготовить диапазон изменения и диапазон значений для диаграммы.
2. Выделить подготовленный диапазон и воспользоваться мастером построения диаграмм (вызывается командой Вставка- Диаграмма либо кнопкой мастера диаграмм панели инструментов Стандартная).
3. Отформатировать полученную диаграмму.
Зная уравнение линии в полярных координатах, легко построить график в декартовой системе координат. Для этого следует:
1. Подготовить диапазон изменения координаты φ.
2. Рассчитать значение функции на данном диапазоне в полярных координатах ρ=ρ(φ).
3. Рассчитать значения х и у в декартовой системе по формулам: x=ρCOSφ, y=ρSINφ
4. Выделить диапазон области определения и области значения функции, т. е. все значения х и у на рабочем листе, и воспользоваться мастером построения диаграмм. Для построения графиков лучше использовать типы диаграмм График и Точечная.
5. Отформатировать полученный график.
Работа по построению поверхности предполагает использование следующей методики:
1. Подготовить диапазон изменения функции по двум координатам, расположив изменения одной координаты вдоль некоторого столбца вниз, а другой— вдоль прилегающей строки вправо.
2. Ввести на пересечении координат необходимую формулу для построения поверхности и воспользоваться маркером автозаполнения для ее копирования на всю область построения поверхности.
3. Выделить подготовленные данные и воспользоваться мастером построения диаграмм (тип диаграммы — Поверхность).
4. Отформатировать полученную поверхность.Рекомендации по построению
диаграмм, графиков функций и поверхностей -
13 слайд
Операции, которые можно производить с диаграммами
С диаграммами можно производить следующие операции:
1. Добавлять и удалять ряды данных — с помощью мастера диаграмм либо из контекстного меню диаграммы командой Исходные данные. Возможно также использование клавиши <DELETE>, перетаскивание мышью данных на построенную диаграмму и др.
2. Изменять (редактировать) данные в диаграмме и на рабочем листе — с помощью средства Подбор параметра (если данные, на которых построена диаграмма, выражены через формулу).
3. Переставлять ряды данных на диаграмме — это касается, в основном, диаграмм гистограммного типа.
4. Вставлять текст в любом месте диаграммы — выделить диаграмму (т. е. щелкнуть на ней мышью), а затем в строке формул ввести необходимый текст, который можно буксировать по всей диаграмме и форматировать как надпись.
5. Редактировать, форматировать и добавлять различные элементы диаграмм — с помощью контекстного меню для необходимого объекта диаграммы.
6. Изменять пространственную ориентацию трехмерных диаграмм — выделить диаграмму и воспользоваться командой меню Диаграмма- Объемный вид, можно также щелкнуть мышью на конце любой оси координат— появятся черные крестики, а затем, удерживая мышь на любом из них, изменять расположение трехмерной диаграммы в пространстве.
Операции, которые можно
производить с диаграммами -
14 слайд
7. Добавлять различные графические объекты (например, стрелки, выноски и т. д.) — с помощью кнопок панели инструментов Рисование либо посредством команд меню Вставка-Рисунок.
8. Настраивать оси и выбирать шкалу — с помощью контекстного меню для данной оси.
9. Строить составные диаграммы (различные типы графиков в одной системе координат) — используя нестандартные типы диаграмм.
10. Изменять типы диаграмм— выбрав команду Тип диаграммы из ее контекстного меню.
11. Создавать рисованные диаграммы (вместо цветовой заливки — рисунки). В данном случае необходимо выбрать некоторый ряд данных и использовать для него команду контекстного меню Формат рядов данных.
12. Связывать текст на диаграмме с ячейками рабочего листа.
13. Создавать диаграммы на основе структурированных данных.
14. Применять диаграммы для анализа данных, т. е. строить различные линии тренда и делать прогнозы.
Операции, которые можно
производить с диаграммами -
15 слайд
Для выполнения задания:
Введите данные на рабочий лист в соответствии с рис.
Выделите мышью диапазон А5:В12 и выполните команду Вставка | Диаграмма либо нажмите кнопку мастера диаграмм панели инструментов Стандартная.
Далее работа с мастером диаграмм осуществляется в пошаговом режиме:
Выбор вида диаграммы — с учетом того, что в примере предложены дискретные статистические данные, подходящий вид диаграммы — гистограммного типа.
• Нажав кнопку Далее, переходим к шагу 2. На вкладке Ряд укажите:
► какой ряд выбран в качестве значения данных (заполните поля Ряд и Значения). В нашем случае в поле Ряд вносим Объем и в поле Значения — диапазон $в$5-$в$12;
► какой ряд будет служить подписями по оси X—в поле Подписи по оси X вносим год и указываем диапазон $А$5:$А$12.
• Перейдя к следующему шагу мастера диаграмм (кнопкой Далее), установим необходимые параметры диаграммы
• На последнем этапе выберем расположение будущей диаграммы.
4. Отформатируйте полученную диаграмму, используя контекстное меню каждого ее элемента.Задание №1: построить диаграмму
-
16 слайд
Построить график функции: y=cos³(πx).
Для выполнения задания:
1.Задайте область определения X вводом начальных данных: 0 и 0.1, а затем маркером автозаполнения подготовьте весь диапазон A8:A28.
2.В ячейку B8 введите формулу =(cos(пи()*А8))^3 и скопируйте ее на диапазон B8:B28.Задание №2: построить график функции
-
17 слайд
Построить функцию, заданную уравнением в полярных координатам: ρ=asin(3φ):
-
18 слайд
Построить поверхность: z=(x³/2)-(y+2)²
Задание №3: построить поверхность
-
19 слайд
Задание №4: построить
гиперболический параболоид -
20 слайд
абсолютная ссылка — указание адреса ячейки в абсолютной системе координат независимо от адреса активной ячейки. Имеет вид: $А$5, $Е$24.
автозаполнения — автоматическое заполнение ячеек.
адрес ячейки — определяется по названию (имени) столбца и названию (номеру строки), на пересечении которых образована ячейка.
влияющая ячейка — от которой зависит значение данной ячейки. В частности, если данная ячейка содержит формулу с ссылкой на некоторую, то последняя считается непосредственно влияющей на первую.
всплывающая подсказка — небольшое «окошко», описывающее назначение объекта. Если указатель установить «поверх» объекта, всплывающая подсказка появится возле него примерно через секунду.
зависимая ячейка — от которой зависит значение данной ячейки (в частности, ячейка, содержащая ссылку на данную ячейку.
защищаемая ячейка — недоступная для редактирования после защиты листа.
значок — картинка (пиктограмма), двойным щелчком которой можно открыть документ, папку или запустить программу.
контекстное меню — вызываемое щелчком правой кнопки мыши; набор команд контекстного меню зависит от того, в каком месте экрана был выполнен щелчок.
легенда — сообщение на диаграмме, содержащее обозначения и названия рядов данных.
лист— электронная таблица, состоящая из 65 536 строк и 256 столбцов и используемая для упорядочения и анализа данных.
маркер заполнения— маленький черный квадрат в правом нижнем углу выделенной ячейки или диапазона.
несмежные ячейки— отделенные друг от друга, несоприкасающиеся.
относительная ссылка— указание адреса ячейки, вычисляемое в относительной системе координат с началом в текущей ячейке. Имеет вид: А5, Е24 и т.д.
очистка содержимого ячейки— удаление данных из ячейки, при этом сама ячейки остается на листе.
поле имен— часть строки формул, содержащая имена ячеек, элементов диаграмм или графических объектов.
раскрывающееся меню — список команд, появляющийся на экране при выборе (подсветке) меню операционной системы и/или приложения.
редактирование — изменение содержания документа.
ряд данных— группа связанных элементов на диаграмме, источником которых является отдельная строка или отдельный столбец на листе.
смежные ячейки— соприкасающиеся ячейки диапазона.
формула— комбинация постоянных значений, знаков арифметических действий, адресов ячеек, имен, функций. Формула вводится в ячейку и определяет правила вычисления в ячейке.
функция— заранее созданная формула, которая выполняет операции над заданными значениями и вычисляет новые значения.
ячейка— часть листа, образованная пересечением столбца и строки. Выделенная ячейка называется активной.
СЛОВАРЬ ТЕРМИНОВ: -
21 слайд
подготовка
к контрольной работе
Задание:
построить
поверхность
Задание:
построить
график
функции -
22 слайд
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
Справка: Microsoft Excel
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 210 267 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 04.01.2021
- 1355
- 0
- 04.01.2021
- 1434
- 0
- 03.01.2021
- 3037
- 15
- 03.01.2021
- 1686
- 0
- 03.01.2021
- 1637
- 1
- 03.01.2021
- 1444
- 3
- 03.01.2021
- 1241
- 0
- 03.01.2021
- 1747
- 13
Вам будут интересны эти курсы:
-
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
-
Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС технических направлений подготовки»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация менеджмента в туризме»
-
Курс профессиональной переподготовки «Управление сервисами информационных технологий»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
-
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
-
Курс профессиональной переподготовки «Гостиничный менеджмент: организация управления текущей деятельностью»
-
Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
-
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
-
Курс профессиональной переподготовки «Осуществление и координация продаж»
-
Курс профессиональной переподготовки «Управление качеством»
ГАПОУ АО Астраханский социально-педагогический колледж
Специальность 39.02.01 «Социальная работа»
Сообщение на тему:
Информация и информационные системы
Студент 2 курса группы «С»
Деревенский Никита Михайлович
Проверила:
Коржова А.П.
_________ отметка за урок
Астрахань, 2022г.
Введение
В современном обществе к статистическим методам проявляется повышенный интерес как к одному из важнейших аналитических инструментариев в сфере поддержки процессов принятия решений. Статистикой пользуются все- от политиков, желающих предсказать исход выборов, до предпринимателей, стремящихся оптимизировать прибыль при тех или иных вложениях капитала. Большим шагом вперёд к развитию статистической науки послужило применение экономико-математических методов и использование компьютерной техники в анализе социально-экономических явлений.
Программа обработки электронных таблиц MS Excel- мощная и достаточно простая в использовании программа, предназначенная для решения широкого круга планово-экономических, учетно-статистических, научно-технических и других задач, в которых числовая, текстовая или графическая информация с некоторой регулярной, повторяющейся структурой представлена в табличном виде.
Программа MS Excel предоставляет богатые возможности создания и изменения таблиц, которые могут содержать числа, тексты, даты, денежные единицы, графику, а также математические и иные формулы для выполнения вычислений.
Предусмотрены средства представления числовых данных в виде диаграммы, создания, сортировки и фильтрации списков, статического анализа данных и решения оптимизационных задач.
В данной работе я постараюсь показать, какие возможности для обработки статистических данных имеет программа MS Excel.
Объектом исследования данной работы являются возможности табличного процессора.
Предметом исследования является применение программы MS Excel для решения статистических задач.
Актуальность работы обусловлена недостаточной реализацией возможностей MS Excel для решения статистических задач.
Цель настоящего исследования заключается в формировании устойчивых знаний о возможностях MS Excel для решения статистических задач.
Для достижения поставленной цели потребовалось решить следующие задачи:
1. Раскрыть сущность возможностей MS Excel.
2. Определить способы применения этих возможностей при решении задач статистики.
В качестве гипотезы выдвигается следующее:
Использование возможностей программы MS Excel облегчает и ускоряет решения задач статистики.
Глава 1. Применение Microsoft Excel для решения
статистических задач.
Работа с данными
В состав Microsoft Excel входит набор средств анализа данных (так называемый пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для проведения анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие средства позволяют представить результаты анализа в графическом виде.
Графические изображения используются, прежде всего, для наглядного представления статистических данных, благодаря ним существенно облегчается их восприятие и понимание. Существенна их роль и тогда, когда речь идет о контроле полноты и достоверности исходного статистического материала, используемого для обработки и анализа.
Статистические данные приводятся в виде длинных и сложных статистических таблиц, поэтому бывает весьма трудно обнаружить в них имеющиеся неточности и ошибки.
В процессе анализа данных, как правило, присутствуют следующие основные этапы:
1. Ввод данных
Введенные данные обычно отражаются в форме электронной таблицы или матрицы данных, где столбцы представляют различные переменные (например, рост, вес), а строки — измерение значений этих переменных, произведенные в различных условиях, в различное время, у различных объектов и т.п.
2. Преобразование данных
Данные в электронной таблице можно просмотреть и скорректировать методами ручного редактирования или же полуавтоматического преобразования к виду, адекватному выбранному методу анализа. Здесь может быть использован широкий набор алгебраических, матричных, структурных преобразований, а также комбинирование этих операций в требуемой последовательности.
3. Визуализация данных
На данные обязательно следует просто посмотреть, чтобы составить общее (в том числе и интуитивное) представление о характере их изменения, специфических особенностях и закономерностях, что очень важно при выборе стратегии и тактики дальнейшего анализа. Для этого можно использовать как исходное числовое представление, так и различные формы графического изображения.
4. Статистический анализ
Собственно выбор метода, анализ данных и интерпретация результатов.
5. Представление результатов
Для наглядности производимых выводов полученные результаты желательно представлять в виде адекватных, убедительных и эффектных графиков.
Для успешного применения процедур анализа необходимы начальные знания в области статистических и инженерных расчетов, для которых эти инструменты были разработаны
В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и дисперсионного анализа.
При машинной обработке исходной информации на ЭВМ, оснащенных пакетами стандартных программ ведения анализов, вычисление параметров применяемых математических функций является быстро выполняемой счетной операцией.
Возможность использования формул и функций является одним из важнейших свойств программы обработки электронных таблиц. Это, в частности, позволяет проводить статистический анализ числовых значений в таблице.
Текст формулы, которая вводится в ячейку таблицы, должен начинаться со знака равенства (=), чтобы программа Excel могла отличить формулу от текста. После знака равенства в ячейку записывается математическое выражение, содержащее аргументы, арифметические операции и функции.
В качества аргументов в формуле обычно используются числа и адреса ячеек. Для обозначения арифметических операций могут использоваться следующие символы: + (сложение); — (вычитание); * (умножение); / (деление).
Формула может содержать ссылки на ячейки, которые расположены на другом рабочем листе или даже в таблице другого файла. Однажды введенная формула может быть в любое время модифицирована. Встроенный Менеджер формул помогает пользователю найти ошибку или неправильную ссылку в большой таблице.
Кроме этого, программа Excel позволяет работать со сложными формулами, содержащими несколько операций. Для наглядности можно включить текстовый режим, тогда программа Excel будет выводить в ячейку не результат вычисления формулы, а собственно формулу.
Программа Excel интерпретирует вводимые данные либо как текст (выравнивается по левому краю), либо как числовое значение (выравнивается по правому краю). Для ввода формулы необходимо ввести алгебраическое выражение, которому должен предшествовать знак равенства (=). [7]
Ввод формул можно существенно упростить, используя маленький трюк. После ввода знака равенства следует просто щелкнуть мышью по первой ячейке, затем ввести операцию деления и щелкнуть по второй ячейке.
Инструменты пакета анализа в Microsoft Excel
Дисперсионный анализ
Пакет анализа включает в себя три средства дисперсионного анализа. Выбор конкретного инструмента определяется числом факторов и числом выборок в исследуемой совокупности данных. [6]
Однофакторный дисперсионный анализ
Однофакторный дисперсионный анализ используется для проверки гипотезы о сходстве средних значений двух или более выборок, принадлежащих одной и той же генеральной совокупности. Этот метод распространяется также на тесты для двух средних (к которым относится, например, t-критерий).
Двухфакторный дисперсионный анализ с повторениями.
Представляет собой более сложный вариант однофакторного анализа, включающий более чем одну выборку для каждой группы данных. Рассмотрим пример применения данной функции Microsoft Excel. Требуется при уровне α=0,05 выяснить, влияют ли на урожайность пшеницы вид удобрений и способ химической обработки почвы. Выборочные данные об урожайности пшеницы, выращенной на участках, на которые вносились различные виды удобрений и которые подвергались различной химической обработке, приведены в таблице ниже.
|
B |
C |
D |
E |
F |
G |
|
|
32 |
Номер участка |
Вид удобрения |
Способ химической обработки |
|||
|
33 |
Способ 1 |
Способ 2 |
Способ 3 |
Способ 4 |
||
|
34 |
Участок1 |
Удобрение1 |
21,4 |
20,9 |
19,6 |
17,6 |
|
35 |
Участок2 |
21,2 |
20,3 |
18,8 |
16,6 |
|
|
36 |
Участок3 |
20,1 |
19,8 |
16,4 |
17,5 |
|
|
37 |
Участок1 |
Удобрение2 |
12,0 |
13,6 |
13,0 |
13,3 |
|
38 |
Участок2 |
14,2 |
13,3 |
13,7 |
14,0 |
|
|
39 |
Участок3 |
12,1 |
11,6 |
12,0 |
13,9 |
|
|
40 |
Участок1 |
Удобрение3 |
13,5 |
14,0 |
12,9 |
12,4 |
|
41 |
Участок2 |
11,9 |
15,6 |
12,9 |
13,7 |
|
|
42 |
Участок3 |
13,4 |
13,8 |
12,1 |
13,0 |
|
|
43 |
Участок1 |
Удобрение4 |
12,8 |
14,1 |
14,2 |
12,0 |
|
44 |
Участок2 |
13,8 |
13,2 |
13,6 |
14,6 |
|
|
45 |
Участок3 |
13,7 |
15,3 |
13,3 |
14,0 |
Рассматриваемый в задаче эксперимент представляет собой факторный эксперимент типа 4×4, при котором четыре вида удобрений(фактор А) пересекаются с использованием четырёх способов химической обработки почвы(фактор В). Таким образом, в плане эксперимента имеется 16 условий. Но здесь каждому условию соответствует не одно, а три значения(3 участка земли, засеянных пшеницей).
Для решения задачи используем режим работы «Двухфакторный дисперсионный анализ с повторениями». Значения параметров, установленных в одноименном диалоговом окне, и рассчитанные в данном режиме показатели представлены в таблице, расположенной ниже .
|
B |
C |
D |
E |
F |
G |
||
|
48 |
Двухфакторный дисперсионный анализ с повторениями |
||||||
|
49 |
|||||||
|
50 |
ИТОГИ |
Способ1 |
Способ2 |
Способ3 |
Способ4 |
Итого |
|
|
51 |
Удобрение1 |
||||||
|
52 |
Счёт |
3 |
3 |
3 |
3 |
12 |
|
|
53 |
Сумма |
62,7 |
61 |
54,8 |
51,7 |
230,2 |
|
|
54 |
Среднее |
20,90 |
20,33 |
18,27 |
17,23 |
19,18 |
|
|
55 |
Дисперсия |
0,49 |
0,30 |
2,77 |
0,30 |
3,13 |
|
|
56 |
|||||||
|
57 |
Удобрение2 |
||||||
|
58 |
Счёт |
3 |
3 |
3 |
3 |
12 |
|
|
59 |
Сумма |
38,3 |
38,5 |
38,7 |
41,2 |
156,7 |
|
|
60 |
Среднее |
12,77 |
12,83 |
12,90 |
13,73 |
13,06 |
|
|
61 |
Дисперсия |
1,54 |
1,16 |
0,73 |
0,14 |
0,82 |
|
|
62 |
|||||||
|
63 |
Удобрение3 |
||||||
|
64 |
Счёт |
3 |
3 |
3 |
3 |
12 |
|
|
65 |
Сумма |
38,8 |
43,4 |
37,9 |
39,1 |
159,2 |
|
|
66 |
Среднее |
12,93 |
14,47 |
12,63 |
13,03 |
13,27 |
|
|
67 |
Дисперсия |
0,80 |
0,97 |
0,21 |
0,42 |
0,99 |
|
|
68 |
|||||||
|
69 |
Удобрение4 |
||||||
|
70 |
Счёт |
3 |
3 |
3 |
3 |
12 |
|
|
71 |
Сумма |
40,3 |
42,6 |
41,1 |
40,6 |
164,6 |
|
|
72 |
Среднее |
13,43 |
14,20 |
13,70 |
13,53 |
13,72 |
|
|
73 |
Дисперсия |
0,30 |
1,11 |
0,21 |
1,85 |
0,73 |
|
|
74 |
|||||||
|
75 |
Итого |
||||||
|
76 |
Счёт |
12 |
12 |
12 |
12 |
||
|
77 |
Сумма |
180,1 |
185,5 |
172,5 |
172,6 |
||
|
78 |
Среднее |
15,01 |
15,46 |
14,38 |
14,38 |
||
|
79 |
Дисперсия |
13,26 |
9,71 |
6,39 |
3,52 |
||
|
B |
C |
D |
E |
F |
G |
H |
|
|
82 |
Дисперсионный анализ |
||||||
|
83 |
Источник вариации |
SS |
df |
MS |
F |
P-значение |
F критическое |
|
84 |
Выборка |
309,26 |
3 |
103,09 |
123,64 |
1,11Е-17 |
2,90 |
|
85 |
столбцы |
9,97 |
3 |
3,32 |
3,99 |
0,016 |
2,90 |
|
86 |
Взаимодействие |
25,68 |
9 |
2,85 |
3,42 |
0,005 |
2,19 |
|
87 |
Внутри |
26,68 |
32 |
0,83 |
|||
|
88 |
|||||||
|
89 |
Итого |
371,59 |
47 |
Так как попадает в критическую область, то гипотезу отвергаем, т.е. считаем, что вид удобрения влияет на урожайность пшеницы.
Выборочный коэффициент детерминации для фактора А
показывает, что 83 процента общей выборочной вариации урожайности пшеницы связано с влиянием вида удобрения.
Расчётное значение F- критерия фактора В (способ химической обработки) , а критическая область образуется правосторонним интервалом (2,90; +∞) . Так как попадает в критическую область, то гипотезу отвергаем, т.е. считаем, что способ химической обработки почвы также влияет на урожайность пшеницы.
Выборочный коэффициент детерминации для фактора В
показывает, что только около 3 процентов общей выборочной вариации урожайности пшеницы связано с влиянием способа химической обработки почвы.
Значимость фактора взаимодействия попадает в критический интервал (2,19;+∞) и указывает на то, что эффективность различных видов удобрения варьируется при различных способах химической обработки почвы. [6]
Двухфакторный дисперсионный анализ без повторения.
Представляет собой двухфакторный анализ дисперсии, не включающий более одной выборки на группу. Используется для проверки гипотезы о том, что средние значения двух или нескольких выборок одинаковы (выборки принадлежат одной и той же генеральной совокупности). Этот метод распространяется также на тесты для двух средних, такие как t-критерий.
Корреляционный и ковариационный анализ.
Ковариация выражает степень статистической зависимости между двумя множествами данных и определяется из следующего соотношения:
где:
X, Y — множества значений случайных величин размерности m;
M(X) — математическое ожидание случайной величины Х;
M(Y) — математическое ожидание случайной величины Y.
Как следует из формулы, положительная ковариация наблюдается в том случае, когда большим значениям случайной величины Х соответствуют большие значения случайной величины Y, т.е. между ними существует тесная прямая взаимосвязь. Соответственно отрицательная ковариация будет иметь место при соответствии малым значениям случайной величины Х больших значений случайной величины Y. При слабо выраженной зависимости значение показателя ковариации близко к 0.
Ковариация зависит от единиц измерения исследуемых величин, что ограничивает ее применение на практике. Более удобным для использования в анализе является производный от нее показатель — коэффициент корреляции R, вычисляемый по формуле:
Коэффициент корреляции обладает теми же свойствами, что и ковариация, однако является безразмерной величиной и принимает значения от -1 (характеризует линейную обратную взаимосвязь) до +1 (характеризует линейную прямую взаимосвязь). Для независимых случайных величин значение коэффициента корреляции близко к 0.
Определение количественных характеристик для оценки тесноты взаимосвязи между случайными величинами в ППП EXCEL может быть осуществлено двумя способами:
с помощью статистических функций КОВАР и КОРРЕЛ ;
с помощью специальных инструментов статистического анализа.
Если число исследуемых переменных больше 2, более удобным является использование инструментов анализа.
Инструмент анализа данных «Корреляция»
Выберите в главном меню тему «Сервис» пункт «Анализ данных». Результатом выполнения этих действий будет появление диалогового окна «Анализ данных», содержащего список инструментов анализа.
Выберите из списка «Инструменты анализа» пункт «Корреляция» и нажмите кнопку «ОК» (рис.1). Результатом будет появление окна диалога инструмента «Корреляция».
Заполните поля диалогового окна, как показано на рис. 2 и нажмите кнопку «ОК».
Результаты корреляционного анализа представлены в ЭТ в виде квадратной матрицы, заполненной только наполовину, поскольку значение коэффициента корреляции между двумя случайными величинами не зависит от порядка их обработки. Нетрудно заметить, что эта матрица симметрична относительно главной диагонали, элементы которой равны 1, так как каждая переменная коррелирует сама с собой.
Полезность проведения последующего статистического анализа результатов имитационного эксперимента заключается также в том, что во многих случаях он позволяет выявить некорректности в исходных данных, либо даже ошибки в постановке задачи. Следует отметить, что близкие к нулевым значения коэффициента корреляции R указывают на отсутствие линейной связи между исследуемыми переменными, но не исключают возможности нелинейной зависимости. Кроме того, высокая корреляция не обязательно всегда означает наличие причинной связи, так как две исследуемые переменные могут зависеть от значений третьей. [12]
Для проверки гипотезы о нормальном распределении случайной величины применяются специальные статистические критерии: Колмогорова-Смирнова, . В целом ППП EXCEL позволяет быстро и эффективно осуществить расчет требуемого критерия и провести статистическую оценку гипотез.
Однако в простейшем случае для этих целей можно использовать такие характеристики распределения, как асимметрия и эксцесс. Для вычисления коэффициента асимметрии и эксцесса в EXCEL реализованы специальные статистические функции — СКОС () и ЭКСЦЕСС(). [3]
Инструмент анализа данных «Описательная статистика»
Чем больше характеристик распределения случайной величины нам известно, тем точнее мы можем судить об описываемых ею процессов. Инструмент «Описательная статистика» автоматически вычисляет наиболее широко используемые в практическом анализе характеристики распределений. При этом значения могут быть определены сразу для нескольких исследуемых переменных.
Определим параметры описательной статистики. Для этого необходимо выполнить следующие шаги.
Выберите в главном меню тему «Сервис» пункт «Анализ данных». Результатом выполнения этих действий будет появление диалогового окна «Анализ данных», содержащего список инструментов анализа.
Выберите из списка «Инструменты анализа» пункт «Описательная статистика» и нажмите кнопку «ОК». Результатом будет появление окна диалога инструмента «Описательная статистика».
Заполните поля диалогового окна, как показано на рис. 4 и нажмите кнопку «ОК».
Результатом выполнения указанных действий будет формирование отдельного листа, содержащего вычисленные характеристики описательной статистики для исследуемых переменных. Выполнив операции форматирования, можно привести 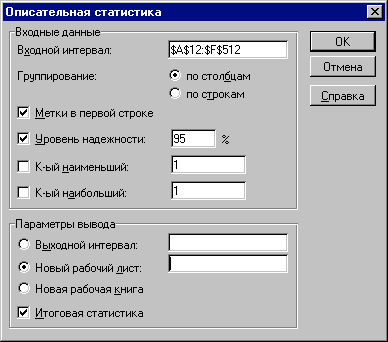
полученную ЭТ к более наглядному виду
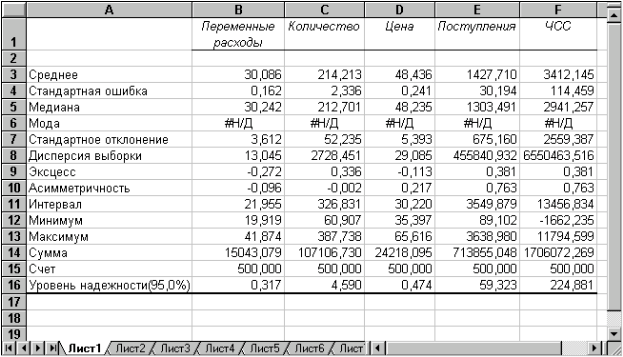
Вторая строка ЭТ содержит значения стандартных ошибок для средних величин распределений. Другими словами среднее или ожидаемое значение случайной величины М (Е) определено с погрешностью . [1]
Медиана — это значение случайной величины, которое делит площадь, ограниченную кривой распределения, пополам (т.е. середина численного ряда или интервала). Как и математическое ожидание, медиана является одной из характеристик центра распределения случайной величины. В симметричных распределениях значение медианы должно быть равным или достаточно близким к математическому ожиданию.
Мода — наиболее вероятное значение случайной величины (наиболее часто встречающееся значение в интервале данных). Для симметричных распределений мода равна математическому ожиданию. Иногда мода может отсутствовать. В данном случае ППП EXCEL вернул сообщение об ошибке. Таким образом, вычисление моды не представляется возможным.
Эксцесс характеризует остроконечность (положительное значение) или пологость (отрицательное значение) распределения по сравнению с нормальной кривой. Теоретически, эксцесс нормального распределения должен быть равен 0. Однако на практике для генеральных совокупностей больших объемов его малыми значениями можно пренебречь. [2]
Асимметричность (коэффициент асимметрии или скоса — s) характеризует смещение распределения относительно математического ожидания. При положительном значении коэффициента распределение скошено вправо, т.е. его более длинная часть лежит правее центра (математического ожидания) и обратно. Для нормального распределения коэффициент асимметрии равен 0. На практике, его малыми значениями можно пренебречь.
Для вычисления коэффициента асимметрии используется статистическая функция СКОС (). Формула для проверки значимости показателя эксцесса задается аналогичным образом. Числителем этой формулы будет функция ЭКСЦЕСС (), а знаменателем соотношение, реализованное средствами ППП EXCEL.
Оставшиеся показатели описательной статистики представляют меньший интерес. Величина «Интервал» определяется как разность между максимальным и минимальным значением случайной величины (численного ряда). Параметры «Счет» и «Сумма» представляют собой число значений в заданном интервале и их сумму соответственно. [3]
Последняя характеристика «Уровень надежности» показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия. По умолчанию уровень надежности принят равным 95%.
Анализ данных
Дополнение «Анализ данных» содержит целый ряд других полезных инструментов, позволяющих быстро и эффективно осуществить требуемый вид обработки данных. Вместе с тем, большинство из них требует осмысленного применения и соответствующей подготовки пользователя в области математической статистики.
Это средство анализа служит для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
Экспоненциальное сглаживание
Предназначается для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. Использует константу сглаживания a, по величине которой определяет, насколько сильно влияют на прогнозы погрешности в предыдущем прогнозе. [4]
Анализ Фурье
Предназначается для решения задач в линейных системах и анализа периодических данных, используя метод быстрого преобразования Фурье (БПФ). Эта процедура поддерживает также обратные преобразования, при этом, инвертирование преобразованных данных возвращает исходные данные.
Двухвыборочный F-тест для дисперсий
Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей. Например, F-тест можно использовать для выявления различия в дисперсиях временных характеристик, вычисленных по двум выборкам.
Гистограмма
Используется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений, при этом, генерируются числа попаданий для заданного диапазона ячеек.
Скользящее среднее
Используется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Каждое прогнозируемое значение основано на формуле:
где
N число предшествующих периодов, входящих в скользящее среднее
Aj фактическое значение в момент времени j
Fj прогнозируемое значение в момент времени j
Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Процедура может использоваться для прогноза сбыта, инвентаризации и других процессов.
Проведение t-теста
Пакет анализа включает в себя три средства анализа среднего для совокупностей различных типов:
Двухвыборочный t-тест с одинаковыми дисперсиями
Двухвыборочный t-тест Стьюдента служит для проверки гипотезы о равенстве средних для двух выборок. Эта форма t-теста предполагает совпадение дисперсий генеральных совокупностей и обычно называется гомоскедастическим t-тестом.
Двухвыборочный t-тест с разными дисперсиями
Двухвыборочный t-тест Стьюдента используется для проверки гипотезы о равенстве средних для двух выборок данных из разных генеральных совокупностей. Эта форма t-теста предполагает несовпадение дисперсий генеральных совокупностей и обычно называется гетероскедастическим t-тестом.
Парный двухвыборочный t-тест для средних
Парный двухвыборочный t-тест Стьюдента используется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные. Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды. [7]
Генерация случайных чисел
Используется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью данной процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей.
Ранг и персентиль
Используется для вывода таблицы, содержащей порядковый и процентный ранги для каждого значения в наборе данных. Данная процедура может быть применена для анализа относительного взаиморасположения данных в наборе. Рассмотрим пример применения данной функции.
Требуется с помощью коэффициента Спирмена определить зависимость между величиной уставного капитала предприятий Х и количеством выставленных акций Y. Данные о предприятиях города, выставивших акции на чековый аукцион, приведены ниже в таблице 1.
Таблица1
|
B |
C |
D |
|
|
21 |
Номер предприятия |
Уставный капитал, млн. руб. Х |
Число выставленных акций Y |
Продолжение таблицы 1
|
22 |
1 |
2954 |
856 |
|
23 |
2 |
1605 |
930 |
|
24 |
3 |
4102 |
1563 |
|
25 |
4 |
2350 |
682 |
|
26 |
5 |
2625 |
616 |
|
27 |
6 |
1795 |
495 |
|
28 |
7 |
2813 |
815 |
|
29 |
8 |
1751 |
858 |
|
30 |
9 |
1700 |
467 |
|
31 |
10 |
2264 |
661 |
Для решения задачи используем режим работы «Ранг и персентиль». Результаты выполнения данного режима приведены ниже в таблице.
|
B |
C |
D |
E |
F |
G |
H |
I |
||
|
35 |
Точка |
Столбец1 |
Ранг |
Процент |
Точка |
Столбец1 |
Ранг |
Процент |
|
|
36 |
3 |
4102 |
1 |
100,00 |
3 |
1563 |
1 |
100,00 |
|
|
37 |
1 |
2954 |
2 |
88,80 |
2 |
930 |
2 |
88,80 |
|
|
38 |
7 |
2813 |
3 |
77,70 |
8 |
858 |
3 |
77,70 |
|
|
39 |
5 |
2625 |
4 |
66,60 |
1 |
856 |
4 |
66,60 |
|
|
40 |
4 |
2350 |
5 |
55,50 |
7 |
815 |
5 |
55,50 |
|
|
41 |
10 |
2264 |
6 |
44,40 |
4 |
682 |
6 |
44,40 |
|
|
42 |
6 |
1795 |
7 |
33,30 |
10 |
661 |
7 |
33,30 |
|
|
43 |
8 |
1751 |
8 |
22,20 |
5 |
616 |
8 |
22,20 |
|
|
44 |
9 |
1700 |
9 |
11,10 |
6 |
495 |
9 |
11,10 |
|
|
45 |
2 |
1605 |
10 |
11,10 |
9 |
467 |
10 |
11,10 |
По данным этой сгенерированной таблицы заполняем в следующей таблице графы Ранг и Ранг
, на основании которых производим вычисления квадратов разности рангов
.
|
B |
C |
D |
E |
F |
G |
|
|
21 |
Номер предприятия |
Уставный капитал, млн. руб. Х |
Число выставленных акций Y |
Ранг |
Ранг |
Квадрат разности рангов |
|
22 |
1 |
2954 |
856 |
2 |
4 |
4 |
|
23 |
2 |
1605 |
930 |
10 |
2 |
64 |
|
24 |
3 |
4102 |
1563 |
1 |
1 |
0 |
|
25 |
4 |
2350 |
682 |
5 |
6 |
1 |
|
26 |
5 |
2625 |
616 |
4 |
8 |
16 |
|
27 |
6 |
1795 |
495 |
7 |
9 |
4 |
|
28 |
7 |
2813 |
815 |
3 |
5 |
4 |
|
29 |
8 |
1751 |
858 |
8 |
3 |
25 |
|
30 |
9 |
1700 |
467 |
9 |
10 |
1 |
|
31 |
10 |
2264 |
661 |
6 |
7 |
1 |
|
32 |
|
120 |
Заключительным этапом решения задачи является вычисление коэффициента Спирмена по формуле
,
подставляя в которую исходные данные и рассчитанные данные задачи получим
.
Значение коэффициента Спирмена свидетельствует о слабой связи между рассматриваемыми признаками. [9]
Регрессия
Регрессионный анализ называют основным методом современной математической статистики для выявления неявных и завуалированных связей между данными наблюдений. Электронные таблицы делают такой анализ легко доступным. Таким образом, регрессионные вычисления и подбор хороших уравнений — это ценный, универсальный исследовательский инструмент в самых разнообразных отраслях деловой и научной деятельности (маркетинг, торговля, медицина и т. д.). Усвоив технологию использования этого инструмента, можно применять его по мере необходимости, получая знание о скрытых связях, улучшая аналитическую поддержку принятия решений и повышая их обоснованность.
Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных. [8]
Выборка
Создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. [5]
Двухвыборочный z-тест для средних
Двухвыборочный z-тест для средних с известными дисперсиями используется для проверки гипотезы о различии между средними двух генеральных совокупностей.
Статистические функции
FРАСП Возвращает F-распределение вероятности. Эту функцию можно использовать, чтобы определить, имеют ли два множества данных различные степени плотности. Например, можно исследовать результаты тестирования мужчин и женщин, окончивших высшую школу, и определить отличается ли разброс результатов для мужчин и женщин.[10]
FРАСПОБР Возвращает обратное значение для F-распределения вероятности
БЕТАОБР Возвращает обратную функцию к интегральной функции плотности бета-вероятности
БЕТАРАСП Возвращает интегральную функцию плотности бета-вероятности
БИНОМРАСП Возвращает отдельное значение биномиального распределения
ВЕЙБУЛЛ Возвращает распределение Вейбулла
ВЕРОЯТНОСТЬ Возвращает вероятность того, что значение из диапазона находится внутри заданных пределов
ГАММАНЛОГ Возвращает натуральный логарифм гамма функции
ГАММАОБР Возвращает обратное гамма-распределение
ГАММАРАСП Возвращает гамма-распределение
ГИПЕРГЕОМЕТ Возвращает гипергеометрическое распределение
ДОВЕРИТ Возвращает доверительный интервал для среднего значения по генеральной совокупности
КВАРТИЛЬ Возвращает квартиль множества данных
КВПИРСОН Возвращает квадрат коэффициента корреляции Пирсона
КРИТБИНОМ Возвращает наименьшее значение, для которого биномиальная функция распределения меньше или равна заданному значению
ЛГРФПРИБЛ Возвращает параметры экспоненциального тренда
ЛИНЕЙН Возвращает параметры линейного тренда
ЛОГНОРМОБР Возвращает обратное логарифмическое нормальное распределение
ЛОГНОРМРАСП Возвращает интегральное логарифмическое нормальное распределение
МАКСА Возвращает максимальное значение из списка аргументов, включая числа, текст и логические значения
МИНА Возвращает минимальное значение из списка аргументов, включая числа, текст и логические значения
НАИБОЛЬШИЙ Возвращает k-ое наибольшее значение из множества данных
НАИМЕНЬШИЙ Возвращает k-ое наименьшее значение в множестве данных
НАКЛОН Возвращает наклон линии линейной регрессии
НОРМАЛИЗАЦИЯ Возвращает нормализованное значение
НОРМОБР Возвращает обратное нормальное распределение
НОРМРАСП Возвращает нормальную функцию распределения
НОРМСТОБР Возвращает обратное значение стандартного нормального распределения
ОТРБИНОМРАСП Возвращает отрицательное биномиальное распределение
ОТРЕЗОК Возвращает отрезок, отсекаемый на оси линией линейной регрессии
ПЕРЕСТ Возвращает количество перестановок для заданного числа объектов
ПИРСОН Возвращает коэффициент корреляции Пирсона
ПРОЦЕНТРАНГ Возвращает процентную норму значения в множестве данных
ПУАССОН Возвращает распределение Пуассона
РОСТ Возвращает значения в соответствии с экспоненциальным трендом
СРГАРМ Возвращает среднее гармоническое
СРГЕОМ Возвращает среднее геометрическое
СРЗНАЧ Возвращает среднее арифметическое аргументов
СРЗНАЧА Возвращает среднее арифметическое аргументов, включая числа, текст и логические значения.
СРОТКЛ Возвращает среднее абсолютных значений отклонений точек данных от среднего
СТАНДОТКЛОН Оценивает стандартное отклонение по выборке
СТАНДОТКЛОНА Оценивает стандартное отклонение по выборке, включая числа, текст и логические значения
СТАНДОТКЛОНП Вычисляет стандартное отклонение по генеральной совокупности
СТАНДОТКЛОНПА Вычисляет стандартное отклонение по генеральной совокупности, включая числа, текст и логические значения
СТЬЮДРАСП Возвращает t-распределение Стьюдента
СТЬЮДРАСПОБР Возвращает обратное t-распределение Стьюдента
СЧЁТЗ Подсчитывает количество значений в списке аргументов
ТЕНДЕНЦИЯ Возвращает значения в соответствии с линейным трендом
ТТЕСТ Возвращает вероятность, соответствующую критерию Стьюдента
УРЕЗСРЕДНЕЕ Возвращает среднее внутренности множества данных
ФИШЕР Возвращает преобразование Фишера
ФИШЕРОБР Возвращает обратное преобразование Фишера
ФТЕСТ Возвращает результат F-теста
ХИ2ОБР Возвращает обратное значение односторонней вероятности распределения хи-квадрат
ХИ2РАСП Возвращает одностороннюю вероятность распределения хи-квадрат
ХИ2ТЕСТ Возвращает тест на независимость
ЧАСТОТА Возвращает распределение частот в виде вертикального массива
ЭКСПРАСП Возвращает экспоненциальное распределение
1.6 Применение графических возможностей Excel
Графические изображения уже давно нашли широкое применение в самых разнообразных видах человеческой деятельности. Но, пожалуй, ни в одной области знаний и практической деятельности графические изображения не играют такой исключительной роли, как в статистике и экономике, имеющих дело с обработкой и анализом огромных массивов информации о социально- экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимают графические изображения статистических данных.
Графические изображения широко используются, прежде всего, для наглядного представления статистических данных, благодаря ним существенно облегчается их восприятие и понимание.
Огромные возможности для автоматического построения различных видов графических изображений статистических данных представляет программа обработки электронных таблиц Microsoft Excel.
Статистическая диаграмма- это особый способ наглядного представления и изложения с помощью геометрических знаков и других графических средств статистической информации с целью её обобщения и анализа. Основным и наиболее важным свойством статистических диаграмм является их наглядность. Непосредственная наглядность статистических диаграмм делает их более выразительными и наглядными. [11]
При анализе статистических данных диаграммы могут использоваться для решения таких задач:
Отображать распределение единиц статистической совокупности по значениям или разновидностям исследуемого признака;
Характеризовать развитие изучаемых явлений во времени, их общую тенденцию развития, сезонность колебаний, абсолютную и относительную скорость их развития и изменения;
Сравнивать размеры различных явлений, их разных частей, а также тенденцию их развития и изменения во времени и пространстве;
Выявлять структуру изучаемых явлений и её изменения, т.е. структурные сдвиги;
Устанавливать взаимозависимость между явлениями или их признаками, а также степень тесноты существующей между ними связи;
Отображать степень распространения изучаемых явлений по той или иной территории и интенсивности этого распространения.
Статистические диаграммы являются очень ценным средством при проведении разного рода сравнений статистических данных.
Графические изображения статистических данных осуществляются в основном посредством геометрических плоскостных знаков- точек, линий, плоскостей, фигур, различного сочетания и их расположения. Графические изображения, как плоскостные, так и объёмные, бывают разнообразными, но почти каждое из них состоит из одних и тех, же основных элементов: поле диаграммы, графического образа, пространственных и масштабных ориентиров, экспликации диаграммы.
В Excel вместо понятия «поле диаграмм» применяются такие понятия, как область построения диаграммы и область диаграммы.
Область построения диаграмма- это область, в которой отображается только координатные оси и сама диаграмма, а область диаграммы — это область, в которой кроме координатных осей и самой диаграммы, заголовок диаграммы, обозначение единиц измерения координатных осей, легенда.
Каждый элемент диаграммы можно выделить, активизировать, а потом осуществлять с ним различные преобразования, как-то: изменять размеры, редактировать, форматировать (оформлять). [5]
С помощью перетаскивания можно перемещать область диаграммы и область построения диаграммы и область диаграммы, кроме того, можно изменять их размеры, а, следовательно, и размеры самой диаграммы и отдельных её элементов.
Кроме того, Excel позволяет изменять внешний вид области построения диаграммы и области диаграммы, т.е. изменять форму линий рамки обрамления, цвет и узор заполнения их внутренних частей.
Графический образ- это совокупность геометрических или графических знаков, с помощью которых отображаются статистические данные.
Графические средства Excel позволяют в качестве графического образа использовать различные знаки – символы, в том числе и рисунки. Точнее говоря, Excel автоматически заменяет геометрические знаки негеометрическими.
Изобразительные диаграммы, которые строятся с помощью негеометрических знаков, широко используется для пропаганды и популяризации статистических данных.
Excel имеет многочисленный арсенал средств для построения и оформления основных элементов диаграммы: линии могут быть разноцветными (существует 56 вариантов цветов) или иметь различную форму (тип) – сплошные, штриховые, точечные, штрих – пунктирные, а также разную толщину – тонкие, средние, полутолстые (полужирные) и толстые(жирные); точки данных могут быть изображены в виде маленьких кружков, квадратиков, треугольников, ромбов и других геометрических знаков с разными узорами. Excel предлагает 48 видов штриховки, а также позволяет изменять цвета, узоры, обрамления основных элементов диаграммы, в том числе, самых больших её частей – области построения диаграммы и области диаграммы. [5]
В Excel вместо понятия графического образа используется термин маркер данных. Вид символа маркера зависит от вида диаграммы: на гистограмме это (обычно) прямоугольники, на круговой диаграмме – сектора и т.п.
Пространственные ориентиры – это элементы диаграммы, определяющие порядок размещения графических знаков в поле диаграммы. Такой порядок задаётся определённой системой координат – совокупностью элементов, определяющих положение точки на прямой или кривой линии, на плоскости и в пространстве. При построении статистических диаграмм обычно применяются прямоугольная или декартова, полярная, треугольная или тригональная системы координат.
Прямоугольная система координат чаще всего применяется для статистических диаграмм по причине простоты её построения и наилучшей выразительности различных соотношений и зависимостей между изображаемыми статистическими величинами. Прямоугольная система координат образуется совокупностью двух пересекающихся перпендикулярных прямых, называемых осями координат. [11]
Для облегчения построения и чтения диаграммы её поля в пределах осей координат покрывают параллельными горизонтальными и вертикальными линиями, которые в совокупности образуют так называемую координатную сетку.
В Excel координатная сетка на плоскостных диаграммах наносится на область построения диаграммы, а на объёмных диаграммах, которые имеют две стенки и основания на них.
Графические средства Excel позволяют наносить линии координатной сетки либо на одну из осей, причём линии сетки могут проходить или через основные деления – основные линии, или через промежуточные деления – промежуточные линии.
Excel по умолчанию автоматически строит и размещает координатные оси в нужном месте диаграммы, используя встроенные установки для типа осевых линий, делений и размещений меток деления. Но все эти параметры можно изменять, а также управлять вводом, выводом и удалением координатных осей.
Можно задать нужный тип линий координатных осей и настроить её деления и метки делений.
Экспликация диаграммы – это пояснение содержания диаграммы и её основных элементов.
Экспликация включает общий заголовок диаграммы, подписи вдоль масштабных шкал и пояснительные надписи, раскрывающие смысл отдельных элементов графического образа. [5]
Excel располагает множеством инструментов, позволяющих выполнить экспликацию диаграммы, при этом каждый из элементов экспликации может быть отформатирован (оформлен) различными способами в зависимости от типа и вида диаграммы.
При построении диаграммы Excel по умолчанию, т.е. автоматически, размещает заголовок диаграммы в центре верхней области построения диаграммы, а надписи координатных осей возле каждой оси.
Отметим, что Excel имеет несколько инструментов, которые позволяют просто и быстро отформатировать любой текст т числа, имеющиеся на диаграмме. Они позволяют выбрать типы шрифтов и их размеры, способы выравнивания текста, оформления его жирным шрифтом, курсивом и подчеркиванием, а также добавить к нему рамки, узоры и цвет.
Excel позволяет выравнивать на диаграмме выделенный текст по горизонтали и вертикали, а также менять ориентацию текста, т.е. выравнивать его под определённым углом.
Кроме ввода, редактирования и форматирования заголовка диаграммы и надписей осей, Excel позволяет просто и быстро поместить на саму диаграмму дополнительные надписи, так называемые ярлыки, поясняющие её смысл и значение отдельных элементов. Этот дополнительный текст можно поместить в любое место диаграммы, изменить его размеры и отформатировать.
Excel позволяет форматировать имеющиеся на диаграмме объекты, в частности стрелки и надписи.
Специальное пояснение к маркерам или элементам, используемым в диаграмме, носит название легенды. Excel автоматически создаёт легенду из названий. Но также позволяет самостоятельно создавать легенду и перемещать её в нужное место.
Классификация статистических диаграмм
Диаграммы, применяемые для изображения статистических данных, очень разнообразны и имеют ряд особенностей, что обуславливает необходимость их классификации.
Классификация статистических диаграмм имеет чрезвычайное значение для их правильного построения и изучения. Она облегчает понимание отличительных особенностей различных типов и видов диаграмм, их возможностей в решении конкретных задач статистического исследования.
В Excel классификация диаграмм осуществлена по форме графического образа. По этому признаку выделено 14 основных, встроенных, или, как их принято называть, стандартных типов диаграмм, и 20 дополнительных, нестандартных, или специальных типов диаграмм. Каждый тип диаграмм представлен несколькими видами (форматами) как плоскостных, так и объёмных диаграмм, которые могут быть применены к данному типу диаграммы. Кроме того, Excel предоставляет пользователю возможность построения собственных типов диаграмм. [5]
Помимо основных, стандартных, типов диаграмм предлагает большое количество нестандартных, специальных, типов диаграмм. Основой нестандартных диаграмм являются стандартные типы диаграмм. Некоторые встроенные нестандартные типы диаграмм подобны стандартным типам. Вместе с тем они содержат дополнительные графические средства, которые расширяют не только наглядные, но и познавательные и аналитические возможности. В частности, они содержат такие встроенные графические элементы: легенду, координатную сетку, логарифмическую шкалу, объяснительные надписи; они имеют, скажем, более привлекательный вид, поскольку их форматирование выполнено с помощью специальных приёмов.
Кроме использования стандартных и нестандартных типов диаграмм, Excel предоставляет пользователю возможность создавать собственные типы диаграмм, сохранять и применять таким же образом, как и любые другие типы диаграмм. [5]
Чтобы создать собственный тип диаграммы, необходимо располагать диаграммой, которая будет служить основой для создания собственного типа диаграммы, при этом в качестве основы можно взять любой тип и вид уже построенной диаграммы, поскольку в любой момент графические средства Excel позволяют изменить его или создать диаграмму требуемого вида и типа.
Заключение
В развитых странах практически любое решение: политическое, финансовое, техническое, научно-исследовательское и даже бытовое решение принимается только после всестороннего анализа данных. Поэтому изучение прикладной статистики и методов анализа данных является неотъемлемым компонентом образования на всех уровнях, а компьютерные пакеты для аналитических исследований и прогнозирования являются настольным рабочим инструментом любого специалиста, так или иначе связанного с информационной сферой.
Таким образом, обработка статистических данных уже давно применяется в самых разнообразных видах человеческой деятельности. Вообще говоря, трудно назвать ту сферу, в которой она бы не использовалась. Но, пожалуй, ни в одной области знаний и практической деятельности обработка статистических данных не играет такой исключительно большой роли, как в экономике, имеющей дело с обработкой и анализом огромных массивов информации о социально-экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимают возможности табличного процессора MS Excel.
Представление экономических и других данных в электронных таблицах в наши дни стало простым и естественным. Оснащение же электронных таблиц средствами анализа способствует тому, что из группы сложных, глубоко научных и потому редко используемых, почти экзотических методов, статистический анализ превращается для специалиста в повседневный, эффективный и оперативный аналитический инструмент. Электронные таблицы делают такой анализ легко доступным.
Усвоив технологию использования табличного процессора MS Excel, можно применять его по мере необходимости, получая знание о скрытых связях, улучшая аналитическую поддержку принятия решений и повышая их обоснованность.
В данной работе я показала, что табличный процессор MS Excel обладает огромными возможностями для решения задач статистики, облегчая работу специалистов, работающих в этой области.
Список литературы
Бернс Дж., Берроуз Э. ,Секреты Excel 97. – М.:Веста, 1999.
Фигурнов В. Э. ,IBM PC для пользователя. – М.:ИНФРА, 1998.
А. Гончаров «Microsoft Excel 7.0 в примерах» — С.-П.:Питер, 1996
Пробитюк А., Excel 7.0 для Windows 95 в бюро. – К.:BHV, 1996
Лаврёнов С.М.,Excel: сборник примеров и задач-М: финансы и статистика,2000.-336с.
Макарова Н.В.,Трофимец В.Я., Статистика в Excel:учеб. пособие.-М.:финансы и статистика,2003.-386с.
Сидоров М.Г., Обработка данных в Excel //информатика и образование.-2000.-№6.-с. 25-36.
Гутовская Г.В., Использование Excel для решения финансово-экономических задач//информатика и образование.-2003.-№3.-с. 15-21.
Ивинская Н.Л., решение прикладных задач в Excel//информатика и образование.-2003.-№6.-с.62-64.
Кирей Е.А., Базовый курс Excel для учащихся профильных экономических классов//информатика и образование.-2004.-№5.-с.39-41.
Андрусенко Н.Е., Использование стандартных функций Excel для поиска и связи данных в таблице//информатика и образование.-2003.-№11.-с.7-12.
Содержание
- Создание графиков в Excel
- Построение обычного графика
- Редактирование графика
- Построение графика со вспомогательной осью
- Построение графика функции
- Вопросы и ответы
График позволяет визуально оценить зависимость данных от определенных показателей или их динамику. Эти объекты используются и в научных или исследовательских работах, и в презентациях. Давайте рассмотрим, как построить график в программе Microsoft Excel.
Каждый пользователь, желая более наглядно продемонстрировать какую-то числовую информацию в виде динамики, может создать график. Этот процесс несложен и подразумевает наличие таблицы, которая будет использоваться за базу. По своему усмотрению объект можно видоизменять, чтобы он лучше выглядел и отвечал всем требованиям. Разберем, как создавать различные виды графиков в Эксель.
Построение обычного графика
Рисовать график в Excel можно только после того, как готова таблица с данными, на основе которой он будет строиться.
- Находясь на вкладке «Вставка», выделяем табличную область, где расположены расчетные данные, которые мы желаем видеть в графике. Затем на ленте в блоке инструментов «Диаграммы» кликаем по кнопке «График».
- После этого открывается список, в котором представлено семь видов графиков:
- Обычный;
- С накоплением;
- Нормированный с накоплением;
- С маркерами;
- С маркерами и накоплением;
- Нормированный с маркерами и накоплением;
- Объемный.
Выбираем тот, который по вашему мнению больше всего подходит для конкретно поставленных целей его построения.
- Дальше Excel выполняет непосредственное построение графика.
Редактирование графика
После построения графика можно выполнить его редактирование для придания объекту более презентабельного вида и облегчения понимания материала, который он отображает.
- Чтобы подписать график, переходим на вкладку «Макет» мастера работы с диаграммами. Кликаем по кнопке на ленте с наименованием «Название диаграммы». В открывшемся списке указываем, где будет размещаться имя: по центру или над графиком. Второй вариант обычно более уместен, поэтому мы в качестве примера используем «Над диаграммой». В результате появляется название, которое можно заменить или отредактировать на свое усмотрение, просто нажав по нему и введя нужные символы с клавиатуры.
- Задать имя осям можно, кликнув по кнопке «Название осей». В выпадающем списке выберите пункт «Название основной горизонтальной оси», а далее переходите в позицию «Название под осью».
- Под осью появляется форма для наименования, в которую можно занести любое на свое усмотрение название.
- Аналогичным образом подписываем вертикальную ось. Жмем по кнопке «Название осей», но в появившемся меню выбираем «Название основной вертикальной оси». Откроется перечень из трех вариантов расположения подписи: повернутое, вертикальное, горизонтальное. Лучше всего использовать повернутое имя, так как в этом случае экономится место на листе.
- На листе около соответствующей оси появляется поле, в которое можно ввести наиболее подходящее по контексту расположенных данных название.
- Если вы считаете, что для понимания графика легенда не нужна и она только занимает место, то можно удалить ее. Щелкните по кнопке «Легенда», расположенной на ленте, а затем по варианту «Нет». Тут же можно выбрать любую позицию легенды, если надо ее не удалить, а только сменить расположение.
Построение графика со вспомогательной осью
Существуют случаи, когда нужно разместить несколько графиков на одной плоскости. Если они имеют одинаковые меры исчисления, то это делается точно так же, как описано выше. Но что делать, если меры разные?
- Находясь на вкладке «Вставка», как и в прошлый раз, выделяем значения таблицы. Далее жмем на кнопку «График» и выбираем наиболее подходящий вариант.
- Как видим, формируются два графика. Для того чтобы отобразить правильное наименование единиц измерения для каждого графика, кликаем правой кнопкой мыши по тому из них, для которого собираемся добавить дополнительную ось. В появившемся меню указываем пункт «Формат ряда данных».
- Запускается окно формата ряда данных. В его разделе «Параметры ряда», который должен открыться по умолчанию, переставляем переключатель в положение «По вспомогательной оси». Жмем на кнопку «Закрыть».
- Образуется новая ось, а график перестроится.
- Нам только осталось подписать оси и название графика по алгоритму, аналогичному предыдущему примеру. При наличии нескольких графиков легенду лучше не убирать.
Построение графика функции
Теперь давайте разберемся, как построить график по заданной функции.
- Допустим, мы имеем функцию
Y=X^2-2. Шаг будет равен 2. Прежде всего построим таблицу. В левой части заполняем значения X с шагом 2, то есть 2, 4, 6, 8, 10 и т.д. В правой части вбиваем формулу. - Далее наводим курсор на нижний правый угол ячейки, щелкаем левой кнопкой мыши и «протягиваем» до самого низа таблицы, тем самым копируя формулу в другие ячейки.
- Затем переходим на вкладку «Вставка». Выделяем табличные данные функции и кликаем по кнопке «Точечная диаграмма» на ленте. Из представленного списка диаграмм выбираем точечную с гладкими кривыми и маркерами, так как этот вид больше всего подходит для построения.
- Выполняется построение графика функции.
- После того как объект был построен, можно удалить легенду и сделать некоторые визуальные правки, о которых уже шла речь выше.

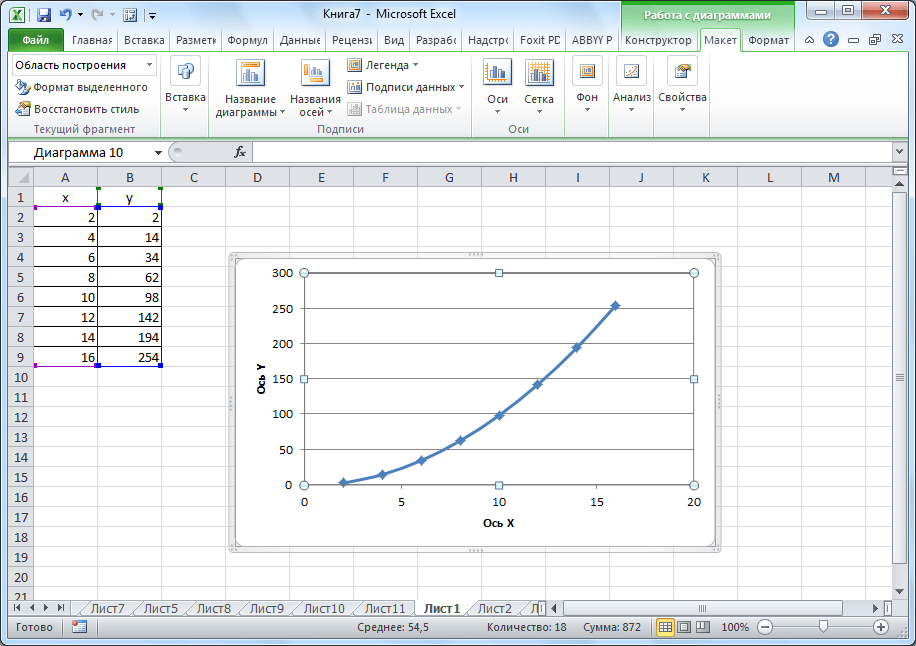
Как видим, Microsoft Excel предлагает возможность построения различных типов графиков. Основным условием для этого является создание таблицы с данными. Созданный график можно изменять и корректировать согласно целевому назначению.
Еще статьи по данной теме: