Содержание
- Основные функции Excel (они помогут при решении задачи №19 ГИА)
- Задание 14 ОГЭ информатика по теме «Электронные таблицы Excel»
- Объяснение заданий 14 ОГЭ по информатике
- Типы ссылок в ячейках
- Стандартные функции Excel
- Построение диаграмм
- Решение 14 задания ОГЭ
- Решение заданий ОГЭ прошлых лет для тренировки
- Формулы в электронных таблицах
- Анализ диаграмм
Основные функции Excel (они помогут при решении задачи №19 ГИА)
Основные функции Excel (они помогут при решении задачи №19 ГИА).
Вычисляет сумму чисел в ячейках указанного диапазона.
— вычисляет сумму чисел в ячейках от A1 до A10
Вычисляет среднее арифметическое чисел в ячейках в ячейках указанного диапазона.
— вычисляет среднее арифметическое чисел в ячейках от A1 до A10
Выводит минимальное число из диапазона ячеек
=МИН(A1:A10) – выведет минимальное число диапазона A1:A10
Выводит максимальное число из диапазона ячеек
=МАКС(A1:A10) – выведет максимальное число диапазона A1:A10
Считает количество ячеек с числами (любыми!)
=СЧЁТ(A1:A10) – вычисляет количество ячеек с числами в диапазоне от A1 до A10
Считает количество ячеек, данные в которых соответствуют условию.
=СЧЁТЕСЛИ(A1:A10;”Иванов”) – вычислит количество ячеек, где записано слово Иванов.
=СЧЁТЕСЛИ(A1:A10;50) – вычислит количество ячеек, где записано число 50.
=СЧЁТЕСЛИ(A1:A10;” 10,»Больше 10″,»10 или меньше») возвращает строку «Больше 10» «, если значение в ячейке A1 больше 10, и «10 или меньше», если оно меньше или равно 10.
Пример №1. Дана таблица и в ячейке B1 записана формула =СЧЁТ(A1:A10):
В этом примере всего ячеек – 10. Из них – одна пустая и одна – с текстом. Будет выдан ответ 8.

Источник
Задание 14 ОГЭ информатика по теме «Электронные таблицы Excel»
Объяснение заданий 14 ОГЭ по информатике
Типы ссылок в ячейках
Формулы, записанные в ячейках таблицы, бывают относительными, абсолютными и смешанными.
- Имена ячеек в относительной формуле автоматически меняются при переносе или копировании ячейки с формулой в другое место таблицы:
Относительная адресация:
имя столбца вправо на 1
номер строки вниз на 1
Абсолютная адресация:
имена столбцов и строк при копировании формулы остаются неизменными
Стандартные функции Excel
В ОГЭ встречаются в формулах следующие стандартные функции. Ниже рассмотрен их смысл. Наводите курсор на пример для просмотра ответа.
| русский | англ. | действие | синтаксис |
|---|---|---|---|
| СУММ | SUM | Суммирует все числа в интервале ячеек | СУММ(число1;число2) |
| Пример: | |||
| =СУММ(3; 2) =СУММ(A2:A4) |
|||
| СЧЁТ | COUNT | Подсчитывает количество всех непустых значений указанных ячеек | СЧЁТ(значение1, [значение2],…) |
| Пример: | |||
| =СЧЁТ(A5:A8) | |||
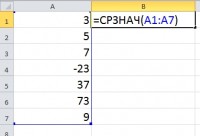
| СРЗНАЧ | AVERAGE | Возвращает среднее значение всех непустых значений указанных ячеек | СРЕДНЕЕ(число1, [число2],…) |
| Пример: | |||
| =СРЗНАЧ(A2:A6) | |||
| МАКС | MAX | Возвращает наибольшее значение из набора значений | МАКС(число1;число2; …) |
| Пример: | |||
| =МАКС(A2:A6) | |||
| МИН | MIN | Возвращает наименьшее значение из набора значений | МИН(число1;число2; …) |
| Пример: | |||
| =МИН(A2:A6) | |||
| ЕСЛИ | IF | Проверка условия. Функция с тремя аргументами: первый аргумент — логическое выражение; если значение первого аргумента — истина, то результатом выполнения функции является второй аргумент. Если ложно — третий аргумент. | ЕСЛИ(лог_выражение; значение_если_истина; значение_если_ложь) |
| Пример: | |||
| =ЕСЛИ(A2>B2;»Превышение»;»ОК») | |||
| СЧЁТЕСЛИ | COUNTIF | Количество непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. | СЧЁТЕСЛИ(диапазон, критерий) |
| Пример: | |||
| =СЧЁТЕСЛИ(A2:A5;»яблоки») | |||
| СУММЕСЛИ | SUMIF | Сумма непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. | СУММЕСЛИ (диапазон, критерий, [диапазон_суммирования]) |
| Пример: | |||
| =СУММЕСЛИ(B2:B25;»>5″) |
В качестве параметра функции везде указывается диапазон ячеек: МИН(А2:А240)
следует иметь в виду, что при использовании функции СРЗНАЧ не учитываются пустые ячейки и текстовые ячейки; например, после ввода формулы в C2 появится значение 2 (не учитывается пустая А2):
Построение диаграмм
- Диаграммы используются для наглядного представления табличных данных.
- Разные типы диаграмм используются в зависимости от необходимого эффекта визуализации.
- Так, круговаяи кольцеваядиаграммы отображают соотношение находящихся в выбранном диапазоне ячеек данных к их общей сумме. Иными словами, эти типы служат для представления доли отдельных составляющих в общей сумме.
- Соответствие секторов круговой диаграммы (если она намеренно НЕ перевернута) начинается с «севера»: верхний сектор соответствует первой ячейке диапазона.
Типы диаграмм Линейчатаяи Гистограмма(на левом рис.), а также Графики Точечная(на рис. справа) отображают абсолютные значения в выбранном диапазоне ячеек.

Решение 14 задания ОГЭ
В электронную таблицу занесли данные о тестировании учеников по выбранным ими предметам.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | Округ | Фамилия | Предмет | Баллы |
| 2 | С | Ученик 1 | Физика | 240 |
| 3 | В | Ученик 2 | Физкультура | 782 |
| 4 | Ю | Ученик 3 | Биология | 361 |
| 5 | СВ | Ученик 4 | Обществознание | 377 |
В столбце A записан код округа, в котором учится ученик;
в столбце B – код фамилии ученика;
в столбце C – выбранный учеником предмет;
в столбце D – тестовый балл.
Всего в электронную таблицу были занесены данные по 1000 учеников.
Откройте файл с данной электронной таблицей (расположение файла Вам сообщат организаторы экзамена). На основании данных, содержащихся в этой таблице, выполните задания.
- Сколько учеников, которые проходили тестирование по информатике, набрали более 600 баллов? Ответ запишите в ячейку H2 таблицы.
- Каков средний тестовый балл учеников, которые проходили тестирование по информатике? Ответ запишите в ячейку H3 таблицы с точностью не менее двух знаков после запятой.
- Постройте круговую диаграмму, отображающую соотношение числа участников тестирования из округов с кодами «В», «Зел» и «З». Левый верхний угол диаграммы разместите вблизи ячейки G6 . В поле диаграммы должны присутствовать легенда (обозначение соответствия данных определённому сектору диаграммы) и числовые значения данных, по которым построена диаграмма.
Полученную таблицу необходимо сохранить под именем, указанным организаторами экзамена.
- Поскольку спрашивается об учениках, которые проходили тестирование по информатике и набрали более 600 баллов, то здесь необходимо учесть одновременно два условия. Поэтому будем использовать функцию ЕСЛИ с логическим оператором И (одновременное выполнение нескольких условий). В ячейку E2 запишем формулу:
или для англоязычного интерфейса:
Ответ: 32
Решение задания 2:
- В ячейку F2 внесем формулу:
или для англоязычной раскладки:
Ответ: 546,82
Решение задания 3:

Ответ: Секторы диаграммы должны визуально соответствовать соотношению 32:29:108.
Выполните задание:
Откройте файл с данной электронной таблицей (расположение файла Вам сообщат организаторы экзамена). На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Сколько учеников в Северо-Восточном округе (СВ) выбрали в качестве любимого предмета математику? Ответ на этот вопрос запишите в ячейку Н2 таблицы.
- Каков средний тестовый балл у учеников Южного округа (Ю)? Ответ на этот вопрос запишите в ячейку Н3 таблицы с точностью не менее двух знаков после запятой.
Ответ: 17
Возможны и другие варианты решения.
Ответ: 525,70
Разбор задания 14.2 :
В электронную таблицу занесли данные о калорийности продуктов. Ниже приведены первые пять строк таблицы. 
в столбце B – содержание в нём жиров;
в столбце C – содержание белков;
в столбце D – содержание углеводов и
в столбце Е – калорийность этого продукта.
Всего в электронную таблицу были занесены данные по 1000 продуктам.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Сколько продуктов в таблице содержат меньше 50 г углеводов и меньше 50 г белков? Запишите число, обозначающее количество этих продуктов, в ячейку H2 таблицы.
- Какова средняя калорийность продуктов с содержанием жиров менее 1 г? Запишите значение в ячейку H3 таблицы с точностью не менее двух знаков после запятой.
Поскольку в задании используется условие, то начнем с него: два условия, значит будем использовать функцию ЕСЛИ с логической операцией И . Формула будет выполняться по значениям каждой строки, поэтому запишем ее сначала для второй строки таблицы, там, где начинаются основные данные. В ячейке F2:
Ответ: 864
Возможны и другие варианты решения.
Ответ: 51,10.
Всего в электронную таблицу были занесены данные по 370 перевозкам в хронологическом порядке.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- На какое суммарное расстояние были произведены перевозки с 1 по 3 октября? Ответ на этот вопрос запишите в ячейку H2 таблицы.
- Какова средняя масса груза при автоперевозках, осуществлённых из города Липки? Ответ на этот вопрос запишите в ячейку H3 таблицы с точностью не менее одного знака после запятой.
Таким образом, смотрим, что последняя запись за «3 октября» соответствует ячейке A118. Значит, для получения суммарного расстояния будем вычислять сумму по диапазону ячеек D2:D118 (столбец Расстояние). Используем функцию СУММ .
Ответ: 28468
Задание 1 второй способ:
Ответ: 28468
Возможны и другие варианты решения, например, сортировка строк по значению столбца B с дальнейшим выбором необходимых диапазонов для функций.
Ответ: 760,9
Всего в электронную таблицу были занесены данные по 272 учащимся. Порядок записей в таблице произвольный.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Сколько учащихся школы № 2 набрали по информатике больше баллов, чем по географии? Ответ на этот вопрос запишите в ячейку F2 таблицы.
- Сколько процентов от общего числа участников составили ученики, получившие по географии больше 50 баллов? Ответ с точностью до одного знака после запятой запишите в ячейку F3 таблицы.
Ответ: 37
- Задание 2:
Найдём количество участников, набравших по географии более 50 баллов. Воспользуемся одной из возможных в таких случаях функций — функцией СЧЁТЕСЛИ(диапазон;критерий). В качестве критерия укажем условие «>50», обязательно указанное в кавычках. Запишем формулу в свободной ячейке H2:
Возможны и другие варианты решения.
Ответ: 74,6
Всего в электронную таблицу были занесены данные по 266 учащимся. Порядок записей в таблице произвольный.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Чему равна средняя сумма баллов по двум предметам среди учащихся школ округа «Южный»? Ответ на этот вопрос запишите в ячейку F2 таблицы.
- Сколько процентов от общего числа участников составили ученики школ округа «Западный»? Ответ с точностью до одного знака после запятой запишите в ячейку F3 таблицы.
Необходимо найти среднюю сумму баллов по двум предметам. Значит, для учащихся южного округа посчитаем сумму баллов по двум ячейкам со значениями баллов по предметам. Так как предусмотрено условие, то будем использовать функцию ЕСЛИ , а в случае истинности значения — выводить сумму двух ячеек. Для этого в ячейке G2 (свободный столбец) запишем формулу:
Ответ: 117,15;
Ответ: 15,4.
Каждая строка таблицы содержит запись об одном поэте. В столбце А записана фамилия, в столбце В — имя, в столбце С — отчество, в столбце D — год рождения, в столбце Е — год смерти.
Всего в электронную таблицу были занесены данные по 150 поэтам Серебряного века в алфавитном порядке.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Определите количество поэтов, родившихся в 1889 году. Ответ на этот вопрос запишите в ячейку H2 таблицы.
- Определите в процентах, сколько поэтов, умерших позже 1940 года, носили имя Сергей. Ответ с точностью не менее 2 знаков после запятой запишите в ячейку НЗ таблицы.
Ответ: 8.
Ответ: 6,02.
Каждая строка таблицы содержит запись об одном ученике. В столбце А записана фамилия, в столбце В — имя; в столбце С — класс; в столбце D — рост, в столбце Е — вес учеников.
Всего в электронную таблицу были занесены данные по 211 ученикам в алфавитном порядке.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Каков рост самого высокого ученика 10 класса? Ответ на этот вопрос запишите в ячейку H2 таблицы.
- Какой процент учеников 8 класса имеет вес больше 65? Ответ с точностью не менее 2 знаков после запятой запишите в ячейку НЗ таблицы.
Ответ: 1) 199; 2) 53,85.
В столбце А указана фамилия; в столбце В — имя; в столбце С — пол; в столбце D — год рождения; в столбце Е — результаты в беге на 1000 метров; в столбце F — результаты в беге на 30 метров; в столбце G — результаты по прыжкам в длину с места.
Всего в электронную таблицу были занесены данные по 1000 учащимся.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Сколько процентов участников пробежало дистанцию в 1000 м меньше, чем за 5 минут? Ответ запишите в ячейку L1 таблицы.
- Найдите разницу в см с точностью до десятых между средним результатом у мальчиков и средним результатом у девочек в прыжках в длину. Ответ на этот вопрос запишите в ячейку L2 таблицы.
Ответ: 1) 59,4; 2)6,4.
Результаты сдачи выпускных экзаменов по алгебре, русскому языку, физике и информатике учащимися 9 класса некоторого города были занесены в электронную таблицу. На рисунке приведены первые строки получившейся таблицы:
Всего в электронную таблицу были занесены результаты 1000 учащихся.
Выполните задание:
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
- Какое количество учащихся получило только четвёрки или пятёрки на всех экзаменах? Ответ на этот вопрос запишите в ячейку I2 таблицы.
- Для группы учащихся, которые получили только четвёрки или пятёрки на всех экзаменах, посчитайте средний балл, полученный ими на экзамене по алгебре. Ответ на этот вопрос запишите в ячейку I3 таблицы с точностью не менее двух знаков после запятой.
- В задании необходимо посчитать количество определенных данных, в зависимости от условий. Можно было бы использовать функцию СЧЁТЕСЛИ(), но ситуация осложняется тем, что в задании несколько условий: только четвёрки или пятёркина всех (четырех!) экзаменах.
- Если заданы несколько условий, то следует использовать сначала логическую функцию ЕСЛИ с логической операцией И для выполнения четырех условий для четырех экзаменов одновременно.
- При этом заметим, что оценка 4 или 5, означает условие оценка > 3. Применим данную функцию сначала для первой строки с данными. Для этого в ячейке G2 (свободный столбец) запишем формулу:
Ответ: 1)88; 2)4,32.
Решение заданий ОГЭ прошлых лет для тренировки
Рассмотрим, как решается задание 14 ОГЭ по информатике.
Формулы в электронных таблицах
Подробный видеоразбор по ОГЭ 14 задания:
Перемотайте видеоурок на решение заданий, если не хотите слушать теорию.
📹 Видеорешение на RuTube здесь
Какая из формул, приведённых ниже, может быть записана в ячейке A2, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку?
- Вычислим значения в ячейках согласно заданным формулам:
- Вспомним, что круговая диаграмма отображает части целого. Из вычисленных значений имеем три подряд идущих сектора, равных соответственно: 4, 16 и 8. Секторы должны следовать подряд, т.к. в заданном диапазоне A2:D2 эти значения тоже идут друг за другом (по часовой стрелке).
- Расставим в диаграмме известные значения в те секторы, которые подходят им по размеру:
Ответ: 4
Разбор задания 14.2:
Дан фрагмент электронной таблицы:
Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку?
- Обратим внимание, что ни в одной формуле указанного диапазона ячеек не встречается ячейка A1. То есть оставим ее пустой.
- Вычислим значения в ячейках согласно заданным формулам:
- Вспомним, что круговая диаграмма отображает части целого. Из вычисленных значений имеем три подряд идущих сектора, равных соответственно: 1, 1 и 1. Секторы должны следовать подряд, т.к. в заданном диапазоне A2:D2 эти значения тоже идут друг за другом (по часовой стрелке).
- По диаграмме видим, что четвертый сектор должен быть равен сумме трёх рассмотренных секторов, т.е. 1+1+1 = 3. Подставим это значение для формулы ячейки D2:
- Получили B1 = 6. Это соответствует варианту 2 .
Ответ: 2
Разбор задания 14.3:
Дан фрагмент электронной таблицы:
Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку?
- Обратим внимание, что ни в одной формуле указанного диапазона ячеек не встречается ячейка D1. То есть оставим ее пустой.
- Вычислим значения в ячейках согласно заданным формулам:
- Вспомним, что гистограмма отображает абсолютное значение в выбранном диапазоне ячеек. Из вычисленных значений имеем три подряд идущих столбика, равных соответственно: 2, 4 и 1. Столбики должны следовать подряд, т.к. в заданном диапазоне A2:D2 эти значения тоже идут друг за другом (слева направо).
- По диаграмме видим, что четвертый столбик должен быть равен значению третьего столбика, умноженного на 3 (1 * 3 = 3), или разности значений второго и третьего столбика (4 — 1 = 3), т.е. значение 3. Подставим это значение для формулы ячейки D2:
- Получили B1 = 4. Это соответствует варианту 4 .
Ответ: 4
Анализ диаграмм
На диаграмме отображено количество участников тестирования по предметам в разных регионах России. 
Какая из диаграмм правильно отражает соотношение общего количества участников (из всех трех регионов) по каждому из предметов тестирования? 
✍ Решение:
- столбчатая диаграмма позволяет определить числовые значения. Так, например, в Татарстане по биологии количество участников 400 и т.п. Найдем с помощью нее общее количество участников со всех регионов по каждому предмету. Для этого посчитаем значения абсолютно всех столбцов в диаграмме:
- по круговой диаграмме можно определить только доли отдельных составляющих в общей сумме: в нашем случае это доли участников по различным предметам тестирования;
- для того чтобы разобраться, какая круговая диаграмма подходит, сначала посчитаем самостоятельно долю участников, тестирующихся по отдельным предметам; для этого из столбчатой диаграммы вычислим сумму участников по каждому предмету и разделим на уже полученное в первом пункте общее количество участников:
- Теперь сравним полученные данные с круговыми диаграммами. Данные соответствуют диаграмме под номером 1 .
Результат: 1
Предлагаем посмотреть подробный разбор данного 7 задания на видео:
📹 Видеорешение на RuTube здесь
На диаграмме отображено количество участников тестирования по предметам в разных регионах России. 
Какая из диаграмм правильно отражает соотношение количества участников тестирования по истории в регионах? 
✍ Решение:
Подробный разбор задания смотрите на видео:
📹 Видеорешение на RuTube здесь
Источник
На уроке рассмотрен разбор 19, 20, 21 задания ЕГЭ по информатике: дается подробное объяснение и решение задания
Содержание:
- Объяснение заданий 19, 20 и 21 ЕГЭ по информатике
- Теория игр. Поиск выигрышной стратегии
- Решение 19, 20, 21 заданий ЕГЭ по информатике
- Игра с двумя кучами камней или табличка
- Задания для тренировки 19, 20, 21 заданий ЕГЭ (взяты из КИМ и сборников прошлых лет)
- Игра с одной кучей камней
- Игра с набором слов
Объяснение заданий 19, 20 и 21 ЕГЭ по информатике
19-е задание: «Анализ алгоритма логической игры»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение анализировать алгоритм логической игры
20-е задание: «Поиск выигрышной стратегии»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение найти выигрышную стратегию игры
21-е задание: «Дерево игры для выигрышной стратегии»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 10 минут.
Проверяемые элементы содержания: Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию
До ЕГЭ 2021 года — эти задания были объединены в задание № 26 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Для пункта 2 или 3 в представленной стратегии рассмотрены не все возможные ходы проигрывающего игрока, которые он может сделать при игре выигрывающего игрока по выигрышной стратегии.
Для пункта 3 представлено дерево игры, содержащее лишние ветви, не относящиеся к выигрышной стратегии.
Дерево, являющееся частью ответа на пункт 3, представлено с использованием ссылок на
фрагменты, являющиеся решениями других пунктов задания.
В задании спрашивается, в частности, кто выиграет, а в ответе не указан в явном виде выигрывающий игрок. На все вопросы, поставленные в задании, должны быть даны чёткие ответы. Ответ на вопрос о выигрышной стратегии в стиле «Может выиграть первый игрок, но если он неправильно пойдёт, то выиграет второй» является ошибочным, поскольку выигрышная стратегия одного игрока не оставляет возможности победы другому игроку»
ФГБНУ «Федеральный институт педагогических измерений»
* Некоторые изображения и примеры страницы взяты из материалов презентации К. Полякова
Теория игр. Поиск выигрышной стратегии
Для решения 19 задания необходимо вспомнить следующие темы и понятия:
- для того чтобы найти выигрышную стратегию в несложных играх, достаточно использовать метод перебора всех возможных вариантов ходов игроков;
- для решения задач 19 задания чаще всего для этого применяется метод построения деревьев;
- если от каждого узла дерева отходят две ветви, т.е. возможные варианты хода, то такое дерево называется двоичным (если из каждой позиции есть три варианта продолжения, дерево будет троичным).
- все позиции в простых играх делятся на выигрышные и проигрышные;
- выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, обязательно выиграет при любых действиях соперника, если не допустит ошибки; при этом говорят, что у данного игрока есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть;
- если игрок, делающий первый ход, находится в проигрышной позиции, то он обязательно проиграет, если ошибку не сделает его оппонент; в этом случае говорят, что у данного игрока нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для оппонента;
- выигрышные и проигрышные позиции характеризуются так:
- позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
- позиция, из которой хотя бы один из последующих возможных ходов ведет в проигрышную позицию — выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для оппонента) позицию.
- для того чтобы определить, какой из игроков выиграет при стратегически правильной игре, необходимо ответить на вопросы:
- Может ли какой-либо из игроков выиграть, независимо от ходов других игроков?
- Что должен сделать игрок с выигрышной стратегией первым ходом, чтобы он смог выиграть, независимо от действий ходов игроков?
Выигрышная стратегия
Выигрышные и проигрышные позиции
Кто выиграет при стратегически правильной игре?
Рассмотрим пример:
Игра: в кучке лежит 5 спичек; играют два игрока, которые по очереди убирают спички из кучки; условие: за один ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку
Решение:
- Будем использовать метод построения дерева. Первый играющий может убрать одну спичку (в этом случае их останется 4) или сразу 2 (останется 3), эти два варианта отобразим при помощи дерева:
- если первый игрок оставил 4 спички, второй может своим ходом оставить 3 или 2; а если после первого хода осталось 3 спички, второй игрок может выиграть, взяв две спички и оставив одну:
- если осталось 3 или 2 спички, то 1-ый игрок (в обеих ситуациях) выиграет своим ходом:
- если первый игрок своим первым ходом взял две спички, то второй сразу выигрывает; если же он взял одну спичку, то своим вторым ходом он может выиграть, независимо от хода второго игрока;
- итак, убрав всего одну спичку первым ходом, 1-ый игрок всегда может выиграть на следующем ходу;
- тогда как второй игрок не может выиграть, независимо от действий первого: потому что, если первый игрок сначала убрал одну спичку, второй всегда проиграет.
проанализируем стратегию игры:
Ответ: при правильной игре (стратегии игры) выиграет первый игрок; для этого ему достаточно своим первым ходом убрать одну спичку.
Решение 19, 20, 21 заданий ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Игра с двумя кучами камней или табличка
19_8:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 59. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 59 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 53.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Задание 20 ЕГЭ.
Найдите минимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Задание 21 ЕГЭ.
Найдите два значения S, при которых одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Найденные значения запишите в ответе в порядке возрастания.
✍ Решение:
- Нарисуем таблицу, в первом столбце которой будем откладывать количество камней в первой куче, а в первой строке — количество камней во второй куче. Получим матрицу. Поскольку в первой куче количество начинается с 5, то это и будет первым значением в таблице. Во второй куче начнем с наибольшего возможного числа — 53. Таблица пригодится для решения заданий 20 и 21:
- Для начала найдем все выигрышные позиции для первой строки таблицы, т.е. для первого хода. Обозначим их плюсами (
+): - Для того, чтобы получить наименьшее значение
S, в качестве первого хода Пети необходимо увеличивать в два раза вторую кучу. Т.е. для решения задания необходимо найти такое наименьшееS, при котором Петя походил неверно, и попал своим ходом в выигрышную позицию для своего соперника, т.е. в ячейку с плюсом:
Выигрышные позиции для первой строки ищем по принципу увеличения количества камней S в 2 два раза: 5 + S*2 >=59. Получим S>=27
S = 14 1 ход Петя: 14*2 = (5,28) 2 ход Ваня: 28*2 = (5,56), Сумма = 61, Выигрыш!
Ответ: 14
✎ Задание 20:
- Проанализируем таблицу, и для каждой строки найдем выигрышные позиции с одного хода. Т.е. которые позволят игроку, оказавшемуся «на них», выиграть за один ход (получить суммарно 59 и более камней):
- Найдем проигрышные позиции: те, которые ведут только в выигрышные позиции для соперника (ведут только в плюсы)
- В задании требуется найти минимальное
S, котором выиграет Петя, но выиграет он НЕ первым своим ходом, а вторым. То есть в нашем случае необходимо найтиS, которое может перевести соперника в проигрышную позицию. То есть в минус. Для первой строки (так как первым будет ходить Петя) таких значений два: - Наименьшее S = 24
При заполнении таблицы выигрышными позициями можно проследить закономерность «узора», а заполнять позиции по аналогии.
Проигрышные позиции: (6,26) (8,25) (10,24) (12,23) (14,22)
- Для решения этого задания найдем выигрышные позиции со второго хода, т.е. которые могут перевести соперника в проигрышную позицию (с минусом):
- Чтобы выиграл Ваня, но выиграл не первым ходом, а вторым, необходимо, чтобы Петя находился в такой позиции, которая ведет его только на выигрышные позиции со второго хода:

Ответ: 23 25
>19_9:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя.
За один ход игрок может убрать из одной из куч один камень или уменьшить количество камней в куче в два раза (если количество камней в куче нечётно, остаётся на 1 камень больше, чем убирается).
Например, пусть в одной куче 6, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (5, 9), (3, 9), (6, 8), (6, 5).
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не более 20. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 20 или меньше камней. В начальный момент в первой куче было 10 камней, во второй куче – S камней, S > 10.
Найдите значение S, при котором Ваня выигрывает своим первым ходом при любой игре Пети?
Задание 20 ЕГЭ.
Найдите минимальное и максимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Задание 21 ЕГЭ.
Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
✍ Решение (Excel):
✎ Задание 19:
- В столбце
Аотложим значения — количество камней в первой куче. Начнем с ячейкиА2, в которую внесем начальное количество камней, т.е. 10. Автозаполнением продлим значения вниз до 0: - В строке 1 таблицы (начиная с ячейки
B1) отложим значения для второй кучи. Поскольку в задании говорится, что победа будет достигнута при S<=20, и достигнуть этого значения более сильной командой можно уменьшив кол-во камней во второй куче в два раза, начиная с числа 40: 40/20. То есть возьмем значение больше 40, примерно 45. Используем автозаполнение до значения 11: - Из двух команд, которые могут выполнять игроки, выберем наиболее сильную, т.е. благодаря которой можно быстрее достичь выигрышного диапазона и попасть в значения S<=20. Это команда уменьшения количества камней в два раза, т.е.
/2. - Для каждой из ячеек полученной таблицы рассчитаем значение, полученное в результате уменьшения в два раза той кучи камней, в которой большее количество камней (так как это даст меньший результат). Например, для ячейки
С5, в которой игрок имеет в первой куче 7 камней, а во второй куче 44 камня, мы бы выполнили действие 44/2+7. Т.е. уменьшили вдвое вторую кучу, т.к. в ней больше камней. Еще необходимо обращать внимание на четность и нечетность значений (в Excel это функцияЕНЕЧЁТ— возвращает ИСТИНУ, если значение нечетно). - Чтобы автоматизировать процесс необходимо использовать формулу, в которой найдем максимальное значение из двух вариантов:
Минимальное из (ЕСЛИ(ЕНЕЧЁТ(1-я куча)то(1-я куча+1)/2+2-я куча,иначе1-я куча/2+2-я куча);ЕСЛИ(ЕНЕЧЁТ(2-я куча)то(2-я куча+1)/2+1-я куча,иначе2-я куча/2+1-я куча)).
B2:= МИН(ЕСЛИ(ЕНЕЧЁТ($A2);($A2+1)/2+B$1;$A2/2+B$1);ЕСЛИ(ЕНЕЧЁТ(B$1);(B$1+1)/2+$A2;B$1/2+$A2))
$ будем использовать для фиксации столбца А и строки 1 при копировании формулы.
Ответ: 21
✎ Задание 20:
- Продолжаем работать с той же таблицей, что и в задании 19. Выделим все проигрышные позиции (из которых можно походить только в выигрышные позиции для соперника, т.е. в выделенные ячейки):
- Петя может выиграть свои вторым ходом, если он не может выиграть первым ходом, но может выполнить ход в позицию, проигрышную для соперника (в ячейку, выделенную красным). Такие позиции назовем выигрышные позиции со второго хода. Найдем минимальное и максимальное значение
Sпри таком первом ходе Пети:
При S=44 Пете необходимо уменьшить 2-ю кучу вдвое (44/2 = 22), чтобы оказаться в проигрышной позиции для соперника.
Ответ: 22 44
✎ Задание 21:
- Выделим все такие выигрышные позиции со второго хода:
- Далее придерживаемся следующей логики: Ваня сможет выиграть свои первым или вторым ходом, но при этом не гарантированно первым ходом, если у Пети будет возможность выполнить ходы только в позиции выигрышные со второго хода. Найдем такое S:
При S = 24 Петя сможет уменьшить кучи на один камень, и тогда оказывается в выделенной зеленой области — выигрышные позиции со второго хода для Вани, либо уменьшить количество камней вдвое, и тогда Ваня оказывается в выигрышной позиции с первого хода (розовая область).
Ответ: 24
19_7: с экзамена ЕГЭ 2020г. (со слов учащегося):
Два игрока, Петя и Ваня, играют в следующую игру. На табличке написаны два значения. Оба игрока в свой ход могут заменить одно из значений на сумму обеих (по своему выбору). Первый ход делает Петя. Игра считается законченной когда сумма обеих значений равняется не меньше 56. То есть выигрывает игрок, получивший 56 или более в сумме. Начальное значение (10, S).
Найдите максимальное S при котором Петя не может выиграть первым ходом.
Задание 20 ЕГЭ.
У кого из игроков есть выигрышная стратегия при начальном значении (9, 15).
Задание 21 ЕГЭ.
У кого из игроков есть выигрышная стратегия при начальном значении (3,7)? Опишите эту стратегию и изобразите дерево всех возможных партий
при этой стратегии
.
Типовые задания для тренировки
✍ Решение:
- Задание 19.
Максимальное S при котором Петя НЕ может выиграть своим первым ходом S = 22. Петя проиграет, если в сумме получится 55 и меньше. Первое значение = 10, необходимо найти второе значение, при этом максимальное. Схематично отобразим варианты ходов:
(10,22) - ход Пети - (10+22, 22) - итог суммы обеих значений таблички: 32 + 22 = 54 (<56)
Для того, чтобы сделать сумму большей, Петя заменит первое значение на сумму, так как оно меньше второго значения (10<22)
В начальной позиции (9, 15) выигрышная стратегия есть у Вани. Для себя отобразим схематично выигрышную партию Вани:
Зеленым цветом выделены выигрышные ходы.
В начальной позиции (3, 7) выигрышная стратегия есть у Вани. Изобразим дерево всех возможных партий при этой стратегии (раз говорится «при этой стратегии» имеем в виду, выигрышную стратегию Вани):

Дерево для выигрышной стратегии Вани: для Вани отображены только ходы по стратегии, для Пети — все возможные ходы. Зеленым цветом — выигрышный ход, красная обводка — ход по стратегии.
Решение подобного задания в Excel смотрите на видео:
📹 Видео
📹 Видеорешение на RuTube здесь
19_6:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) два камня или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 44.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 44 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 38.
Задание 19 ЕГЭ.
При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
Задание 20 ЕГЭ.
Назовите одно любое значение S, при котором Петя может выиграть своим вторым ходом.
Задание 21 ЕГЭ.
Назовите значение S, при котором Ваня выигрывает своим первым или вторым ходом.
✍ Решение:
- Нарисуем таблицу, в первом столбце которой будем откладывать количество камней в первой куче, а в первой строке — количество камней во второй куче. Получим матрицу. Поскольку в первой куче количество начинается с 5, то это и будет первым значением в таблице. Во второй куче начнем с наибольшего возможного числа — 38:
- Далее будем рассуждать так: Петя может выиграть первым ходом, выполнив команду *2 (увеличить количество камней в куче в два раза), если вместо S (кол-во камней во второй куче), мы будем изменять значение, начиная от 20, до последнего возможного по условию значения 38:
Задание 19 а):
5 + 20*2 = 45 (>44) * 5 - кол-во камней в первой куче, оно не меняется по условию
+ означает выигрышную позицию с первого хода:Ответ 1 а):
S = [20;38] (На ЕГЭ пояснить ходы, например: (5; 20) -> (Ход Пети)-> (5;40); 40 + 5 = 45)
Задание 19 б):
+). Отметим такие позиции, учитывая, что это первый ход Пети, и кол-во камней в первой куче должно быть 5. Найденные позиции будут проигрышными позициями (-):S = 19 (На ЕГЭ пояснить ходы, например: (5; 19) -> (Ходы Пети): (5;21),(5;28);(7;19);(7;28). Везде следующим ходом выиграет Ваня, см. предыдущ. пункт)
Задание 20:
2+):
S = 16, 17 или 18 (На ЕГЭ пояснить ходы, ссылаясь на объяснения в предыдущих пунктах)
Задание 21:
+), либо в позицию выигрышную со второго хода или n-го хода (2+). Это позиция при S = 14:
Ответ 3: S = 14 (На ЕГЭ пояснить ходы, ссылаясь на объяснения в предыдущих пунктах)
📹 YouTube здесь
Видеорешение на RuTube здесь
Задания для тренировки 19, 20, 21 заданий ЕГЭ (взяты из КИМ и сборников прошлых лет)
Игра с одной кучей камней
19_3: Демоверсия ЕГЭ 2018 информатика:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Задание 19 ЕГЭ
а) Укажите такие значения числа S, при которых Петя может выиграть в один ход.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 20 ЕГЭ
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причем:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для указанных значений S опишите выигрышную стратегию Пети.
Задание 21 ЕГЭ
Укажите значение S, при котором:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции
Дерево не должно содержать партий, невозможных при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.
✍ Решение:
-
Задание 19.
- а) Петя может выиграть, если S = 15, … 28
15, ..., 28 - выигрышные позиции с первого хода
S = 14 Петя: 14 + 1 = 15 выигрышная позиция (см. п. а). Выигрывает Ваня Петя: 14 * 2 = 28 выигрышная позиция (см. п. а). Выигрывает Ваня 14 - проигрышная позиция
Задание 20.
S = 7 Петя: 7 * 2 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Петя S = 13 Петя: 13 + 1 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Петя 7, 13 - выигрышные позиции со второго хода
Задание 21.
S = 12 Петя: 12 + 1 = 13 Ваня: 13 + 1 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Ваня вторым ходом!
В таблице изображено дерево возможных партий (и только их) при описанной стратегии Вани. Заключительные позиции (в них выигрывает Ваня) подчеркнуты. На рисунке это же дерево изображено в графическом виде.
Дерево всех партий, возможных при стратегии Вани:
* красный круг означает выигрыш
19_4: Досрочный егэ по информатике 2018, вариант 1. Задание 19:
Два игрока, Паша и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в пять раз. Игра завершается в тот момент, когда количество камней в куче становится не менее 69.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 69 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 68.
а) Укажите все такие значения числа S, при которых Паша может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
б)Укажите такое значение S, при котором Паша не может выиграть за один ход, но при любом ходе Паши Вася может выиграть своим первым ходом. Опишите выигрышную стратегию Васи.
Задание 20 ЕГЭ.
Укажите 2 таких значения S, при которых у Паши есть выигрышная стратегия, причём Паша не может выиграть за один ход и может выиграть своим вторым ходом независимо от того, как будет ходить Вася. Для каждого указанного значения S опишите выигрышную стратегию Паши.
Задание 21 ЕГЭ.
Укажите хотя бы одно значение S, при котором у Васи есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Паши, и у Васи нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Васи. Постройте дерево всех партий, возможных при этой выигрышной стратегии Васи (в виде рисунка или таблицы).
Типовые задания для тренировки
✍ Решение:
-
19.
а) S ≥ 14. При количестве камней в куче от 14 и выше Паше необходимо увеличить их количество в пять раз, тем самым получив 70 или более камней.
S ≥ 14 выигрышные позиции
б) S = 13. Паша своим первым ходом может сделать 14, 17 или 65 камней, после этого Вася увеличивает количество в пять раз, получая 70, 85 или 325 камней в куче.
S = 13 Паша 1 ход: 13 + 1 = 14 Паша 1 ход: 13 + 4 = 17 Паша 1 ход: 13 * 5 = 65 Ваня 1 ход: [14, 17, 65] * 5 = S ≥ 14 Ваня выигрывает 13 - проигрышная позиция
20. S = 9, 12. Для данных случаев Паше необходимо прибавить 4 камня к куче из 9 камней, либо 1 камень к куче из 12, и получить кучу из 13 камней.
После чего игра сводится к стратегии, описанной в пункте 1б.
S = 13 Паша 1 ход: 9 + 4 = 13 Паша выигрывает Паша 1 ход: 12 + 1 = 13 Паша выигрывает 9, 12 - выигрышные позиции со второго хода
21. S = 8. Своим первым ходом Паша может сделать количество камней в куче 9, 12 или 40. Если Паша увеличивает кол-во в пять раз, тогда Вася выигрывает своим первым ходом, увеличивая количество камней в пять раз.
Для случая 9 и 12 камней Вася использует стратегию, указанную в п.2.
S = 8 Паша 1 ход: 8 + 1 = 9 Ваня Выигрывает (см. п.2) Паша 1 ход: 8 + 4 = 12 Ваня Выигрывает (см. п.2) Паша 1 ход: 8 * 5 = 40

Аналитическое решение 19 задания смотрите на видео:
📹 YouTube здесь
Видеорешение на RuTube здесь
19_1:
Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 7 камней, за один ход можно получить кучу из 14 или 8 камней. У каждого игрока, чтобы сделать ход, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 28. Если при этом в куче осталось не более 44 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 23 камня, и Паша удвоит количество камней в куче, то игра закончится и победителем будет Валя. В начальный момент в куче было S камней, 1≤ S ≤ 27.
Задание 19 ЕГЭ
а) При каких значениях числа S Паша может выиграть в один ход? Укажите все такие значения и соответствующие ходы Паши.
б) У кого из игроков есть выигрышная стратегия при S = 26, 25, 24? Опишите выигрышные стратегии для этих случаев.
Задание 20 ЕГЭ
У кого из игроков есть выигрышная стратегия при S = 13, 12? Опишите соответствующие выигрышные стратегии.
Задание 21 ЕГЭ
У кого из игроков есть выигрышная стратегия при S = 11? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции.
✍ Решение:
а) Паша имеет выигрышную стратегию и может выиграть за один ход, если S = 27: тогда ему достаточно добавить один камень, чтобы игра закончилась при 28 камнях в куче; или если S = 14, 15, 16, 17, 18, 19, 20, 21, 22 (44/2 = 22 и 28/2 = 14, т.е. от 14 до 22): тогда необходимо удвоить кучу.
S=27 Паша: 27 + 1 = 28 - Выигрыш! 27 - выигрышная позиция
б) При S = 26 выигрышная стратегия есть у Вали. Паша делает ход первым, у него есть возможность либо удвоить количество камней в куче, и тогда количество превысит 44, — выигрывает Валя; либо увеличить количество на один камень, станет 27 камней: следующая Валя, — она может положить один камень и выиграть.
S=26 Паша: 26 * 2 = 52 Валя выигрывает! или: Паша: 26 + 1 = 27 Валя: 27 + 1 = 28 - Выигрыш! 26 - проигрышная позиция
При S = 25 выигрышная стратегия есть у Паши. Удваивать количество камней нет смысла, т.к. количество превысит 44, значит, Паша добавит один камень, их станет 26, следующая Валя, — она может либо добавить камень (станет 27 камней, следующим ходом выиграет Паша) либо удвоить — и сразу проиграть, т.к. станет более 44 камней.
S=25 Паша: 25 + 1 = 26 Валя: 26 ... проигрышная позиция (см. выше) Паша выигрывает! 25 - выигрышная позиция
При S = 24 выигрышная стратегия есть у Вали. Паша делает ход первым: удваивать кучу нет смысла, т.к. в ней станет более 44, значит, Паша добавит один камень, их станет 25; следующая — Валя: она может только добавить один камень (станет 26 камней, следующим ходом Паша оказывается в проигрышной позиции, см. пункт при S = 26).
S=24 Паша: 24 + 1 = 25 Валя: 25 ... выигрышная позиция (см. выше) Валя выигрывает! 24 - проигрышная позиция
Задание 20 ЕГЭ:
При S = 13 или S = 12 выигрышная стратегия есть у Паши. Паша удваивает количество и в куче остается 26 или 24 камня. Это проигрышная позиция для того, кто ходит (см. п. 1 б), а следующий ход за Валей.
Задание 21 ЕГЭ:
При S = 11 выигрышная стратегия есть у Вали. Паша делает первый ход: в куче остается либо 22, либо 12 камней. Обе эти позиции выигрышные для того, кто ходит. При S = 12 последовательность игры описана в пункте 2, а при S = 22 — в пункте 1а.
Дерево возможных партий:
* Для Вали отображены только ходы по стратегии
** красный круг означает выигрыш
*** фиолетовый круг — конец игры (проигрыш)
Подробное объяснение 19 задания ЕГЭ смотрите на видео (аналитическое решение):
📹 YouTube здесь
Видеорешение на RuTube здесь
Игра с двумя кучами камней или табличка
19_5:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 73.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.
Задание 1.
Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2.
Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию.
Задание 3.
Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Постройте дерево всех партий, возможных при указанной вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
✍ Решение:
- Задание 1. В начальных позициях (6, 33), (8, 32) выигрышная стратегия есть у Вани.
- Задание 2. В начальных позициях (6, 32), (7, 32) и (8, 31) выигрышная стратегия есть у Пети.
- Задание 3. В начальной позиции (7, 31) выигрышная стратегия есть у Вани.

Видео решения 19 задания с двумя кучами (аналитическое решение):
📹 YouTube здесь
Видеорешение на RuTube здесь
Игра с набором слов
19_2: 2017 год (один из вариантов со слов выпускника):
Петя и Ваня играют в игру: есть набор слов, необходимо последовательно называть буквы этих слов. Побеждает тот игрок, который называет последнюю букву любого слова из набора. Петя ходит первым.
Например, есть набор слов {Волк, Информатика, Страшно}; для заданного набора слов Петя своим первым ходом может назвать букву В, И или С. Если Петя выберет букву В, то победит Ваня (следующие ходы: Петя — В, Ваня — О, Петя — Л, Ваня — К).
Задание 1
А) Даны 2 слова (набора букв) {ИКЛМНИКЛМНХ, НМЛКИНМЛКИ}. Определить выигрышную стратегию.
Б) Даны 2 слова {ТРИТРИТРИ…ТРИ, РИТАРИТАРИТАРИТА…РИТА}. В первом слове 99 букв, во втором 164. Определить выигрышную стратегию.
Задание 2
Необходимо поменять две буквы местами из набора пункта 1А в слове с наименьшей длинной так, чтобы выигрышная стратегия была у другого игрока. Объяснить выигрышную стратегию.
Задание 3
Дан набор слов {Ворона, Волк, Волна, Производная, Прохор, Просо}. У кого из игроков есть выигрышная стратегия? Обосновать ответ и написать дерево всех возможных партий для выигрышной стратегии.
✍ Решение:
- Если поменять местами во втором слове (НМЛКИНМЛКИ) буквы Н и И, то получится следующий набор слов:
{ИКЛМНИКЛМНХ, ИМЛКННМЛКИ}Для данного набора выигрышная стратегия есть у Вани. Петя в любом случае должен будет выбрать букву И, а Ваня следующим ходом может перевести игру в проигрышную позицию для Пети, т.е. перейти на второе слово, назвав букву М. Такая стратегия приведет Ваню к выигрышу, так как последнюю букву слова — И — запишет именно он.
- Выигрышная стратегия есть у Вани, так как при любом выборе Пети, Ваня может перевести игру в проигрышную позицию для Пети, т.е. «перейти» на слово с четным количеством букв. Такая стратегия позволит Ване написать последнюю букву и тем самым выиграть игру.
А) Для выигрыша Пете достаточно выбрать первую букву слова с нечетным количеством букв, тогда последний ход делает Петя. При исходном наборе слов выигрышная стратегия есть у Пети. Она заключается в том, что своим первым ходом он должен выбрать букву И (слово ИКЛМНИКЛМНХ из 11 букв). Ване придется выбрать букву К. Таким образом, они последовательно будут называть буквы первого слова, пока Петя не выберет последнюю букву Х. На этом игра закончится выигрышем Пети. При данной стратегии возможна только одна партия. Заключением партии будет написано слово ИКЛМНИКЛМНХ.
Б) При исходном наборе слов выигрышная стратегия есть у Пети. Она заключается в том, чтобы выбрать слово с нечетным количеством букв, т.к. при такой стратегии последнюю букву в любом случае записывает Петя. Т.о., Петя должен выбрать букву Т, т.к. в первом слове 99 букв.
Дерево возможных партий:
* Для Вани отображены только ходы по стратегии
** Красный круг означает выигрыш
Подробней с решением задания про слова ознакомьтесь в видеоуроке (аналитическое решение):
📹 YouTube здесь
Видеорешение на RuTube здесь
Разбор заданий 19,20,21 ЕГЭ по информатике в Excel.
Задание 19.
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10камней, а в другой 5 камней; такую позицию в игре будем обозначать (10,5). Тогда за один ход можно получить любую из четырёх позиций: (11,5), (20,5), (10,6), (10,10). Для того чтобы делать ход, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент впервой куче было семь камней, вовторой куче – S камней: 1S69
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение.
Поскольку у нас 2 кучикамней, будем использовать 2 ячейки. В ячейку A4 введём 7 (количество камней в первой куче) и поскольку количество камней во второй куче неизвестно, введём в ячейкуB4 Excelпроизвольное число, например 10. Распишем ходы Пети.
Для того чтобы Ваня гарантировано выиграл первым ходом, последний ход его должен быть самым сильным. Для этого количество камней из кучи с максимальным количеством камней умножаем на 2 и прибавляем количество камней из другой кучи. В ячейку E4 вводим формулу
=МАКС(C4:D4)*2 + МИН(C4:D4). Копируем эту формулу в ячейки E5:E7.
т.к. по условию задачи Ваня должен выиграть своим первым ходом, то суммарное количество камней в двух кучах должно быть 77. При этом количество камней во второй куче должно быть минимальным. Будем подбирать количество камней во второй куче, пока не найдем минимальное, при котором суммарное количество камней количество камней у Вани не станет 77.
И
Для наглядности выполним условное форматирование. Выделим ячейки E4:E7. Выбираем Условное форматирование – Правила выделения ячеек – другие правила – значения 77 – форма – заливка – зеленая – ОК — ОК
такое количество камней во второй куче будет равно 18.
Задание 20. Для игры, описанной в предыдущем задании, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Ответ:
Решение.
Введём в ячейку A10количество камней в первой куче — 7, в ячейку B10 – количество камней во второй куче, т.к. количество камней во второй куче неизвестно, введём 10 (число произвольное). Скопируем таблицу, полученную в первом задании, в ячейку C9.
Так как Петя должен сделать свои 4 хода, а затем Ваня свои ходы, скопируем таблицу из первого задания ещё три раза. Распишем все первые ходы Пети. Ходы Вани и второй ход Пети при этом рассчитываются автоматически.
При S=10 Петя выигрывает своим вторым ходом только при одном ходе Вани (7,40), а нам надо, чтобы Петя после своего первого хода при любом ходе Вани выигрывал своим вторым ходом, т.е. нам нужно найти такое S, при котором все вторые ходы Пети в одном из прямоугольников были 77. Кроме того, нам надо будет следить за последним ходом Вани, т.к. может случиться так,что Петя выигрывает своим вторым ходом, но до этого побеждает Ваня. Для этого создадим дополнительный столбец, в который будем записывать сумму камней в двух кучах у Вани и следить, чтобы это значение было 77. В ячейку H10вводим формулу =E10 + F10и копируем её в ячейки H11:H25. Для наглядности выполним условное форматирование.
Меняя значение Sво второй куче, находим решение задачи. Первое значение S=31 ивторое значение S=34
Ответ: 3134
Задание 21.
Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани естьвыигрышная стратегия,позволяющая ему выиграть первым иливторым ходом при
любой игре Пети;
— у Вани нет стратегии,которая позволит ему гарантированно выиграть первым ходом.
Решение.
Скопируем таблицу из второго задания в ячейку K3 и снова поменяем местами Петя, Ваня, Петя. В ячейку I4 введём количество камней в первой куче, в ячейку J4 – число, например, 10 (количество камней во второй куче). Тогда при первом ходе Пети K4 =I4+1, L4=J4.
Выделим данный фрагмент таблицы жирным. Так как Петя не должен выиграть своим первым ходом, скопируем полученную таблицу ещё 3 раза. Введём формулы в ячейкиK20=I4, L20=J4+1, K36=I4*2, L36=J4, K52=I4, L52=J4*2. Также надо проверить, не выиграет ли Ваня своим первым ходом. Для этого в ячейку M5 введём формулу =M4+N4. Скопируем эту формулу в ячейкиM9, M13,M17, M21, M25, M29, M33, M37, M41, M45, M49. Снова будем проверять, используя условное форматирование. Меняя значение вячейке J4, находим такое минимальное S, при которому Вани естьвыигрышная стратегия,позволяющая ему выиграть первым иливторым ходом прилюбой игре Пети;у Вани нет стратегии,которая позволит ему гарантированно выиграть первым ходом.
Разбор задания 19 на примере 2-х задач из ГИА 9
Задания приведены с решениями.
На данной странице вы найдёте два задания типа 19 из ОГЭ по информатике для 9-х классов.
Задания приведены с решениями. Сами электронные таблицы с ответами и формулами можно скачать по ссылкам.
Задание 1. Тип 19 ОГЭ по информатике
В электронную таблицу занесли данные о тестировании учеников. Ниже приведены первые пять строк таблицы:
|
A |
B |
C |
D |
|
|
1 |
округ |
фамилия |
предмет |
балл |
|
2 |
C |
Ученик 1 |
обществознание |
246 |
|
3 |
В |
Ученик 2 |
немецкий язык |
530 |
|
4 |
Ю |
Ученик 3 |
русский язык |
576 |
|
5 |
СВ |
Ученик 4 |
обществознание |
304 |
В столбце А записан округ, в котором учится ученик; в столбце В — фамилия; в столбце С — любимый предмет; в столбце D — тестовый балл. Всего в электронную таблицу были занесены данные по 1000 ученикам.
Выполните задание.
Откройте файл с данной электронной таблицей (расположение файла Вам сообщат организаторы экзамена). На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
1. Сколько учеников в Юго-Западном округе (ЮЗ) выбрали в качестве любимого предмета обществознание? Ответ на этот вопрос запишите в ячейку Н2 таблицы.
2. Каков средний тестовый балл у учеников Центрального округа (Ц)? Ответ на этот вопрос запишите в ячейку Н3 таблицы с точностью не менее двух знаков после запятой.

Решение
1. Добавляем фильтр к заголовкам таблицы. Фильтруем данные. Оставляем округ «ЮЗ» и затем фильтруем данные столбца С. Оставляем только предмет «Обществознание». Затем выделяем отображённые ячейки по 1 столбцу. Внизу окна программы мы получим количество ячеек. Вписываем ответ в ячейку H2
2. Отключаем установленную ранее фильтрацию так, чтобы отобразились все данные. В столбце А настраиваем фильтрацию на отображение только округа «Ц». Выделяем столбец D. Внизу окна программы смотрим среднее значение. Вписываем ответ.
Задание 2. Тип 19 ОГЭ по информатике
На метеостанции данные о погоде занесли в электронную таблицу. Ниже приведены первые пять строк таблицы, в которую были занесены данные о погоде в период с января 2013 года по январь 2014 года.
Каждая строка таблицы содержит запись о погоде одного дня. В столбце A записана дата; в столбце B — температура воздуха; в столбце C — атмосферное давление; в столбце D – скорость ветра; в столбце E – облачность. Всего в электронную таблицу были занесены данные о погоде за 396 дней.
Выполните задание.
Откройте файл с данной электронной таблицей. На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
1. Сколько дней за данный период атмосферное давление было ниже 760 мм ртутного столба? Ответ на этот вопрос запишите в ячейку H2 таблицы.
2. Какое среднее атмосферное давление было в дни с температурой воздуха ниже 0 °C? Ответ на этот вопрос с точностью не менее 2 знаков после запятой запишите в ячейку H3 таблицы.

Решение
1. Возможно решение при помощи фильтрации данных и автоматического подсчёта количества записей программой Excel, как это делалось в прошлом задании.
Так же возможно ответить на первый вопрос задания при помощи формулы СЧЁТЕСЛИ
=СЧЁТЕСЛИ(C2:C397;»<760″)
Формула работает по принципу =СЧЁТЕСЛИ([Диапазон, в котором будут считаться количество ячеек]; «[условие, при котором ячейка посчитается]».
2. Добавляем любой свободный столбец формулу условия, которое будет выводить нам атм.давление при условии, если температура будет меньше 0. =ЕСЛИ(B2<0;C2). Затем считаем среднее значение по нашему столбцу. =СРЗНАЧ(F2:F397)
Какую задачу считает формула?
1. 2 способа решение задачи 14 ОГЭ с помощью формулы или фильтров в EXCEL
Для решение описанных в видеороликах задач необходимы таблица Excel. ЕЕ вы можете скачать с сайта решу ОГЭ, также познакомится с условием задачи.
*Если нет Excel на домашнем компьютере, то воспользуйтесь Google-таблицами (не забудьте скачать таблицу себе на Google-диск команда Файл/создать копию, открыть доступ к таблице и послать ссылку учителю)
Решите задание 1 способом.
Видео 1 ссылка>> Решение задачи с помощью формул
Выпишите все формулы, которые использовались в ролике в тетрадь, с пояснениями.
Решите задание 2 способом.
Видео 2 ссылка>> Решение задачи с помощью фильтров
2. Реши три задачи EXCEL вариант № 11945871 на решу ОГЭ любым способом.
Скачай таблицу, отредактируй ее и прикрепи к тесту или отправь в чат учителю в дневнике.
В результате выполнения классной работы должно получится
5 решенных задач EXCEL , отправленных учителю.
Записи в тетради новых формул в EXCEL
Решение задачи 1 ОГЭ

27.03.2014
При подготовки к ГИА и ЕГЭ необходимо владеть прикладным программным обеспечением, в частности, табличными процессорами. Функция ЕСЛИ в Excel поможет успешно решить задачи на работу с таблицами.

Абсолютные и относительные ссылки в Excel
26.02.2014
Мы с вами знаем, что в умелых руках Excel — очень мощный инструмент. При произведении расчетов с помощью этого табличного редактора мы можем оперировать как содержимым ячеек так и их адресами (ссылками). И вот эти самые ссылки бывают двух типов — абсолютные и относительные.

Функции МИН и МАКС Excel
25.12.2013
Продолжаем изучать функции Excel, которые помогут нам решить задачу 19 ГИА по информатике. В прошлый раз мы рассмотрели функцию СРЗНАЧ — рекомендую освежить в памяти эту информацию.
Функция СРЗНАЧ Excel
23.12.2013
При подготовке к ГИА по информатике для успешного решения задачи 19 из части 3 необходимо знать некоторые функции Excel. Одна из таких функций — СРЗНАЧ. Рассмотрим ее подробнее.
Задания № 19 . Обработка большого массива данных с использованием средств электронной таблицы или базы данных.
Работа состоит из 8 вариантов заданий в Excel для подготовки к ОГЭ по информатике в 2017 году. Задачи + ответы + шаблоны.
Источник: ГИА по информатике.
Скачать файл
Слайд 1
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №8 поселка

Катасон Буденновского района» Ставропольского края
«Методы и способы решения
задания 19 ОГЭ
по информатике»
Баграмова Ирина Александровна
Учитель информатики и ИКТ
МОУ СОШ №8 п.Катасон
*
Слайд 2
Для работы в Excel надо знать основные принципы

записи адреса ячейки и правила копирования формул и ещё
несколько формул для обработки.
В 19 задании чаще всего задаются
несколько вопросов и в зависимости от вопроса целесообразно использовать либо одну, либо другую формулу (предварительно нажав в нужной ячейке знак «=» равно). Формулы находятся на вкладке «Формулы» в верхней части листа, так можно вводить и с клавиатуры.
Слайд 3
Функции в программе Excel позволяют выполнять сложные действия

вычислительного характера.
Основные встроенные функции табличного процессора:
МАКС (
) — возвращает наибольшее значение из набора значений.
МИН ( ) — возвращает
наименьшее значение из набора значений.
СРЗНАЧ ( ) — возвращает среднее значение (среднее арифметическое) аргументов.
ЕСЛИ ( ) — возвращает одно значение, если указанное условие дает в результате значение ИСТИНА, и другое значение, если условие дает в результате значение ЛОЖЬ.
СЧЕТЕСЛИ ( ) — подсчитывает количество ячеек в диапазоне, которые соответствуют одному указанному пользователем критерию.
СУММ ( ) — вычисляет сумму всех чисел, указанных в качестве аргументов.
Слайд 4
1.Если в условии задачи необходимо найти количество чего-либо,

то используем функцию СЧЁТЕСЛИ(диапазон; критерий)
2.Если в условии задачи необходимо найти процент чего-либо,
то используем функции СУММЕСЛИ(диапазон, условие, [диапазон_суммирования]),
СЧЁТЕСЛИ(диапазон; критерий),
ЕСЛИ(лог_выражение; [значение_если_истина]; [значение_если_ложь])
3.Если в задании необходимо проверить одновременное выполнение двух условий, то можно использовать функции
ЕСЛИ(лог_выражение; [значение_если_истина]; [значение_если_ложь])
И(логическое_значение1, [логическое_значение2], …)
4.Если в задаче необходимо найти среднее чего-либо, то используем функции СУММЕСЛИ(диапазон, условие, [диапазон_суммирования]),
СЧЁТЕСЛИ(диапазон; критерий),
Слайд 5
Формулы
ЕСЛИ(IF)
Возвращает одно значение, если заданное условие при вычислении

дает значение ИСТИНА, и другое значение, если ЛОЖЬ.
Функция ЕСЛИ
используется при проверке условий для значений и формул.
Синтаксис
ЕСЛИ(лог_выражение;значение_если_истина;значение_если_ложь)
Например, =ЕСЛИ(И(D2
может являться число, текст и формула
Логическая операция
(может быть И(AND), ИЛИ(OR),НЕ(NOT))
Слайд 6
Формулы
СУММ(SUM)
Суммирует все числа в интервале ячеек.
Синтаксис
СУММ(число1;число2; …)
Число1, число2,…

— от 1 до 30 аргументов, для которых требуется
определить итог или сумму.
Например, =СУММ(A2:A4)
Диапазон ячеек, сумму которых необходимо найти,
начиная с А2 и до А4 включительно
Слайд 7
Формулы
СУММЕСЛИ (SUMIF)
Суммирует ячейки, заданные критерием.
Синтаксис
СУММЕСЛИ(диапазон;критерий;диапазон_суммирования)
Например, =СУММЕСЛИ(A2:A5;»>160000″;B2:B5)
Диапазон — диапазон вычисляемых
ячеек.
Критерий — критерий в форме числа, выражения или текста, определяющего
суммируемые ячейки. Например, критерий может быть выражен как 32, «32»,
«>32», «яблоки».
Диапазон_суммирования — фактические ячейки для суммирования.
Если «диапазон_суммирования» опущен,
то суммируются ячейки в аргументе «диапазон».
Слайд 8
Формулы
СЧЁТЕСЛИ
Подсчитывает количество ячеек внутри диапазона, удовлетворяющих заданному критерию.
Синтаксис
СЧЁТЕСЛИ(диапазон;критерий)
Например,
=СЧЕТЕСЛИ(B2:B5;»>55″)
Диапазон — диапазон, в котором нужно подсчитать ячейки.
Критерий — критерий в
форме числа, выражения или текста, который определяет, какие ячейки надо
подсчитывать. Например, критерий может быть выражен следующим образом: 32, «32», «>32», «яблоки».
Слайд 9
Задание 19 №1 ОГЭ по информатике
Выполните задание
Откройте файл

с данной электронной таблицей (Рабочий стол/Решение задания 19 ОГЭ
по информатике/Задание1).
На основании данных, содержащихся в этой таблице, ответьте
на два вопроса.
1. Сколько продуктов в таблице содержат меньше 50 г углеводов и
меньше 50 г белков? Запишите число этих продуктов в ячейку H2
таблицы.
2. Какова средняя калорийность продуктов с содержанием жиров
менее 1 г? Ответ на этот вопрос запишите в ячейку H3 таблицы с
точностью не менее двух знаков после запятой
Слайд 10
Определим: Сколько продуктов в таблице содержат меньше 50

г углеводов и меньше 50 г белков.
В данном
задании 2 условия: углеводов < 50, белков < 50.
Используем столбец
F для дополнительных вычислений.
Напротив каждого продукта будем писать 1, если условия выполняются, 0 — если условия не выполняются. Обратим внимание на союз, соединяющий эти условия — И. Т.е. данные условия должны выполняться одновременно и условие 1 и условие 2.
Для реализации этого воспользуемся функцией ЕСЛИ ( условие;если истина; если ложь):
Логическое выражение в нашем случае сложное — состоит из двух: углеводов < 50, белков < 50. Для ячейки F2 формула будет выглядеть следующим образом И(D2<50;C2<50). Два условия помещаются в скобки и разделяются точкой с запятой. Перед скобкой стоит союз И.
Значение_если_истина — ставим 1
Значение_если_ложь — ставим 0
F2=ЕСЛИ(И(D2<50;C2<50);1;0)
Используя автозаполнение, копируем ячейку с формулой в ячейки F3:F1001. Получили в ячейках единицу, где условия выполняются, ноль — где нет.
Слайд 11
1. Сколько продуктов в таблице содержат меньше 50

г углеводов и меньше 50 г белков? Запишите число
этих продуктов в ячейку H2 таблицы.
Windows Excel
F2=ЕСЛИ(И(D2
Скопируем формулу во все ячейки диапазона F3:F1001
Слайд 12
Windows Excel
H2=СУММ(F2:F1001)

Остается с
помощью функции
СУММ ( ) суммировать единички в диапазоне F2:F1001
и мы получим количество таких продуктов, удовлетворяющих двум условиям. Записываем формулу =СУММ(F2:F1001) в ячейку H2
(так указано в задании).
Слайд 13
1. Сколько продуктов в таблице содержат меньше 50

г углеводов и меньше 50 г белков? Запишите число
этих продуктов в ячейку H2 таблицы.
Слайд 14
Вопрос 2
Определим: Какова средняя калорийность продуктов с содержанием

жиров менее 1 г.
Для ответа на вопрос нужно выполнить
три действия:
1. Найти общую сумму калорий продуктов с содержанием жиров
менее 1 г.
2. Выделить из всего списка продуктов те, которые удовлетворяют поставленным условиям (содержание жиров менее 1 г.)
3. Найти среднюю калорийность выбранных продуктов
Для выполнения первого пункта нам потребуются дополнительные ячейки: возьмем столбец H для промежуточных вычислений. Выберем из общего списка продукты, удовлетворяющие требованию с помощью функции СУМЕСЛИ (диапазон 1;условие;диапазон2условие;), т.е. диапазон 1 сравнивает количество жиров меньше 1г., а диапазон 2 складывает калории.
Запишем в ячейку Н5 формулу: H5=СУММЕСЛИ(B2:B1001;»<1″;E2:E1001)
Используя автозаполнение копируем формулу для каждого продукта.
Слайд 15
Теперь как посчитать количество продуктов с содержанием жиров

меньше 1г.
Используем функцию СЧЁТЕСЛИ(диапазон;условие) т.е диапазон будет с
жирами,а условие меньше 1 г.
=СЧЁТЕСЛИ(B2:B1001;»
Н3 найдем среднее арифметическое полученных значений , сумму поделим на количество, т.е. первая функция нашла сумму калорий, вторая посчитала все ячейки с количеством жиров менее 1 г.
Слайд 16
2. Какова средняя калорийность продуктов с содержанием жиров

менее 1 г? Ответ на этот вопрос запишите в
ячейку H3 таблицы с точностью не менее двух знаков после
запятой
Windows Excel
H5=СУММЕСЛИ(B2:B1001;»<1″;E2:E1001)
H6= СЧЁТЕСЛИ(B2:B1001;»<1″)
H3=H5/H6
Слайд 17
2. Какова средняя калорийность продуктов с содержанием жиров

менее 1 г? Ответ на этот вопрос запишите в
ячейку H3 таблицы с точностью не менее двух знаков после
запятой
Слайд 18
Задание 19 № 2 ОГЭ по информатике.
В электронную

таблицу занесли данные о тестировании учеников. Ниже приведены первые
пять строк таблицы:
В столбце А записан округ, в котором
учится ученик; в столбце В — фамилия; в столбце С — любимый предмет; в столбце D — тестовый балл. Всего в электронную таблицу были занесены данные по 1000 ученикам.
Выполните задание.
Откройте файл с данной электронной таблицей (расположение файла (Рабочий стол/Решение задания 19 ОГЭ по информатике/Задание2). На основании данных, содержащихся в этой таблице, ответьте на два вопроса.
1. Сколько учеников в Восточном округе (В) выбрали в качестве любимого предмета информатику? Ответ на этот вопрос запишите в ячейку Н2 таблицы.
2. Каков средний тестовый балл у учеников Северного округа (С)? Ответ на этот вопрос запишите в ячейку НЗ таблицы с точностью не менее двух знаков после запятой.
Слайд 19
1. Сколько учеников в Восточном округе (В) выбрали

в качестве любимого предмета информатику? Ответ на этот вопрос
запишите в ячейку Н2 таблицы.
Запишем в ячейку E2 следующую формулу
=ЕСЛИ(A2=»В»;C2;0) и скопируем ее в диапазон E3:E1001. В ячейку столбца E будет записываться название предмета, если ученик из Восточного округа и «0», если это не так.
Применив операцию F=ЕСЛИ(E2=»информатика»;1;0) , получим столбец (F): с единицами и нулями.
Далее, используем операцию =СУММ(F2:F1001). Получим количество учеников, которые считают своим любимым предметом информатику.
Таких 10 человек.
Слайд 20
2. Какова средняя скорость ветра в дни с

облачностью 100%? Ответ на этот вопрос с точностью не
менее двух знаков после запятой запишите в ячейку H3 таблицы.
Для
ответа на второй вопрос в столбце G для каждого дня запишем скорость ветра, если в этот день облачность 100%, и 0 в обратном случае. В ячейку G2 запишем формулу
=ЕСЛИ(E2=100;D2;»»)
Скопируем формулу во все ячейки диапазона G2:G397.
Далее, чтобы определить среднюю скорость ветра, запишем формулу в ячейку H3:
=СРЗНАЧ(G2:G397)
Если задание выполнено правильно и при выполнении задания использовались файлы, специально подготовленные для проверки выполнения данного задания, то должны получиться следующие ответы:
на первый вопрос: 73; на второй вопрос: 1,58.
Слайд 21
Задача 3
В электронную таблицу внести результаты тестирования

20 учащихся Западного, Восточного, Южного, Северного и Центрального округов
по физике и информатике.
1. Чему равна наибольшая сумма баллов по
двум предметам среди учащихся Центрального округа? Ответ на этот вопрос запишите в ячейку G2 таблицы.
2. Сколько процентов от общего числа участников составили ученики, получившие по информатике 40 баллов? Ответ с точностью до одного знака после запятой запишите в ячейку G4 таблицы.
Слайд 22
Пояснение:
1. В столбце Е для каждого ученика вычислим

сумму баллов по двум предметам если это ученик Центрального
округа. Для ученика другого округа ячейка будет содержать пустую строку.
В ячейку Е2 запишем формулу:
= ЕСЛИ (В2 = «Центральный»; С2 + D2; « »)
Скопируем формулу во все ячейки диапазона Е3:Е21. Непустые значения строк будут равны суммам баллов учеников Центрального округа.
Для определения наибольшей суммы в ячейку G2 введём формулу:
= МАКС (Е2:Е21).
2. В дополнительной ячейке, например в Н3, найдём количество участников, набравших по информатике менее 40 баллов.
=СЧЁТЕСЛИ(D2:D21; « <40 »)
Выразим полученное значение в процентах от общего числа участников тестирования. Результат запишем в ячейку G4:
=H3/20*100
Слайд 23
В электронную таблицу внести результаты тестирования 20 учащихся

Западного, Восточного, Южного, Северного и Центрального округов по физике
и информатике.
1. Чему равна наименьшая сумма баллов по двум предметам
среди учащихся Западного округа? Ответ на этот вопрос запишите в ячейку G2 таблицы.
2. Сколько процентов от общего числа участников составили ученики, получившие по информатике не менее 71 балла? Ответ с точностью до одного знака после запятой запишите в ячейку G4 таблицы.
Задача 4
Слайд 24
Пояснение:
1. В столбце Е для каждого ученика вычислим

сумму баллов по двум предметам если это ученик Западного
округа. Для ученика другого округа ячейка будет содержать пустую строку.
В ячейку Е2 запишем формулу:
= ЕСЛИ (В2 = «Западный»; С2 + D2; « »)
Скопируем формулу во все ячейки диапазона Е3:Е21. Непустые значения строк будут равны суммам баллов учеников Западного округа.
Для определения наибольшей суммы в ячейку G2 введём формулу:
= МАКС (Е2:Е21).
2. В дополнительной ячейке, например в Н3, найдём количество участников, набравших по информатике не менее 71 балла.
=СЧЁТЕСЛИ(D2:D21; « >70»)
Выразим полученное значение в процентах от общего числа участников тестирования. Результат запишем в ячейку G4:
=H3/20*100
Слайд 25
В электронную таблицу внести результаты тестирования 20 учащихся

1, 2, 3, 4 и 5 школ по географии
и информатике. информатике.
1. У какого количества учеников школ, набравших более
60 баллов по информатике, разность баллов по информатике и по географии по абсолютной величине превышает 15 баллов? Ответ на этот вопрос запишите в ячейку F1 таблицы.
2. Каков средний балл среди участников тестирования, получивших зачётные баллы по информатике (не менее 44 баллов)? Ответ с точностью не менее двух знаков после запятой запишите в ячейку G1 таблицы.
Задача 5
Слайд 26
Пояснение:
1. В ячейку Е2 запишем формулу:
= ЕСЛИ(D2>60; ABS(C2

– D2);0)
Скопируем формулу во все ячейки диапазона Е3:Е21.
2.
Для того чтобы найти искомое количество школьников в ячейку F1
введём формулу:
= СЧЁТЕСЛИ(Е2:Е21; « >15 »)
В ячейку G1 запишем формулу:
= СУММЕСЛИ(D2:D21; «>=44 ») / СЧЁТЕСЛИ(D2:D21; « >=44 »)
Слайд 27
В электронную таблицу внести результаты тестирования 20 учащихся

1, 2, 3, 4 и 5 школ по географии
и информатике. информатике.
1. Сколько процентов от общего числа участников тестирования
составили ученики, получившие неудовлетворительные баллы хотя бы по одному предмету (т. е. менее 40 баллов по географии или менее 44 баллов по информатике)? Ответ с точностью не менее двух знаков после запятой запишите в ячейку F1 таблицы.
2. Каким оказался средний балл по географии? Ответ с точностью не менее двух знаков после запятой запишите в ячейку G1 таблицы.
Задача 6
Слайд 28
Пояснение:
1. В ячейку Е1 запишем формулу:
= ЕСЛИ(ИЛИ(С2

40; D2 < 44); 1;0)
Скопируем формулу во все
ячейки диапазона Е3:Е21.
2. Для того чтобы найти искомое количество
школьников в ячейку F1 внесём формулу:
= СЧЁТЕСЛИ(Е2:Е21; « > 15 »)
В ячейку G1 запишем формулу для вычисления среднего балла по географии:
= СУММЕ(C2:C21) / 20
Слайд 29
В электронную таблицу внести результаты тестирования 20 учащихся

Западного, Восточного, Южного, Северного и Центрального округов по физике
и информатике.
1. Чему равна наибольшая сумма баллов по двум предметам
среди учащихся Северного округа? Ответ на этот вопрос запишите в ячейку G1 таблицы.
2. Сколько процентов от общего числа участников составили ученики, получившие по физике больше 60 баллов? Ответ с точностью до одного знака после запятой запишите в ячейку G3 таблицы.
Задача 7
Слайд 30
Пояснение:
1. В столбце Е для каждого ученика вычислим

сумму баллов по двум предметам если это ученик Северного
округа. Для ученика другого округа ячейка будет содержать пустую строку.
В ячейку Е2 запишем формулу:
= ЕСЛИ (В2 = «Северный»; С2 + D2; « »)
Скопируем формулу во все ячейки диапазона Е3:Е21. Непустые значения строк будут равны суммам баллов учеников Северного округа.
Для определения наибольшей суммы в ячейку G1 введём формулу:
= МАКС (Е2:Е21).
2. В дополнительной ячейке, например в Н3, найдём количество участников, набравших по информатике более 60 баллов.
=СЧЁТЕСЛИ(С2:С21; «>60 »)
Выразим полученное значение в процентах от общего числа участников тестирования. Результат запишем в ячейку G3:
=H3/20*100


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 24.11.2022 17:18
Румянцева Надежда Александровна
учитель информатики
3 881
9 050
04.11.2018 23:11
Тематические тесты для подготовки к ОГЭ. Задание 19 (высокий уровень). Тема: Обработка большого массива данных с использованием средств электронной таблицы.
Просмотр содержимого документа
«Задание 19 (варианты 1-5)»
Просмотр содержимого документа
«Функции Еxcel»
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Скачать материал
Выберите документ из архива для просмотра:
УСЛОВ_ФУНКЦИЯ1.xls
условная функция2.xls
условная функцияExcel.ppt
Выбранный для просмотра документ условная функцияExcel.ppt

Скачать материал


- Курс добавлен 19.01.2023


- Сейчас обучается 83 человека из 28 регионов


- Сейчас обучается 342 человека из 65 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Excel. Условная функция и логические выражения.
-
2 слайд
Условная функция Общий вид функции следующий: ЕСЛИ <условие>,<выражение1>,<выражение2>) Условие – это логическое выражение, которое может принимать значение ИСТИНА или ЛОЖЬ. <выражение1> и <выражение2> могут быть числами, формулами или текстами
-
3 слайд
Условная функция Условная функция выполняется так: Если условие истинно, то значение данной ячейки определяет <выражение1>, в противном случае – <выражение2> Пример условной функции для линейного уравнения ЕСЛИ(А2<>0;=-B2/A2;”решений нет”)
-
4 слайд
В некоторых задачах необходимо, чтобы в зависимости от некоторого условия получалось то или иное решение. Для таких задач применяют условную функцию и логические выражения
-
5 слайд
Логические выражения Логические выражения строятся с помощью операций отношения (<,>,<=,>=,<>) и логических операций (логическое И, логическое ИЛИ, логическое отрицание НЕ) Результатом вычисления логического выражения являются логические величины ИСТИНА или ЛОЖЬ
-
6 слайд
Особенность записи логических операций в Excel. Сначала записывается имя логической операции (И, ИЛИ, НЕ), а затем в круглых скобках перечисляются логические операнды, т.е. И(А3<=14,A3>=5,B1<>0) таким образом, условная функция будет выглядеть ЕСЛИ(И(А3<=14,A3>=5,B1<>0),”да”,”нет”)
-
7 слайд
Задача 1 Разработать таблицу, содержащую следующие сведения об абитуриентах (не менее 10 чел): Фамилия, оценки за экзамены (матем, русский яз., ин. яз.), сумма баллов за три экзамена и информацию о зачислении (если сумма баллов больше или равна проходному баллу и оценка за экзамен по матем. – 4 или 5, то абитуриент зачислен, в противном случае –нет) Указание. Исходной информацией являются фамилии, оценки и проходной балл, а сумма баллов и информация вычисляются с помощью формул. (Запустите MS Excel и выполните предложенные задачи) АВСDEF 1Проходной балл13 2ФамилияМатематикаРусский языкИн. языкСумма балловЗачислен (да /нет) 3Иванов453 4Петров355
-
8 слайд
Задача 1 (Подсказки) Формула в ячейке Е3 вычисляет сумму баллов за три экзамена =B3+C3+D3 или =СУММ(B3:D3) Формула в ячейке F3 задается с помощью условной функции =ЕСЛИ(И(Е3>=$C$1;B3>3);”да”;”нет”)
-
9 слайд
Задача 2 Даны коэффициенты a, b, c квадратного уравнения (а≠0). Определить, имеет ли это уравнение действительные корни или нет. Указание. Исходной информацией являются коэффициенты a, b, c. В ячейке D2 вычисляется дискриминант , а в ячейке Е2 должен быть ответ на поставленный вопрос в ячейке Е1 — «да» или «нет» (напомним, что квадратное уравнение имеет действительные корни, если дискриминант больше или равен нулю) ABCDE 1abcдискриминантЕсть действительные корни? 2
-
10 слайд
Задача 3 Создайте таблицу «Прием в секцию волейбола », заполнив ее не менее, чем 10 записями. Выведите сообщение в котором будет отображаться принять учащийся в секцию или нет. Учащийся 6-го класса ростом не менее 164 см. будет принят в секцию и подсчитайте, сколько учащихся в итоге поступило в секцию. № ФамилияКлассВозрастРостЗачисление в секцию
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 210 305 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 17.02.2016
- 584
- 0
- 17.02.2016
- 1192
- 1
- 17.02.2016
- 774
- 1
- 17.02.2016
- 875
- 0
- 17.02.2016
- 3802
- 3
- 17.02.2016
- 278
- 0
- 17.02.2016
- 309
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс повышения квалификации «Облачные технологии в образовании»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»


























































