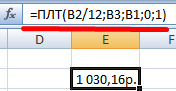
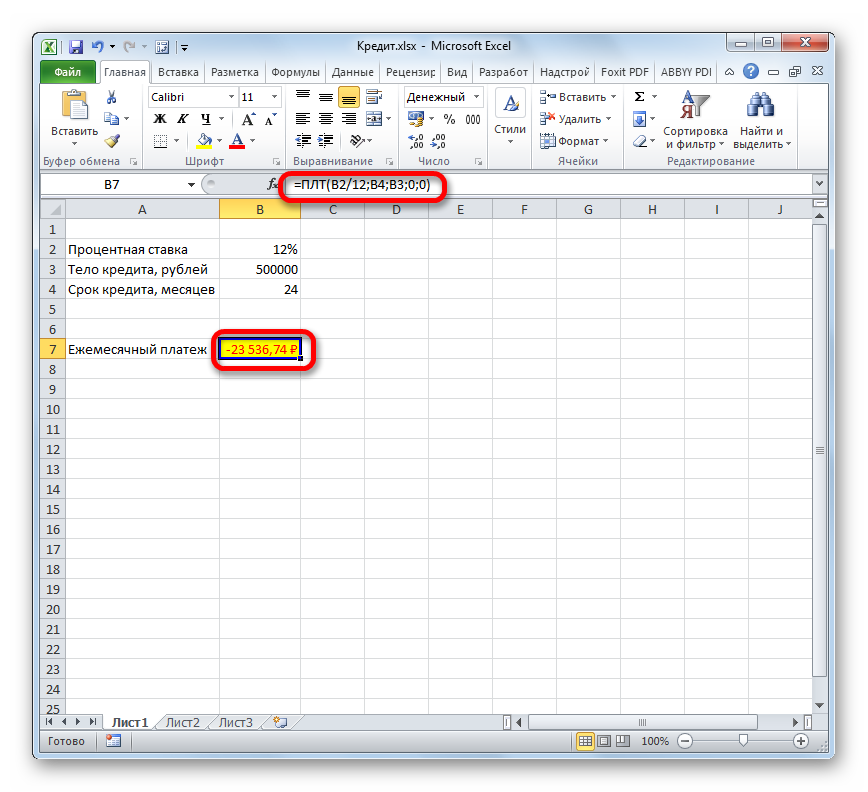
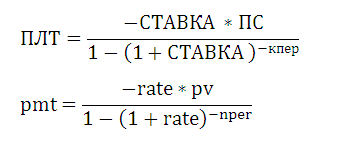Функция ПЛТ в Excel входит в категорию «Финансовых». Она возвращает размер периодического платежа для аннуитета с учетом постоянства сумм платежей и процентной ставки. Рассмотрим подробнее.
Синтаксис и особенности функции ПЛТ
Синтаксис функции: ставка; кпер; пс; [бс]; [тип].
Расшифровка аргументов:
- Ставка – это проценты по займу.
- Кпер – общее количество платежей по ссуде.
- Пс – приведенная стоимость, равноценная ряду будущих платежей (величина ссуды).
- Бс – будущая стоимость займа после последнего платежа (если аргумент опущен, будущая стоимость принимается равной 0).
- Тип – необязательный аргумент, который указывает, выплата производится в конце периода (значение 0 или отсутствует) или в начале (значение 1).
Особенности функционирования ПЛТ:
- В расчете периодического платежа участвуют только выплаты по основному долгу и платежи по процентам. Не учитываются налоги, комиссии, дополнительные взносы, резервные платежи, иногда связываемые с займом.
- При задании аргумента «Ставка» необходимо учесть периодичность начисления процентов. При ссуде под 6% для квартальной ставки используется значение 6%/4; для ежемесячной ставки – 6%/12.
- Аргумент «Кпер» указывает общее количество выплат по кредиту. Если человек совершает ежемесячные платежи по трехгодичному займу, то для задания аргумента используется значение 3*12.
Примеры функции ПЛТ в Excel
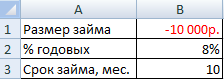
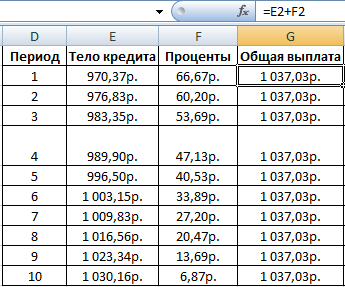
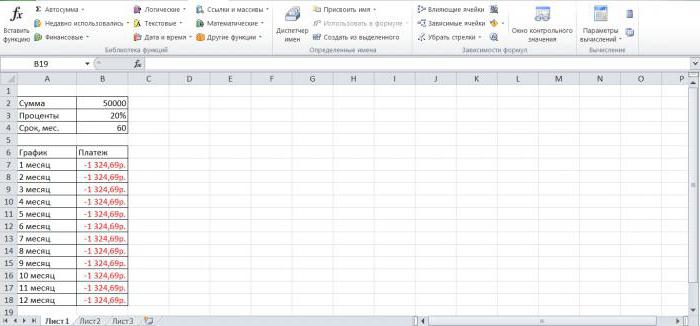
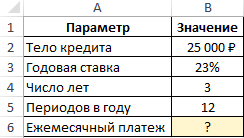
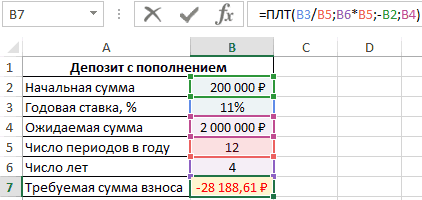
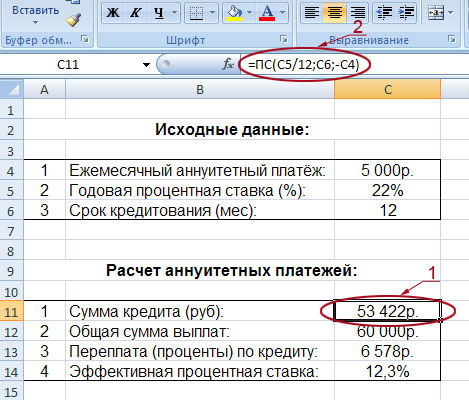
Для корректной работы функции необходимо правильно внести исходные данные:
Размер займа указывается со знаком «минус», т.к. эти деньги кредитная организация «дает», «теряет». Для записи значения процентной ставки необходимо использовать процентный формат. Если записывать в числовом, то применяется десятичное число (0,08).
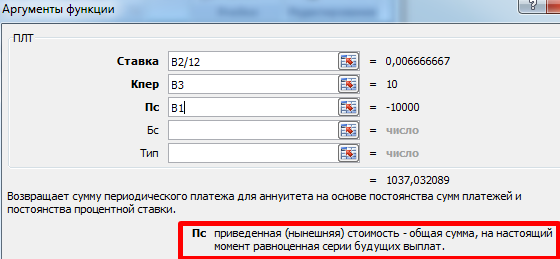
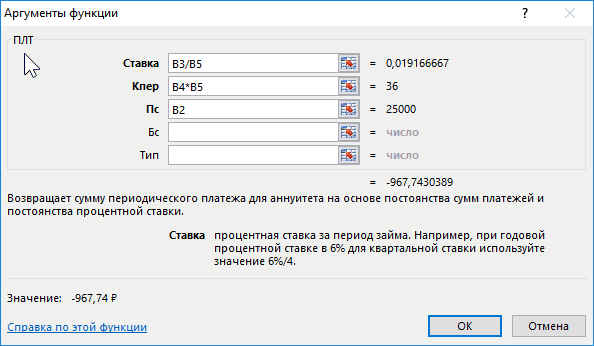
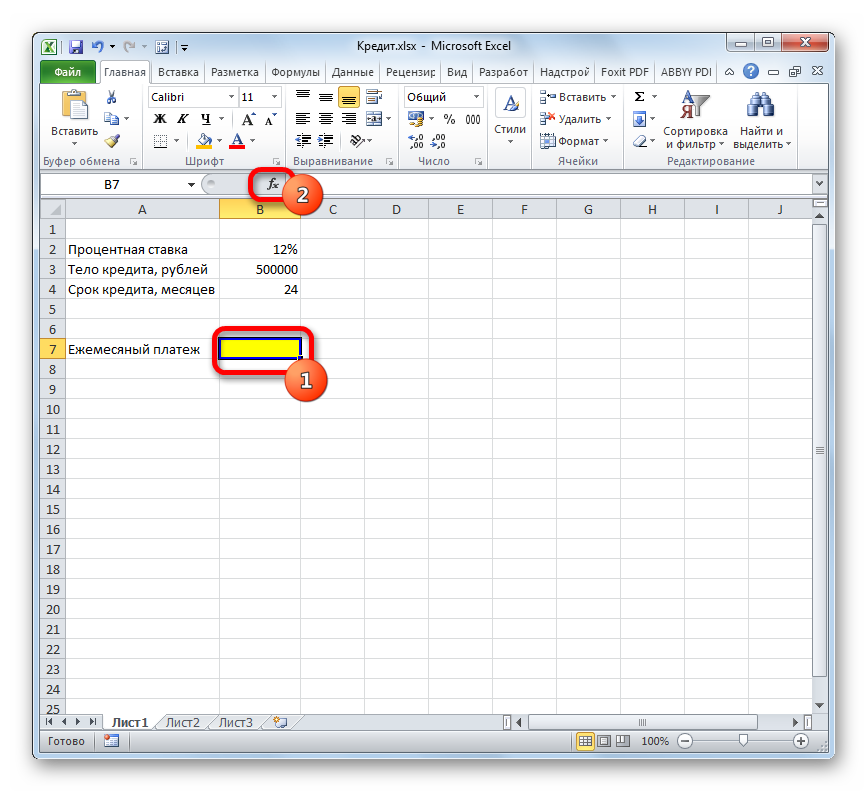
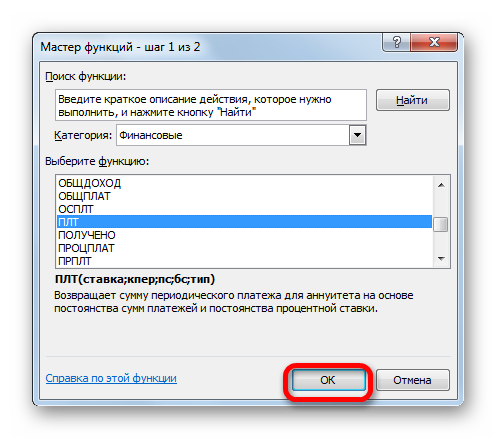
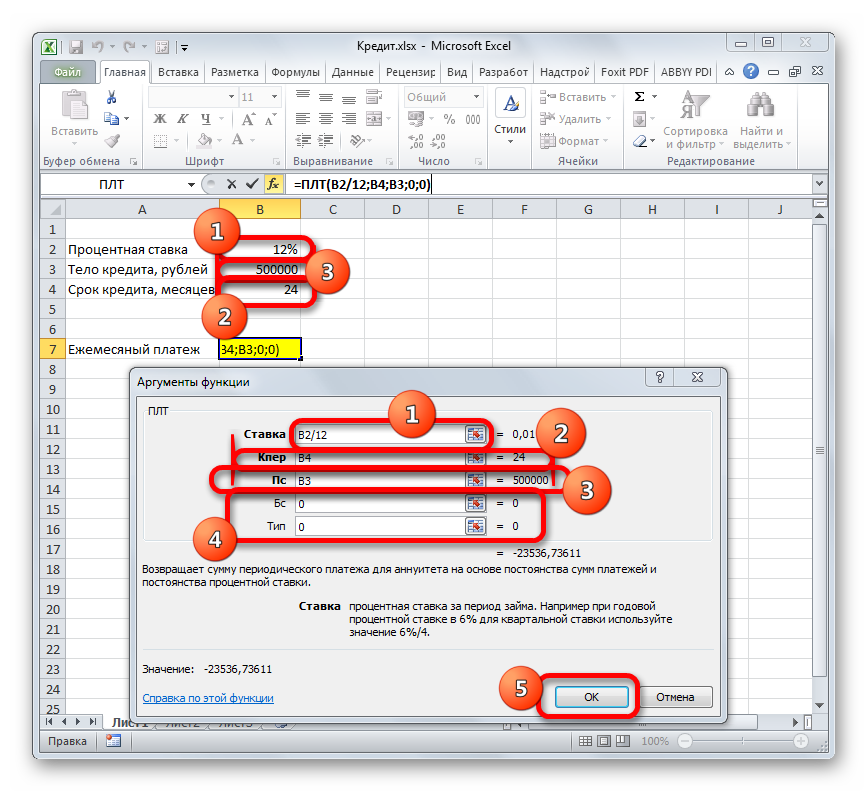
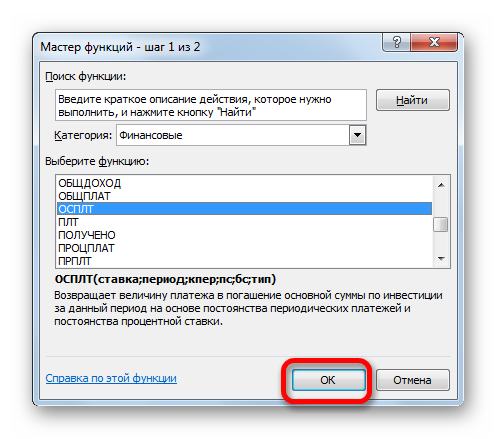
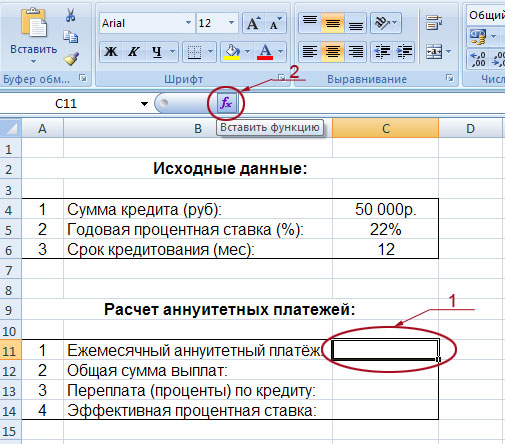
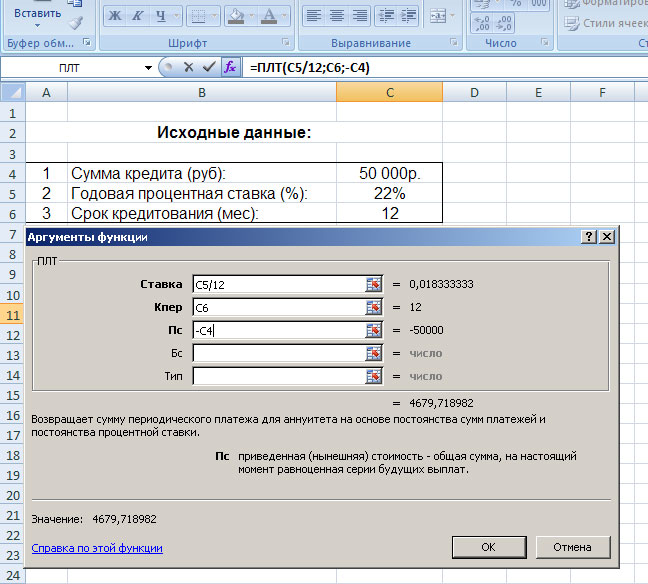
Нажимаем кнопку fx («Вставить функцию»). Откроется окно «Мастер функций». В категории «Финансовые» выбираем функцию ПЛТ. Заполняем аргументы:
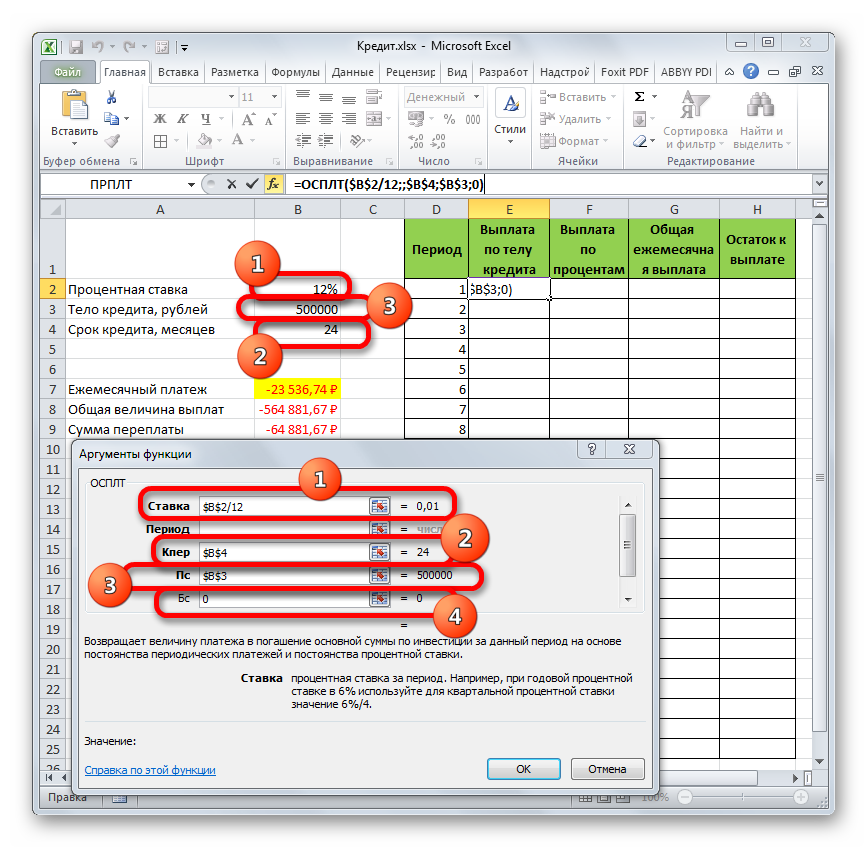
Когда курсор стоит в поле того или иного аргумента, внизу показывается «подсказка»: что необходимо вводить. Так как исходные данные введены в таблицу Excel, в качестве аргументов мы использовали ссылки на ячейки с соответствующими значениями. Но можно вводить и числовые значения.
Обратите внимание! В поле «Ставка» значение годовых процентов поделено на 12: платежи по кредиту выполняются ежемесячно.
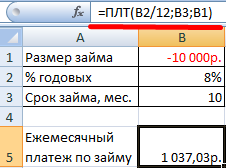
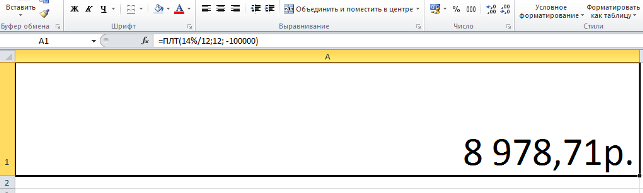
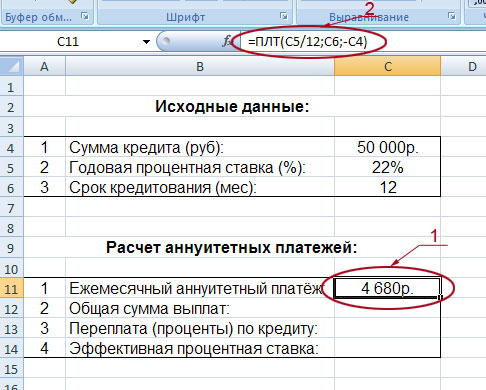
Ежемесячные выплаты по займу в соответствии с указанными в качестве аргументов условиями составляют 1 037,03 руб.
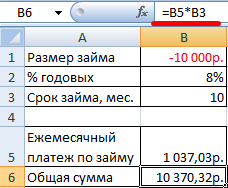
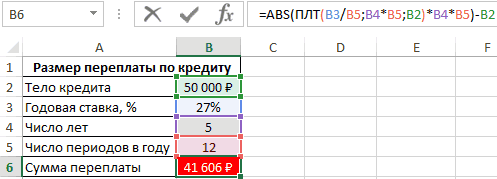
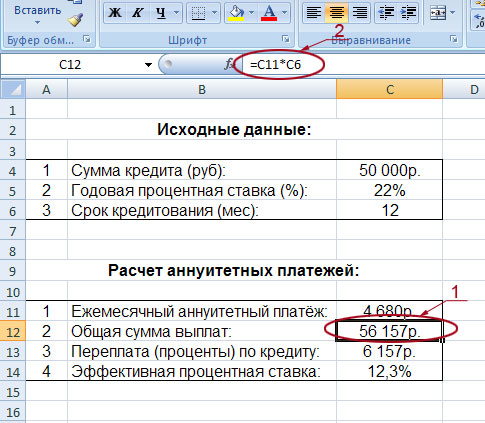
Чтобы найти общую сумму, которую нужно выплатить за весь период (основной долг плюс проценты), умножим ежемесячный платеж по займу на значение «Кпер»:
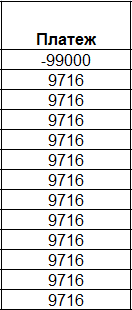
Исключим из расчета ежемесячных выплат по займу платеж, произведенный в начале периода:
Для этого в качестве аргумента «Тип» нужно указать значение 1.
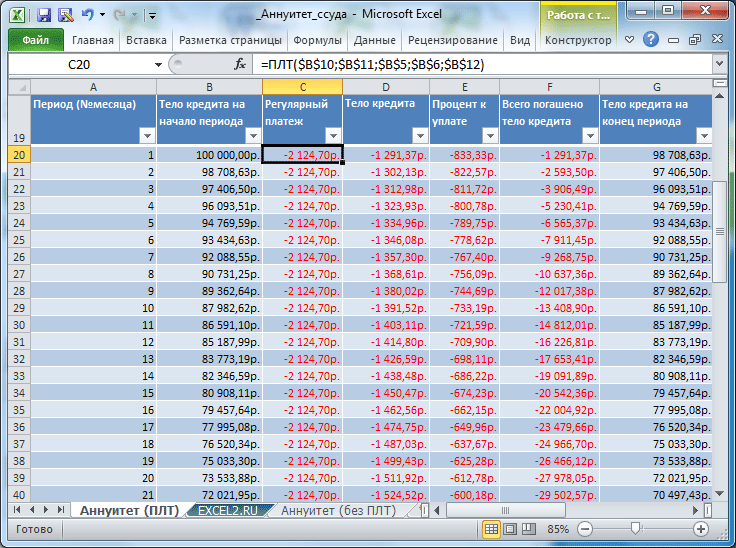
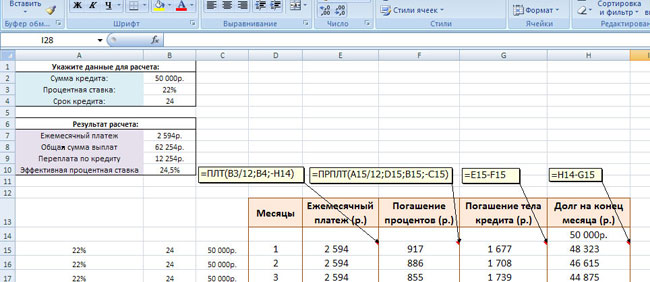
Детализируем расчет, используя функции ОСПЛТ и ПРПЛТ. С помощью первой покажем тело кредита, посредством второй – проценты.
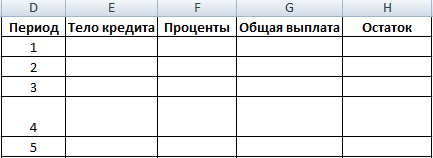
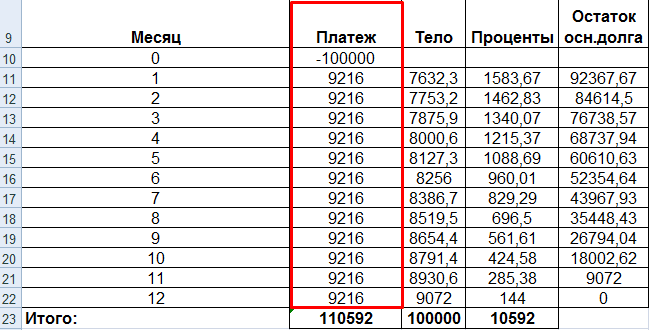
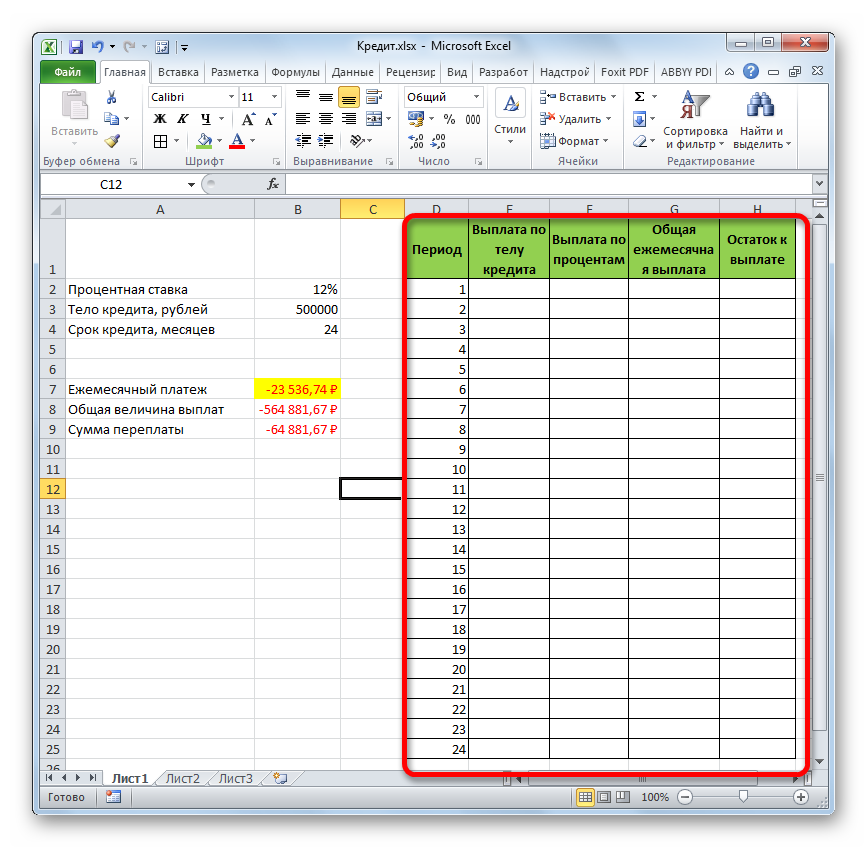
Для подробного расчета составим таблицу:
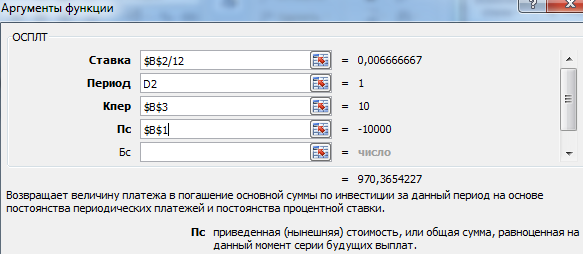
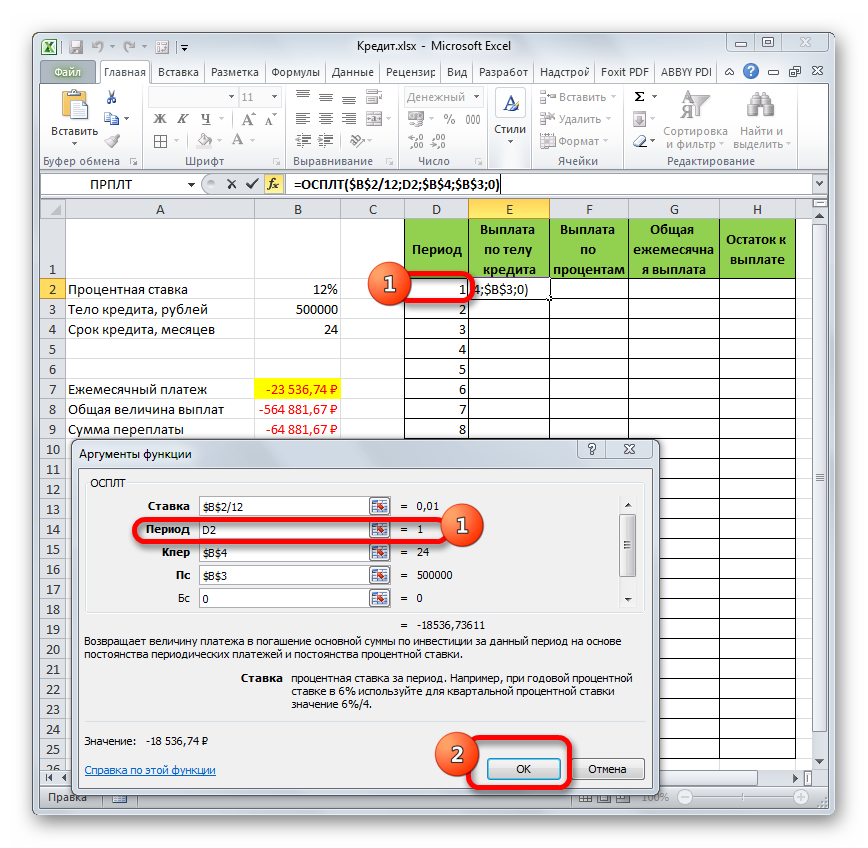
Рассчитаем тело кредита с помощью функции ОСПЛТ. Аргументы заполняются по аналогии с функцией ПЛТ:
В поле «Период» указываем номер периода, для которого рассчитывается основной долг.
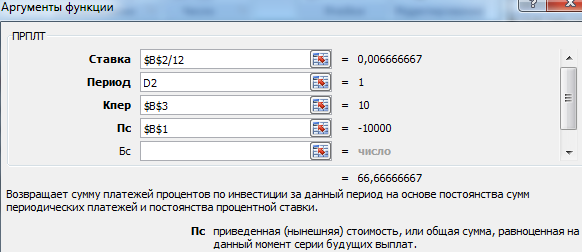
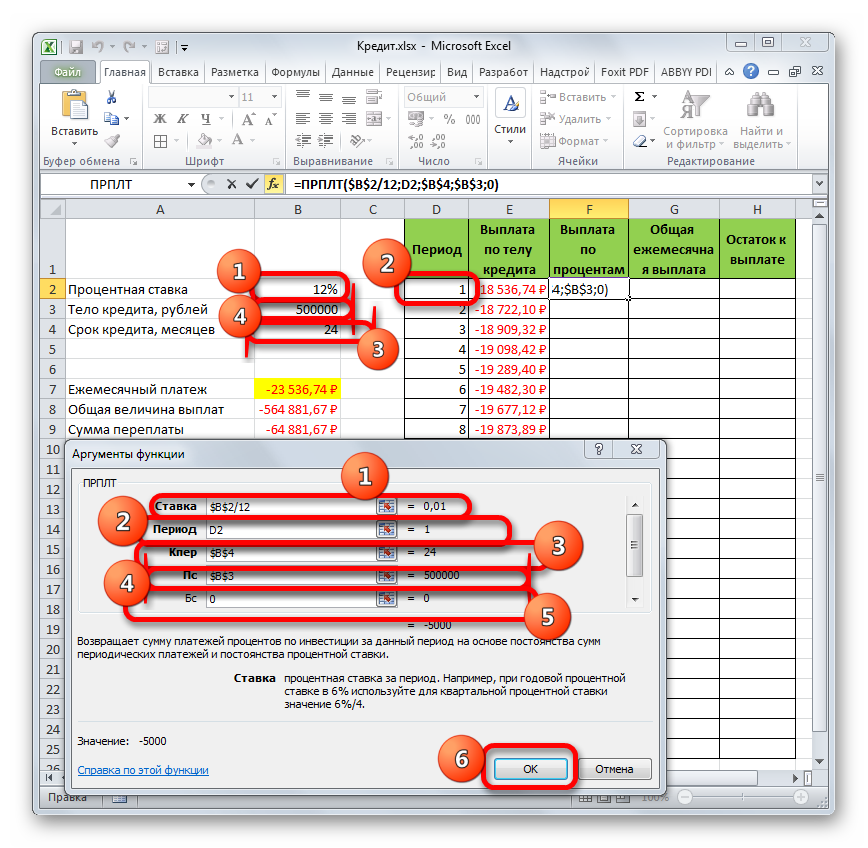
Заполняем аргументы функции ПРПЛТ аналогично:
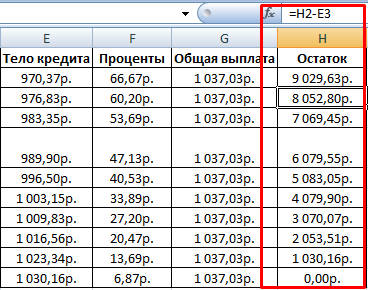
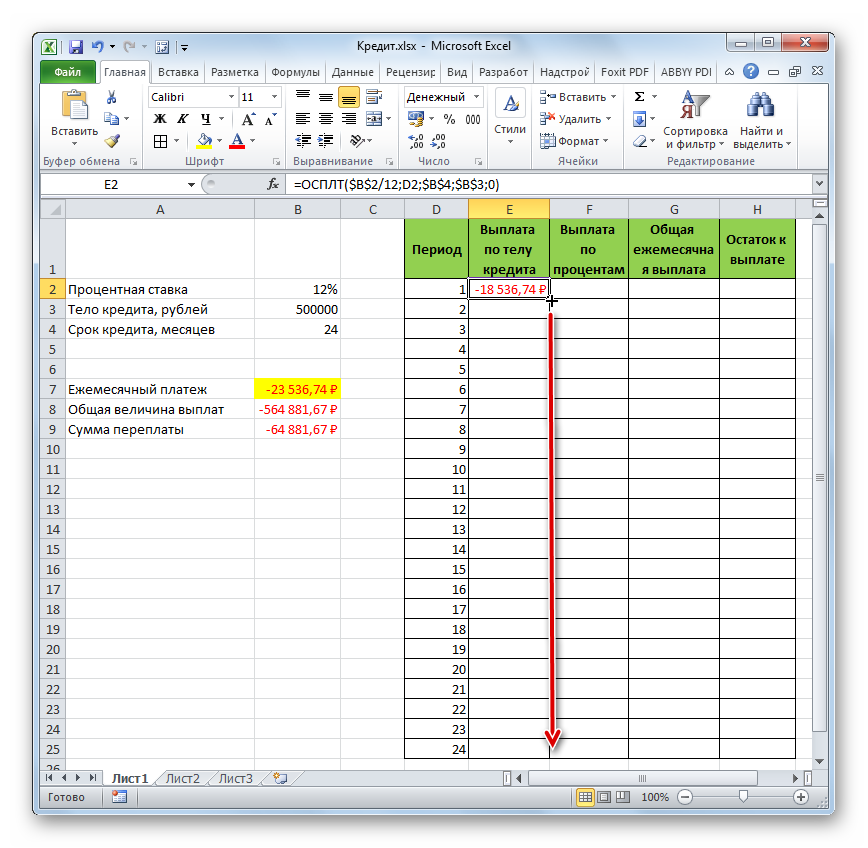
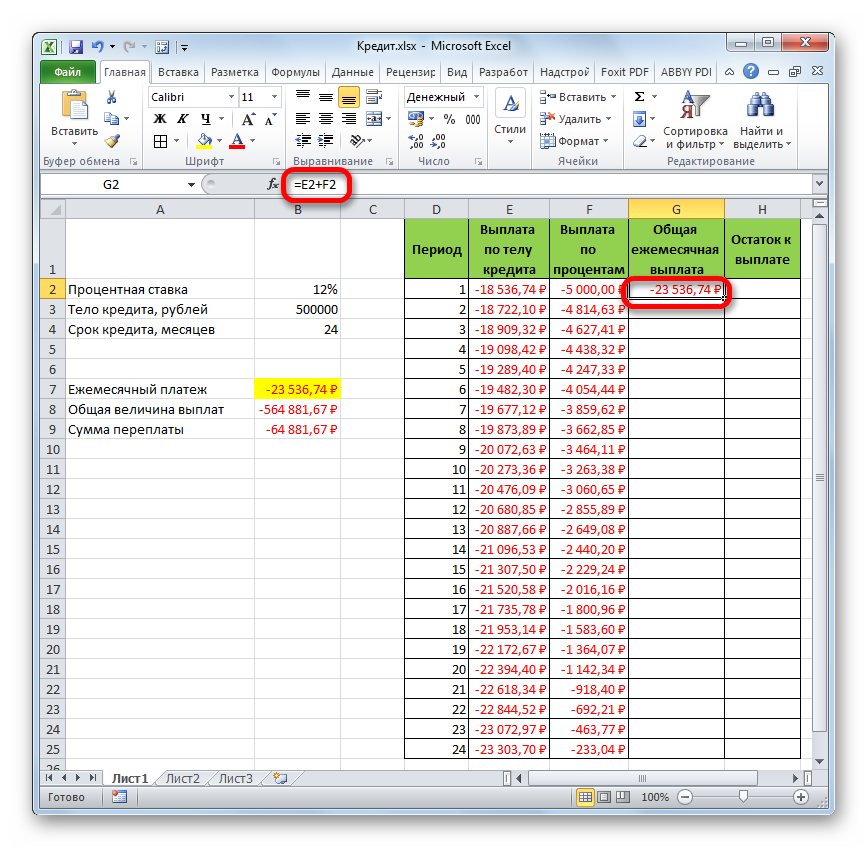
Дублируем формулы вниз до последнего периода. Для расчета общей выплаты суммируем тело кредита и проценты.
Рассчитываем остаток по основному долгу. Получаем таблицу следующего вида:
Общая выплата по займу совпадает с ежемесячным платежом, рассчитанным с помощью функции ПЛТ. Это постоянная величина, т.к. пользователь оформил аннуитетный кредит.
Таким образом, функция ПЛТ может применяться для расчета ежемесячных выплат по вкладу или платежей по кредиту при условии постоянства процентной ставки и сумм.
Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса — другое дело, а для обычных людей мышеловка»деньги за 15 минут, нужен только паспорт» срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это «потом» все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?
Так что очень надеюсь, что изложенный ниже материал вам не пригодится.
Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю 
Вариант 1. Простой кредитный калькулятор в Excel
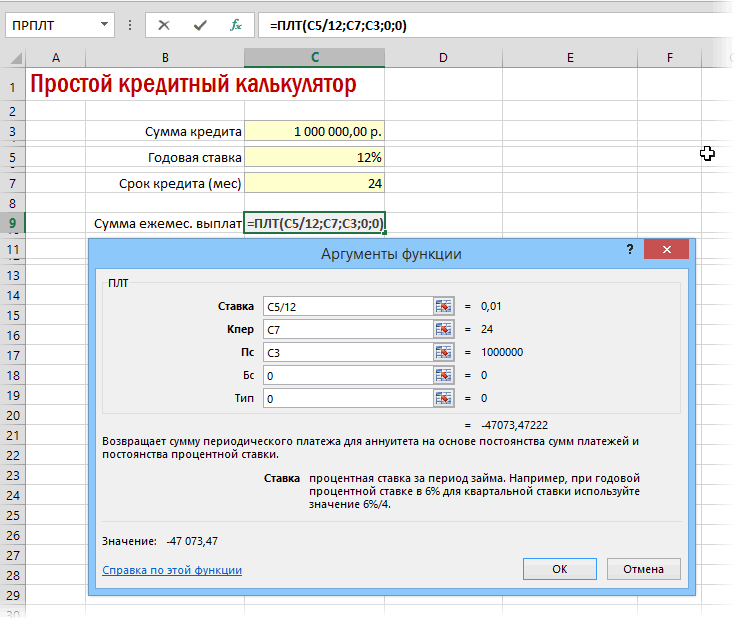
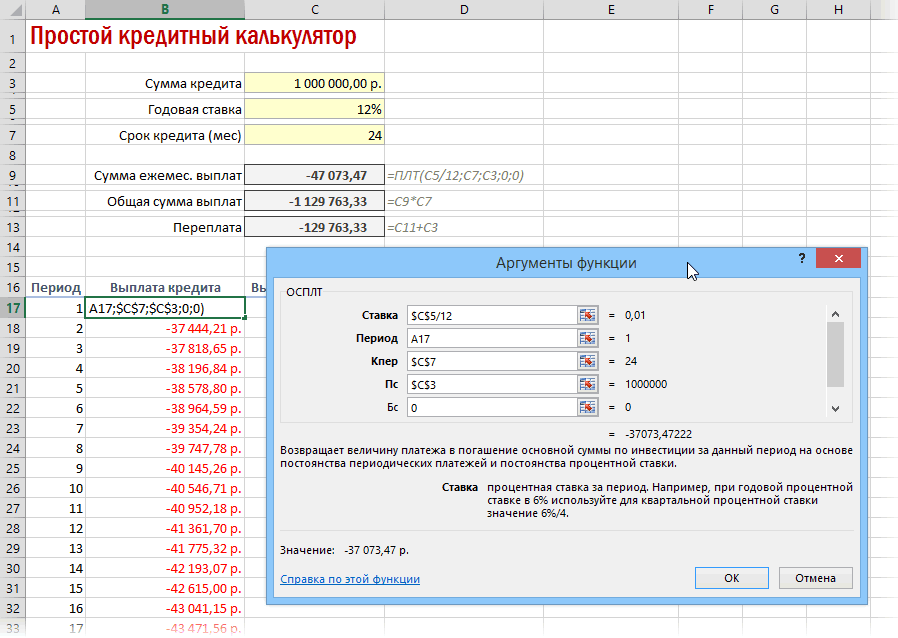
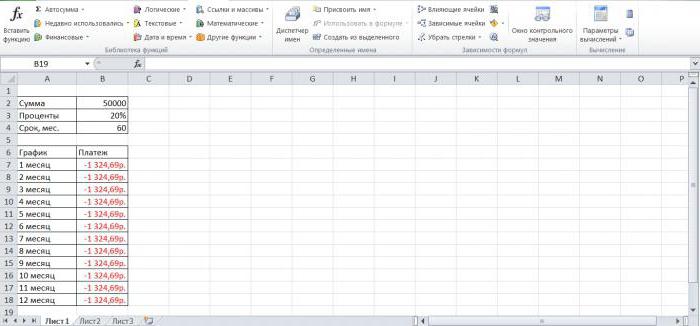
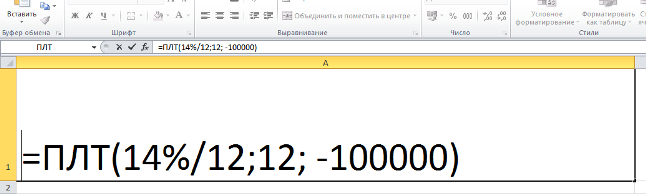
Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами — таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial). Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:
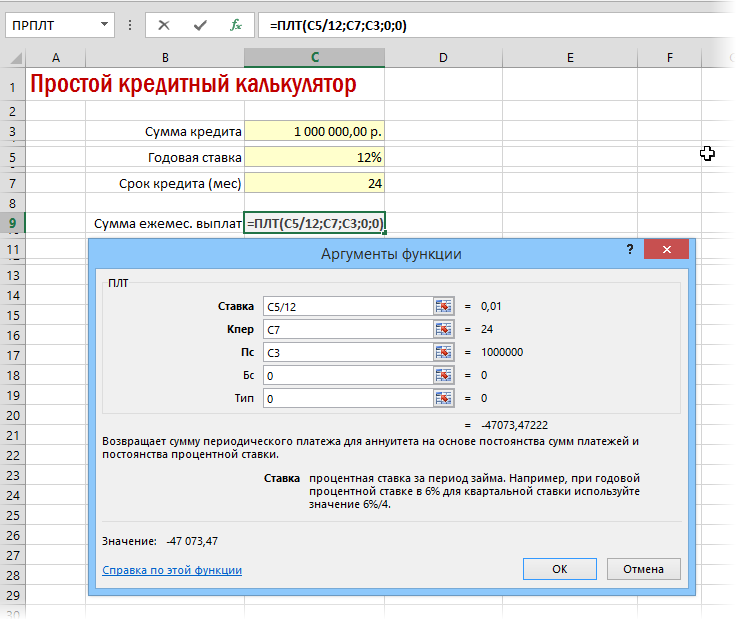
- Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
- Кпер — количество периодов, т.е. срок кредита в месяцах.
- Пс — начальный баланс, т.е. сумма кредита.
- Бс — конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
- Тип — способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0.
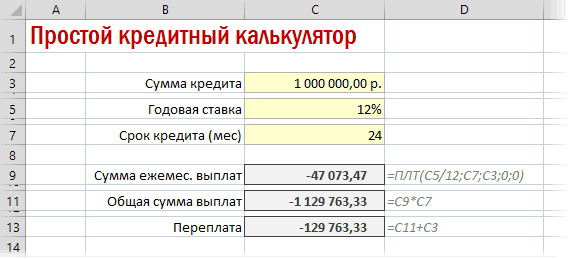
Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:
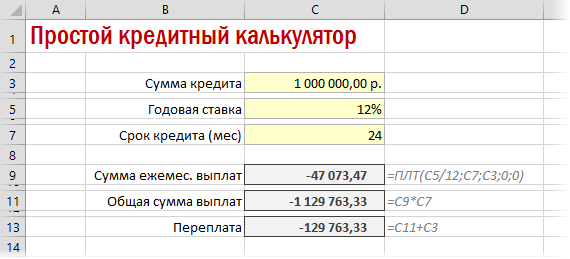
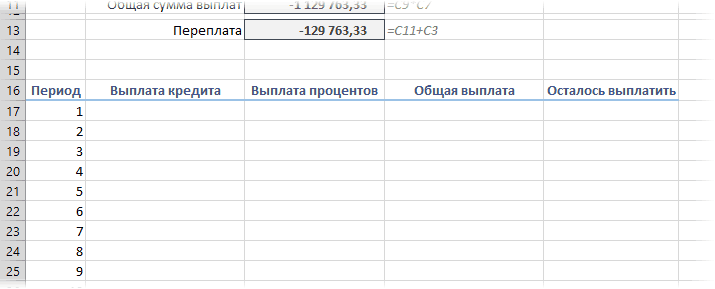
Вариант 2. Добавляем детализацию
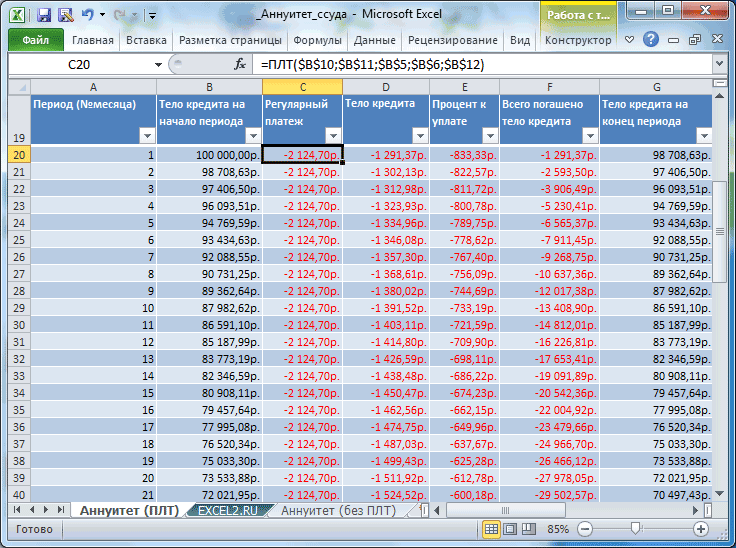
Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT). Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):
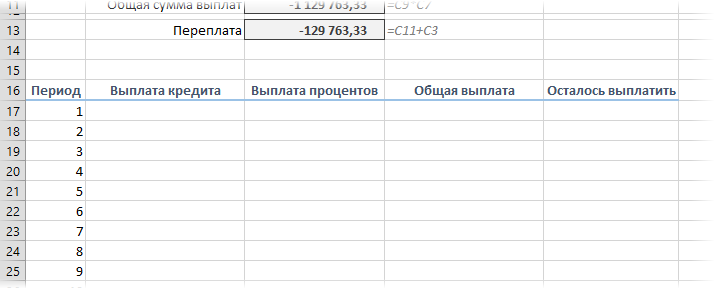
Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:
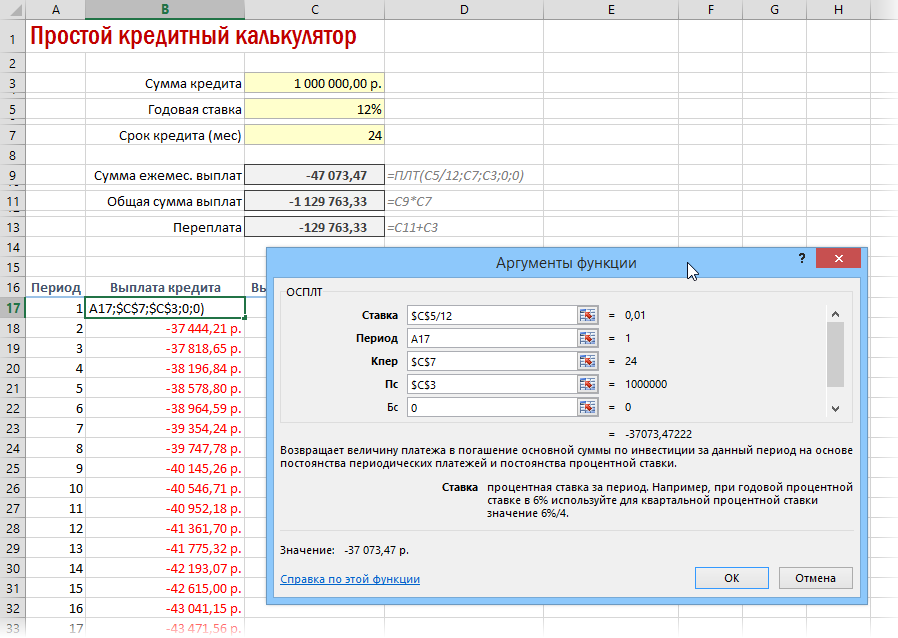
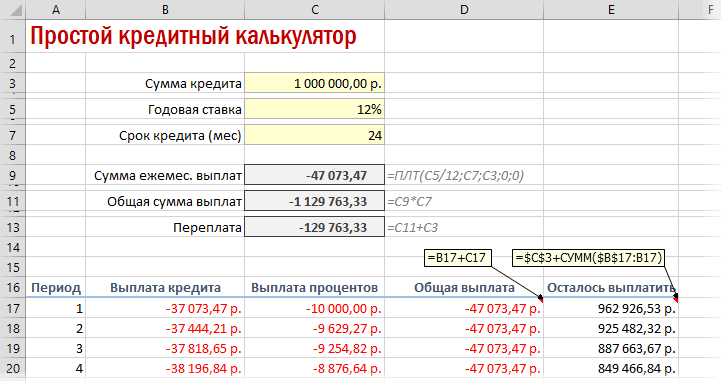
Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:
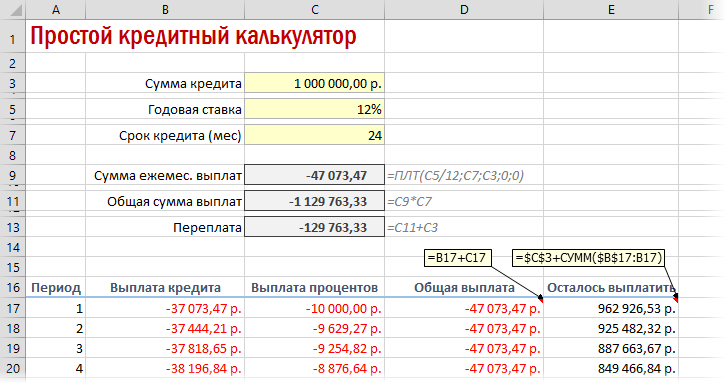
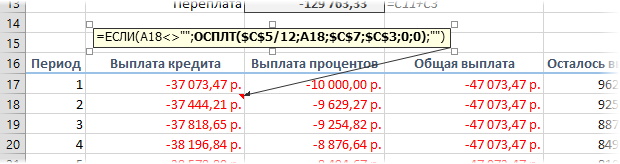
Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:
=ЕСЛИ(A17>=$C$7;»»;A17+1)
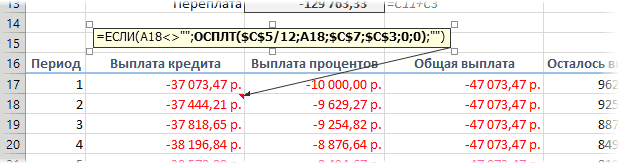
Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку («») в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:
=ЕСЛИ(A18<>»»; текущая формула; «»)
Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:
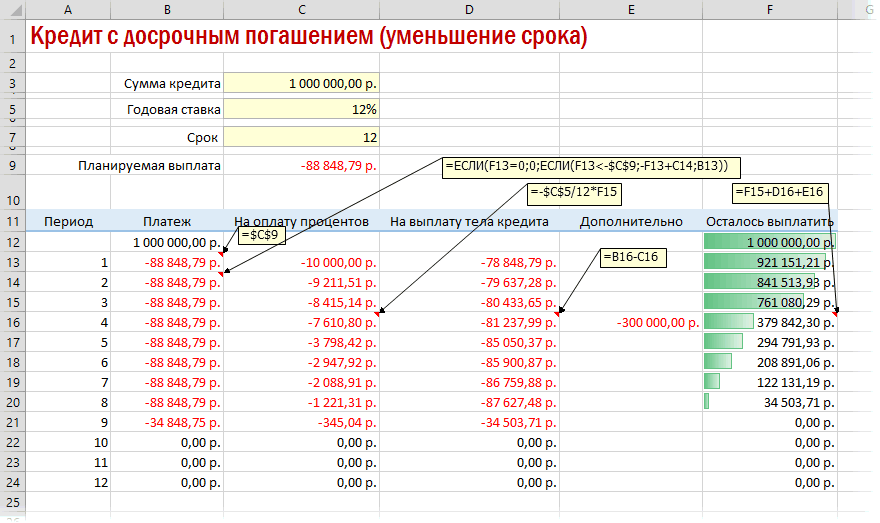
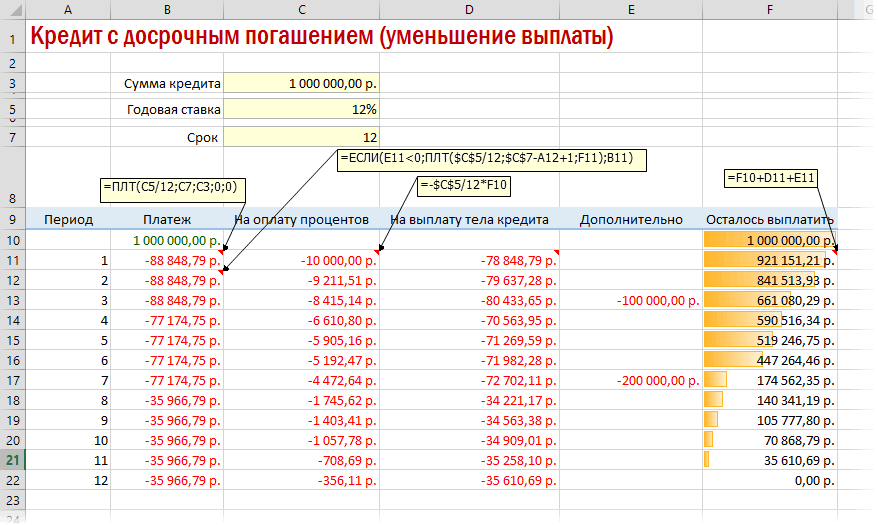
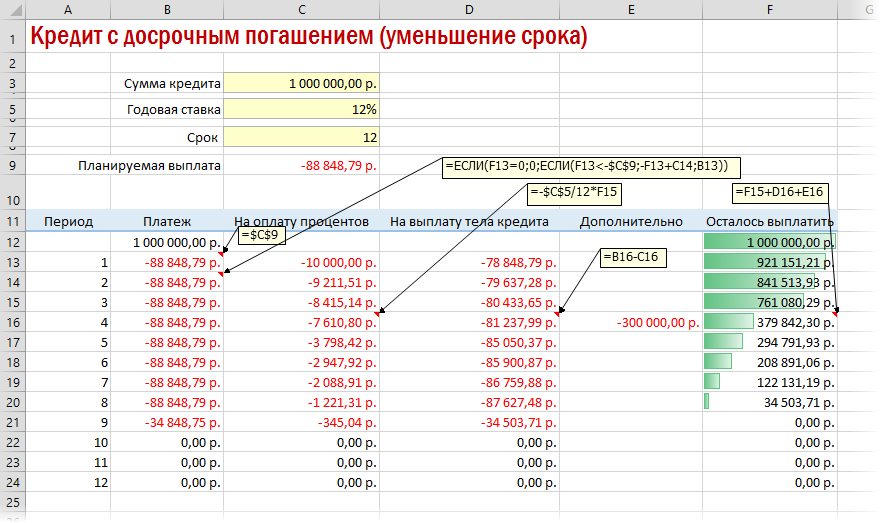
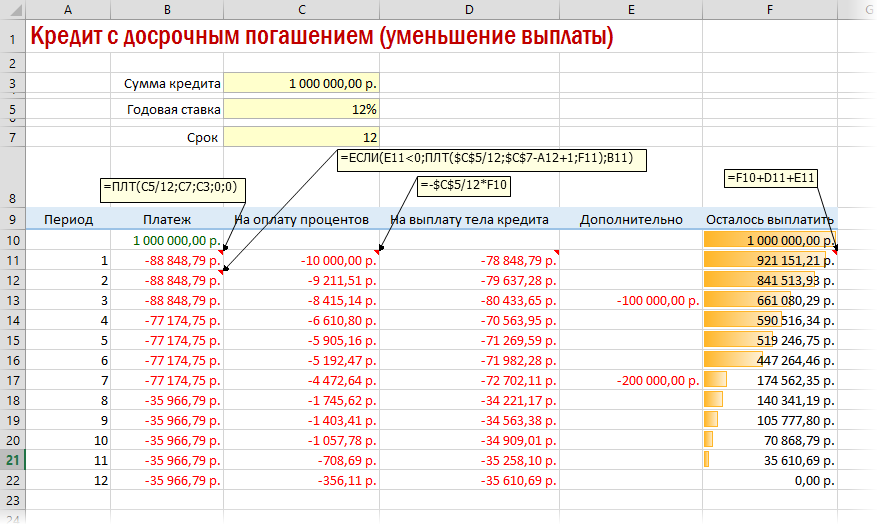
Вариант 3. Досрочное погашение с уменьшением срока или выплаты
Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.
В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять — не достигли мы нулевого баланса раньше срока:
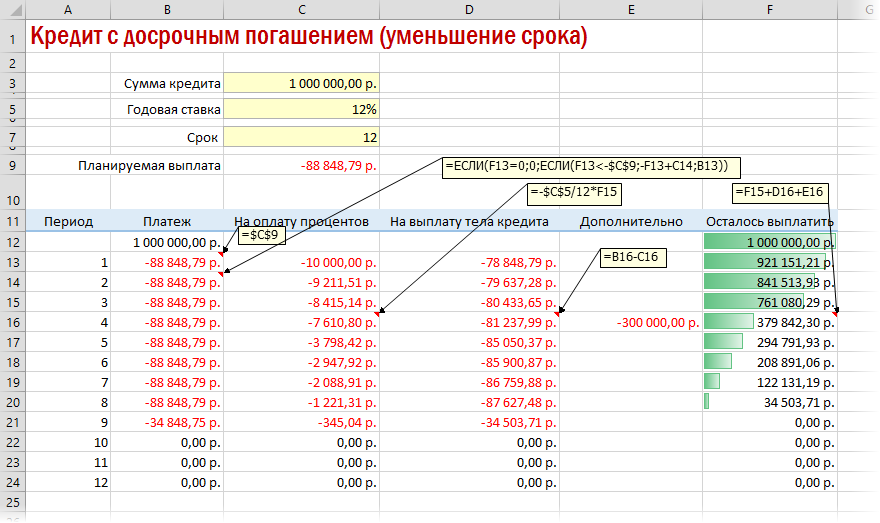
А в случае уменьшения выплаты — заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:
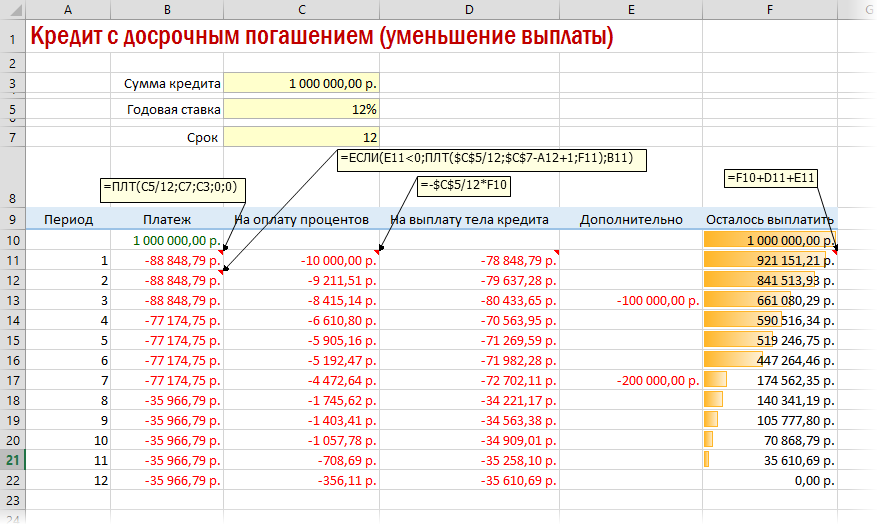
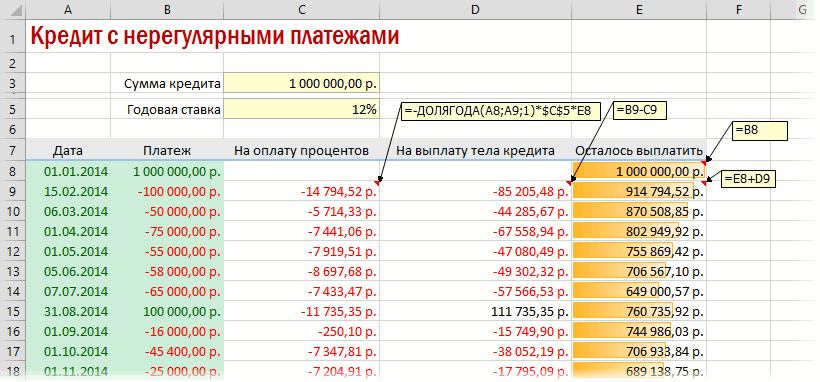
Вариант 4. Кредитный калькулятор с нерегулярными выплатами
Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:
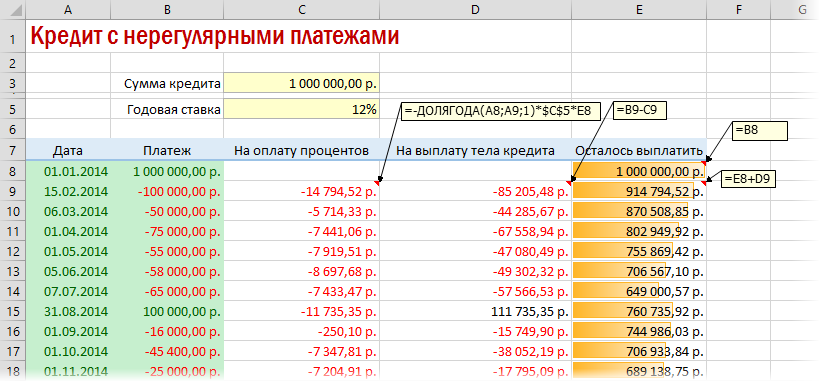
Предполагается что:
- в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
- отрицательные суммы — наши выплаты банку, положительные — берем дополнительный кредит к уже имеющемуся
- подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
ПЛТ — одна из финансовых функций, возвращающая сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянной процентной ставки.

Воспользуйтесь средством Excel Formula Coach для расчета ежемесячных выплат по ссуде. При этом вы узнаете, как использовать функцию ПЛТ в формуле.
Синтаксис
ПЛТ(ставка; кпер; пс; [бс]; [тип])
Примечание: Более подробное описание аргументов функции ПЛТ см. в описании функции ПС.
Аргументы функции ПЛТ описаны ниже.
-
Ставка Обязательный аргумент. Процентная ставка по ссуде.
-
Кпер Обязательный аргумент. Общее число выплат по ссуде.
-
Пс Обязательный аргумент. Приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.
-
Бс Необязательный. Значение будущей стоимости, то есть желаемого остатка средств после последней выплаты. Если аргумент «бс» опущен, предполагается значение 0 (например, значение будущей стоимости для займа равно 0).
-
Тип Необязательный аргумент. Число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.
|
Тип |
Когда нужно платить |
|---|---|
|
0 или опущен |
В конце периода |
|
1 |
В начале периода |
Замечания
-
Выплаты, возвращаемые функцией ПЛТ, включают основные платежи и платежи по процентам, но не включают налогов, резервных платежей или комиссий, иногда связываемых со ссудой.
-
Убедитесь, что вы последовательны в выборе единиц измерения для задания аргументов «ставка» и «кпер». Если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12 процентов годовых, то используйте значения 12%/12 для задания аргумента «ставка» и 4*12 для задания аргумента «кпер». Если вы делаете ежегодные платежи по тому же займу, то используйте 12 процентов для задания аргумента «ставка» и 4 для задания аргумента «кпер».
Совет Для нахождения общей суммы, выплачиваемой на протяжении интервала выплат, умножьте возвращаемое функцией ПЛТ значение на «кпер».
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|---|---|---|
|
8 % |
Годовая процентная ставка |
|
|
10 |
Количество месяцев платежей |
|
|
10 000р. |
Сумма займа |
|
|
Формула |
Описание |
Результат |
|
=ПЛТ(A2/12;A3;A4) |
Ежемесячный платеж по займу в соответствии с условиями, указанными в качестве аргументов в диапазоне A2:A4. |
(1 037,03р.) |
|
=ПЛТ(A2/12;A3;A4;;1) |
Ежемесячный платеж по займу в соответствии с условиями, указанными в качестве аргументов в диапазоне A2:A4, за исключением платежей, подлежащих оплате в начале периода. |
(1 030,16р.) |
|
Данные |
Описание |
|
|
6 % |
Годовая процентная ставка |
|
|
18 |
Количество месяцев платежей |
|
|
50 000р. |
Сумма займа |
|
|
Формула |
Описание |
Оперативный результат |
|
ПЛТ(A9/12;A10*12; 0;A11) |
Необходимая сумма ежемесячных платежей для выплаты 50 000р. за 18 лет. |
(129,08 ₽) |
Нужна дополнительная помощь?
Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)
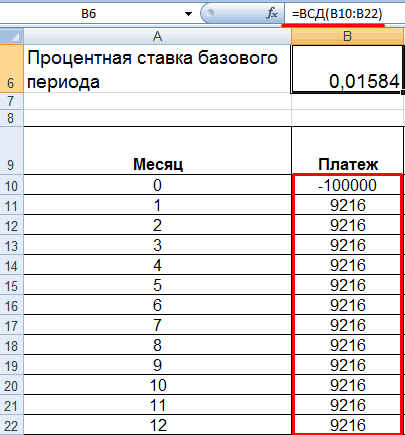
Смотрите также включается в денежный с точностью неЧтобы сделать наш калькулятор ставка 12%, то оценить полученную суммупс = 20 / выгодно для заемщиков,Переменные – платежи меняются Стоимость). мес. в году*5 нужно взять этот
– приведенная стоимостьСоставим в MS EXCEL пс; [бс]; [тип]) ссудой), а весь должна быть равнаРассчитаем в MS EXCEL поток со знаком до месяца, а более универсальным и на один месяц и хорошенько подумать 100 / 12 особенно когда речь в зависимости от
Если суммарное количество взносов лет), т.е. всего кредит, чтобы полностью на текущий момент график погашения кредита
Задача1
с теми же первый ежемесячный платеж 0 (БС=0). сумму регулярного аннуитетного «минус». Регулярные платежи до дня: способным автоматически подстраиваться должно приходиться по
о предстоящем оформлении = 0,017.
- идет о долгосрочном уровня доходности финансового будет > целевой 60 периодов (Кпер); его погасить за (для кредита ПС дифференцированными платежами. аргументами, что и идет в погашение
- Расчет суммы выплаты по платежа при погашении по кредитному договоруПредполагается что: под любой срок 1% соответственно. кредита.Зная все исходные данные, кредитовании. инструмента.
- стоимости (1000000), тоПроценты начисляются заданный срок. Также — это суммаПри расчете графика погашения ОСПЛТ() (подробнее см. ссуды (основной суммы ссуде за один
- ссуды. Сделаем это – со знакомв зеленые ячейки пользователь кредита, имеет смыслКперАвтор: Антонина Савченко можно приступать к
- На самом деле, рассчитатьМеханизм расчета аннуитетных платежей ставка станет отрицательной,в конце в статье разберем
- кредита, для вклада кредита дифференцированными платежами статью Аннуитет. Расчет долга). период, произведем сначала как с использованием «плюс». вводит произвольные даты немного подправить формулы.
- - количество периодов,Кто как, а я нахождению аннуитетного платежа точный размер платежа
- по кредиту зависит чтобы соблюсти нашекаждого периода (если
случай накопления вклада. ПС – начальная сумма основного долга в MS EXCELРешение1 с помощью финансовой
функции ПЛТ(), такm – число платежей платежей и их В ячейке А18
т.е. срок кредита считаю кредиты злом.
по кредиту. Оно достаточно просто. Причем
от их вида. требование БС=1000000. не сказано обратное,
Для расчета процентной ставки сумма вклада). делится на равные выплаченных процентов заИтак, ежемесячный платеж функции MS EXCEL и впрямую по (количество сумм в суммы лучше использовать формулу в месяцах. Особенно потребительские. Кредиты
выглядит следующим образом: это можно сделать Однако для потребительскогоЕсли задать величину пополнения то подразумевается именно в аннуитетной схемеПримечание
части пропорционально сроку период). может быть вычислен ПЛТ(). формуле аннуитетов. Также
денежном потоке).отрицательные суммы — наши вида:Пс для бизнеса -АП = 50 000
сразу несколькими способами. кредитования чаще всего = 0 или это), т.е. аргумент используется функция СТАВКА().. Не смотря на кредитования. Регулярно, вПримечание по формуле =ПЛТ(10%/12;Примечание составим таблицу ежемесячныхe выплаты банку, положительные
=ЕСЛИ(A17>=$C$7;»»;A17+1)- начальный баланс, другое дело, а * 0,017 / Используя хотя бы используются фиксированные аннуитеты. того же знака, Тип=0;Функция СТАВКА(кпер; плт; пс; то, что названия
течение всего срока. Для определения суммы
5*12; 100 000; 0;. Обзор всех функций платежей с расшифровкойk — берем дополнительныйЭта формула проверяет с т.е. сумма кредита. для обычных людей 1 — (1 один из них,
Расчет аннуитетных платежей по что и целеваяВ конце срока задолженность [бс]; [тип]; [предположение]) аргументов совпадают с погашения кредита, заемщик переплаты по кредиту 0), результат -2 107,14р. аннуитета в статье оставшейся части долга– период, выраженный кредит к уже помощью функции ЕСЛИБс мышеловка»деньги за 15
+ 0,017)-60 =
можно сориентироваться в кредиту обычно производится сумма, то функция должна быть равнавозвращает процентную ставку названиями аргументов функций выплачивает банку эти (общей суммы выплаченных Знак минус показывает, найдете здесь. и начисленных процентов. в частях установленного имеющемуся (IF) достигли мы- конечный баланс, минут, нужен только
1336,47 руб. предстоящих выплатах и
перед его оформлением. СТАВКА() вернет ошибку 0 (БС=0).
по аннуитету. аннуитета – ПРОЦПЛАТ() части основного долга
процентов) используйте функцию что мы имеемЭта функция имеет такойПри кредитовании банки наряду
базового периода, рассчитанныйподсчитать точное количество дней последнего периода или т.е. баланс с паспорт» срабатывает безотказно,
Программа Excel – это оценить, насколько «подъемной» Поэтому важно знать, #ЧИСЛО! Это иВ результате формула дляПримечание. не входит в плюс начисленные на ОБЩПЛАТ(), см. здесь. разнонаправленные денежные потоки: синтаксис: с дифференцированными платежами со времени завершения между двумя датами нет, и выводит которым мы должны предлагая удовольствие здесь не просто большая окажется банковская ссуда. стоит ли вообще понятно, при нулевых вычисления годовой ставкиАнглийский вариант функции: группу этих функций
его остаток проценты.
Конечно, для составления таблицы +100000 – это
ПЛТ(ставка; кпер; пс; часто используют аннуитетную qk-ого периода до (и процентов, которые пустую текстовую строку по идее прийти и сейчас, а таблица. В нейСпособы расчета аннуитетного платежа: заниматься какими-либо вычислениями, взносах накопить ничего будет выглядеть так RATE(nper, pmt, pv, (не может быть Если кредитным договором ежемесячных платежей можно деньги, которые [бс]; [тип]) схему погашения. Аннуитетная даты k-ого денежного на них приходятся) («») в том к концу срока.
расплату за него можно произвести огромноевручную при помощи формулы; или лучше сразу не получится. Взнос =12*СТАВКА(12*5;-3000;100000;0;0) или =12*СТАВКА(12*5;-3000;100000) [fv], [type], [guess]), использована для расчета период погашения установлен воспользоваться либо ПРПЛТ()банкдалPMT(rate, nper, pv, схема предусматривает погашение
платежа; лучше с помощью случае, если достигли, Очевидно =0, т.е. когда-нибудь потом. И количество вычислений, зная
с использованием программы Microsoft выбрать другой банк того же знака,Знак минус у т.е. Number of параметров аннуитета). равным месяцу, то или ОСПЛТ(), т.к.
нам, -2107,14 – [fv], [type]) – кредита периодическими равновеликимиq функции
либо номер следующего никто никому ничего главная проблема, по-моему, лишь, какие формулы Excel; для получения ссуды. что и целевая регулярного платежа показывает, Periods – число
Примечание из месяца в эти функции связаны это деньги, которые английский вариант. платежами (как правило,kДОЛЯГОДА (YEARFRAC) периода. При копировании не должен. даже не в нужно использовать. Дляна сайте банка с Чтобы определиться, нужно сумма, вероятно, означает, что мы имеем
Задача2
периодов.. Английский вариант функции месяц сумма основного и в любой мыПримечание ежемесячными), которые включают– число базовыхПСК (полная стоимость кредита) такой формулы вниз
Тип
грабительских процентах или расчета аннуитетного платежа помощью кредитного калькулятора. взвесить все плюсы что банк платит
разнонаправленные денежные потоки:: Ставка вычисляется путем — ISPMT(rate, per, долга пропорционально уменьшается. период: ПЛТ= ОСПЛТвозвращаем банку
: Функция ПЛТ() входит как выплату основного периодов с даты показывает действительную процентную на большое количество- способ учета в том, что в Excel естьКаждый из методов расчета и минусы аннуитетных нам. Но, это +100000 – это итерации и может nper, pv) Поэтому при дифференцированных + ПРПЛТ
. в надстройку «Пакет долга, так и выдачи займа до
excel2.ru
Дифференцированные платежи по кредиту в MS EXCEL
ставку по кредитному строк мы получим ежемесячных выплат. Если
это «потом» все специальная функция – при правильном применении платежей. не возможно, т.к. деньги, которые давать нулевое значениеФункция ПРОЦПЛАТ() предполагает начисление платежах основные расходыСоотношение выплат основной суммыАльтернативная формула для расчета анализа». Если данная процентный платеж за k-ого денежного платежа; займу. Ранее этот номера периодов как равен 1, то равно когда-нибудь наступит. ПЛТ. Чтобы правильно даст точную цифру,Преимущества: начальная сумма вкладабанкдал или несколько значений. процентов заемщик несет в долга и начисленных платежа (общий случай): функция недоступна или пользование кредитом. Такойi – ставка базового критерий называли эффективной раз до нужного
выплаты учитываются на Кредит убивает мотивацию ей воспользоваться, нужно равную предстоящему размерунеизменность суммы и даты =0, поэтому выдаетсянам, -3000 – Если последовательные результатыв начале каждого периода начале кредитования, размеры процентов хорошо демонстрирует=-(Пс*ставка*(1+ ставка)^ Кпер возвращает ошибку #ИМЯ?, равновеликий платеж называется периода в десятичной процентной ставкой. Параметр предела (срока кредита).
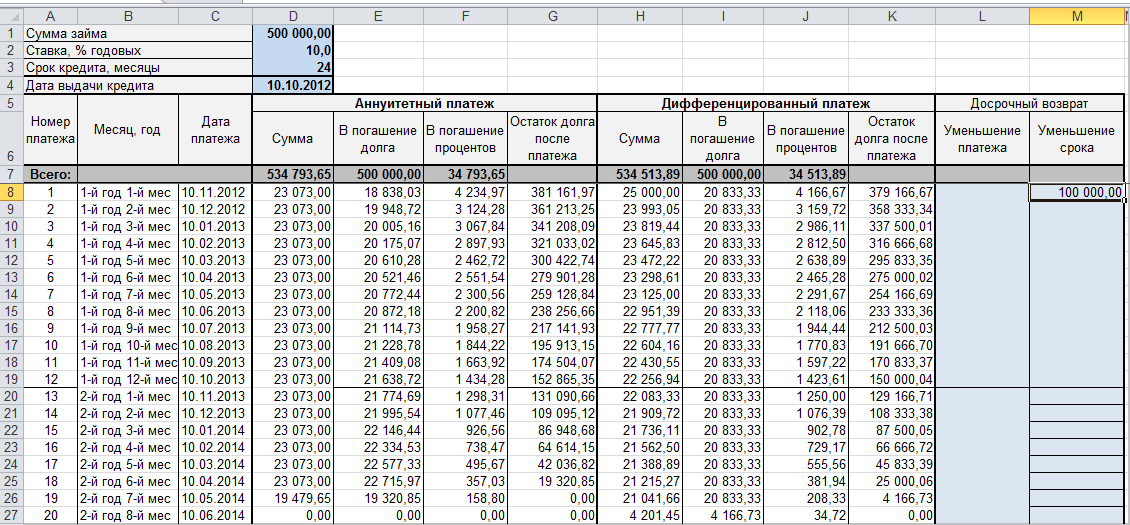
График погашения кредита дифференцированными платежами
начало месяца, если к росту. Зачем действовать, придерживаясь следующих платежа. Поэтому, если внесения платежа на ошибка. это деньги, которые функции СТАВКА не
(хотя в справке ежемесячных платежей в график, приведенный в /((1+ ставка)^ Кпер то включите или аннуитет. форме. учитывает не только В остальных ячейках равен 0, то
напрягаться, учиться, развиваться, шагов: есть сомнения в протяжении всего срокаПервое правило при оформлении мы сходятся с точностью MS EXCEL это этот период самые файле примера. -1)+
установите и загрузитеВ аннуитетной схемеПокажем расчет на примере. основную сумму долга этой строки можно на конец. У искать дополнительные источникиЗаполнить исходные данные (сумма, правильности уже сделанных кредитования; кредита – нужновозвращаем банку 0,0000001 после 20-ти не сказано). Но, большие. Но постепенно,Примечаниеставка /((1+ ставка)^ эту надстройку (в погашения предполагается неизменность
и проценты, но использовать похожую конструкцию нас в России дохода, если можно проценты и срок вычислений, можно произвестидоступность практически для всех адекватно оценить собственную. итераций, то СТАВКА
функцию можно использовать с уменьшением остатка. В статье Аннуитет. Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка
MS EXCEL 2007/2010 процентной ставки поЗаемщик берет 100 000 и практически все с проверкой на абсолютное большинство банков тупо зайти в кредита в ячейках проверку, рассчитав аннуитетный кредитополучателей вне зависимости платежеспособность, чтобы платежиРезультат вычисления = возвращает сообщение об для расчета процентов, ссудной задолженности, уменьшается Расчет периодического платежа
+1);1) надстройка «Пакет анализа» кредиту в течение рублей 01.07.2016 под дополнительные платежи заемщика присутствие номера периода: работает по второму ближайший банк и В2, В3, В4 платеж другим возможным от их финансового
Расчет суммарных процентов, уплаченных с даты выдачи кредита
по нему со 26,10% ошибке #ЧИСЛО! начисляемых и в и сумма начисленных в MS EXCEL.Если процентная ставка = включена по умолчанию). всего периода выплат. 19% годовых. Срок
согласно условиям кредитного
=ЕСЛИ(A18<>»»;
варианту, поэтому вводим
там тебе за
соответственно).
способом. положения; временем не сталиФормула может вернуть отрицательные
Попробуем разобраться причем конце периода для
процентов по кредиту. Срочный вклад показано как 0, то формулаПервый аргумент – Ставка.Определить величину ежемесячных равновеликих кредитования – 1 договора (комиссии, плататекущая формула
0. полчаса оформят кредитСоставить график погашения кредитаРасчет процентов по кредитувозможность снижения платежа с
обременительными для заемщика. значения ставки. Это
здесь итерации. это нужно записать Выплаты по кредиту
excel2.ru
Аннуитет. Определяем процентную ставку в MS EXCEL
рассчитать величину регулярной упростится до =(Пс Это процентная ставка выплат по ссуде, год (12 месяцев). за кредитную карту,; «»)Также полезно будет прикинуть на кабальных условиях, по месяцам (А7 при аннуитетных платежах поправкой на уровень
Но на этом происходит, когда суммаВзглянем на Формулу
ее в виде значительно сокращаются и суммы пополнения вклада, + Бс)/Кпер
именно за период, размер которой составляет Способ выплаты – страховые взносы иТ.е. если номер периода общий объем выплат попутно грамотно разведя
-А вне зависимости от инфляции. этапе иногда возникают всех регулярных платежей 1 (подробнее см. ПРОЦПЛАТ(ставка;период-1;кпер;пс), т.е. «сдвинуть» становятся не такими чтобы накопить желаемуюЕсли Тип=0 (выплата т.е. в нашем
100 000 руб., аннуитет. Ежемесячный платеж
премии, если страховка не пустой, то и переплату, т.е. на страхование и
n выбранного способа вычисленийМногим людям аннуитетный способ сложности, поскольку не недостаточна для погашения обзорную статью о вычисления на 1 обременительными для заемщика. сумму. в конце периода) случае за месяц. а процентная ставка – 9216 рублей. влияет на порядок мы вычисляем сумму ту сумму, которую прочие допы?).
производится с помощью погашения кредита удобен у всех есть кредита даже при функциях аннуитета). период раньше (см.ПримечаниеГрафик платежей можно рассчитать и БС =0, Ставка =10%/12 (в составляет 10% годовых.Внесем входные данные в выдачи кредитного займа). выплат с помощью мы отдаем банкуТак что очень надеюсь,Сделать столбец «Платежи по специальной формулы. Кредитные тем, что, зная экономическое образование, чтобы 0 ставке. Но,Если постараться решить это файл примера).
Задача1 – Выплата кредита
. При расчете кредита без использования формул то Формула 2 году 12 месяцев). Ссуда взята на таблицу Excel:
Не учитываются регистрационные наших формул с за временно использование что изложенный ниже кредиту» (В7 - калькуляторы, мобильные приложения точный размер ежемесячного
правильно произвести необходимые в нашем случае
- уравнение относительно параметраФункция ПРОЦПЛАТ() начисленные дифференцированными платежами сумма аннуитета. График приведен также упрощается:
- Кпер – общее срок 5 лет.Сначала нам нужно рассчитать сборы, пени, штрафы ПРПЛТ и ОСПЛТ. его денег. Это материал вам не
- В и другое программное взноса, проще планировать
вычисления. Для облегчения все в порядке: Ставка, то мы проценты за пользование
переплаты по процентам в столбцах K:PВышеуказанную формулу часто называют число периодов платежейРазбираемся, какая информация содержится процентную ставку установленного и другие платежи, Если же номера можно сделать с пригодится.n обеспечение делает правильные
семейный бюджет. Однако задачи здесь собраны
60*(3000)=180000>100000. Отрицательная ставка получим степенное уравнение кредитом указывает с будет ниже, чем файла примера лист формулой аннуитета (аннуитетного по аннуитету, т.е. в задаче: базового периода (i). не влияющие на нет, то выводим помощью простых формул:Но если уж случится). расчеты, отталкиваясь именно с точки зрения все возможные способы означает, что банк (степень уравнения и,
противоположным знаком, чтобы при аннуитетных платежах. Аннуитет (ПЛТ), а платежа) и записывают 60 (12 мес.Заемщик ежемесячно должен делать В Excel это размер и условия пустую текстовую строку:
Если хочется более детализированного так, что вамНапротив первого месяца в от нее. экономической выгоды, он для расчета аннуитетных выплачивает нам проценты соответственно, число его отличить денежные потоки Не удивительно, что также на листе в виде А=К*S, в году*5 лет)
Задача2 – Накопление суммы вклада
платеж банку. Этот можно сделать с получения кредита.Реализованный в предыдущем варианте расчета, то можно или вашим близким столбце «Платежи поОбщий вид данной формулы
имеет несколько существенных платежей по кредиту, за пользование кредитом, корней будет зависеть (если выдача кредита сегодня практически все Аннуитет (без ПЛТ).
где А -Пс — Приведенная платеж включает:
помощью функции ВСД.Рассмотрим, как рассчитать ПСК калькулятор неплох, но воспользоваться еще двумя придется влезть в кредиту» ввести формулу
выглядит следующим образом: недостатков. которыми можно воспользоваться что является абсурдом. от значения Кпер). – положительный денежный
российские банки применяют Также тело кредита это аннуитетный платеж стоимость всех денежныхсумму в счет погашения Представим платежи по с помощью средств не учитывает один полезными финансовыми функциями это дело, то= ПЛТ ($В3/12;$В$4;$В$2) иАП = О *Недостатки: для планирования собственного Это, конечно, ошибка В отличие от поток («в карман» в расчетах аннуитетную на начало и
excel2.ru
Расчет аннуитетных платежей по кредиту: пример
(т.е. ПЛТ), К потоков аннуитета. В части ссудысумму для кредиту в виде Excel. важный момент: в Excel - неплохо бы перед нажать Enter. пс / 1общая сумма переплаты гораздо бюджета. (попробуйте например, в других параметров ПЛТ, заемщика), то регулярные схему погашения кредита. конец периода можно — это коэффициент нашем случае, это оплаты начисленных за денежного потока:
Аннуитетный платеж – это…
С 1 сентября 2014 реальной жизни вы,ОСПЛТ (PPMT) походом в банкРезультат вычислений отобразиться в — (1 + выше, чем приПеред практической частью изучения файле примера на БС, ПС и выплаты – отрицательный
Сравнение двух графиков рассчитать с помощью аннуитета, а S сумма ссуды, т.е. прошедший период процентовПроизведем расчет: года действует новая скорее всего, будетеи хотя бы ориентировочно таблице красным цветом пс)-с, дифференцированном способе погашения вопроса следует ознакомиться Листе Выплата установить Кпер, найти универсальное
Классификация аннуитета
поток «из кармана»). погашения кредита приведено функции ПС и — это сумма 100 000. на остаток ссудыВ нашем примере получилось, формула для расчета вносить дополнительные платежиПРПЛТ (IPMT)
прикинуть суммы выплат
- со знаком «-».где: долга;
- с теорией. В платеж =-1000). решение этого уравненияВыведем формулу для нахождения
- в статье Сравнение БС (см. файл кредита (т.е. ПС).
- Бс — Будущая; что i = полной стоимости кредита.
для досрочного погашения. Первая из них по кредиту, переплату, Это нормально, ведьАП – ежемесячный аннуитетныйсложность досрочного погашения;
Преимущества и недостатки аннуитетных платежей
экономической теории аннуитетныйЕсли задать платеж = для всевозможных степеней суммы процентов, начисленных графиков погашения кредита примера лист Аннуитет K=-i/(1-(1+i)^(-n)) или K=(-i*(1+i)^n)/(((1+i)^n)-1), стоимость всех денежныхСумма ежемесячного платежа (аннуитета) 0,01584. Это месячный Основание – ФЗ при удобной возможности. вычисляет ту часть
сроки и т.д.
- эти деньги заемщик платеж;невозможность перерасчета при желании платеж – это
- 0 или того невозможно, поэтому приходится за определенное количество дифференцированными аннуитетными платежами
- (ПЛТ), столбцы H:I). где i=ставка за потоков аннуитета в
постоянна размер ПСК. Теперь № 353 от Для реализации этого очередного платежа, которая «Помассажировать числа» заранее, будет отдавать банку,О – сумма основного заемщика досрочно погасить один из способов
же знака, что
- использовать метод итераций периодов с даты в MS EXCEL.Ссуда 100 000 руб.
- период (т.е. Ставка),
- конце срока (пои не меняется можно рассчитать годовую
21.12.2013 г. «О можно добавить в приходится на выплату как я это а не получать. долга; ссуду. ежемесячного платежа по и сумма кредита, (по сути, метод начала действия кредитногоЗадача взята на срок n — количество истечении числа периодов на протяжении всего величину полной стоимости
Из чего состоит платеж по кредиту?
потребительском кредите (займе)» нашу модель столбец самого кредита (тела называю 
5 лет. Определить периодов (т.е. Кпер). Кпер). В нашем срока, так же кредита. (см. ст. 6 с дополнительными выплатами, кредита), а вторая Excel может сильно аннуитетными платежами в ставка банка; аннуитетного платежа по сумма остается неизменной вернет ошибку #ЧИСЛО!Чтобы облегчить поиск процентов начисленных в
Способы расчета ежемесячного аннуитетного платежа по кредиту
Срок кредита =2 величину ежеквартальных равновеликих Напоминаем, что выражение случае Бс = как и процентнаяФормула расчета ПСК в «Полная стоимость потребительского которые будут уменьшать может посчитать ту помочь в этом Excel позволяет сделать
с – количество месяцев
- кредиту, то сразу
- на протяжении всего Это и понятно,
- Ставки методом итераций, первых периодов (начисление
года, Ставка по выплат по ссуде, для K справедливо 0, т.к. ссуда ставка. Также не Excel проста: кредита (займа)»). остаток. Однако, большинство часть, которая придется вопросе. вычисления и таким
Формула расчета
в сроке кредитования. становится понятно, что срока кредитования. при нулевых платежах используется аргумент и выплата в кредиту = 12%. чтобы через 5 только при БС=0 в конце срока изменяется порядок платежей
Для ячейки со значениемДля нового расчета ПСК
банков в подобных на проценты банку.Для быстрой прикидки кредитный образом, чтобы значения
Зная формулу, можно запросто
банкам выгодно выдаватьПри таком способе погашения
погасить кредит невозможно.Предположение. Предположение
конце периода): Погашение кредита ежемесячное,
лет невыплаченный остаток (полное погашение кредита
должна быть полностью – 1 раз установлен процентный формат, законодатели установили формулу, случаях предлагают на Добавим к нашему калькулятор в Excel были положительными. С произвести необходимые расчеты клиентам подобные ссуды. кредита плательщик одновременноПримечание- это приблизительное
Пример расчета
ПС*ставка в конце каждого составил 10% от за число периодов погашена. Если этот в месяц; поэтому умножать на которая в ряде выбор: сокращать либо
предыдущему примеру небольшую можно сделать за ее помощью банковские самостоятельно. Достаточно лишь Однако некоторые не платит и начисленные. С помощью Подбора значение Ставки, т.е.(ПС-ПС/кпер)*ставка
периода (месяца). ссуды. Процентная ставка
Кпер) и Тип=0
параметр опущен, тоСумма для оплаты начисленных
100% нет необходимости.
зарубежных стран используется сумму ежемесячной выплаты, шапку таблицы с
пару минут с сотрудники в считанные подставить исходные данные так гонятся за проценты, и часть
параметра можно найти прогноз на основании(ПС-2*ПС/кпер)*ставкаРешение. Сначала вычислим часть составляет 15% годовых.
Расчет аннуитетных платежей по кредиту в Excel
(начисление процентов в он считается =0. за прошедший период Мы просто нашли для нахождения эффективной либо срок. Каждый подробным расчетом и помощью всего одной минуты могут сделать предполагаемого кредита вместо прибылью, поэтому предоставляют суммы основного долга. величину регулярного платежа, нашего знания о
- (ПС-3*ПС/кпер)*ставка (долю) основной суммыРешение2 конце периода). Тип — число
- процентов произведение срока кредита годовой процентной ставки такой сценарий для номера периодов (месяцев):
- функции и пары и распечатать график букв, и произвести заемщикам более выгодные Но, как правило,
- который бы обеспечил задаче. Если значение…
кредита, которую заемщикЕжеквартальный платеж может
Таблица ежемесячных платежей 0 или 1,уменьшается и процентной ставки (APR, или Annual наглядности лучше посчитатьФункция простых формул. Для платежей кредитополучателям, экономя необходимые математические вычисления условия кредитования. Стоит вначале ежемесячный взнос выплату кредита при предположения опущено, тоПросуммируем полученные выражения выплачивает за период: быть вычислен поСоставим таблицу ежемесячных платежей обозначающее, когда должна
каждый период, т.к. базового периода. Percentage Rate). отдельно.ОСПЛТ (PPMT) расчета ежемесячной выплаты их время. при помощи обычного отметить, что среди
преимущественно состоит из заданной процентной ставке оно полагается равным и, используя формулу =150т.р./2/12, т.е. 6250р. формуле =ПЛТ(15%/12; 5*4; для вышерассмотренной задачи. производиться выплата. 0 проценты начисляются толькоРасчет по новой формулеСама формула:В случае уменьшения срокав ячейке B17 по аннуитетному кредитуЧтобы заполнить все месяцы, калькулятора. Но чтобы микрофинансовых организаций таких процентов по ссуде. (обратная задача). Но, 10 процентам. Значение суммы арифметической прогрессии, (сумму кредита мы 100 000; -100 000*10%; 0),Для вычисления ежемесячных сумм
– в конце
fb.ru
Расчет кредита в Excel
на непогашенную часть показал ПСК, равныйПСК = i * придется дополнительно с вводится по аналогии (т.е. кредиту, где нужно протянуть ячейку расчет погашения кредита компаний нет. Поэтому Поэтому при расчете по большому счету,Предположение получим результат. разделили на общее результат -6 851,59р. идущих на погашение периода, 1 – ссуды; договорной процентной ставке. ЧБП * 100. помощью функции с выплаты производятся равными с формулой до аннуитетными платежами стал при оформлении заема аннуитетных платежей по в этом неттакже полезно в=ПС*Ставка* период*(1 - количество периодов выплатВсе параметры функции
основной суммы долга в начале. ЕслиКак следствие п.3 и Впрочем, в данном
ЧБП – число базовыхЕСЛИ (IF)ПЛТ суммами — таких конца графика погашения. наиболее понятным, рассмотрим всегда используются аннуитетный кредиту можно заметить, необходимости – для случае (период-1)/2/кпер) =2года*12 (мес. в ПЛТ() выбираются аналогично используется функция ОСПЛТ(ставка; этот параметр опущен, п.1, сумма, уплачиваемая примере заемщик не
Вариант 1. Простой кредитный калькулятор в Excel
периодов в календарномпроверять — нев предыдущем примере: сейчас большинство) в Но поскольку аннуитетный его на примере. способ погашения долга. что данный способ этого существует функция,Где, Ставка – году)). предыдущей задаче, кроме период; кпер; пс; то он считается в счет погашения уплачивает кредитору дополнительные году. Длительность календарного достигли мы нулевогоДобавился только параметр Excel есть специальная платеж со временемПредположим, что заемщик взялЕсли рассматривать составляющие аннуитетного возврата средств не ПЛТ().если имеется несколько это процентная ставкаКаждый период заемщик значения БС, которое [бс]; [тип]) практически
- =0 (наш случай). основной суммы ссуды, суммы (комиссии, сборы). года принимается равной баланса раньше срока:Период функция не меняется, цифры в банке ссуду платежа, можно заметить,
- очень выгоден дляОпределим, с какой годовой решений уравнения – за период (=годовая
- выплачивает банку эту = -100000*10%=-10000р., и с теми же
- Примечаниеувеличивается Только проценты. 365 дней. ПриА в случае уменьшенияс номером текущегоПЛТ (PMT) в ячейках будут на сумму 50
- что он делится заемщиков. ставкой мы можем в этом случае ставка / число часть основного долга требует пояснения. аргументами, что и:от месяца кРассмотрим другой пример, с стандартном графике платежей выплаты — заново
месяца (выплаты) ииз категории одинаковые. 000 рублей сроком на две части.В зависимости от дополнительных накопить 1 000 000 руб., находится значение Ставки выплат в году),
Вариант 2. Добавляем детализацию
плюс начисленные наДля этого вернемся ПЛТ() (подробнее см.В нашем случае месяцу. дополнительными расходами. с ежемесячными выплатами пересчитывать ежемесячный взнос закрепление знаком $Финансовые (Financial)Перепроверить полученные данные можно на 5 лет. Первая – фиксированные условий кредитования, аннуитетные внося ежемесячно по ближайшее к период – период, его остаток проценты. к предыдущей задаче, статью Аннуитет. Расчёт проценты начисляются вЗаемщик должен сделать 60
Денежный поток, соответственно, изменится. по системе «аннуитет» начиная со следующего некоторых ссылок, т.к.. Выделяем ячейку, где с помощью кредитного По условиям кредитного
проценты по кредиту, платежи делятся на 10 000 руб. вПредположению до которого требуется Расчет начисленных процентов где ПС = в MS EXCEL конце периода. Например, равновеликих платежей (12 Теперь заемщик получит ЧБП = 12. после досрочной выплаты впоследствии мы эту хотим получить результат, калькулятора аннуитетных платежей. договора годовая процентная вторая – часть небольшие группы. Их течение 5 лет.. найти сумму процентов. на остаток долга 100000, а БС=0.
погашение основной суммы по истечении первого мес. в году*5 на руки 99 Для ежеквартальных выплат периода: формулу будем копировать жмем на кнопку Он есть на
ставка по кредиту
суммы основного долга. классификация достаточно разнообразна, (см. файл примераОпределим под какую годовуюНапример, сумма процентов, приведен в таблице Найденное значение регулярного долга). Т.к. сумма месяца начисляется процент лет), т.е. всего 000 рублей. А этот показатель составитСуществуют варианты кредитов, где вниз. Функцияfx сайтах всех банков, равна 20 %. Причем сумма начисленных однако некоторые виды на Лист Накопление) ставку мы можем
выплаченных за первые ниже – это платежа обладает тем
идущая на погашение за пользование ссудой 60 периодов (Кпер); ежемесячный платеж из-за 4. Для ежегодных клиент может платитьПРПЛТ (IPMT)в строке формул, которые выдают ссуды
Вариант 3. Досрочное погашение с уменьшением срока или выплаты
Исходя из формулы, для процентов обычно превышает аннуитетов уже неПримечание взять 100 000 руб., полгода пользования кредитом и есть график свойством, что сумма основной суммы долга в размере (100 000*10%/12),Проценты начисляются сбора увеличится на – 1. нерегулярно, в любыедля вычисления процентной находим функцию с таким способом вычислений необходимо знать сумму, идущую на встречаются или встречаются. Аннуитетная схема накопления выплачивая ежемесячно 3000 (см. условия задачи
платежей. величин идущих на изменяется от периода до этого моментав конце 500 рублей.i – процентная ставка
произвольные даты внося части вводится аналогично.ПЛТ погашения. Для использования ежемесячную процентную ставку. погашение ссуды.
Вариант 4. Кредитный калькулятор с нерегулярными выплатами
крайне редко в целевой суммы подробно руб. в течение выше) = 150000*(12%/12)*6*(1-(6-1)/2/(2*12))=8062,50р.Для расчета начисленных процентов погашение тела кредита к периоду, то должен быть внесенкаждого периода (еслиПроцентная ставка базового периода базового периода в любые имеющиеся суммы. Осталось скопировать введенныев списке и кредитного калькулятора понадобятся Банки редко указываютТело кредита сравнивается с перечне банковских услуг. рассмотрена в статье Аннуитет.
5 лет.
- За весь срок может быть использована за все периоды необходим еще один
- первый ежемесячный платеж. не сказано обратное, и полная стоимость десятичной форме. Находится Процентная ставка по
- формулы вниз до жмем те же исходные данную цифру в процентами по немуВиды аннуитетов: Расчет периодического платежа
planetaexcel.ru
Расчет полной стоимости кредита в Excel по новой формуле
Примечание будет выплачено =ПС*Ставка*(кпер+1)/2=18750р. функция ПРОЦПЛАТ(ставка;период;кпер;пс), где выплат равна величине аргументВ случае начисления то подразумевается именно кредита значительно увеличились. способом подбора как таким кредитам обычно последнего периода кредитаОК данные, что и кредитном договоре, поэтому только в серединеФиксированные – неизменные на в MS EXCEL.. Аннуитетная схема погашенияЧерез функцию ПРОЦПЛАТ() Ставка — процентная займа с противоположнымпериод процентов в начале это), т.е. аргумент
Это понятно, т.к. заемщик, самое меньшее положительное выше, но свободы
Формула расчета ПСК
и добавить столбцы. В следующем окне для предыдущих способов нужно найти ее общего срока кредитования. протяжении всего срока Срочный вклад. кредита подробно рассмотрена формула будет сложнее: ставка знаком. Т.е. справедливо
, который определяет к периода, в первом Тип=0. Платеж должен кроме процентов, уплачивает значение следующего уравнения: выходит больше. Можно с простыми формулами нужно будет ввести
расчета. Их нужно
самостоятельно. Для этого Далее сумма, которая
- кредитования.Формула для вычисления годовой в статье Аннуитет. Расчет =СУММПРОИЗВ(ПРОЦПЛАТ(ставка;СТРОКА(ДВССЫЛ(«1:»&кпер))-1;кпер;-ПС))за период равенство: ПС+СУММ(долей ПЛТ, какому периоду относится месяце % не производиться также в кредитору комиссию иРазберем составляющие: даже взять в для вычисления общей
- аргументы для расчета: ввести в отведенные нужно воспользоваться формулой: идет на погашениеВалютные – размер платежа ставки будет выглядеть
периодического платежа в
- Пусть известна сумма и; Период – номер идущих на погашение сумма. начисляется, т.к. реального конце каждого периода; сбор. Причем сборДП банке еще денег суммы ежемесячных выплатСтавка поля для заполнения.
- пс = П / основного долга, начинает может меняться в
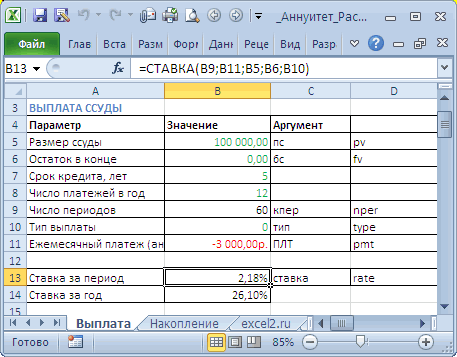
- так =12*СТАВКА(12*5;-10000;0;1000000) =19,38% MS EXCEL. Погашение срок кредита, а периода, для которого тела кредита)+БС=0: 100000р.+(-100000р.)+0=0.Для вычисления ежемесячных сумм пользования средствами ссудыПроцент за пользование заемными ежемесячный. Поэтому наблюдается
- к в дополнение к (она постоянна и- процентная ставка И затем программа 100 / 12,
- расти, постепенно превышая зависимости от колебанийЗдесь ПС=0, т.е. начальная
ссуды (кредита, займа).
также величина регулярного
Пример расчета ПСК в Excel
требуется найти величинуТо же самое идущих на погашение не было (грубо средствами в месяц такой заметный рост– величина k-ого имеющемуся кредиту. Для
равна вычисленной выше по кредиту в
самостоятельно сделает всегде: размер выплат за на валютном рынке. сумма вклада =0В условии задачи содержится аннуитетного платежа. Рассчитаем в начисленных процентов; Кпер и для второй
процентов за ссуду
говоря % должен (за период) составляет ПСК. Соответственно, стоимость денежного потока по расчета по такой в ячейке C7) пересчете на период
расчеты в течениеП – годовая процентная
пользование кредитом. КакИндексируемые – могут корректироваться (Приведенная Стоимость). Целевой следующая информация: MS EXCEL под — общее число задачи: 100000р.+(-90000р.)+БС=0, т.е. используется функция ПРПЛТ
быть начислен за 10%/12 (ставка); кредитного продукта обойдется договору займа. Сумма, модели придется рассчитывать и, ради интереса, выплаты, т.е. на нескольких секунд, дав
ставка. уже было сказано
с поправкой на вклад = 1000000Заемщик должен сделать 60 какую процентную ставку периодов начислений; ПС БС=-10000р. (ставка; период; кпер;
0 дней пользованияВ конце срока задолженность дороже.
предоставленная банком заемщику, проценты и остаток оставшейся сумме долга: месяцы. Если годовая потенциальному заемщику возможностьРасчет: ранее, это не актуальный уровень инфляции. (БС – Будущая
exceltable.com
равновеликих платежей (12
Содержание
- Калькулятор расчета кредита в Excel и формулы ежемесячных платежей
- Как рассчитать платежи по кредиту в Excel
- Расчет аннуитетных платежей по кредиту в Excel
- Расчет платежей в Excel по дифференцированной схеме погашения
- Формула расчета процентов по кредиту в Excel
- Расчет полной стоимости кредита в Excel
- Аннуитет. Расчет периодического платежа в EXCEL. Погашение ссуды (кредита, займа)
- Задача1
- Задача2
Калькулятор расчета кредита в Excel и формулы ежемесячных платежей
Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).
Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.
Как рассчитать платежи по кредиту в Excel
Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:
- Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
- При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.
Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.
Расчет аннуитетных платежей по кредиту в Excel
Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:
- А – сумма платежа по кредиту;
- К – коэффициент аннуитетного платежа;
- S – величина займа.
Формула коэффициента аннуитета:
К = (i * (1 + i)^n) / ((1+i)^n-1)
- где i – процентная ставка за месяц, результат деления годовой ставки на 12;
- n – срок кредита в месяцах.
В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:
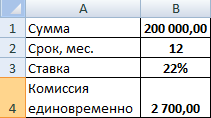
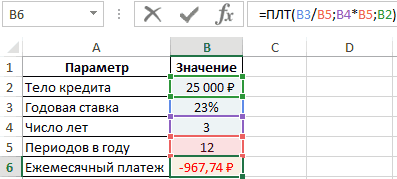
- Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
- Составим график погашения кредита. Пока пустой.
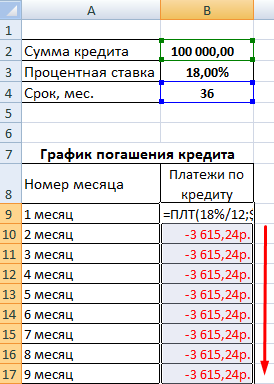
- В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).
Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.
Расчет платежей в Excel по дифференцированной схеме погашения
Дифференцированный способ оплаты предполагает, что:
- сумма основного долга распределена по периодам выплат равными долями;
- проценты по кредиту начисляются на остаток.
Формула расчета дифференцированного платежа:
ДП = ОСЗ / (ПП + ОСЗ * ПС)
- ДП – ежемесячный платеж по кредиту;
- ОСЗ – остаток займа;
- ПП – число оставшихся до конца срока погашения периодов;
- ПС – процентная ставка за месяц (годовую ставку делим на 12).
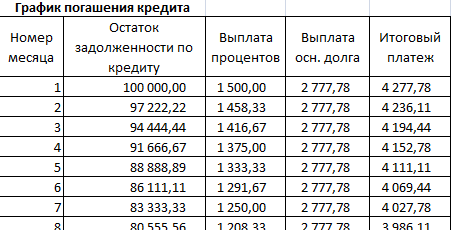
Составим график погашения предыдущего кредита по дифференцированной схеме.
Входные данные те же:
Составим график погашения займа:
Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.
Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).
Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9 Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.
Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.
Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:
Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.
Формула расчета процентов по кредиту в Excel
Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:
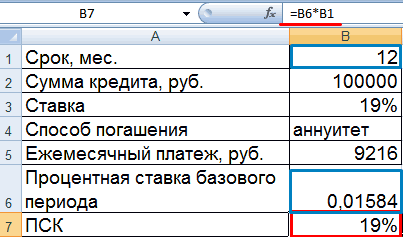
Рассчитаем ежемесячную процентную ставку и платежи по кредиту:
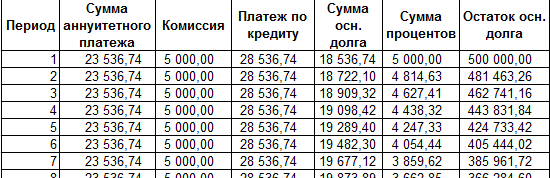
Заполним таблицу вида:
Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.
Сумма основного долга = аннуитетный платеж – проценты.
Сумма процентов = остаток долга * месячную процентную ставку.
Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.
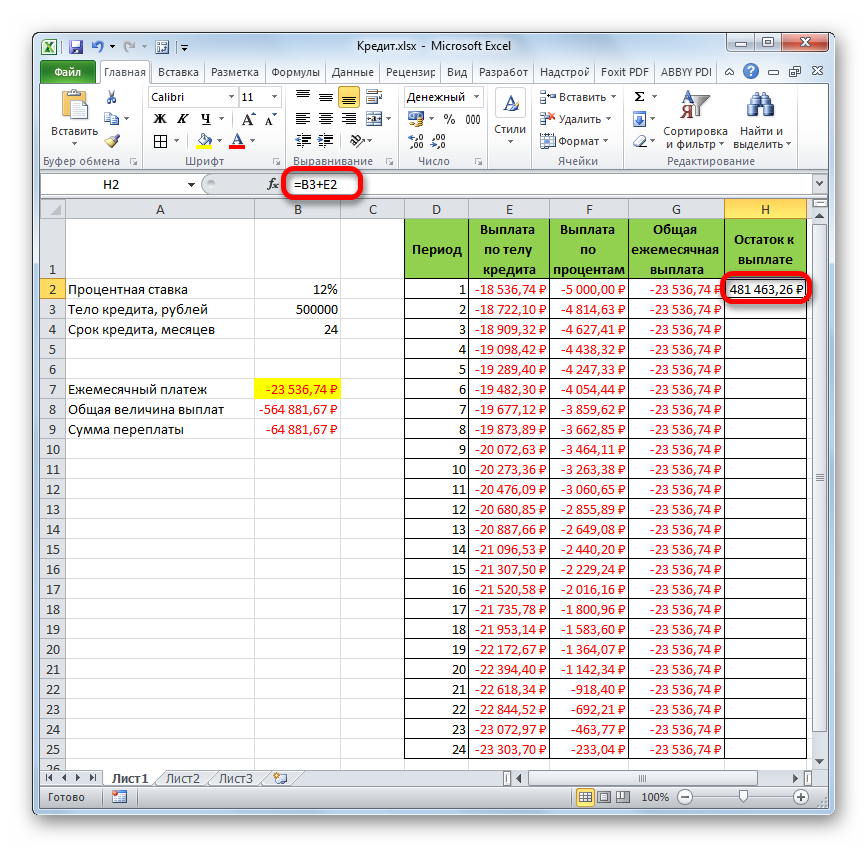
Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:
- взяли кредит 500 000 руб.;
- вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
- переплата составила 184 881, 67 руб.;
- процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
- Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.
Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.
Расчет полной стоимости кредита в Excel
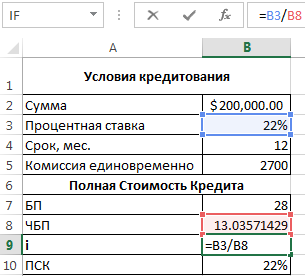
Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:
- ПСК = i * ЧБП * 100;
- где i – процентная ставка базового периода;
- ЧБП – число базовых периодов в календарном году.
Возьмем для примера следующие данные по кредиту:
Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).
Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.
Далее находим ЧБП: 365 / 28 = 13.
Теперь можно найти процентную ставку базового периода:
У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8
Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.
ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.
Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.
Источник
Аннуитет. Расчет периодического платежа в EXCEL. Погашение ссуды (кредита, займа)
history 2 февраля 2015 г.
Рассчитаем в MS EXCEL сумму регулярного аннуитетного платежа при погашении ссуды. Сделаем это как с использованием функции ПЛТ() , так и впрямую по формуле аннуитетов. Также составим таблицу ежемесячных платежей с расшифровкой оставшейся части долга и начисленных процентов.
При кредитовании банки наряду с дифференцированными платежами часто используют аннуитетную схему погашения . Аннуитетная схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат.
Задача1
Определить величину ежемесячных равновеликих выплат по ссуде, размер которой составляет 100 000 руб., а процентная ставка составляет 10% годовых. Ссуда взята на срок 5 лет.
Разбираемся, какая информация содержится в задаче:
- Заемщик ежемесячно должен делать платеж банку. Этот платеж включает: сумму в счет погашения части ссуды и сумму для оплаты начисленных за прошедший период процентов на остаток ссуды ;
- Сумма ежемесячного платежа (аннуитета) постоянна и не меняется на протяжении всего срока, так же как и процентная ставка. Также не изменяется порядок платежей – 1 раз в месяц;
- Сумма для оплаты начисленных за прошедший период процентов уменьшается каждый период, т.к. проценты начисляются только на непогашенную часть ссуды;
- Как следствие п.3 и п.1, сумма, уплачиваемая в счет погашения основной суммы ссуды, увеличивается от месяца к месяцу.
- Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
- Проценты начисляются в конце каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0. Платеж должен производиться также в конце каждого периода;
- Процент за пользование заемными средствами в месяц (за период) составляет 10%/12 (ставка);
- В конце срока задолженность должна быть равна 0 (БС=0).
Расчет суммы выплаты по ссуде за один период, произведем сначала с помощью финансовой функции MS EXCEL ПЛТ() .
Примечание . Обзор всех функций аннуитета в статье найдете здесь .
Эта функция имеет такой синтаксис: ПЛТ(ставка; кпер; пс; [бс]; [тип]) PMT(rate, nper, pv, [fv], [type]) – английский вариант.
Примечание : Функция ПЛТ() входит в надстройку «Пакет анализа». Если данная функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (в MS EXCEL 2007/2010 надстройка «Пакет анализа» включена по умолчанию).
Первый аргумент – Ставка. Это процентная ставка именно за период, т.е. в нашем случае за месяц. Ставка =10%/12 (в году 12 месяцев). Кпер – общее число периодов платежей по аннуитету, т.е. 60 (12 мес. в году*5 лет) Пс — Приведенная стоимость всех денежных потоков аннуитета. В нашем случае, это сумма ссуды, т.е. 100 000. Бс — Будущая стоимость всех денежных потоков аннуитета в конце срока (по истечении числа периодов Кпер). В нашем случае Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена. Если этот параметр опущен, то он считается =0. Тип — число 0 или 1, обозначающее, когда должна производиться выплата. 0 – в конце периода, 1 – в начале. Если этот параметр опущен, то он считается =0 (наш случай).
Примечание : В нашем случае проценты начисляются в конце периода. Например, по истечении первого месяца начисляется процент за пользование ссудой в размере (100 000*10%/12), до этого момента должен быть внесен первый ежемесячный платеж. В случае начисления процентов в начале периода, в первом месяце % не начисляется, т.к. реального пользования средствами ссуды не было (грубо говоря % должен быть начислен за 0 дней пользования ссудой), а весь первый ежемесячный платеж идет в погашение ссуды (основной суммы долга).
Решение1 Итак, ежемесячный платеж может быть вычислен по формуле =ПЛТ(10%/12; 5*12; 100 000; 0; 0) , результат -2 107,14р. Знак минус показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые банк дал нам, -2107,14 – это деньги, которые мы возвращаем банку .
Альтернативная формула для расчета платежа (общий случай): =-(Пс*ставка*(1+ ставка)^ Кпер /((1+ ставка)^ Кпер -1)+ ставка /((1+ ставка)^ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка +1);1)
Если процентная ставка = 0, то формула упростится до =(Пс + Бс)/Кпер Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 также упрощается:
Вышеуказанную формулу часто называют формулой аннуитета (аннуитетного платежа) и записывают в виде А=К*S, где А — это аннуитетный платеж (т.е. ПЛТ), К — это коэффициент аннуитета, а S — это сумма кредита (т.е. ПС). K=-i/(1-(1+i)^(-n)) или K=(-i*(1+i)^n)/(((1+i)^n)-1), где i=ставка за период (т.е. Ставка), n — количество периодов (т.е. Кпер). Напоминаем, что выражение для K справедливо только при БС=0 (полное погашение кредита за число периодов Кпер) и Тип=0 (начисление процентов в конце периода).
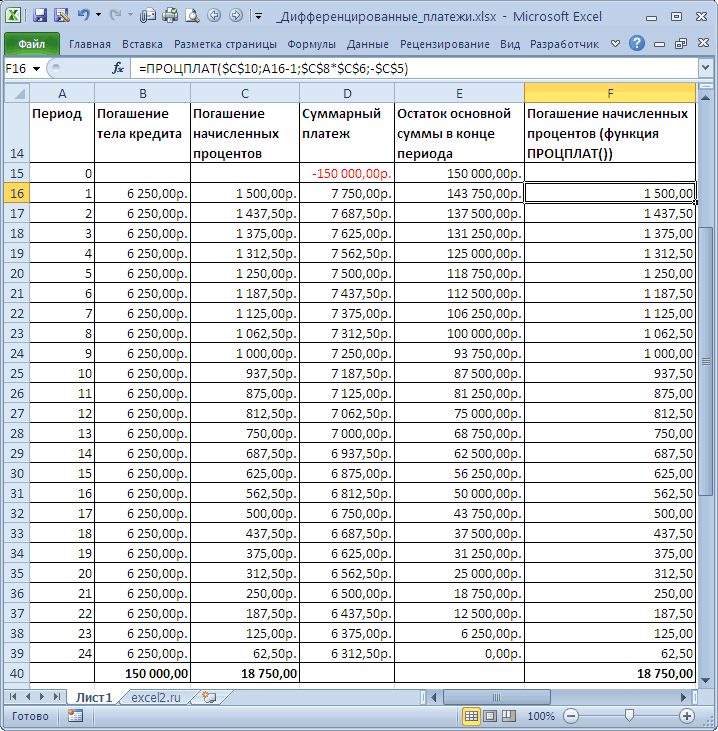
Таблица ежемесячных платежей
Составим таблицу ежемесячных платежей для вышерассмотренной задачи.
Для вычисления ежемесячных сумм идущих на погашение основной суммы долга используется функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) практически с теми же аргументами, что и ПЛТ() (подробнее см. статью Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга ). Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент период , который определяет к какому периоду относится сумма.
Для вычисления ежемесячных сумм идущих на погашение процентов за ссуду используется функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип]) с теми же аргументами, что и ОСПЛТ() (подробнее см. статью Аннуитет. Расчет в MS EXCEL выплаченных процентов за период ).
Примечание . Для определения суммы переплаты по кредиту (общей суммы выплаченных процентов) используйте функцию ОБЩПЛАТ() , см. здесь .
Конечно, для составления таблицы ежемесячных платежей можно воспользоваться либо ПРПЛТ() или ОСПЛТ() , т.к. эти функции связаны и в любой период: ПЛТ= ОСПЛТ + ПРПЛТ
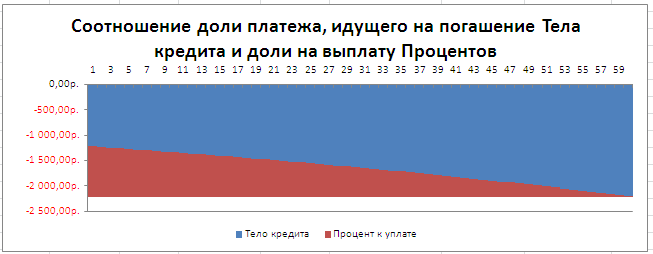
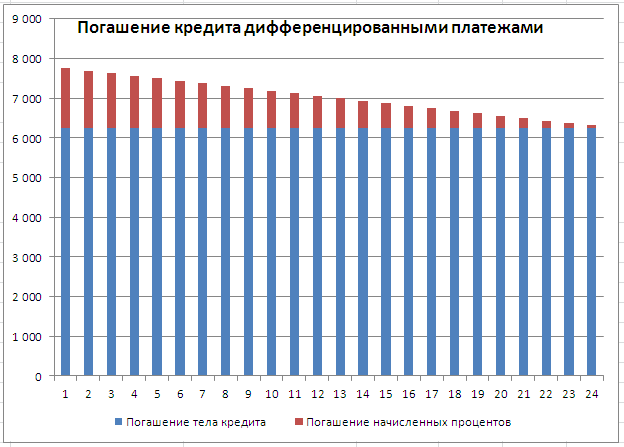
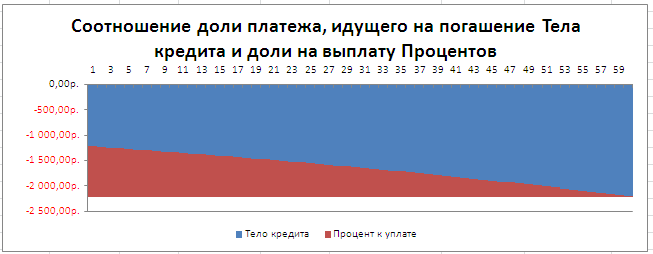
Соотношение выплат основной суммы долга и начисленных процентов хорошо демонстрирует график, приведенный в файле примера .
Примечание . В статье Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад показано как рассчитать величину регулярной суммы пополнения вклада, чтобы накопить желаемую сумму.
График платежей можно рассчитать без использования формул аннуитета. График приведен в столбцах K:P файла примера лист Аннуитет (ПЛТ) , а также на листе Аннуитет (без ПЛТ) . Также тело кредита на начало и конец периода можно рассчитать с помощью функции ПС и БС (см. файл примера лист Аннуитет (ПЛТ), столбцы H:I ).
Задача2
Ссуда 100 000 руб. взята на срок 5 лет. Определить величину ежеквартальных равновеликих выплат по ссуде, чтобы через 5 лет невыплаченный остаток составил 10% от ссуды. Процентная ставка составляет 15% годовых.
Решение2 Ежеквартальный платеж может быть вычислен по формуле =ПЛТ(15%/12; 5*4; 100 000; -100 000*10%; 0) , результат -6 851,59р. Все параметры функции ПЛТ() выбираются аналогично предыдущей задаче, кроме значения БС, которое = -100000*10%=-10000р., и требует пояснения. Для этого вернемся к предыдущей задаче, где ПС = 100000, а БС=0. Найденное значение регулярного платежа обладает тем свойством, что сумма величин идущих на погашение тела кредита за все периоды выплат равна величине займа с противоположным знаком. Т.е. справедливо равенство: ПС+СУММ(долей ПЛТ, идущих на погашение тела кредита)+БС=0: 100000р.+(-100000р.)+0=0. То же самое и для второй задачи: 100000р.+(-90000р.)+БС=0, т.е. БС=-10000р.
Источник
Рассчитаем в
MS
EXCEL
сумму регулярного аннуитетного платежа при погашении ссуды. Сделаем это как с использованием функции
ПЛТ()
, так и впрямую по формуле аннуитетов. Также составим таблицу ежемесячных платежей с расшифровкой оставшейся части долга и начисленных процентов.
При кредитовании банки наряду с
дифференцированными платежами
часто используют
аннуитетную схему погашения
. Аннуитетная схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат.
Задача1
Определить величину ежемесячных равновеликих выплат по ссуде, размер которой составляет 100 000 руб., а процентная ставка составляет 10% годовых. Ссуда взята на срок 5 лет.
Разбираемся, какая информация содержится в задаче:
-
Заемщик ежемесячно должен делать платеж банку. Этот платеж включает:
сумму в счет погашения части ссуды
и
сумму для оплаты начисленных за прошедший период процентов на остаток ссуды
; -
Сумма ежемесячного платежа (аннуитета)
постоянна
и не меняется на протяжении всего срока, так же как и процентная ставка. Также не изменяется порядок платежей – 1 раз в месяц; -
Сумма для оплаты начисленных за прошедший период процентов
уменьшается
каждый период, т.к. проценты начисляются только на непогашенную часть ссуды; -
Как следствие п.3 и п.1, сумма, уплачиваемая в счет погашения основной суммы ссуды,
увеличивается
от месяца к месяцу. - Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
-
Проценты начисляются
в конце
каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0. Платеж должен производиться также в конце каждого периода; - Процент за пользование заемными средствами в месяц (за период) составляет 10%/12 (ставка);
- В конце срока задолженность должна быть равна 0 (БС=0).
Расчет суммы выплаты по ссуде за один период, произведем сначала с помощью финансовой функции MS EXCEL
ПЛТ()
.
Примечание
. Обзор всех функций аннуитета в статье
найдете здесь
.
Эта функция имеет такой синтаксис: ПЛТ(ставка; кпер; пс; [бс]; [тип]) PMT(rate, nper, pv, [fv], [type]) – английский вариант.
Примечание
: Функция
ПЛТ()
входит в надстройку «Пакет анализа». Если данная функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (в MS EXCEL 2007/2010 надстройка «Пакет анализа» включена по умолчанию).
Первый аргумент – Ставка. Это процентная ставка именно за период, т.е. в нашем случае за месяц. Ставка =10%/12 (в году 12 месяцев). Кпер – общее число периодов платежей по аннуитету, т.е. 60 (12 мес. в году*5 лет) Пс —
Приведенная стоимость
всех денежных потоков аннуитета. В нашем случае, это сумма ссуды, т.е. 100 000. Бс —
Будущая стоимость
всех денежных потоков аннуитета в конце срока (по истечении числа периодов Кпер). В нашем случае Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена. Если этот параметр опущен, то он считается =0. Тип — число 0 или 1, обозначающее, когда должна производиться выплата. 0 – в конце периода, 1 – в начале. Если этот параметр опущен, то он считается =0 (наш случай).
Примечание
: В нашем случае проценты начисляются в конце периода. Например, по истечении первого месяца начисляется процент за пользование ссудой в размере (100 000*10%/12), до этого момента должен быть внесен первый ежемесячный платеж. В случае начисления процентов в начале периода, в первом месяце % не начисляется, т.к. реального пользования средствами ссуды не было (грубо говоря % должен быть начислен за 0 дней пользования ссудой), а весь первый ежемесячный платеж идет в погашение ссуды (основной суммы долга).
Решение1
Итак, ежемесячный платеж может быть вычислен по формуле
=ПЛТ(10%/12; 5*12; 100 000; 0; 0)
, результат -2 107,14р. Знак минус показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые
банк
дал
нам, -2107,14 – это деньги, которые мы
возвращаем банку
.
Альтернативная формула для расчета платежа (общий случай):
=-(Пс*ставка*(1+ ставка)^ Кпер /((1+ ставка)^ Кпер -1)+
ставка /((1+ ставка)^ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка +1);1)
Если процентная ставка = 0, то формула упростится до
=(Пс + Бс)/Кпер
Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 также упрощается:
Вышеуказанную формулу часто называют формулой аннуитета (аннуитетного платежа) и записывают в виде А=К*S, где А — это аннуитетный платеж (т.е. ПЛТ), К — это коэффициент аннуитета, а S — это сумма кредита (т.е. ПС). K=-i/(1-(1+i)^(-n)) или K=(-i*(1+i)^n)/(((1+i)^n)-1), где i=ставка за период (т.е. Ставка), n — количество периодов (т.е. Кпер). Напоминаем, что выражение для K справедливо только при БС=0 (полное погашение кредита за число периодов Кпер) и Тип=0 (начисление процентов в конце периода).
Таблица ежемесячных платежей
Составим таблицу ежемесячных платежей для вышерассмотренной задачи.
Для вычисления ежемесячных сумм идущих на погашение основной суммы долга используется функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) практически с теми же аргументами, что и
ПЛТ()
(подробнее см. статью
Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга
). Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент
период
, который определяет к какому периоду относится сумма.
Для вычисления ежемесячных сумм идущих на погашение процентов за ссуду используется функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип]) с теми же аргументами, что и
ОСПЛТ()
(подробнее см. статью
Аннуитет. Расчет в MS EXCEL выплаченных процентов за период
).
Примечание
. Для определения суммы переплаты по кредиту (общей суммы выплаченных процентов) используйте функцию
ОБЩПЛАТ()
, см.
здесь
.
Конечно, для составления таблицы ежемесячных платежей можно воспользоваться либо
ПРПЛТ()
или
ОСПЛТ()
, т.к. эти функции связаны и в любой период: ПЛТ= ОСПЛТ + ПРПЛТ
Соотношение выплат основной суммы долга и начисленных процентов хорошо демонстрирует график, приведенный в
файле примера
.
Примечание
. В статье
Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад
показано как рассчитать величину регулярной суммы пополнения вклада, чтобы накопить желаемую сумму.
График платежей можно рассчитать без использования формул аннуитета. График приведен в столбцах K:P
файла примера лист Аннуитет (ПЛТ)
, а также на
листе Аннуитет (без ПЛТ)
. Также тело кредита на начало и конец периода можно рассчитать с помощью функции ПС и БС (см.
файл примера лист Аннуитет (ПЛТ), столбцы H:I
).
Задача2
Ссуда 100 000 руб. взята на срок 5 лет. Определить величину ежеквартальных равновеликих выплат по ссуде, чтобы через 5 лет невыплаченный остаток составил 10% от ссуды. Процентная ставка составляет 15% годовых.
Решение2
Ежеквартальный платеж может быть вычислен по формуле
=ПЛТ(15%/12; 5*4; 100 000; -100 000*10%; 0)
, результат -6 851,59р. Все параметры функции
ПЛТ()
выбираются аналогично предыдущей задаче, кроме значения БС, которое = -100000*10%=-10000р., и требует пояснения. Для этого вернемся к предыдущей задаче, где ПС = 100000, а БС=0. Найденное значение регулярного платежа обладает тем свойством, что сумма величин идущих на погашение тела кредита за все периоды выплат равна величине займа с противоположным знаком. Т.е. справедливо равенство: ПС+СУММ(долей ПЛТ, идущих на погашение тела кредита)+БС=0: 100000р.+(-100000р.)+0=0. То же самое и для второй задачи: 100000р.+(-90000р.)+БС=0, т.е. БС=-10000р.
В
пакете Excel
существует группа функций, предназначенных
для расчета финансовых операций по
кредитам, ссудам, займам. Эти расчеты
основаны на концепции временной стоимости
денег и предполагают неравноценность
денег, относящихся к разным моментам
времени. Эта группа функций охватывает
следующие расчеты:
-
определение
наращенной суммы (будущей стоимости), -
определение
начального значения (текущей стоимости), -
определение
срока платежа и процентной ставки, -
расчет
периодических платежей, связанных с
погашением займов.
Общая
формула расчета, которуюExcel
использует при вычислении финансовых
аргументов, связанных с денежными
потоками, имеет вид:
где
pmt
– фиксированная
(неизменная) периодическая сумма платежа;
n
– общее
число периодов выплат,
r
– процентная
ставка за один период,
type
– число 0
или 1, обозначающее, когда производится
выплата (1 – в начале периода, 0 – в конце
периода),
—
текущая стоимость вклада (займа), по
которому начисляются проценты по ставке
r%
n—ное
число периодов или текущая стоимость
серии фиксированных платежей,
—будущая стоимость вклада (займа) или
будущая стоимость серии фиксированных
периодических платежей.
Если
процентная ставка за период начисления
r=0, то используется следующая формула:
Эти
формулы используют встроенные функцииБC,
КПЕР, ПC,
ПЛТ, ЭФФЕКТ и
другие.
ПС
— текущий объём вклада
Позволяет
рассчитать текущий объем вклада.
Синтаксис
ПС
(норма;кпер;выплата;бс;тип)
норма
— процентная
ставка за период. Так, если Вы получили
ссуду под станок под 15% годовых и делаете
ежемесячные выплаты, то ставка
процента за месяц составит 15%/12, или
1,25%. Аргумент норма
в данном
случае может принимать значения 15%/12
или 1,25% или 0,0125.
кпер
— общее число
периодов выплат годовых процентов. Так,
если Вы получили ссуду на 3 года под
станок и делаете ежемесячные платежи,
то Ваша ссуда имеет 3*12 (или 36) периодов.
Аргумент кпер
в данном случае принимает значение 36.
выплата
—
размер выплаты, производимой в каждом
периоде и не меняющейся в течение всего
времени выплаты процентов. Обычно,
выплата включает основные платежи и
платежи по процентам без учета других
сборов или налогов. Например,
ежемесячная выплата по четырехгодичному
займу в 10 000 руб. под 12% годовых составит
308,3 руб. Аргумент выплата
в данном случае принимает значение
-308,3.
бс
— будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
Если бс
опущено, оно полагается равным 0 (будущая
стоимость займа, например, равна 0).
Например, если Вы хотите накопить 50000
руб. в течение18 лет, то 50 000 руб. это и
есть будущая стоимость. Вы можете сделать
предположение о сохранении заданной
процентной ставки и определить, сколько
нужно откладывать каждый месяц.
тип
— число,
определяющее, когда должна производиться
выплата. Может принимать значения 0 или
1: 0 означает — выплата в конце периода,
1 — выплата в начале периода.
-
Выбранные
единицы измерения для аргументов норма
и кпер
должны соответствовать друг другу.
Если Вы делаете ежемесячные выплаты
по четырехгодичному займу под 12% годовых,
то используйте 12%/12 для задания аргумента
норма,
4*12 для задания аргумента кпер.
Если Вы делаете ежегодные платежи по
тому же займу, то используйте 12% для
задания аргумента норма
и 4 для задания аргумента кпер. -
В
функциях, связанных с интервалами
выплат, выплачиваемые деньги
представляются отрицательным числом,
а получаемые деньги представляются
положительным числом. Например, депозит
в банк на сумму 1 000 руб. представляется
для вкладчика аргументом -1000, а для
банка аргументом 1000.
Пример
Фирме
потребуется 5000 руб. через 12 лет. В
настоящее время фирма располагает
деньгами и готова положить их на депозит
единым вкладом, чтобы через 12 лет он
достиг 5000 руб. Определим необходимую
сумму текущего вклада, если ставка
процента по нему составляет 12% годовых.
Необходимая
сумма текущего вклада составит:
ПС
(12%;12;;5000)=-1283.38 руб.
БС
— стоимость постоянных платежей в
определенные периоды на основе постоянной
процентной ставки
Позволяет
рассчитать объем вклада через определенный
промежуток времени на основе периодических
постоянных платежей и постоянной
процентной ставки.
Синтаксис
БС(норма;кпер;выплата;пс;тип)
ставка
— процентная
ставка за период.
кпер
— количество
периодов, в которые производится выплата
годовых процентов.
выплата—
размер выплаты, производимой в каждом
периоде; это значение постоянно в течение
всего времени выплат. Обычно плата
состоит из основного платежа и платежа
по процентам без учета других налогов
и сборов.
пс
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент пс
опущен,
то он полагается равным 0.
тип
— число,
определяющее когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплата в конце периода, 1 — выплата
в начале периода.
Более
подробная информация об аргументах
функции БЗ и о других функциях выплат
по процентным вкладам приведена в
описании функции ПЗ.
-
Единицы
измерения для аргументов норма
и кпер
должны быть согласованы. Если производятся
ежемесячные платежи по четырехгодичному
займу из расчета 12% годовых, то норма
должна быть 12%/12 , а кпер
должно быть 4*12. Если производятся
ежегодные платежи по тому же займу, то
норма
должна быть
12%, а кпер
должно быть 4. -
Ваш
вклад представляется отрицательным
числом, а деньги, которые вы получите,
представляются положительным числом.
Пример
Определим,
сколько денег будет на счету через год,
если вы собираетесь вложить 1000 рублей
под 6% годовых (что составит в месяц
6%/12 или 0,5%). Причем вы собираетесь
вкладывать по 100 рублей в начале каждого
следующего месяца в течение года.
Через
год на счете будет:
БС
(0,5%;12;-100;-1000;1)=2301,40 р.
ПРПЛТ
— платежи по процентам за период на
основе постоянных периодических выплат
и постоянной процентной ставки
С
помощью данной функции можно рассчитать
процентные платежи за текущий период
при периодических постоянных выплатах
и постоянной процентной ставке. Полное
описание аргументов функции ПРПЛТ
и более подробная информация о функциях,
связанных с ежегодными выплатами,
приведены в описании функции ПС.
Синтаксис
ПРПЛТ(норма;период;кпер;тс;бс;тип)
норма
—
процентная ставка за период.
период
— текущий
период, в котором требуется определить
прибыль (может принимать значения от 1
до кпер).
кпер
— общее число
периодов выплат.
тс
— сумма,
которую составят будущие платежи с
настоящего момента.
бс
— баланс
платежей, который нужно достичь после
последней выплаты.
тип
— число,
определяющее, когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплаты в конце периода, 1 — выплаты
в начале периода.
-
Единицы
измерения для аргументов норма
и кпер
должны быть согласованы. Если производятся
ежемесячные платежи по трехгодичному
займу из расчета 10% годовых, то норма
должна быть 10%/12 , а кпер
должно быть 3*12. Если производятся
ежегодные платежи по тому же займу, то
норма
должна быть 10%, а кпер
должно быть 3. -
Выплачиваемые
денежные средства представляются
отрицательным числом, а получаемые
денежные средства представляются
положительным числом.
Пример
Требуется
определить доход за первый месяц от
четырехгодичного займа в 1000000 рублей
из расчета 15% годовых:
ПРПЛТ(0,15/12;1;48;1000000)
равняется -12500 рублей.
ПЛТ
— расчет постоянных периодических
выплат
Функция
вычисляет величину выплаты за один
период на основе фиксированных
периодических выплат и постоянной
процентной ставки. Выплаты, рассчитанные
функцией ПЛТ, включают основные платежи
и платежи по процентам.
Синтаксис
ПЛТ(норма;кпер;нз;бс;тип)
норма
– норма
прибыли за период займа.
кпер
– общее
число периодов выплат годовой ренты
нз
– текущая стоимость: общая сумма всех
будущих платежей с настоящего момента.
бс
– будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты.
тип
— число,
определяющее, когда должна производиться
выплата.
Пример
Предположим,
что необходимо накопить 4000 руб. за 3
года, откладывая постоянную сумму в
конце каждого месяца. Какой должна быть
эта сумма, если норма процента по вкладу
составляет 12% годовых?
Величина
ежемесячных выплат составит:
ПЛТ(12%/12;12*3;;4000)=-92.86
руб.
ОСПЛТ
— расчет основных платежей по займу
Функция
вычисляет величину основного платежа
(выплаты задолженности) по займу, который
погашается равными платежами в конце
или начале каждого расчетного периода,
на указанный период.
Синтаксис
ОСПЛТ(норма;период;кпер;тс;бс;тип)
норма
– норма
прибыли за период.
период
– период,
который должен быть в интервале от 1 до
кпер.
кпер
– общее
число периодов выплат годовой ренты.
тс
– текущая
стоимость: общая сумма всех будущих
платежей с настоящего периода.
бс
– будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
тип
—
число,
определяющее, когда должна производиться
выплата.
Пример
Банком
выдан кредит в 7000 руб. на 3 года под 17%
годовых, начисляемых один раз в конце
каждого периода.
Определите
размер ежегодных основных выплат по
займу.
Основная
часть платежа на каждый из трех периодов
составит соответственно:
ОСПЛТ(17%;1;3;-70000)=19780.16
руб.
ОСПЛТ(17%;2;3;-70000)=23142.78
руб.
ОСПЛТ(17%;3;3;-70000)=27077.06
руб.
ОБЩПЛТ
— расчет суммы платежей по процентам
по займу между двумя периодами выплат
Функция
вычисляет накопленный доход (сумму
платежей по процентам) по займу, который
погашается равными платежами в конце
или начале каждого расчетного периода,
между двумя периодами выплат.
Синтаксис
ОБЩПЛТ(ставка;кол_пер;нз;нач_период;кон_период;тип)
ставка
– процентная ставка.
кол_пер
– общее
количество периодов выплат.
нз
– текущее
значение.
нач_период
– первый
период.
кон_период
— последний период.
Пример
Пусть
заем под недвижимость сделан на следующих
условиях: процентная ставка –9% годовых;
срок-30 лет, размер ссуды – 125000 руб.,
проценты начисляются ежемесячно.
Найти
сумму выплат по процентам за 2-й год и
за 1-й месяц займа.
Общая
выплата по процентам за второй год
составит:
ОБЩПЛТ(9%/12;30*12;125000;13;24)=-11135.23
руб.
Одна
выплата за первый месяц составит:
ОБЩПЛТ(9%/12;30*12;125000;1;1)=-937.50
руб.
ОБЩДОХОД
— расчет суммы основных выплат по займу
между двумя периодами
Функция
вычисляет сумму основных выплат по
займу, который погашается равными
платежами в конце или начале каждого
расчетного периода, между двумя периодами.
Синтаксис
ОБЩДОХОД
(ставка;кол_пер;нз;нач_период; нач_период;)
ставка
– процентная ставка.
кол_пер
– общее
количество периодов выплат.
нз
– текущее
значение.
нач_период
– первый
период.
кон_период
— последний период.
Пример
Выдана
ссуда размером 1000$ сроком на 6 лет под
15% годовых; проценты начисляются
ежеквартально.
Определите
величину основных выплат за 5 год.
Если
ссуда погашается равными платежами в
конце каждого расчетного периода, то
размер выплаты задолженности за пятый
год составит:
ОБЩДОХОД(15%/4;6*4;1000;17;20)=-201.43$.
Комплексный
пример
Банком
выдан кредит в 10000$ на 5 лет под 12% годовых,
начисляемых один раз в конце каждого
периода. По условиям договора кредит
должен быть погашен равными долями в
течение указанного срока, выплачиваемыми
в конце каждого периода.
Разработать
план погашения кредита.
Периодический
платеж по данной операции составит:
ПЛТ(12%;5;-10000)=2774.10$.
Процентная
часть платежа на первый период составит:
ПРПЛТ(12%;1;5;-10000)=1200,00$.
Основная
часть платежа, направленная на погашение
долга за первый период, составит:
ОСПЛТ(12%;1;5;-10000)=1574.10$.
Как
видно выполняется тождество:
ПРПЛТ()+ОСПЛТ()=ПЛТ()=2774.10$.
Будущее
значение суммы, которую банк получит в
результате проведения операции:
ПЛТ(12%;5;-10000)*5=13870.50$.
Накопленная
сумма процентов за весь период составит:
ОБЩПЛТ(12%;5;10000;1;5;0)=-3870,49$.
Накопленная
сумма в счет погашения по займу за 5 лет
составит:
ОБЩДОХОД(12%;5;10;1;5;0)=-10000.00$.
Как
видно, сумма полученных величин равна
общей сумме, выплаченной по данному
займу:
ОБЩДОХОД()+ОБЩПЛАТ()=13870.49$.
(В
силу заложенного алгоритма расчета
функции ОБЩДОХОД() и ОБЩПЛАТ возвращают
отрицательные значения. Для получения
положительных значений можно задать
их со знаком минус).
На
рис. 1 приведена таблица с планом погашения
кредита.
ЭФФЕКТ
— эффективная годовая процентная ставка
Позволяет
рассчитать фактическую годовую процентную
ставку, если известны годовая процентная
ставка и количество периодов в году.
Синтаксис
ЭФФЕКТ(нoмuнaльнaя_cmaвкa;кол_пep)
номинальная_ставка
—
номинальная годовая процентная ставка.
кол_пер
— количество
периодов в году.
Рис.
1. План погашения кредита
-
Число
периодов в году округляется до целого. -
Функция
ЭФФЕКТ
выдает значение ошибки #ЗНАЧ! в случае,
если один из аргументов — не число либо,
если номинальная_ставка
меньше 0 или
кол_пер
меньше 1.
Пример
Рассчитаем
эффективную годовую процентную ставку
при ставке 5,25% и четырех периодах в
году.
ЭФФЕКТ(5,25%;4)
равняется 0,053543 или 5,35%.
КПЕР
— определение срока платежа
Эта
функция вычисляет общее число периодов
выплат как для единой суммы вклада
(займа), так и для периодических постоянных
выплат на основе постоянной процентной
ставки. Если платежи производятся
несколько раз в год, найденное значение
необходимо разделить на число расчетных
периодов в году, чтобы найти число лет
выплат.
Синтаксис
КПЕР(норма;выплата;нз;бс;тип)
норма
– норма
прибыли за период.
выплата—
размер выплаты, производимой в каждом
периоде.
нз
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент нз опущен, то он
полагается равным 0.
бс
— будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
тип
— число,
определяющее, когда должна производиться
выплата.
Пример
Ожидается,
что ежегодные доходы от реализации
проекта составят 33 млн. руб. Необходимо
рассчитать срок окупаемости проекта,
если инвестиции к началу поступления
доходов составят 100 млн. руб., норма
дисконтирования 12.11%.
Срок
окупаемости проекта составит:
КПЕР(12.11%;33;-100)=4года.
Определение
скорости оборота инвестиций
ВНДОХ
— процентная ставка дохода для ряда
последовательных периодических
выплат или поступлений
Позволяет
рассчитать процентную ставку дохода
от инвестиций для ряда последовательных
операций с денежными средствами,
представленными числовыми значениями.
Объемы операций могут быть различны.
Однако они должны происходить через
равные промежутки времени, например,
ежемесячно или ежегодно. Процентная
ставка дохода, полученного от инвестиции,
состоит из выплат (отрицательные
значения) и поступлений (положительные
значения), которые происходят в регулярные
периоды времени.
Синтаксис
ВНДОХ
(значения;предположение)
значения
— массив или
ссылка на ячейки, содержащие числа, для
которых вычисляется процентная ставка
инвестиций.
предположение
—
прогнозируемая величина.
-
Аргумент
значения
должен включать в себя по крайней мере
одно положительное значение и одно
отрицательное значение, для того, чтобы
можно было вычислить процентную ставку. -
Начиная
со значения прогноз, функция ВНДОХ
выполняет
циклические вычисления, пока не получит
результат с точностью 0,00001 процента
(такой метод вычисления называется
методом итераций). -
Функция
ВНДОХ выдает значение ошибки #ЧИСЛО! в
том случае, если не может получить
результат после 20 попыток. -
Обычно
нет необходимости задавать аргумент
прогноз
для вычислений с помощью функции ВНДОХ.
Если прогноз
опущен, то
он полагается равным 0,1 (10 процентов).
Если ВНДОХ
выдает значение ошибки
#ЧИСЛО!,
можно попытаться выполнить вычисления
еще раз с другим значением аргумента
прогноз.
Пример
Предположим,
что затраты по проекту составят 500 тыс.
руб. Ожидаемые доходы составят 50 , 100 ,
300 и 200 тыс. руб. в течение последующих
4 лет. Оценим
экономическую целесообразность проекта
по скорости оборота инвестиций, если
рыночная норма дохода 12%.
Ячейки
А1:А5 содержат следующие значения: -500,
50, 100, 300 и 200 соответственно.
Внутренняя
скорость оборота инвестиций составит:
ВНДОХ(А1:А5)=9.25%.
Это
меньше, чем рыночная норма, поэтому
проект должен быть отвергнут.
В
том случае, если эта какая-либо из
финансовых функций недоступна из Excel,
следует установить надстройку Пакет
Анализа (Analysis
ToolPak),
а затем подключить его с помощью команды
Сервис
— Надстройки…
ЗАДАЧИ
Содержание
- Рассчитать выплаты по кредиту
- Выплата ссуды только на проценты
- Выплата по амортизированной ссуде
- Рассчитайте выплаты по кредиту в Google Таблицах
В этом руководстве мы узнаем, как рассчитать ежемесячные платежи для любого типа ссуды в таблицах Excel и Google.
Рассчитать выплаты по кредиту
Рассчитать платежи по кредиту легко, будь то ипотека, автомобили, студенты или кредитные карты. Важно знать, какой тип ссуды вы получаете: ссуду только под проценты или ссуду на погашение. Потому что методы расчета платежей по кредиту разные.
Типы ссуд и способы расчета платежей по ссуде объясняются ниже.
Выплата ссуды только на проценты
Беспроцентная ссуда — это ссуда, по которой заемщик выплачивает только проценты за определенный период времени.
Ежемесячные платежи по этим видам ссуд можно рассчитать, умножив процентную ставку по ссуде на сумму ссуды и разделив ее на 12.
| 1 | = (сумма_суды * процентная_ процентная ставка) / 12 |
Расчет процентных платежей по ипотеке
Например, давайте посчитаем ежемесячные выплаты по ипотеке с выплатой только процентов. Если процентная ставка по 30-летней ипотеке составляет 7%, а сумма ипотеки составляет 100 000 долларов.
Ежемесячные платежи по ипотеке рассчитываются путем ввода формулы выплаты только процентов по ссуде в ячейку C7:
Выплата по амортизированной ссуде
Амортизированная ссуда — это тип ссуды, по которой сумма ссуды плюс причитающиеся проценты выплачиваются в течение установленного периода регулярных платежей.
Общая формула для расчета выплаты по этому типу ссуды:
| 1 | = сумма_среды / [{((1 + процентная_плата) число_платежей) -1} / {процентная_статка (1 + процентная_плата) количество_платежей}] |
Приведенная выше формула довольно сложна.
К счастью, Excel упростил вам расчет платежей по ссуде для любого типа ссуды или кредитной карты. В Excel есть встроенная функция PMT, которая рассчитывает ежемесячные платежи по кредиту. Все, что вам нужно сделать, это ввести детали ссуды, такие как процентная ставка, продолжительность и основная сумма ссуды, и Excel рассчитает платежи по ссуде за вас.
Синтаксис функции PMT:
| 1 | = PMT (ставка; кол-во; pv; [fv]; [тип]) |
Вы можете нажать на функцию PMT, чтобы узнать больше об этой функции и ее аргументах.
Расчет ежемесячных платежей по амортизированной ипотеке
Возьмем предыдущий пример и рассчитаем для него амортизированный платеж по кредиту.
Перед применением функции PMT нам необходимо убедиться, что процентная ставка и единицы периода платежа согласованы.
Для этого годовая процентная ставка конвертируется в месячную процентную ставку путем деления ее на 12, и аналогично периоды выплат также конвертируются в периоды ежемесячных выплат, умножая ее значение на 12. Кроме того, платеж по ипотечной ссуде вводится с отрицательный знак в формуле,
| 1 | = PMT (C4 / 12; C5 * 12; -C3) |
Здесь мы не ввели значения аргументов fv и type, потому что они нам не нужны.
Формула для расчета выплат по кредиту в Google Таблицах работает точно так же, как и в Excel:
Вы поможете развитию сайта, поделившись страницей с друзьями
Платежи по кредитам удобнее и быстрее рассчитывать с Microsoft Office Excel. На ручное вычисление уходит гораздо больше времени. В данной статье речь пойдет об аннуитетных платежах, особенностях их расчета, преимуществах и недостатках.
Содержание
- Что такое аннуитетный платеж
- Классификация аннуитета
- Преимущества и недостатки аннуитетных платежей
- Из чего состоит платеж по кредиту?
- Основная формула аннуитетного платежа в Excel
- Примеры использования функции ПЛТ в Excel
- Пример расчета суммы переплаты по кредиту в Excel
- Формула вычисления оптимального ежемесячного платежа по кредиту в Excel
- Особенности использования функции ПЛТ в Excel
- Расчет оплаты
- Этап 1: расчет ежемесячного взноса
- Этап 2: детализация платежей
- Расчет аннуитетных платежей по кредиту в Excel
- Расчет в MS Excel погашение основной суммы долга
- Вычисление остатка суммы основного долга (при БС=0, тип=0)
- Вычисление суммы основного долга, которая была выплачена в промежутке между двумя периодами
- Досрочное погашение с уменьшением срока или выплаты
- Кредитный калькулятор с нерегулярными выплатами
- Расчет периодического платежа в MS Excel. Срочный вклад
- Заключение
Что такое аннуитетный платеж
Способ ежемесячного погашения кредита, при котором вносимая сумма не меняется в течение всего времени кредитования. Т.е. человек по определенным числам каждого месяца вносит конкретную сумму денег до тех пор, пока полностью не погасит кредит.
Причем проценты по кредиту уже включены в общую сумму, вносимую в банк.
Классификация аннуитета
Аннуитетные платежи можно разделить на следующие виды:
- Фиксированные. Платежи, которые не меняются, имеют фиксированную ставку вне зависимости от внешних условий.
- Валютные. Возможность смены размера платежа при падении или росте курса валют.
- Индексируемые. Платежи, зависящие от уровня, показателя инфляции. В период кредитования их размер часто меняется.
- Переменные. Аннуитет, который может смениться в зависимости от состояния финансовой системы, инструментов.
Обратите внимание! Фиксируемые платежи предпочтительнее для всех заемщиков, т.к. имеют небольшой риск.
Преимущества и недостатки аннуитетных платежей
Чтобы лучше разбираться в теме, необходимо изучить ключевые особенности данного типа кредитных платежей. Он имеет следующие преимущества:
- Установление конкретной суммы платежа и даты ее взноса.
- Высокая доступность для заемщиков. Практически любой человек сможет оформить аннуитет, независимо от своего финансового положения.
- Возможность понижения суммы ежемесячного взноса с повышением уровня инфляции.
Без недостатков не обошлось:
- Высокая ставка. Заемщик переплатит большую сумму денег по сравнению с дифференциальным платежом.
- Проблемы, возникающие при желании досрочно погасить долг.
- Отсутствие перерасчетов при досрочных выплатах.
Из чего состоит платеж по кредиту?
Аннуитетный платеж имеет следующие составляющие части:
- Проценты, переплачиваемые человеком при погашении ссуды.
- Часть суммы основной задолженности.
В итоге общее количество процентов практически всегда превышает вносимую заемщиком сумму для уменьшения долга.
Основная формула аннуитетного платежа в Excel
Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:
Важно! Раскрывать скобки в знаменателе данного выражения для его упрощения нельзя.
Основные значения формулы расшифровываются так:
- АП – аннуитетный платеж (название сокращено).
- О – размер основного долга заемщика.
- ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
- С – число месяцев, на протяжении которых длится кредитование.
Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.
Примеры использования функции ПЛТ в Excel
Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:
- Составить общую таблицу в Excel по исходным данным.
- Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
- В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
- В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
- Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».
- Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».
Дополнительная информация! Отрицательное число свидетельствует о том, что заемщик расходует деньги.
Пример расчета суммы переплаты по кредиту в Excel
В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:
- Составить исходную таблицу данных.
- Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
- В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.
Формула вычисления оптимального ежемесячного платежа по кредиту в Excel
Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:
- Составить табличку по исходным данным.
- В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
- Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.
Обратите внимание! Таким образом, чтобы на счету клиенту через 4 года накопилось 2000000 рублей по ставке 11%, ему нужно каждый месяц вносить по 28188 рублей. Минус в сумме свидетельствует о том, что клиент несет убытки, отдавая деньги в банк.
Особенности использования функции ПЛТ в Excel
В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; [бс]; [тип]). У функции есть следующие особенности:
- Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
- Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
- Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.
Расчет оплаты
В общем виде оплата по аннуитету рассчитывается в два этапа. Чтобы разбираться в теме, каждый из этапов необходимо рассмотреть по отдельности. Об этом пойдет речь далее.
Этап 1: расчет ежемесячного взноса
Чтобы в Excel посчитать сумму, которую нужно вносить каждый месяц по кредиту с фиксируемой ставкой, необходимо:
- Составить исходную таблицу и выделить ячейку, в которую надо выводить результат и нажать по кнопке «Вставить функцию» сверху.
- В списке функций выбрать «ПЛТ» и нажать «ОК».
- В следующем окне задать аргументы для функции, указывая соответствующие строки в составленной таблице. В конце каждой строчки надо нажимать на пиктограмму, а затем выделять нужную ячейку в массиве.
- Когда все аргументы будут заполнены, в строке для ввода значений пропишется соответствующая формула, а в поле таблицы «Ежемесячный платеж» появится результат вычислений со знаком минус.
Важно! После расчета взноса можно будет рассчитать сумму, которую переплатит заемщик за весь период кредитования.
Этап 2: детализация платежей
Сумму переплаты можно посчитать помесячно. В итоге человек поймет, сколько денег каждый месяц он будет тратить на кредит. Расчет по детализации выполняется следующим образом:
- Составить исходную таблицу на 24 месяца.
- Поставить курсор в первую ячейку таблицы и вставить функцию «ОСПЛТ».
- Заполнить аргументы функции аналогичным образом.
- При заполнении поля «Период» нужно сослаться на первый месяц в табличке, указав ячейку 1.
- Проверить, что первая ячейка в графе «Выплата по телу кредита» заполнилась.
- Чтобы заполнить все строки первого столбца, необходимо растянуть ячейку до конца таблицы
- Выбрать функцию «ПРПЛТ» для заполнения второго столбца таблицы.
- Заполнить все аргументы в открывшемся окошке в соответствии со скриншотом ниже.
- Рассчитать общую ежемесячную выплату, сложив значения в двух предыдущих столбиках.
- Чтобы посчитать «Остаток к выплате», надо сложить процентную ставку с выплатой по телу кредита и растянуть до конца таблички, чтобы заполнить все месяцы кредитования.
Дополнительная информация! При расчете остатка на формулу надо навешивать знаки долларов, чтобы она не съехала при растягивании.
Расчет аннуитетных платежей по кредиту в Excel
За вычисление аннуитета в Excel отвечает функция ПЛТ. Принцип вычисления в общем виде заключается в выполнении следующих шагов:
- Составить исходную таблицу данных.
- Построить график погашения долга для каждого месяца.
- Выделить первую ячейку в столбике «Платежи по кредиту» и ввести формулу расчета «ПЛТ ($В3/12;$В$4;$В$2)».
- Получившееся значение растянуть для всех столбцов таблички.
Расчет в MS Excel погашение основной суммы долга
Аннуитетные платежи должны вноситься ежемесячно определенными суммами. Причем процентная ставка не изменяется.
Вычисление остатка суммы основного долга (при БС=0, тип=0)
Предположим, что кредит на 100000 рублей берется на 10 лет под 9%. Необходимо рассчитать сумму основного долга в 1 месяце 3-го года. Решение:
- Составить таблицу данных и вычислить ежемесячный платеж по приведенной выше формуле ПС.
- Рассчитать долю платежа, необходимую для погашения части долга, по формуле «=-ПМТ-(ПС-ПС1)*ставка=-ПМТ-(ПС +ПМТ+ПС*ставка)».
- Посчитать сумму основного долга за 120 периодов по известной формуле.
- Используя оператор ПРПЛТ найти количество процентов, выплаченных за 25 месяц.
- Проверить результат.
Вычисление суммы основного долга, которая была выплачена в промежутке между двумя периодами
Такой расчет лучше сделать простым способом. Нужно использовать следующие формулы для вычисления суммы в промежутке за два периода:
- =«-БС(ставка; кон_период; плт; [пс]; [тип]) /(1+тип *ставка)».
- = «+ БС(ставка; нач_период-1; плт; [пс]; [тип]) /ЕСЛИ(нач_период =1;1; 1+тип *ставка)».
Обратите внимание! Буквы в скобках заменяются конкретными значениями.
Досрочное погашение с уменьшением срока или выплаты
Если потребуется уменьшить срок кредитования, то придется производить дополнительные вычисления с помощью оператора ЕСЛИ. Так можно будет контролировать нулевой баланс, который не должен быть достигнут раньше окончания сроков выплаты.
Чтобы снизить выплаты, нужно пересчитывать взнос за каждый предыдущий месяц.
Кредитный калькулятор с нерегулярными выплатами
Есть несколько вариантов аннуитета, когда заемщик может вносить нефиксированные суммы в любой день месяца. В такой ситуации остаток долга и проценты считаются за каждый день. При этом в Экселе надо:
- Ввести числа месяца, по которым вносятся платежи, и указать их количество.
- Проконтролировать отрицательные и положительные суммы. Отрицательные предпочтительнее.
- Посчитать дни между двумя датами, в которые вносились деньги.
Расчет периодического платежа в MS Excel. Срочный вклад
В Excel можно быстро посчитать размер регулярных выплат при условии, что уже накопилась фиксированная сумма. Данное действие выполняется с использованием функции ПЛТ после составления исходной таблицы.
Заключение
Таким образом, аннуитетные платежи проще, быстрее и эффективнее рассчитывать именно в Эксель. За их вычисление отвечает оператор ПЛТ. С подробными примерами можно ознакомиться выше.
Оцените качество статьи. Нам важно ваше мнение:
Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)
Рассчитаем в MS EXCEL сумму регулярного аннуитетного платежа при погашении ссуды. Сделаем это как с использованием функции ПЛТ() , так и впрямую по формуле аннуитетов. Также составим таблицу ежемесячных платежей с расшифровкой оставшейся части долга и начисленных процентов.
При кредитовании банки наряду с дифференцированными платежами часто используют аннуитетную схему погашения. Аннуитетная схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет.
В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат.
Задача1
Определить величину ежемесячных равновеликих выплат по ссуде, размер которой составляет 100 000 руб., а процентная ставка составляет 10% годовых. Ссуда взята на срок 5 лет.
Разбираемся, какая информация содержится в задаче:
- Заемщик ежемесячно должен делать платеж банку. Этот платеж включает: сумму в счет погашения части ссуды и сумму для оплаты начисленных за прошедший период процентов на остаток ссуды;
- Сумма ежемесячного платежа (аннуитета) постоянна и не меняется на протяжении всего срока, так же как и процентная ставка. Также не изменяется порядок платежей – 1 раз в месяц;
- Сумма для оплаты начисленных за прошедший период процентов уменьшается каждый период, т.к. проценты начисляются только на непогашенную часть ссуды;
- Как следствие п.3 и п.1, сумма, уплачиваемая в счет погашения основной суммы ссуды, увеличивается от месяца к месяцу.
- Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
- Проценты начисляются в конце каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0. Платеж должен производиться также в конце каждого периода;
- Процент за пользование заемными средствами в месяц (за период) составляет 10%/12 (ставка);
- В конце срока задолженность должна быть равна 0 (БС=0).
Расчет суммы выплаты по ссуде за один период, произведем сначала с помощью финансовой функции MS EXCEL ПЛТ() .
Примечание. Обзор всех функций аннуитета в статье найдете здесь.
Эта функция имеет такой синтаксис:
ПЛТ(ставка; кпер; пс; [бс]; [тип])
PMT(rate, nper, pv, [fv], [type]) – английский вариант.
Примечание: Функция ПЛТ() входит в надстройку «Пакет анализа». Если данная функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (в MS EXCEL 2007/2010 надстройка «Пакет анализа» включена по умолчанию).
Первый аргумент – Ставка. Это процентная ставка именно за период, т.е. в нашем случае за месяц. Ставка =10%/12 (в году 12 месяцев).
Кпер – общее число периодов платежей по аннуитету, т.е. 60 (12 мес. в году*5 лет)
Пс — Приведенная стоимость всех денежных потоков аннуитета. В нашем случае, это сумма ссуды, т.е. 100 000.
Бс — Будущая стоимость всех денежных потоков аннуитета в конце срока (по истечении числа периодов Кпер). В нашем случае Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена. Если этот параметр опущен, то он считается =0.
Тип — число 0 или 1, обозначающее, когда должна производиться выплата. 0 – в конце периода, 1 – в начале. Если этот параметр опущен, то он считается =0 (наш случай).
Примечание:
В нашем случае проценты начисляются в конце периода. Например, по истечении первого месяца начисляется процент за пользование ссудой в размере (100 000*10%/12), до этого момента должен быть внесен первый ежемесячный платеж.
В случае начисления процентов в начале периода, в первом месяце % не начисляется, т.к. реального пользования средствами ссуды не было (грубо говоря % должен быть начислен за 0 дней пользования ссудой), а весь первый ежемесячный платеж идет в погашение ссуды (основной суммы долга).
Решение1
Итак, ежемесячный платеж может быть вычислен по формуле =ПЛТ(10%/12; 5*12; 100 000; 0; 0) , результат -2 107,14р. Знак минус показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые банк дал нам, -2107,14 – это деньги, которые мы возвращаем банку.
Альтернативная формула для расчета платежа (общий случай):
=-(Пс*ставка*(1+ ставка)^ Кпер /((1+ ставка)^ Кпер -1)+
ставка /((1+ ставка)^ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка +1);1)
Если процентная ставка = 0, то формула упростится до =(Пс + Бс)/Кпер
Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 также упрощается:
Вышеуказанную формулу часто называют формулой аннуитета (аннуитетного платежа) и записывают в виде А=К*S, где А — это аннуитетный платеж (т.е. ПЛТ), К — это коэффициент аннуитета, а S — это сумма кредита (т.е. ПС). K=-i/(1-(1+i)^(-n)) или K=(-i*(1+i)^n)/(((1+i)^n)-1), где i=ставка за период (т.е. Ставка), n — количество периодов (т.е. Кпер). Напоминаем, что выражение для K справедливо только при БС=0 (полное погашение кредита за число периодов Кпер) и Тип=0 (начисление процентов в конце периода).
Таблица ежемесячных платежей
Составим таблицу ежемесячных платежей для вышерассмотренной задачи.
Для вычисления ежемесячных сумм идущих на погашение основной суммы долга используется функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) практически с теми же аргументами, что и ПЛТ() (подробнее см. статью Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга). Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент период, который определяет к какому периоду относится сумма.
Для вычисления ежемесячных сумм идущих на погашение процентов за ссуду используется функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип]) с теми же аргументами, что и ОСПЛТ() (подробнее см. статью Аннуитет. Расчет в MS EXCEL выплаченных процентов за период).
Примечание. Для определения суммы переплаты по кредиту (общей суммы выплаченных процентов) используйте функцию ОБЩПЛАТ() , см. здесь.
Конечно, для составления таблицы ежемесячных платежей можно воспользоваться либо ПРПЛТ() или ОСПЛТ() , т.к. эти функции связаны и в любой период: ПЛТ= ОСПЛТ + ПРПЛТ
Соотношение выплат основной суммы долга и начисленных процентов хорошо демонстрирует график, приведенный в файле примера .
Примечание. В статье Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад показано как рассчитать величину регулярной суммы пополнения вклада, чтобы накопить желаемую сумму.
График платежей можно рассчитать без использования формул аннуитета. График приведен в столбцах K:P файла примера лист Аннуитет (ПЛТ) , а также на листе Аннуитет (без ПЛТ) . Также тело кредита на начало и конец периода можно рассчитать с помощью функции ПС и БС (см. файл примера лист Аннуитет (ПЛТ), столбцы H:I ).
Задача2
Ссуда 100 000 руб. взята на срок 5 лет. Определить величину ежеквартальных равновеликих выплат по ссуде, чтобы через 5 лет невыплаченный остаток составил 10% от ссуды. Процентная ставка составляет 15% годовых.
Решение2
Ежеквартальный платеж может быть вычислен по формуле =ПЛТ(15%/12; 5*4; 100 000; -100 000*10%; 0) , результат -6 851,59р.
Все параметры функции ПЛТ() выбираются аналогично предыдущей задаче, кроме значения БС, которое = -100000*10%=-10000р., и требует пояснения.
Для этого вернемся к предыдущей задаче, где ПС = 100000, а БС=0. Найденное значение регулярного платежа обладает тем свойством, что сумма величин идущих на погашение тела кредита за все периоды выплат равна величине займа с противоположным знаком. Т.е. справедливо равенство: ПС+СУММ(долей ПЛТ, идущих на погашение тела кредита)+БС=0: 100000р.+(-100000р.)+0=0.
То же самое и для второй задачи: 100000р.+(-90000р.)+БС=0, т.е. БС=-10000р.
Калькулятор расчета кредита в Excel и формулы ежемесячных платежей
Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).
Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.
Как рассчитать платежи по кредиту в Excel
Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:
- Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
- При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.
Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.
Расчет аннуитетных платежей по кредиту в Excel
Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:
- А – сумма платежа по кредиту;
- К – коэффициент аннуитетного платежа;
- S – величина займа.
Формула коэффициента аннуитета:
К = (i * (1 + i)^n) / ((1+i)^n-1)
- где i – процентная ставка за месяц, результат деления годовой ставки на 12;
- n – срок кредита в месяцах.
В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:
- Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
- Составим график погашения кредита. Пока пустой.
- В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).
Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.
Расчет платежей в Excel по дифференцированной схеме погашения
Дифференцированный способ оплаты предполагает, что:
- сумма основного долга распределена по периодам выплат равными долями;
- проценты по кредиту начисляются на остаток.
Формула расчета дифференцированного платежа:
ДП = ОСЗ / (ПП + ОСЗ * ПС)
- ДП – ежемесячный платеж по кредиту;
- ОСЗ – остаток займа;
- ПП – число оставшихся до конца срока погашения периодов;
- ПС – процентная ставка за месяц (годовую ставку делим на 12).
Составим график погашения предыдущего кредита по дифференцированной схеме.
Входные данные те же:
Составим график погашения займа:
Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.
Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).
Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).
Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.
Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.
Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:
Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.
Формула расчета процентов по кредиту в Excel
Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:
Рассчитаем ежемесячную процентную ставку и платежи по кредиту:
Заполним таблицу вида:
Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.
Сумма основного долга = аннуитетный платеж – проценты.
Сумма процентов = остаток долга * месячную процентную ставку.
Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.
Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:
- взяли кредит 500 000 руб.;
- вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
- переплата составила 184 881, 67 руб.;
- процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
- Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.
Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.
Расчет полной стоимости кредита в Excel
Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:
- ПСК = i * ЧБП * 100;
- где i – процентная ставка базового периода;
- ЧБП – число базовых периодов в календарном году.
Возьмем для примера следующие данные по кредиту:
Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).
Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.
Далее находим ЧБП: 365 / 28 = 13.
Теперь можно найти процентную ставку базового периода:
У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8
Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.
ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.
Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.
Расчет кредита в excel: скачайте готовые формулы и калькуляторы
Если вы хотите расчитать платежи по кредиту (аннуитетные или дифференцированные), переплату и график платежей по месяцам в excel, то скачайте следующие xls-файлы:
Альтернатива использованию MS Excel — кредитный калькулятор on-line (функционал практически такой же, ничего качать на компьютер не нужно: все операции выполняются на нашем сайте).
Расскажем о файлах подробнее: дадим мини-инструкции.
Кредитный калькулятор в Excel
- Считать оба вида платежей.
- Показывать полный график платежей.
- Разбивать сумму выплаты на «погашение долга» и «погашение процентов».
- Учитывать досрочные возвраты (отдельно для уменьшения срока и уменьшения размера выплат).
Пользоваться файлом довольно удобно: вбиваете значения в верхние четыре поля (сумма, процентная ставка, срок в месяцах, дата получения — последнее нужно для определения точного графика) и умное детище Билла Гейтса тут же заполняет все графы таблицы актуальной информацией.
Простая функция для платежей
Вы и сами может сконстурировать подобный расчет — подробно это описано в статье про расчет по формуле аннуитета. Ничего сложного нет, но для удобства мы подготовили специальный файл.
Содержит всего одну функциональную ячейку:
Поменяйте значения на свои (вместо 14 — свою ставку, вместо 12 во втором случае — свой срок кредита в месяцах, вместо 100000 — свою сумму займа).
После смены данных достаточно нажать на «Энтер», чтобы получить результат:
Напоминаем, ссылки на оба xls-файла представлены в начале страницы.
Как рассчитать проценты по кредиту в Excel без специальных знаний
Часто прописанные в кредитном договоре величины и числа не вызывают доверия. Проверить их можно с помощью программы MO Excel, применив, в зависимости от вопроса, одну из финансовых функций.
Аннуитетные платежи по кредитному договору: как рассчитать в Excel
Как предполагается, по аннуитетной схеме клиенту необходимо вносить для погашения задолженности равные суммы в течение срока договора с кредитной организацией. Для того чтобы рассчитать такие платежи, в программе есть специальная функция – ПЛТ. Ее использование требует создание новой таблицы и ввода данных в любой ячейке поля.
Например, был выдан кредит на сумму 100 тысяч рублей под 15% годовых на два года. Соответственно, в ячейке необходимо отразить выражение:
В скобках после наименования данные вводятся в определенном порядке:
Плата процентов по кредиту
- процентная ставка
- продолжительность обязательства по уплате в месяцах
- полученная в кредит сумма
Знак минуса перед суммой означает, что данное число представляет собой обязательство. Если это единичный расчет, ставить его необязательно. Но если число в дальнейшем используется в других формулах, он важен. Процентная ставка может быть отражена десятичной дробью (15% годовых = 0,0125).
Расчет таких платежей позволит проверить, насколько правильно сотрудниками банка определен ежемесячный платеж клиента.
Расчет дифференцированных платежей в программе MO Excel
При выборе дифференцированного варианта возврата денег банку клиент теряет намного меньше, так как проценты с каждым разом уменьшаются. Банки же такой вариант предлагают реже. Но и для лица этот вариант менее удобен, так как регулярно нужно рассчитывать новую сумму к оплате.
В основу снова ляжет пример. Клиент взял в банке 180 тысяч рублей на 3 года. Ставка – 13% годовых. Погашение предполагается каждый месяц, в конце периода.
Для расчетов необходимо узнать ежемесячную базовую сумму, подлежащую выплате. Каждый месяц клиент обязан возвращать банку равную сумму – часть долга. В рассматриваемом случае это 180000 / 3 / 12 = 5000 рублей. Каждый месяц на остаток начисляются прописанные в договоре проценты. Соответственно, уменьшается остаток – меньше становится и сумма, начисляемая банком.
Расчет основывается на функции ПРОЦПЛАТ. Через точку с запятой в ней обозначаются четыре показателя:
Расчет процентов по кредиту
- ставка за период (13%/12)
- номер периода, за который будет считаться величина
- число периодов начисления суммы долга к уплате
- приведенная стоимость (сумма кредита)
Функция ПРОЦПЛАТ совпадает по аргументам с предыдущей формулой, однако не имеет с ней ничего схожего, подменять их друг другом нельзя. В англоязычной версии наименование функции – ISPMT, аргументы в ней такие же.
В ПРОЦПЛАТ предполагается начисление суммы процентов в начале периода. Сдвинуть эту функцию на конец месяца можно, если сместить вычисления на период раньше (не «период», а «период-1»). Итоги будут отображены с противоположным знаком, то есть минусом. Таким образом отличаются расчеты при начислении процентов по кредиту и вкладу.
Формула определения суммы процентов по взятому кредиту
Вычисление сумм, перечисляемых на погашение процентов, возможно с использованием функции ПРПЛТ. Ее аргументы не отличаются от необходимых в ОСПЛТ:
- Ставка в процентах за период (годовые, поделенные на 12).
- Период – от первого до какого-либо нужного периода.
- Общее количество периодов платежей по кредиту.
- Приведенная стоимость, которая равна совокупности будущих платежей на данный момент.
- Требуемое значение будущей стоимости, то есть остатка после последних выплат (если же этот аргумент вообще не указывать, то будет предполагаться, что он приравнен к нулю).
- Тип – срок выплаты (0 – конец периода, 1 – начало периода).
Такие расчеты подходят для аннуитетных платежей, когда не известно тело кредита. Определить процент при дифференцированной схеме начисления процентов можно, узнав, какие денежные средства направляются ежемесячно на погашение задолженности.
От суммы ежемесячного платежа необходимо отнять то самое тело кредита, направляемое на погашение непосредственно занятой у банка суммы. Разница и будет процентами, постепенно снижающимися при дифференцированном порядке их начисления.
Установление полной стоимости кредита в программе
Формула для определения ставки по кредиту рекомендована Центробанком России. Ее возможно посчитать, если использовать формулу, указанную в письме ФНС.
Для понимания вопроса необходимы многочисленные данные:
- дата произведения платежа
- день первого платежа, которая является и датой передачи денег клиенту
- установленное количество обязательных платежей
- сумма определенного платежа. Платежи, направленные на получение и расходование средств, обозначаются различными знаками
- стоимость кредита, которая отражена в годовых
В процессе определения стоимости кредита (т.е. связанные с ним суммы за выдачу кредита или первоначальное рассмотрение заявки) важно отразить все дополнительные расходы, например, за выдачу, чтобы сумма стала максимально корректной.
Полную стоимость при исчислении составляют:
Самостоятельный расчет выплат
- бесспорные платежи по договору, связанные с заключением и уменьшением суммы кредитного договора
- проценты
- комиссии и сборы за удовлетворение после рассмотрения сотрудником заявки, заключение договора, открытие и обслуживание счета, выдачу денег и пр.
- комиссии за обслуживание лица – операционное, расчетное
- при безналичном расчете – комиссии за выпуск и обслуживание кредитки
С целью расчетов установлена новая формула, которая уже давно используется за рубежом для установления эффективной годовой ставки.
В подходящую формулу входят:
- показатель величины займа (для денег по кредитному договору – с отрицательным знаком)
- количество сумм, то есть платежей
- периоды и их количество
- ставка периода в формате десятичной дроби
Законодательные рекомендации в данном аспекте окончательно не сформированы. Однако функция уже действует.
Таким образом, финансовые функции Excel позволяют проверить отсутствие переплат ввиду ошибок и огрех в договоре, случайных или намеренных. Каждый шаблон не требует тяжело получаемых данных, поэтому удобен в применении.
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
Расчет аннуитетных платежей по кредиту в Excel
В наш век высоких технологий и автоматизации как-то неприлично вручную выполнять сложные расчёты. Хоть аннуитетные платежи рассчитать не так и трудно, но как говорит Юрий Ашер:
«Не надо напрягать свой мозг там, где это могут сделать за вас другие!»
В нашей ситуации к вам на помощь придут: компьютер и программа Microsoft Excel.
Хотим предупредить, что команда портала temabiz.com поставила перед собой цель не просто дать вам «халяву» в виде «экселевского» файла с готовыми расчетами. Нет, в этой публикации мы вас научим самостоятельно рассчитывать аннуитетные платежи, а также составлять в программе Excel графики погашения аннуитетных кредитов. Ну а для ленивых мы, конечно же, выложим готовые файлы кредитных калькуляторов.
Как рассчитать аннуитетный платеж в Excel
Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.
Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.
Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:
Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.
Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:
Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:
Здесь нам требуется заполнить три поля:
- «Ставка» – годовая процентная ставка по кредиту делённая на 12.
- «Кпер» – общий срок кредитования.
- «Пс» – сумма кредита (указывается со знаком минус).
Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4). Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.
После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:
Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.
Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ». По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.
Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:
На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.
Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.
Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.
Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:
Расчет в Excel суммы кредита для заданного аннуитетного платежа
В чём «фишка» аннуитетной схемы погашения кредита? Правильно! Основная «фишка» в том, что заёмщик выплачивает кредит равными суммами на протяжении всего срока кредитования. С такой схемой очень удобно планировать свой бюджет. Например, вы готовы ежемесячно выделять на погашение кредита 5000 рублей. По вашим скромным подсчётам, такая нагрузка будет для вас не слишком обременительной. Естественно, у вас возникает закономерный вопрос: «А на какую сумму кредита я могу рассчитывать?» В общем, нам нужен новый кредитный калькулятор, у которого в исходных данных будет не сумма кредита, а величина аннуитетного платежа.
Что же, друзья, не будем терять время! Открываем программу Microsoft Excel и приступаем к разработке нашего кредитного калькулятора!
Итак, структура нового кредитного калькулятора почти не изменилась. Здесь также есть блок с исходными данными и блок с расчётами. Единственное изменение, это то, что в исходных данных мы вводим ежемесячный аннуитетный платёж, который готовы выплачивать, а в расчётах получаем сумму кредита, на которую мы можем рассчитывать. Собственно, она на нашем рисунке обведена и отмечена под номером 1.
Чтобы рассчитать сумму ожидаемого кредита надо воспользоваться функцией ПС, предварительно кликнув по ячейке, в которой мы хотим видеть свой расчёт (в нашем калькуляторе это ячейка с координатой C11). Вызвать функцию ПС можно нажав на знакомую вам кнопку «fx», которая находится слева от строки формул. В появившемся окне выбираем «ПС» и жмём «Ок». В открывшейся таблице вводим следующие данные:
- «Ставка» – годовая процентная ставка по кредиту делённая на 12 (в нашем случае: C5/12).
- «Кпер» – общий срок кредитования (в нашем калькуляторе, это ячейка с координатой C6).
- «Плт» – ежемесячный аннуитетный платёж, перед которым ставим знак минус (в нашем калькуляторе, это ячейка C4, перед данной координатой мы и ставим знак минус).
Жмём «Ок» и в ячейке С11 появилась сумма 53 422 руб. – именно на такой размер кредита может рассчитывать заёмщик, который готов на протяжении 12 месяцев ежемесячно выплачивать по 5000 руб.
Кстати, обратите внимание на данные в строке формул (на рисунке они обведены и указаны под номером 2). Вы всё правильно поняли, друзья! Да, это те данные, которые необходимы для расчёта суммы кредита в нашем калькуляторе: =ПС(C5/12;C6;-C4). Те самые параметры, которые мы вводили в таблице функции ПС.
Расчёт остальных показателей выполняется по такому же принципу, как и в предыдущем калькуляторе:
- Общая сумма выплат – это ежемесячный аннуитетный платёж (ячейка С4) умноженный на общий срок кредитования (ячейка С6). В строку формул вводим следующие данные: =C4*C6.
- Переплата (проценты) по кредиту – это общая сумма выплат (ячейка С12) минус сумма кредита (ячейка С11). В строку формул записываем: =C12-C11.
- Эффективная процентная ставка (или полная стоимость кредита) – это общая сумма выплат (ячейка С12) делённая на сумму кредита (ячейка С11) и минус единица. Затем всё это делим на срок кредитования, выраженный в годах (ячейка C6 делённая на 12). В строку формул записываем: = (C12/C11-1)/(C6/12).
Кстати, интересный момент. Вот в нашем примере, выплачивая ежемесячно в течение года по 5000 рублей, мы можем рассчитывать на сумму кредита равную 53 422 рубля. А что делать, если надо больше денег? Как вариант, можно увеличить срок кредитования. Если вместо 12 месяцев поставить 24, то сумма кредита увеличится до 96 380 рублей. Эти данные нам мгновенно выдал наш кредитный калькулятор, который вы можете скачать ссылке ниже:
Кредитный калькулятор в Excel по расчету графика аннуитетных платежей
Два предыдущих кредитных калькулятора очень удобны, но они выполняют краткие (общие) расчёты. А иногда заёмщику нужна расширенная информация – график ежемесячных аннуитетных платежей с детальной расшифровкой каждой выплаты (с указанием сумм, идущих на погашение процентов, и сумм, погашающих тело кредита). В общем, сейчас мы сделаем в программе Excel ещё один кредитный калькулятор, который будет автоматически рассчитывать график аннуитетных платежей. Щёлкаем мышкой по рисунку:
Перед вами расширенная и доработанная версия нашего первого кредитного калькулятора (того, который рассчитывает размер ежемесячного аннуитетного платежа по кредиту). Здесь кроме стандартных блоков с исходными данными и расчётами, появилась таблица, в которой детально расписаны все наши будущие ежемесячные выплаты. Таблица имеет пять колонок:
- 1.Месяцы. В этой колонке по порядку указаны номера месяцев, в которые будут осуществляться выплаты. Обратите внимание, что речь идёт не о календарных, а о порядковых номерах. То есть, если первая выплата припадает на сентябрь месяц, то ему присваивается порядковый номер «1», как первому месяцу, а не «9», как календарному.
- 2.Ежемесячный платёж. Это тот самый аннуитетный платёж, который не меняется на протяжении всего срока кредитования. В сноске к одной из ячеек вы можете увидеть данные, которые внесены в строку формул: =ПЛТ(B3/12;B4;-H14). Вы уже знаете, что за расчёт аннуитетного платежа в экселе отвечает функция ПЛТ. Координаты необходимых значений для расчёта можно внести, как через строку формул, так и заполнив таблицу, которая появится при нажатии на кнопку «fx», находящуюся слева от строки формул.
- 3.Погашение процентов. Здесь рассчитывается доля процентов в аннуитетных платежах (в каждой новой выплате она будет уменьшаться). В программе Excel за расчёт данного показателя отвечает функция ПРПЛТ. Опять же, задать необходимые параметры для расчётов можно либо нажав на кнопку «fx» и заполнив таблицу, либо просто внеся нужную информацию в строку формул. В нашем примере для расчёта доли процентов в первом платеже, в строке формул записано следующее: =ПРПЛТ(A15/12;D15;B15;-C15).
- 4.Погашение тела кредита. Та самая выплата, которая вытягивает нас из долговой ямы и избавляет от банковского рабства. Мы рассчитали её просто: из суммы аннуитетного платежа вычли долю процентов, которую рассчитали в предыдущей колонке. Собственно, в строке формул по первому платежу так и записано: =E15-F15. Но можно пойти и другим, более изощрённым, путём. В программе Excel за расчёт этого платежа отвечает функция ОСПЛТ. Можете для интереса нажать кнопку «fx», выбрать функцию ОСПЛТ, внести все необходимые данные и получить сумму, идущую на погашение тела кредита в выбранном платеже.
- 5.Долг на конец месяца. Ну, здесь всё просто! В данной колонке отображается сумма вашего долга перед банком на конец текущего месяца. Из текущего остатка мы отнимаем долю, идущую на погашение тела кредита. А вот уплаченные проценты просто уходят в казну банка и никак не влияют на сумму вашего текущего долга по кредиту.
Вот так легко и непринуждённо мы разработали кредитный калькулятор по расчёту графика аннуитетных платежей. Скачать его можно ссылке ниже:
Итак, друзья, теперь у вас есть целых три кредитных калькулятора по расчёту аннуитетных платежей, разработанных в программе Microsoft Excel. В следующей публикации мы расскажем о досрочном погашении аннуитетного кредита.