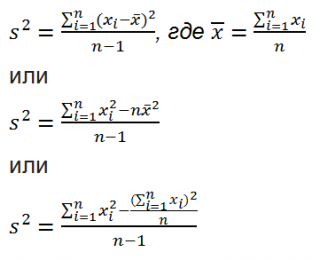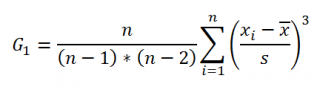Содержание
- Выполнение выборки
- Способ 1: применение расширенного автофильтра
- Способ 2: применение формулы массива
- Способ 3: выборка по нескольким условиям с помощью формулы
- Способ 4: случайная выборка
- Вопросы и ответы
При работе с таблицами Excel довольно часто приходится проводить отбор в них по определенному критерию или по нескольким условиям. В программе сделать это можно различными способами при помощи ряда инструментов. Давайте выясним, как произвести выборку в Экселе, используя разнообразные варианты.
Выполнение выборки
Выборка данных состоит в процедуре отбора из общего массива тех результатов, которые удовлетворяют заданным условиям, с последующим выводом их на листе отдельным списком или в исходном диапазоне.
Способ 1: применение расширенного автофильтра
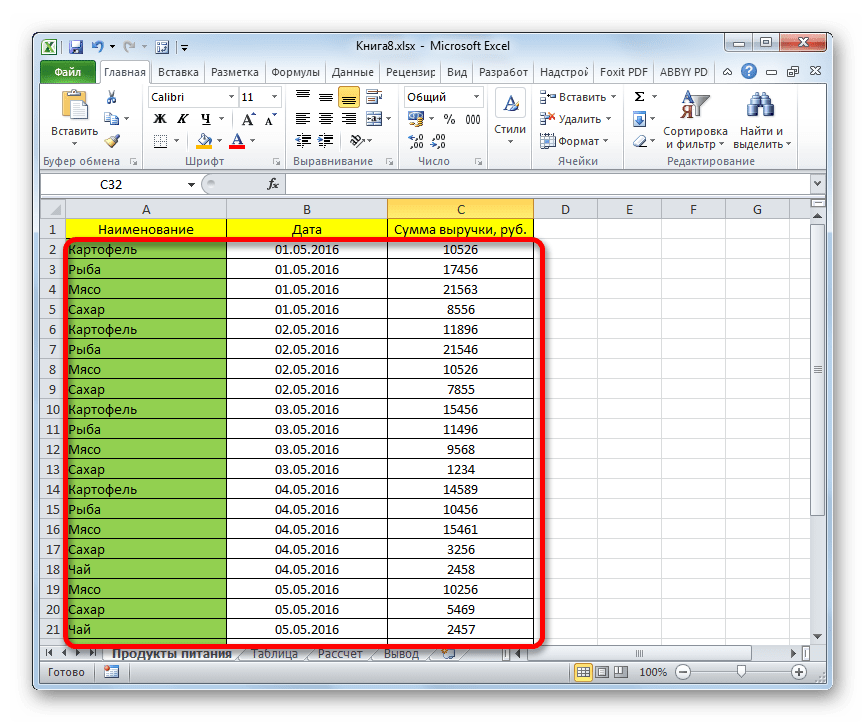
Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.
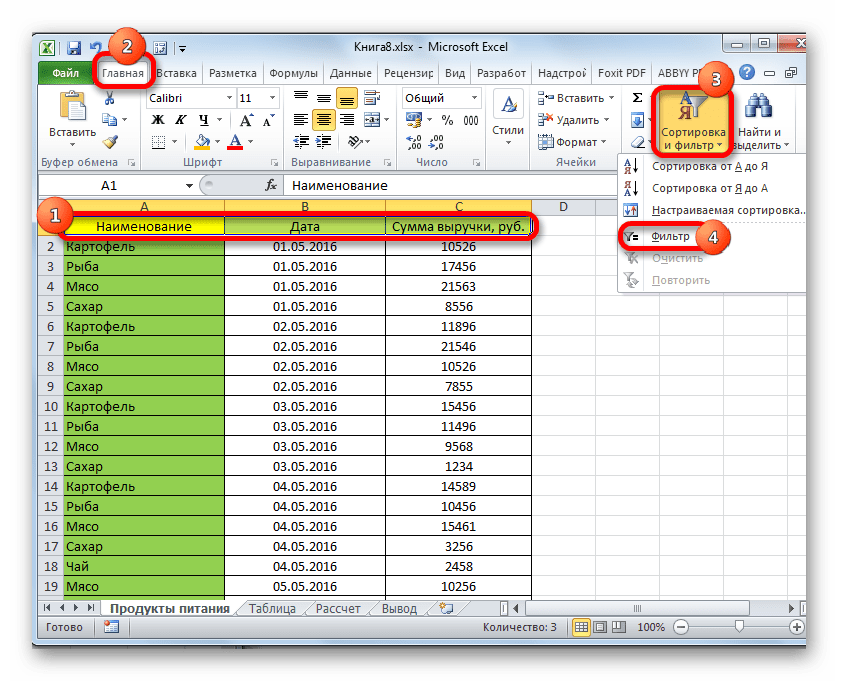
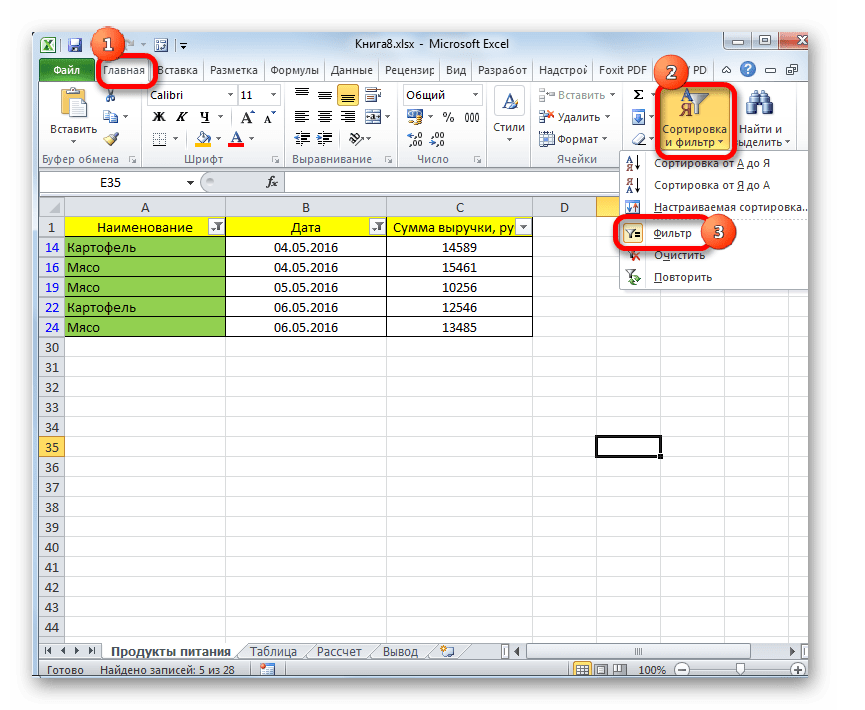
- Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».
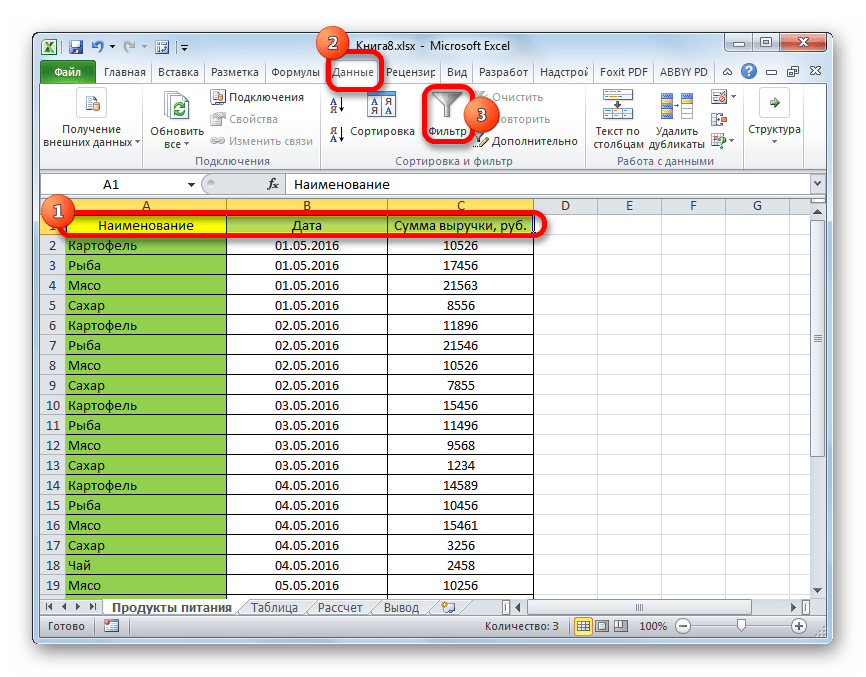
Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».
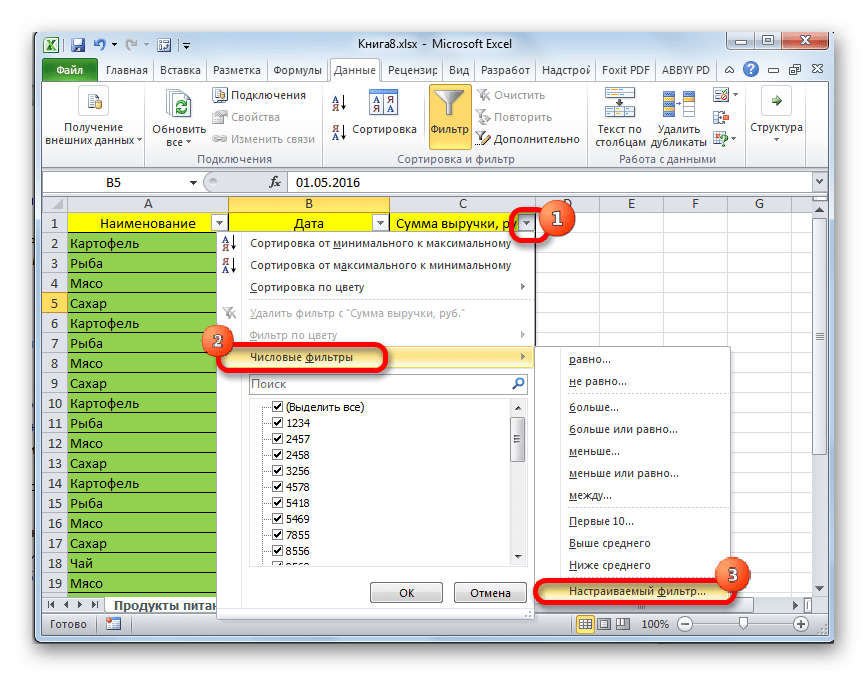
- После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».
- Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
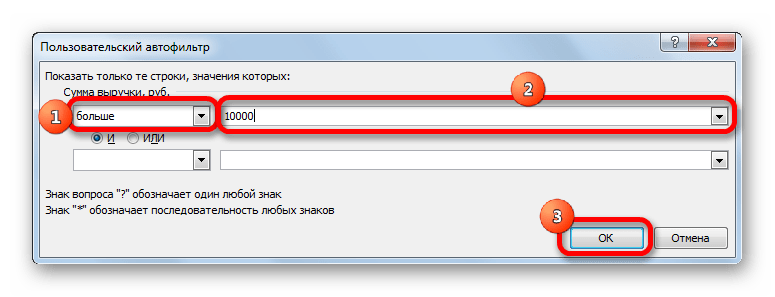
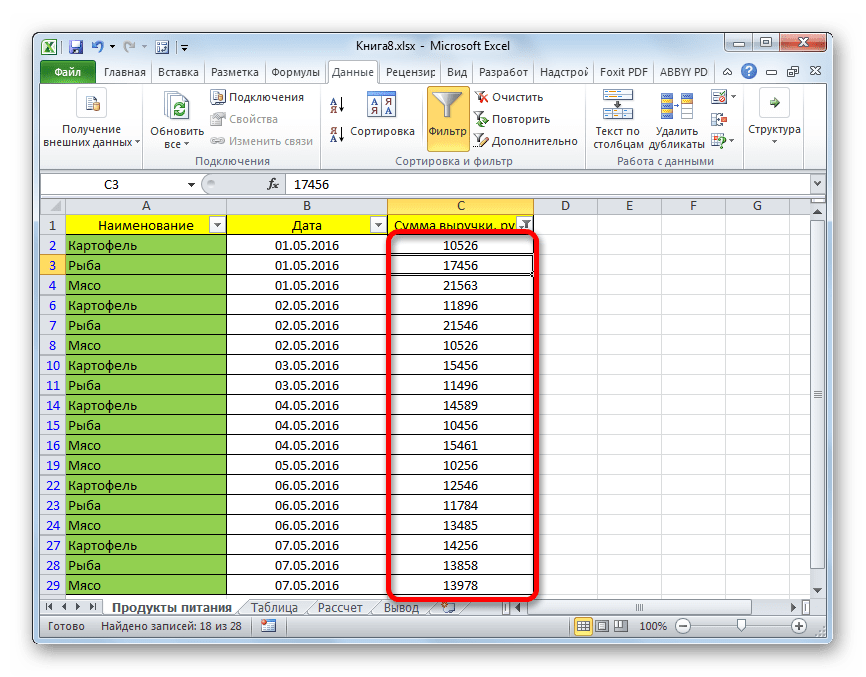
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».
- Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.
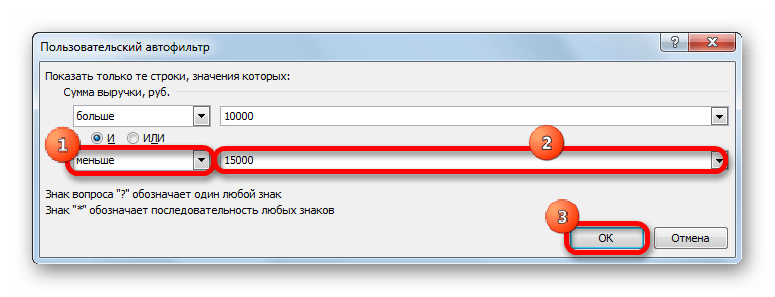
- Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».
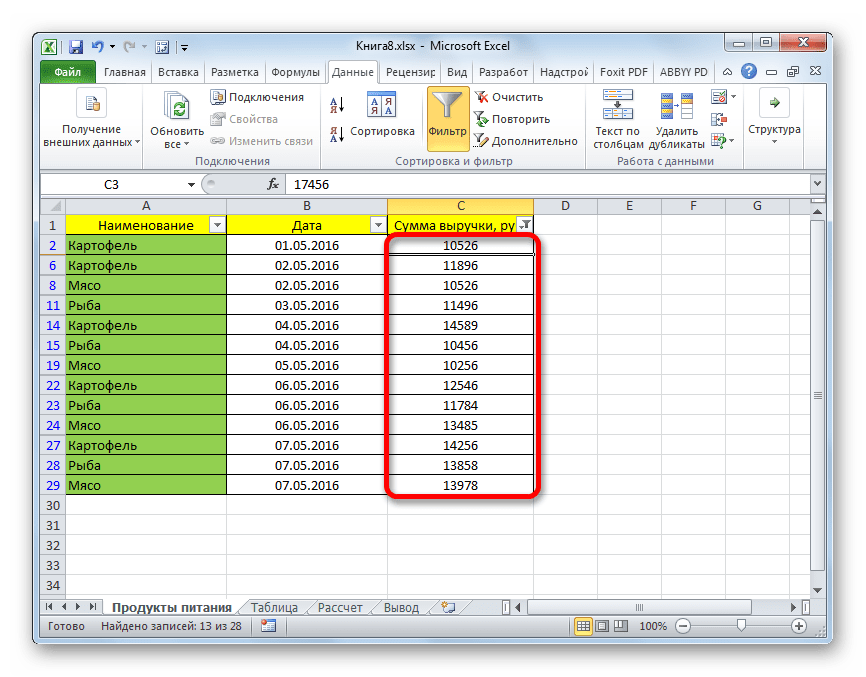
- Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.
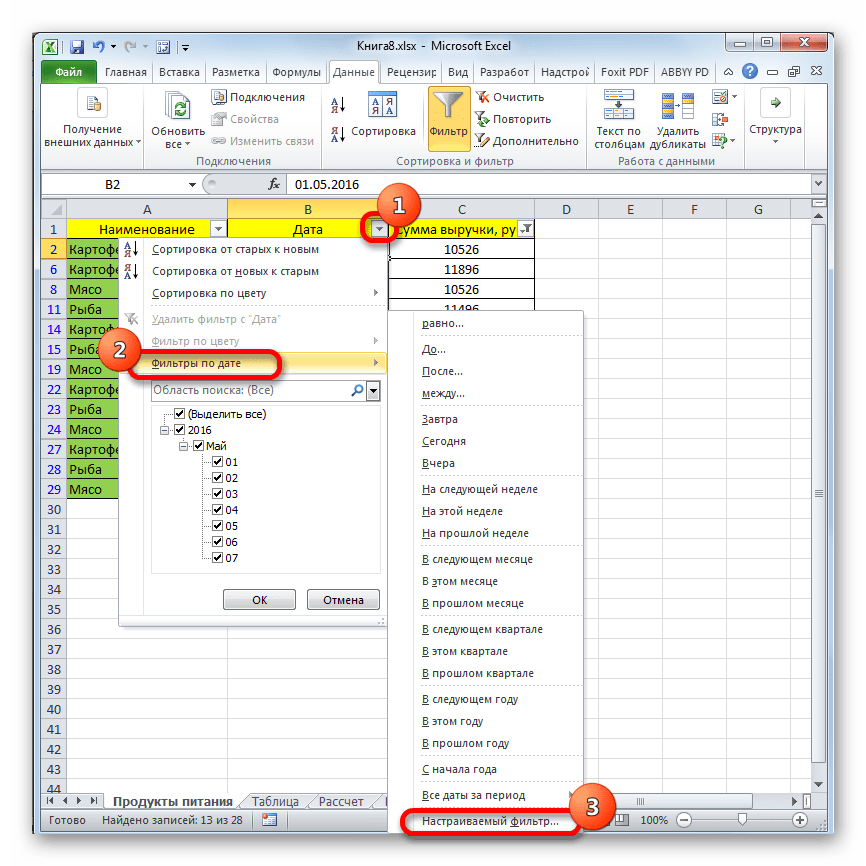
- Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».
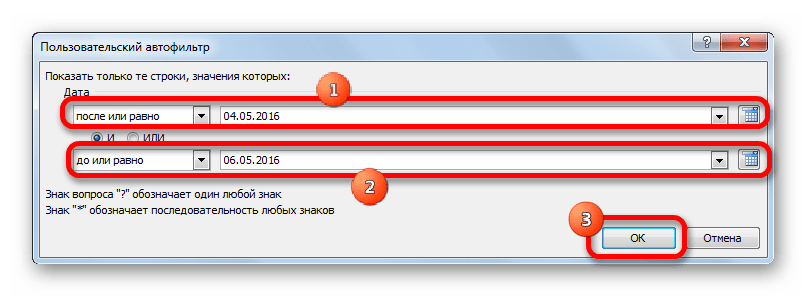
- Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».
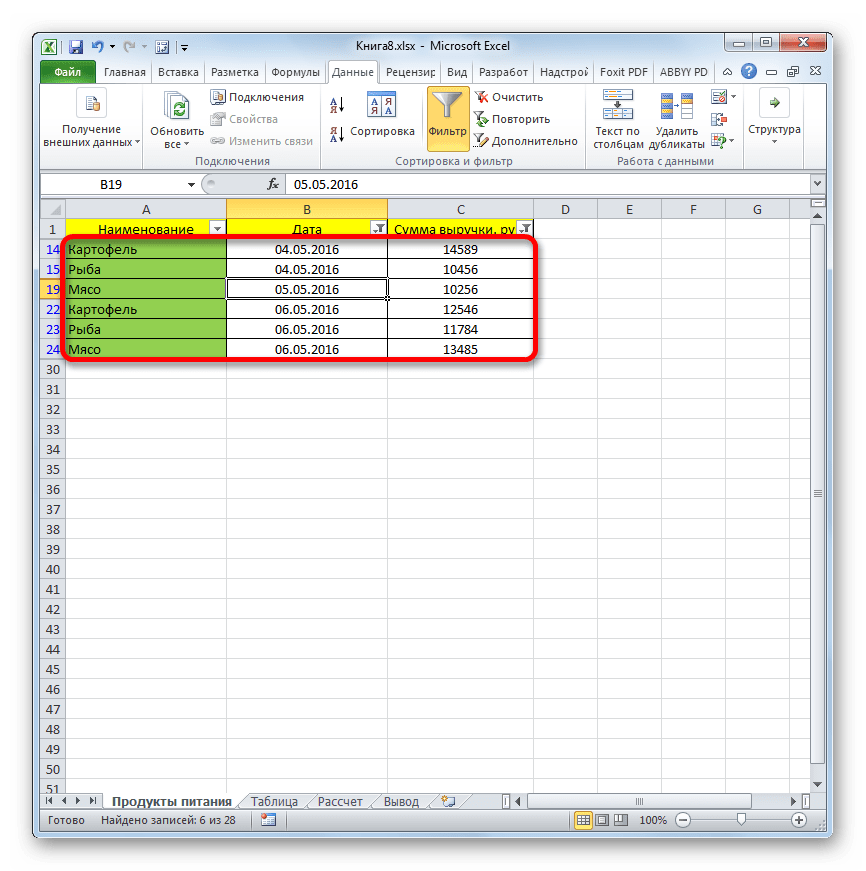
- Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.
- Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».
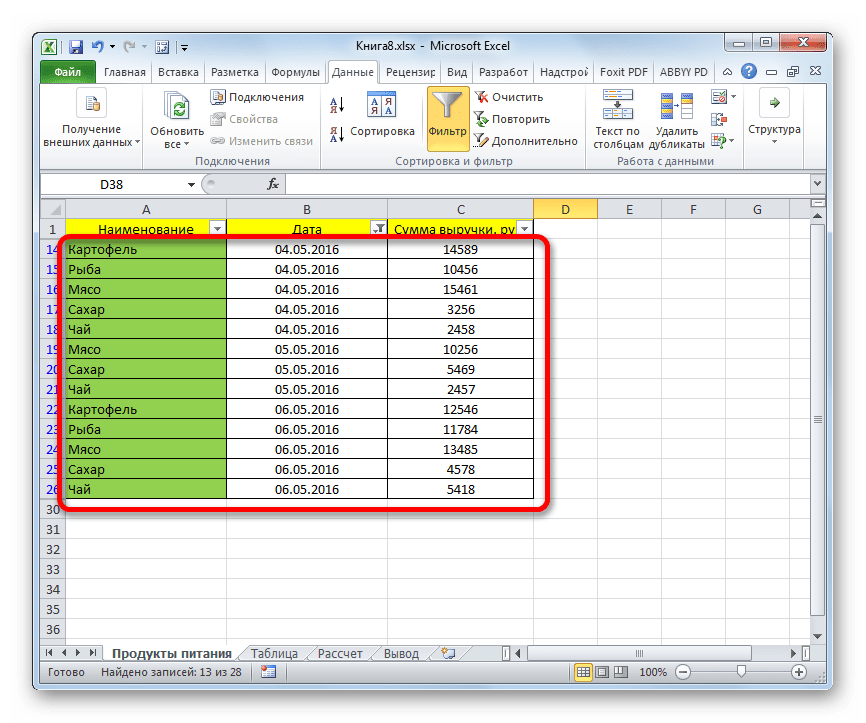
- Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).
- В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
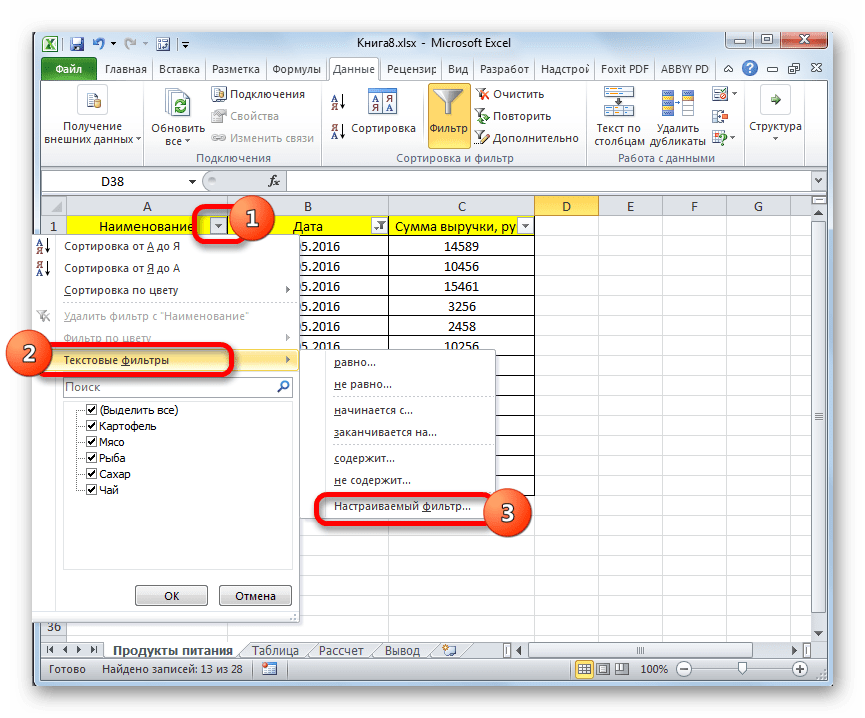
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».
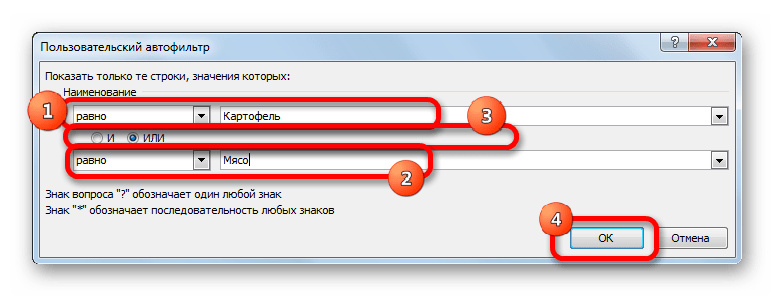
- Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».
- Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.
- Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».
Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».
При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.
Урок: Функция автофильтр в Excel
Способ 2: применение формулы массива
Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.
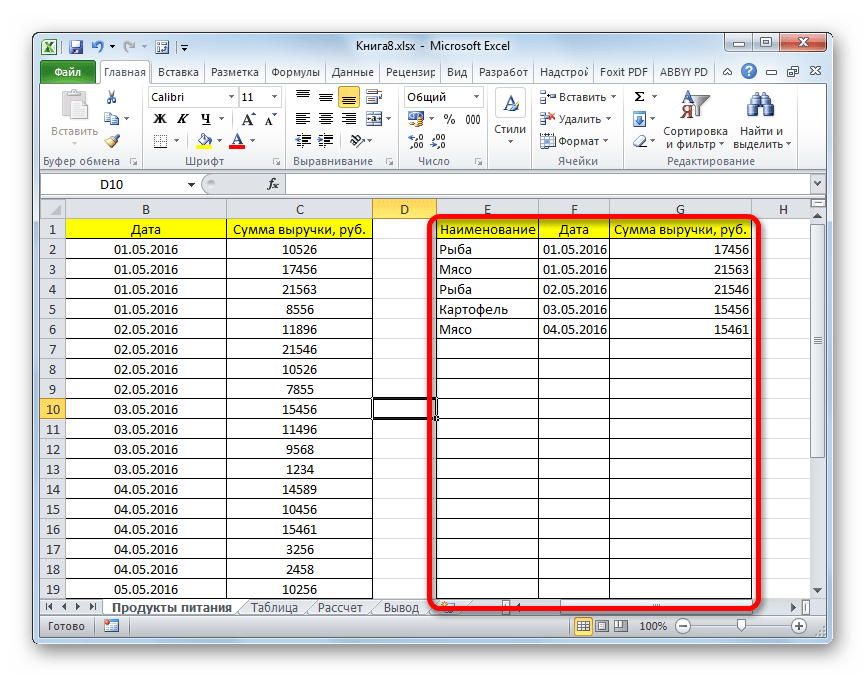
- На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.
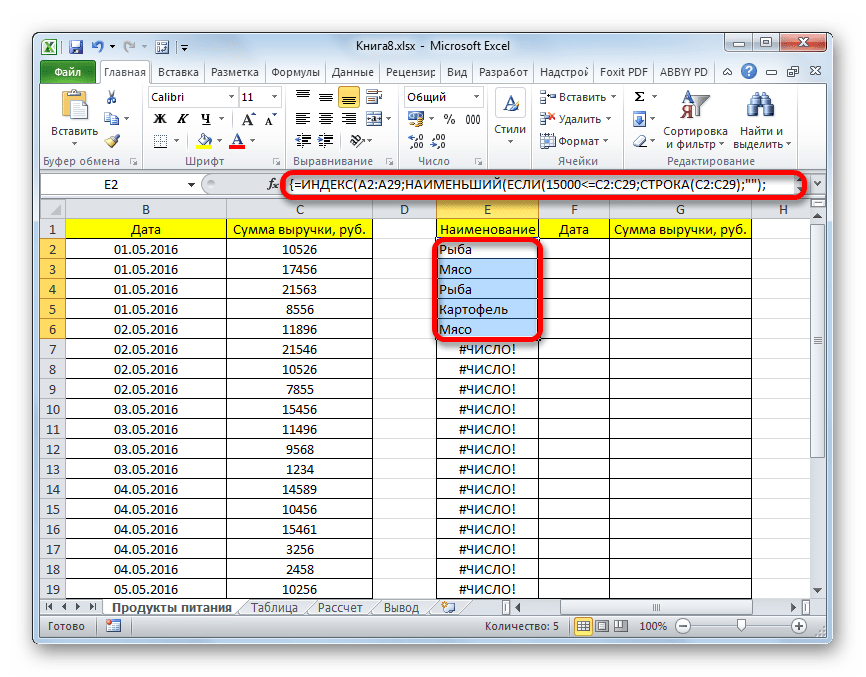
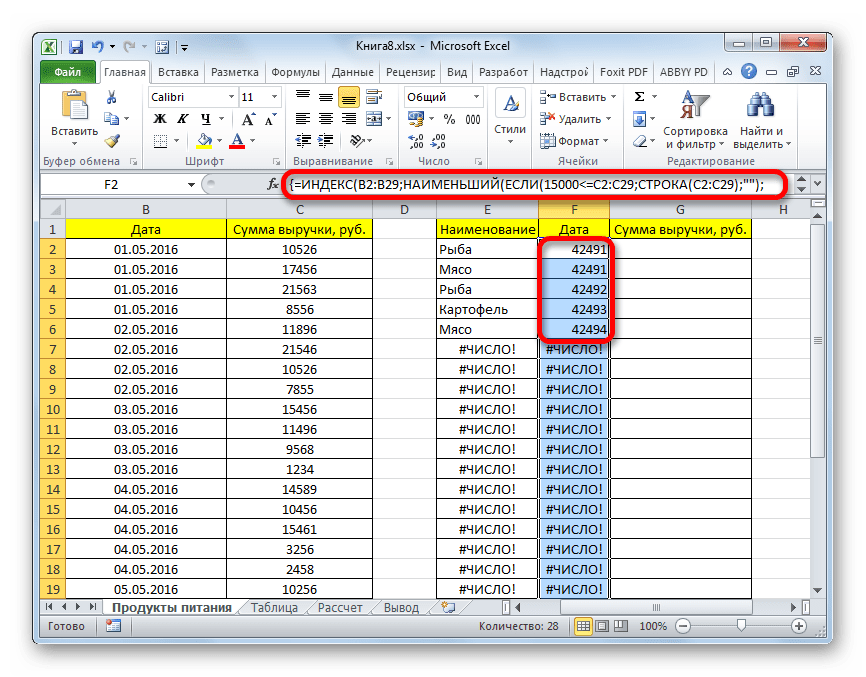
- Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.
- Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.
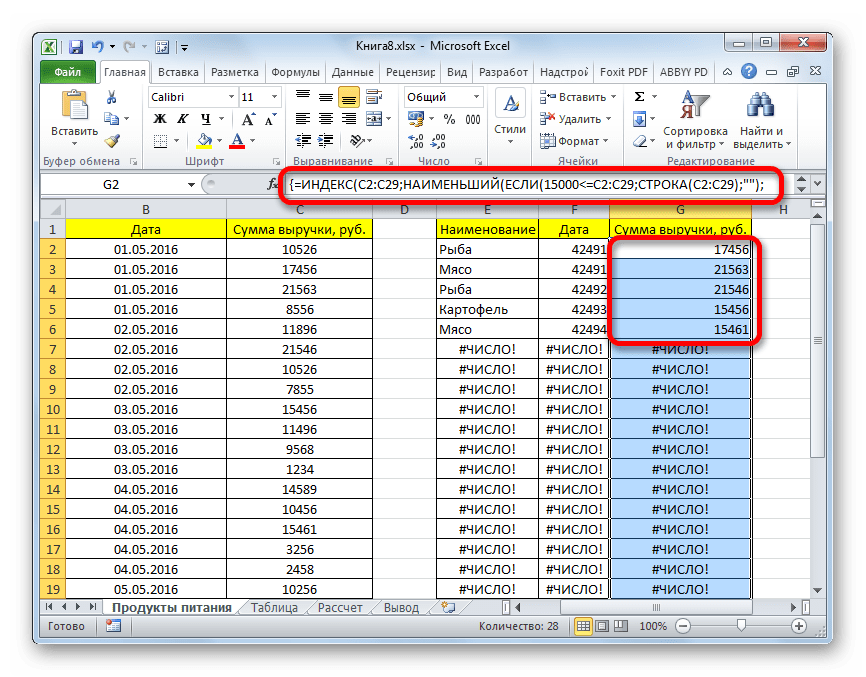
- Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Жмем сочетание клавиш Ctrl+Shift+Enter.
- Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Опять набираем сочетание клавиш Ctrl+Shift+Enter.
Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.
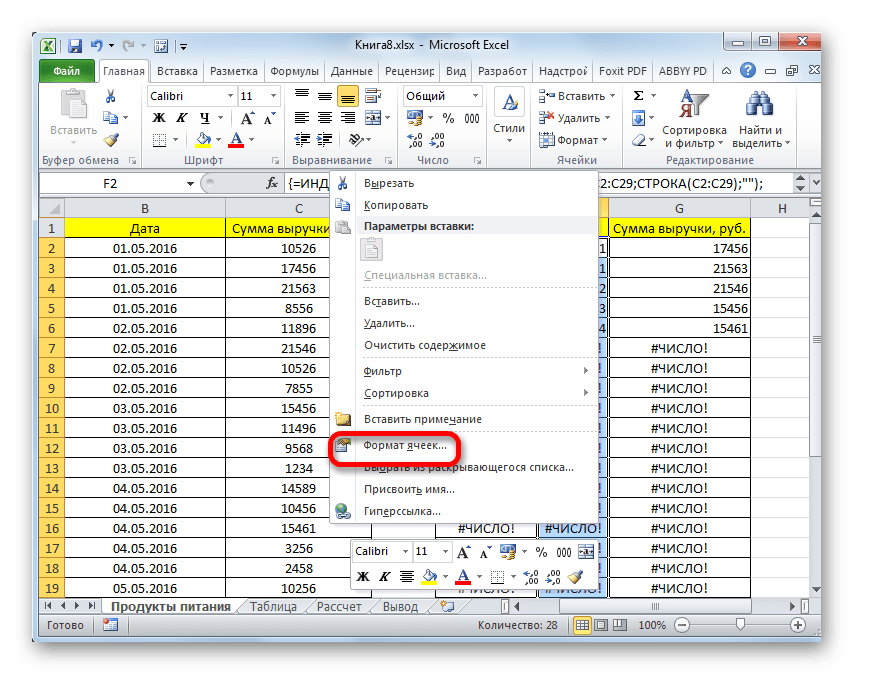
- Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».
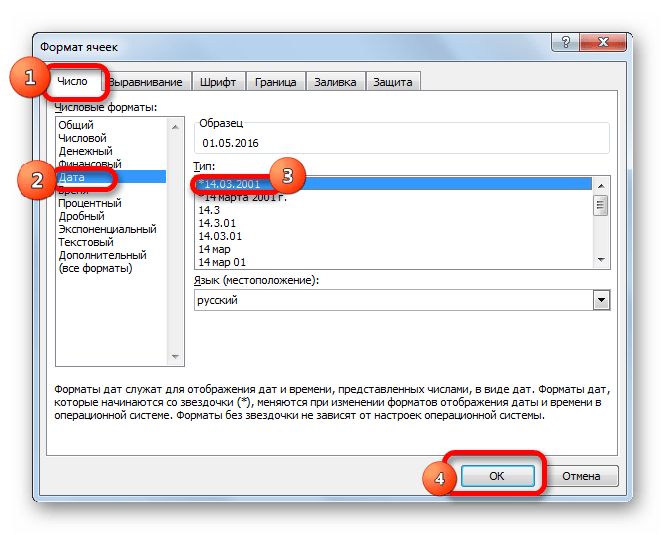
- В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».
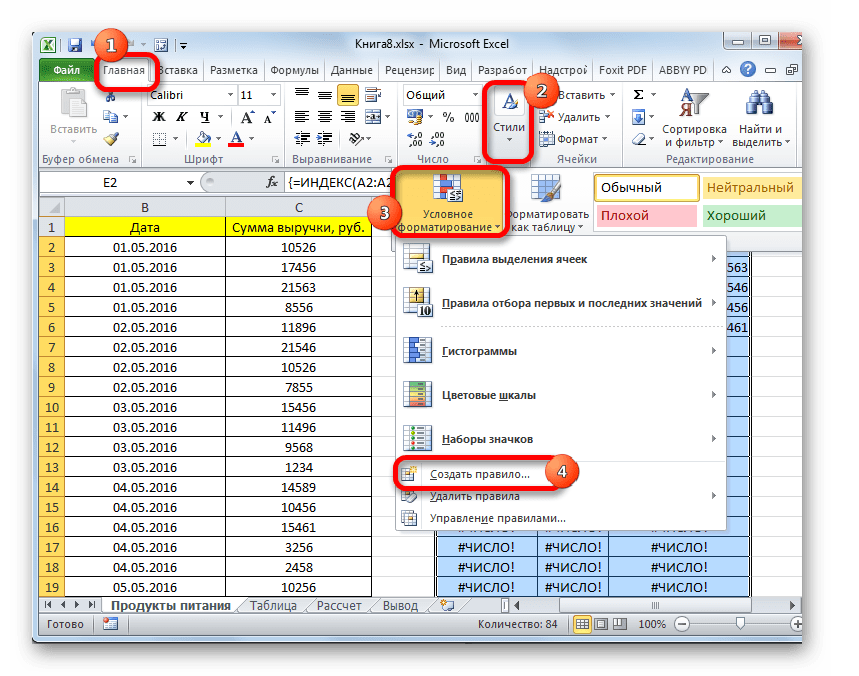
- Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».
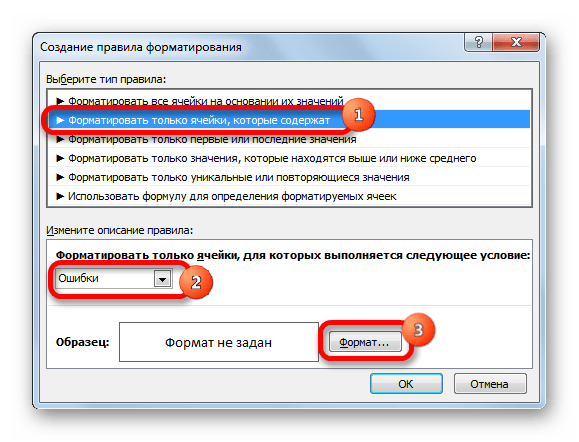
- В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».
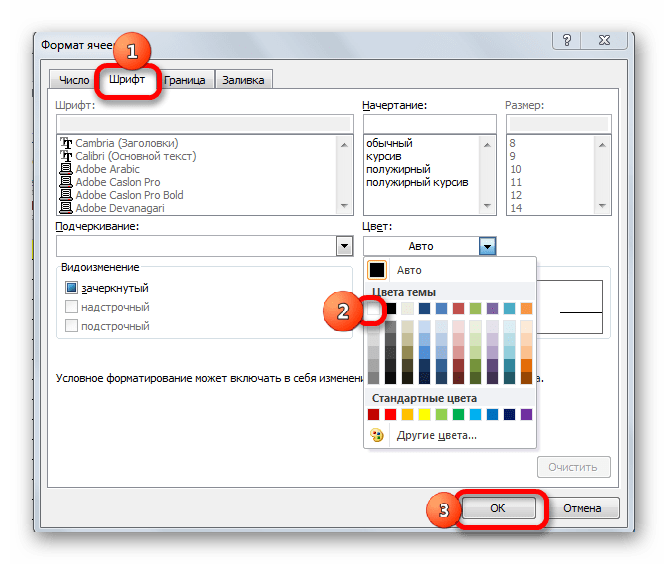
- В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».
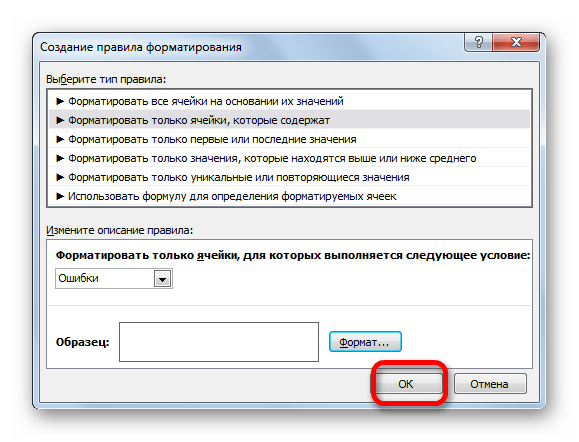
- На кнопку с точно таким же названием жмем после возвращения в окно создания условий.
Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.
Урок: Условное форматирование в Excel
Способ 3: выборка по нескольким условиям с помощью формулы
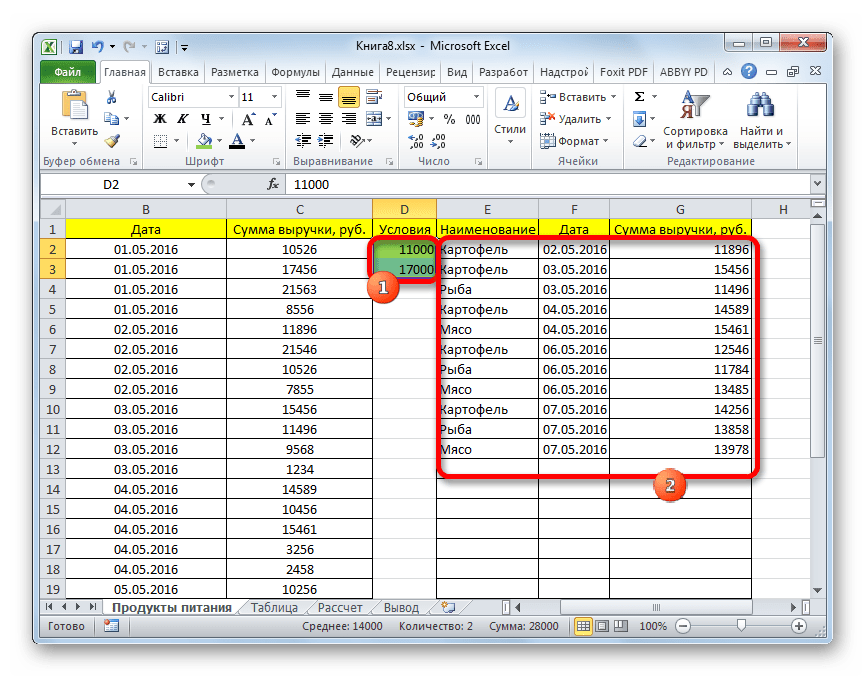
Так же, как и при использовании фильтра, с помощью формулы можно осуществлять выборку по нескольким условиям. Для примера возьмем всю ту же исходную таблицу, а также пустую таблицу, где будут выводиться результаты, с уже выполненным числовым и условным форматированием. Установим первым ограничением нижнюю границу отбора по выручке в 15000 рублей, а вторым условием верхнюю границу в 20000 рублей.
- Вписываем в отдельном столбце граничные условия для выборки.
- Как и в предыдущем способе, поочередно выделяем пустые столбцы новой таблицы и вписываем в них соответствующие три формулы. В первый столбец вносим следующее выражение:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(($D$2=C2:C29);СТРОКА(C2:C29);"");СТРОКА(C2:C29)-СТРОКА($C$1))-СТРОКА($C$1))В последующие колонки вписываем точно такие же формулы, только изменив координаты сразу после наименования оператора ИНДЕКС на соответствующие нужным нам столбцам, по аналогии с предыдущим способом.
Каждый раз после ввода не забываем набирать сочетание клавиш Ctrl+Shift+Enter.
- Преимущество данного способа перед предыдущим заключается в том, что если мы захотим поменять границы выборки, то совсем не нужно будет менять саму формулу массива, что само по себе довольно проблематично. Достаточно в колонке условий на листе поменять граничные числа на те, которые нужны пользователю. Результаты отбора тут же автоматически изменятся.
Способ 4: случайная выборка
В Экселе с помощью специальной формулы СЛЧИС можно также применять случайный отбор. Его требуется производить в некоторых случаях при работе с большим объемом данных, когда нужно представить общую картину без комплексного анализа всех данных массива.
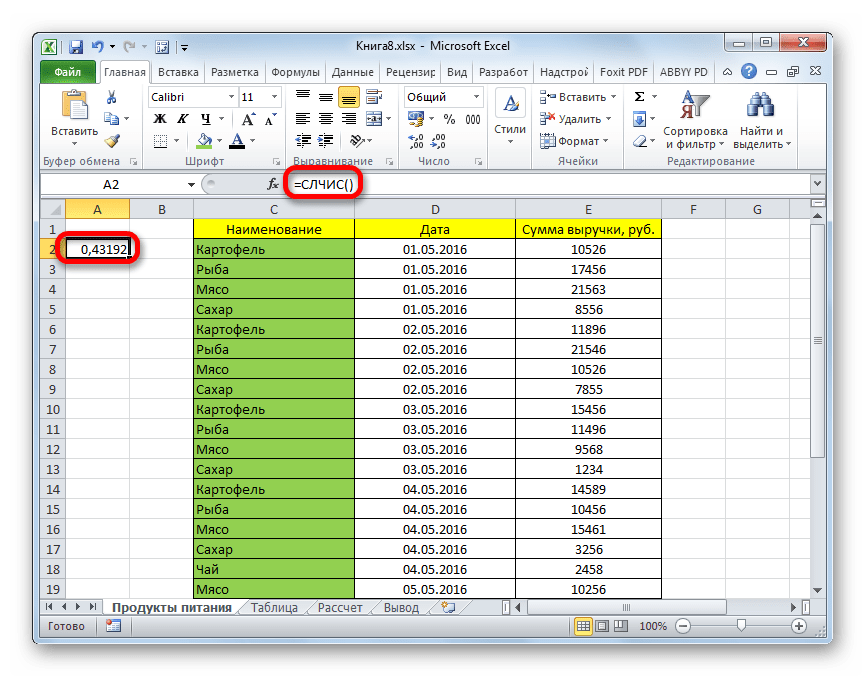
- Слева от таблицы пропускаем один столбец. В ячейке следующего столбца, которая находится напротив первой ячейки с данными таблицы, вписываем формулу:
=СЛЧИС()Эта функция выводит на экран случайное число. Для того, чтобы её активировать, жмем на кнопку ENTER.
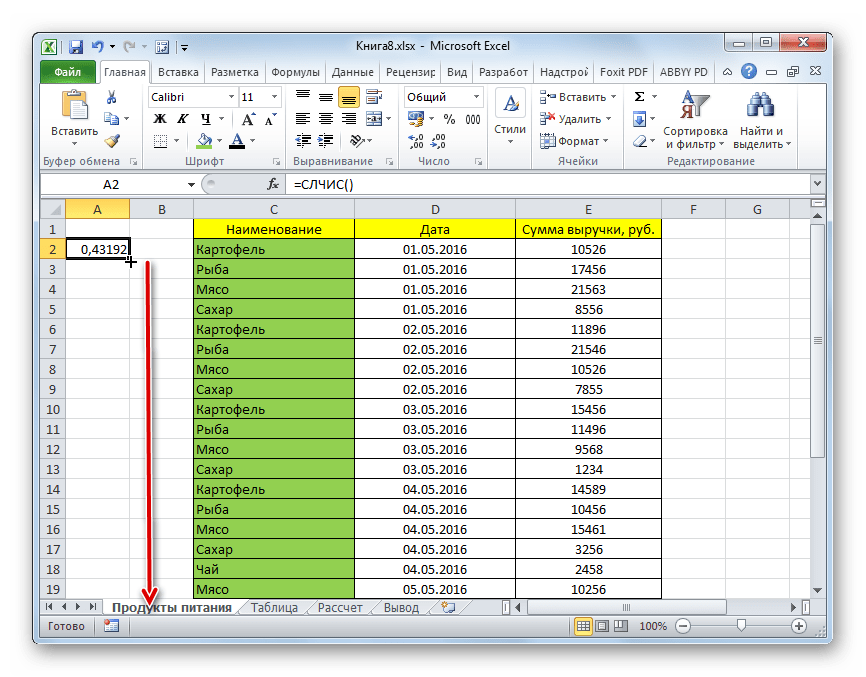
- Для того, чтобы сделать целый столбец случайных чисел, устанавливаем курсор в нижний правый угол ячейки, которая уже содержит формулу. Появляется маркер заполнения. Протягиваем его вниз с зажатой левой кнопкой мыши параллельно таблице с данными до её конца.
- Теперь у нас имеется диапазон ячеек, заполненный случайными числами. Но, он содержит в себе формулу СЛЧИС. Нам же нужно работать с чистыми значениями. Для этого следует выполнить копирование в пустой столбец справа. Выделяем диапазон ячеек со случайными числами. Расположившись во вкладке «Главная», щелкаем по иконке «Копировать» на ленте.
- Выделяем пустой столбец и кликаем правой кнопкой мыши, вызывая контекстное меню. В группе инструментов «Параметры вставки» выбираем пункт «Значения», изображенный в виде пиктограммы с цифрами.
- После этого, находясь во вкладке «Главная», кликаем по уже знакомому нам значку «Сортировка и фильтр». В выпадающем списке останавливаем выбор на пункте «Настраиваемая сортировка».
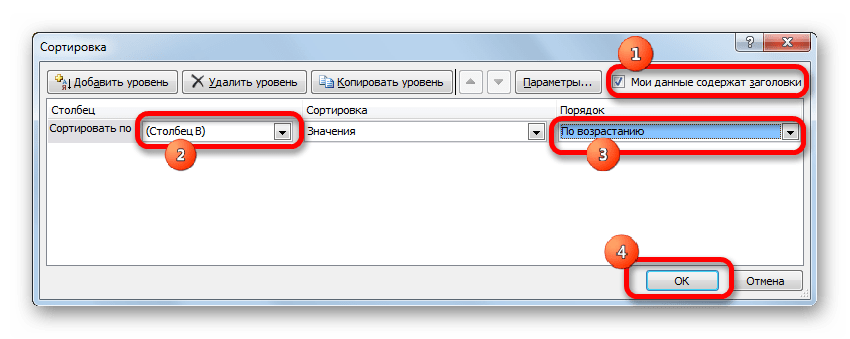
- Активируется окно настройки сортировки. Обязательно устанавливаем галочку напротив параметра «Мои данные содержат заголовки», если шапка имеется, а галочки нет. В поле «Сортировать по» указываем наименование того столбца, в котором содержатся скопированные значения случайных чисел. В поле «Сортировка» оставляем настройки по умолчанию. В поле «Порядок» можно выбрать параметр как «По возрастанию», так и «По убыванию». Для случайной выборки это значения не имеет. После того, как настройки произведены, жмем на кнопку «OK».
- После этого все значения таблицы выстраиваются в порядке возрастания или убывания случайных чисел. Можно взять любое количество первых строчек из таблицы (5, 10, 12, 15 и т.п.) и их можно будет считать результатом случайной выборки.
Урок: Сортировка и фильтрация данных в Excel
Как видим, выборку в таблице Excel можно произвести, как с помощью автофильтра, так и применив специальные формулы. В первом случае результат будет выводиться в исходную таблицу, а во втором – в отдельную область. Имеется возможность производить отбор, как по одному условию, так и по нескольким. Кроме того, можно осуществлять случайную выборку, использовав функцию СЛЧИС.
Еще статьи по данной теме:
Помогла ли Вам статья?
Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.
Задача
описательной статистики
(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений
выборки
к нескольким итоговым показателям, которые дают представление о
выборке
.В качестве таких статистических показателей используются:
среднее
,
медиана
,
мода
,
дисперсия, стандартное отклонение
и др.
Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные
статистические выводы о распределении
, из которого была взята
выборка
. Например, если у нас есть
выборка
значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой
выборки
мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.
Содержание статьи:
- Надстройка Пакет анализа;
-
Среднее выборки
;
-
Медиана выборки
;
-
Мода выборки
;
-
Мода и среднее значение
;
-
Дисперсия выборки
;
-
Стандартное отклонение выборки
;
-
Стандартная ошибка
;
-
Ассиметричность
;
-
Эксцесс выборки
;
-
Уровень надежности
.
Надстройка Пакет анализа
Для вычисления статистических показателей одномерных
выборок
, используем
надстройку Пакет анализа
. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.
СОВЕТ
: Подробнее о других инструментах надстройки
Пакет анализа
и ее подключении – читайте в статье
Надстройка Пакет анализа MS EXCEL
.
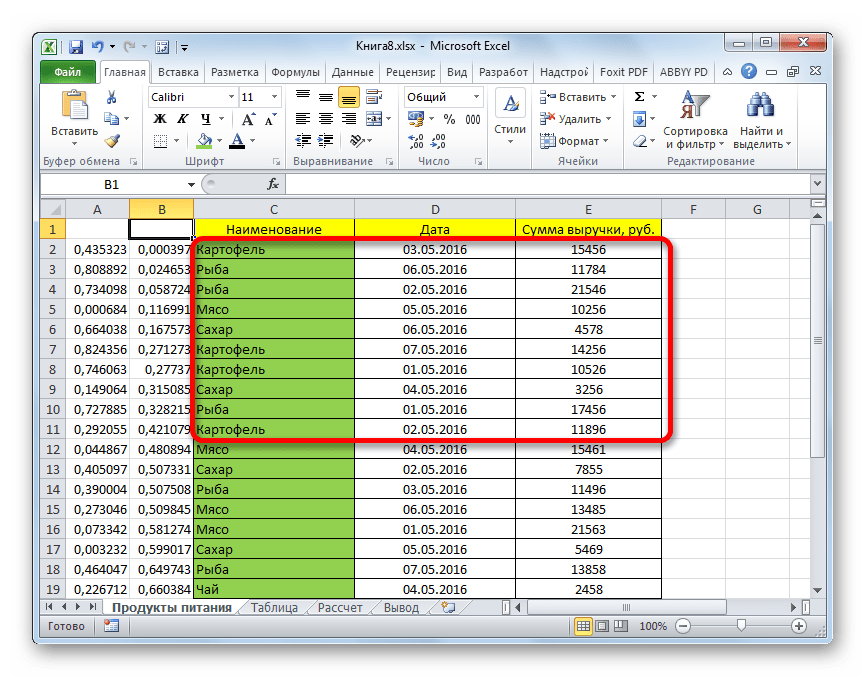
Выборку
разместим на
листе
Пример
в файле примера
в диапазоне
А6:А55
(50 значений).
Примечание
: Для удобства написания формул для диапазона
А6:А55
создан
Именованный диапазон
Выборка.
В диалоговом окне
Анализ данных
выберите инструмент
Описательная статистика
.
После нажатия кнопки
ОК
будет выведено другое диалоговое окно,
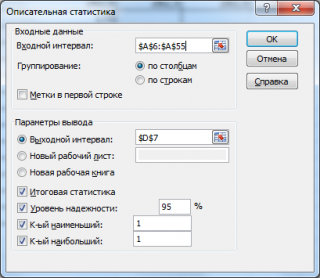
в котором нужно указать:
входной интервал
(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле
Метки в первой строке (
Labels
in
first
row
).
В этом случае заголовок будет выведен в
Выходном интервале.
Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал
(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (
Summary
Statistics
)
. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:
среднее, медиана, мода, стандартное отклонение
и др.;-
Также можно поставить галочки напротив полей
Уровень надежности (
Confidence
Level
for
Mean
)
,
К-й наименьший
(Kth Largest) и
К-й наибольший
(Kth Smallest).
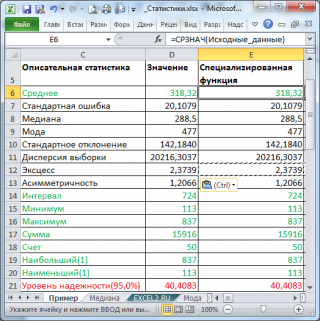
В результате будут выведены следующие статистические показатели:
Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.
Если во
входном интервале
указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во
Входной интервал
и установите галочку в поле
Метки в первой строке
). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.
Зеленым цветом на картинке выше и в
файле примера
выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:
Интервал
(Range) — разница между максимальным и минимальным значениями;
Минимум
(Minimum) – минимальное значение в диапазоне ячеек, указанном во
Входном интервале
(см.статью про функцию
МИН()
);
Максимум
(Maximum)– максимальное значение (см.статью про функцию
МАКС()
);
Сумма
(Sum) – сумма всех значений (см.статью про функцию
СУММ()
);
Счет
(Count) – количество значений во
Входном интервале
(пустые ячейки игнорируются, см.статью про функцию
СЧЁТ()
);
Наибольший
(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.статью про функцию
НАИБОЛЬШИЙ()
);
Наименьший
(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.статью про функцию
НАИМЕНЬШИЙ()
).
Ниже даны подробные описания остальных показателей.
Среднее выборки
Среднее
(mean, average) или
выборочное среднее
или
среднее выборки
(sample average) представляет собой
арифметическое среднее
всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция
СРЗНАЧ()
.
Выборочное среднее
является «хорошей» (несмещенной и эффективной) оценкой
математического ожидания
случайной величины (подробнее см. статью
Среднее и Математическое ожидание в MS EXCEL
).
Медиана выборки
Медиана
(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем
медиана
, а половина чисел меньше, чем
медиана
. Для определения
медианы
необходимо сначала
отсортировать множество чисел
. Например,
медианой
для чисел 2, 3, 3,
4
, 5, 7, 10 будет 4.
Если множество содержит четное количество чисел, то вычисляется
среднее
для двух чисел, находящихся в середине множества. Например,
медианой
для чисел 2, 3,
3
,
5
, 7, 10 будет 4, т.к. (3+5)/2.
Если имеется длинный хвост распределения, то
Медиана
лучше, чем
среднее значение
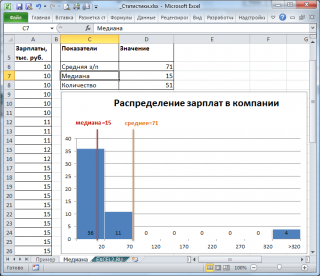
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что
как минимум
у 50% сотрудников зарплата меньше или равна 15 тыс. руб.
Для определения
медианы
в MS EXCEL существует одноименная функция
МЕДИАНА()
, английский вариант — MEDIAN().
Медиану
также можно вычислить с помощью формул
=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).
Подробнее о
медиане
см. специальную статью
Медиана в MS EXCEL
.
СОВЕТ
: Подробнее про
квартили
см. статью, про
перцентили (процентили)
см. статью.
Мода выборки
Мода
(Mode) – это наиболее часто встречающееся (повторяющееся) значение в
выборке
. Например, в массиве (1; 1;
2
;
2
;
2
; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это
мода
. Для вычисления
моды
используется функция
МОДА()
, английский вариант MODE().
Примечание
: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье
Есть ли повторы в списке?
Начиная с
MS EXCEL 2010
вместо функции
МОДА()
рекомендуется использовать функцию
МОДА.ОДН()
, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция
МОДА.НСК()
, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.
Например, в массиве (1; 1;
2
;
2
;
2
; 3;
4
;
4
;
4
; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются
модами
. Функции
МОДА.ОДН()
и
МОДА()
вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.
файл примера
, лист
Мода
).
Чтобы исправить эту несправедливость и была введена функция
МОДА.НСК()
, которая выводит все
моды
. Для этого ее нужно ввести как
формулу массива
.
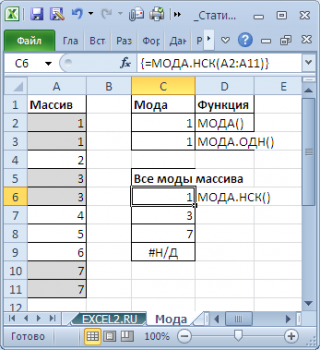
Как видно из картинки выше, функция
МОДА.НСК()
вернула все три
моды
из массива чисел в диапазоне
A2:A11
: 1; 3 и 7. Для этого, выделите диапазон
C6:C9
, в
Строку формул
введите формулу
=МОДА.НСК(A2:A11)
и нажмите
CTRL+SHIFT+ENTER
. Диапазон
C
6:
C
9
охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству
мод
. Если ячеек больше чем м
о
д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если
мода
только одна, то все выделенные ячейки будут заполнены значением этой
моды
.
Теперь вспомним, что мы определили
моду
для выборки, т.е. для конечного множества значений, взятых из
генеральной совокупности
. Для
непрерывных случайных величин
вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция
МОДА()
вернет ошибку.
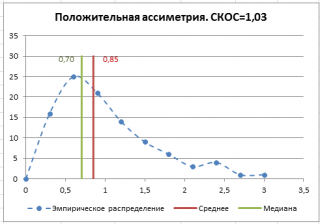
Даже в нашем массиве с
модой
, которая была определена с помощью
надстройки Пакет анализа
, творится, что-то не то. Действительно,
модой
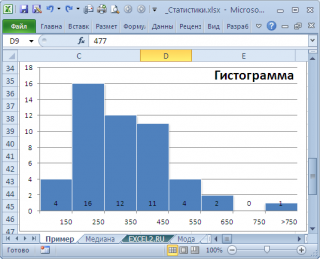
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на
гистограмму распределения
, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).
Проблема в том, что мы определили
моду
как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,
моду
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для
логнормального распределения
мода
(наиболее вероятное значение непрерывной случайной величины х), вычисляется как
exp
(
m
—
s
2
)
, где m и s параметры этого распределения.
Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для
моды
распределения, из которого взята
выборка
(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).
Для того, чтобы получить оценку
моды
распределения, из
генеральной совокупности
которого взята
выборка
, можно, например, построить
гистограмму
. Оценкой для
моды
может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.
Вывод
: Значение
моды
для
выборки
, рассчитанное с помощью функции
МОДА()
, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер
выборки
существенно превышает количество этих значений.
Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),
модой
является число 15 (17 значений из 51, т.е. 33%). В этом случае функция
МОДА()
дает хорошую оценку «наиболее вероятного» значения зарплаты.
Примечание
: Строго говоря, в примере с зарплатой мы имеем дело скорее с
генеральной совокупностью
, чем с
выборкой
. Т.к. других зарплат в компании просто нет.
О вычислении
моды
для распределения
непрерывной случайной величины
читайте статью
Мода в MS EXCEL
.
Мода и среднее значение
Не смотря на то, что
мода
– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из
Генеральной совокупности
максимальна), не следует ожидать, что
среднее значение
обязательно будет близко к
моде
.
Примечание
:
Мода
и
среднее
симметричных распределений совпадает (имеется ввиду симметричность
плотности распределения
).
Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.
Модой
является 6, а среднее значение – 3,6666.
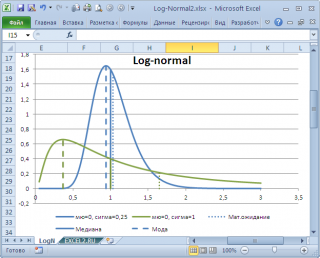
Другой пример. Для
Логнормального распределения
LnN(0;1)
мода
равна =EXP(m-s2)= EXP(0-1*1)=0,368, а
среднее значение
1,649.
Дисперсия выборки
Дисперсия выборки
или
выборочная дисперсия (
sample
variance
) характеризует разброс значений в массиве, отклонение от
среднего
.
Из формулы №1 видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии выборки
используется функция
ДИСП()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию
ДИСП.В()
.
Дисперсию
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)
–
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
.
Чем больше величина
дисперсии
, тем больше разброс значений в массиве относительно
среднего
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность
дисперсии
будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии – стандартное отклонение
.
Подробнее о
дисперсии
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартное отклонение выборки
Стандартное отклонение выборки
(Standard Deviation), как и
дисперсия
, — это мера того, насколько широко разбросаны значения в выборке
относительно их среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х
выборок
: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у
выборок
существенно отличается.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
СТАНДОТКЛОН()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
СТАНДОТКЛОН.В()
.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Подробнее о
стандартном отклонении
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартная ошибка
В
Пакете анализа
под термином
стандартная ошибка
имеется ввиду
Стандартная ошибка среднего
(Standard Error of the Mean, SEM).
Стандартная ошибка среднего
— это оценка
стандартного отклонения
распределения
выборочного среднего
.
Примечание
: Чтобы разобраться с понятием
Стандартная ошибка среднего
необходимо прочитать о
выборочном распределении
(см. статью
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
) и статью про
Центральную предельную теорему
.
Стандартное отклонение распределения выборочного среднего
вычисляется по формуле σ/√n, где n — объём
выборки, σ — стандартное отклонение исходного
распределения, из которого взята
выборка
. Т.к. обычно
стандартное отклонение
исходного распределения неизвестно, то в расчетах вместо
σ
используют ее оценку
s
—
стандартное отклонение выборки
. А соответствующая величина s/√n имеет специальное название —
Стандартная ошибка среднего.
Именно эта величина вычисляется в
Пакете анализа.
В MS EXCEL
стандартную ошибку среднего
можно также вычислить по формуле
=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))
Асимметричность
Асимметричность
или
коэффициент асимметрии
(skewness) характеризует степень несимметричности распределения (
плотности распределения
) относительно его
среднего
.
Положительное значение
коэффициента асимметрии
указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.
Коэффициент асимметрии
идеально симметричного распределения или выборки равно 0.
Примечание
:
Асимметрия выборки
может отличаться расчетного значения асимметрии теоретического распределения. Например,
Нормальное распределение
является симметричным распределением (
плотность его распределения
симметрична относительно
среднего
) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в
выборке
из соответствующей
генеральной совокупности
не обязательно должны располагаться совершенно симметрично относительно
среднего
. Поэтому,
асимметрия выборки
, являющейся оценкой
асимметрии распределения
, может отличаться от 0.
Функция
СКОС()
, английский вариант SKEW(), возвращает коэффициент
асимметрии выборки
, являющейся оценкой
асимметрии
соответствующего распределения, и определяется следующим образом:
где n – размер
выборки
, s –
стандартное отклонение выборки
.
В
файле примера на листе СКОС
приведен расчет коэффициента
асимметрии
на примере случайной выборки из
распределения Вейбулла
, которое имеет значительную положительную
асимметрию
при параметрах распределения W(1,5; 1).
Эксцесс выборки
Эксцесс
показывает относительный вес «хвостов» распределения относительно его центральной части.
Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-
σ
.
Примечание
: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение
Эксцесса
как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение
Эксцесса
ничего не говорит о форме пика распределения.
Согласно определения,
Эксцесс
равен четвертому
стандартизированному моменту:
Для
нормального распределения
четвертый момент равен 3*σ
4
, следовательно,
Эксцесс
равен 3. Многие компьютерные программы используют для расчетов не сам
Эксцесс
, а так называемый Kurtosis excess, который меньше на 3. Т.е. для
нормального распределения
Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.
Примечание
: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как
Эксцесс
(от англ. excess — «излишек»). Например, функция MS EXCEL
ЭКСЦЕСС()
на самом деле вычисляет Kurtosis excess.
Функция
ЭКСЦЕСС()
, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку
эксцесса распределения
случайной величины и определяется следующим образом:
Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из
нормального распределения
формула вернет близкое к 0 значение.
Если задано менее четырех точек данных, то функция
ЭКСЦЕСС()
возвращает значение ошибки #ДЕЛ/0!
Вернемся к
распределениям случайной величины
.
Эксцесс
(Kurtosis excess) для
нормального распределения
всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений
Эксцесс
зависит от параметров распределения: см., например,
распределение Вейбулла
или
распределение Пуассона
, для котрого
Эксцесс
= 1/λ.
Уровень надежности
Уровень
надежности
— означает вероятность того, что
доверительный интервал
содержит истинное значение оцениваемого параметра распределения.
Вместо термина
Уровень
надежности
часто используется термин
Уровень доверия
. Про
Уровень надежности
(Confidence Level for Mean) читайте статью
Уровень значимости и уровень надежности в MS EXCEL
.
Задав значение
Уровня
надежности
в окне
надстройки Пакет анализа
, MS EXCEL вычислит половину ширины
доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Тот же результат можно получить по формуле (см.
файл примера
):
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)
s —
стандартное отклонение выборки
, n – объем
выборки
.
Подробнее см. статью про
построение доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Если вам нужно разработать сложный статистический или инженерный анализ, вы можете сэкономить время и этапы с помощью этого средства. Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.
Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.
Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопкуАнализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа».
-
Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
-
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
-
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
-
Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
-
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
-
Примечание: Чтобы включить Visual Basic для приложений (VBA) для надстройки «Надстройка анализа», вы можете загрузить надстройку VBA так же, как и надстройку «Надстройка анализа». В поле Доступные надстройки выберите «Надстройка анализа — VBA».
Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.
Однофакторный дисперсионный анализ
Этот инструмент выполняет простой анализ дисперсии данных для двух или более выборок. Анализ дает проверку гипотезы о том, что каждая выборка взята из одного и того же распределения вероятности на основе альтернативной гипотезы о том, что для всех выборок распределение вероятности не одно и то же. Если есть только два примера, можно использовать функцию T.ТЕСТ. В более чем двух примерах нет удобного обобщения T.ВМЕСТОэтого можно использовать модель Anova для одного фактора.
Двухфакторный дисперсионный анализ с повторениями
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий {удобрение, температура}, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:
-
Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.
-
Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.
Извлечены ли шесть выборок, представляющих все пары значений {удобрение, температура}, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар {удобрение, температура} превышает влияние отдельно удобрения и отдельно температуры.
Двухфакторный дисперсионный анализ без повторений
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров {удобрение, температура} из предыдущего примера).
Функции CORREL и PEARSON вычисляют коэффициент корреляции между двумя переменными измерения, если для каждой переменной наблюдаемы измерения по каждому из N-объектов. (Любые отсутствующие наблюдения по любой теме вызывают игнорирование в анализе.) Средство анализа корреляции особенно удобно использовать, если для каждого субъекта N имеется более двух переменных измерения. Она содержит выходную таблицу — матрицу корреляции, которая показывает значение CORREL (или PEARSON),примененного к каждой из возможных пар переменных измерения.
Коэффициент корреляции, как и ковариана, — это мера степени, в которой две единицы измерения «различаются». В отличие от ковариации коэффициент корреляции масштабирован таким образом, что его значение не зависит от единиц измерения, выраженных в двух переменных измерения. (Например, если двумя переменными измерения являются вес и высота, то значение коэффициента корреляции не изменяется, если вес преобразуется из фунта в фунты.) Значение любого коэффициента корреляции должно быть включительно от -1 до +1 включительно.
Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).
Средства корреляции и коварианс могут использоваться в одном и том же параметре, если у вас есть N различных переменных измерения, наблюдаемые для набора людей. Каждый из инструментов корреляции и ковариции дает выходную таблицу — матрицу, которая показывает коэффициент корреляции или коварианс между каждой парой переменных измерения соответственно. Разница заключается в том, что коэффициенты корреляции масштабироваться в зависимости от -1 и +1 включительно. Соответствующие ковариансы не масштабироваться. Коэффициент корреляции и коварианс — это показатели степени, в которой две переменные «различаются».
Инструмент Ковариана вычисляет значение функции КОВАРИАНА. P для каждой пары переменных измерения. (Прямое использование КОВАРИАНА. P вместо ковариана является разумной альтернативой, если есть только две переменные измерения, то есть N=2.) Запись в диагонали выходной таблицы средства Коварица в строке i, столбце i — коварианс i-й переменной измерения. Это только дисперсия по численности населения для этой переменной, вычисляемая функцией ДИСПЕРС.P.
Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).
Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
Инструмент анализа «Экспоненциальное сглаживание» применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.
Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.
Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.
Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.
С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f < 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики меньшего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение меньше 1 для выбранного уровня значимости «Альфа». Если f > 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики большего f при равных дисперсиях генеральной совокупности и F критическом одностороннем дает критическое значение больше 1 для «Альфа».
Инструмент «Анализ Фурье» применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.

Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.
Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.
Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.
Инструмент анализа «Скользящее среднее» применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:
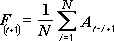
где
-
N — число предшествующих периодов, входящих в скользящее среднее;
-
A
j — фактическое значение в момент времени j; -
F
j — прогнозируемое значение в момент времени j.
Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.
Средство анализа Ранг и процентиль создает таблицу, которая содержит порядковую и процентную ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. В этом средстве используются функции РАНГ. EQ и PERCENTRANK. INC. Если вы хотите учитывать связанные значения, используйте РАНГ. Функция EQ, которая обрабатывает связанные значения как имеющие одинаковый ранг или использует РАНГ.Функция AVG, которая возвращает средний ранг связанных значений.
Инструмент анализа «Регрессия» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
В средстве регрессии используется функция LINEST.
Инструмент анализа «Выборка» создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.
Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.
Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как «t-статистика» в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t < 0 «P(T <= t) одностороннее» дает вероятность того, что наблюдаемое значение t-статистики будет более отрицательным, чем t. При t >=0 «P(T <= t) одностороннее» делает возможным наблюдение значения t-статистики, которое будет более положительным, чем t. «t критическое одностороннее» дает пороговое значение, так что вероятность наблюдения значения t-статистики большего или равного «t критическое одностороннее» равно «Альфа».
«P(T <= t) двустороннее» дает вероятность наблюдения значения t-статистики, по абсолютному значению большего, чем t. «P критическое двустороннее» выдает пороговое значение, так что значение вероятности наблюдения значения t- статистики, по абсолютному значению большего, чем «P критическое двустороннее», равно «Альфа».
Парный двухвыборочный t-тест для средних
Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.
Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:
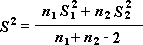
Двухвыборочный t-тест с одинаковыми дисперсиями
Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных поступили из распределения с одинаковыми дисперсиями. Его называют гомике t-тестом. Этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения.
Двухвыборочный t-тест с различными дисперсиями
Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных были полученными из распределения с неравными дисперсиями. Его называют гетероскестическими t-тестами. Как и в предыдущем примере с равными дисперсиями, этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения. Этот тест можно использовать, если в двух примерах есть отдельные объекты. Используйте тест Парный, описанный в примере, если существует один набор тем и две выборки представляют измерения по каждой теме до и после обработки.
Для определения тестовой величины t используется следующая формула.
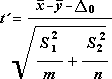
Следующая формула используется для вычисления степеней свободы (df). Так как результат вычисления обычно не является integer, значение df округлится до ближайшего другого, чтобы получить критическое значение из таблицы t. Функция Excel T .Test использует вычисляемую величину df без округлений, так как можно вычислить значение для T.ТЕСТ с неинтегрированной df. Из-за этих разных подходов к определению степеней свободы результаты T.Тест и этот t-тест будут отличаться в случае неравных дисперсий.
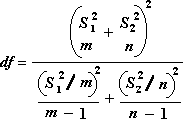
Z-тест. Средство анализа «Две выборки для середины» выполняет два примера z-теста для средств со известными дисперсиями. Этот инструмент используется для проверки гипотезы NULL о том, что между двумя значениями численности населения нет различий между односторонними или двухбокльными альтернативными гипотезами. Если дисперсии не известны, функция Z .Вместо этого следует использовать тест.
При использовании этого инструмента следует внимательно просматривать результат. «P(Z <= z) одностороннее» на самом деле есть P(Z >= ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. «P(Z <= z) двустороннее» на самом деле есть P(Z >= ABS(z) или Z <= -ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. Двусторонний результат является односторонним результатом, умноженным на 2. Инструмент «z-тест» можно также применять для гипотезы об определенном ненулевом значении разницы между двумя средними генеральных совокупностей. Например, этот тест можно использовать для определения разницы выступлений на соревнованиях двух автомобилей разных марок.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Создание гистограммы в Excel 2016
Создание диаграммы Парето в Excel 2016
Загрузка средства анализа в Excel
Инженерные функции (справка)
Общие сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Поиск ошибок в формулах
Сочетания клавиш и горячие клавиши в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Нужна дополнительная помощь?
Если вам по работе или учёбе приходится погружаться в океан цифр и искать в них подтверждение своих гипотез, вам определённо пригодятся эти техники работы в Microsoft Excel. Как их применять — показываем с помощью гифок.
Юлия Перминова
Тренер Учебного центра Softline с 2008 года.
1. Сводные таблицы
Базовый инструмент для работы с огромным количеством неструктурированных данных, из которых можно быстро сделать выводы и не возиться с фильтрацией и сортировкой вручную. Сводные таблицы можно создать с помощью нескольких действий и быстро настроить в зависимости от того, как именно вы хотите отобразить результаты.
Полезное дополнение. Вы также можете создавать сводные диаграммы на основе сводных таблиц, которые будут автоматически обновляться при их изменении. Это полезно, если вам, например, нужно регулярно создавать отчёты по одним и тем же параметрам.
Как работать
Исходные данные могут быть любыми: данные по продажам, отгрузкам, доставкам и так далее.
- Откройте файл с таблицей, данные которой надо проанализировать.
- Выделите диапазон данных для анализа.
- Перейдите на вкладку «Вставка» → «Таблица» → «Сводная таблица» (для macOS на вкладке «Данные» в группе «Анализ»).
- Должно появиться диалоговое окно «Создание сводной таблицы».
- Настройте отображение данных, которые есть у вас в таблице.
Перед нами таблица с неструктурированными данными. Мы можем их систематизировать и настроить отображение тех данных, которые есть у нас в таблице. «Сумму заказов» отправляем в «Значения», а «Продавцов», «Дату продажи» — в «Строки». По данным разных продавцов за разные годы тут же посчитались суммы. При необходимости можно развернуть каждый год, квартал или месяц — получим более детальную информацию за конкретный период.
Набор опций будет зависеть от количества столбцов. Например, у нас пять столбцов. Их нужно просто правильно расположить и выбрать, что мы хотим показать. Скажем, сумму.
Можно её детализировать, например, по странам. Переносим «Страны».
Можно посмотреть результаты по продавцам. Меняем «Страну» на «Продавцов». По продавцам результаты будут такие.
2. 3D-карты
Этот способ визуализации данных с географической привязкой позволяет анализировать данные, находить закономерности, имеющие региональное происхождение.
Полезное дополнение. Координаты нигде прописывать не нужно — достаточно лишь корректно указать географическое название в таблице.
Как работать
- Откройте файл с таблицей, данные которой нужно визуализировать. Например, с информацией по разным городам и странам.
- Подготовьте данные для отображения на карте: «Главная» → «Форматировать как таблицу».
- Выделите диапазон данных для анализа.
- На вкладке «Вставка» есть кнопка 3D-карта.
Точки на карте — это наши города. Но просто города нам не очень интересны — интересно увидеть информацию, привязанную к этим городам. Например, суммы, которые можно отобразить через высоту столбика. При наведении курсора на столбик показывается сумма.
Также достаточно информативной является круговая диаграмма по годам. Размер круга задаётся суммой.
3. Лист прогнозов
Зачастую в бизнес-процессах наблюдаются сезонные закономерности, которые необходимо учитывать при планировании. Лист прогноза — наиболее точный инструмент для прогнозирования в Excel, чем все функции, которые были до этого и есть сейчас. Его можно использовать для планирования деятельности коммерческих, финансовых, маркетинговых и других служб.
Полезное дополнение. Для расчёта прогноза потребуются данные за более ранние периоды. Точность прогнозирования зависит от количества данных по периодам — лучше не меньше, чем за год. Вам требуются одинаковые интервалы между точками данных (например, месяц или равное количество дней).
Как работать
- Откройте таблицу с данными за период и соответствующими ему показателями, например, от года.
- Выделите два ряда данных.
- На вкладке «Данные» в группе нажмите кнопку «Лист прогноза».
- В окне «Создание листа прогноза» выберите график или гистограмму для визуального представления прогноза.
- Выберите дату окончания прогноза.
В примере ниже у нас есть данные за 2011, 2012 и 2013 годы. Важно указывать не числа, а именно временные периоды (то есть не 5 марта 2013 года, а март 2013-го).
Для прогноза на 2014 год вам потребуются два ряда данных: даты и соответствующие им значения показателей. Выделяем оба ряда данных.
На вкладке «Данные» в группе «Прогноз» нажимаем на «Лист прогноза». В появившемся окне «Создание листа прогноза» выбираем формат представления прогноза — график или гистограмму. В поле «Завершение прогноза» выбираем дату окончания, а затем нажимаем кнопку «Создать». Оранжевая линия — это и есть прогноз.
4. Быстрый анализ
Эта функциональность, пожалуй, первый шаг к тому, что можно назвать бизнес-анализом. Приятно, что эта функциональность реализована наиболее дружественным по отношению к пользователю способом: желаемый результат достигается буквально в несколько кликов. Ничего не нужно считать, не надо записывать никаких формул. Достаточно выделить нужный диапазон и выбрать, какой результат вы хотите получить.
Полезное дополнение. Мгновенно можно создавать различные типы диаграмм или спарклайны (микрографики прямо в ячейке).
Как работать
- Откройте таблицу с данными для анализа.
- Выделите нужный для анализа диапазон.
- При выделении диапазона внизу всегда появляется кнопка «Быстрый анализ». Она сразу предлагает совершить с данными несколько возможных действий. Например, найти итоги. Мы можем узнать суммы, они проставляются внизу.
В быстром анализе также есть несколько вариантов форматирования. Посмотреть, какие значения больше, а какие меньше, можно в самих ячейках гистограммы.
Также можно проставить в ячейках разноцветные значки: зелёные — наибольшие значения, красные — наименьшие.
Надеемся, что эти приёмы помогут ускорить работу с анализом данных в Microsoft Excel и быстрее покорить вершины этого сложного, но такого полезного с точки зрения работы с цифрами приложения.
Читайте также:
- 10 быстрых трюков с Excel →
- 20 секретов Excel, которые помогут упростить работу →
- 10 шаблонов Excel, которые будут полезны в повседневной жизни →
В статье рассказывается:
- Суть и методы анализа данных
- Активация и запуск функций анализа данных в Excel
- 4 техники анализа данных в Excel
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Анализ данных в Excel не ограничен простыми функциями деления, умножения, суммирования и сведения значений из разных ячеек. Данный программный продукт от Microsoft – это мощный комплекс, позволяющий работать со сводными таблицами, подтягивать информацию из внешних отчетов, интерпретировать ее, выстраивая наглядные диаграммы и графики.
Чтобы начать работать с данным блоком функций, их нужно активировать в Excel. Никаких сложностей на подготовительном этапе возникнуть не должно – всё делается довольно просто. С аналитикой чуть посложнее, но справиться можно. О том, как выполняется анализ данных в Excel, вы узнаете из нашего материала.
Суть и методы анализа данных
Американский учёный-статистик Джон Тьюки в 1961 году сформулировал определение анализа данных. Под ним он подразумевал как сами процедуры анализа, так и методы интерпретации результатов этих процедур, а также способы планирования сбора данных в целях упрощения и уточнения анализа и результаты математической статистики, используемые для анализа.
В связи с этим анализ данных представляет собой деятельность по извлечению крупных неструктурированных данных из самых разных источников, а также их реорганизацию в информацию, которая может быть использована в целях:
- ответа на вопросы;
- проверки гипотез;
- принятия решений;
- опровержения теорий.
Есть несколько способов анализа данных, которые распространяются на многочисленные области, от маркетинга до науки. Можно выделить несколько базовых вариантов:
Сбор данных
Data Mining – это анализ больших информационных объемов в целях получения прежде неоткрытых, полезных моделей данных, нестандартных данных, а также выявления зависимостей. Стоит упомянуть, что в качестве главной задачи выступает извлечение не самих данных, а шаблонов и знаний из больших информационных объемов.
Анализ данных производится на основе различных методов информатики, в том числе систем искусственного интеллекта, машинного обучения, статистики и баз данных.
Шаблоны, которые извлекаются посредством интеллектуального анализа данных, могут определяться как сводка входных данных. Они в свою очередь могут быть применены в последующем анализе либо для извлечения более детализированных результатов прогнозирования системой поддержки принятия решений.
Скачать файл
Бизнес-аналитика
Суть бизнес-аналитики заключается в сборе и трансформации больших объемов неструктурированных бизнес-данных, что, в свою очередь, необходимо для упрощения определения, разработки и формирования новых стратегических бизнес-возможностей.
Иными словами, главная задача бизнес-аналитики — сделать процесс интерпретации больших объемов данных более простым, чтобы выявлять новые возможности. Все это способствует разработке результативной стратегии, базирующейся на концепциях, которые могут сформировать конкурентное преимущество на рынке и стабилизировать компанию в долгосрочной перспективе.
Статистический анализ
Статистику можно определить как изучение произведенного сбора, анализа, интерпретации, представления и организации данных.
В процессе анализа данных применяют 2 базовых метода статистики:
- Описательная статистика
Данная разновидность статистики предполагает суммирование данных от всей совокупности или выборки посредством числовых дескрипторов. В качестве этих дескрипторов выступают:
- среднее значение, стандартное отклонение для непрерывных данных;
- частота, процент для категориальных данных.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Уже скачали 20406
- Статистическая статистика
В этом случае применяются образцы в выборочных данных в целях формирования выводов о представленной совокупности или учета случайности. Выделяют следующие разновидности выводов:
- ответы на вопросы да / нет о данных (проверка гипотез);
- оценка числовых характеристик данных (оценка);
- описание связей в данных (корреляция);
- моделирование отношений в данных (к примеру, регрессионный анализ).
Прогнозная аналитика
Predictive Analytics применяет статистические модели в целях анализа нынешних и исторических данных. Это необходимо для создания прогнозов относительно дальнейших или иных неизвестных событий. В предпринимательстве эта разновидность анализа применяется в целях определения рисков и возможностей, способствующих принятию правильных решений.
Текстовая аналитика
Text Analytics (Text Mining, Text Data Mining) — это процесс извлечения из текста информации высокого уровня качества. Можно выделить несколько составляющих анализа текста:
- процесс структурирования исходного текста;
- извлечение шаблонов из структурированных данных с применением метода изучения статистических шаблонов и др.;
- оценка и интерпретация полученной информации.
С помощью Microsoft Excel можно использовать целый ряд средств и методов для анализа и интерпретации данных. При этом данные могут быть получены из разных источников. Имеется несколько вариантов трансформации и форматирования данных. Анализ можно осуществлять посредством различных команд, функций и инструментов программы.

Читайте также
В частности, к ним можно отнести условное форматирование, диапазоны, таблицы, текстовые функции, функции даты, функции времени, финансовые функции, промежуточные итоги, быстрый анализ, аудит формул, инструмент Inquire, анализ «что, если», решатели, модель данных, PowerPivot, PowerView, PowerMap и многое другое.
Активация и запуск функций анализа данных в Excel
Excel представляет собой не только редактор таблиц, а еще и отличный инструмент, позволяющий производить всевозможные математические и статистические расчеты. Программа отличается широким функционалом, позволяющим осуществлять вышеописанные процедуры. Однако некоторые из этих функций неактивны по умолчанию. Анализ данных в Excel является как раз такой скрытой возможностью.
Если вы хотите активировать данную функцию, то следует зайти в настройки Microsoft Excel. Причем для разных версий утилиты (2010, 2013 и 2016 года) последовательность действий будет примерно одна и та же. Несущественные расхождения в алгоритме действий имеются лишь для версии 2007 года.
Только до 17.04
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:



Чтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:
Уже скачали 7503
Итак, необходимо выполнить следующие действия:
- Нажать на вкладку «Файл» (либо на логотип Microsoft Office в верхнем левом углу экрана для версии 2007 года).
- Нажать на один из пунктов в левой части открывшегося окна — «Параметры».
- Перейти в подраздел «Надстройки» (второй с конца в списке в левой части окна).
- Здесь нужно обратить внимание на нижнюю часть окна. Следует найти параметр «Управление». Обратите внимание на значение в выпадающей форме — вы должны увидеть «Надстройки Excel». Далее следует нажать на вкладку «Перейти…» справа от этого пункта. Если же в выпадающей форме вы увидите какое-то другое значение, нужно будет сначала вписать то, которое мы указали выше.
- В открывшемся окне доступных надстроек найдите пункт «Пакет анализа» и поставьте возле него галочку. Затем нажмите на кнопку «OK» (в правой верхней части).
Выполнив все перечисленные действия, вы активируете нужную функцию и получите соответствующие инструменты. Найти их можно в ленте Excel.
Чтобы открыть тот или иной инструмент анализа данных, нужно произвести следующие действия:
- Зайти в раздел «Данные».
- Найти блок инструментов «Анализ», который расположен на правом краю ленты и нажать на «Анализ данных».
- Выбрать конкретный инструмент из появившегося списка. Наиболее полезными считаются:
- корреляция;
- гистограмма;
- регрессия;
- выборка;
- экспоненциальное сглаживание;
- генератор случайных чисел;
- описательная статистика;
- анализ Фурье;
- различные виды дисперсионного анализа и т.д.
Выбрав нужный инструмент, нажмите на кнопку «OK». Каждый из доступных инструментов работает на основе своего собственного алгоритма.
Таким образом, блок функций «Пакет анализа» включается с помощью всего лишь нескольких простых шагов. При этом если не знать четкую последовательность действий, пользователю сложно найти нужную кнопку.
4 техники анализа данных в Excel
Сводные таблицы
Это важнейший инструмент для обработки больших информационных объемов. Сводные таблицы позволяют быстро делать выводы на основе неструктурированных данных без ручной сортировки и фильтрации. Создание и настройка таблиц осуществляется довольно быстро. Однако от того, какой именно вариант отображения результата вам нужен, будет зависеть алгоритм настройки.
Кроме того, у пользователя есть возможность создавать сводные диаграммы на базе сводных таблиц. При изменении таблиц диаграммы будут обновляться в автоматическом режиме. Скажем, если вы на регулярной основе формируете отчёты по одним и тем же параметрам, то такая функция вам очень пригодится.
Можно вписать какие угодно исходные параметры, например, данные по продажам, отгрузкам, доставкам и т.д.
Для использования сводной таблицы вам необходимо:
- Открыть файл с таблицей, данные которой необходимо проанализировать.
- Выделить диапазон данных для анализа.
- Перейти на вкладку «Вставка», а затем «Таблица». Далее нужно нажать на «Сводная таблица» (для macOS на вкладке «Данные» в группе «Анализ»). Если вы сделали все правильно, то появится диалоговое окно «Создание сводной таблицы».
- Настроить отображение данных, которые есть у вас в таблице.
3D-карты
Благодаря этому методу визуализации данных с географической привязкой вы сможете проанализировать данные и выявить закономерности, имеющие региональное происхождение.
Однако вам не нужно указывать координаты, ведь если правильно ввести географическое название в таблице, программа сделает все сама.
Для применения инструмента вас нужно:
- Открыть файл с таблицей, информацию из которой необходимо визуализировать. К примеру, с данными по разным городам и странам.
- Подготовить данные для отображения на карте. Для этого нужно нажать на «Главная» и перейти на вкладку «Форматировать как таблицу».
- Обозначить диапазон данных для анализа.
- На вкладке «Вставка» вы увидите кнопку «3D-карта».
На карте имеются точки, обозначающие города. Однако нам нужно увидеть информацию, которая привязана к этим городам, например, суммы, отображающиеся через высоту столбика. Если навести курсор на столбик, то вы увидите сумму.
Вместе с тем, довольно полезной считается круговая диаграмма по годам, в которой размер круга зависит от суммы.
Лист прогнозов
В бизнес-процессах имеют место сезонные закономерности. Их, конечно же, нужно учитывать во время планирования. Для этой цели лучше всего подходит «Лист прогноза», который является самым точным инструментом для осуществления прогнозов в рамках Excel. Его применяют для планирования деятельности коммерческих, финансовых, маркетинговых и прочих служб.
Чтобы сделать прогноз, необходимо иметь информацию за предыдущие периоды. Чем больше информации будет внесено, тем более точный прогноз вы получите (минимальный объём информации для хорошего прогноза — 1 год). Учтите, что нужны одинаковые интервалы между точками данных (скажем, месяц или равное количество дней).
Чтобы использовать данную функцию, вам необходимо:
- Открыть таблицу с данными за период и соответствующими ему параметрами, к примеру, от года.
- Выделить 2 ряда данных.
- На вкладке «Данные» нажать на кнопку «Лист прогноза».
- В окне «Создание листа прогноза» выбрать подходящий график или гистограмму для визуализации прогноза.
- Определить дату окончания прогноза.

Читайте также
Быстрый анализ
Данный инструмент позволяет выполнять процедуры анализа в кратчайшие сроки. Чтобы получить необходимые данные, достаточно нажать всего на несколько кнопок. Вам не нужно будет производить никаких расчетов или указывать какие-либо формулы. Единственное что от вас потребуется — выделить нужный диапазон и выбрать тип результата, который вам необходим на выходе.
Благодаря данному инструменту вы можете формировать всевозможные разновидности диаграмм или спарклайны (микрографики прямо в ячейке) буквально в два счета.
Чтобы работать с инструментом, вам нужно:
- Открыть таблицу с данными для анализа.
- Выделить необходимый для анализа диапазон.
- Во время выделения диапазона в нижней части высвечивается кнопка «Быстрый анализ».
Нажав на эту кнопку, вы сможете произвести целый ряд различных действий, которые предложит программа. К примеру, найти итоги. Кроме того, можно узнать суммы, которые проставляются внизу.
Быстрый анализ предполагает несколько способов форматирования. Чтобы узнать, какие значения больше, а какие меньше, нужно перейти в ячейки гистограммы.
Плюс ко всему, вы можете выставить в ячейках значки разных цветов: зелёные — самые большие значения, красные — самые меньшие.
Все эти инструменты позволят вам ускорить процесс анализа данных и сделать его более простым. Используя различные функции, вы сможете с легкостью освоить Microsoft Excel и извлечь из него максимальную пользу.