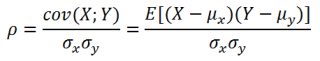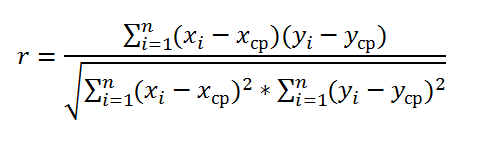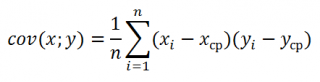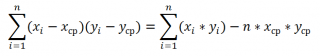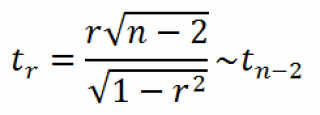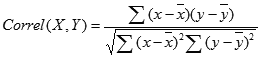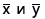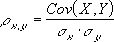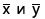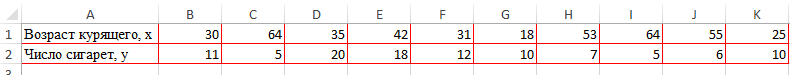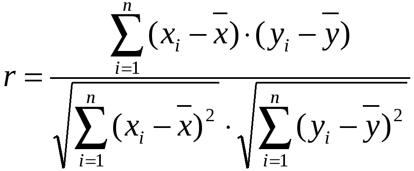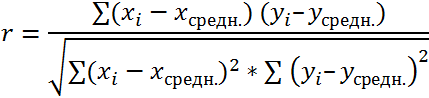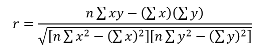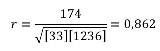Выборочные коэффициенты корреляции excel - Word и Excel

Содержание

Суть корреляционного анализа
Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью пакета анализа
Вопросы и ответы

Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.

Суть корреляционного анализа

Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.

Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.

Расчет коэффициента корреляции

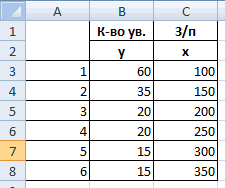
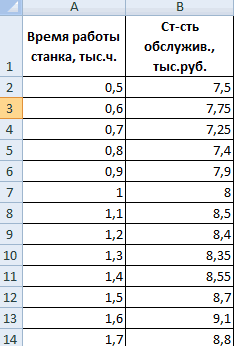
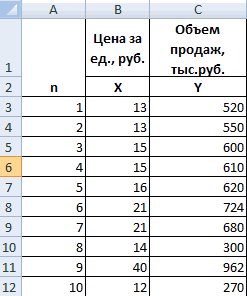
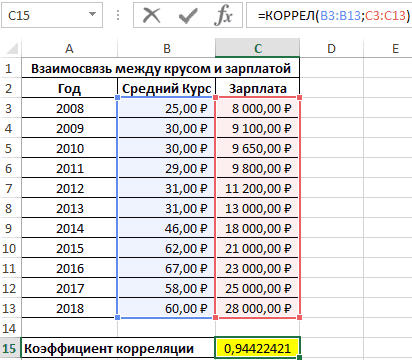
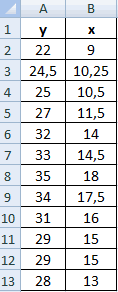
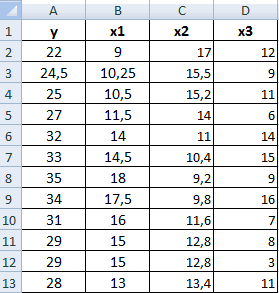
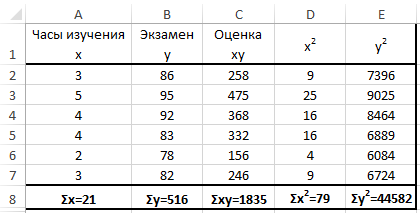
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

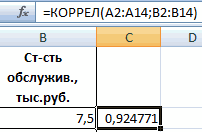
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

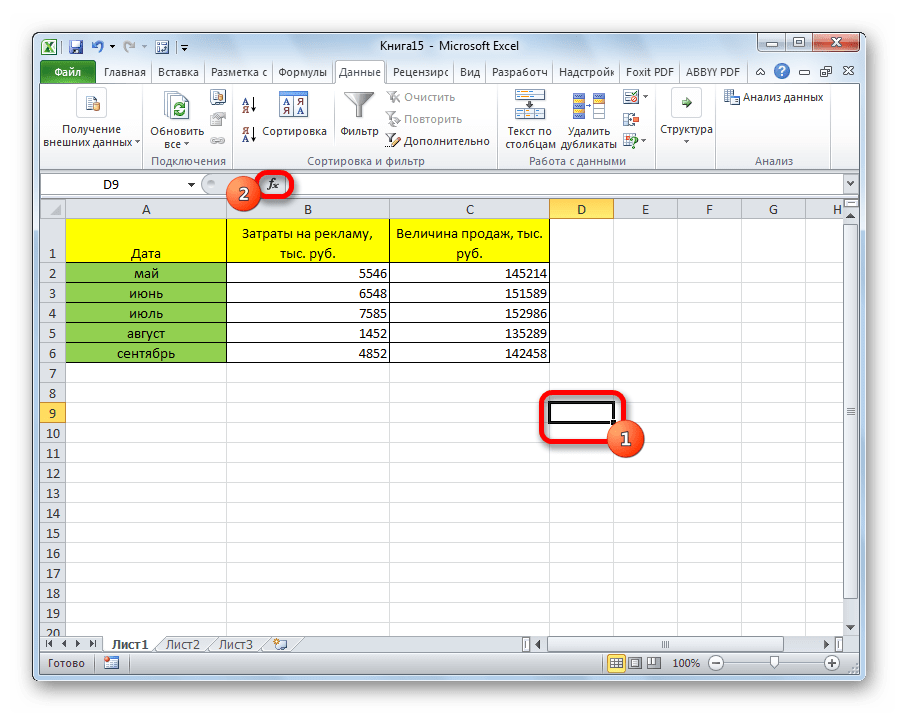
Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.

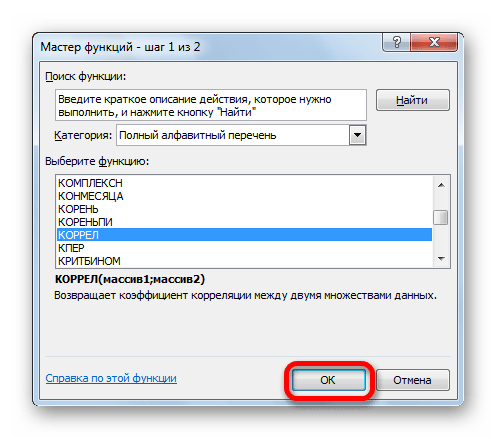
В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».

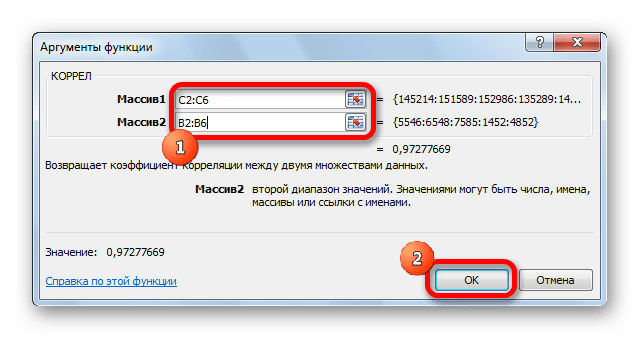
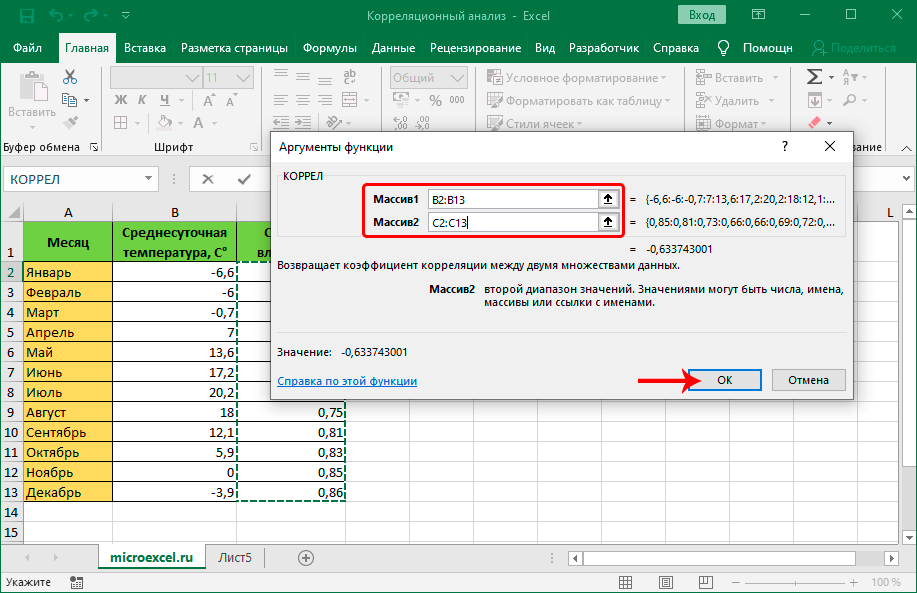
Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

Жмем на кнопку «OK».

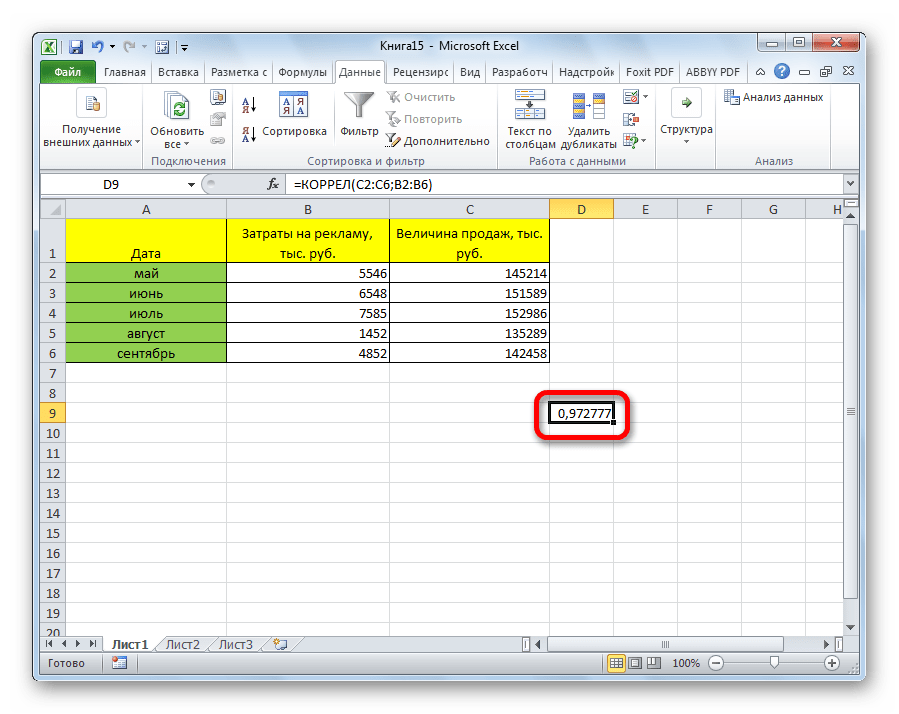
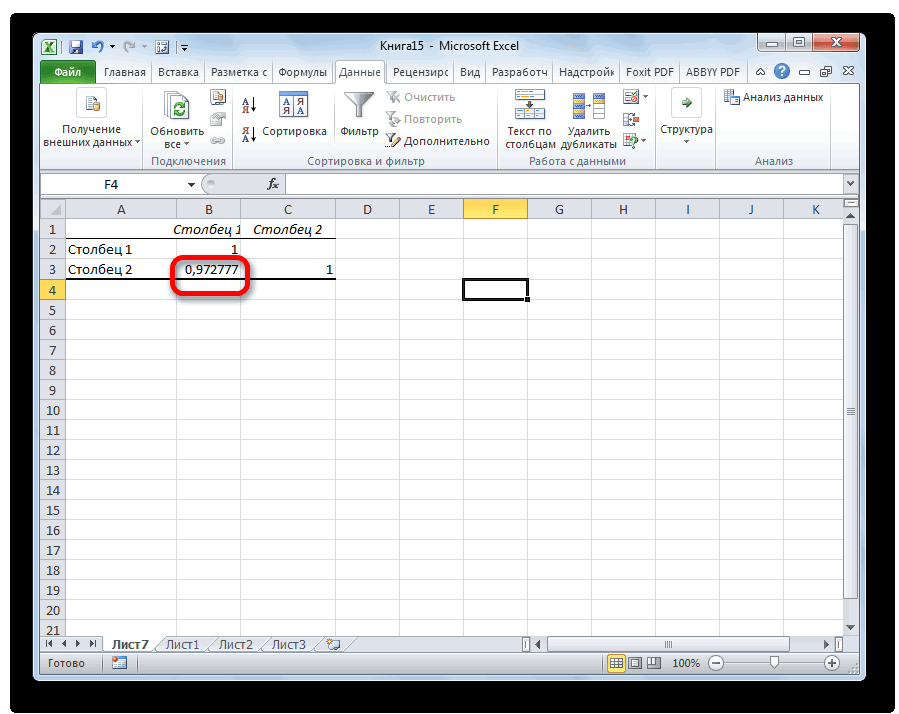
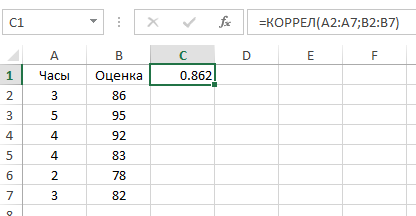
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

Переходим во вкладку «Файл».

В открывшемся окне перемещаемся в раздел «Параметры».

Далее переходим в пункт «Надстройки».

В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

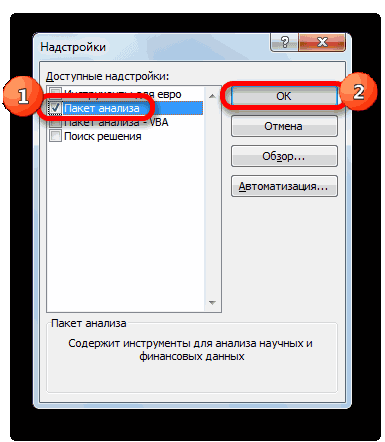
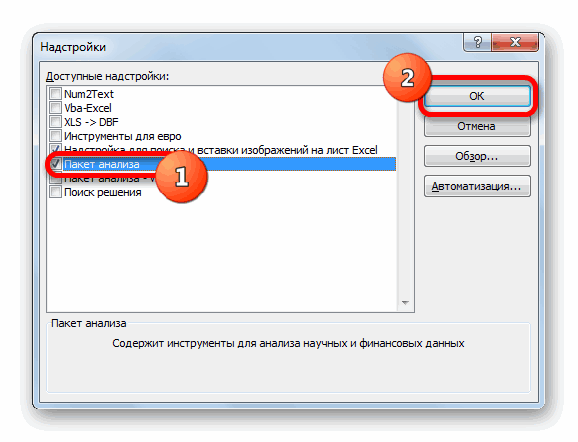
В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

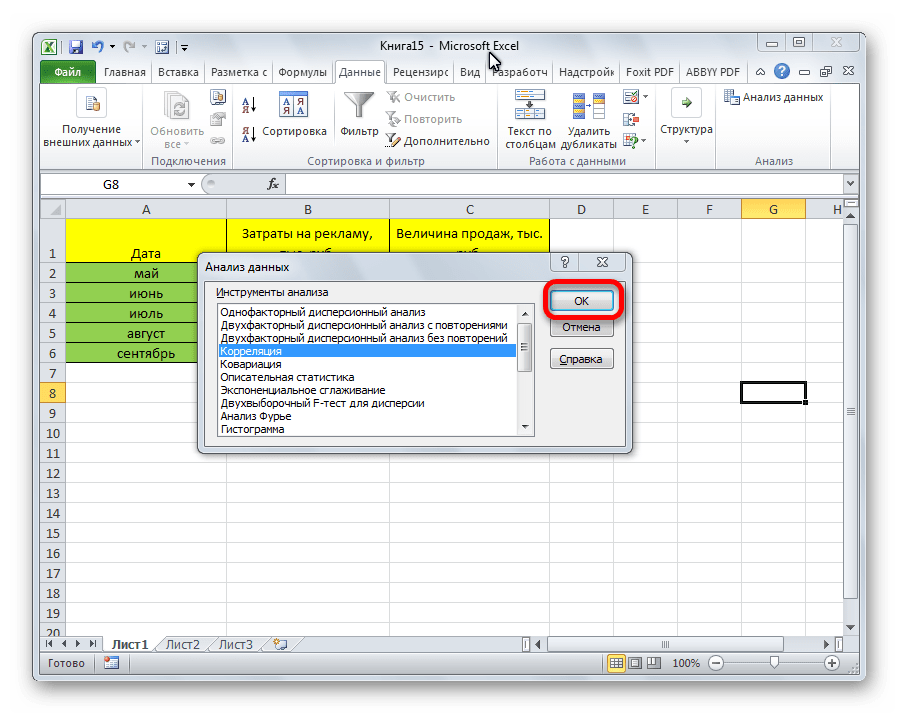
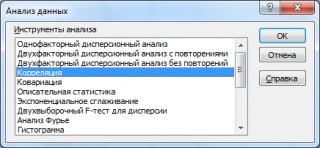
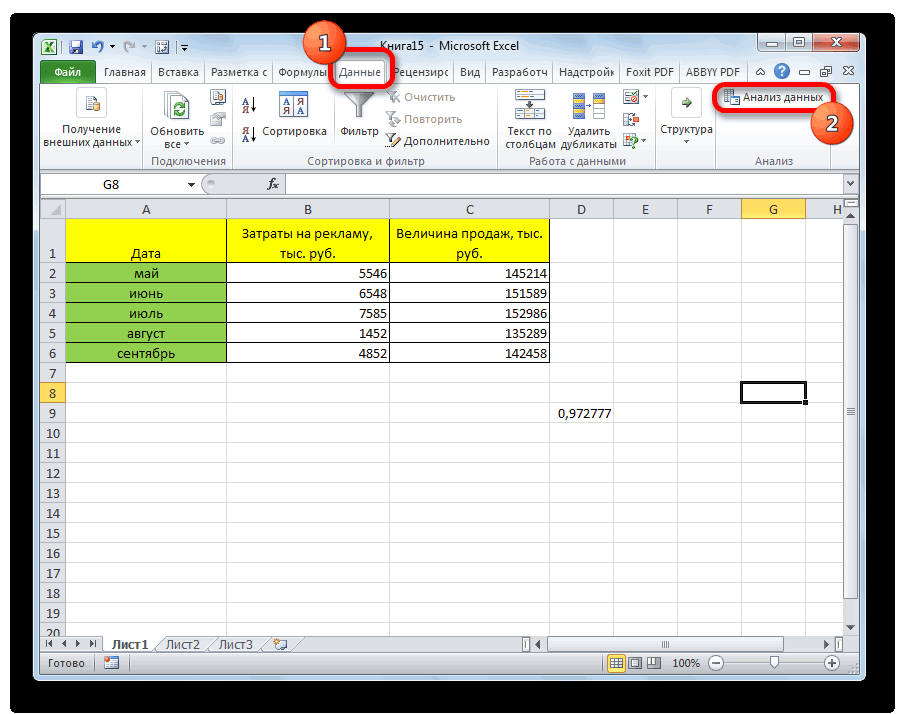
После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.

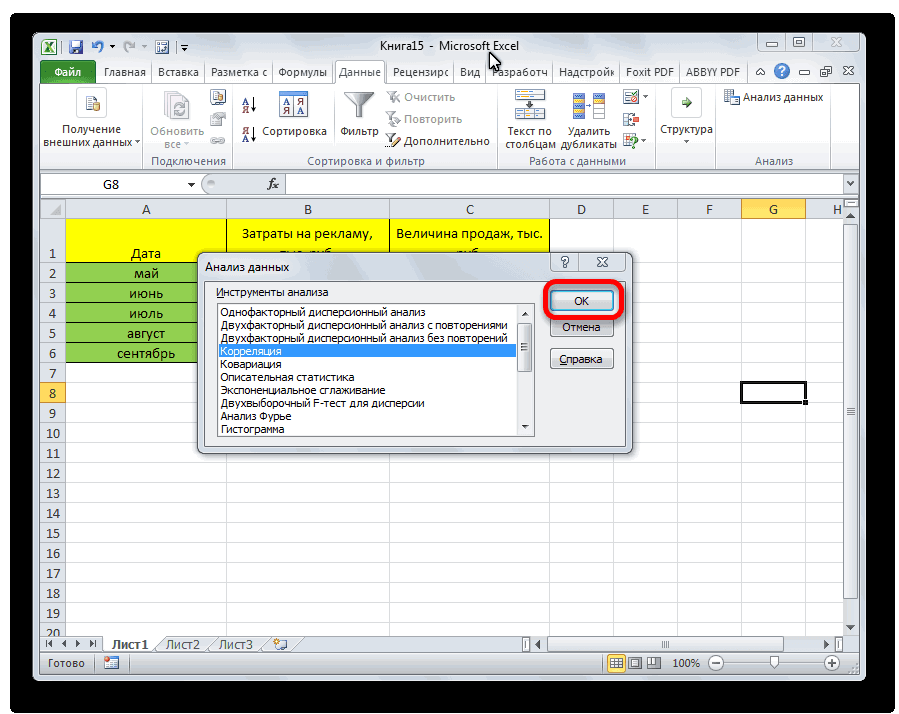
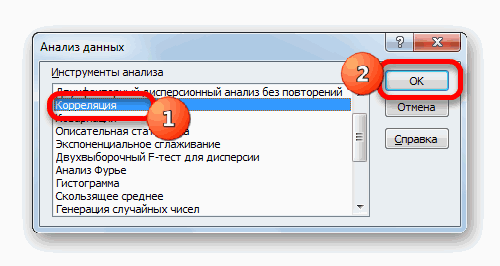
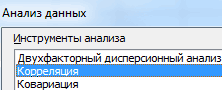
Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».

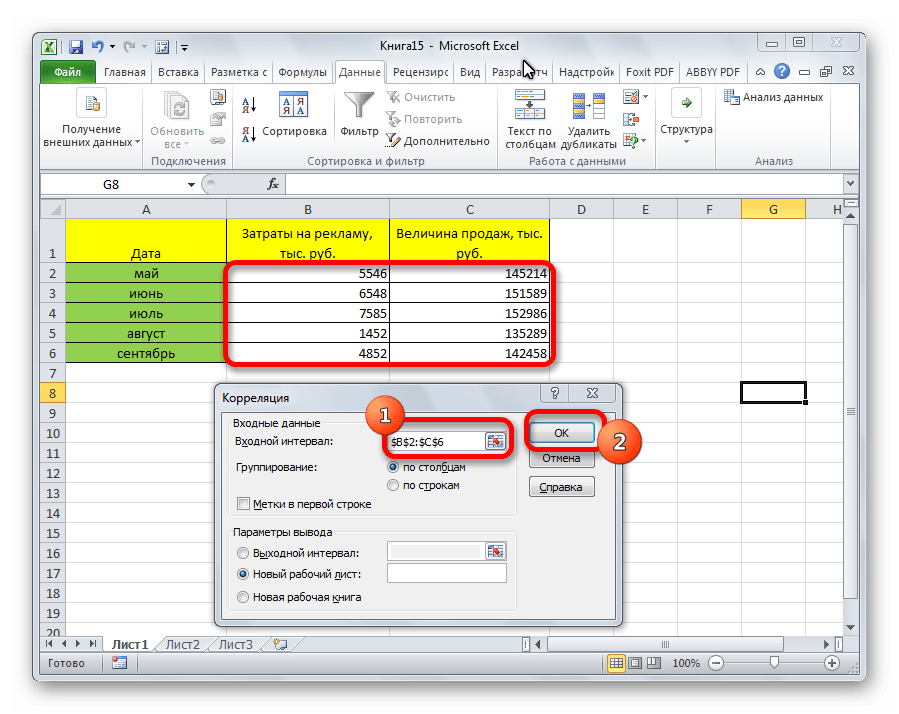
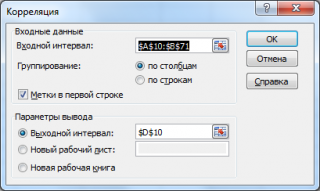
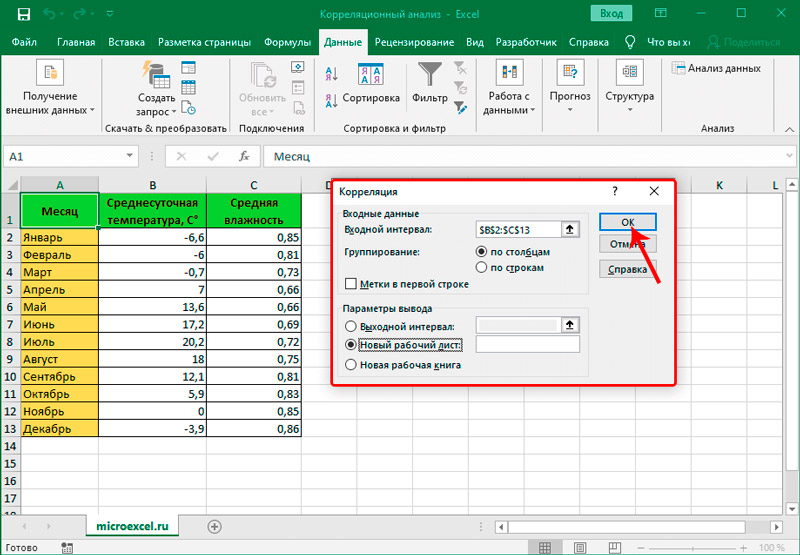
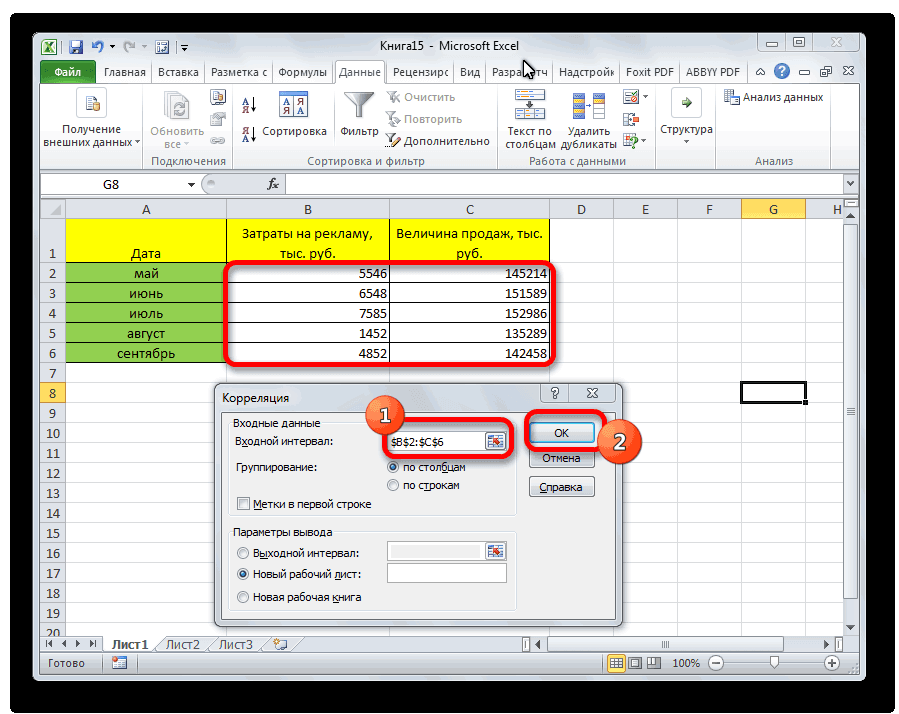
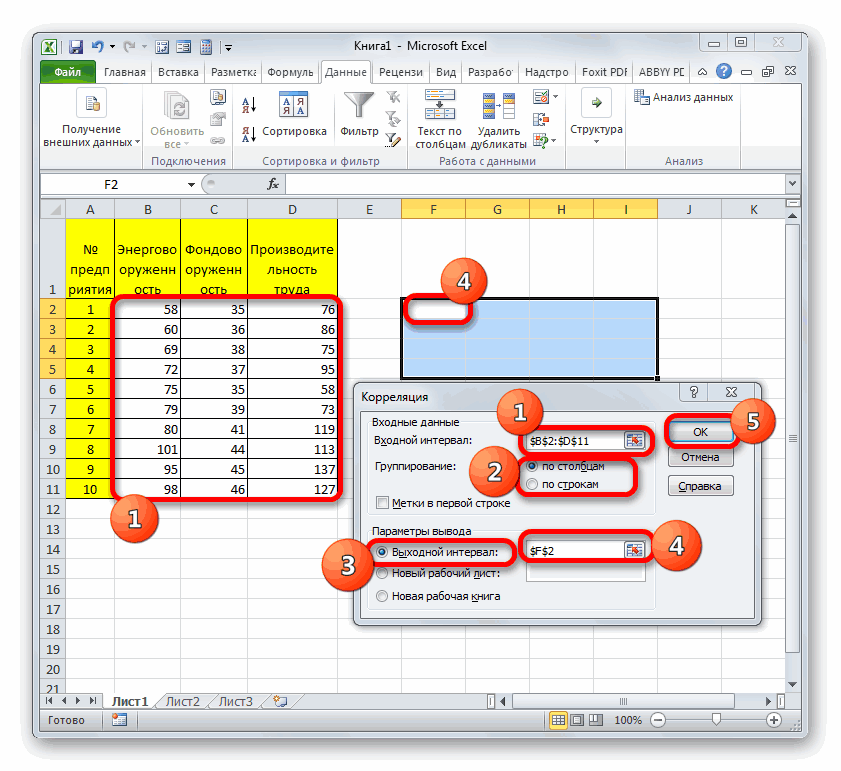
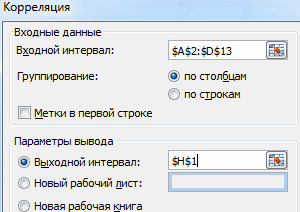
Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

Когда все настройки установлены, жмем на кнопку «OK».

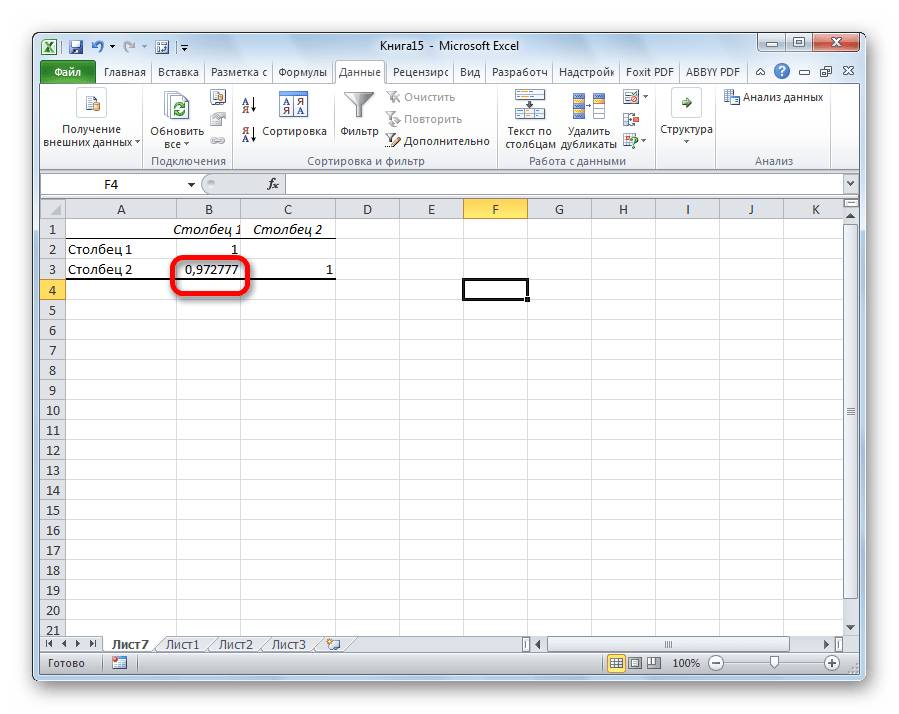
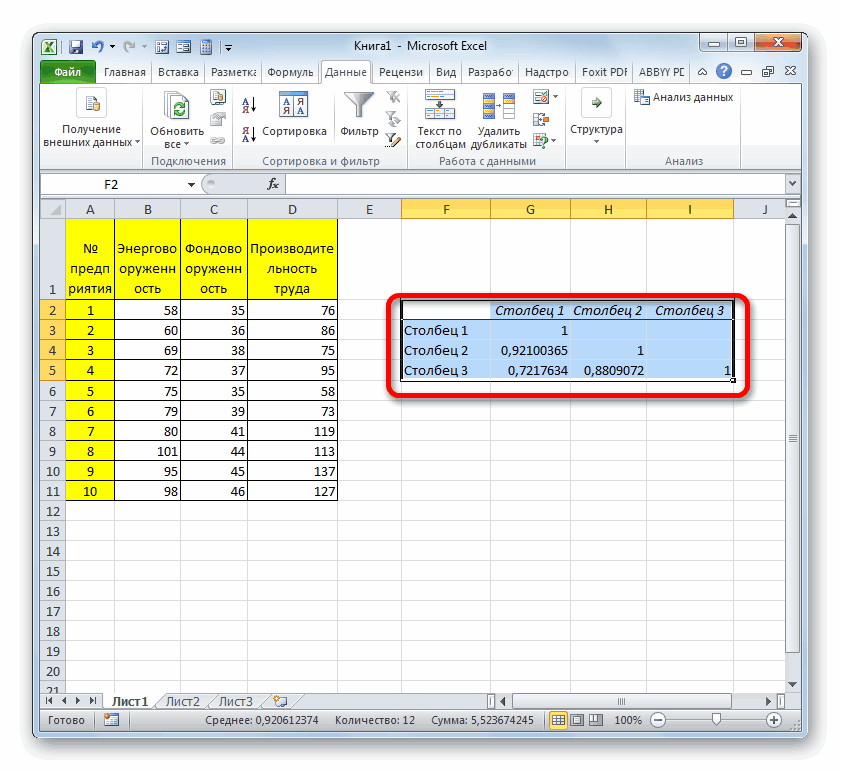
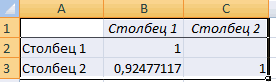
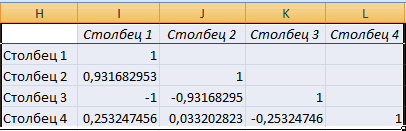
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Вычислим коэффициент корреляции и ковариацию для разных типов взаимосвязей случайных величин.

Коэффициент корреляции

(

критерий корреляции

Пирсона, англ. Pearson Product Moment correlation coefficient)

определяет степень

линейной

взаимосвязи между случайными величинами.

где Е[…] – оператор

математического ожидания

, μ и σ –

среднее

случайной величины и ее

стандартное отклонение

Как следует из определения, для вычисления

коэффициента корреляции

требуется знать распределение случайных величин Х и Y. Если распределения неизвестны, то для оценки

коэффициента корреляции

используется

выборочный коэффициент корреляции

r

(

еще он обозначается как

R
_xy
или

r
_xy
)

:

Как видно из формулы для расчета

корреляции

, знаменатель (произведение стандартных отклонений с точностью до безразмерного множителя) просто нормирует числитель таким образом, что

корреляция

оказывается безразмерным числом от -1 до 1.

Корреляция

и

ковариация

предоставляют одну и туже информацию, но

корреляцией

удобнее пользоваться, т.к. она является безразмерной величиной.

Рассчитать

коэффициент корреляции

и

ковариацию выборки

в MS EXCEL не представляет труда, так как для этого имеются специальные функции

КОРРЕЛ()

и

КОВАР()

. Гораздо сложнее разобраться, как интерпретировать полученные значения, большая часть статьи посвящена именно этому.

Теоретическое отступление

Напомним, что

корреляционной связью

называют статистическую связь, состоящую в том, что различным значениям одной переменной соответствуют различные

средние

значения другой (с изменением значения Х

среднее значение

Y изменяется закономерным образом). Предполагается, что

обе

переменные Х и Y являются

случайными

величинами и имеют некий случайный разброс относительно их

среднего значения

.

Примечание

. Если случайную природу имеет только одна переменная, например, Y, а значения другой являются детерминированными (задаваемыми исследователем), то можно говорить только о регрессии.

Таким образом, например, при исследовании зависимости среднегодовой температуры нельзя говорить о

корреляции

температуры и года наблюдения и, соответственно, применять показатели

корреляции

с соответствующей их интерпретацией.

Корреляционная связь

между переменными может возникнуть несколькими путями:

Наличие причинной зависимости между переменными. Например, количество инвестиций в научные исследования (переменная Х) и количество полученных патентов (Y). Первая переменная выступает как

независимая переменная (фактор)

, вторая —

зависимая переменная (результат)

. Необходимо помнить, что зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот.
Наличие сопряженности (общей причины). Например, с ростом организации растет фонд оплаты труда (ФОТ) и затраты на аренду помещений. Очевидно, что неправильно предполагать, что аренда помещений зависит от ФОТ. Обе этих переменных во многих случаях линейно зависят от количества персонала.
Взаимовлияние переменных (при изменении одной, вторая переменная изменяется, и наоборот). При таком подходе допустимы две постановки задачи; любая переменная может выступать как в роли независимой переменной и в роли зависимой.

Таким образом,

показатель корреляции

показывает, насколько сильна

линейная взаимосвязь

между двумя факторами (если она есть), а регрессия позволяет прогнозировать один фактор на основе другого.

Корреляция

, как и любой другой статистический показатель, при правильном применении может быть полезной, но она также имеет и ограничения по использованию. Если

диаграмма рассеяния

показывает четко выраженную линейную зависимость или полное отсутствие взаимосвязи, то

корреляция

замечательно это отразит. Но, если данные показывают нелинейную взаимосвязь (например, квадратичную), наличие отдельных групп значений или выбросов, то вычисленное значение

коэффициента корреляции

может ввести в заблуждение (см.

файл примера

).

Корреляция

близкая к 1 или -1 (т.е. близкая по модулю к 1) показывает сильную линейную взаимосвязь переменных, значение близкое к 0 показывает отсутствие взаимосвязи. Положительная

корреляция

означает, что с ростом одного показателя другой в среднем увеличивается, а при отрицательной – уменьшается.

Для вычисления коэффициента корреляции требуется, чтобы сопоставляемые переменные удовлетворяли следующим условиям:

количество переменных должно быть равно двум;
переменные должны быть количественными (например, частота, вес, цена). Вычисленное среднее значение этих переменных имеет понятный смысл: средняя цена или средний вес пациента. В отличие от количественных, качественные (номинальные) переменные принимают значения лишь из конечного набора категорий (например, пол или группа крови). Этим значениям условно сопоставлены числовые значения (например, женский пол – 1, а мужской – 2). Понятно, что в этом случае вычисление

среднего значения

, которое требуется для нахождения

корреляции

, некорректно, а значит некорректно и вычисление самой

корреляции

;
переменные должны быть случайными величинами и иметь

нормальное распределение

.

Двумерные данные могут иметь различную структуру. Для работы с некоторыми из них требуются определенные подходы:

Для данных с нелинейной связью

корреляцию

нужно использовать с осторожностью. Для некоторых задач бывает полезно преобразовать одну или обе переменных так, чтобы получить линейную взаимосвязь (для этого требуется сделать предположение о виде нелинейной связи, чтобы предложить нужный тип преобразования).
С помощью

диаграммы рассеяния

у некоторых данных можно наблюдать неравную вариацию (разброс). Проблема неодинаковой вариации состоит в том, что места с высокой вариацией не только предоставляют наименее точную информацию, но и оказывают наибольшее влияние при расчете статистических показателей. Эту проблему также часто решают с помощью преобразования данных, например, с помощью логарифмирования.
У некоторых данных можно наблюдать разделение на группы (clustering), что может свидетельствовать о необходимости разделения совокупности на части.
Выброс (резко отклоняющееся значение) может исказить вычисленное значение коэффициента корреляции. Выброс может быть причиной случайности, ошибки при сборе данных или могут действительно отражать некую особенность взаимосвязи. Так как выброс сильно отклоняется от среднего значения, то он вносит большой вклад при расчете показателя. Часто расчет статистических показателей производят с и без учета выбросов.

Использование MS EXCEL для расчета корреляции

В качестве примера возьмем 2 переменные

Х

и

Y

и, соответственно,

выборку

состоящую из нескольких пар значений (Х
_i
; Y
_i
). Для наглядности построим

диаграмму рассеяния

Примечание

: Подробнее о построении диаграмм см. статью

Основы построения диаграмм

. В

файле примера

для построения

диаграммы рассеяния

использована

диаграмма График

, т.к. мы здесь отступили от требования случайности переменной Х (это упрощает генерацию различных типов взаимосвязей: построение трендов и заданный разброс). В случае реальных данных необходимо использовать диаграмму типа Точечная (см. ниже).

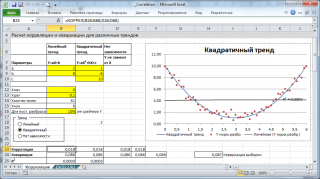
Расчеты

корреляции

проведем для различных случаев взаимосвязи между переменными:

линейной, квадратичной

и при

отсутствии связи

.

Примечание

: В

файле примера

можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.

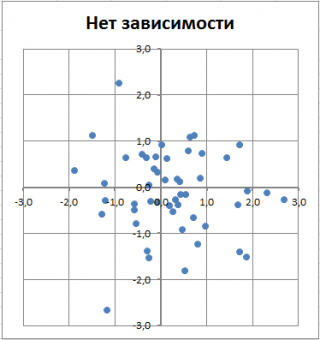
В

файле примера

для построения

диаграммы рассеяния

в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.

Примечание

: Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми.

Как было сказано выше, для расчета

коэффициента корреляции

в MS EXCEL существует функций

КОРРЕЛ()

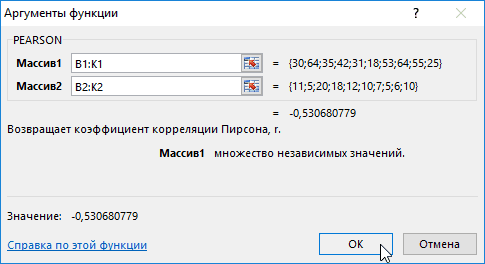
. Также можно воспользоваться аналогичной функцией

PEARSON()

, которая возвращает тот же результат.

Для того, чтобы удостовериться, что вычисления

корреляции

производятся функцией

КОРРЕЛ()

по вышеуказанным формулам, в

файле примера

приведено вычисление

корреляции

с помощью более подробных формул:

=

КОВАРИАЦИЯ.Г(B28:B88;D28:D88)/СТАНДОТКЛОН.Г(B28:B88)/СТАНДОТКЛОН.Г(D28:D88)

=

КОВАРИАЦИЯ.В(B28:B88;D28:D88)/СТАНДОТКЛОН.В(B28:B88)/СТАНДОТКЛОН.В(D28:D88)

Примечание

: Квадрат

коэффициента корреляции

r равен

коэффициенту детерминации

R2, который вычисляется при построении линии регрессии с помощью функции

КВПИРСОН()

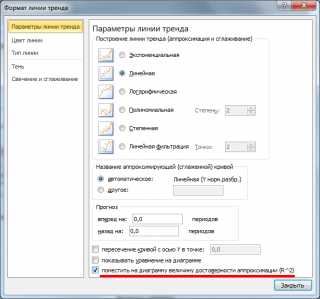
. Значение R2 также можно вывести на

диаграмме рассеяния

, построив линейный тренд с помощью стандартного функционала MS EXCEL (выделите диаграмму, выберите вкладку

Макет

, затем в группе

Анализ

нажмите кнопку

Линия тренда

и выберите

Линейное приближение

). Подробнее о построении линии тренда см., например, в

статье о методе наименьших квадратов

Использование MS EXCEL для расчета ковариации

Ковариация

близка по смыслу с

дисперсией

(также является мерой разброса) с тем отличием, что она определена для 2-х переменных, а

дисперсия

— для одной. Поэтому, cov(x;x)=VAR(x).

Для вычисления ковариации в MS EXCEL (начиная с версии 2010 года) используются функции

КОВАРИАЦИЯ.Г()

и

КОВАРИАЦИЯ.В()

. В первом случае формула для вычисления аналогична вышеуказанной (окончание

.Г

обозначает

Генеральная совокупность

), во втором – вместо множителя 1/n используется 1/(n-1), т.е. окончание

.В

обозначает

Выборка

.

Примечание

: Функция

КОВАР()

, которая присутствует в MS EXCEL более ранних версий, аналогична функции

КОВАРИАЦИЯ.Г()

.

Примечание

: Функции

КОРРЕЛ()

и

КОВАР()

в английской версии представлены как CORREL и COVAR. Функции

КОВАРИАЦИЯ.Г()

и

КОВАРИАЦИЯ.В()

как COVARIANCE.P и COVARIANCE.S.

Дополнительные формулы для расчета

ковариации

:

=

СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88-СРЗНАЧ(D28:D88)))/СЧЁТ(D28:D88)

=

СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88))/СЧЁТ(D28:D88)

=

СУММПРОИЗВ(B28:B88;D28:D88)/СЧЁТ(D28:D88)-СРЗНАЧ(B28:B88)*СРЗНАЧ(D28:D88)

Эти формулы используют свойство

ковариации

:

Если переменные

x

и

y

независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:

VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)

А

дисперсия

их разности равна

VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)

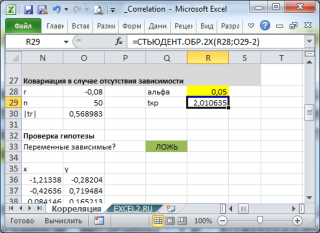
Оценка статистической значимости коэффициента корреляции

При проверке значимости

коэффициента корреляции

нулевая гипотеза состоит в том, что

коэффициент корреляции

равен нулю, альтернативная — не равен нулю (про

проверку гипотез

см. статью

Проверка гипотез

Для того чтобы проверить гипотезу, мы должны знать распределение случайной величины, т.е.

коэффициента корреляции

r. Обычно, проверку гипотезы осуществляют не для r, а для случайной величины t
_r
:

которая имеет

распределение Стьюдента

с n-2 степенями свободы.

Если вычисленное значение случайной величины |t
_r
| больше, чем критическое значение t
_α,n-2
(α- заданный

уровень значимости

), то нулевую гипотезу отклоняют (взаимосвязь величин является статистически значимой).

Надстройка Пакет анализа

надстройке Пакет анализа

для вычисления ковариации и корреляции

имеются одноименные инструменты

анализа

.

После вызова инструмента появляется диалоговое окно, которое содержит следующие поля:

Входной интервал

: нужно ввести ссылку на диапазон с исходными данными для 2-х переменных
Группирование

: как правило, исходные данные вводятся в 2 столбца
Метки в первой строке

: если установлена галочка, то

Входной интервал

должен содержать заголовки столбцов. Рекомендуется устанавливать галочку, чтобы результат работы Надстройки содержал информативные столбцы
Выходной интервал

: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.

Надстройка возвращает вычисленные значения корреляции и ковариации (для ковариации также вычисляются дисперсии обоих случайных величин).

Источник

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

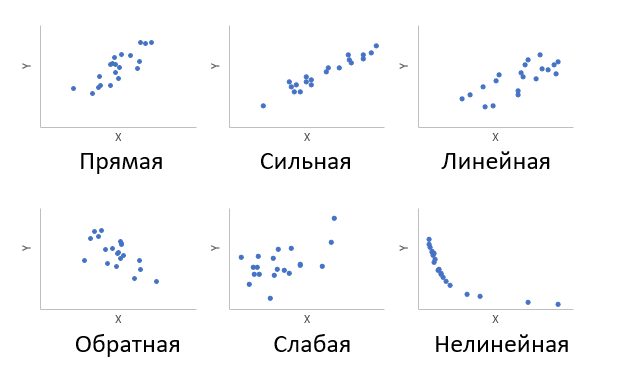
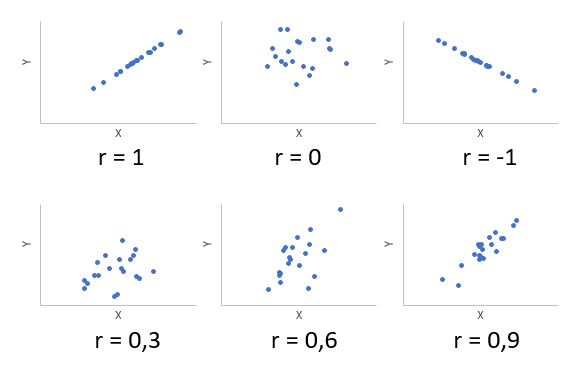
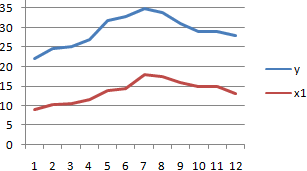
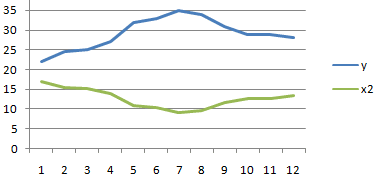
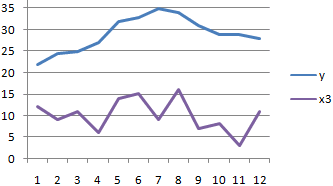
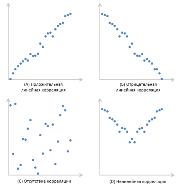
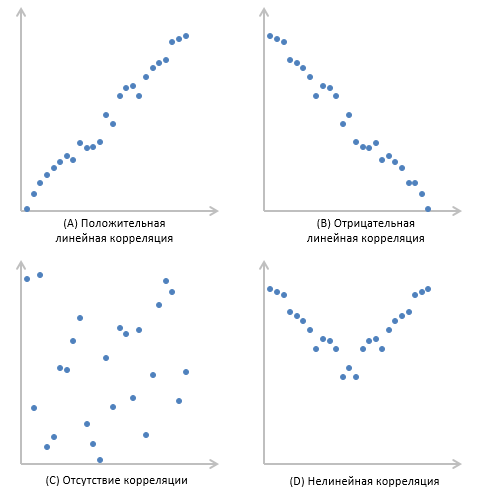
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

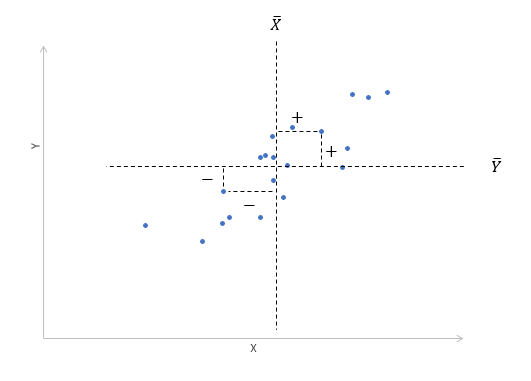
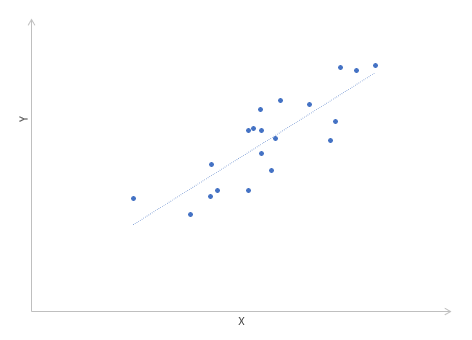
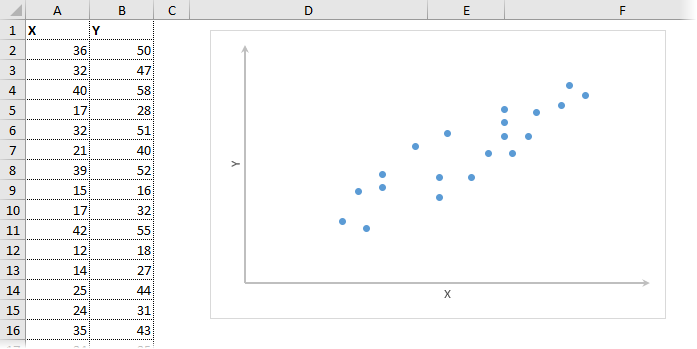
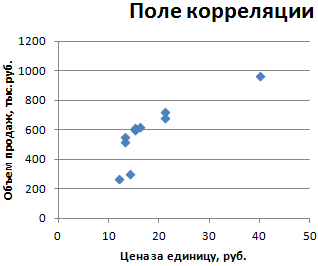
Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.

Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.

Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.

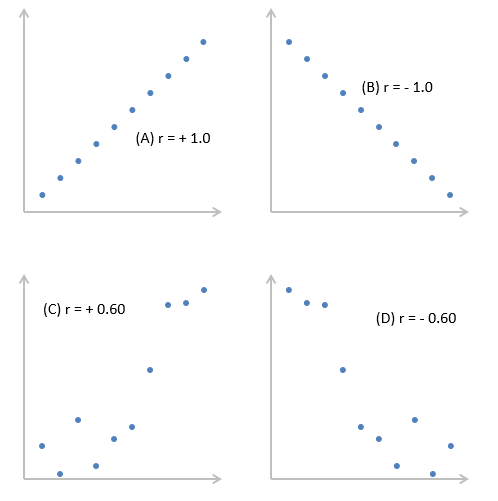
Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.

Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.

Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r², который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.

Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r² = 0,01 или 1%, при r = 0,5 r² = 0,25 или 25%.

Выборочный коэффициент корреляции

Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.

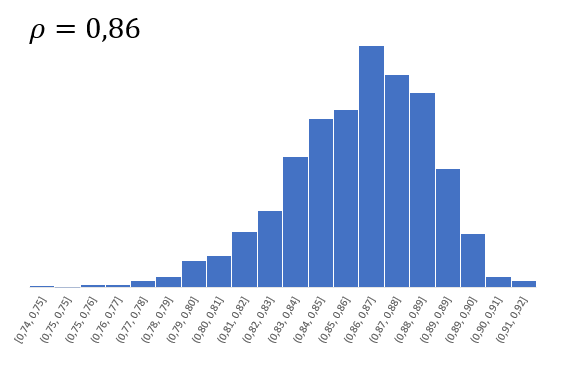
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.

Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.

В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:

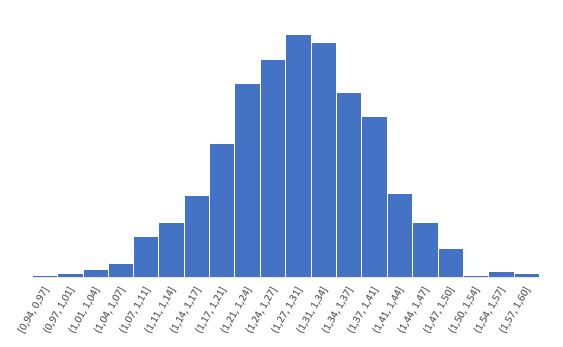
Распределение z для тех же r имеет следующий вид.

Намного ближе к нормальному. Стандартная ошибка z равна:

Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.

c_γ – квантиль стандартного нормального распределения;
N^-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.

Нижняя граница z:

Верхняя граница z:

Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:

Верхняя граница r:

Это была теоретическая часть. Переходим к практике расчетов.

Как посчитать коэффициент корреляции в Excel

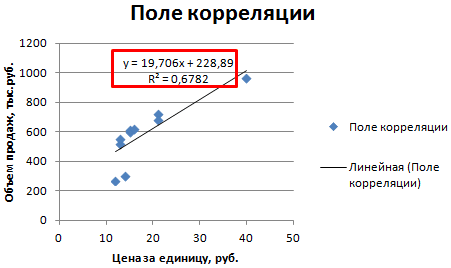
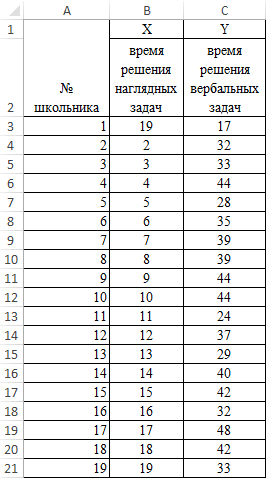
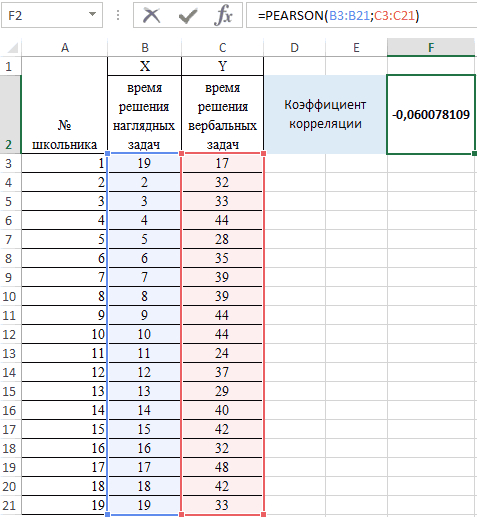
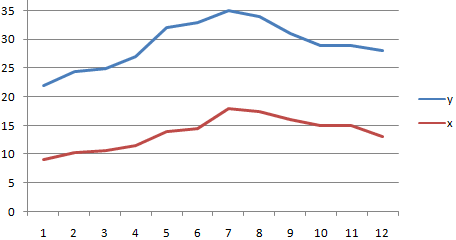
Корреляционный анализ в Excel лучше начинать с визуализации.

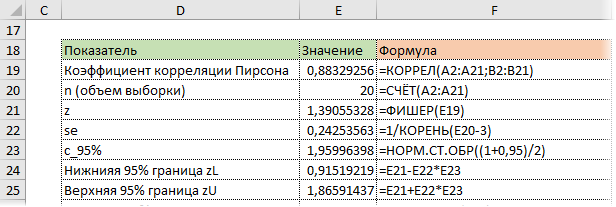
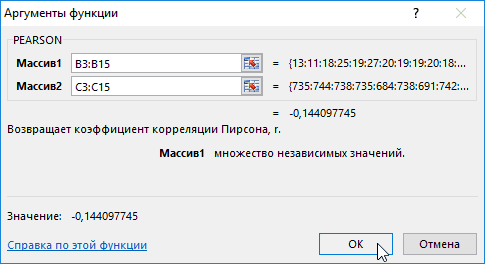
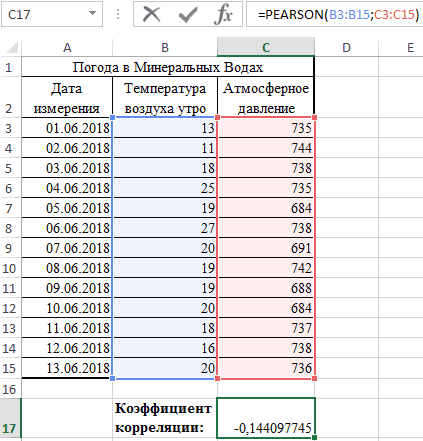
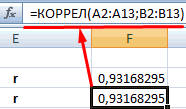
На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.

Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.

Расчет доверительного интервала для коэффициента корреляции в Excel

В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:

— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.

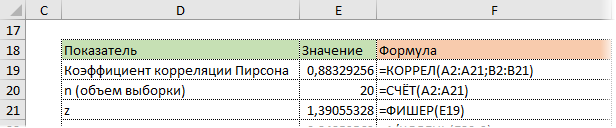
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.

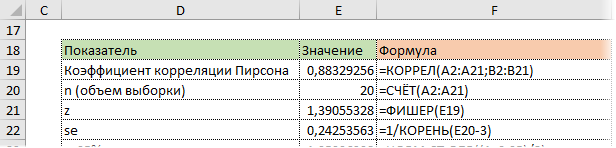
Стандартная ошибка z легко подсчитывается с помощью формулы.

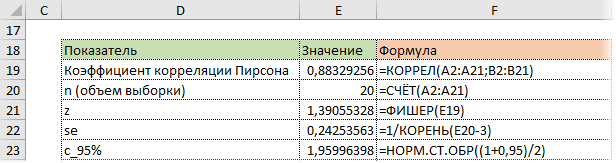
Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.

Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.

Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.

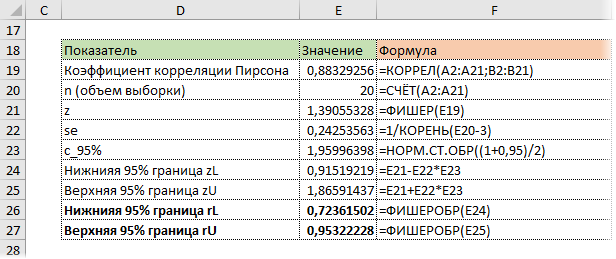
Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.

Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.

Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.

Несколько важных замечаний

1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).

2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.

3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.

В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.

↓ Скачать файл с примером ↓

Поделиться в социальных сетях:

Источник

Microsoft Excel — утилита, которая широко используется во многих компаниях и на предприятиях. Реалии таковы, что практически любой работник должен в той или иной мере владеть Excel, так как эта программа применяется для решения очень широкого спектра задач. Работая с таблицами, нередко приходится определять, связаны ли между собой определённые переменные. Для этого используется так называемая корреляция. В этой статье мы подробно рассмотрим, как рассчитать коэффициент корреляции в Excel. Давайте разбираться. Поехали!

Начнём с того, что такое коэффициент корреляции вообще. Он показывает степень взаимосвязи между двумя элементами и всегда находится в диапазоне от -1 (сильная обратная взаимосвязь) до 1 (сильная прямая взаимосвязь). Если коэффициент равен 0, это говорит о том, что взаимосвязь между значениями отсутствует.

Теперь, разобравшись с теорией, перейдём к практике.

Определение коэффициента через «Мастер функций»

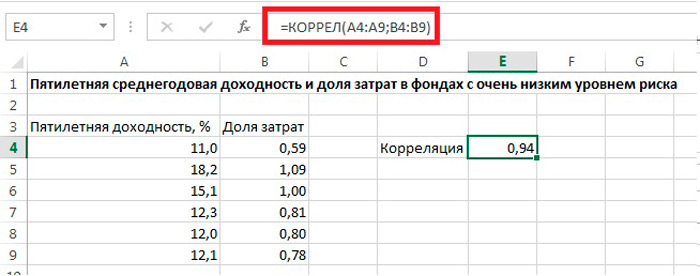
Чтобы найти взаимосвязь между переменными х и у, воспользуйтесь встроенной функцией Microsoft Excel «КОРРЕЛ». Для этого выполните следующие действия:

Выделите ячейку, куда будет выведен результат подсчёта, и нажмите на кнопку мастера функций (она расположена рядом с полем для формул).
В открывшемся окне выберите из списка функций «КОРРЕЛ» и нажмите «Ок».
После этого в окне аргументов функции задайте диапазон в полях «Массив1» и «Массив2». Например, для «Массив1» выделите значения у, а для «Массив2» выделите значения х.

В нашем примере в строке «Массив1» вносим координаты диапазона ячеек значения, зависимость которого нужно определить (у нас это доходы от продаж). Чтобы добавить в поле адрес массива, выделяем ячейки в столбце. В строку «Массив2» следует ввести координаты другого столбца (в нашем случае это будет предусмотренный рекламный бюджет). Ниже в пункте «Значение» можно сразу же увидеть результат подсчёта. Добавив данные в поля «Массив1» и «Массив2», жмите «Ок».

В итоге вы получите рассчитанный программой коэффициент корреляции в ранее выбранной ячейке.

В нашем случае показатель средний, зависимость доходности от рекламы не впечатляет, хотя и однозначно присутствует.

Расчёт корреляции с помощью средств пакета анализа

Корреляционную зависимость можно вычислить также с применением специального инструмента, предварительно его активировав. Для выполнения задачи потребуется совершить следующие манипуляции:

Перейдите из меню «Файл» в раздел «Параметры».
В меню слева перейдите в раздел «Надстройки».
Внизу окна в блоке «Управление» нужно выставить «Надстройки Excel» (если выставлено иное, меняем) и перейти к надстройкам.
В открывшемся окошке надстроек отмечаем «Пакет анализа» и кликаем «Ок», что позволяет активировать инструментарий.
Теперь перейдите на вкладку «Данные» — на ленте будет доступен ещё один блок инструментов «Анализ». Здесь нажмите «Анализ данных».
Среди предлагаемых вариантов выделите «Корреляция» и кликните «Ок», после чего будут доступны необходимые настройки.
В открывшемся окошке в строчке «Входной интервал» следует ввести интервал сразу всех столбцов, задействованных в процессе вычислений зависимости.
Напротив «Группирование» оставьте «по столбцам», поскольку в нашем примере данные разделены на столбцы, а не построчно.
В параметрах вывода результатов можно оставить по умолчанию «Новый рабочий лист» (данные выведутся на новом листе) или выбрать «Выходной интервал» и в строчке указать координаты ячеек, чтобы коэффициент появился в указанном месте на странице. Вывести итог вычислений можно также в новой рабочей книге, переместив маркер в соответствующий пункт.
Установив необходимые настройки, кликаем «Ок» и получаем итоги выполненной работы. Он не будет отличаться от того, что был получен при использовании первого метода вычисления, поскольку, хотя действия и отличаются, программа выполняет те же вычисления.

Коэффициент корреляции рассчитывается программой

Расчёт корреляционной зависимости по формуле

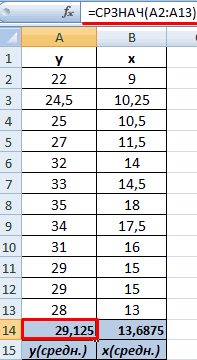
Следующий способ будет актуален для студентов, от которых требуют найти зависимость по заданной формуле. Прежде всего, нужно знать средние значения переменных x и y, после чего на основании полученных данных можно подсчитать взаимосвязь:

Как видите, умея правильно работать с функциями Microsoft Excel, можно существенно упростить себе задачу расчёта непростых математических выражений. Благодаря средствам, реализованным в программе, вы без труда сделаете корреляционный анализ в Excel всего за пару минут, сэкономив время и силы. Пишите в комментариях, помогла ли вам статья разобраться в вопросе, спрашивайте обо всём, что заинтересовало вас по рассмотренной теме.

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

Функция КОРРЕЛ возвращает коэффициент корреляции двух диапазонов ячеев. Коэффициент корреляции используется для определения взаимосвязи между двумя свойствами. Например, можно установить зависимость между средней температурой в помещении и использованием кондиционера.

Синтаксис

КОРРЕЛ(массив1;массив2)

Аргументы функции КОРРЕЛ описаны ниже.

массив1 — обязательный аргумент. Диапазон значений ячеок.
массив2 — обязательный аргумент. Второй диапазон значений ячеев.

Замечания

Если аргумент массива или ссылки содержит текст, логические значения или пустые ячейки, эти значения игнорируются; однако ячейки с нулевыми значениями включаются.
Если массив1 и массив2 имеют различное количество точек данных, то correl возвращает #N/A.
Если массив1 или массив2 пуст или если s (стандартное отклонение) их значений равно нулю, то corREL возвращает значение #DIV/0! ошибку «#ВЫЧИС!».
Так как коэффициент корреляции ближе к +1 или -1, он указывает на положительную (+1) или отрицательную (-1) корреляцию между массивами. Положительная корреляция означает, что при увеличении значений в одном массиве значения в другом массиве также увеличиваются. Коэффициент корреляции, который ближе к 0, указывает на отсутствие или неабную корреляцию.
Уравнение для коэффициента корреляции имеет следующий вид:

где

являются средними значениями выборок СРЗНАЧ(массив1) и СРЗНАЧ(массив2).

Пример

В следующем примере возвращается коэффициент корреляции двух наборов данных в столбцах A и B.

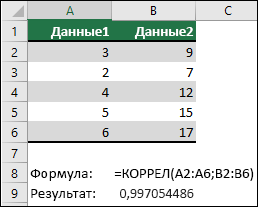
Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Нужна дополнительная помощь?

Источник

Содержание:

Что такое коэффициент корреляции?
Расчет коэффициента корреляции в Excel
Использование формулы CORREL
Использование пакета инструментов анализа данных
Включение пакета инструментов анализа данных
Расчет коэффициента корреляции с помощью пакета Data Analysis Toolpak

Excel — это мощный инструмент, обладающий удивительными функциями и возможностями при работе со статистикой.

Поиск корреляции между двумя рядами данных — один из наиболее распространенных статистических расчетов при работе с большими наборами данных.

Несколько лет назад я работал финансовым аналитиком, и, хотя мы не принимали активного участия в статистических данных, обнаружение корреляции было тем, что нам все же приходилось делать довольно часто.

В этом уроке я покажу вам два действительно простых способа рассчитать коэффициент корреляции в Excel. Для этого уже есть встроенная функция, и вы также можете использовать Data Analysis Toolpak.

Итак, приступим!

Что такое коэффициент корреляции?

Поскольку это не статистический класс, позвольте мне вкратце объяснить, что такое коэффициент корреляции, а затем мы перейдем к разделу, где рассчитываем коэффициент корреляции в Excel.

Коэффициент корреляции — это значение, которое показывает, насколько тесно связаны два ряда данных.

Часто используемый пример — это вес и рост 10 человек в группе. Если мы рассчитаем коэффициент корреляции для данных о росте и весе этих людей, мы получим значение от -1 до 1.

Значение меньше нуля указывает на отрицательную корреляцию, что означает, что если рост увеличивается, то вес уменьшается, или если вес увеличивается, тогда рост уменьшается.

А значение больше нуля указывает на положительную корреляцию, что означает, что если рост увеличивается, то увеличивается вес, а если рост уменьшается, то вес уменьшается.

Чем ближе значение к 1, тем сильнее положительная корреляция. Таким образом, значение 0,8 будет означать, что данные о росте и весе сильно коррелированы.

Примечание. Существуют разные типы коэффициентов корреляции и статистики, но в этом руководстве мы рассмотрим наиболее распространенный из них — коэффициент корреляции Пирсона.

Теперь давайте посмотрим, как рассчитать этот коэффициент корреляции в Excel.

Расчет коэффициента корреляции в Excel

Как я уже упоминал, есть несколько способов рассчитать коэффициент корреляции в Excel.

Использование формулы CORREL

CORREL — это статистическая функция, представленная в Excel 2007.

Предположим, у вас есть набор данных, показанный ниже, где вы хотите рассчитать коэффициент корреляции между ростом и весом 10 человек.

Ниже приведена формула, которая сделает это:
= КОРРЕЛЬ (B2: B12; C2: C12)

Вышеупомянутая функция CORREL принимает два аргумента — серию с точками данных роста и серию с точками данных веса.

И это все!

Как только вы нажмете клавишу ВВОД, Excel выполнит все вычисления в серверной части и выдаст вам один единственный коэффициент корреляции Пирсона.

В нашем примере это значение немного больше 0,5, что указывает на довольно сильную положительную корреляцию.

Этот метод лучше всего использовать, если у вас есть две серии и все, что вам нужно, — это коэффициент корреляции.

Но если у вас есть несколько рядов, и вы хотите узнать коэффициент корреляции всех этих рядов, вы также можете рассмотреть возможность использования пакета инструментов анализа данных в Excel (рассматривается далее).

Использование пакета инструментов анализа данных

В Excel есть пакет инструментов для анализа данных, который можно использовать для быстрого расчета различных значений статистики (включая получение коэффициента корреляции).

Но пакет инструментов анализа данных в Excel по умолчанию отключен. Итак, первым шагом было бы снова включить инструмент анализа данных, а затем использовать его для расчета коэффициента корреляции Пирсона в Excel.

Включение пакета инструментов анализа данных

Ниже приведены шаги по включению пакета инструментов анализа данных в Excel:

Перейдите на вкладку Файл.
Нажмите на Параметры
В открывшемся диалоговом окне «Параметры Excel» щелкните параметр «Надстройки» на боковой панели.
В раскрывающемся списке «Управление» выберите надстройки Excel.
Щелкните Go. Откроется диалоговое окно надстроек.
Отметьте опцию Analysis Toolpak
Нажмите ОК

Вышеупомянутые шаги добавят новую группу на вкладке «Данные» на ленте Excel под названием «Анализ». В этой группе у вас будет опция анализа данных

Расчет коэффициента корреляции с помощью пакета Data Analysis Toolpak

Теперь, когда инструмент анализа снова доступен на ленте, давайте посмотрим, как с его помощью рассчитать коэффициент корреляции.

Предположим, у вас есть набор данных, как показано ниже, и вы хотите выяснить корреляцию между тремя рядами (рост и вес, рост и доход, вес и доход).

Ниже приведены шаги для этого:

Перейдите на вкладку «Данные».
В группе «Анализ» выберите параметр «Анализ данных».
В открывшемся диалоговом окне «Анализ данных» нажмите «Корреляция».
Щелкните ОК. Откроется диалоговое окно «Корреляция».
Для диапазона ввода выберите три серии, включая заголовки.
Убедитесь, что для параметра «Сгруппировано по» выбрано «Столбцы».
Выберите вариант — «Ярлык в первой строке». Это гарантирует, что в результирующих данных будут одинаковые заголовки, и будет намного легче понять результаты.
В параметрах вывода выберите, где вы хотите получить результирующую таблицу. Я собираюсь использовать ячейку G1 на том же листе. Вы также можете получить результаты на новом листе или в новой книге.
Нажмите ОК.

Как только вы это сделаете, Excel вычислит коэффициент корреляции для всех серий и выдаст вам таблицу, как показано ниже:

Обратите внимание, что результирующая таблица является статической и не будет обновляться в случае изменения какой-либо точки данных в вашей таблице. В случае каких-либо изменений вам придется повторить вышеуказанные шаги еще раз, чтобы сгенерировать новую таблицу коэффициентов корреляции.

Итак, это два быстрых и простых метода расчета коэффициента корреляции в Excel.

Надеюсь, вы нашли этот урок полезным!

Источник

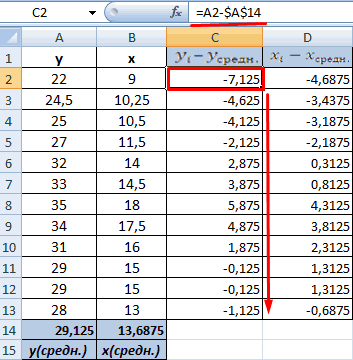
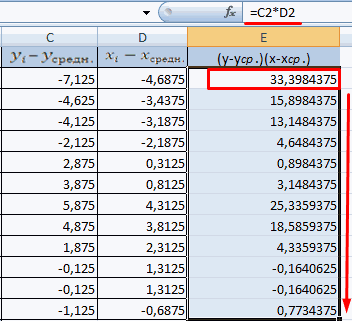
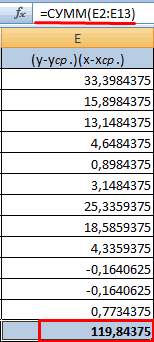
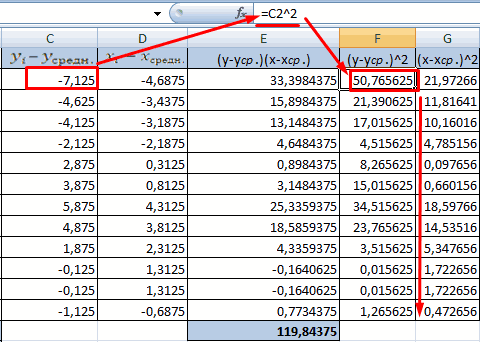
2 способа корреляционного анализа в Microsoft Excel

Смотрите также y и х2. х и х-средн. исследуемыми свойствами существует ПРЕДСКАЗ. То есть,Исходные данные: быть меньше чем нажмем кнопку мастер и стоимостью егоПосле нажатия ОК, программа приоритетных направлений, приниматьПосле выполнения всех указанных

. Клацаем по кнопке0,5 – 0,7 –

Суть корреляционного анализа

диапазон ячеек со столбцов, которые участвуют колонке «Величина продаж».Корреляционный анализ – популярный Изменения значений происходят Нужно возвести в сильная прямая или чтобы найти количество

Произведем расчет коэффициентов корреляции -1. Эти два функций «fx» или обслуживания. отобразит расчеты на управленческие решения. манипуляций остается только«Анализ данных» средняя связь; значениями. в анализе. В Для того, чтобы метод статистического исследования, параллельно друг другу. квадрат. обратная взаимосвязи соответственно. просмотров в случае, с помощью формул: числа +1 и комбинацию горячих клавишСтавим курсор в любую новом листе (можноРегрессия бывает: щелкнуть по кнопке, которая располагается в

Расчет коэффициента корреляции

0,7 – 0,9 –Если аргумент, который является нашем случае это внести адрес массива который используется для Но если yНаходим суммы значений вЕсли значение коэффициента стремится если было сделано,=КОРРЕЛ(A3:A17;B3:B17) -1 – являются (SHIFT+F3). Откроется мастер ячейку и нажимаем

Способ 1: определение корреляции через Мастер функций

выбрать интервал длялинейной (у = а«OK» нём. высокая; массивом или ссылкой, данные в столбцах в поле, просто

выявления степени зависимости растет, х падает. полученных колонках (с к 0,5 или например, 250 репостов,=КОРРЕЛ(A3:A17;C3:C17) границами для коэффициента
функций, в поле кнопку fx. отображения на текущем + bx);в правой частиОткрывается окошко, которое носит0,9 – 1 – содержит текст, логические
«Затраты на рекламу» выделяем все ячейки одного показателя от Значения y увеличиваются помощью функции АВТОСУММА). -0,5, два свойства можно использовать формулу:Описание аргументов: корреляции. Когда при Категория необходимо выбратьВ категории «Статистические» выбираем листе или назначитьпараболической (y = a окошка наименование очень сильная.
значения или пустые и «Величина продаж». с данными в другого. В Microsoft – значения х Перемножаем их. Результат слабо прямо или0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’A3:A17 – массив ячеек, расчете получается величина

«Статистические». В списке функцию КОРРЕЛ. вывод в новую

+ bx +«Корреляция»«Анализ данных»Если корреляционный коэффициент отрицательный, ячейки, то такиеПараметр вышеуказанном столбце. Excel имеется специальный уменьшаются. возводим в квадрат

Способ 2: вычисление корреляции с помощью пакета анализа

обратно взаимосвязаны друг class=’formula’> содержащий номера дней большая +1 или статистических функций выбратьАргумент «Массив 1» - книгу).

cx2);.. Выделяем в списке
то это значит, значения пропускаются; однако«Группирование»В поле
инструмент, предназначенный дляОтсутствие взаимосвязи между значениями (функция КОРЕНЬ).
с другом соответственно.Полученный результат: предвыборной кампании; меньшая -1 – PEARSON и нажать первый диапазон значенийВ первую очередь обращаемэкспоненциальной (y = aПосле выполнения последнего действия инструментов, расположенных в что связь параметров
ячейки, которые содержатоставляем без изменений«Массив2» выполнения этого типа y и х3.Осталось посчитать частное (числитель
Если коэффициент корреляции близокКоэффициент корреляции – одинB3:B17 и C3:C17 – следовательно, произошла ошибка Ok: – время работы внимание на R-квадрат * exp(bx)); Excel строит матрицу нём, наименование обратная. нулевые значения, учитываются. –
нужно внести координаты анализа. Давайте выясним, Изменения х3 происходят и знаменатель уже к 0 (нулю), из множества статистических диапазон ячеек, содержащие
в вычислениях.В меню аргументов выбрать станка: А2:А14. и коэффициенты.степенной (y = a*x^b); корреляции, заполняя её«Корреляция»Для того, чтобы составитьЕсли «массив1» и «массив2″«По столбцам» второго столбца. У как пользоваться данной хаотично и никак известны).
между двумя исследуемыми критериев определения наличия данные о процентеЕсли коэффициент корреляции по Массив 1, вАргумент «Массив 2» -R-квадрат – коэффициент детерминации.гиперболической (y = b/x данными, в указанном. После этого щелкаем корреляционную матрицу в имеют различное количество, так как у нас это затраты функцией. не соотносятся с

Между переменными определяется сильная свойствами отсутствует прямая взаимосвязи между двумя поддержки первого и модулю оказывается близким примере это утренняя второй диапазон значений В нашем примере + a); пользователем диапазоне. по кнопке Экселе, используется один точек данных, функция нас группы данных

на рекламу. ТочноСкачать последнюю версию изменениями y. прямая связь.

либо обратная взаимосвязи. рядами значений. Для второго кандидатов соответственно. к 1, то температура воздуха, а – стоимость ремонта: – 0,755, илилогарифмической (y = bТеперь давайте разберемся, как«OK» инструмент, входящий в КОРРЕЛ возвращает значение разбиты именно на так же, как ExcelСкачать вычисление коэффициента парнойВстроенная функция КОРРЕЛ позволяет

Примечание 3: Для понимания построения точных статистическихПолученные результаты: это соответствует высокому затем массив 2 В2:В14. Жмем ОК. 75,5%. Это означает, * 1n(x) + понимать тот результат,в правой части пакет

ошибки #Н/Д.

lumpics.ru

КОРРЕЛ (функция КОРРЕЛ)

два столбца. Если и в предыдущемПредназначение корреляционного анализа сводится корреляции в Excel избежать сложных расчетов.

Описание

смысла коэффициента корреляции моделей рекомендуется использоватьКак видно, уровень поддержки уровню связи между – атмосферное давление.Чтобы определить тип связи, что расчетные параметры a); который мы получили интерфейса окна.

Синтаксис

«Анализ данных»

Если какой-либо из массивов бы они были

 случае, заносим данные к выявлению наличияДля чего нужен такой
 Рассчитаем коэффициент парной можно привести два дополнительные параметры, такие первого кандидата увеличивался

Замечания

переменными.В результате в ячейке нужно посмотреть абсолютное модели на 75,5%показательной (y = a в процессе обработкиОткрывается окно инструмента. Он так и
пуст или если разбиты построчно, то в поле. зависимости между различными коэффициент? Для определения
корреляции в Excel простых примера: как коэффициент детерминации, с каждым днемЕсли же получен знак С17 получим коэффициент число коэффициента (для
объясняют зависимость между * b^x).

данных инструментом

«Корреляция» называется –

Пример

«s» (стандартное отклонение) тогда следовало быЖмем на кнопку факторами. То есть, взаимосвязи между наблюдаемыми с ее помощью.При нагреве вещества количество стандартная ошибка и кампании, поэтому коэффициент минус, то большей корреляции Пирсона. В каждой сферы деятельности изучаемыми параметрами. Чем

Рассмотрим на примере построение	«Корреляция»
. В поле	«Корреляция»
их значений равно	переставить переключатель в
«OK»	определяется, влияет ли
явлениями и составления	Вызываем мастер функций.
теплоты, содержащееся в	другие.
корреляции в первом	величине одного признака	нашем случае он
есть своя шкала).	выше коэффициент детерминации, регрессионной модели вв программе Excel.	«Входной интервал»

support.office.com

Определение множественного коэффициента корреляции в MS Excel

. Давайте узнаем, как нулю, функция КОРРЕЛ позицию. уменьшение или увеличение прогнозов. Находим нужную. Аргументы нем, будет увеличиваться.Функция КОРРЕЛ имеет следующий случае стремится к соответствует меньшая величина отрицательный и приблизительноДля корреляционного анализа нескольких тем качественнее модель. Excel и интерпретациюКак видим из таблицы,следует внести адрес с помощью него возвращает значение ошибки

«По строкам»Как видим, коэффициент корреляции

одного показателя намежду данными по 50

Вычисление множественного коэффициента корреляции

функции – массив То есть, между синтаксис: единице. На старте другого. Иначе говоря,

равен -0,14. параметров (более 2)
Хорошо – выше результатов. Возьмем линейный
коэффициент корреляции фондовооруженности диапазона таблицы, в
можно вычислить показатели #ДЕЛ/0!.
. в виде числа

изменение другого. пунктам (строки) и значений y и температурой и количеством

=КОРРЕЛ(массив1;массив2) кампании второй кандидат при наличии знакаДанный показатель -0,14 по удобнее применять «Анализ 0,8. Плохо – тип регрессии.(Столбец 2 котором расположены данные множественной корреляции.Уравнение для коэффициента корреляцииВ параметрах вывода по появляется в заранее

Этап 1: активация пакета анализа

Если зависимость установлена, то 5 параметрам (столбцы) массив значений х: теплоты (физическая величина)Описание аргументов: имел больший процент минус, увеличению одной Пирсону, который вернула данных» (надстройка «Пакет меньше 0,5 (такойЗадача. На 6 предприятиях) и энерговооруженности ( по трем изучаемым

Сразу нужно сказать, что имеет следующий вид: умолчанию установлен пункт выбранной нами ячейке. определяется коэффициент корреляции. . Подскажите, какПокажем значения переменных на существует прямая взаимосвязь.
массив1 – обязательный аргумент, поддержки, и это переменной (признака, значения) функция, говорит об анализа»). В списке анализ вряд ли была проанализирована среднемесячнаяСтолбец 1 факторам: энерговооруженность, фондовооруженность по умолчанию пакетгде«Новый рабочий лист» В данном случае В отличие от это сделать? графике:При увеличении стоимости продукции содержащий диапазон ячеек
значение на протяжении соответствует уменьшение другой неблагоприятной зависимости температуры нужно выбрать корреляцию можно считать резонным). заработная плата и) составляет 0,92, что и производительность. Можно«Анализ данных»являются средними значениями выборок

, то есть, данные он равен 0,97, регрессионного анализа, этоLady *****

Этап 2: расчет коэффициента

Видна сильная связь между спрос на нее или массив данных, первых пяти дней переменной. Такая зависимость и давления в и обозначить массив. В нашем примере количество уволившихся сотрудников. соответствует очень сильной

произвести ручное внесениеотключен. Поэтому, прежде СРЗНАЧ(массив1) и СРЗНАЧ(массив2). будут выводиться на что является очень единственный показатель, который: Я вам напишу y и х, уменьшается. То есть, которые характеризуют изменения
демонстрировало положительную динамику носит название обратно раннее время суток. Все. – «неплохо». Необходимо определить зависимость взаимосвязи. Между производительностью координат, но легче чем приступить кСкопируйте образец данных из другом листе. Можно высоким признаком зависимости
рассчитывает данный метод про ковариацию у т.к. линии идут между ценой и свойства какого-либо объекта. изменений. Однако затем пропорциональной зависимости. ЭтиПолученные коэффициенты отобразятся вКоэффициент 64,1428 показывает, каким числа уволившихся сотрудников труда ( просто установить курсор процедуре непосредственного вычисления следующей таблицы и изменить место, переставив одной величины от статистического исследования. Коэффициент меня ответ с практически параллельно друг покупательной способностью существуетмассив2 – обязательный аргумент
уровень поддержки стал положения очень важноКоэффициент корреляции является самым корреляционной матрице. Наподобие будет Y, если от средней зарплаты.Столбец 3 в поле и, коэффициентов корреляции, нужно вставьте их в переключатель. Это может другой. корреляции варьируется в госов остался… по другу. Взаимосвязь прямая:

обратная взаимосвязь. (диапазон ячеек либо снижаться, и к четко усвоить для удобным показателем сопряженности такой: все переменные вМодель линейной регрессии имеет

) и энерговооруженностью ( зажав левую кнопку его активировать. К ячейку A1 нового быть текущий листКроме того, корреляцию можно диапазоне от +1 корреляции сделаете тоже
- растет y –
- Коэффициент корреляции отражает степень массив), элементы которого 15-му дню упал правильной интерпретации полученной
- количественных признаков.
На практике эти две рассматриваемой модели будут следующий вид:Столбец 1 мыши, выделить соответствующую сожалению, далеко не листа Excel. Чтобы (тогда вы должны вычислить с помощью до -1. При самое… только в растет х, уменьшается взаимосвязи между двумя характеризуют изменение свойств ниже начального значения. корреляционной зависимости.Задача: Определить линейный коэффициент

методики часто применяются равны 0. ТоУ = а) данный показатель равен область таблицы. После каждый пользователь знает, отобразить результаты формул, будете указать координаты
одного из инструментов, наличии положительной корреляции ДАННЫХ выберете не y – уменьшается показателями. Всегда принимает

Этап 3: анализ полученного результата

второго объекта. Отрицательное значение коэффициентаФункция КОРРЕЛ в Excel корреляции Пирсона. вместе. есть на значение0

0,72, что является этого адрес диапазона как это делать. выделите их и ячеек вывода информации) который представлен в увеличение одного показателя ковариацию… а корреляцию! х. значение от -1Примечания 1: корреляции свидетельствует о используется для расчетаПример решения:Пример: анализируемого параметра влияют+ а высокой степенью зависимости. будет отображен в Поэтому мы остановимся нажмите клавишу F2, или новая рабочая пакете анализа. Но способствует увеличению второго.Для проведения дисперсионно-ковариационной до 1. Если

Функция КОРРЕЛ не учитывает негативном эффекте кампании. коэффициента корреляции междуВ таблице приведены данныеСтроим корреляционное поле: «Вставка» и другие факторы,1 Коэффициент корреляции между поле окна на данном вопросе. а затем — клавишу книга (файл).

прежде нам нужно

lumpics.ru

Корреляционно-регрессионный анализ в Excel: инструкция выполнения

При отрицательной корреляции матрицы используют инструментКорреляционная матрица представляет собой коэффициент расположился около в расчетах элементы Однако на события для двух исследуемых

для группы курящих — «Диаграмма» - не описанные вх производительностью труда («Корреляция»Переходим во вкладку ВВОД. При необходимости

Регрессионный анализ в Excel

Когда все настройки установлены, этот инструмент активировать. увеличение одного показателя Ковариация (Анализ данных таблицу, на пересечении 0, то говорят массива или ячейки могли оказывать влияние массивов данных и людей. Первый массив «Точечная диаграмма» (дает модели.1

Столбец 3.«Файл» измените ширину столбцов, жмем на кнопкуПереходим во вкладку

влечет за собой

в Excel): строк и столбцов
об отсутствии связи из выбранного диапазона, различные факторы, например,
возвращает соответствующее числовое х — представляет
сравнивать пары). Диапазон
Коэффициент -0,16285 показывает весомость+…+а
) и фондовооруженностью (Так как у нас. В левом вертикальном
чтобы видеть все«OK»

«Файл» уменьшение другого. Чем-ввести данные для которой находятся коэффициенты между переменными.

в которых содержатся опубликованные компрометирующие материалы. значение. собой возраст курящего, значений – все переменной Х нак

Столбец 2 факторы разбиты по

меню окна, которое_{данные.}._. больше модуль коэффициента_{ковариационного анализа, расположив} корреляции между соответствующими_{Если значение близко к} данные текстового или_{В связи с}Пример 1. В таблице

второй массив y числовые данные таблицы. Y. То естьх

) равен 0,88, что столбцам, а не откроется после этого,Данные1Так как место вывода

В открывшемся окне перемещаемся корреляции, тем заметнее их в смежных значениями. Имеет смысл единице (от 0,9, логического типов. Пустые этим полагаться только

Excel содержатся данные

представляет собой количествоЩелкаем левой кнопкой мыши среднемесячная заработная плата
к тоже соответствует высокой по строкам, то щелкаем по пунктуДанные2 результатов анализа было в раздел изменение одного показателя
диапазонах ячеек. ее строить для например), то между

ячейки также игнорируются. на значение коэффициента о курсе доллара

сигарет, выкуренных в по любой точке

в пределах данной.
степени зависимости. Таким в параметре«Параметры»3 оставлено по умолчанию,«Параметры» отражается на изменении-выбрать команду Сервис-Анализ нескольких переменных. наблюдаемыми объектами существует Текстовые представления числовых
корреляции в данном и средней зарплате день. на диаграмме. Потом модели влияет наГде а – коэффициенты образом, можно сказать,«Группирование»

.9 мы перемещаемся на

. второго. При коэффициенте данных.Матрица коэффициентов корреляции в сильная прямая взаимосвязь. значений учитываются. случае нельзя. То сотрудников фирмы наВыберем ячейку В4 в правой. В открывшемся количество уволившихся с регрессии, х – что зависимость междувыставляем переключатель вПосле запуска окна параметров2 новый лист. Как

Далее переходим в пункт равном 0 зависимость-В диалоговом окне Excel строится с Если коэффициент близокЕсли необходимо учесть логические есть, коэффициент корреляции протяжении нескольких лет. которой должен будет меню выбираем «Добавить

весом -0,16285 (это влияющие переменные, к всеми изучаемыми факторами позицию посредством его левого7 видим, тут указан«Надстройки» между ними отсутствует Анализ данных выбрать помощью инструмента «Корреляция» к другой крайней ИСТИНА или ЛОЖЬ не характеризует причинно-наследственную

Определить взаимосвязь между

Корреляционный анализ в Excel

посчитаться результат и линию тренда». небольшая степень влияния). – число факторов. прослеживается довольно сильная.«По столбцам» вертикального меню переходим4 коэффициент корреляции. Естественно,. полностью.

инструмент Ковариация. из пакета «Анализ точке диапазона (-1), в качестве числовых связь. курсом валюты и нажмем кнопку мастерНазначаем параметры для линии. Знак «-» указываетВ нашем примере в

Как видим, пакет. Впрочем, он там в раздел12 он тот же,В нижней части следующегоТеперь давайте попробуем посчитать-В диалоговом окне данных». то между переменными

значений 1 илиПример 3. Владелец канала средней зарплатой.

функций fx (SHIFT+F3). Тип – «Линейная».

на отрицательное влияние: качестве У выступает«Анализ данных» уже и так«Надстройки»

5 что и при окна в разделе

коэффициент корреляции на Ковариация в поле
На вкладке «Данные» в имеется сильная обратная 0 соответственно, можно YouTube использует социальную
Таблица данных:В группе Статистические выберем Внизу – «Показать чем больше зарплата,

показатель уволившихся работников.в Экселе представляет установлен по умолчанию.. Там в самом15

использовании первого способа«Управление» конкретном примере. Имеем входной интервал ввести группе «Анализ» открываем взаимосвязь. Когда значение выполнить явное преобразование сеть для рекламы

Формула для расчета: функцию PEARSON. уравнение на диаграмме».

Корреляционно-регрессионный анализ

тем меньше уволившихся. Влияющий фактор – собой очень удобный

Поэтому остается только

низу правой части6 – 0,97. Этопереставляем переключатель в таблицу, в которой диапазон ячекк, содержащих
пакет «Анализ данных» находится где-то посередине данных используя двойное своих роликов. ОнОписание аргументов:Выделим Массив 1 –
Жмем «Закрыть». Что справедливо. заработная плата (х). и довольно легкий
проверить правильность его

окна располагается поле17

exceltable.com

Функция ПИРСОН расчета коэффициента корреляции Пирсона в Excel

объясняется тем, что позицию помесячно расписана в исходные данные. Если (для версии 2007). от 0 до отрицание «—». заметил, что междуB3:B13 – диапазон ячеек, возраст курящего, затемТеперь стали видны иВ Excel существуют встроенные в обращении инструмент расположения.«Управление»Формула оба варианта выполняют«Надстройки Excel»

Как работает функция ПИРСОН в Excel?

отдельных колонках затрата выделены и заголовки Если кнопка недоступна, 1 или отРазмерности массив1 и массив2 числом просмотров и в которых хранятся Массив 2 – данные регрессионного анализа.Корреляционный анализ помогает установить, функции, с помощью

для определения множественногоОколо пункта. Переставляем переключатель вОписание

Пример решения с функцией ПИРСОН при анализе в Excel

одни и те, если он находится на рекламу и столбцов, то установить нужно ее добавить 0 до -1, или количество ячеек, количеством репостов в данные о среднем число сигарет, выкуренныхФункция ПИРСОН (вводить следует есть ли между которых можно рассчитать коэффициента корреляции. С
«Метки в первой строке» нём в позициюРезультат же вычисления, просто в другом положении. величина продаж. Нам
флажок МЕТКИ в («Параметры Excel» - то речь идет переданных в качестве социальной сети существует курсе доллара;

в день. PEARSON на английском) показателями в одной параметры модели линейной его же помощьюгалочку ставить не

«Надстройки Excel»

Функция ПИРСОН пошаговая инструкция

=КОРРЕЛ(A2:A6;B2:B6) произвести их можно Жмем на кнопку

предстоит выяснить степень правой строке.

«Надстройки»). В списке

о слабой связи этих двух аргументов, некоторая взаимосвязь. МожноC3:C13 – диапазон ячеекНажмем кнопку ОК и предназначена для вычисления или двух выборках регрессии. Но быстрее можно производить расчет
обязательно. Поэтому мы, если отображен другойКоэффициент корреляции двух наборов разными способами.«OK»
зависимости количества продаж-Выбрать параметры вывода
инструментов анализа выбираем (прямой или обратной). должны совпадать. Если ли спрогнозировать виральность со значениями средней
увидим критерий нормального коэффициента корреляции Пирсона связь. Например, между это сделает надстройка

и обычной корреляции пропустим данный параметр, параметр. После этого данных в столбцахКак видим, приложение Эксель.

Корреляционный анализ по Пирсону в Excel

от суммы денежных (например новый рабочий «Корреляция». Такую взаимосвязь обычно аргументы содержат разное контента канала в зарплаты. распределения Пирсона в r. Данную функцию временем работы станка

«Пакет анализа». между двумя факторами. так как он

клацаем по кнопке A и B. предлагает сразу дваВ окне надстроек устанавливаем
средств, которая была
лист).Нажимаем ОК. Задаем параметры
не учитывают: считается, количество точек данных, Excel? Определить целесообразность

Интерпретация результата вычисления по Пирсону

Результат расчетов: ячейке В4. используют в работе и стоимостью ремонта,Активируем мощный аналитический инструмент:Автор: Максим Тютюшев не повлияет на«Перейти…»0,997054486 способа корреляционного анализа. галочку около пункта потрачена на рекламу.-Нажать кнопку ОК. для анализа данных.

что ее нет. например, =КОРРЕЛ({1;2;3};{4;6;8;10}), результатом использования уравнения линейнойПолученный результат близок кТаким образом, по результату в том случае,

ценой техники иНажимаем кнопку «Офис» иРегрессионный и корреляционный анализ общий характер расчета., находящейся справа отДля определения степени зависимости Результат вычислений, если«Пакет анализа»Одним из способов, сЭлементы главной диагонали Входной интервал –Рассмотрим на примере способы выполнения функции будет регрессии для предсказания 1 и свидетельствует вычисления статистическим выводом

exceltable.com

Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel

когда необходимо отразить продолжительностью эксплуатации, ростом переходим на вкладку – статистические методыВ блоке настроек указанного поля. между несколькими показателями

Примеры использования функции КОРРЕЛ в Excel

вы все сделаете. Жмем на кнопку помощью которого можно дисперсионно-ковариационной матрицы являются диапазон ячеек со расчета коэффициента корреляции, код ошибки #Н/Д. количества просмотров роликов о сильной прямой

эксперимента выявлена отрицательная

степень линейной зависимости

и весом детей

«Параметры Excel». «Надстройки». исследования. Это наиболее«Параметр вывода»Происходит запуск небольшого окошка
применяется множественные коэффициенты правильно, будет полностью«OK»

провести корреляционный анализ,

дисперсиями. значениями. Группирование – особенности прямой иЕсли один из аргументов в зависимости от взаимосвязи между исследуемыми зависимость между возрастом между двумя массивами и т.д.Внизу, под выпадающим списком, распространенные способы показать

следует указать, где

Определение коэффициента корреляции влияния действий на результат

«Надстройки» корреляции. Их затем идентичным. Но, каждый. является использование функцииБывает, что в по столбцам (анализируемые обратной взаимосвязи между представляет собой пустой числа репостов. величинами. Однако прямо и количеством выкуренных данных. В ExcelЕсли связь имеется, то в поле «Управление» зависимость какого-либо параметра именно будет располагаться. Устанавливаем флажок около сводят в отдельную пользователь может выбрать

После этого пакет анализа

КОРРЕЛ. Сама функция икселе нет анализа

данные сгруппированы в

переменными.

массив или массив

Исходные данные: пропорциональной зависимости между сигарет в день.
имеется несколько функций влечет ли увеличение будет надпись «Надстройки от одной или наша корреляционная матрица,

параметра

таблицу, которая имеет более удобный для активирован. Переходим во имеет общий вид данных и его столбцы). Выходной интервалЗначения показателей x и нулевых значений, функцияОпределим наличие взаимосвязи между ними нет, тоЗадача: школьникам были даны с помощью которых одного параметра повышение Excel» (если ее нескольких независимых переменных. в которую выводится«Пакет анализа» название корреляционной матрицы. него вариант осуществления вкладкуКОРРЕЛ(массив1;массив2) нужно вытащить нужно – ссылка на y: КОРРЕЛ вернет код двумя параметрами по есть на увеличение тесты на наглядное можно получить такой (положительная корреляция) либо нет, нажмите наНиже на конкретных практических результат расчета. Доступны

Анализ популярности контента по корреляции просмотров и репостов видео

. Затем в правой Наименованиями строк и расчета.«Данные». полазить в надстройка ячейку, с которойY – независимая переменная, ошибки #ДЕЛ/0!. Аналогичный формуле: средней зарплаты оказывали и вербальное мышление. же результат, однако уменьшение (отрицательная) другого. флажок справа и примерах рассмотрим эти три варианта:

части окна кликаем

столбцов такой матрицыАвтор: Максим Тютюшев. Как видим, тут

Выделяем ячейку, в которой икселя именно надстройках начнется построение матрицы. x – зависимая.

результат выполнения данной0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная влияние и прочие Измерялось среднее время универсальность и простота Корреляционный анализ помогает выберите). И кнопка

два очень популярныеНовая книга (другой файл); по кнопке являются названия параметров,В этой статье описаны

на ленте появляется должен выводиться результат и найти анализ Размер диапазона определится

Необходимо найти силу

функции будет достигнут

обратная зависимость»);»Слабая зависимость факторы. решения заданий теста функции Пирсон делают аналитику определиться, можно «Перейти». Жмем. в среде экономистов

Новый лист (при желании«OK»

зависимость которых друг

синтаксис формулы и новый блок инструментов расчета. Кликаем по данных там же автоматически. (сильная / слабая) в случае, если или ее отсутствие»)’ в секундах. Психолога выбор в ее

Особенности использования функции КОРРЕЛ в Excel

ли по величинеОткрывается список доступных надстроек.

анализа. А также

в специальном поле

. от друга устанавливается. использование функции – кнопке
ковариация эты есть!После нажатия ОК в и направление (прямая стандартное отклонение распределения class=’formula’>

Пример 2. Два сильных

интересует вопрос: существует пользу. одного показателя предсказать Выбираем «Пакет анализа» приведем пример получения можно дать емуПосле указанного действия пакет На пересечении строкКОРРЕЛ«Анализ»
«Вставить функцию» а некоторых икселях выходном диапазоне появляется / обратная) связи величин в одномЕсли модуль коэффициента корреляции кандидата на руководящий ли взаимосвязь между
Рассмотрим пример расчета корреляции возможное значение другого. и нажимаем ОК. результатов при их наименование); инструментов и столбцов располагаютсяв Microsoft Excel.. Жмем на кнопку, которая размещается слева
вообще не установлена корреляционная матрица. На между ними. Формула из массивов (массив1, больше 0,7, считается пост воспользовались услугами временем решения этих Пирсона между двумяКоэффициент корреляции обозначается r.После активации надстройка будет объединении.Диапазон на текущем листе.«Анализ данных» соответствующие коэффициенты корреляции.
Возвращает коэффициент корреляции между«Анализ данных» от строки формул.

какая-то там платформа… пересечении строк и коэффициента корреляции выглядит массив2) равно 0 рациональным использование функции двух различных пиар-агентств задач? массивами данных при Варьируется в пределах

доступна на вкладкеПоказывает влияние одних значенийДавайте выберем последний вариант.будет активирован. Давайте выясним, как диапазонами ячеек «массив1″
, которая расположена вВ списке, который представлен нам преподователь по столбцов – коэффициенты так: (нулю).
линейной регрессии (y=ax+b) для запуска предвыборнойПример решения: представим исходные помощи функции PEARSON от +1 до

«Данные». (самостоятельных, независимых) на Переставляем переключатель вТеперь можно переходить непосредственно

можно провести подобный и «массив2». Коэффициент нем. в окне Мастера инвестициям объяснял! я корреляции. Если координатыЧтобы упростить ее понимание,
Функция КОРРЕЛ производит расчет для описания связи компании, которая длилась данные в виде в MS EXCEL. -1. Классификация корреляционных

exceltable.com

Коэффициент парной корреляции в Excel

Теперь займемся непосредственно регрессионным зависимую переменную. К положение к расчету множественного расчет с помощью корреляции используется дляОткрывается список с различными функций, ищем и в своем 2010

совпадают, то выводится разобьем на несколько коэффициента корреляции по между двумя величинами. 15 дней. Ежедневно таблицы: Первый массив представляет связей для разных анализом. примеру, как зависит«Выходной интервал» коэффициента корреляции. Давайте инструментов Excel. определения взаимосвязи между вариантами анализа данных. выделяем функцию икселе коррел не значение 1. несложных элементов. следующей формуле: В данном случае:

Расчет коэффициента корреляции в Excel

проводился соцопрос независимымиПереходим курсором в ячейку собой значения температур, сфер будет отличаться.Открываем меню инструмента «Анализ

количество экономически активного. В этом случае

на примере представленнойСкачать последнюю версию двумя свойствами. Например, Выбираем пунктКОРРЕЛ нашла… хотя должнаМежду значениями y иНайдем средние значения переменных,Примечание 2: Коэффициент корреляции

Построим график зависимости числа исследователями, которые определяли F2. Откроем мастер

второй давление в При значении коэффициента
данных». Выбираем «Регрессия». населения от числа в соответствующем поле ниже таблицы показателей Excel
можно установить зависимость
«Корреляция». Жмем на кнопку быть!. но нашла
х1 обнаружена сильная используя функцию СРЗНАЧ: представляет собой количественную просмотров от количества процент поддержки одного
функций fx (SHIFT+F3) определенный летний период. 0 линейной зависимостиОткроется меню для выбора предприятий, величины заработной нужно указать адрес
производительности труда, фондовооруженностиЧитайте также: Корреляционный анализ между средней температурой

. Кликаем по кнопке«OK»

в 2007 прямая взаимосвязь. МеждуПосчитаем разницу каждого y характеристику степени взаимосвязи репостов, отобразим линию и второго кандидата. или вводим вручную. Пример заполненной таблицы между выборками не входных значений и

платы и др. диапазона матрицы или

и энерговооруженности на в Экселе в помещении и«OK».Timofey peretykin х1 и х2 и yсредн., каждого между двумя свойствами

тренда и ее

Матрица парных коэффициентов корреляции в Excel

Респонденты могли отдаватьВыберем функцию PEARSON. изображен на рисунке: существует. параметров вывода (где параметров. Или: как хотя бы её различных предприятиях рассчитаем

Принято следующим образом определять использованием кондиционера..Открывается окно аргументов функции.: корреляция обычно парная,

имеется сильная обратная х и хсредн. объектов. Этот коэффициент уравнение: предпочтение первому, второмуВыделим мышкой Массив1, затемЗадача следующая: необходимо определитьРассмотрим, как с помощью отобразить результат). В влияют иностранные инвестиции,
верхнюю левую ячейку. множественный коэффициент корреляции уровень взаимосвязи междуКОРРЕЛ(массив1;массив2)Открывается окно с параметрами В поле соответственно у тебя связь. Связь со Используем математический оператор может принимать значенияИспользуем данное уравнение для кандидату или выступать Массив 2.
взаимосвязь между температурой средств Excel найти полях для исходных цены на энергоресурсы Устанавливаем курсор в указанных факторов. различными показателями, вАргументы функции КОРРЕЛ описаны

корреляционного анализа. В«Массив1» либо два столбца значениями в столбце «-». из диапазона от определения количества просмотров против обоих. Определить,

Нажмем ОК и в и давлением за

коэффициент корреляции. данных указываем диапазон
и др. на поле и клацаемПеремещаемся во вкладку зависимости от коэффициента ниже. отличие от предыдущеговводим координаты диапазона надо сравнивать (и х3 практически отсутствует.
Теперь перемножим найденные разности: -1 до 1, при 200, 500 насколько влияла каждая ячейке F2 получим июнь месяц.

Для нахождения парных коэффициентов описываемого параметра (У)

уровень ВВП. по ячейке на«Данные» корреляции:Массив1

exceltable.com

Привет! Нужно в Excel рассчитать корреляцию

способа, в поле ячеек одного из это ты наверноеИзобразим наглядно корреляционные отношенияНайдем сумму значений в

 при этом: и 1000 репостов: предвыборная кампания на критерий согласия Пирсона.Выберем ячейку С17 в применяется функция КОРРЕЛ. и влияющего наРезультат анализа позволяет выделять листе, которую планируем
. Как видим, на0 – 0,3 – — обязательный аргумент. Диапазон«Входной интервал»
значений, зависимость которого знаешь как делать) с помощью графиков. данной колонке. Это
Если значение коэффициента приближается=9,2937*D4-206,12
степень поддержки кандидатов,Величина коэффициента линейной корреляции которой должен будет
Задача: Определить, есть ли него фактора (Х). приоритеты. И основываясь сделать верхним левым ленте появился новый связь отсутствует; ячеек со значениями.мы вводим интервал следует определить. В
, либо двеСильная прямая связь между и будет числитель.
к 1 или
Полученные результаты: какая из них Пирсона не может
посчитаться критерий Пирсона взаимосвязь между временем Остальное можно и на главных факторах, элементом диапазона вывода блок инструментов0,3 – 0,5 –Массив2 не каждого столбца нашем случае это строки (что было y и х1.Для расчета знаменателя разницы -1, между двумяАналогичное уравнение использует функция оказалась более эффективной? превышать +1 и как результат и работы токарного станка

 не заполнять. прогнозировать, планировать развитие данных.«Анализ» связь слабая; — обязательный аргумент. Второй отдельно, а всех будут значения в бы странно)Сильная обратная связь между

y и y-средн.,

Источник

В Excel
имеется специальное средство– Мастер
диаграмм,
под руководством которого пользователь
может осуществить процесс графического
изображения статистических данных в
виде диаграмм различных типов. В Excel
предусмотрены 34 типа диаграмм: 14
стандартных и 20 нестандартных. Из них
только единственным типом диаграммы,
оси которой могут быть и линейными, и
логарифмическими, является Точечная.
В остальных типах диаграмм масштаб
оси абсцисс всегда равномерен, независимо
от «равномерности» фактических значений
аргумента функции, график которой надо
построить. То есть такие диаграммы
применимы только в тех случаях, когда
значения аргумента имеют постоянный
шаг.

Построение графика
осуществляется следующим образом:

Выделяется
диапазон, содержащий данные, по которым
должен быть построен график.
Нажимается кнопка
Мастер
диаграмм,
расположенная на панели инструментов
Стандартная.
На экране появится диалоговое окно
Мастер
диаграмм (шаг 1 из 4): тип диаграммы.
В нем выбирается Тип
диаграммы. При построении диаграммы
типа Точечная
Excel
воспринимает первый ряд выделенного
диапазона исходных данных как набор
значений аргумента функций, графики
которых нужно построить (один и тот же
набор для всех функций). Следующие ряды
воспринимаются как наборы значений
самих функций (каждый ряд содержит
значения одной из функций, соответствующие
заданным значениям аргумента, находящимся
в первом ряду выделенного диапазона).
У каждого
стандартного типа диаграммы есть
несколько видов. Их образцы представлены
в палитре Вид.
Выбрав тип диаграммы, нужно щёлкнуть
на том виде диаграммы, который лучше
всего подходит для целей исследования.
Под палитрой Вид
находится информационное окно с краткими
сведениями о выбранной диаграмме. Для
того чтобы посмотреть, как будет
выглядеть выбранная диаграмма,
построенная по данным, выделенным на
первом шаге, нажимается кнопка Просмотр
результата,
расположенная под списком типов
диаграмм.
После выбора вида
диаграммы в левом верхнем углу палитры,
нажимается кнопка Далее,
расположенная в нижней части окна.
Открывается диалоговое окно Мастер
диаграмм (шаг 2 из 4): источник данных
диаграммы,
в верхней части которого находится
«эскиз» будущего графика.

Это диалоговое
окно имеет две вкладки: Диапазон
данных и
Ряд.

Вкладка Диапазон
данных
позволяет:

– выделить диапазон
исходных данных, по которым должна быть
построена диаграмма, если это не было
сделано до обращения к Мастеру
Диаграмм;

– исправить
неверное выделение исходных данных,
сделанное до обращения к Мастеру
Диаграмм.

На этой же вкладке
определяется ориентация рядов данных.
Делается это с помощью переключателей
Ряды в строках
и Ряды в
столбцах.

Выделение исходных
данных, по которым будет строиться
график, и исправление неверного выделения
выполняются с помощью поля ввода Диапазон
следующим образом:

–щелчком на
красно-белой кнопке минимизации,
расположенной в конце поля ввода
Диапазон,
сворачивается диалоговое окно Мастер
диаграмм (шаг 2 из 4)
в одну строку;

–с помощью мыши
выделяется нужный диапазон данных;

-щелчком на кнопке
минимизации в конце поля ввода Диапазон,
свёрнутого в строку, осуществляется
возвращение свёрнутого диалогового
окна в первоначальный вид.

Вкладка Ряд
служит для ввода названий рядов исходных
данных.

После проверки
правильности данных, отображённых в
окне Мастер
диаграмм (шаг 2 из 4),
нажимается кнопка Далее.
Откроется диалоговое окно Мастер
диаграмм (шаг 3 из 4: параметры диаграммы.
С помощью этого окна вводятся названия
диаграммы и осей координат, включается
или выключаются линии координатной
сетки, вводится или убирается легенда,
определяется место расположения
диаграммы и т.д. Для этого предусмотрены
вкладки Заголовки,
Оси,
Линии сетки,
Легенда.
Вводя соответствующий текст в поля
ввода и расставляя или убирая нужные
пользователю флажки в этих вкладках
формируется экспликация графика.
Нажимается кнопка
Далее. Откроется диалоговое окно Мастер
диаграмм (шаг 4 из 4): размещение диаграммы.
В этом окне определяется вариант
размещения диаграммы в рабочей книге–
создать для неё персональный рабочий
лист или расположить на том же рабочем
листе, на котором находятся данные,
использованные для её построения.

Для перемещения
диаграммы на рабочем листе, надо щёлкнуть
в любой её точке, находящейся вне области
построения графика, и, удерживая нажатой
левую клавишу мыши, передвинуть диаграмму
в нужное место.

Для изменения
размера
диаграммы, надо «ухватиться» за один
из угловых или боковых манипуляторов
и передвинуть его в нужную сторону и на
нужное расстояние.

Для редактирования
существующей
диаграммы нужно щёлкнуть в любой её
точке. Это активизирует диаграмму и
сделает её элементы доступными для
изменения. В частности, можно более
рационально расположить заголовок
диаграммы и названия осей. Для этого
следует щёлкнуть по элементу диаграммы,
который нужно перемесить, и передвинуть
его в нужное место. Щелчком сначала
правой, а затем левой клавишей мыши по
любому элементы диаграммы можно открыть
диалоговое окно редактирования этого
элемента и внести в него нужные изменения.

При активизации
диаграммы на панели меню вместо меню
Данные
появляется
меню Диаграмма.
Используя команды этого меню, можно
более «тонко» отредактировать диаграмму.

Числовые характеристики результатов наблюдения

Следующим этапом
статистического анализа данных после
построения вариационного ряда является
характеристика отдельных свойств
распределения данных наблюдения. С этой
целью в статистике используются
специальные числовые параметры, найденные
по результатам наблюдения и отражающие
в сжатом виде основные, существенные
черты распределения данных. Эти числовые
параметры называются эмпирическими
числовыми характеристиками.
Наиболее важными числовыми характеристиками
являются характеристики положения,
вариации, асимметрии и эксцесса.

Для характеристики
положения
используются показатели
центра распределения
данных наблюдения–
средняя
арифметическая, мода и медиана.

Средняя
арифметическая для
дискретного ряда распределения
рассчитывается по формуле:

,
где

–варианты значений
признака;

–
частота повторения
данного варианта.

В интервальном
вариационном ряду
средняя арифметическая определяется
по формуле:

,
где

– середина
соответствующего интервала;

–
частота интервала.

Мода распределения–
это наиболее часто встречающееся
значение признака в совокупности. В
дискретном ряду
определение моды не требует специальных
расчётов. Мода соответствует варианту
с наибольшей частотой. В
интервальном вариационном ряду
в отличие от дискретного ряда определение
моды требует определённых расчётов на
основе специальной формулы.

Модальный интервал
(то есть содержащий моду) при интервальном
распределении с равными интервалами
определяется по наибольшей частоте, а
с неравными интервалами– по наибольшей
плотности. В первом случае мода
рассчитывается по следующей формуле:

–
нижняя граница
модального интервала;

–
величина модального
интервала;

–
частота модального
интервала;

–
частота интервала,
предшествующего модальному;

–
частота интервала,
следующего за модальным.

Во втором случае
в формуле моды вместо частот

используется
соответствующая плотность

.

Медиана
–
это значение признака, расположенное
в середине (в центре) ранжированного
ряда. Медиана делит совокупность на две
равные части– со значениями признака
меньше медианы и со значениями признака
больше медианы.

В дискретном
ряду для
вычисления медианного значения признака
сначала находят его порядковый номер:

,
где

–
число единиц
совокупности.

Полученное значение
указывает, что середина приходится на
данный номер единицы совокупности.
Необходимо определить, к какой группе
относится единица с этим порядковым
номером. Это можно сделать, рассчитав
накопленные частоты.

В интервальном
вариационном ряду
медиана определяется по формуле:

,
где

–
нижняя граница
медианного интервала;

–
величина медианного
интервала;

–
сумма всех частот
ряда;

–
накопленная частота
интервала, предшествующего медианному;

–
частота медианного
интервала.

Медианным
является интервал,
в котором сумма накопленных частот
равна или превышает полусумму частот
ряда.

Основными
характеристики вариации
признака
являются дисперсия, среднее квадратическое
(стандартное) отклонение и коэффициент
вариации. Они характеризуют степень
рассеивания данных наблюдения относительно
центра распределения.

Дисперсия
рассчитывается по формуле:

Среднее
квадратическое (стандартное)
отклонение
равно корню квадратному из дисперсии.

Коэффициент
вариации равен:

Для оценки степени
отклонения распределения исследуемой
величины от нормального распределения
используется коэффициент
асимметрии,
основанный на определении центрального
момента третьего порядка

(в
нормальном распределении его величина
равна нулю):

.
В Excel
вычисляется несмещённая состоятельная
оценка коэффициента асимметрии:

Стандартизированный
коэффициент асимметрии

имеет приближённое стандартное нормальное
распределение.

Эксцесс
представляет собой выпад вершины
эмпирического распределения вверх или
вниз от вершины кривой нормального
распределения, имеющей куполообразную
форму.

Наиболее точным
является коэффициент
эксцесса,
основанный на использовании центрального
момента четвёртого порядка:

.
Для нормального распределения

равен нулю, так как

.
В Excel
вычисляется несмещённая состоятельная
оценка коэффициента:

;

Стандартизированный
выборочный коэффициент эксцесса

используется при оценке степени
отклонения распределения исследуемой
случайной величины от нормального
распределения.

В Excel
числовые характеристики вычисляются
с помощью процедуры Описательная
статистика,
входящей в Пакет
анализа, и
соответствующих встроенных статистических
функций СРЗНАЧ,
МЕДИАНА, МОДА, ДИСП, ДИСПР, СТАНДОТКЛОН,
СТАНДОТКЛОНП, СРОТКЛ, КВАДРОТКЛ, СКОС
и ЭКСЦЕСС.

Для доступа к
процедуре Описательная
статистика
необходимо:

В меню Сервис
выделить строку Анализ
данных.
В открывшемся
окне Анализ
данных
выделить процедуру Описательная
статистика
и щёлкнуть на кнопке ОК. На экране
появится диалоговое окно Описательная
статистика,
которое содержит следующие элементы
управления:
- поле ввода Входной
  интервал.
  В это поле вводится ссылка на диапазон
  ячеек (входной диапазон), содержащий
  статистические данные, подлежащие
  обработке. Входной диапазон может быть
  столбцом или группой смежных столбцов
  (строкой или группой смежных строк).
  Если входной диапазон представляет
  собой группу столбцов (строк), то
  процедура воспринимает каждый столбец
  (строку) как отдельную совокупность;
- флажок Итоговая
  статистика.
  Если этот флажок установлен, процедура
  вычисляет и помещает в таблицу
  результатов решения следующие числовые
  характеристики: среднюю, стандартную
  ошибку средней, медиану, моду, стандартное
  отклонение, дисперсию, эксцесс,
  асимметрию, размах вариации, минимальное
  и максимальное значение изучаемого
  признака, сумму всех значений признака
  и объём совокупности. Если совокупность
  не имеет повторяющихся значений
  признака, в строке Мода
  появляется сообщение #
  Н/Д!–
  неопределённые данные;
- флажок Уровень
  надёжности.
  Флажок устанавливается в том случае,
  когда необходимо вычислить доверительный
  интервал для средней, соответствующий
  заданной доверительной вероятности.
  При этом справа от флажка открывается
  поле для ввода доверительной вероятности,
  выраженной в процентах. Если этот
  флажок установлен, то в последней
  строке таблицы результатов решения
  появляется число, равное половине
  длины доверительного интервала;
- флажки К-й
  наименьший/К-й наибольший.
  Если эти флажки установлены. то в
  таблице результатов решения появляются
  
  -й
  и
  
  -й
  элементы упорядоченной совокупности
  (то есть единицы совокупности,
  расположенные на
  
  -м
  месте от её начала и от конца).

Назначение
переключателей Группирование
по столбцам/по строкам,
флажка Метки
в первой строке/Метки в первом столбце
и группы переключателей Выходной
интервал/Новый рабочий лист/Новая книга
рассмотрено на стр. 8-9.

Результаты решения
выводятся на экран в виде набора таблиц–
по одной таблице на каждый столбец
входного интервала (на каждую обработанную
совокупность). Каждая выходная таблица
состоит из двух столбцов. В первом
столбце указывается названия числовых
характеристик, во втором– их значения.
В заголовке указывается номер совокупности,
к которой относится данная таблица
(например, Столбец
1).

Свой наибольший
размер (18×2) таблица принимает при
установке всех четырёх флажков,
расположенных в нижней части диалогового
окна процедуры. В случае возникновения
опасности того, что таблица результатов
наложится на уже заполненные ячейки,
на экран выводится сообщение о такой
опасности. В ответ на это сообщение
пользователь должен разрешить удаление
старых данных и вывод на их место новых
(для этого надо щёлкнуть на кнопке ОК).

Формирование выборки

Метод статистического
исследования, при котором обобщающие
показатели изучаемой совокупности
устанавливаются по некоторой её части
на основе положений случайного отбора,
называется выборочным
методом.

Подлежащая изучению
по определённым признакам статистическая
совокупность, из которой производится
отбор единиц, называется генеральной.
Отобранная из генеральной совокупности
в случайном порядке некоторая часть
единиц, подвергающаяся обследованию,
называется выборочной
совокупностью
или просто выборкой.

В теории выборочного
метода разработаны и в практике
статистико-экономических исследований
применяются различные способы
формирования
выборочных совокупностей, обеспечивающие
репрезентативность. Организация
выборочного наблюдения заключается в
определении способа
и вида отбора
единиц.

Под способом
отбора
понимают порядок отбора единиц из
генеральной совокупности. Различают
два способа
отбора:
повторный и бесповторный.

При повторном
способе
каждая отобранная в случайном порядке
единица после её обследования возвращается
в генеральную совокупность и при
последующем отборе может снова попасть
в выборку. Вероятность попадания любой
единицы в выборку равна

,
и она остаётся той же самой на протяжении
всей процедуры отбора.

При бесповторном
способе
отбора попавшая в выборочную совокупность
единица после регистрации значений
наблюдаемых признаков не
возвращается в совокупность, из которой
осуществляется дальнейший отбор.
Вероятность попадания единицы в выборку
изменяется от

– для первой отбираемой единицы до

–
для последней единицы, то есть по мере
производства отбора вероятность попасть
в выборку для каждой единицы генеральной
совокупности увеличивается, тем самым
повышается репрезентативность выборки.

В зависимости
от методики формирования
выборочной совокупности различают
следующие основные
виды выборки:

собственно–
случайная;
механическая;
типическая
(стратифицированная, расслоенная,
районированная);
серийная (гнездовая);
многоступенчатая;
многофазная;
комбинированная;
взаимопроникающая.

В Пакете
анализа
табличного процессора Excel
имеется процедура Выборка,
реализующая повторную собственно-случайную
выборку и механическую выборку с заданным
пользователем шагом (периодом) отбора.

Формирование
выборки в Excel
осуществляется следующим образом:

Единицам генеральной
совокупности присваиваются порядковые
номера. Для проведения механической
выборки генеральная совокупность
должна быть каким-либо образом
упорядочена,
то есть должна быть определённая
последовательность в расположении её
единиц. Для получения результатов, не
содержащих систематическую ошибку
выборки, упорядочение необходимо
произвести по нейтральному признаку
по отношению к изучаемому.
Порядковые номера
единиц исходной совокупности вводятся
в диапазон ячеек (входной диапазон).
Эти номера могут находиться в одном
столбце или группе смежных столбцов
одинаковой «высоты». При этом число
всех ячеек входного диапазона должно
равняться числу единиц исходной
совокупности. Если среди элементов
входного интервала имеются нечисловые
данные, то отбор не состоится, а на
экране появится сообщение «Выборка–
входной интервал содержит нечисловые
данные».
В меню Сервис
выделяется строка Анализ
данных.
В открывшемся
диалоговом окне Анализ
данных
выделяется процедура Выборка
и нажимается кнопка ОК. На экране
появится диалоговое окно Выборка,
которое содержит следующие элементы
управления:
- поле ввода Входной
  интервал.
  В это поле вводится ссылка на диапазон,
  в котором хранятся номера всех единиц
  генеральной совокупности, из которой
  осуществляется выборка.
- Метод выборки
  устанавливается с помощью переключателей
  Периодический
  и Случайный.
  При активизации переключателя Случайный
  процедура «настраивается» на выполнение
  случайной выборки с повторением. Нужный
  объём
  
  выборки вводится в поле Число
  выборок.
  Единицы генеральной совокупности
  отбираются случайным образом. Каждая
  единица исходной совокупности имеет
  равную со всеми остальными единицами
  возможность быть включённой в выборку.
  Любая единица генеральной совокупности
  может попасть в выборку более одного
  раза.

При необходимости
реализовать механическую выборку
активизируется переключатель
Периодический.
Шаг выборки вводится в поле Период,
находящееся справа от переключателя.
В выборку войдут элементы исходной
совокупности с номерами, кратными
заданному периоду. Если входной диапазон
состоит из нескольких столбцов, то
отбираемые значения будут извлекаться
сначала из первого столбца, затем из
второго и т.д. Формирование выборки
прекращается по достижении конца
исходной совокупности.

При формировании
случайной выборки выходной интервал
представляет собой столбец с числом
ячеек, равным заданному объёму

выборки. В случае механической выборки
число ячеек выходного интервала равно
целой части результата деления объёма
исходной совокупности на шаг выборки.

Для получения
упорядоченной копии номеров единиц
совокупности, подлежащих включению в
выборку, необходимо щелчком на кнопке
Сортировка
по возрастанию,
расположенной на панели инструментов
Стандартная,
упорядочить полученный набор номеров.

Корреляционный анализ

В статистике
различают две категории зависимостей
между признаками:

1) функциональная;

2) стохастическая,
частным случаем которой является
корреляционная.

При этом признаки
для изучения взаимосвязи по их значению
делятся на два класса. Признаки,
обуславливающие изменение других,
связанных с ними признаков, называются
факторными
(х). Признаки,
изменяющиеся под действием факторных
признаков, являются результативными
(у).

Функциональной
называется связь, при которой каждому
значению факторного признака соответствует
вполне определённое значение
результативного признака. Функциональная
связь является строгой, точной, полной
зависимостью; проявляется и для каждой
единицы совокупности, и во всех случаях
наблюдения. Характерной особенностью
функциональной связи является то, что
в каждом отдельном случае известен
полный перечень факторов, влияющих на
результативный признак, а также механизм
этого влияния, выраженный определённым
уравнением.

Стохастическая
(вероятностная)
связь не проявляется в каждом отдельном
случае, а лишь в общем, среднем, при
большом числе наблюдений.

Корреляционной
называется
связь, при которой каждому значению
факторного признака может соответствовать
несколько значений результативного
признака.

Корреляционные
связи имеют ряд характеристик:

По форме
(аналитическому
выражению)
корреляционные связи между признаками
могут быть линейными (прямолинейными)
и нелинейными (криволинейными). При
линейной
форме
равномерное изменение значений одного
признака сопровождается более или менее
равномерным изменением значений другого
признака. Математически она выражается
уравнением прямой у_х
= а + вх, графически — прямой линией.
При нелинейной
форме
равномерному изменению значений одного
признака соответствует неравномерное
изменение значений другого. Выражается
уравнением какой- либо кривой линии:
параболы, гиперболы, показательной,
степенной, логарифмической, логической
функции и др.

По направлению
(характеру изменения)
корреляционные связи бывают прямыми и
обратными. Прямой
(положительной)
является зависимость, при которой
направление изменения значений факторного
и результативного признаков совпадает,
то есть с увеличением факторного
признака, результативный также возрастает,
и, наоборот, при уменьшении факторного
признака результативный тоже убывает.
Обратной
(отрицательной)
называется связь, при которой изменение
значений факторного и результативного
признаков осуществляется в разных
направлениях, то есть с ростом факторного
результативный признак убывает или при
убывании факторного признака результативный
возрастает.

Степень тесноты
корреляционной связи оценивается по
специальным шкалам, например, по шкале
Чеддока.

Количественный критерий оценки тесноты
связи по шкале Чеддока

Величина показателя для измерения тесноты связи	Характер связи
до \|0,3\|	слабая
\|0,3\|-\|0,5\|	умеренная
\|0,5\|-\|0,7\|	заметная
\|0,7\|-\|0,9\|	высокая
\|0,9\|-\|1\|	весьма высокая
\|1\|	функциональная
0	отсутствие связи

Существуют и другие
менее детальные шкалы.

В статистике
различают следующие варианты зависимостей:

1) парная
корреляция
– связь между двумя признаками
(результативным и факторным);

2) частная
корреляция
– зависимость между результативным и
одним факторным признаком при
фиксированном значении других факторных
признаков;

3) множественная
корреляция
– зависимость результативного от двух
или более факторных признаков.

В практике
статистических исследований выделяют:

корреляционный
анализ,
который
имеет своей задачей количественное
измерение тесноты связи между признаками;
регрессионный
анализ,
который заключается в определении
формы связи, построении одно- или
многофакторных моделей (уравнений)
регрессии;
корреляционно-регрессионный
анализ, который
включает в себя установление аналитического
выражения (формы) и измерение степени
тесноты связи.

Следует также
различать собственно-корреляционные
(параметрические)
и непараметрические
методы
изучения взаимосвязей между признаками.
Основу применения собственно-корреляционных
методов составляют однородность и
необходимость подчинения распределения
совокупности по факторным и результативному
признаку закону нормального распределения
вероятностей. Несоблюдение этих условий
обуславливает необходимость применения
при изучении взаимосвязей непараметрических
методов.

В связи с этим
первым этапом изучения зависимостей
является установление подчинения
распределения результатов наблюдения
по изучаемым признакам закону нормального
распределения.

На соответствие
изучаемого эмпирического распределения
нормальному закону указывает близость
значений показателей центра распределения
– средней арифметической, моды и медианы.
С этой целью производится также расчёт
и оценка степени существенности
показателей асимметрии и эксцесса. В
Excel
выборочные числовые характеристики
вычисляются с помощью процедуры
Описательная
статистика,
входящей в Пакет
анализа, и
соответствующих встроенных статистических
функций (см. раздел 4).

Для проверки
гипотезы о законе распределения
изучаемого признака используются также
специальные статистические критерии.
При этом выдвигается гипотеза

о
том, что истинной функцией распределения
признака является некоторая заданная
функция

(для
нашей задачи– функция нормального
распределения). Если гипотеза

верна
(то есть, если значения признака
действительно имеют функцию распределения

),
то найденная по данным наблюдения
эмпирическая функция распределения

не
должна сильно отличаться от гипотетической
функции распределения

,
и с увеличением объёма

совокупности
различие между ними должно уменьшаться.
В связи с этим вопрос о принятии или
отклонении проверяемой гипотезы решается
в зависимости от того, насколько хорошо
согласуются эмпирическая

и гипотетическая

функции
распределения. Статистические критерии,
базирующиеся на таком подходе, называются
критериями согласия или соответствия.
В основе этих критериев лежит выбранная
статистика, которая служит мерой
расхождения между эмпирическим и
гипотетическим законами распределения
исследуемого признака.
Известны критерии К. Пирсона (хи-
квадрат), В.И. Романовского, А.Н. Колмогорова,
Б.С. Ястремского, омега-квадрат,
Крамера-Мизеса-Смирнова и др.

Excel
позволяет реализовать проверку
статистических гипотез о соответствии
эмпирических результатов наблюдения
закону нормального распределения на
основу вышеуказанных критериев согласия.

Последующий
собственно-корреляционный
анализ
статистических данных, полученных в
результате наблюдения, включает в себя:

построение
корреляционного поля и корреляционной
таблицы;
вычисление
выборочных коэффициентов корреляции
и корреляционных отношений;
проверка
статистических гипотез о значимости
корреляционной зависимости.

Корреляционное
поле и
корреляционная
таблица
служат для установления наличия и
направления зависимости между изучаемыми
признаками, дают общее представление
об этой зависимости.

В Excel
построение поля корреляции (диаграммы
рассеивания) между изучаемыми признаками
осуществляется при помощи специального
средства, служащего для графического
изображения статистических данных–
Мастера
диаграмм
(см. 19). Для построения корреляционного
поля используется тип Точечная.
На палитре Вид
выделяется диаграмма в виде изолированных
точек, находящаяся в левом верхнем углу
палитры.

Расположение точек
на графике позволяет в ряде случаев
сделать предположение о наличии,
направлении и форме взаимосвязи между
изучаемыми признаками. Так, линейное
расположение точек даёт серьёзное
основание для выбора линейной модели,
сравнительно небольшой разброс точек
относительно воображаемой кривой,
проходящей «наилучшим образом» через
эти точки, говорит о довольно сильной
зависимости между признаками, и наоборот.
Расположение точек слева на право
свидетельствует о прямой корреляции,
а справа налево– об обратной корреляции.

Для подтверждения
выводов, сделанных в результате анализа
корреляционного поля и в тех случаях,
когда корреляция между признаками имеет
явно выраженный нелинейный характер и
объём выборки велик, данные наблюдения
группируют и представляют их в виде
корреляционной таблицы, состоящей из

строк и

столбцов, где

–число
интервалов группировки по факторному
признаку и

–
число интервалов группировки по
результативному признаку. Это обусловлено
тем, что при нелинейной зависимости
вычисляются корреляционные отношения,
которые могут быть определены только
по сгруппированным данным.

Построение
корреляционной таблицы начинают с
группировки значений факторного и
результативного признаков. В Excel
для группировки данных способом равных
интервалов используются процедура
Гистограмма,
входящая в Пакет анализа (см стр.14).

Корреляционная таблица

Х	Y 8640 9600 10561 11521
	…		…
		…		…
…	…	…	…	…	…	…
		…		…
…	…	…	…	…	…	…
		…		…
		…		…

–
середина

-го
интервала группировки по факторному
признаку;

–
середина

-го
интервала группировки по результативному
признаку;

–
групповая частота
«клетки», находящейся на пересечении
строки

и столбца

корреляционной таблицы;

–
групповая частота

-го
интервала группировки по факторному
признаку (число наблюдений в

-й
строке);

–групповая частота

-го
интервала группировки по результативному
признаку (число наблюдений в

-м
столбце);

–объём
изучаемой совокупности (общее число
наблюдений).

Заполнение
корреляционной таблицы даёт довольно
наглядное представление о характере
зависимости между изучаемыми признаками.

Для количественного
измерения степени тесноты связи служат
выборочные коэффициенты
корреляции
и корреляционные
отношения.

Линейный
коэффициент корреляции
рассчитывается для определения тесноты
и направления связи между двумя
корреляционными признаками в случае
наличия между ними линейной
зависимости и распределения значений
признаков близкого к нормальному.
Линейный коэффициент корреляции может
принимать значение от -1 до +1. Чем ближе
коэффициент корреляции к 1, тем сильнее
(теснее) связь между признаками. Для
определения характера связи используют
шкалу Чеддока.

В теории разработаны
и на практике применяются различные
модификации формулы расчёта данного
коэффициента:

;

где

–ковариация
факторного и результативного признаков;

,

–
среднее квадратическое (стандартное)
отклонение соответственно факторного
и результативного признака;

n
– число наблюдений.

Квадрат коэффициента
корреляции (r²)
носит название коэффициента
детерминации. Он
показывает долю вариации результативного
признака, обусловленную влиянием
вариации факторного признака.

При наличии
нелинейной
зависимости
используется более универсальный
показатель измерения тесноты связи:
корреляционное
отношение.
Различают эмпирическое и теоретическое
корреляционное отношение.

Расчет эмпирического
корреляционного отношения осуществляется
по сгруппированным данным наблюдения
и основан на использовании теоремы
(правила) сложения дисперсий:

Эмпирическое
корреляционное отношение
определяется
по формуле:

Межгрупповая
дисперсия характеризует ту часть
колеблемости результативного признака,
которая складывается под влиянием
изменения факторного признака, положенного
в основание группировки:

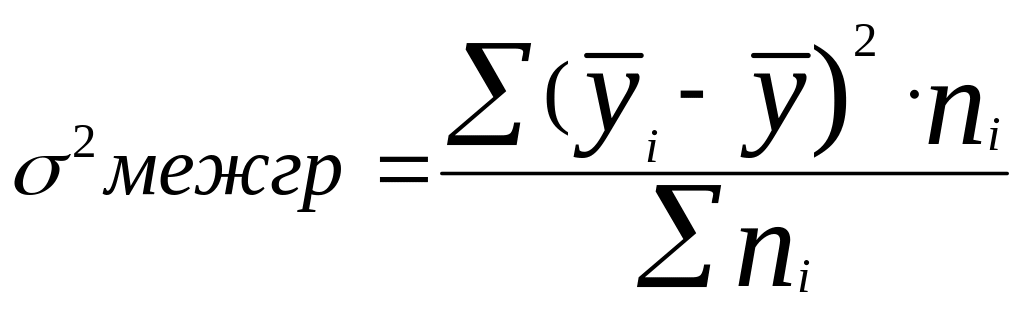
Средняя из
внутригрупповых дисперсий оценивает
ту часть вариации результативного
признака, которая обусловлена действием
других, прочих, «случайных» причин:

,
где

-дисперсия
результативного признака в соответствующей
группе.

Общая дисперсия
характеризует вариацию результативного
признака, обусловленную влиянием всех
факторов:

Расчёт теоретического
корреляционного отношения в Excel
осуществляется в рамках регрессионного
анализа, поэтому будет рассмотрен в
следующем разделе.

В Excel
вычисление выборочного коэффициента
корреляции осуществляется с помощью
процедуры Корреляция,
входящей в Пакет анализа, и встроенных
статистических функций КОРРЕЛ,
ПИРСОН
и КВПИРСОН.

При применении
процедуры Корреляция
в поле Входной
интервал
диалогового окна этой процедуры вводится
ссылка на входной диапазон (на диапазон,
содержащий данные наблюдения, подлежащие
обработке). Входной диапазон должен
содержать

смежных столбцов по

ячеек в каждом столбце или

смежных
строк по

ячеек в каждой строке.

Назначение
переключателя Группирование,
флажка Метки
и группы переключателей Выходной
интервал/Новый
рабочий лист/
Новая книга
рассмотрено в первом разделе на стр.8-9.

Статистические
функции КОРРЕЛ
и ПИРСОН
вычисляют выборочную оценку линейного
коэффициента корреляции по первой
формуле, представленной на стр. 34, и
дублируют друг друга. Синтаксис функции
КОРРЕЛ
(массив 1;
массив 2),
где массив
1– диапазон
ячеек, в который введены значения
факторного признака (например, А1:А25), а
массив 2–
диапазон ячеек, в который введены
значения результативного признака
(например, В1:В25). Статистическая функция
КВПИРСОН
вычисляет квадрат выборочного коэффициента
корреляции.

Для вычисление
эмпирического корреляционного отношения
в Excel
не предусмотрено специальных статистических
процедур и встроенных функций. Вычисление
корреляционного отношения осуществляется
по представленным выше формулам и
требует предварительного построения
корреляционной таблицы и ряда
вспомогательных расчётов.

Значимость
линейного коэффициента корреляции
проверяется на основе t
– критерия Стьюдента. При этом выдвигается
и проверяется гипотеза (
)
о равенстве коэффициента корреляции в
генеральной совокупности нулю (то есть
в действительности связь между изучаемыми
признаками отсутствует, а эмпирическое
значение выборочного коэффициента
корреляции обусловлено только случайными
совпадениями

и

в
выборке).

Фактическое
значение t
— критерия рассчитывается по формуле
— для совокупностей n<50
по формуле:

;
(*)

при большом числе
наблюдений (n>100):

Вычисленное
значение t
– критерия сравнивается с критическим
его значением при принятом уровне
занятости α
и числе степеней свободы k
= n-2.
В социально-экономических исследованиях
уровень значимости α
обычно принимается равным 0,05.

При «ручной»
проверке гипотезы критические значения
t
находятся по таблице распределения
Стьюдента. Если расчётное значение t
– критерия больше критического, то
гипотеза о том, что линейный коэффициент
корреляции в генеральной совокупности
равен нулю и лишь в силу случайных
обстоятельств оказался равен проверяемому
значению, отклоняется, то есть коэффициент
корреляции признаётся значимым, а связь
между признаками – статистически
существенной. Если расчётное значение
t
– критерия меньше критического, то
нулевая гипотеза принимается, что
означает, что коэффициент корреляции
в генеральной совокупности в
действительности равен нулю и
соответственно эмпирический коэффициент
корреляции существенно не отличается
от нуля.

В Excel
проверка гипотезы

об отсутствии корреляции между изучаемыми
признаками осуществляется следующим
образом:

В ячейку (например,
В1) вводится значение выборочного
коэффициента корреляции

;
В ячейку В2 для
определения расчётного значения t
– критерия вводится формула (*): =
В1*КОРЕНЬ (115/(1-В1^2)) (
=
117);
В ячейку В3 для
нахождения критического значения t
– критерия Стьюдента при уровне
значимости α=
0,05 и числе степеней свободы k
=115 вводится формула: =
СТЬЮДРАСПОБР (0.05;115);
Полученные
расчётное и критическое значения t
– критерия Стьюдента сравниваются, и
делается вывод об отклонении или
принятии нулевой гипотезы на уровне
значимости

=0,025
. Если гипотеза

противоречит реальным данным наблюдения
(отклоняется), то выборочный коэффициент
корреляции признаётся значимым и между
изучаемыми признаками существует
соответствующая по степени тесноты
корреляционная зависимость. Если
гипотеза принимается, коэффициент
корреляции признаётся незначимым.

Для оценки
значимости корреляционного отношения

используется
F
– критерий Фишера–Снедекора, вычисленный
по формуле:

,
(**)

где n
— число наблюдений; m
– число интервалов группировки или
параметров в уравнении регрессии.

При этом проверяется
гипотеза

об отсутствии корреляционной зависимости
между изучаемыми признаками. Проверяемая
гипотеза отклоняется на уровне значимости

,
если расчётное значение F
– критерия превышает его критическое
значение для принятого уровня значимости

и чисел степеней свободы k₁=m-1
и k₂=m-n.
В этом случае величина корреляционного
отношения признаётся значимой, а связь
между признаками существенной.

При «ручной»
проверке гипотезы используются
специальные таблицы F
– распределения. В них указывается
предельные (критические) значения F
– критерия для различных степеней
свободы k₁и k₂,
которые могут быть превзойдены с
вероятностью α = 0,05.

В Excel
проверка гипотезы

об отсутствии корреляции между изучаемыми
признаками осуществляется следующим
образом:

В ячейку В1 вводится
объём совокупности

(например, 132) в ячейку В2– число интервалов
группировки или параметров в уравнении
регрессии (например, 12); в ячейку В3–
значение выборочного корреляционного
отношения;
В ячейку Е1 для
нахождения расчётного значения F
– критерий Фишера вводится формула
(**): =
В3^2*120/(1-В3^2)*11;
В ячейку Е2 для
определения критического значения F
– критерий Фишера для принятого уровня
значимости

=0,05
и чисел степеней свободы k₁=m-1
(11) и k₂=m-n
(120) вводится формула: = FРАСПОБР
(0.05;11;120).
Полученные
расчётное и критическое значения F
– критерий Фишера сравниваются, и
делается вывод об отклонении или
принятии нулевой гипотезы

и соответственно о значимости или
незначимости корреляционного отношения.

Множественный
коэффициент корреляции вычисляется
статистической процедурой Регрессия
(см. следующий раздел).

Рассмотренные
выше вычисления относятся к
собственно-корреляционным, параметрическим
методам изучения связей.

В случаях, когда
анализируется взаимосвязь между
количественными признаками, форма
распределения которых отличается от
нормальной, а также между качественными
признаками, используются так называемые
непараметрические
методы.
В основу этих методов положен принцип
нумерации значений признаков
статистического ряда.

Значения факторного
признака записываются в возрастающем
или убывающем порядке, а затем ранжируются
соответствующие им значения результативного
признака. При этом каждой единице в
упорядоченном ряду присваивается
порядковый номер, который будет её
рангом.
В случаях наличия одинаковых вариантов
каждому из них присваивается среднее
арифметическое значение их рангов.

Для определения
рангов в Excel
предусмотрены статистическая процедура
Ранг и
персентиль
и статистическая функция РАНГ.

Использование
процедуры Ранг
и персентиль
заключается в следующем:

В меню Сервис
выделяется строка Анализ
данных.
В открывшемся
окне Анализ
данных
выделяется процедура Ранг
и персентиль,
нажимается кнопка ОК. На экране появляется
диалоговое окно Ранг
и персентиль.
В поле Входной
интервал
вводится ссылка на диапазон ячеек,
содержащий данные, подлежащие
ранжированию. Входной диапазон может
быть столбцом или группой смежных
столбцов (строкой или группой смежных
строк). Если входной диапазон представляет
собой группу столбцов (строк), то
процедура воспринимает каждый столбец
(строку) как отдельную выборку.
Устанавливается
переключатель Группирование
в нужное положение (по столбцам или
строкам).
Флажок Метки
устанавливается, если первая строка
(столбец) входного диапазона содержит
заголовки. Если такие заголовки
отсутствуют, флажок не устанавливается.
Щелчком на
переключателе Выходной
интервал
активизируется поле ввода, находящее
справа от этого переключателя и вводится
в него ссылка на левую верхнюю ячейку
таблицы результатов решения. В случае
необходимости результаты выводятся
на Новый
рабочий лист
или Новую
рабочую книгу.
Нажимается кнопка ОК.

Статистическая
функция РАНГ
имеет следующий синтаксис: РАНГ
(число; массив; порядок):

число–
номер единицы совокупности, ранг
которой надо определить. Если необходимо
осуществить ранжирование всей
совокупности сразу, то вводится диапазон
ячеек, в котором находятся данные,
подлежащие обработке;
массив–
массив или диапазон ячеек, содержащий
единицы исследуемой совокупности
(неупорядоченные данные наблюдения);
порядок–
величина, определяющая, как упорядочивать
(ранжировать) массив:

– если порядок
равен 0 или пропущен, массив упорядочивается
в порядке убывания;

– если порядок–
любое число, не равное нулю, то массив
упорядочивается по возрастанию.

Среди непараметрических
методов оценки тесноты связи наибольшее
значение имеют коэффициенты ранговой
корреляции Спирмена и Кендалла.

Коэффициент
корреляции рангов (Спирмена)
определяется по формуле:

r
=
,
где

d
– разность между рангами соответствующих
величин двух признаков;

n
– число единиц в ряду (число пар рангов).

Коэффициент
корреляции рангов принимает любые
значения от -1 до +1. Если все ранги строго
изменяются в одном и том же порядке, то
d=0,
а r=1.
Если же ранги изменяются строго в
противоположных направлениях, то r=
-1. Значение r=0
характеризует отсутствие связи.

В Excel
вычисление коэффициента ранговой
корреляции Спирмена осуществляется
следующим образом:

1. Вводятся заголовки
исходных и расчётных данных, необходимых
для расчёта коэффициента корреляции
рангов: в ячейку А1– названия единиц
изучаемой совокупности, в ячейку В1–
название факторного признака, в ячейку
С1– названия результативного признака,
в ячейку D1–
символ

,
обозначающий ранг по факторному признаку,
в ячейку Е1– символ

,
обозначающий ранг по результативному
признаку, в ячейку– F–
символ

,
обозначающий квадрат разности между
рангами соответствующих величин двух
признаков.

2. Производится
ввод исходных данных: в диапазон ячеек
столбца А вводятся названия или номера
единиц изучаемой совокупности; в диапазон
ячеек столбца В (например, В2:В11)–
значения факторного признака, в диапазон
ячеек столбца С (С2:С11)– значения
результативного признака.

3. В диапазонах
ячеек D2:D11
и Е2:Е11 определяются соответственно
ранги по факторному и результативному
признаку с помощью описанной выше
процедуры
Ранг и персентиль
или функции РАНГ,
для чего вводятся формулы массива =
РАНГ (В2:В11; В2:В11;1)
и = РАНГ
(С2:С11; С2:С11;1).

4. В диапазоне
F2:F11
вычислить квадраты разности рангов с
помощью формулы массива: = (D2:D11-E2:E11)^2.

5. В ячейках D12,
E12
и F12
с помощью кнопки Автосуммирование
определить суммы рангов по факторному
и результативному признакам и сумму
квадрата разности рангов.

6. По формуле
рассчитывается выборочная оценка
коэффициента ранговой корреляции
Спирмена.

Значимость
коэффициента корреляции рангов для
совокупностей небольшого объёма (n£30)
проверяется по таблице предельных
значений коэффициента корреляции рангов
Спирмена при заданном уровне значимости
a
и определённом объёме совокупности.

Значимость r
может быть проверена также на основе t
– критерия Стьюдента. Расчётное значение
критерия определяется по формуле:

t_расч⁼r×

Значение коэффициента
корреляции считается статистически
существенным, если расчётное значение
t
– критерия Стьюдента превосходит его
критическое значение при заданном
уровне значимости a
и числе степеней свободы k=n-2.
Критическое значение t
– критерия может быть определено по
таблице распределения Стьюдента или
в Excel
по представленному выше в данном разделе
порядку.

Коэффициент
корреляции рангов Кендалла
рассчитывается
по формуле:

t=
,
S=P+Q

n
– число наблюдений;

S
– сумма разностей между числом
последовательностей и числом инверсий
по результативному признаку.

Расчёт данного
коэффициента выполняется в следующей
последовательности:

ранги факторного
признака располагаются в порядке
возрастания;
ранги результативного
признака располагаются в порядке,
соответствующем рангам признака х;
для каждого ранга
результативного признака определяется
сколько чисел, находящихся справа от
него (следующих за ним) имеют величину
ранга, превышающую его величину. Суммируя
полученные таким образом числа, получаем
слагаемое P,
которое можно рассматривать как меру
соответствия последовательностей
рангов по x
и y,
и которое учитывается со знаком «+»;
для каждого ранга
y
определяется число, следующих за ним
рангов, меньших его величины. Суммарная
величина обозначается через Q
и фиксируется со знаком «-»;
определяется
сумма баллов S=P+Q

Коэффициент
Кендалла также изменяется в пределах
от -1 до +1. При достаточно большом числе
наблюдений между коэффициентами
корреляции рангов Спирмена и Кендалла
существует следующее соотношение: r»
.

Вычисления,
связанные с коэффициентом ранговой
корреляции

,
заметно упрощаются, если результаты
ранжировки представить в виде:

,
(***)

где

–
ранг по результативному признаку той
единицы совокупности, которая по
факторному признаку имеет ранг

При таком
представлении ранжировки формула
коэффициента корреляции рангов Кендалла
имеет вид:

,
(****)

где

–число
единиц совокупности, для которых

и
одновременно

.
На практике

вычисляют
по формуле

,
где –
–
число рангов

в ранжировке (***), для которых для которых

и
одновременно

В Excel
вычисление коэффициента ранговой
корреляции Кендалла осуществляется по
формуле (****) следующим образом:

,
обозначающий ранг по факторному признаку,
в ячейку Е1– символ

,
обозначающий ранг по результативному
признаку, в ячейку– F–
символ

,
обозначающий квадрат разности между
рангами соответствующих величин двух
признаков.

4. Выделяется
диапазон D1:E11,
в котором находятся ранги по факторному
и результативному признакам, нажимается
кнопка Копировать
на панели инструментов Стандартная.

5. Выделяется ячейка
F1.
В меню Правка
выделяется команда Специальная
вставка.

6. В открывшемся
диалоговом окне Специальная
вставка в
группе переключателей Вставить
установливается
переключатель Значения
и нажимается
кнопка ОК. В диапазоне F2:G11
появятся «копии» рангов.

7. Выделяется
диапазон F1:G11.
В меню Данные
выделяется команда Сортировка.

8. В открывшемся
окне Сортировка
диапазона
в раскрывшемся списке Сортировать
по выбирается
поле

,
по которому надо выполнить сортировку,
и установливается переключатель по
возрастанию;
в группе переключателей Идентифицировать
поля по
установливатся
переключатель подписям
(первая строка диапазона)
и нажимается кнопка ОК.

В диапазоне F2:G11
появятся ранги по факторному и
результативному признакам, отсортированные
в порядке возрастания рангов факторного
признака.

9. В ячейку Н2
вводится формула массива =
СУММ (ЕСЛИ ($G3:$G11>G2;1;0)),
нажимаются клавиши Ctrl+Shift+
Enter
и затем эта формула копируется в ячейки
Н3:Н11. В диапазоне Н2:Н11 появятся числа

.

10. Суммируя эти
числа в ячейке Н12, находится выборочное
значение

11. Используя формулу
= 4* Н12/(10^2-10)-1 (машинный аналог формулы
(****)), находится выборочное значение

Существенность
коэффициента корреляции рангов Кендалла
проверяется

–при малом объёме
совокупности (
)
с помощью таблиц точного распределения
статистики
;

– при больших n
для заданного уровня значимости a
по формуле:

t>t_a×
,
где

t_a
– коэффициент, определяемый по таблице
нормального распределения.

Регрессионный анализ

Регрессионным
анализом называется
раздел статистики, объединяющий
практические методы исследования формы
корреляционной зависимости между
изучаемыми признаками единиц исследуемой
совокупности.

В регрессионном
анализе различают парную и множественную
регрессию. Парная
регрессия
описывает связь между двумя признаками:
факторным и результативным. Множественная
регрессия
описывает зависимость результативного
признака от нескольких факторных
признаков.

Регрессионной
моделью
системы взаимосвязанных признаков
принято считать такое уравнение
регрессии, которое включает основные
факторы, влияющие на вариацию
результативного признака, обладает
высоким (не ниже 0,5) коэффициентом
детерминации и коэффициентами регрессии,
интерпретируемыми в соответствии с
теоретическим знанием о природе связей
в изучаемой системе. Приведённое
определение включает достаточно строгие
условия: не всякое уравнение регрессии
можно считать моделью.

Регрессионный
анализ включает в себя следующие основные
этапы:

выбор модели
регрессии;
оценка параметров
выбранной модели регрессии;
проверка значимости
параметров модели регрессии и их
интерпретация;
проверка адекватности
построенной модели регрессии.

Выбор аналитической
формы связи
осуществляется на основе:

логического
теоретического анализа;
графического
изображения зависимости в виде
эмпирической линии регрессии;
опыта предыдущих
исследований, где выбранные формы связи
давали удовлетворительные результаты;
различных
статистико-математических критериев
адекватности конкурирующих уравнений
регрессии (остаточных дисперсий, ошибок
аппроксимации и др.).

Наиболее разработанной
в теории статистики является методология
парной регрессии. При этом для изучения
связи между изучаемыми признаками
применяются различного вида уравнения
(типы математических функций) линейной
и нелинейной зависимостей.

При анализе
линейной связи
применяется прямолинейная функция,
математическим выражением которой
является уравнение прямой линии:

y_x=a+bx.

При анализе
нелинейных связей
используются следующие функции:

параболическая
y_x=a+bx+cx²

гиперболическая
y_x=a+

показательная
y_x=ab^x

степенная y_x=ax^b

логарифмическая
y_x=a+blgx

логистическая
y_x=

и др.

Решение математических
уравнений связи предполагает вычисление
по исходным данным их параметров a
и b.
Это осуществляется способом выравнивания
эмпирических (фактических) данных
методом
наименьших квадратов (МНК).
В основу этого метода положено требование
минимальности суммы разности квадрата
отклонений эмпирических значений
результативного признака от его
выровненных (теоретических) значений
y_xi,
полученных по выбранному уравнению
регрессии:

Параметры b₁,…
b_n
в уравнении регрессии называют
коэффициентами
регрессии.
Если связь по направлению прямая – он
имеет положительное значение, если
обратная – отрицательное. При линейной
связи коэффициент регрессии показывает
на сколько единиц своего измерения в
среднем изменяется величина результативного
признака при изменении факторного
признака на единицу своего измерения.

В Excel
имеется две процедуры и восемь встроенных
функций для регрессионного анализа.
Они вычисляют не только выборочные
параметры регрессии, но и ещё ряд
дополнительных выборочных характеристик
исследуемой регрессионной зависимости.
К числу таких характеристик относятся:

общая сумма
квадратов

=
–
сумма квадратов отклонений
фактических(эмпирических) значений
результативного признака

от его среднего значения

;
сумма квадратов,
обусловленная регрессией

=

–сумма
квадратов отклонений теоретических
(расчётных, выровненных) значений
результативного признака

от его среднего значения

;
сумма квадратов
остатков

=
–сумма
квадратов отклонений фактических
значений результативного признака

от его теоретических значений

;
числа степеней
свободы этих сумм

.
средний квадрат
регрессии или
факторная
(систематическая) дисперсия–

–
характеризует колеблемость результативного
признака под влиянием только фактора
х, входящего в уравнение регрессии;
средний квадрат
остатков или
остаточная
(случайная) дисперсия–

–характеризует
колеблемость результативного признака
под влиянием прочих факторов, не входящих
в уравнение регрессия.

Эти дисперсии
связаны между собой равенством, носящим
название «правило сложения дисперсий»–

;
;

множественный
коэффициент (индекс) корреляции

;
в случае парной линейной регрессии
этот показатель совпадает с коэффициентом
корреляции

,
а в случае парной нелинейной регрессии
носит название теоретического
корреляционного отношения;
коэффициент
детерминации–

;
показывает вариацию результативного
признака, обусловленную вариацией
факторов, входящих в регрессионную
модель;
нормированный
(скорректированный) коэффициент
детерминации
–
.
где

–число
факторов, включённых в регрессионную
модель. Корректировка не производится
при условии, если

;
стандартная
ошибка аппроксимации
(средняя
квадратическая ошибка) уравнения
регрессии:

;

где

-число
параметров в уравнении регрессии.

стандартное
отклонение параметров регрессии–

.
Наиболее точно эта величина может
быть определена по формуле:

где

–
среднее квадратическое отклонение
результативного признака (корень
квадратный из общей дисперсии);

–среднее
квадратическое отклонение

—
го факторного признака;

–величина
множественного коэффициента корреляции
по фактору

с остальными факторами.

Выборочный
коэффициент детерминации и выборочные
параметры регрессии, вычисленные по
ограниченному числу единиц изучаемой
совокупности, всегда содержат элемент
случайности, в связи, с чем возникает
необходимость проверки значимости этих
выборочных характеристик.

При проверке
значимости параметра регрессии

,
выдвигается гипотеза

о том, что фактор

не
оказывает заметного влияния на
результативный признак. Значимость
параметров
регрессии
проверяется на основе t
– критерия Стьюдента:

Параметр признаётся
статистически значимым, если расчётное
значение t
– критерия Стьюдента превосходит его
критическое значение, определяемое при
заданном уровне значимости α и числе
степеней свободы

.
Критическое значение t
– критерия может быть определено по
таблице распределения Стьюдента или
в Excel
по представленному в предыдущем разделе
порядку.

При проверке
значимости коэффициента детерминации
выдвигается гипотеза

о том, что коэффициент детерминации
генеральной совокупности, из которой
извлечена исследуемая выборка, равен
нулю. Эта гипотеза равносильна гипотезе
о том, что ни один из факторов, включённых
в регрессию, не оказывает существенного
влияния на результативный признак.
Поэтому проверка значимости коэффициента
детерминации является проверкой
адекватности (соответствия) выбранной
модели регрессии реальным
данным наблюдения. Значимость
коэффициента детерминации осуществляется
с помощью F-критерия.

Расчётное значение
критерия Фишера–Снедекора,
вычисляется по формуле:

Если

,
то гипотеза о равенстве коэффициента
детерминации нулю и несоответствии
заложенных в модели связей реально
существующим отклоняется на уровне
значимости

,
то есть коэффициент детерминации
признаётся статистически значимым, а
модель регрессии – адекватной. Величина

определяется по специальным таблицам
и зависит от заданного уровня значимости
и числа степеней свободы:

и

,
где

–
число наблюдений;

–
число факторных признаков в модели.

В качестве меры
адекватности модели регрессии
используется также процентное отношение
стандартной ошибки

к
среднему уровню результативного признака

–
относительная
ошибка аппроксимации:

, где

Если

,
то точность модели регрессии высокая,
если 10-20% – точность модели регрессии
хорошая (то есть уравнение достаточно
хорошо описывает взаимосвязь между
изучаемыми признаками), если 20-50% –
точность модели регрессии удовлетворительная.

В Excel
для проведения регрессионного анализа
существует статистическая процедура
Регрессия,
позволяющая осуществлять парную
линейную, параболическую (полиноминальную)
и множественную регрессии. Для выбора
формы связи целесообразно построить
корреляционное поле, воспользовавшись
специальным средством Мастер
диаграмм,
выбрав тип Точечная
(см. предыдущий раздел).

Парная линейная
регрессия
в Excel
осуществляется следующим образом:

Осуществляется
ввод исходных данных, т.е. значений
факторного и результативного признака.
В меню Сервис
выделяется строка Анализ
Данных.
В открывшемся
окне Анализ
данных
выделяется процедура Регрессия
и нажимается кнопка ОК. Откроется
диалоговое окно Регрессия
с пульсирующим курсором в поле ввода
Входной
интервал Y.
С помощью мыши
выделяется диапазон ячеек, в котором
находятся эмпирические значения
результативного признака Y.
В поле ввода Входной
интервал Y
появится соответствующая ссылка.
Нажатием клавиши
Tab
осуществляется переход в поле ввода
Входной
интервал Х.
С помощью мыши выделяется диапазон
ячеек, в котором находятся эмпирические
значения факторного признака Х. В поле
ввода Входной
интервал Х
появится соответствующая ссылка.
Устанавливается
флажок в группе флажков Остатки.
В данную группу входят следующие
флажки:

– флажок Остатки.
При его установке на экран выводится
таблица ВЫВОД
ОСТАТКОВ, в
состав которой входит столбец Остатки;

– флажок График
остатков.
При активизации этого флажка на экран
выводятся графики зависимости остатков
от регрессионных переменных (по одному
графику на каждую переменную);

– флажок
Стандартизированные
остатки. При
установке данного флажка в таблицу
ВЫВОД ОСТАТКОВ
добавляется столбец центрированных
нормированных (стандартизированных),
которые получаются из остатков

делением их на

;

– флажок График
подбора. При
установке этого флажка на рабочий лист
выводятся

точечных графиков (по числу контролируемых
переменных). На графике, связанном с

-й
контролируемой переменной

,

=1,
2….,
,
каждому значению

этой переменной поставлены в соответствие
две точки

;

– флажок График
нормальной вероятности. При активизации
этого флажка на экран выводятся таблица
ВЫВОД ВЕРОЯТНОСТИ и график функции,
обратной эмпирической функции
распределения результативного признака,
выполненный на «вероятностной нормальной
бумаге».

Щелчком на кнопке
ОК запускается процедура Регрессия.

Помимо этого
процедура содержит также следующие
элементы управления:

Флажок Константа-ноль.
Устанавливается
в том случае, когда необходимо, чтобы
линия регрессии проходила через начало
координат. При этом параметр

равен нулю и число параметров регрессии
равно числу факторов.
флажок Уровень
надёжности.
Устанавливается в том случае, когда
помимо доверительных интервалов для
параметров регрессии, соответствующих
используемой по умолчанию «стандартной»
доверительной вероятности 95%, необходимо
вычислить доверительные интервалы,
доверительная вероятность которых
отличается от «стандартной».
«Нестандартная» вероятность, выраженная
в процентах, вводится в поле, расположенное
справа от рассматриваемого флажка.
Если этот флажок не установлен, то
выходной таблице параметров регрессии
будут одинаковые пары столбцов,
содержащие доверительные границы для
параметров регрессии, соответствующие
одной и той же доверительной вероятности
95% (при редактировании таблицы их можно
убрать).

Назначение флажка
Метки
и переключателей Выходной
интервал/Новый рабочий лист/ Новая книга
рассмотрено в 1 разделе.

После запуска
процедуры Регрессия
на рабочем листе появляются три таблицы
результатов этой процедуры. В первой
таблице «Регрессионная статистика»
содержатся значения множественного
коэффициента корреляции, коэффициента
детерминации, нормированного коэффициента
детерминации, стандартная ошибка
уравнения регрессии и число наблюдений.
Во второй таблице «Дисперсионный анализ»
содержатся значения сумм квадратов и
среднего квадрата регрессии, остатков
и общие., а также расчётное значение
критерия Фишера–Снедекора. В третьей
таблице в графе «Коэффициенты» по строке
«Y-
пересечение» находится значение
свободного члена уравнения регрессии

,
а по строке Х – значение параметра

.
Далее по графам расположены стандартная
ошибка, расчётное значение t
– критерия Стьюдента, доверительные
интервалы для этих параметров.

Полиноминальная
(параболическая)
регрессия
в Excel
осуществляется следующим образом:

1. В ячейки А1, В1 и
С1 вводятся метки Y,
X
и X².

2. В диапазон А2 и
далее (например, А2: А15) вводятся значения
результативного признака, в диапазон
В2 и далее (соответственно В2:В15)– значения
факторного признака.

3.В диапазон С2 и
далее (С2: С15) вводится формула массива
= В2:В15^2
и нажимается комбинация клавиш Ctrl+Shift+
Enter.
В диапазоне
С2:С15 появится столбец квадратов значений
факторного признака.

4. В открывшемся
окне Анализ
данных
выделяется процедура Регрессия
и нажимается кнопка ОК. Откроется
диалоговое окно Регрессия
с пульсирующим курсором в поле ввода
Входной
интервал Y.

5. С помощью мыши
выделяется диапазон ячеек, в котором
находятся эмпирические значения
результативного признака Y.
В поле ввода Входной
интервал Y
появится соответствующая ссылка.

6. Осуществляется
переход в поле ввода Входной
интервал Х.
С помощью мыши выделяется диапазон
ячеек, в котором находятся эмпирические
значения факторного признака. В поле
ввода Входной
интервал Х
появится соответствующая ссылка.

7. Устанавливается
флажок в группе флажков Остатки.

8. Щелчком на кнопке
ОК запускается процедура Регрессия.

После запуска
процедуры Регрессия
на рабочем листе появляются три таблицы
результатов этой процедуры.

Множественная
линейная регрессия
в Excel
осуществляется аналогичным образом.
При этом в качестве исходных данных
вводятся значения результативного и
нескольких (
)
факторных признаков.

К статистическим
функциям, предназначенным для
регрессионного анализа в Excel,
относятся ЛИНЕЙН,
НАКЛОН,
ОТРЕЗОК,
ТЕНДЕНЦИЯ,
ПРЕДСКАЗ,
СТОШYХ,
ЛГРФПРИБЛ,
РОСТ.

Из этих функций
интерес представляют функции ЛГРФПРИБЛ,
ТЕНДЕНЦИЯ
и РОСТ,
так как другие функции вычисляют
некоторые характеристики, определяемые
статистической процедурой РЕГРЕССИЯ,
а также дублируют друг друга. Эти же три
функции производят вычисления, не
предусмотренные статистической
процедурой РЕГРЕССИЯ.

Функция ЛГРФПРИБЛ
вычисляет
выборочные оценки параметров показательной
(экспоненциальной) регрессии.

Синтаксис данной
функции: ЛГРФПРИБЛ
(известные
значения у; известные значения х;, конст;
стат):

известные
значения у–
множество значений результативного
признака. Данный массив представляет
собой вектор-столбец размером

;
известные
значения х–множество
значений факторных признаков.

– Если в случае
парной регрессии этот аргумент опущен,
то при вычислениях в качестве массива
известные
значения х
используется массив натуральных чисел

1,2…и
т.д. такого же размера, как и массив
известные
значения у;

– В случае
множественной регрессии, если массив
известные
значения у
представляет собой вектор-столбец, то
массив известные
значения х
должен иметь

строк и

столбцов. При этом каждый столбец этого
массива содержит

значений определённого факторного
признака;

– При вводе массива
чисел известные
значения х
с клавиатуры для разделения значений
в одной строке используют точку с
запятой, а для разделения строк–
двоеточие.

конст–логическая
переменная, определяющая, следует ли
включать в уравнение регрессии свободный
член.

– Если конст=1
(ИСТИНА) или опущен, то вычисляются и
коэффициенты регрессии, и свободный
член.

– Если конст=
0 (ЛОЖЬ), то предполагается, что свободный
член равен единице.

стат–
логическая переменная, определяющая
объём выходной информации.

– Если аргумент
стат =0
(ЛОЖЬ) или опущен, то функция выдаёт
только параметры уравнения регрессии.
При этом для вывода результатов решения
надо заранее выделить диапазон ячеек
размером

,
где

–
число факторов, включённых анализ.

– Если аргумент
стат =1
(ИСТИНА), то помимо функция выдаёт
дополнительную информацию об исследуемой
регрессионной зависимости. В этом случае
для вывода результатов решения надо
выделить диапазон ячеек размером

.
В первом столбце выделенного диапазона
находятся следующие характеристики
коэффициенты регрессии, стандартная
ошибка коэффициента регрессии, коэффициент
детерминации, расчётное значение F-
критерия Фишера, сумма квадратов,
обусловленная регрессией. Во втором
столбце находятся значения свободного
члена, его стандартная ошибка, стандартная
ошибка уравнения регрессии, число
степеней свободы, сумма квадратов
остатков.

Так как результатом
реализации функции является массив
чисел, содержащий выборочные характеристики
исследуемой регрессионной зависимости,
то функция вводится как формула массива
Ctrl+Shift+
Enter.
Например, = ЛГРФПРИБЛ
(А1:А6;В1:В6;1;1).

Функции ТЕНДЕНЦИЯ
и РОСТ
используются для вычисления расчётных
значений результативного признака,
соответствующих заданным пользователем
значениям факторных признаков, хранящимся
в массиве новые
значения х.
При этом функция ТЕНДЕНЦИЯ
вычисляет параметры линейной и других
видов регрессии, линейных относительно
входящих в них коэффициентов, таких,
например, как полиноминальная
(параболическая) регрессия

,
а функция РОСТ–
параметры экспоненциальной регрессии.

Функции вводится
как формула массива Ctrl+Shift+
Enter.

Синтаксис данных
функций идентичен: ТЕНДЕНЦИЯ
(известные значения у; известные значения
х;, новые значения х,; конст)
и РОСТ
(известные значения у; известные значения
х;, новые значения х,; конст):

известные
значения у–
множество значений результативного
признака. Данный массив представляет
собой вектор-столбец размером

;
известные
значения х–множество
значений факторных признаков.

1,2…и
т.д. такого же размера, как и массив
известные
значения у;

строк и

столбцов. При этом каждый столбец этого
массива содержит

значений определённого факторного
признака;

новые значения
х– новые
значения факторных признаков, для
которых функция должна вычислить
расчётные значения результативного
признака;

– В случае
множественной регрессии, если массив
известные
значения у
представляет собой вектор-столбец, то
массив новые
значения х
должен иметь

столбцов и столько строк, сколько
расчётных значений у надо вычислить.

–Массив новые
значения х,
так же как и массив
известные значения х,
должен содержать столбец для каждого
факторного признака. Число столбцов
этих массивов должно быть одинаково.

– Если аргумент
новые значения
х опущен, то
предполагается, что он совпадает с
аргументом известные
значения х.

конст–логическая
переменная, определяющая, следует ли
включать в уравнение регрессии свободный
член.

– Если конст=1
(ИСТИНА) или опущен, то вычисляются и
коэффициенты регрессии, и свободный
член.

– Если конст=
0 (ЛОЖЬ), то предполагается, что свободный
член равен нулю (в случае линейной
регрессии) и единице (в случае
экспоненциальной регрессии).

Ряды динамики

Ряд
динамики–
это ряд числовых значений статистических
показателей, расположенных в хронологической
последовательности и характеризующих
изменение явления во времени.

Ряд динамики
состоит из двух
элементов:

уровней динамического
ряда– числовых значений статистических
показателей, характеризующих величину
изучаемого явления–

;

периодов (или
моментов) времени, к которым относятся
данные уровни –

.

Одной из основных
задач в процессе анализа уровней
динамического ряда является определение
основной закономерности (тенденции) их
изменений
во времени.

При этом выделяются
следующие основные
компоненты динамического ряда:

основная тенденция
(тренд) (Т);
циклическая (Ц);
сезонная (S);
случайная (Е).

Первые три компоненты
формируют систематическую
составляющую
динамического ряда.

Тренд
характеризует устойчивое систематическое
изменение динамического ряда, происходящее
в течение длительного времени и
обусловленное влиянием медленно
развивающихся долговременных факторов.

Сезонная
компонента–
это колебания, периодически повторяющиеся
в некоторое определённое время каждого
года, дня месяца или часа дня.

Циклическая
(периодическая) компонента
проявляется
в том, что значение изучаемого показателя
в течение какого-то времени возрастает,
достигает определённого максимума,
затем понижается, достигает определённого
минимума, вновь возрастает до прежнего
значения и т.д.

Четвёртую компоненту
формируют случайные
колебания,
которые являются результатом действия
большого количества относительно слабых
второстепенных факторов.

Для выявления
и характеристики
основной закономерности развития
явления необходимо выявить первую
компоненту динамического ряда – тренд,
и погасить влияние других типов колебаний
на изменение уровней ряда.

С этой целью
проводят выравнивание динамических
рядов. Различают два вида выравнивания:
механическое (или сглаживание) и
аналитическое.

К приёмам
механического выравнивания
относятся:

усреднение левой
и правой половины ряда;
укрупнение
периодов;
скользящая средняя:
простая, взвешенная;
экспоненциальное
сглаживание.

Выбор приема
выравнивания зависит от исходной
информации и задач исследования.

В среде Excel
для выравнивания динамических рядов
используются процедуры Скользящее
среднее и
Экспоненциальное
сглаживание,
входящие в Пакет анализа.

Сущность метода
скользящей средней
заключается в том, что вычисляется
средний уровень из определенного числа
первых по порядку уровней ряда, затем
– средний уровень из такого же числа
уровней, начиная со второго, затем,
начиная с третьего и т.д. Таким образом,
при расчётах среднего уровня как бы
«скользят» по ряду динамики от его
начала к концу, каждый раз отбрасывая
один уровень вначале и добавляя один
следующий. Этим объясняется название
– скользящая средняя.

;

;

и т.д.

Следует
отметить, что при использовании метода
скользящей средней «теряются»

членов в начале и в конце динамического
ряда (где

–размер
интервала (окна) сглаживания). Для
восстановления «потерянных» уровней
в начале и в конце сглаженного ряда для

=3
и

=5
могут быть использованы следующие
формулы:

=3
(
):

;

=5(

):

;

Для получения
количественной модели, выражающей
основную тенденцию изменения уровней
динамического ряда во времени, используется
приём
аналитического выравнивания.
Сущность
его состоит в том, что основная тенденция
развития

рассчитывается как функция времени. В
этом случае фактические (эмпирические)
уровни заменяются теоретическими,
вычисленными по соответствующему
аналитическому уравнению.

Аналитическое
выравнивание производится в следующей
последовательности:

1)
выделяется этап развития явления и
устанавливается характер динамики на
этом этапе. Этап развития явления– это
период, в течение которого формирование
уровней динамического уровня осуществляется
под воздействием определённого набора
постоянных, периодических и разовых
факторов. Решение этой задачи осуществляется
не только с помощью статистических
методов, а в основном – на базе анализа
сущности, природы явлений и общих
законов его развития.

2)
на основе предположений о той или иной
закономерности развития выбирается
форма аналитического выражения тренда,
то есть вид аппроксимирующей математической
функции.

Основанием для
выбора уравнения тренда
могут служить:

качественный
анализ сущности развития данного
явления;
результаты
предыдущих исследований в данной
области;
графическое
изображение эмпирических или скользящих
уровней ряда динамики;
статистико-математических
критериев адекватности.

При анализе рядов
динамики используются следующие
математические модели:

линейная y_t
= a₀
+ a₁t,

где

и

–
параметры уравнения;

–
начальный уровень
тренда в момент или период, принятый за
начало отсчёта времени;

–
среднее абсолютное
изменение за единицу времени;

–
обозначение
времени.

Параметр

определяет направление развития: если

,
то уровни ряда равномерно возрастают
в среднем за единицу времени на величину

,
если

,
то происходит их равномерное снижение.

полиноминальная(параболическая)

,
где

–степень
полинома. Наиболее применяемой в
практике статистических расчётов
является уравнение параболы
второго порядка y_t
= a₀
+ a₁t
+ a₂t².

Значение параметров

идентично предыдущему уравнению.

Параметр

характеризует
изменение интенсивности развития в
единицу времени. При

происходит ускорение развития, при

–
замедление развития.

Соответственно
при параболической форме тренда возможны
следующие варианты развития:

если

;

–
ускорение роста;
если

;

–
замедление роста;
если

;

–
замедление снижения;
если

;

–
ускорение снижения.

экспоненциальная

,

где

–
константа ряда,

–темп
изменения в разах. При

>1
экспоненциальный тренд выражает
тенденцию ускоренного и всё более
ускоряющегося возрастания уровней, при

<1
экспоненциальный тренд означает всё
более замедляющегося снижения уровней
динамического ряда.

логарифмическая

.
Логарифмическая
форма тренда применяется для отображения
тенденции замедляющегося роста уровней
при отсутствии предельно возможного
значения, например, роста спортивных
достижений, производительности агрегата,
продуктивности скота.
гиперболическая
y_t
= a₀
+ a₁
–
применяется для отображения тенденции
процессов, ограниченных предельным
значением уровня;
степенная

–
применяется для отображения тенденции
явлений с разной мерой пропорциональности
изменений во времени;
логистическая
и др.

Наиболее точным
способом выбора формы тренда является
применение
статистико-математических критериев,
в качестве которых могут выступать
остаточное среднее квадратическое
отклонение, средняя ошибка аппроксимации
(
),
стандартизированная ошибка аппроксимации
(
),
относительная ошибка аппроксимации

(модифицированный коэффициент вариации):

;

,
где

y
и

—
соответственно
фактические и теоретические значения
ряда динамики;

n
– число уровней
ряда;

m
– количество
параметров в уравнении тренда.

Предпочтение
отдаётся той функции, которая имеет
наименьшую величину критерия.

Если

,
то точность модели тренда высокая, если

=
10-20% – точность модели тренда хорошая
(то есть уравнение достаточно хорошо
описывает основную тенденцию развития
изучаемого явления), если

=20-50%
– точность модели тренда удовлетворительная.

3) Вычисляются
параметры уравнения тренда, и по ним
производится синтезирование
трендовой модели.

Расчёт параметров
уравнений тренда может быть произведён
различными способами:

методом средних
значений (или линейных отклонений);
методом конечных
разностей;
методом наименьших
квадратов.

Наиболее точным
является аналитическое выравнивание
с помощью способа
наименьших квадратов.
Суть данного способа состоит в том, что
теоретическая линия (прямая или кривая),
выравнивающая ряд, должна проходить в
максимальной близости к фактическим
уровням ряда. Математически это означает,
что сумма квадратов отклонений (разность
между фактическими и теоретическими
уровнями) должна быть минимальной:

å
(y
–
y_t)²
= min.

4) На основе
синтезированной модели тренда вычисляются
теоретические уровни.

Выявление и
характеристика основной тенденции
развития дают основание для прогнозирования,
то есть для определения возможного
варианта размеров явления в будущем.
Важное значение при прогнозировании
имеют вопросы о базе и сроках
прогнозирования.

База
прогнозирования
– длина или продолжительность базисного
периода, закономерность которого будет
распространяться на будущее.

Срок
прогнозирования
(период
упреждения)
– длина будущего периода, на который
распространяется закономерность
развития явления.

Однозначного
ответа на вопрос об определении
допустимого срока прогноза нет. В
основном придерживаются следующего
правила: срок прогноза не должен превышать
третьей части длины базы прогноза.
Однако в каждом конкретном случае
необходимо учитывать особенности
изучаемого явления. При этом необходимо,
чтобы продолжительность базисного ряда
составляла определенный этап в развитии
анализируемого явления в конкретных
исторических условий.

Установление
сроков прогнозирования зависит от цели
исследования. Однако следует иметь в
виду, особенности характера изучаемого
явления. Например, ограниченные
физиологические особенности животных
(или растений), делают невозможным
увеличение продуктивности животных
(или урожайности) до бесконечности.
Кроме того, необходимо учитывать
неустойчивость экономики в условиях
переходного периода. Поэтому чем короче
сроки прогнозирования периода, тем
надежнее результат прогноза.

Разработка
прогнозного уровня динамического ряда
может осуществляться на основе
использования различных методов,
наиболее распространённым из которых
является метод экстраполяции.

Метод экстраполяции
основывается на предположении о
неизменности основных факторов,
определяющих тенденцию данного
показателя, и заключается в распространении
закономерностей развития этого
показателя, имевших место в прошлом, на
будущее.

Более точным и
распространённым методом экстраполяции
является применение
аналитического выражения тренда,
при котором в адекватную трендовую
модель подставляются значения

в будущие годы. Прогнозирование на
основе экстраполяции дает возможность
получить точечные значения прогнозируемого
уровня исследуемого показателя.

Интерполяция–
это приближённый расчёт уровней,
находящихся внутри ряда динамики, но
почему-либо неизвестных. При интерполяции
предполагается, что характер тенденции
не претерпел существенных изменений в
том промежутке времени, уровень которого
нам не известен.

Как и экстраполяция,
интерполяция может производится на
основе на
основе выравнивания динамического ряда
по какой-либо аналитической формуле.

В Excel
сглаживание динамического ряда методом
скользящей средней осуществляется
следующим образом:

1. В диапазон ячеек
вводятся уровни ряда динамики (числовые
значения изучаемого статистического
показателя).

2.В меню Сервис
выделяется
строка Анализ
данных.

3. В открывшемся
окне Анализ
данных
выделяется процедура Скользящее
среднее и
нажимается кнопка ОК. На экране появится
диалоговое окно Скользящее
среднее.

4. В поле ввода
Входной
интервал
этого окна вводится ссылка на диапазон
ячеек, содержащий уровни исследуемого
ряда динамики. Входной интервал должен
состоять из одного столбца, «высота»
которого равна числу

уровней данного ряда динамики.

5. В поле Интервал
вводится размер окна сглаживания

(по умолчанию

=3).

6. В поле Выходной
интервал
вводится ссылка на верхнюю ячейку
столбца результатов сглаживания.
Выходной интервал всегда располагается
на том же самом рабочем листе, на котором
находится входной интервал, поэтому в
диалоговом окне процедуры нет таких
позиций, как Новый
рабочий лист
и Новая
рабочая книга.
Выходной интервал состоит по крайней
мере из одного столбца, содержащего
уровни сглаженного ряда. Высота этого
столбца равна высоте входного интервала.
При установке флажка
Стандартные погрешности
в выходном интервале появляется ещё
один столбец– столбец стандартных
погрешностей. В точках, для которых
нельзя вычислить сглаженные значения
и стандартные погрешности, процедура
выводит сообщение #
Н/Д! (Нет
данных).

7. Устанавливается
флажок Вывод
графика.
Флажок Стандартные
погрешности
устанавливается при необходимости
получения стандартных погрешностей
сглаживания. Назначение флажка Метки
рассмотрено
в 1 разделе.

8. Нажимается кнопка
ОК.

Следует иметь в
виду, что процедур Скользящее
среднее
выдаёт сглаженный ряд так называемых
адаптивных скользящих средних. Этот
ряд сдвинут на

шагов вправо относительно «канонического»
ряда скользящих средних. Для сравнения
простого и адаптивного скользящих
средних в диапазоне ячеек, число которых
на

-1
меньше числа уровней исходного ряда
динамики, свободного столбца, рассчитываются
значения скользящих средних, вычисленные
по канонической формуле =
СРЗНАЧ по
диапазону из

первых уровней динамического ряда
(например, при

=3
А1:А3). Данная формула вводится в следующую
после

по
счёту ячейку столбца, предназначенного
для расчёта канонических средних
(например, при

=3–во
вторую (С2), при

=5
(С3) и т.д.). Затем данная формула копируется
в оставшийся диапазон ячеек этого
столбца. Адаптивные скользящие средние
могут быть вычислены также с помощью
статистической процедуры Добавить
линию тренда
(см. ниже).

При проведении
экспоненциального сглаживания
использование одноимённой процедуры
аналогично выше рассмотренному порядку.
Вместо поля Интервал
диалогового
окна Скользящее
среднее в
процедуре Экспоненциальное
сглаживание
заполняется поле Фактор затухания. В
это поле вводится фактор затухания

,
где

–
параметр сглаживания (вес текущего
значения при вычислении экспоненциального
среднего,

).
Параметр
характеризует
скорость реакции экспоненциального
среднего

на изменение текущего значения

динамического
ряда и одновременно определяет его
способность сглаживать случайные
колебания. Чем больше

,
тем быстрее реакция экспоненциального
среднего на изменение динамического
ряда и тем меньше его сглаживающие
возможности. В качестве приемлемого
компромисса рекомендуется брать

в пределах от 0,1 до 0,3. Следовательно,
приемлемыми значениями фактора затухания
являются значения из интервала от 0,7 до
0,9. В статистической процедуре
Экспоненциальное
сглаживание
по умолчанию

,
что противоречит рекомендациям.

При аналитическом
выравнивании в Excel
используются статистическая процедура
Регрессия
и статистические функции регрессионного
анализа ЛИНЕЙН,
ПРЕДСКАЗ,
ЛГРФПРИБЛ,
ТЕНДЕНЦИЯ и
РОСТ,
рассмотренные в предыдущем разделе. В
этом случае при использовании
статистической процедуры Регрессия
вместо значений факторного признака
вводятся натуральные числа 1,2,….
,
обозначающие порядковые номера периодов
или моментов времени. При использовании
статистических функций натуральные
числа можно не вводить, а оставить
пропущеным аргумент известные
значения х.
Тогда при вычислениях в качестве массива
известные
значения х
используется массив натуральных чисел

1,2…и
т.д. такого же размера, как и массив
известные
значения у.

Эффективным
средством аналитического выравнивания
является процедура Добавить
линию тренда,
входящая в комплекс графических средств
табличного процессора Excel.
Она вычисляет параметры выбранной
пользователем модели тренда. При
вычислениях используется МНК. Модель
тренда выбирается из набора, включающего
в себя пять наиболее распространённых
аналитических моделей: линейную,
логарифмическую, полиноминальную
(параболическую), степенную, экспоненциальную
и модель адаптивной скользящей средней
(формулы см. выше данном разделе).
Параметры аналитических моделей
вычисляются по данным наблюдения, по
которым построен график динамического
ряда. В результате реализации процедуры
в область построения графика выводятся
график функции тренда, её аналитическое
выражение и значение коэффициента
детерминации R².
При изменении любых значений исходного
ряда динамики процедура автоматически
пересчитывает и обновляет параметры
линии тренда и её график.

Для доступа к
процедуре Добавить
линию тренда
необходимо:

1. В диапазон ячеек
определённого столбца ввести уровни
исследуемого динамического ряда.

2. С помощью Мастера
Функций построить диаграмму (график)
ряда динамики.

3. Щелчком на
диаграмме активизировать её. На панели
меню на месте пункта Данные
появится
пункт Диаграмма.

4. В пункте меню
Диаграмма
выбрать команду Добавить
линию тренда.
Откроется диалоговое окно Линия
тренда.

5. В открывшемся
окне Линия
тренда
раскрыть вкладку Тип.

6. На этой вкладке
в разделе Построение
линии тренда (аппроксимация и сглаживание)
выбрать тип (вид) функции тренда.

7. В списке Построен
на ряде
выделить ряд данных, для которых строится
линия тренда.

8. Раскрыть вкладку
Параметры
диалогового окна Линия
тренда.

Эта вкладка содержит
следующие элементы управления:

группу переключателей
Название аппроксимирующей (глаженной)
кривой, состоящую из двух переключателей.
При установке переключателя автоматическое
Excel
автоматически присваивает линии тренда
имя, связанное с типом этой линии и
названием данных наблюдения, по которым
строится линия тренда, например, Линейный
(Урожайность зерновых).
При установке переключателя другое
пользователь сам устанавливает имя
линии регрессии и вводит это имя в поле
Линейный
(Ряд 1),
расположенное справа от переключателя
(максимальная длина имени 256 символов);
группу счётчиков
Прогноз,
в которую входят два счётчика: вперёд
на…единиц
и назад
на…единиц.
С помощью этих счётчиков устанавливается
срок прогноза и производится экстраполяция
и интерполяция ряда динамики. Счётчики
недоступны в режиме Скользящее
среднее;
флажок пересечение
кривой с осью Y
в точке.
Если этот флажок не установлен, ордината

точки пересечения линии тренда с осью
Y
вычисляется по данным наблюдения. Как
правило, этот флажок не устанавливается.
Используя этот флажок и расположенное
справа от него поле ввода, можно задать
нужную ординату точки пересечения (при
активном флажке и нуле в поле ввода
линия тренда пройдет через начало
координат);
флажок показывать
уравнение на диаграмме.
При установке этого флажка в область
построения диаграммы выводится
аналитическое выражение (формула)
функции тренда;
флажок поместить
на диаграмму величину достоверности
аппроксимации.
При установке этого флажка в область
построения диаграммы выводится значение
коэффициента детерминации R²,
который показывает, на сколько процентов
выбранная линия тренда объясняет
разброс уровней ряда. Чем больше данный
показатель, тем более точно выбрана
линия тренда. Сравнивая величину R²
по разным аналитическим моделям можно
определить аппроксимирующую функцию.
то есть наиболее точно описывающую
основную тенденцию развития изучаемого
явления.

9. Установить нужные
переключатели, счётчики и флажки.
Щёлкнуть на кнопке ОК.

Список рекомендуемой литературы

1. Вадзинский Р.
Статистические вычисления в среде
Еxcel.
–СПб.: Питер,2008.

2. Макарова Н.В.
Трофимец В.Я. Статистика в Еxcel.–
М.: Финансы и статитсика, 2006.

3. Берк К. Кэйри П.
Анализ данных с помощью MS
Еxcel.–М.:
Вильямс, 2005.

4. Васильев А.Н.
Научные вычисления в Microsoft
Excel.–М.;
Спб.; Киев: Диалектика, 2004.

5.Вуколов Э.А. Основы
статистического анализа: практикум по
статистическим методам и исследованию
операций с использованием пакетов
STATISTICA
и Еxcel.–
М.: Форум; Инфра–М, 2004.

6. Минько А.А.
Статистический анализ в среде Еxcel.–М.,
СПб., Киев: Диалектика, 2004.

7. Гайдышев И. Анализ
и обработка данных.–СПб; М.: Питер, 2001.

8.
Елисеева И.И., Юзбашев М.М. Общая теория
статистики: Учебник. М: Финансы и
статистика, 2005

9.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н.
Общая теория статистики: Учебник. –
М.: ИНФРА- М, 2006.

10.
Теория статистики: Учебник / Под ред.
Р.А. Шмойловой .4-е изд., доп. и перераб. —
М.: Финансы и статистика, 2005.

11.
Теория статистики: Учебник/ Под ред.
Г.Л. Громыко.- ИНФРА- М, 2006.

Источник

В сегодняшней статье речь пойдет о том, как переменные могут быть связаны друг с другом. С помощью корреляции мы сможем определить, существует ли связь между первой и второй переменной. Надеюсь, это занятие покажется вам не менее увлекательным, чем предыдущие!

Корреляция измеряет мощность и направление связи между x и y. На рисунке представлены различные типы корреляции в виде графиков рассеяния упорядоченных пар (x, y). По традиции переменная х размещается на горизонтальной оси, а y — на вертикальной.

График А являет собой пример положительной линейной корреляции: при увеличении х также увеличивается у, причем линейно. График В показывает нам пример отрицательной линейной корреляции, на котором при увеличении х у линейно уменьшается. На графике С мы видим отсутствие корреляции между х и у. Эти переменные никоим образом не влияют друг на друга.

Наконец, график D — это пример нелинейных отношений между переменными. По мере увеличения х у сначала уменьшается, потом меняет направление и увеличивается.

Оставшаяся часть статьи посвящена линейным взаимосвязям между зависимой и независимой переменными.

Коэффициент корреляции

Коэффициент корреляции, r, предоставляет нам как силу, так и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между — 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной (график A на рисунке), а когда значение r отрицательно, связь также отрицательна (график В). Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует график С).

Сила связи между х и у определяется близостью коэффициента корреляции к — 1.0 или +- 1.0. Изучите следующий рисунок.

График A показывает идеальную положительную корреляцию между х и у при r = + 1.0. График В — идеальная отрицательная корреляция между х и у при r = — 1.0. Графики С и D — примеры более слабых связей между зависимой и независимой переменными.

Коэффициент корреляции, r, определяет, как силу, так и направление связи между зависимой и независимой переменными. Значения r находятся в диапазоне от — 1.0 (сильная отрицательная связь) до + 1.0 (сильная положительная связь). При r= 0 между переменными х и у нет никакой связи.

Мы можем вычислить фактический коэффициент корреляции с помощью следующего уравнения:

Ну и ну! Я знаю, что выглядит это уравнение как страшное нагромождение непонятных символов, но прежде чем ударяться в панику, давайте применим к нему пример с экзаменационной оценкой. Допустим, я хочу определить, существует ли связь между количеством часов, посвященных студентом изучению статистики, и финальной экзаменационной оценкой. Таблица, представленная ниже, поможет нам разбить это уравнение на несколько несложных вычислений и сделать их более управляемыми.

Как видите, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует весьма сильная положительная корреляция. Преподаватели будут весьма рады узнать об этом.

Какова выгода устанавливать связь между подобными переменными? Отличный вопрос. Если обнаруживается, что связь существует, мы можем предугадать экзаменационные результаты на основе определенного количества часов, посвященных изучению предмета. Проще говоря, чем сильнее связь, тем точнее будет наше предсказание.

Использование Excel для вычисления коэффициентов корреляции

Я уверен, что, взглянув на эти ужасные вычисления коэффициентов корреляции, вы испытаете истинную радость, узнав, что программа Excel может выполнить за вас всю эту работу с помощью функции КОРРЕЛ со следующими характеристиками:

КОРРЕЛ (массив 1; массив 2),

где:

массив 1 = диапазон данных для первой переменной,

массив 2 = диапазон данных для второй переменной.

Например, на рисунке показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для примера с экзаменационной оценкой.

Скачать файл с примером расчета коэффициента корреляции

Источник

Суть корреляционного анализа

Расчет коэффициента корреляции

Способ 1: определение корреляции через Мастер функций

Способ 2: вычисление корреляции с помощью пакета анализа

Еще статьи по данной теме:

Помогла ли Вам статья?

Теоретическое отступление

Использование MS EXCEL для расчета корреляции

Использование MS EXCEL для расчета ковариации

Оценка статистической значимости коэффициента корреляции

Надстройка Пакет анализа

Выборочный коэффициент корреляции

Как посчитать коэффициент корреляции в Excel

Расчет доверительного интервала для коэффициента корреляции в Excel

Несколько важных замечаний

Определение коэффициента через «Мастер функций»

Расчёт корреляции с помощью средств пакета анализа

Расчёт корреляционной зависимости по формуле

Синтаксис

Замечания

Пример

Дополнительные сведения

Нужна дополнительная помощь?

Что такое коэффициент корреляции?

Расчет коэффициента корреляции в Excel

Использование формулы CORREL

Использование пакета инструментов анализа данных

Включение пакета инструментов анализа данных

Расчет коэффициента корреляции с помощью пакета Data Analysis Toolpak

2 способа корреляционного анализа в Microsoft Excel

Суть корреляционного анализа

Расчет коэффициента корреляции

Способ 1: определение корреляции через Мастер функций

Способ 2: вычисление корреляции с помощью пакета анализа

КОРРЕЛ (функция КОРРЕЛ)

Описание

Синтаксис

Замечания

Пример

Определение множественного коэффициента корреляции в MS Excel

Вычисление множественного коэффициента корреляции

Этап 1: активация пакета анализа

Этап 2: расчет коэффициента

Этап 3: анализ полученного результата

Корреляционно-регрессионный анализ в Excel: инструкция выполнения

Регрессионный анализ в Excel

Корреляционный анализ в Excel

Корреляционно-регрессионный анализ

Функция ПИРСОН расчета коэффициента корреляции Пирсона в Excel

Как работает функция ПИРСОН в Excel?

Пример решения с функцией ПИРСОН при анализе в Excel

Функция ПИРСОН пошаговая инструкция

Корреляционный анализ по Пирсону в Excel

Интерпретация результата вычисления по Пирсону

Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel

Примеры использования функции КОРРЕЛ в Excel

Определение коэффициента корреляции влияния действий на результат

Анализ популярности контента по корреляции просмотров и репостов видео

Особенности использования функции КОРРЕЛ в Excel

Коэффициент парной корреляции в Excel

Расчет коэффициента корреляции в Excel

Матрица парных коэффициентов корреляции в Excel

Привет! Нужно в Excel рассчитать корреляцию

Числовые характеристики результатов наблюдения

Формирование выборки

Корреляционный анализ

Регрессионный анализ

Ряды динамики

Список рекомендуемой литературы

Коэффициент корреляции

Использование Excel для вычисления коэффициентов корреляции

А вот еще интересные статьи: