Выбрать комбинацию в excel

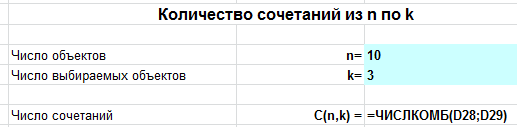
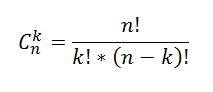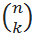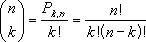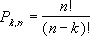Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).

Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:

(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)

Примечание

: Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье — плохая идея.

Отличие Сочетаний от Размещений

В отличие от

Размещений

следующие 3-х элементные комбинации (1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 1; 3); (3; 2; 1); (3; 1; 2) считаются одинаковыми, и в набор

Сочетаний

включается только одна из этих комбинаций. Очевидно, что для тех же n и k число

Сочетаний

всегда меньше чем число

Размещений

(так как при размещениях порядок важен, а для сочетаний — нет), причем в k! раз.

Подсчет количества Сочетаний

Число всех

Сочетаний

из n элементов по k можно вычислить по формуле:

Например, количество 4-х элементных комбинаций из 6 чисел {1; 2; 3; 4; 5; 6}  равно 15=6!/(4!(6-4)!)

Примечание

:  Для

Сочетаний

из n элементов по k также используется и другая запись:

В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ() , английское название функции — COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4) , разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4) .

Очевидно, что k меньше или равно n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются). При k=n количество сочетаний всегда равно 1.

Примечание

: О Сочетаниях с повторениями (с возвращением элементов) можно прочитать в статье

Сочетания с повторениями: Комбинаторика в MS EXCEL

Вывод всех комбинаций Сочетаний

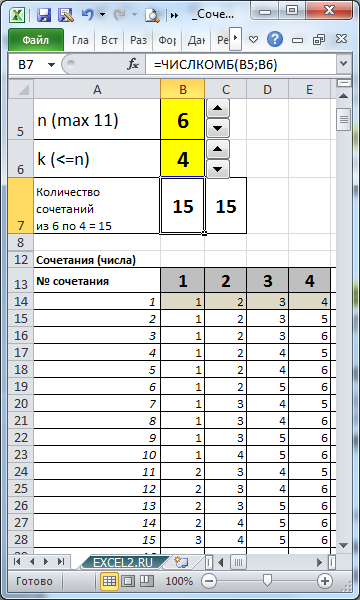
В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.

Задавая с помощью

элементов управления Счетчик

количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.

В файле примера не забывайте увеличивать количество строк с формулами, чтобы поместились все ваши комбинации. Для этого выделите последние ячейки с формулами (сочетание №330) и скопируйте их вниз на нужно количество строк. При увеличении строк с формулами размер файла быстро растет, а скорости пересчета листа падает. Если строк 4 тысячи, то размер файла составляет около 2 Мб.

Задача

Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.

Нам нужно определить число

Сочетаний

7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.

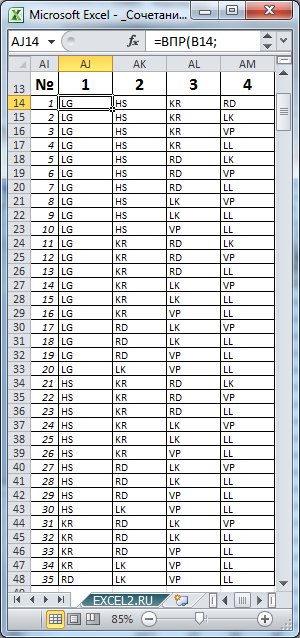
Воспользуемся файлом примера (ссылка внизу статьи) , чтобы наглядно убедиться, что мы решили задачу правильно.

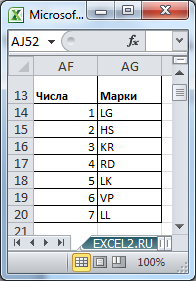
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …

Выставив в ячейках

В5

и

В6

значения 7 и 4 соответственно, определим все варианты размещений машин в автовозе (см. столбцы AJ:AM).

Примечание

: О Перестановках можно прочитать в статье

Перестановки без повторений: Комбинаторика в MS EXCEL

, а о Размещениях в статье

Размещения без повторений: Комбинаторика в MS EXCEL

.

Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.

Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!

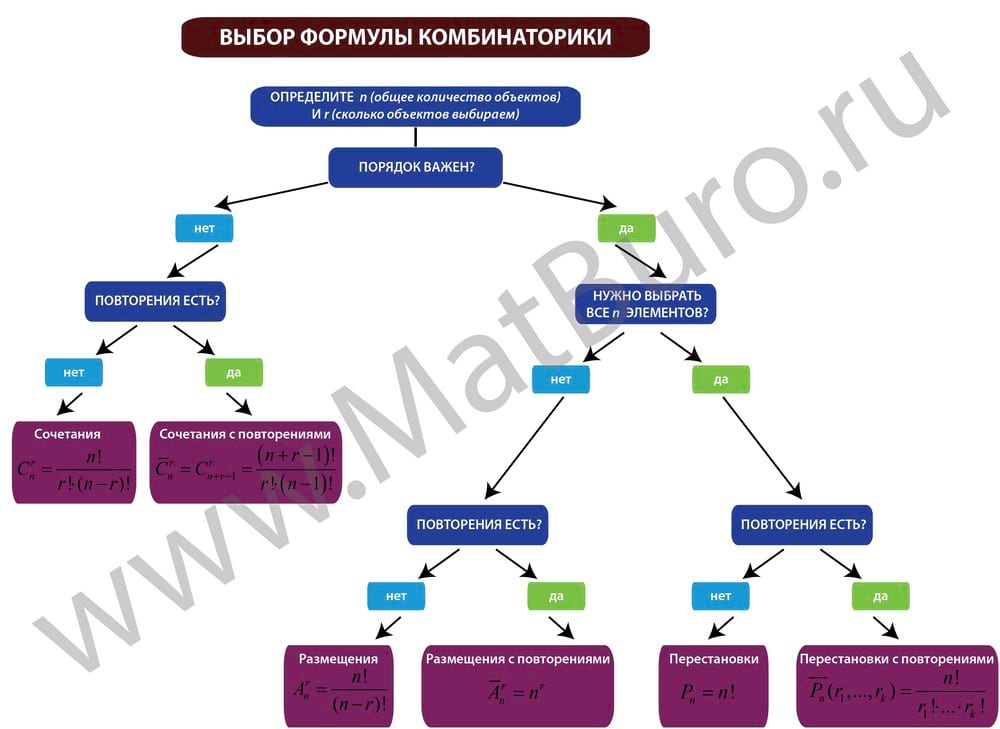
Как выбрать формулу комбинаторики?

Нужно последовательно (см. схему выше) ответить на несколько вопросов:

• Сколько у нас есть объектов (число $n$)?
• Важен ли их порядок в комбинации?
• Могут ли встречаться повторяющиеся элементы?
• Нужно выбрать все элементы или только $klt n$?

Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:

Схема выбора формул с примерами задач

Перестановки в Excel

Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

$$P_n=n!=1cdot 2cdot 3 cdot … cdot (n-1) cdot n$$

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Подробнее: факториал в эксель.

Для нахождения числа перестановок в Excel можно использовать одну из двух функций:

=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$), где $n$ — число переставляемых объектов.

Задача. Сколькими способами можно расставить 10 различных книг на одной полке?

Вводим число объектов 10 и получаем ответ: 3628800 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок.

Перестановки с повторениями в Excel

Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа,… $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?

Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть

$$ P_n (n_1,n_2,…,n_k)=frac{n!}{n_1! cdot n_2!cdot … cdot n_k!}. $$

Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР(), которая находит факториал чисел и обычные действия (умножение, деление).

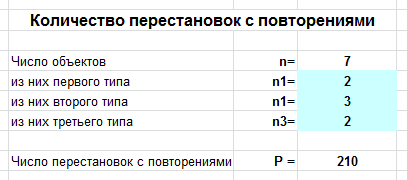
Задача. Сколько различных слов можно составить из букв слова «колокол»?

Вводим число букв $n=7$, а также $n_1=2$ (2 буквы «к»), $n_2=3$ (3 буквы «о»), $n_3=2$ (2 буквы «л»), и получаем ответ: 210 слов.

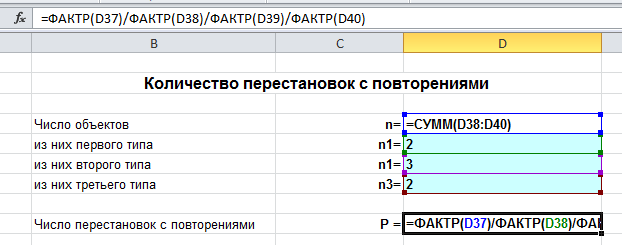
В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок c повторениями.

Размещения в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно

$$A_n^k=frac{n!}{(n-k)!}=ncdot (n-1)cdot … cdot (n-k+1) $$

Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$).

Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений.

Размещения с повторениями в Excel

Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле

$$overline{A}_n^k=ncdot ncdot … cdot n = n^k. $$

Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$).

Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?

Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений с повторениями.

Сочетания в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно

$$C_n^k=frac{n!}{(n-k)!cdot k!} $$

Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$).

Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний.

Сочетания с повторениями в Excel

Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле

$$overline{C}_n^k=C_{k+n-1}^k=frac{(k+n-1)!}{(n-1)!cdot k!}$$

Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$).

Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?

Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний с повторениями.

Полезные ссылки

Для собственных расчетов скачайте файл: Комбинаторика в Excel.

Решебник задач по комбинаторике

Подбор слагаемых для нужной суммы

Не очень частый, но и не экзотический случай. На моих тренингах такой вопрос задавали не один и не два раза  Суть в том, что мы имеем конечный набор каких-то чисел, из которых надо выбрать те, что дадут в сумме заданное значение.

В реальной жизни эта задача может выглядеть по-разному.

• Например, мы выгрузили из интернет-банка все платежи, которые поступили на наш счет за последний месяц. Один из клиентов разбивает сумму своего платежа на несколько отдельных счетов и платит частями. Мы знаем общую сумму оплаты и количество счетов, но не знаем их сумм. Надо подобрать те суммы в истории платежей, которые дадут в общем заданное значение.
• У нас есть несколько рулонов стали (линолеума, бумаги…), из которых надо подобрать под заказ те, что дадут заданную длину.
• Блэкджек или в народе «очко». Надо набрать карты суммарной стоимостью максимально близкой к 21 баллу, но не превысить этот порог.

В некоторых случаях может быть известна разрешенная погрешность допуска. Она может быть как нулевой (в случае подбора счетов), так и ненулевой (в случае подбора рулонов), или ограниченной снизу или сверху (в случае блэкджека).

Давайте рассмотрим несколько способов решения такой задачи в Excel.

Способ 1. Надстройка Поиск решения (Solver)

Эта надстройка входит в стандартный набор пакета Microsoft Office вместе с Excel и предназначена, в общем случае, для решения линейных и нелинейных задач оптимизации при наличии списка ограничений. Чтобы ее подключить, необходимо:

• в Excel 2007 и новее зайти Файл — Параметры Excel — Надстройки — Перейти (File — Excel Options — Add-ins — Go)
• в Excel 2003 и старше — открыть меню Сервис — Надстройки (Tools — Add-ins)

и установить соответствующий флажок. Тогда на вкладке или в меню Данные (Data) появится нужная нам команда.

Чтобы использовать надстройку Поиск решения для нашей задачи необходимо будет слегка модернизировать наш пример, добавив к списку подбираемых сумм несколько вспомогательных ячеек и формул:

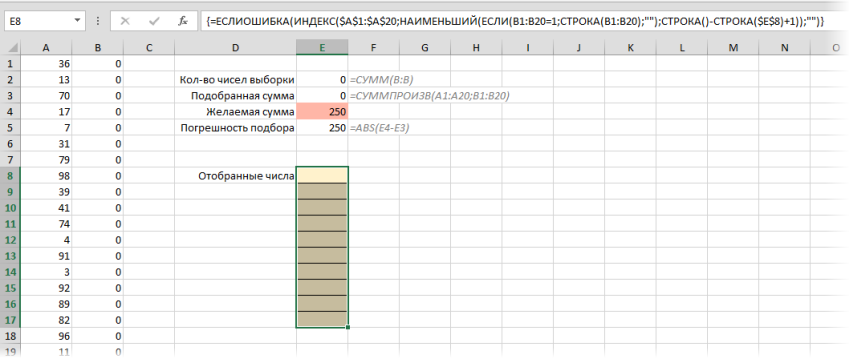
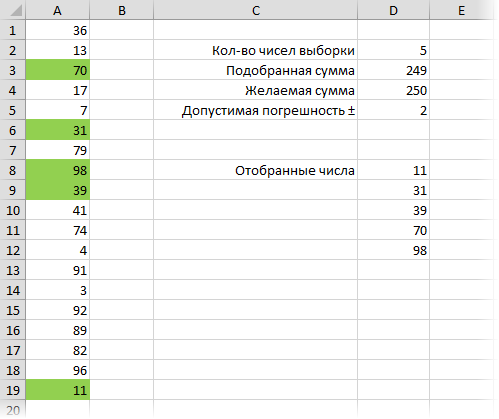
• Диапазон A1:A20 содержит наши числа, из которых мы будем выбирать нужные, чтобы «вписаться» в заданную сумму.
• Диапазон В1:B20 будет своего рода набором переключателей, т.е. будет содержать нули или единички, показывая, отбираем мы данное число в выборку или нет.
• В ячейке E2 стоит обычная автосумма всех единичек по столбцу B, подсчитывающая кол-во выбранных чисел.
• В ячейке E3 с помощью функции СУММПРОИЗВ (SUMPRODUCT) считается сумма попарных произведений ячеек из столбцов А и B (то есть A1*B1+A2*B2+A3*B3+…). Фактически, здесь подсчитывается сумма чисел из столбца А, отобранных единичками из столбца В.
• В розовую ячейку E4 пользователь вводит желаемую сумму для подбора.
• В ячейке E5 вычисляется абсолютное по модулю значение погрешности подбора с целью ее будущей минимизации.
• Все желтых ячейках Е8:E17 хотелось бы получить список отобранных чисел, т.е. тех чисел из столбца А, напротив которых в столбце В есть единички. Для этого необходимо выделить сразу все (!) желтые ячейки и в них ввести вот такую формулу массива:

=ЕСЛИОШИБКА(ИНДЕКС($A$1:$A$20;НАИМЕНЬШИЙ(ЕСЛИ(B1:B20=1;СТРОКА(B1:B20);»»);СТРОКА()-СТРОКА($E$8)+1));»»)

=IFERROR(INDEX($A$1:$A$20;SMALL(IF(B1:B20=1;ROW(B1:B20);»»);ROW()-ROW($E$8)+1));»»)

После ввода формулы ее необходимо ввести не как обычную формулу, а как формулу массива, т.е. нажать не Enter, а Ctrl+Shift+Enter. Похожая формула используется в примере о ВПР, выдающей сразу все найденные значения (а не только первое).



Теперь перейдем на вкладку (или в меню) Данные и запустим инструмент Поиск решения (Data — Solver):

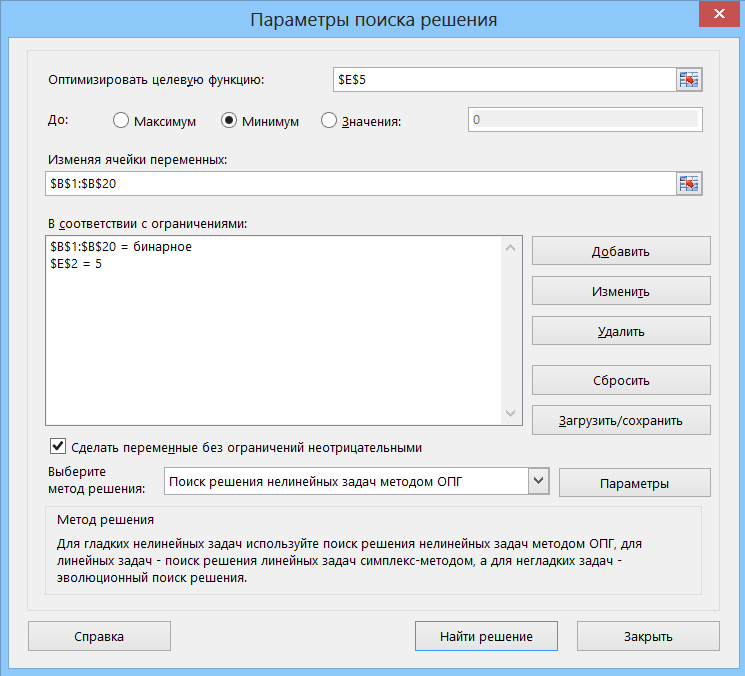
В открывшемся окне необходимо:

• Задать как целевую функцию (Target Cell) — ячейку вычисления погрешности подбора E5. Чуть ниже выбрать опцию — Минимум, т.к. мы хотим подобрать числа под заданную сумму с минимальной (а лучше даже нулевой) погрешностью.
• В качестве изменяемых ячеек переменных (Changing cells) задать диапазон столбца переключателей B1:B20.
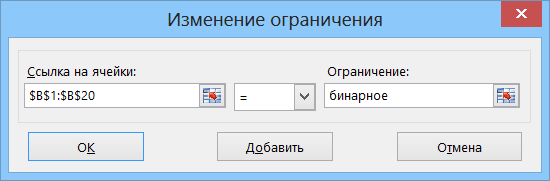
• С помощью кнопки Добавить (Add) создать дополнительное условие на то, что ячейки диапазона B1:B20 должны быть бинарными (т.е. содержать только 0 или 1):

  

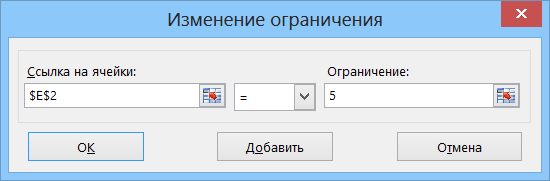
• С помощью той же кнопки, при необходимости, создать ограничение на количество чисел в выборке. Например, если мы знаем, что сумма была разбита на 5 счетов, то:

  

После ввода всех параметров и ограничений запускаем процесс подбора кнопкой Найти решение (Solve). Процесс подбора занимает от нескольких секунд до нескольких минут (в тяжелых случаях) и заканчивается появлением следующего окна:

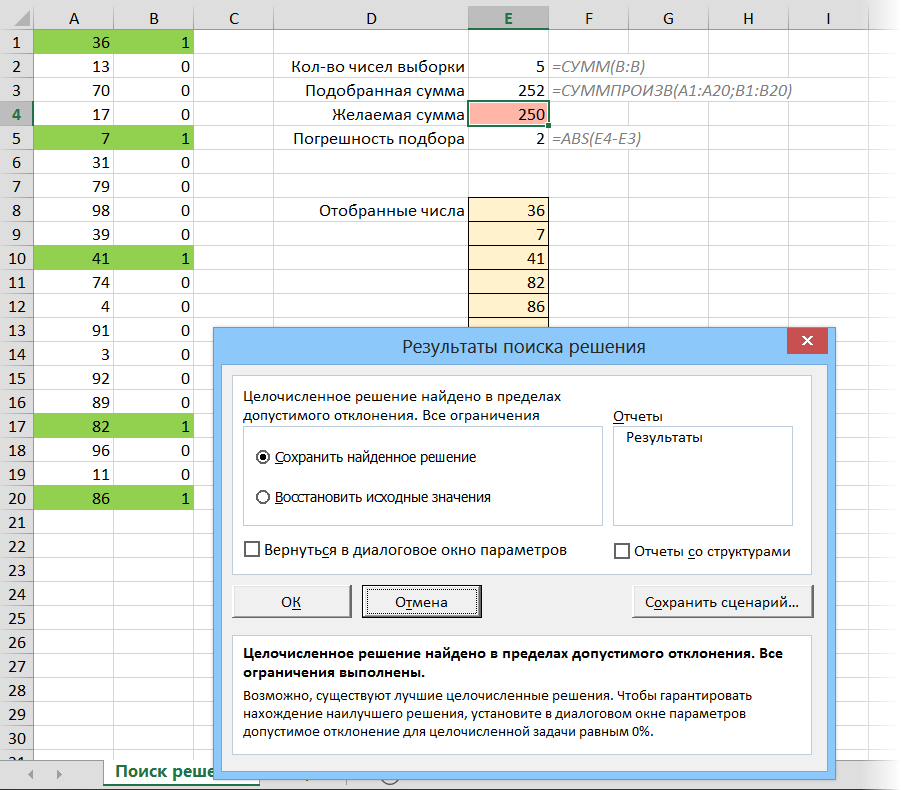
Теперь можно либо оставить найденное решение подбора (Сохранить найденное решение), либо откатиться к прежним значениям (Восстановить исходные значения).

Необходимо отметить, что для такого класса задач существует не одно, а целое множество решений, особенно, если не приравнивать жестко погрешность к нулю. Поэтому запуск Поиска решения с разными начальными данными (т.е. разными комбинациями 0 и 1 в столбце В) может приводить к разным наборам чисел в выборках в пределах заданных ограничений. Так что имеет смысл прогнать эту процедуру несколько раз, произвольно изменяя переключатели в столбце В.

Найденные комбинации можно сохранять виде сценариев (кнопка Сохранить сценарий), чтобы вернуться к нем позднее с помощью команды Данные — Анализ «что-если» — Диспетчер сценариев (Data — What-If Analysis — Scenario Manager):

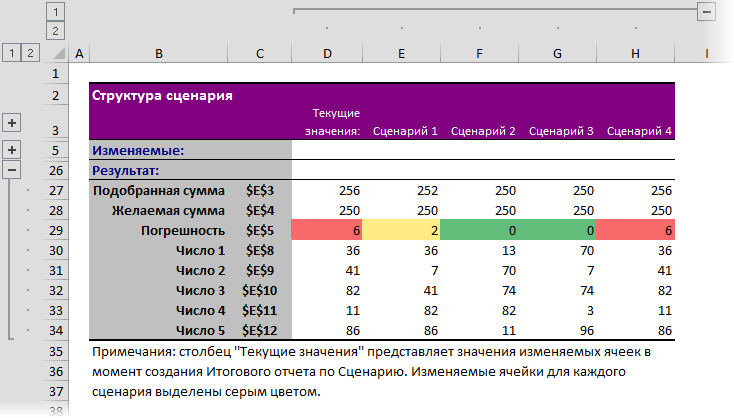
И весьма удобно будет вывести все найденные решения, сохраненные в виде сценариев, в одной сравнительной таблице с помощью кнопки Отчет (Summary):

Способ 2. Макрос подбора

В этом способе всю работу делает макрос, который тупо перебирает случайные комбинации чисел, пока не наткнется на нужную сумму в пределах разрешенной погрешности. Добавлять столбец с нулями и единичками и формулы в этом случае не нужно.

Для использования макроса нажмите сочетание Alt+F11, в открывшемся окне редактора Visual Basic вставьте новый модуль через меню Insert — Module и скопируйте туда этот код:

Sub Combinator()
    Dim Data() As Variant, Selected() As Variant
    Dim goal As Double, sel_count As Integer, prec As Double
    Const LIMIT = 1000000
    
    prec = Range("D5").Value
    sel_count = Range("D2").Value
    goal = Range("D4").Value
    
    Set OutRange = Range("D8")
    Set InputRange = Range("A1", Range("A1").End(xlDown))
    input_count = InputRange.Cells.Count
    Data = InputRange.Value
    ReDim Selected(1 To sel_count) As Variant

NewTry:
    For j = 1 To sel_count
Start:
        RandomIndex = Int(Rnd * input_count + 1)
        RandomValue = Data(RandomIndex, 1)
        
        'начиная со второго элемента дополнительно проверяем, чтобы такой уже не был выбран
        If j > 1 Then
            For k = 1 To j - 1
                If Selected(k) = RandomValue Then GoTo Start
            Next k
        End If
        Selected(j) = RandomValue
    Next j
    
    If Abs(WorksheetFunction.Sum(Selected) - goal) <= prec Then
        Range("D3").Value = WorksheetFunction.Sum(Selected)
        MsgBox "Подбор завершен. Необходимая точность достигнута."
        Range(OutRange, OutRange.End(xlDown)).ClearContents
        OutRange.Resize(sel_count, 1).Value = Application.Transpose(Selected)
        Exit Sub
    Else
        iterations = iterations + 1
        If iterations > LIMIT Then
            MsgBox "Достигнут лимит попыток. Решение не найдено."
            Exit Sub
        Else
            GoTo NewTry
        End If
    End If
End Sub

Аналогично первому способу, запуская макрос несколько раз, можно получать разные наборы подходящих чисел.

P.S. Сейчас набегут энтузиасты с мехмата МГУ с криками «Тупой перебор — это неэстетично!» Да, я в курсе, что прямой перебор вариантов — это не самый оптимальный способ поиска. Да, существует много умных алгоритмов поиска решения таких задач, которые сокращают время поиска и находят нужную комбинацию заметно быстрее. Могу даже рассказать про парочку. Но мне на данном этапе существующей скорости «тупого перебора» вполне достаточно — обработка массива из 1000 ячеек идет меньше секунды. Готов подождать

Ссылки по теме

• Оптимизация бизнес-модели с помощью надстройки Поиск решения (Solver)
• Что такое макросы, куда и как вставлять код макросов на VBA

In this guide, we’re going to show you how to find all combinations of two lists in Excel by using Power Query.

Download Workbook

In our example, we have two lists that contain Pokémon names and we want to see the combinations of matched Pokémon.

We can join these two tables to compare them by using Get & Transform Data. Get & Transform Data feature consists of tools, previously known as Power Query. You can get more information about this here: Power Query 101.

Creating queries from tables

First step is to convert the tables into Power Query structure.

1. Select one of your tables.
2. Open the Data tab and click the corresponding icon under the Get & Transform Data section to get data from your workbook.
   1. (Microsoft 365 / Excel 2019) From Sheet
      
      
   2. (Excel 2016) From Table/Range
   3. (Excel 2010 / Excel 2013) Use Power Pivot tab instead of Data
3. Clicking the button opens the Power Query Editor.
   
4. Once you are done with the changes, click Custom Column in Add Column. We will add a helper column which will be a common point between the two tables.
   
5. Enter a friendly name for your new column and enter =1 into the formula section.
   
6. Click OK to save.
   
7. After adding the helper column, return to the Home tab and click Close & Load To item in Close & Load list to see options.
   
8. Make sure to select Only Create Connection in the Import Data This option will save the table as a connection rather that populating the queried data in the worksheet.
   
9. Apply the same steps to the other table. At the end you should have two queries corresponding with your tables. You can see these tables in Queries & Connections pane in Excel.
   

Joining queries to find all combinations of two lists

Next step is to join (merge) the queries on a new table which will allow us to see any differences between the tables.

1. Once the queries from the tables are ready, go to Data > Get Data > Combine Queries > Merge to open the Merge dialog of Power Query.
   
2. Select each table in the drop downs.
3. Click on the column for each table to select them.
4. Finally select Full Outer option for Join Kind to join by all rows from both tables.
5. Click OK to apply selections.
   
6. You will see three columns after merging. The first one is the items of the first list. Right-click on the column in the middle and select Remove to delete the helper column.
   
7. Click the button next to the column title.
8. Make sure that the Expand option is selected in the popup menu.
9. Uncheck the helper column.
10. Uncheck Use original column as prefix.
11. Click OK to populate the data of the second table.
    
12. You will see the combinations in Power Query. When you are OK with the outcome, click Close & Load, this time to populate the entire data into your worksheet.
    

After populating the merged table, you can see all combinations of the two lists.