|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
1 |
|
Знак принадлежит в математических формулах20.02.2017, 01:12. Показов 72503. Ответов 11
Где в формулах в ворде знак принадлежности одного множества другому?
0 |
|
8927 / 4839 / 1885 Регистрация: 11.02.2013 Сообщений: 10,246 |
|
|
20.02.2017, 08:04 |
2 |
|
На вкладке работы с формулами Миниатюры
1 |
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
20.02.2017, 18:18 [ТС] |
3 |
|
ViterAlex, мне нужен знак принадлежности множества множеству, а не элемента множеству.
0 |
|
8927 / 4839 / 1885 Регистрация: 11.02.2013 Сообщений: 10,246 |
|
|
20.02.2017, 19:18 |
4 |
|
РешениеА они разные? Ну ладно, раскрой список, там море этих операторов. Неужели это так сложно? Миниатюры
1 |
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
21.02.2017, 13:15 [ТС] |
5 |
|
ViterAlex, в заскриненном вами списке нет знака принадлежности одного множества другому. Данный знак выглядит как тот, который Вы предложили изначально, лишь только без чёрточки посредине. В списке есть похожий на искомый мною знак, но этот из списка слишком высокий.
0 |
|
5942 / 3154 / 698 Регистрация: 23.11.2010 Сообщений: 10,524 |
|
|
21.02.2017, 14:45 |
6 |
|
Решениеoobarbazanoo, Вы об этом? Миниатюры
1 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,666 Записей в блоге: 4 |
|
|
21.02.2017, 14:50 |
7 |
|
А разве не проще напечатать на клавиатуре, а не искать по спискам?
1 |
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
21.02.2017, 15:05 [ТС] |
8 |
|
А на форуме почему запись subset в символ не превращается? Тут отличный от ворда текстовый редактор?
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,666 Записей в блоге: 4 |
|
|
21.02.2017, 15:28 |
9 |
|
oobarbazanoo, должно превратиться. У меня же превратилось. Наведите мышку на эти символы и дождитесь всплывающего окна. Там есть исходный код этой формулы.
1 |
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
21.02.2017, 22:44 [ТС] |
10 |
|
palva, не превращается ведь. Миниатюры
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,666 Записей в блоге: 4 |
|
|
21.02.2017, 23:35 |
11 |
|
oobarbazanoo, Теперь я понял вопрос. Эта запись, как и любой текст LATEX работает только в тэгах LATEX. Можно поставить эти тэги с клавиатуры, а можно выделить текст, записанный на LATEX, и нажать метку LATEX, расположенную выше окна текстового редактора форума, так же как вы выделяете C++ или PHP.
1 |
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
21.02.2017, 23:43 [ТС] |
12 |
|
palva,
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
21.02.2017, 23:43 |
|
Помогаю со студенческими работами здесь
Составить программу, которая определяет, принадлежит или не принадлежит круг полностью в квадрат Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 12 |
Содержание
- 1 Доступные наборы символов
- 1.1 Вставка символа
- 1.2 Вставка специального знака
- 2 Вставка символов Юникода
- 2.1 Выбор знака Юникода в окне “Символ”
- 2.2 Добавление знака Юникода с помощью кода
В Word можно вставлять математические символы в уравнения и текст.
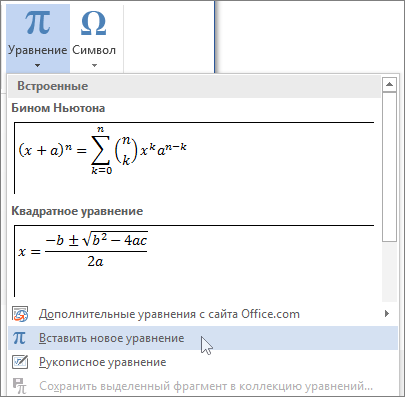
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
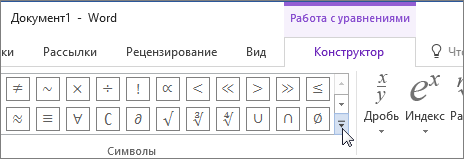
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Щелкните стрелку рядом с названием набора символов и выберите набор символов, который вы хотите отобразить.
Щелкните нужный символ.
Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
Основные математические символы
Часто используемые математические символы, такие как > и
Вероятнее всего, вы хотя бы раз сталкивались с необходимостью вставить в MS Word знак или символ, которого нет на компьютерной клавиатуре. Это могло быть, к примеру, длинное тире, символ градуса или правильной дроби, а также много чего другого. И если в некоторых случаях (тире и дроби) на помощь приходит функция автозамены, то в других все оказывается намного сложнее.
Мы уже писали о вставке некоторых специальных символов и знаков, в этой статье мы расскажем о том, как быстро и удобно добавлять в документ MS Word любые из них.
Вставка символа
1. Кликните в том месте документа, куда необходимо вставить символ.
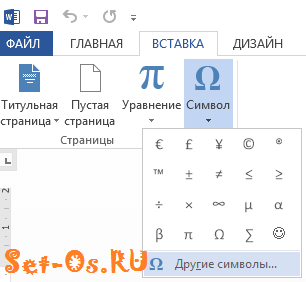
2. Перейдите во вкладку “Вставка” и нажмите там кнопку “Символ”, которая находится в группе “Символы”.
3. Выполните необходимое действие:
- Выберите в развернувшемся меню нужный символ, если он там есть.
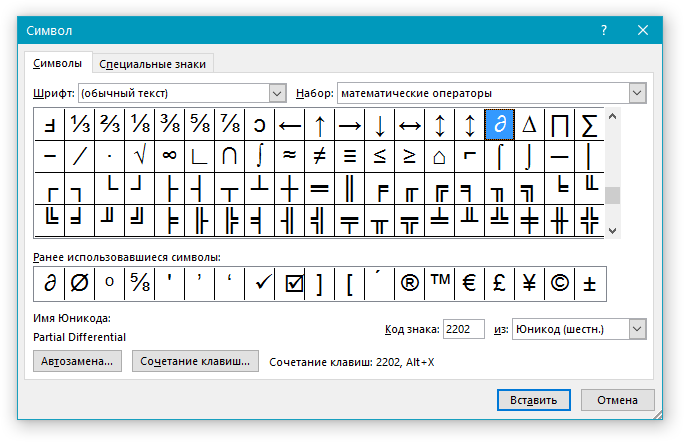
- Если же нужный символ в этом небольшом окошке будет отсутствовать, выберите пункт “Другие символы” и найдите его там. Кликните по необходимому символу, нажмите кнопку “Вставить” и закройте диалоговое окно.
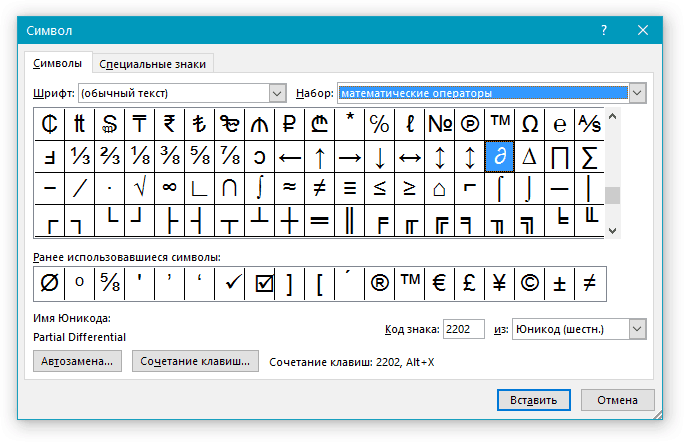
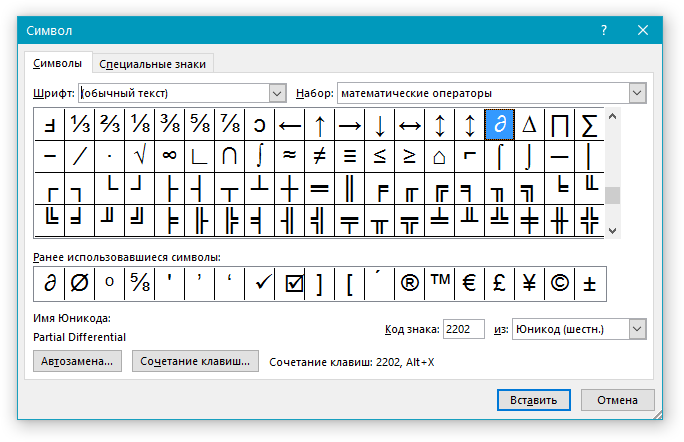
Примечание: В диалоговом окне “Символ” содержится очень много различных символов, которые сгруппированы по тематикам и стилям. Для того, чтобы быстрее найти нужный символ, вы можете в разделе “Набор” выбрать характерный для этого символа, например, “Математические операторы” для того, чтобы найти и вставить математические символы. Также, можно изменять шрифты в соответствующем разделе, ведь во многих из них тоже есть различные символы, отличные от стандартного набора.
4. Символ будет добавлен в документ.
Вставка специального знака
1. Кликните в том месте документа, куда необходимо добавить специальный знак.
2. Во вкладке “Вставка” откройте меню кнопки “Символы” и выберите пункт “Другие символы”.
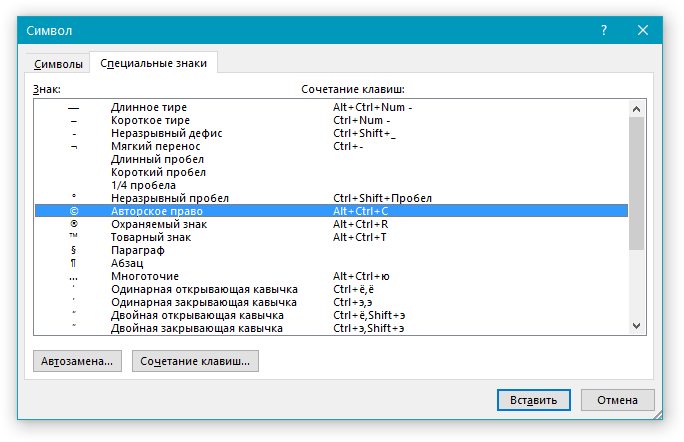
3. Перейдите во вкладку “Специальные знаки”.
4. Выберите необходимый знак, кликнув по нему. Нажмите кнопку “Вставить”, а затем “Закрыть”.
5. Специальный знак будет добавлен в документ.
Примечание: Обратите внимание, что в разделе “Специальные знаки” окна “Символ”, помимо самих специальных знаков вы также можете увидеть горячие комбинации клавиш, которые можно использовать для их добавления, а также настроить автозамену для конкретного символа.
Вставка символов Юникода
Вставка знаков Юникода мало чем отличается от вставки символов и специальных знаков, за исключением одного важного преимущества, заметно упрощающего рабочий процесс. Более подробная инструкция о том, как это сделать, изложена ниже.
Выбор знака Юникода в окне “Символ”
1. Кликните в том месте документа, куда нужно добавить знак Юникода.
2. В меню кнопки “Символ” (вкладка “Вставка”) выберите пункт “Другие символы”.
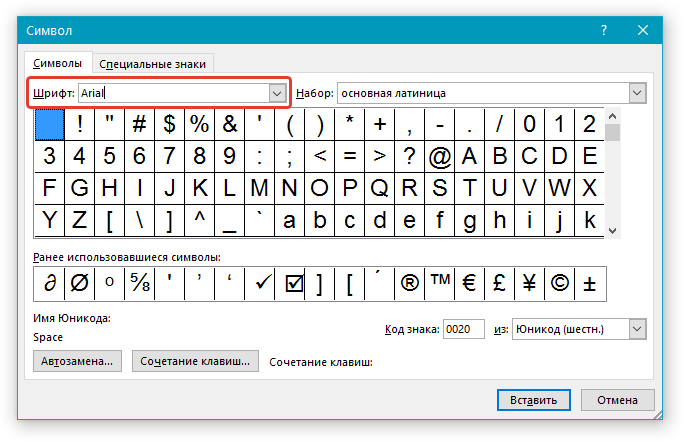
3. В разделе “Шрифт” выберите необходимый шрифт.
4. В разделе “Из” выберите пункт “Юникод (шестн)”.
5. Если поле “Набор” будет активно, выберите необходимый набор символов.
6. Выбрав нужный символ, кликните по нему и нажмите “Вставить”. Закройте диалоговое окно.
7. Знак Юникода будет добавлен в указанное вами место документа.
Урок: Как в Word поставить символ галочки
Добавление знака Юникода с помощью кода
Как уже было сказано выше, у знаков Юникода есть одно важное преимущество. Заключается оно в возможности добавления знаков не только через окно “Символ”, но и с клавиатуры. Для этого необходимо ввести код знака Юникода (указан в окне “Символ” в разделе “Код”), а затем нажать комбинацию клавиш.
Очевидно, что запомнить все коды этих знаков невозможно, но самые необходимые, часто используемые выучить точно можно, ну, или хотя бы записать их где-нибудь и хранить под рукой.
1. Кликните левой кнопкой мышки там, где требуется добавить знак Юникода.
2. Введите код знака Юникода.
Примечание: Код знака Юникода в Word всегда содержит буквы, вводить их необходимо в английской раскладке заглавным регистром (большими).
3. Не перемещая указатель курсора с этого места, нажмите клавиши “ALT+X”.
4. В указанном вами месте появится знак Юникода.
Вот и все, теперь вы знаете о том, как вставить в Майкрософт Ворд специальные знаки, символы или знаки Юникода. Желаем вам положительных результатов и высокой продуктивности в работе и обучении.
Отблагодарите автора, поделитесь статьей в социальных сетях.
| Состояние | отпатрулирована |
В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeX, объяснения и примеры использования. Список и смысл обозначений соответствует международным стандартам ISO 31-11 и ISO 80000-2.
Кроме указанных символов, иногда используются их зеркальные отражения, например, A ⊂ B <displaystyle Asubset B> 
Знаки операций, или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.
Таблица математических символов. Сокращённая запись математического текста, математические обозначения. Математический алфавит. Математическая скоропись. Негламурный эксклюзив от Проекта DPVA.info
- Сортировка знак / легенда
- Сортировка легенда / знак
|
Знак (символ, сокращение) |
Пояснения (расшифровка, легенда) |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
т.о. |
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
ЧТД QED |
Конец доказательства = «Что и требовалось доказать» = quod erat demonstrandum | |||||||||||||||||||||||
|
|
Что и требовалось доказать = окончание доказательства | |||||||||||||||||||||||
|
|
Что и требовалось доказать = окончание доказательства | |||||||||||||||||||||||
|
|
Что и требовалось доказать = окончание доказательства | |||||||||||||||||||||||
|
= |
Равенство | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
Записывается a |
|||||||||||||||||||||||
|
|
По определению логически эквивалентно | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Неравенство | |||||||||||||||||||||||
|
|
Меньше | |||||||||||||||||||||||
|
|
Больше | |||||||||||||||||||||||
|
|
Много меньше | |||||||||||||||||||||||
|
|
Много больше | |||||||||||||||||||||||
|
<= |
Меньше или равно | |||||||||||||||||||||||
|
>= |
Больше или равно | |||||||||||||||||||||||
|
|
Сведение по Карпу (Karp reduction) — теория сложности, левое сводимо по Карпу к правому, левое «не сложнее правого», естественно возможно и использование знака острием вправо (но нам лень было рисовать) |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Разделить | |||||||||||||||||||||||
|
|
Если G -группа, а H- ее нормальная подгруппа, то G/H — факторгруппа G по H, т.е. группа классов смежности H в G
Если X — множество с заданным на нем отношением эквивалентности |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Минус плюс — имеет смысл только при употреблении вместе со знаком плюс минус cos(x ± y) = cos(x) cos(y) |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
P(A|B) — вероятность события А, при условии, что событие B уже произошло
Если функция f определена на R, то f|N определена только на N и принимает на N те же значения, что и f
A={x | |x|<1} читается: «А — множество x таких, что модуль x меньше 1» и значит, что множество А — множество элементов числовой прямой, лежащих между -1 и 1. |
|||||||||||||||||||||||
|
|
a||b — параллельные прямые a и b
Если X — множество с отношением частичного порядка ≤, а a и b — его элементы, то a||b — a и b несравнимы, если про них невозможно сказать ни a≤b, ни b≤a
|
|||||||||||||||||||||||
|
|
n# — произведение простых чисел, не превышающих n |
|||||||||||||||||||||||
|
|
Алеф — кардинальное число, характеризующее мощность бесконечного вполне упорядоченного множества |
|||||||||||||||||||||||
|
|
Бет — кардинальное число, характеризующее мощность бесконечного множества |
|||||||||||||||||||||||
|
|
мощность континуума — теория множеств |
|||||||||||||||||||||||
|
: |
E:K значит, что E — это расширение поля K
|
|||||||||||||||||||||||
|
! |
n!=1*2*3…..*(n-1)*n читается n-факториал
!A=1, если А=0, !А=0, если А=1, читается не А. |
|||||||||||||||||||||||
|
|
сплетение групп в теории групп (Также обозначается как АwrВ) | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Антисоединение отношений (Antijoin) — операция реляционной алгебры, которая оставляет только те кортежи первого отношения, для которых не найдется кортежей второго отношения, совпадающих с ними по общему атрибуту. |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Естественное соединение отношений (Natural Join)- операция реляционной алгебры, результатом которой является набор всех возможных комбинаций кортежей исходных отношений, то есть комбинаций тех кортежей, у которых совпадают общие атрибуты |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
импликация (материальная) логика |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Материальная эквивалентность, равносильность= «тогда и только тогда» |
|||||||||||||||||||||||
|
|
Материальная эквивалентность, равносильность= «тогда и только тогда» |
|||||||||||||||||||||||
|
|
Логическое отрицание = не |
|||||||||||||||||||||||
|
|
Логическое отрицание = не |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
исключающее ИЛИ (только в логике) |
|||||||||||||||||||||||
|
|
обозначение понятия — любой, читается как — «для любого», «для всех», «для каждого» |
|||||||||||||||||||||||
|
|
обозначение понятия — существует, читается как «найдется», «существует», «существуют»… |
|||||||||||||||||||||||
|
|
обозначение понятия — существует единственный, читается как «найдется ровно один «, «существует один и только один «, «существует единственный «… |
|||||||||||||||||||||||
|
|
внутри скобок записываются элементы множества |
|||||||||||||||||||||||
|
|
значок множества со значком определяющего признака элементов множеств. Читается, как элементы «икс», такие что «для всех икс верно….». |
|||||||||||||||||||||||
|
|
значок множества со значком определяющего признака элементов множеств. Читается, как элементы «икс», такие что «для всех икс верно….». |
|||||||||||||||||||||||
|
|
значок пустого множества |
|||||||||||||||||||||||
|
|
значок пустого множества |
|||||||||||||||||||||||
|
|
значок пустого множества |
|||||||||||||||||||||||
|
|
значок принадлежности к множеству — читается «принадлежит…» |
|||||||||||||||||||||||
|
|
значок не принадлежности к множеству — читается «не принадлежит…» |
|||||||||||||||||||||||
|
|
Знак подмножества. А |
|||||||||||||||||||||||
|
|
Знак собственного (строгого = истинного ) подмножества. А |
|||||||||||||||||||||||
|
|
Знак надмножества. А |
|||||||||||||||||||||||
|
|
Знак строгого = истинного надмножества. А |
|||||||||||||||||||||||
|
|
В теории множеств-объединение множеств. С= А |
|||||||||||||||||||||||
|
|
В теории множеств — пересечение множеств. С= А |
|||||||||||||||||||||||
|
|
В теории множеств — симметрическая разность множеств. С= А |
|||||||||||||||||||||||
|
|
В теории множеств — разность множеств (или относительное дополнение одного множества до другого). С= А |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Стрелка, определяющая отображение (функцию) f. Запись f: a Наример, f: x |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Множество натуральных чисел. В зависимости от контекста и области применения этого обозначения за  обозначают либо множество {1, 2, 3, 4, …}, либо множество {0, 1, 2, 3, 4…}. обозначают либо множество {1, 2, 3, 4, …}, либо множество {0, 1, 2, 3, 4…}. |
|||||||||||||||||||||||
|
|
Множество целых чисел.
Также можно написать |
|||||||||||||||||||||||
|
|
Множество положительных целых чисел. Т.е. множество {1, 2, 3, …} | |||||||||||||||||||||||
|
|
Множество неотрицательных целых чисел. Т.е. множество {0, 1, 2, …} | |||||||||||||||||||||||
|
Z/(n)Z Z/(n) |
Кольцо вычетов по модулю n. Стоит понимать, что вместо n может стоять любая буква, а в частном случае цифра. |
|||||||||||||||||||||||
|
|
Множество p-адических чисел вида Стоит понимать, что вместо p может стоять любая буква, а в частном случае цифра. |
|||||||||||||||||||||||
|
|
Проективное пространство. В частности,  n n-мерное проективное пространство. n n-мерное проективное пространство. |
|||||||||||||||||||||||
|
P(X) Pr(X) P[X] Pr[X] |
В теории вероятности — вероятность. |
|||||||||||||||||||||||
|
|
Множество рациональных чисел.
|
|||||||||||||||||||||||
|
|
Множество действительных чисел | |||||||||||||||||||||||
|
|
Множество комплексных чисел.
|
|||||||||||||||||||||||
|
|
Множество кватернионов (кватернионов Гамильтона).
Другими словами, a — это рациональное число, а b i +c j +d k — это вектор трехмерного пространства с координатами {b, c, d}. |
|||||||||||||||||||||||
|
O |
O-большое в исследовании ассимптотического поведения функций. Описывает ассимптотическое поведение функции, когда ее аргумент стремится к числу или к бесконечности. Запись f(x)=O(g(x)) при x |
|||||||||||||||||||||||
|
|
Бесконечность. Элемент расширенной числовой прямой, который больше любого числа. Чаще всего употребляется, когда речь идет о пределах. | |||||||||||||||||||||||
|
|
Огругление числа до целого в меньшую сторону.
Например, |
|||||||||||||||||||||||
|
|
Огругление числа до целого в большую сторону.
Например, |
|||||||||||||||||||||||
|
|
Огругление числа до ближайшего целого к нему. Например, |
|||||||||||||||||||||||
|
|
[E:K] — это по определению размерность векторного пространства E над K. Например, [
|
|||||||||||||||||||||||
|
|
Например, [2=3]=0; [4<5]=1.
Иными словами, f[X]={f(x) | x∈X} |
|||||||||||||||||||||||
|
|
[g, h] = g-1h-1gh, если g, h∈G, где G — группа. [a,b]=ab-ba, если a, b∈R, где R — кольцо. [A, B]=AB-BA, если A и B — операторы.
|
|||||||||||||||||||||||
|
|
Смешанное произведение векторов. | |||||||||||||||||||||||
|
|
f(x) — образ x при применении f.
Иными словами, f(X)={f(x) | x∈X}
|
|||||||||||||||||||||||
| (( )) |
Количество мультимножеств -число различных мультимножеств мощности k, состоящих из элементов, выбранных из множества мощности n |
|||||||||||||||||||||||
|
|
(a, b)=НОД(a, b) — наибольший общий делитель чисел a и b.
(a,b)={x∈
|
|||||||||||||||||||||||
|
|
Интервал (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый слева) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый слева) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый справа) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый справа) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
<S> — среднее значение элементов множества S.
Если S — подмножество линейного пространства L, <S> — линейная оболочка множества S, т.е. прересечение всех подпространств линейного пространства L, содержащих в себе множество S.
Если S — некоторое подмножество элементов группы G, то <S> — подгруппа G, порожденная S, т.е. минимальная подгруппа G, содержащая S. |
|||||||||||||||||||||||
|
|
Если a1, a2…,an — векторы линейного пространства L, то <a1, a2…,an> — линейная оболочка векоторов a1, a2…,an т.е. пересечение всех подпространств пространства L, содержащих в себе векторы a1, a2…,an.
Если a1, a2…,an— некоторые элементы группы G, то <a1, a2…,an> — подгруппа G, порожденная элементами a1, a2…,an, т.е. минимальная подгруппа G, содержащая в себе элементы a1, a2…,an.
|
|||||||||||||||||||||||
|
|
Скалярное произведение векторов в предгильбертовом пространстве. (Следует понимать, что скалярное произведение может быть определено множеством способов) | |||||||||||||||||||||||
|
|
Скалярное произведение векторов в предгильбертовом пространстве. (Следует понимать, что скалярное произведение может быть определено множеством способов) | |||||||||||||||||||||||
|
|
В обозначениях Дирака — кет-вектор. |φ> — вектор φ некоторого гильбертого пространства | |||||||||||||||||||||||
|
|
В обозначениях Дирака — бра-вектор из пространства, сопряженного некоторому гильбертовому пространству. <φ| — бра вектор, соответствующий кет-вектору |φ> (говорят, даже, совпадающий с кет-фектором |φ>), задающий линейный функционал, ставящий в соответствие каждому кет-вектору |ψ> скалярное произведение <φ|ψ>. | |||||||||||||||||||||||
|
|
число советаний из r элементов, выбранных из n элементов | |||||||||||||||||||||||
|
|
Сумма, ряд.
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
В теории категорий — копроизведение (категорная сумма) | |||||||||||||||||||||||
|
|
Производная. f'(x) — значение производной функции f в точке x (Тангенс угла наклона касательно к функции f в точке x). | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Интеграл по контуру (поверхности — знак интеграла удваивается, объему-знак интеграла утраивается). | |||||||||||||||||||||||
|
|
Если вектор
Если вектор где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то |
|||||||||||||||||||||||
|
|
Если M — некоторое множество, то
Если f — многочлен, то |
|||||||||||||||||||||||
|
|
Оператор Лапласа ставит функции от n переменных в соответствие ее дифференциал второго порядка.
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Операция, которая из заданного отношения (таблицы) выбирает подмножество, которое получается выбором нескольких из имеющихся атрибутов и (если потребуется) вычеркиванием повторяющихся кортежей. Результатом перации Например: Если в изначальной таблице ЛЮДИ атрибутами являются рост, вес, пол, то результатом операции
Математическая константа, равная отношению длины окружности к ее диаметру. |
|||||||||||||||||||||||
|
|
В реляционной алгебре — выборка Операция |
|||||||||||||||||||||||
|
|
В теории порядка — покрытие (понятие, определяющее смежность вершин диаграммы Хассе некоторого частично-упорядоченного множества). Если X — множество с отношением частичного порядка ≤ , а отношение < на этом множестве задается следующим образом : a<b, если a≤b и а ≠ b, то элемент y покрывает элемент x и пишется x x<z<y. Если a |
|||||||||||||||||||||||
|
|
В теории типов — подтип (подкласс, дочерний тип(класс)). Часто используется в объектно-ориентированном программировании. S  T значит, что S — подтип T, т.е. все элементы S являются элементами типа Т, и их объединяет какое-то общее свойство. T значит, что S — подтип T, т.е. все элементы S являются элементами типа Т, и их объединяет какое-то общее свойство. Например, Круги  Фигуры. Фигуры.S  T значит, что любой элемент типа S можно использовать в том месте, где ожидается использование элемента типа T, и при этом не возникнет ошибки. T значит, что любой элемент типа S можно использовать в том месте, где ожидается использование элемента типа T, и при этом не возникнет ошибки. |
|||||||||||||||||||||||
|
|
Эрмитово-сопряженная (комплексно-сопряженная) матрица. A† — матрица, полученная из матрицы A транспонированием и заменой каждого элемента матрицы A комплексно-сопряженным ему. Чаще всего такая матрица обозначается A*, а также встречаются обозначения A*T, AT*, |
|||||||||||||||||||||||
|
|
Транспонирование матрицы. AT — матрица, в которой в качестве строк записаны столбцы матрицы А. |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
x⊥y значит, что векторы (прямые) x и y перпендикулярны, или, в более общем случае, ортогональны.
Если W — подпространство предгильбертового пространства V, то W⊥ — ортогональное дополнение подпространства W, т.е. множество векторов пространства V, перпендикулярных каждому из векторов подпространства W.
a⊥b значит, что наибольший общий делитель чисел a и b равен единице. Часто записывается как (a, b)=1
A⊥B значит, что случайные события A и B независимы, т.е. наступление одного из них не влияет на вероятность наступления другого.
⊥ — наименьший (нижний) элемент решетки
⊥ — тип, у которого нет подтипов
x⊥y значит, что элементы x и y частично упорядоченного множества сравнимы, т.е. про них известно, что x≤y или y≤x |
|||||||||||||||||||||||
|
|
Импликация (логическое следование) — в теории моделей A |
|||||||||||||||||||||||
|
|
Вывод — в логике высказываний (предикатов). A |
|||||||||||||||||||||||
|
|
Тензорное произведение (модулей) — в линейной алгебре. Если A и B — линейные пространства, то Если а
a Если A и B — модули над коммутативным кольцом R, то A |
|||||||||||||||||||||||
|
|
a
где f, g — функции, определенные и интегрируемые относительно меры Лебега на пространстве Rd
z* — число, комплексно-сопряженное к z. Если z=a+bi, то z*=a-bi
R* — группа обратимых элементов кольца R
R* — расширение множества R действительных чисел, в котором каждый элемент представляется в виде суммы действительного числа и бесконечно малой добавки, бесконечно малые величины в котором являются величинами постоянными. В R* входят также бесконечно большие числа. Вместо R можно использовать также другие множества, например, N*.
Линейный оператор из пространства p-векторов в пространства (n-p)-форм. Если вектор v — поливектор степени p, то *v — дифференциальная форма степени n-p. |
|||||||||||||||||||||||
|
|
Если S — некоторое подмножество топологического пространства, то |
- Сортировка знак / легенда
- Сортировка легенда / знак
|
Легенда (пояснение, расшифровка) |
Символ (знак, сокращение) |
|||
| Следовательно, таким образом, поэтому |
1. 2. т.о. 3. |
|||
| Потому что, из-за того что, вследствие того что, поскольку, в результате того, что |
|
|||
| Конец доказательства, что и требовалось доказать |
1. ЧТД, QED (Что и требовалось доказать, quod erat demonstrandum) 2. 3. 4. |
|||
| Таких что, так что, такие что |
1. A={x | |x|<1} читается: «А — множество x таких, что модуль x меньше 1» и значит, что множество А — множество элементов числовой прямой, лежащих между -1 и 1. 2. :
|
|||
| Материальная эквивалентность, равносильность, тогда и только тогда |
1. 2. |
|||
| Любой, для любого | ||||
| Существует, найдется | ||||
| Существует единственный | ||||
| Или | ||||
| Бесконечность |  |
|||
| Приращение, изменение |  |
|||
| Стремится |  |
|||
| Равно | = | |||
| По определению равно | 1. 2. 3. 4. 5. 6. |
|||
| По определению эквивалентно | ||||
| Равно по модулю |
Записывается a |
|||
| Не равно | ||||
| Приблизительно равно | ||||
| Сложение, ряд |
1. 2.
|
|||
| Вычитание | ||||
| Умножение, произведение |
1. 2. 3. * 4.
|
|||
| Деление, разделить |
1. : 2. 3. |
|||
| Квадратный корень (действительный, мнимый) | ||||
| Возведение в степень |
2^3 = 23 |
|||
| Факториал |
! n!=1*2*3…..*(n-1)*n читается n-факториал |
|||
| Модуль числа |
1. |a| — модуль а 2. Abs(a) |
|||
| Плюс-минус, минус-плюс |
1. 2. имеет смысл только при употреблении вместе со знаком плюс минус cos(x ± y) = cos(x) cos(y) |
|||
| Больше | ||||
| Больше или равно |
1. 2. >= |
|||
| Меньше | ||||
| Меньше или равно |
1. 2. <= |
|||
| Много больше | ||||
| Много меньше | ||||
| Числа одного порядка | ||||
| Приоритет операций | ( ) | |||
| Число сочетаний из n по r |
1. 2. |
|||
| Количество мультимножеств, число различных мультимножеств мощности k, состоящих из элементов, выбранных из множества мощности n |
(( )) |
|||
| Число Пи |  |
|||
| Кортеж , упорядоченный набор (список) некоторых величин, или горизонтальный вектор |
1. 2. |
|||
| Среднее значение, усреднение |
1. 2. |
|||
| Множество, знак множества |
1. 2. 3. |
|||
| Пустое множество |
1. 2. 3. |
|||
| Знак принадлежности множеству, принадлежит | ||||
| Знак «не принадлежит множеству» |  |
|||
| Множество натуральных чисел |
|
|||
| Множество целых чисел |
1. 2. 3. |
|||
| Множество рациональных чисел |
|
|||
| Множество действительных чисел |
|
|||
| Множество комплексных чисел |
|
|||
| Множество кватернионов |
|
|||
| Множество p-адических чисел |
Стоит понимать, что вместо p может стоять любая буква, а в частном случае цифра. |
|||
| Множество гипердействительных чисел |
R* — расширение множества R действительных чисел, в котором каждый элемент представляется в виде суммы действительного числа и бесконечно малой добавки, бесконечно малые величины в котором являются величинами постоянными. В R* входят также бесконечно большие числа. |
|||
| Мощность множества, кардинальное число, количество элементов |
1. 2. |
|||
|
Алеф — кардинальное число, характеризующее мощность бесконечного вполне упорядоченного множества |
||||
|
Бет — кардинальное число, характеризующее мощность бесконечного множества |
||||
|
Континуум, мощность континуума |
||||
| Знак подмножества |
1. А 2. А |
|||
| Знак надмножества |
1. А 2. А |
|||
| Объединение (множеств) |  |
|||
| Пересечение (множеств) |  |
|||
| Симметрическая разность (множеств) |
1. 2. |
|||
| Разность множеств |
1. 2. — (редко) |
|||
| Прямое (декартово) произведение множеств | 1. 
2. |
|||
| Прямая сумма | ||||
| Несвязное объединение, несвязная сумма, дизъюнктное объединение | ||||
| Логическое отрицание |
1. 2. 3. ! |
|||
| Логическая конъюнкция |
1. 2. & |
|||
| Логическая дизъюнкция | ||||
| Исключающее или | ||||
| Импликация (логическое следование) |
1. 2. 3. 4. |
|||
| Вывод в логике высказываний |  |
|||
| Нотация Айверсона, или скобка Айверсона. Сопоставляет некоторому утверждению 1 или 0, в зависимости от того, истинно или ложно данное утверждение. |  |
|||
| Сведение по Карпу (Karp reduction) — теория сложности, левое сводимо по Карпу к правому, левое «не сложнее правого», естественно возможно и использование знака острием вправо (но нам лень было рисовать) |
1. 2. |
|||
| Делитель, делит/ не делит нацело |
1. 2. |
|||
| Точный делитель (при разложении числа в произведение степеней простых чисел — простое число в максимальной степени, делящее исходное) | ||||
| Взаимно простые числа |  |
|||
| Примориал или праймориал | ||||
| Наибольший общий делитель |
1. 2. НОД |
|||
| Окргугление числа до целого |
1. 2. 3. 4. 5. 6. Round(x) — до ближайшего целого 7. Nint(x) — до ближайшего целого |
|||
| Сопряжение комплексных чисел |
1. z* — число, комплексно-сопряженное к z 2.
|
|||
| Пропорциональность | ||||
| Отрезок |  |
|||
| Интервал |
1. 2. |
|||
| Полуинтервал |
1. 2. 3. 4. |
|||
| Норма, длина вектора |
1. 2. |
|||
| Обозначения Дирака: кет-вектор |  |
|||
| Обозначения Дирака: бра-вектор |  |
|||
| Скалярное произведение |
1. 2. 3. 4. 5. |
|||
| Векторное произведение векторов |
1. 2. |
|||
| Смешанное произведение векоторов |  |
|||
| Ортогональность (перпендикулярность) |  |
|||
| Параллельность | ||||
| Эквивалентность матриц | ||||
| Скалярное произведение матриц | : | |||
| Определитель матрицы |
1. 2. det(A), где А — матрица 3. |
|||
| Транспонирование матрицы |
АТ — транспонированная матрица А |
|||
| Эрмитово-сопряженная (комплексно-сопряженная) матрица к матрице А |
1. A† 2.A* 3.А*T 4. AT* 5. 6. |
|||
| Произведение Адамара двух матриц одинакового размера | ||||
| Определение функции, область определения и область значений функции |
Запись f : X |
|||
| Определение функции (отображения) , задание функции |
Запись f: a |
|||
| Образ элемента/множества |
1. f(x) — образ элемента x; f(X) — образ множества X 2. f[X] — образ множества X |
|||
| Ограничение функции на множестве, сужение области определения функции |
Если функция f определена на R, то f|N определена только на N и принимает на N те же значения, что и f |
|||
| Композиция функций | ||||
| Производная |
1. 2.
3. |
|||
| Интеграл, первообразная |
1. 2. 3. 4. |
|||
| Свертка функция |
|
|||
| Градиент |
|
|||
| Дивергенция |
|
|||
| Ротор |
|
|||
| Эквивалентность функций при определенной базе | ||||
| О-большое | O | |||
| Степень многочлена |
1.
2. deg f |
|||
| Лапласиан, оператор Лапласа |  |
|||
| Кольцо вычетов по модулю n | 1. 
2. 3. Z/(n)Z 4. Z/(n) |
|||
| Проективное пространство |
1. 2. |
|||
| Изоморфизм |
1. 2. |
|||
| Конгруэнтность | ||||
| Коммутатор |
[g, h] = g-1h-1gh, если g, h∈G, где G — группа. [a,b]=ab-ba, если a, b∈R, где R — кольцо. [A, B]=AB-BA, если A и B — операторы |
|||
| Группа, порожденная подмножеством/элементом группы |
1. Если S — некоторое подмножество элементов группы G, то <S> — подгруппа G, порожденная S 2. Если a1, a2…,an— некоторые элементы группы G, то <a1, a2…,an> — подгруппа G, порожденная элементами a1, a2…,an |
|||
| Линейная оболочка подмножества/векторов линейного пространства |
1. Если S — подмножество линейного пространства L, <S> — линейная оболочка множества S 2. Если a1, a2…,an — векторы линейного пространства L, то <a1, a2…,an> — линейная оболочка векоторов a1, a2…,an т.е. пересечение всех подпространств пространства L, содержащих в себе векторы a1, a2…,an. |
|||
| Ортогональное дополнение подпространства |
Если W — подпространство предгильбертового пространства V, то W⊥ — ортогональное дополнение подпространства W |
|||
| Тензорное произведение |  |
|||
| Нормальная (инвариантная) подгруппа | ||||
| Идеал кольца | ||||
| Индекс подгруппы |
Если H — подгруппа группы G, то [G:H] — индекс подгруппы H |
|||
| Расширение поля |
: E:K значит, что E — это расширение поля K |
|||
| Степень расширения поля |
[E:K] — это степень расширения поля E:K, где E — это расширение поля K. |
|||
| Факторгруппа |
Если G -группа, а H- ее нормальная подгруппа, то G/H — факторгруппа G по H, т.е. группа классов смежности H в G |
|||
| Фактормножество |
Если X — множество с заданным на нем отношением эквивалентности |
|||
| Сплетение групп |
1. 2. АwrВ |
|||
| Граница множества |
Если M — некоторое множество, |
|||
| Группа единиц (обратимых элементов) кольца |
1. R* 2. Rx 3. U(R) |
|||
| Звезда Ходжа |  |
|||
| Замыкание (алгебраическое, топологическое) |  |
|||
| Полупрямое произведение групп | ||||
| Копроизведение (категорная сумма) |  |
|||
| Антисоединение отношений (Antijoin) — реляционная алгебра | ||||
| Полусоединение отношений (Semijoin) — реляционная алгебра | ||||
| Естественное соединение отношений (Natural Join) — реляционная алгебра | ||||
| Проекция — реляционная алгебра |
|
|||
| Выборка — реляционная алгебра |
|
|||
| Отношение эквивалентности, принадлежность одному классу эквивалентности | ||||
| Класс эквивалентности |
[a] — это множество элементов, эквивалентных a. Более точная запись — [a]R означает класс эквивалентности, порожденный элементом a относительно отношения эквивалентности R |
|||
| Вероятность события X |
1. 2. 3. P(X) 4. Pr(X) 5. P[X] 6. Pr[X] |
|||
| Условная вероятность |
P(A|B) — вероятность события А, при условии, что событие B уже произошло |
|||
| Независимость случайных событий |  |
|||
| Распределение вероятности случайной величины | ||||
| Несравнимость в теории порядка | ||||
| Сравнимость в теории порядка |  |
|||
| Покрытие в теории порядка |
x |
|||
| Наибольший (верхний )элемент решетки в теории порядка |  |
|||
| Наименьший (нижний) элемент решетки |  |
|||
| Подтип, подкласс, дочерний класс в теории типов |
S |
|||
| Высший (универсальный) тип в теории типов |  |
|||
| Нижайший тип (универсальный подтип) в теории типов |  |
|||
| Дельта-функция |
|
|||
| Символ Кронекера, индикатор равенства переменных |
|
- Сортировка знак / легенда
- Сортировка легенда / знак
Математические символы
1) Если вы скопировали символ, вставили его в ваш документ, а он превратился
в нечто непонятное, не расстраивайтесь: просто выберите для него другой шрифт.
2) Левая и правая угловые скобки отображаются здесь некорректно.
Но при копировании в документ Word они отображаются правильно.
|
надчеркивание |
‾ |
|
дробная черта |
⁄ |
|
рукописная P |
℘ |
|
мнимая часть числа |
ℑ |
|
действительная часть числа |
ℜ |
|
алеф |
ℵ |
|
стрелка влево |
← |
|
стрелка вверх |
↑ |
|
стрелка вправо |
→ |
|
стрелка вправо из вертикальной черты |
↦ |
|
стрелка вниз |
↓ |
|
стрелка влево-вправо |
↔ |
|
знак обратимости (реакция идет в обе стороны) |
⇄ |
|
возврат каретки |
↵ |
|
двойная стрелка влево |
⇐ |
|
двойная стрелка вверх |
⇑ |
|
двойная стрелка вправо |
⇒ |
|
двойная стрелка вниз |
⇓ |
|
двойная стрелка влево-вправо |
⇔ |
|
квантор всеобщности |
∀ |
|
знак дифференциала |
∂ |
|
квантор существования |
∃ |
|
пустое множество |
∅ |
|
набла |
∇ |
|
принадлежит множеству |
∈ |
|
не принадлежит множеству |
∉ |
|
является членом |
∋ |
|
n-арное произведение |
∏ |
|
n-арная сумма |
∑ |
|
знак минус |
− |
|
радикал |
√ |
|
пропорционально |
∝ |
|
бесконечность |
∞ |
|
угол |
∠ |
|
логическое И |
∧ |
|
логическое ИЛИ |
∨ |
|
пересечение |
∩ |
|
объединение |
∪ |
|
интеграл |
∫ |
|
следовательно |
∴ |
|
оператор тильда |
~ |
|
приблизительно равно |
≅ |
|
асимптотически равно |
≈ |
|
не равно |
≠ |
|
тождественно равно |
≡ |
|
меньше или равно |
≤ |
|
больше или равно |
≥ |
|
подмножество |
⊂ |
|
надмножество |
⊃ |
|
не подмножество |
⊄ |
|
подмножество или равно |
⊆ |
|
надмножество или равно |
⊇ |
|
прямая сумма |
⊕ |
|
векторное произведение |
⊗ |
|
перпендикулярно |
⊥ |
|
левый верхний угол |
⌈ |
|
правый верхний угол |
⌉ |
|
левый нижний угол |
⌊ |
|
правый нижний угол |
⌋ |
|
левая угловая скобка |
⟨ |
|
правая угловая скобка |
⟩ |
|
ромб |
◊ |
Альт коды – таблица всех символов
Приветствую вас снова на нашем сайте! Вы знали, что с помощью самой обыкновенной клавиатуры можно вводить гораздо больше символов, чем на ней нарисовано? Ну, скорее всего, знали, если вы попали в эту статью с поиска. Если нет, то сегодня вы узнаете, что такое альт коды и как ими пользоваться, а также, почему они могут не сработать.
Если вам нужны только таблицы альт кодов со всеми символами, то сразу проматывайте статью до картинок с таблицами. Если же хотите узнать что-то другое, то читайте статью внимательно.
Как знак принадлежит?
Теория множеств и теория чисел
| Символ TeX (Команда TeX) | Символ (Юникод) | Название |
|---|---|---|
| Произношение | ||
| (varnothing) | ∅ <> | «Пустое множество» |
| (in) (notin) | ∈ ∉ | Принадлежность/непринадлежность к множеству |
| «принадлежит», «из» «не принадлежит» |
Для написания нужного символа следует зажать клавишу Alt и ввести на дополнительной цифровой клавиатуре число 0185 (для примера), не отпуская. (Для активации дополнительной цифровой клавиатуры должен быть включен NumLock.)
Кнопки на клавиатурной панели
На клавиатуре знаки располагаются в разных местах. Обычно специальные символы можно найти справа и слева от основного алфавита или над ним. Речь идет о кнопках с цифрами.
При наборе символов посредством клавиш на клавиатуре используют или русскую раскладку, или английскую. Например, чтобы поставить точку, можно:
- нажать на кнопку, расположенную слева от правого «Шифта», находясь на наборе «русского»;
- перейти на английскую раскладку и нажать на букву «Ю».
Как правило, знаки на клавиатуре, набранные подобным образом, ограничиваются слэшами, скобками и символами препинания. Набрать их не составляет никакого труда.
Как поставить обелюс — символ знака деления
На компьютерной клавиатуре клавиши обелюса нет. Чтобы напечатать символ в WORD или другой программе, следует использовать комбинацию Alt Num.
Переключитесь на английскую раскладку. Поставьте курсор в нужное место. Одной рукой нажмите клавишу Alt и, удерживая её, другой рукой введите число 0247 на цифровой клавиатуре. После набора цифр, отпустите клавишу Alt — появится знак ÷
Юникод — U+00F7
HTML-код — ÷ или ÷
Автор — Михаил Апсолямов
Создаю и продвигаю сайты с 2010 года. Провожу аудиты, настраиваю контекстную рекламу. Подробнее об услугах.
Знак деления в Ворд 2016, 2013
Чтобы вставить дробное значение необходимо повторить шаги:
- Вкладка «Вставка» раздел «Символы» и кнопка «Уравнение»;
- В выпадающем окне выбрать пункт «Вставить новое уравнение»;
- В меню «Конструктор» нажать на «Дробь». Далее выбрать соответствующий вариант: либо дробь через слеш, либо с помощью горизонтальной линии.
Как вводить символы и знаки на клавиатуре компьютера?!
Начинающие пользователи персонального компьютера часто задают вопрос — как набрать специальные символы, которые нарисованы на клавишах цифрового блока — *?:%;№»!~.
Тут всё дело в том, что для того, чтобы если бы мы задались целью для каждого символа сделать отдельную клавишу, то получили примерно такой результат:
Именно поэтому на одной клавише совмещают по 2-3 символа, а в некоторых случая — даже 4. Помимо этого есть куча спецсимволов, которых нет и на клавиатуре — как набирать их?!
Начнём со спецсимволов на клавиатуре. Для того, чтобы набрать символ, которой написан на клавише над цифрой нужно выполнить 3 действия:
— переключиться на английскую раскладку
— нажать и удерживать кнопку CTRL
— нажать кнопку с цифрой
Вот например, как поставить значок собака:
Теперь давайте рассмотрим как ставить символы в текстовых редакторах. В самом полурном — MS Word для этого существует специальный пункт меню Вставка >>> Символ:
Как Вы видите на скриншоте — в списке открываются самые часто употребляемые знаки и значки. Для того, чтобы открыть весь список — надо кликнуть на ссылку «Другие символы».
В других текстовых редакторах, например, в Блокноте, Notepad++ или AkelPad можно воспользоваться специальными кодами для вставки знаков. Правда, тут есть небольшая хитрость. Чтобы ввести код спецсимвола, цифры в этих кодах надо набирать на цифровом блоке справа при отключенной клавише NumLock.
Вот список кодов клавиатуры (спецсимволов) в Windows:
alt+1 = ☺ (обычный смайл)
alt+2 = ☻ (инверсный «черный» смайл)
alt+3 = ♥ (значок «черви»)
alt+4 = ♦ (значок «бубны»)
alt+5 = ♣ (значок «трефы»)
alt+6 = ♠ (значок «пики»)
alt+7 = • (жирная точка)
alt+8 = ◘ (инверсная точка)
alt+9 = ○ (круг)
alt+10 = ◙ (круг в квадрате)
alt+11 = ♂ (мужской символ)
alt+12 = ♀ (женский символ)
alt+13 = ♪ (значок ноты)
alt+14 = ♫ (значок двойной ноты)
alt+15 = ☼ (солнце)
alt+16 = ► (вправо)
alt+17 = ◄ (влево)
alt+18 = ↕ (туда-сюда)
alt+19 = ‼ (двойное восклицание)
alt+20 = ¶ (перевод строки)
alt+21 = § (параграф)
alt+22 = ▬ (жирное тире)
alt+23 = ↨
alt+24 = ↑ (стрелка вверх)
alt+25 = ↓ (стрелка вниз)
alt+26 = → (стрелка вправо)
alt+27 = ← (стрелка влево)
alt+28 = ∟ (прямой угол)
alt+29 = ↔ (стрелка влево-вправо)
alt+30 = ▲ (курсор вверх)
alt+31 = ▼ (курсор вниз)
alt+177 = ▒
alt+987 = █
alt+0130 ‚ (бинарная нижняя кавычка)
alt+0132 „ (двойная нижняя кавычка)
alt+0133 … (троеточие)
alt+0136 € (значок евро)
alt+0139 ‹ (значок «меньше»)
alt+0145 ‘ (апостроф перевернутый)
alt+0146 ’ (апостроф обычный)
alt+0147 “ (перевернутые закрывающие кавычки)
alt+0148 ” (закрывающие кавычки)
alt+0149 • (жирная точка)
alt+0150 – (минус, короткое тире)
alt+0151 — (длинное тире)
alt+0153 ™ (зачок «торговая марка» (Trade mark)
alt+0155 › (значок «больше»)
alt+0167 § (параграф)
alt+0169 © (Значок Copyright)
alt+0171 « (русские открывающие кавычки)
alt+0174 ® (Значок Registered)
alt+0176 ° (значок градуса)
alt+0177 ± (плюс-минус)
alt+0183 · (точка по центру)
alt+0187 » (русские закрывающие кавычки)


 Сообщение было отмечено oobarbazanoo как решение
Сообщение было отмечено oobarbazanoo как решение




 — матрица того же размера, элементы которой равны произведению соответствующих элементов перемножаемых матриц
— матрица того же размера, элементы которой равны произведению соответствующих элементов перемножаемых матриц 





 , где m≥0; ak — целые числа, а p — простое число.
, где m≥0; ak — целые числа, а p — простое число.









 x
x — это наибольшее целое число, меньшее или равное х.
— это наибольшее целое число, меньшее или равное х.
 x
x -это наименьшее целое число, большее или равное х.
-это наименьшее целое число, большее или равное х.

























 =vx i +vy j +vz k , где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то
=vx i +vy j +vz k , где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то




 — граница множества M (другими словами, множество всех граничных точек множества M)
— граница множества M (другими словами, множество всех граничных точек множества M) — степень многочлена f. Чаще встречается обозначение deg f.
— степень многочлена f. Чаще встречается обозначение deg f.





 ,
,  .
.



 — топологическое замыкание подмножества S, т.е. пересечение всех замкнутых надмножеств подмножества S.
— топологическое замыкание подмножества S, т.е. пересечение всех замкнутых надмножеств подмножества S.
 — строгое, истинное подмножество
— строгое, истинное подмножество